Skip to main content
Global

9.8E: تمارين

  1. Last updated
  2. Save as PDF
  • Page ID
    201658

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    الممارسة تجعل من الكمال

    التمارين\(\PageIndex{23}\) Graph Quadratic Functions of the Form \(f(x)=x^{2}=k\)

    في التمارين التالية،

    1. رسم بياني للدوال التربيعية على نفس نظام الإحداثيات المستطيلة
    2. وصف تأثير إضافة ثابت،\(k\)، إلى الدالة على المكافئ الأساسي.
      1. \(f(x)=x^{2}, g(x)=x^{2}+4, \text { and } h(x)=x^{2}-4\)
      2. \(f(x)=x^{2}, g(x)=x^{2}+7, \text { and } h(x)=x^{2}-7\)
    إجابة

    1.


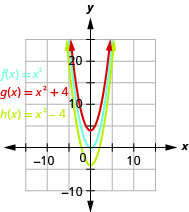
    1. يوضح هذا الشكل 3 بارابولات تفتح صعوديًا على مستوى الإحداثيات x y. المنحنى الأوسط هو الرسم البياني لـ f of x يساوي x مربعًا وله رأس (0، 0). توجد نقاط أخرى على المنحنى في (سالب 1، 1) و (1، 1). تم نقل المنحنى العلوي لأعلى 4 وحدات، وتم نقل الجزء السفلي لأسفل 4 وحدات.
      الشكل 9.7.71
    2. الرسم البياني\(g(x)=x^{2}+4\) هو نفس الرسم البياني\(4\) للوحدات\(f(x)=x^{2}\) ولكن المحولة لأعلى. الرسم البياني\(h(x)=x^{2}-4\) هو نفس الرسم البياني\(4\) للوحدات\(f(x)=x^{2}\) ولكن بالتحويل لأسفل.
    التمارين\(\PageIndex{24}\) Graph Quadratic Functions of the Form \(f(x)=x^{2}=k\)

    في التمارين التالية، قم برسم بياني لكل دالة باستخدام التحول الرأسي.

    1. \(f(x)=x^{2}+3\)
    2. \(f(x)=x^{2}-7\)
    3. \(g(x)=x^{2}+2\)
    4. \(g(x)=x^{2}+5\)
    5. \(h(x)=x^{2}-4\)
    6. \(h(x)=x^{2}-5\)
    إجابة

    1.

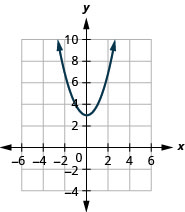
    يوضح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على مستوى الإحداثيات x y. له قمة (0، 3) ونقاط أخرى (7، 2) و (7، سالب 2).
    الشكل 9.7.72

    3.

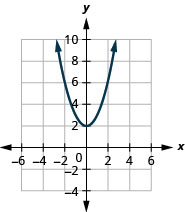
    يوضح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على مستوى الإحداثيات x y. لها قمة (0، 2) ونقاط أخرى (سالب 2، 6) و (2، 6).
    الشكل 9.7.73

    5.

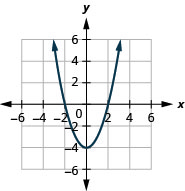
    يوضح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على مستوى الإحداثيات x y. له قمة (0، سالب 4) ونقاط أخرى (سالب 2، 0) و (2، 0).
    الشكل 9.7.74
    التمارين\(\PageIndex{25}\) Graph Quadratic Functions of the Form \(f(x)=(x-h)^{2}\)

    في التمارين التالية،

    1. رسم بياني للدوال التربيعية على نفس نظام الإحداثيات المستطيلة
    2. وصف تأثير إضافة ثابت داخل الأقواس\(h\)
      1. \(f(x)=x^{2}, g(x)=(x-3)^{2}, \text { and } h(x)=(x+3)^{2}\)
      2. \(f(x)=x^{2}, g(x)=(x+4)^{2}, \text { and } h(x)=(x-4)^{2}\)
    إجابة

    1.


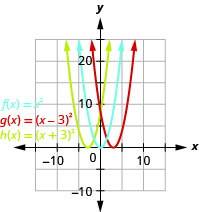
    1. يوضح هذا الشكل 3 بارابولات تفتح صعوديًا على مستوى الإحداثيات x y. واحد هو الرسم البياني لـ f of x يساوي x مربعًا وله رأس (0، 0). توجد نقاط أخرى على المنحنى في (سالب 1، 1) و (1، 1). يتم تحويل الرسم البياني إلى اليمين بمقدار 3 وحدات إلى اليمين لإنتاج g من x يساوي كمية x ناقص 3 مربعًا. يُنقل الرسم البياني إلى اليسار بمقدار ٣ وحدات إلى اليسار لإنتاج h من x يساوي كمية x زائد ٣ مربعًا.
      الشكل 9.7.75
    2. الرسم البياني\(g(x)=(x−3)^{2}\) هو نفس الرسم البياني\(3\) للوحدات اليمنى\(f(x)=x^{2}\) ولكن تم تحويلها. الرسم البياني\(h(x)=(x+3)^{2}\) هو نفس الرسم البياني\(3\) للوحدات اليسرى\(f(x)=x^{2}\) ولكن تم تحويلها.
    التمارين\(\PageIndex{26}\) Graph Quadratic Functions of the Form \(f(x)=(x-h)^{2}\)

    في التمارين التالية، قم برسم بياني لكل دالة باستخدام الإزاحة الأفقية.

    1. \(f(x)=(x-2)^{2}\)
    2. \(f(x)=(x-1)^{2}\)
    3. \(f(x)=(x+5)^{2}\)
    4. \(f(x)=(x+3)^{2}\)
    5. \(f(x)=(x-5)^{2}\)
    6. \(f(x)=(x+2)^{2}\)
    إجابة

    1.

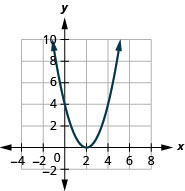
    يوضح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على مستوى الإحداثيات x y. وتتكون قمته من (2، 0) ونقاط أخرى (0، 4) و (4، 4).
    الشكل 9.7.76

    3.

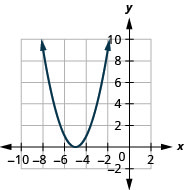
    يوضح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على مستوى الإحداثيات x y. له قمة (سالب 5، 0) ونقاط أخرى (سالب 7، 4) و (سالب 3، 4).
    الشكل 9.7.77

    5.

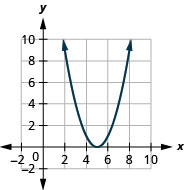
    يوضح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على مستوى الإحداثيات x y. وتتكون قمته من (5، 0) ونقاط أخرى (3، 4) و (7، 4).
    الشكل 9.7.78
    التمارين\(\PageIndex{27}\) Graph Quadratic Functions of the Form \(f(x)=(x-h)^{2}\)

    في التمارين التالية، قم برسم بياني لكل دالة باستخدام التحويلات.

    1. \(f(x)=(x+2)^{2}+1\)
    2. \(f(x)=(x+4)^{2}+2\)
    3. \(f(x)=(x-1)^{2}+5\)
    4. \(f(x)=(x-3)^{2}+4\)
    5. \(f(x)=(x+3)^{2}-1\)
    6. \(f(x)=(x+5)^{2}-2\)
    7. \(f(x)=(x-4)^{2}-3\)
    8. \(f(x)=(x-6)^{2}-2\)
    إجابة

    1.

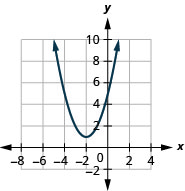
    يوضح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على مستوى الإحداثيات x y. له قمة (سالب 2، 1) ونقاط أخرى (سالب 4، 5) و (0، 5).
    الشكل 9.7.79

    3.

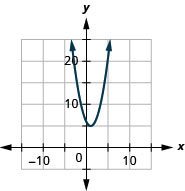
    يوضح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على مستوى الإحداثيات x y. لها قمة (1، 5) ونقاط أخرى (سالب 1، 9) و (3، 9).
    الشكل 9.7.80

    5.

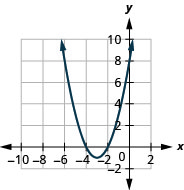
    يوضح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على مستوى الإحداثيات x y. له قمة (سالب 3، 1) ونقاط أخرى (سالب 4، 0) و (سالب 2، 0).
    الشكل 9.7.81

    7.

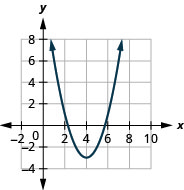
    يوضح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على مستوى الإحداثيات x y. له قمة (4، سالب 2) ونقاط أخرى (3، سالب 2) و (5، سالب 2).
    الشكل 9.7.82
    التمارين\(\PageIndex{28}\) Graph Quadratic Functions of the Form \(f(x)=ax^{2}\)

    في التمارين التالية، قم برسم بياني لكل وظيفة.

    1. \(f(x)=-2 x^{2}\)
    2. \(f(x)=4 x^{2}\)
    3. \(f(x)=-4 x^{2}\)
    4. \(f(x)=-x^{2}\)
    5. \(f(x)=\frac{1}{2} x^{2}\)
    6. \(f(x)=\frac{1}{3} x^{2}\)
    7. \(f(x)=\frac{1}{4} x^{2}\)
    8. \(f(x)=-\frac{1}{2} x^{2}\)
    إجابة

    1.

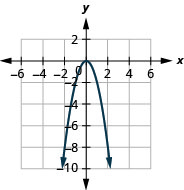
    يوضِّح هذا الشكل الأشكال المظلية التي تفتح هبوطًا على مستوى الإحداثيات x y. له قمة (0، 0) ونقاط أخرى (سالب 1، سالب 2) و (1، سالب 2).
    الشكل 9.7.83

    3.

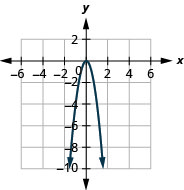
    يوضِّح هذا الشكل الأشكال المظلية التي تفتح هبوطًا على مستوى الإحداثيات x y. له قمة (0، 0) ونقاط أخرى (سالب 1، سالب 4) و (1، سالب 4).
    الشكل 9.7.84

    5.

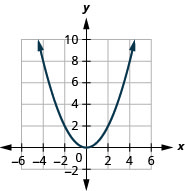
    يوضح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على مستوى الإحداثيات x y. لها قمة (0، 0) ونقاط أخرى (سالب 2، 2) و (2، 2).
    الشكل 9.7.85

    7.

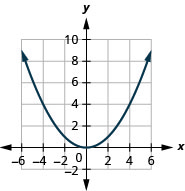
    يوضِّح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على المستوى الإحداثي x y. له قمة (0، 0) ونقاط أخرى (2، 1) و (سالب 2، 1).
    الشكل 9.7.86
    التمارين\(\PageIndex{29}\) Graph Quadratic Functions Using Transformations

    في التمارين التالية، أعد كتابة كل دالة في\(f(x)=a(x−h)^{2}+k\) النموذج بإكمال المربع.

    1. \(f(x)=-3 x^{2}-12 x-5\)
    2. \(f(x)=2 x^{2}-12 x+7\)
    3. \(f(x)=3 x^{2}+6 x-1\)
    4. \(f(x)=-4 x^{2}-16 x-9\)
    إجابة

    1. \(f(x)=-3(x+2)^{2}+7\)

    3. \(f(x)=3(x+1)^{2}-4\)

    التمارين\(\PageIndex{30}\) Graph Quadratic Functions Using Transformations

    في التمارين التالية،

    1. أعد كتابة كل وظيفة في\(f(x)=a(x−h)^{2}+k\) النموذج
    2. قم برسم بياني باستخدام التحويلات
      1. \(f(x)=x^{2}+6 x+5\)
      2. \((x)=x^{2}+4 x-12\)
      3. \(f(x)=x^{2}+4 x-12\)
      4. \(f(x)=x^{2}-6 x+8\)
      5. \(f(x)=x^{2}-6 x+15\)
      6. \(f(x)=x^{2}+8 x+10\)
      7. \(f(x)=-x^{2}+8 x-16\)
      8. \(f(x)=-x^{2}+2 x-7\)
      9. \(f(x)=-x^{2}-4 x+2\)
      10. \(f(x)=-x^{2}+4 x-5\)
      11. \(f(x)=5 x^{2}-10 x+8\)
      12. \(f(x)=3 x^{2}+18 x+20\)
      13. \(f(x)=2 x^{2}-4 x+1\)
      14. \(f(x)=3 x^{2}-6 x-1\)
      15. \(f(x)=-2 x^{2}+8 x-10\)
      16. \(f(x)=-3 x^{2}+6 x+1\)
    إجابة

    1.

    1. f (x) = (x+3) ^ {2} -4
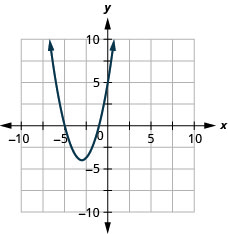
    يوضِّح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على المستوى الإحداثي x y. وله رأس (سالب 3، 3)، والجزء المقطوع من الصادات (0، 5)، ومحور التماثل الموضح عند x يساوي سالب 3.
    الشكل 9.7.87

    3.

    1. \(f(x)=(x+2)^{2}-1\)
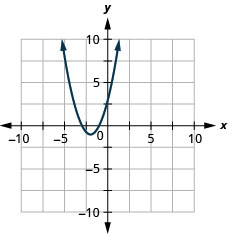
    يوضِّح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على المستوى الإحداثي x y. له رأس (سالب 2، سالب 1)، نقطة التقاطع y (0، 3)، ومحور التماثل الموضح عند x يساوي سالب 2.
    الشكل 9.7.88

    5.

    1. \(f(x)=(x-3)^{2}+6\)
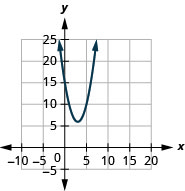
    يوضِّح هذا الشكل الأشكال المظلية ذات الفتحة الصاعدة على المستوى الإحداثي x y. وله رأس (٣، ٦)، وقطرفه الصادي (٠، ١٠)، ومحور التماثل الموضح عند س يساوي ٣.
    الشكل 9.7.89

    7.

    1. \(f(x)=-(x-4)^{2}+0\)
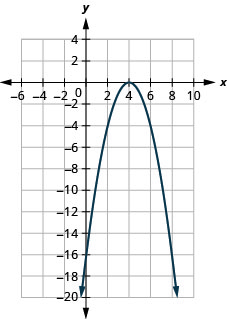
    يوضِّح هذا الشكل المكافئ المتجه نحو الأسفل على مستوى الإحداثيات x y. وله رأس (٤، ٠)، وقطرفه الصادي (٠، سالب ١٦)، ومحور التماثل الموضح عند س يساوي ٤.
    الشكل 9.7.90

    9.

    1. \(f(x)=-(x+2)^{2}+6\)
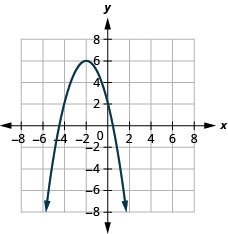
    يوضِّح هذا الشكل المكافئ المتجه نحو الأسفل على مستوى الإحداثيات x y. له رأس (سالب 2، 6)، والجزء المقطوع على شكل حرف y (0، 2)، ومحور التماثل الموضح عند x يساوي سالب 2.
    الشكل 9.7.91

    11.

    1. \(f(x)=5(x-1)^{2}+3\)
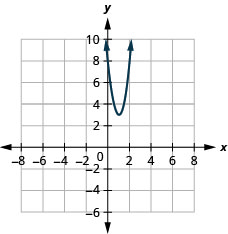
    يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. رأسه (1، 3)، والجزء المقطوع من الصادات يساوي (0، 8)، ومحور التماثل الموضح عند x يساوي 1.
    الشكل 9.7.92

    13.

    1. \(f(x)=2(x-1)^{2}-1\)
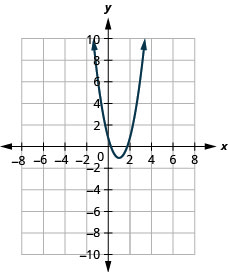
    يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. له رأس (1، سالب 1)، نقطة التقاطع y (0، 1)، ومحور التماثل الموضح عند x يساوي 1.
    الشكل 9.7.93

    15.

    1. \(f(x)=-2(x-2)^{2}-2\)
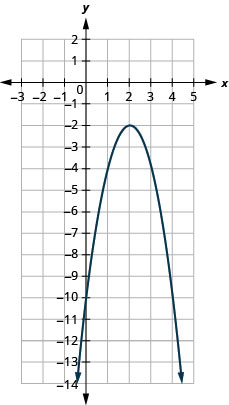
    يوضِّح هذا الشكل المكافئ المتجه نحو الأسفل على مستوى الإحداثيات x y. له رأس (2، سالب 2)، محور التقاطع y (0، سالب 10)، ومحور التماثل الموضح عند x يساوي 2.
    الشكل 9.7.94
    التمارين\(\PageIndex{31}\) Graph Quadratic Functions Using Transformations

    في التمارين التالية،

    1. أعد كتابة كل وظيفة في\(f(x)=a(x−h)^{2}+k\) النموذج
    2. قم برسمها باستخدام الخصائص
      1. \(f(x)=2 x^{2}+4 x+6\)
      2. \(f(x)=3 x^{2}-12 x+7\)
      3. \(f(x)=-x^{2}+2 x-4\)
      4. \(f(x)=-2 x^{2}-4 x-5\)
    إجابة

    1.

    1. \(f(x)=2(x+1)^{2}+4\)
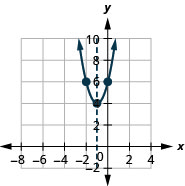
    يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. له رأس (سالب 1، 4)، والجزء المقطوع على شكل حرف y (0، 6)، ومحور التماثل الموضح عند x يساوي سالب 1.
    الشكل 9.7.95

    3.

    1. \(f(x)=-(x-1)^{2}-3\)
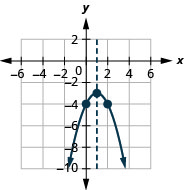
    يوضِّح هذا الشكل المكافئ المتجه نحو الأسفل على مستوى الإحداثيات x y. له رأس (1، سالب 3)، محور التقاطع y (0، سالب 4)، ومحور التماثل الموضح عند x يساوي 1.
    الشكل 9.7.96
    التمارين\(\PageIndex{32}\) Matching

    في التمارين التالية، قم بمطابقة الرسوم البيانية بإحدى الوظائف التالية:

    1. \(f(x)=x^{2}+4\)
    2. \(f(x)=x^{2}-4\)
    3. \(f(x)=(x+4)^{2}\)
    4. \(f(x)=(x-4)^{2}\)
    5. \(f(x)=(x+4)^{2}-4\)
    6. \(f(x)=(x+4)^{2}+4\)
    7. \(f(x)=(x-4)^{2}-4\)
    8. \(f(x)=(x-4)^{2}+4\)

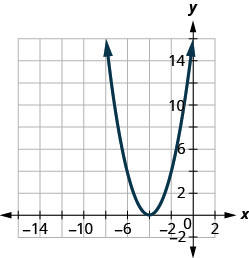
      1. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. له قمة (سالب 4، 0) ونقاط أخرى (سالب 4، 4) و (سالب 2، 4).
        الشكل 9.7.97

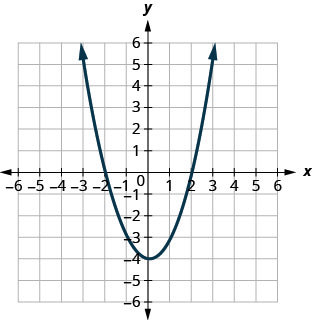
      2. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. له قمة (0، سالب 4) ونقاط أخرى (سالب 2، 0) و (2، 0).
        الشكل 9.7.98

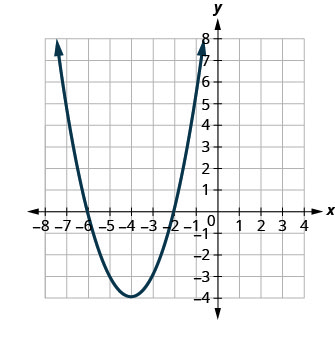
      3. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. له قمة (سالب 4، سالب 4) ونقاط أخرى (سالب 4، 0) و (سالب 2، 0).
        الشكل 9.7.99

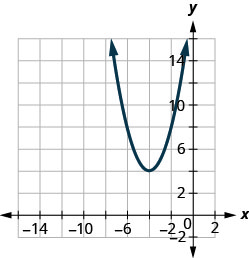
      4. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. له قمة (سالب 4، 4) ونقاط أخرى (سالب 6، 8) و (سالب 2، 8).
        الشكل 9.7.100

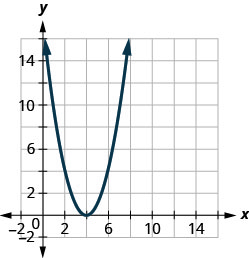
      5. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. وتتكون قمته من (4، 0) ونقاط أخرى (2، 4) و (2، 4).
        الشكل 9.7.101

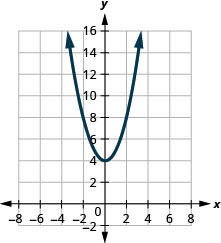
      6. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. لها قمة (0، 4) ونقاط أخرى (سالب 2، 8) و (2، 8).
        الشكل 9.7.102

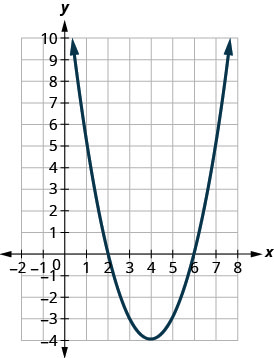
      7. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. له قمة (4، سالب 4) ونقاط أخرى (2,0) و (6,0).
        الشكل 9.7.103

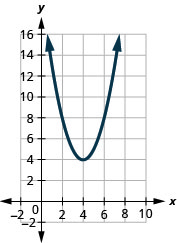
      8. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. وتتكون قمته من (4، 4) ونقاط أخرى (2,8) و (6,8).
        الشكل 9.7.104
    إجابة

    1. ج

    3.

    5. د

    7. جرام

    التمارين\(\PageIndex{33}\) Find a Quadratic Function from its Graph

    في التمارين التالية، اكتب الدالة التربيعية في\(f(x)=a(x−h)^{2}+k\) الشكل الذي يظهر الرسم البياني الخاص به.


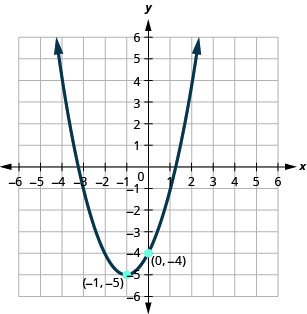
    1. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. وله قمة (سالب 1، سالب 5) ونقطة تقاطع y (0، سالب 4).
      الشكل 9.7.105

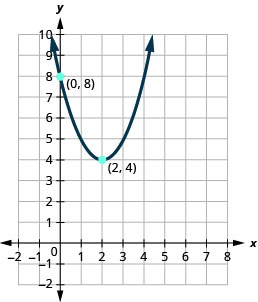
    2. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. وتتكون قمته من (2,4) ونقطة التقاطع y (0، 8).
      الشكل 9.7.106

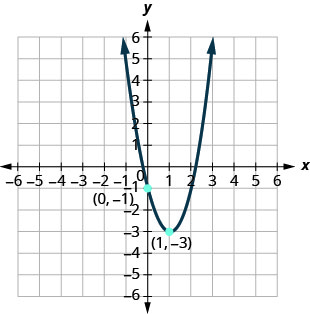
    3. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. له قمة (1، سالب 3) ونقطة تقاطع y (0، سالب 1).
      الشكل 9.7.107

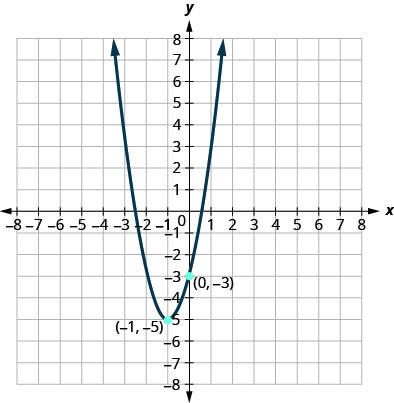
    4. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على مستوى الإحداثيات x y. وله قمة (سالب 1، سالب 5) ونقطة تقاطع y (0، سالب 3).
      الشكل 9.7.108
    إجابة

    1. \(f(x)=(x+1)^{2}-5\)

    3. \(f(x)=2(x-1)^{2}-3\)

    التمارين\(\PageIndex{34}\) Writing Exercise
    1. قم برسم بياني للدالة التربيعية\(f(x)=x^{2}+4x+5\) أولاً باستخدام الخصائص كما فعلنا في القسم الأخير ثم رسمها بيانيًا باستخدام التحويلات. ما الطريقة التي تفضلها؟ لماذا؟
    2. قم برسم بياني للدالة التربيعية\(f(x)=2x^{2}−4x−3\) أولاً باستخدام الخصائص كما فعلنا في القسم الأخير ثم رسمها بيانيًا باستخدام التحويلات. ما الطريقة التي تفضلها؟ لماذا؟
    إجابة

    1. قد تختلف الإجابات.

    فحص ذاتي

    أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.

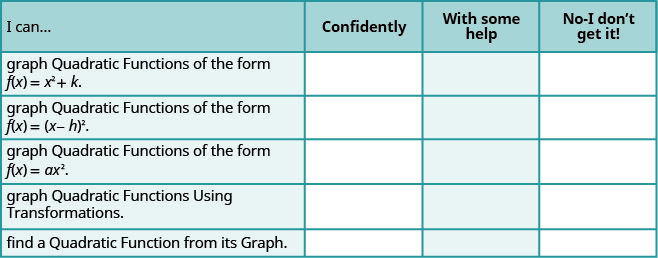
    هذا الشكل عبارة عن قائمة لتقييم فهمك للمفاهيم المقدمة في هذا القسم. يحتوي على 4 أعمدة تحمل علامة «يمكنني»، بكل ثقة، مع بعض المساعدة، ولا يمكنني الحصول عليها™! يوجد أدناه رسم بياني للدوال التربيعية في الصورة f لـ x يساوي x مربعًا زائد k؛ الرسم البياني الدوال التربيعية في صورة f من x يساوي الكمية x ناقص h مربعًا؛ الرسم البياني الدوال التربيعية بالشكل f من x يساوي x مربعًا؛ رسم بياني للدوال التربيعية في صورة x يساوي x مربعًا؛ رسم بياني للدوال التربيعية باستخدام التحويلات؛ أوجد الدالة التربيعية من الرسم البياني الخاص بها. يتم ترك الأعمدة الأخرى فارغة لك للتحقق من فهمك.
    الشكل 9.7.109

    ب- بعد الاطلاع على قائمة المراجعة، هل تعتقد أنك مستعد جيدًا للقسم التالي؟ لماذا أو لماذا لا؟