9.8: رسم بياني للدوال التربيعية باستخدام التحويلات
- Page ID
- 201653
في نهاية هذا القسم، ستكون قادرًا على:
- رسم بياني للدوال التربيعية للنموذج\(f(x)=x^{2}+k\)
- رسم بياني للدوال التربيعية للنموذج\(f(x)=(x−h)^{2}\)
- رسم بياني للدوال التربيعية للنموذج\(f(x)=ax^{2}\)
- رسم بياني للدوال التربيعية باستخدام التحويلات
- ابحث عن دالة تربيعية من الرسم البياني الخاص بها
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- رسم بياني للدالة\(f(x)=x^{2}\) من خلال رسم النقاط.
إذا فاتتك هذه المشكلة، راجع المثال 3.54. - عامل بالكامل:\(y^{2}−14y+49\).
إذا فاتتك هذه المشكلة، راجع المثال 6.24. - عامل بالكامل:\(2x^{2}−16x+32\).
إذا فاتتك هذه المشكلة، راجع المثال 6.26.
تمثيل بياني للدوال التربيعية للنموذج\(f(x)=x^{2}+k\)
في القسم الأخير، تعلمنا كيفية رسم الدوال التربيعية بيانيًا باستخدام خصائصها. تتضمن الطريقة الأخرى البدء بالرسم البياني الأساسي\(f(x)=x^{2}\) و «تحريكه» وفقًا للمعلومات الواردة في معادلة الدالة. نسمي هذا التمثيل البياني للدوال التربيعية باستخدام التحويلات.
في المثال الأول، سنقوم برسم الدالة التربيعية\(f(x)=x^{2}\) برسم النقاط. ثم سنرى التأثير الذي ستحدثه إضافة ثابت\(k\)، إلى المعادلة على الرسم البياني للدالة الجديدة\(f(x)=x^{2}+k\).
رسم بياني\(f(x)=x^{2}\)\(g(x)=x^{2}+2\)،\(h(x)=x^{2}−2\) وعلى نفس نظام الإحداثيات المستطيلة. وصف تأثير إضافة ثابت إلى الدالة على المكافئ الأساسي.
الحل:
سيساعدنا رسم النقاط على رؤية تأثير الثوابت على الرسم\(f(x)=x^{2}\) البياني الأساسي. نملأ الرسم البياني لجميع الوظائف الثلاث.
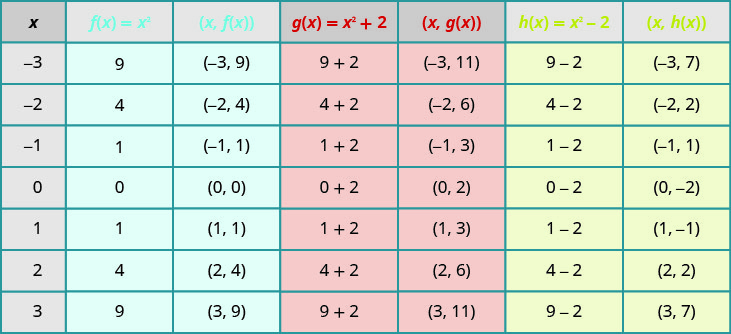
\(g(x)\)القيم تزيد بمقدار اثنين عن\(f(x)\) القيم. كما أن\(h(x)\) القيم أقل بمقدار اثنين من\(f(x)\) القيم. الآن سنقوم برسم جميع الوظائف الثلاث على نفس نظام الإحداثيات المستطيل.
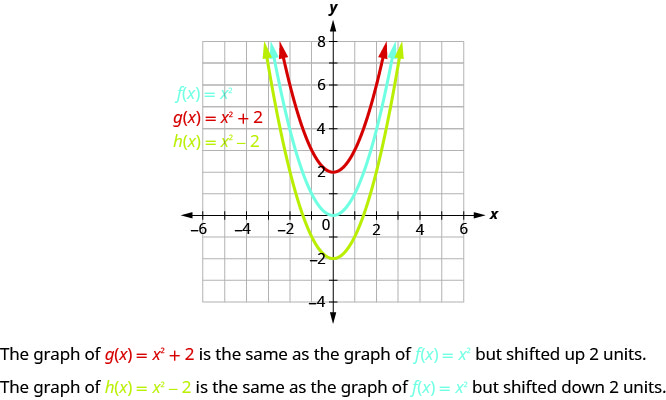
الرسم البياني\(g(x)=x^{2}+2\) هو نفس الرسم البياني\(2\) للوحدات\(f(x)=x^{2}\) ولكن المحولة لأعلى.
الرسم البياني\(h(x)=x^{2}−2\) هو نفس الرسم البياني\(2\) للوحدات\(f(x)=x^{2}\) ولكن المحولة لأسفل.
- رسم بياني\(f(x)=x^{2}, g(x)=x^{2}+1,\)\(h(x)=x^{2}-1\) وعلى نفس نظام الإحداثيات المستطيلة.
- وصف تأثير إضافة ثابت إلى الدالة على المكافئ الأساسي.
- إجابة
-
أ.
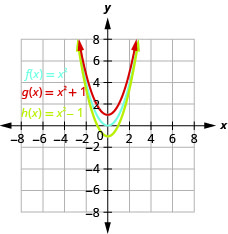
الشكل 9.7.3 ب- الرسم البياني\(g(x)=x^{2}+1\) هو نفس الرسم البياني\(1\) للوحدة\(f(x)=x^{2}\) ولكن تم تحويلها لأعلى. الرسم البياني\(h(x)=x^{2}−1\) هو نفس الرسم البياني\(1\) للوحدة\(f(x)=x^{2}\) ولكن تم تحريكها لأسفل.
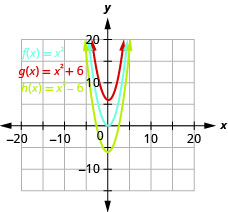
- رسم بياني\(f(x)=x^{2}, g(x)=x^{2}+6,\)\(h(x)=x^{2}-6\) وعلى نفس نظام الإحداثيات المستطيلة.
- وصف تأثير إضافة ثابت إلى الدالة على المكافئ الأساسي.
- إجابة
-
أ.
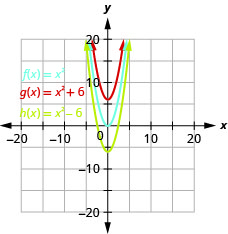
الشكل 9.7.4 ب- الرسم البياني\(h(x)=x^{2}+6\) هو نفس الرسم البياني\(6\) للوحدات\(f(x)=x^{2}\) ولكن المحولة لأعلى. الرسم البياني\(h(x)=x^{2}-6\) هو نفس الرسم البياني\(6\) للوحدات\(f(x)=x^{2}\) ولكن المحولة لأسفل.
يوضح لنا المثال الأخير أنه لرسم دالة تربيعية للنموذج\(f(x)=x^{2}+k\)، نأخذ الرسم البياني المكافئ الأساسي\(f(x)=x^{2}\) ونقوم بتحريكه رأسيًا لأعلى\((k>0)\) أو تحريكه لأسفل\((k<0)\).
هذا التحول يسمى التحول الرأسي.
رسم بياني للدالة التربيعية للنموذج\(f(x)=x^{2}+k\) باستخدام التحول الرأسي
يغير الرسم\(f(x)=x^{2}+k\) البياني الرسم البياني\(k\) للوحدات\(f(x)=x^{2}\) الرأسية.
- إذا قمت\(k>0\) بتحريك القطع المكافئ رأسيًا إلى أعلى\(k\) بالوحدات.
- إذا قمت\(k<0\) بتحريك القطع المكافئ رأسيًا إلى\(|k|\) أسفل.
الآن بعد أن رأينا تأثير الثابت\(k\)، أصبح من السهل رسم وظائف النموذج\(f(x)=x^{2}+k\). نبدأ فقط بالمكافأ الأساسي\(f(x)=x^{2}\) ثم ننقله لأعلى أو لأسفل.
قد يكون من المفيد ممارسة الرسم\(f(x)=x^{2}\) بسرعة. نحن نعرف القيم ويمكننا رسم الرسم البياني من هناك.
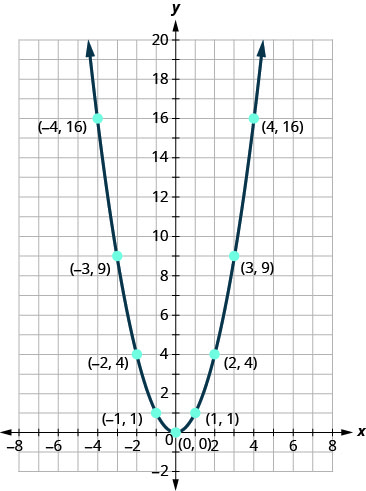
بمجرد أن نعرف هذا المكافئ، سيكون من السهل تطبيق التحولات. سيتطلب المثال التالي تحولًا رأسيًا.
رسم بياني\(f(x)=x^{2}−3\) باستخدام التحول الرأسي.
الحل:
| نرسم أولاً الرسم البياني\(f(x)=x^{2}\) على الشبكة. | 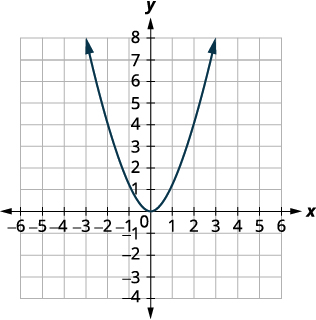 |
| تحديد\(k\). | 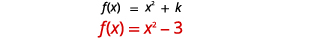 |
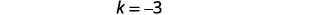 |
|
| قم بتحويل الرسم البياني\(f(x)=x^{2}\) لأسفل\(3\). | 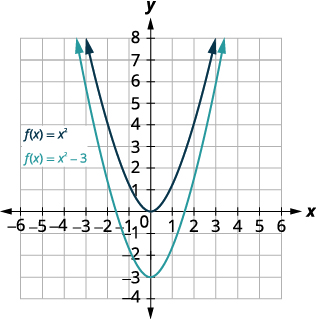 |
رسم بياني\(f(x)=x^{2}−5\) باستخدام التحول الرأسي.
- إجابة
-
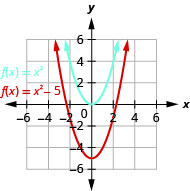
الشكل 9.7.10
رسم بياني\(f(x)=x^{2}+7\) باستخدام التحول الرأسي.
- إجابة
-
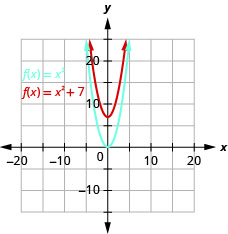
الشكل 9.7.11
تمثيل بياني للدوال التربيعية للنموذج\(f(x)=(x-h)^{2}\)
في المثال الأول، قمنا برسم الدالة\(f(x)=x^{2}\) التربيعية برسم النقاط ثم رأينا تأثير إضافة ثابت\(k\) إلى الدالة على الرسم البياني الناتج للدالة الجديدة\(f(x)=x^{2}+k\).
سنستكشف الآن تأثير طرح الثابت\(h\)، من\(x\) Has على الرسم البياني الناتج للدالة الجديدة\(f(x)=(x−h)^{2}\).
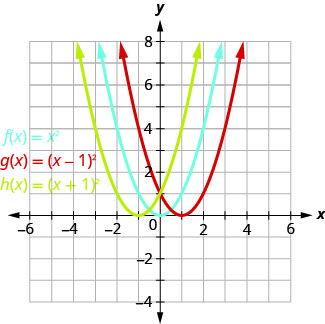
رسم بياني\(f(x)=x^{2}, g(x)=(x-1)^{2},\)\(h(x)=(x+1)^{2}\) وعلى نفس نظام الإحداثيات المستطيلة. وصف تأثير إضافة ثابت إلى الدالة على المكافئ الأساسي.
الحل:
سيساعدنا رسم النقاط على رؤية تأثير الثوابت على الرسم\(f(x)=x^{2}\) البياني الأساسي. نملأ الرسم البياني لجميع الوظائف الثلاث.
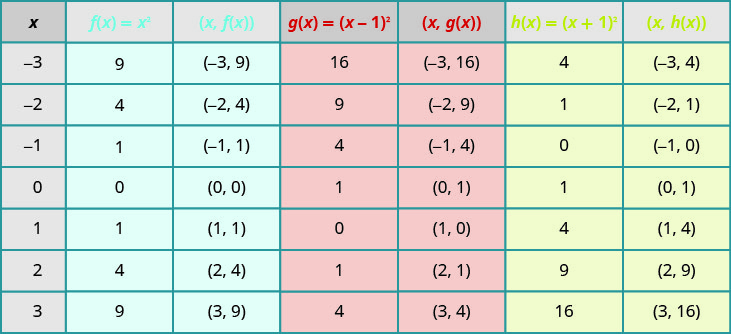
تشترك\(g(x)\) القيم\(h(x)\) والقيم في الأرقام الشائعة\(0, 1, 4, 9\)\(16\)، ولكن يتم تغييرها.

- رسم بياني\(f(x)=x^{2}, g(x)=(x+2)^{2},\)\(h(x)=(x-2)^{2}\) وعلى نفس نظام الإحداثيات المستطيلة.
- وصف تأثير إضافة ثابت إلى الدالة على المكافئ الأساسي.
- إجابة
-
أ.
الشكل 9.7.15 ب- الرسم البياني\(g(x)=(x+2)^{2}\) هو نفس الرسم البياني\(2\) للوحدات اليسرى\(f(x)=x^{2}\) ولكن تم تحويلها. الرسم البياني\(h(x)=(x−2)^{2}\) هو نفس الرسم البياني للوحدات\(f(x)=x^{2}\) ولكن قم بتغيير\(2\) الوحدات الصحيحة.
- رسم بياني\(f(x)=x^{2}, g(x)=x^{2}+5,\)\(h(x)=x^{2}-5\) وعلى نفس نظام الإحداثيات المستطيلة.
- وصف تأثير إضافة ثابت إلى الدالة على المكافئ الأساسي.
- إجابة
-
أ.
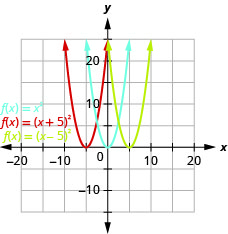
الشكل 9.7.16 ب- الرسم البياني\(g(x)=(x+5)^{2}\) هو نفس الرسم البياني\(5\) للوحدات اليسرى\(f(x)=x^{2}\) ولكن تم تحويلها. الرسم البياني\(h(x)=(x-5)^{2}\) هو نفس الرسم البياني\(5\) للوحدات اليمنى\(f(x)=x^{2}\) ولكن تم تحويلها.
يوضح لنا المثال الأخير أنه لرسم دالة تربيعية للنموذج\(f(x)=(x−h)^{2}\)، نأخذ الرسم البياني المكافئ الأساسي\(f(x)=x^{2}\) ونحوله إلى اليسار\((h>0)\) أو نحوله إلى اليمين\((h<0)\).
هذا التحول يسمى التحول الأفقي.
رسم بياني للدالة التربيعية للنموذج\(f(x)=(x-h)^{2}\) باستخدام التحول الأفقي
يغير الرسم\(f(x)=(x-h)^{2}\) البياني الرسم البياني\(f(x)=x^{2}\)\(h\) للوحدات الأفقية.
- إذا\(h>0\)، قم بتحويل\(h\) وحدات القطع المكافئ أفقيًا إلى اليسار.
- إذا\(h<0\)، قم بتحويل\(|h|\) وحدات القطع المكافئ أفقيًا إلى اليمين.
الآن بعد أن رأينا تأثير الثابت\(h\)، أصبح من السهل رسم وظائف النموذج\(f(x)=(x−h)^{2}\). نبدأ فقط بالمكافأ الأساسي ثم نحوله إلى اليسار أو اليمين.\(f(x)=x^{2}\)
سيتطلب المثال التالي تحولًا أفقيًا.
رسم بياني\(f(x)=(x−6)^{2}\) باستخدام التحول الأفقي.
الحل:
| نرسم أولاً الرسم البياني\(f(x)=x^{2}\) على الشبكة. | 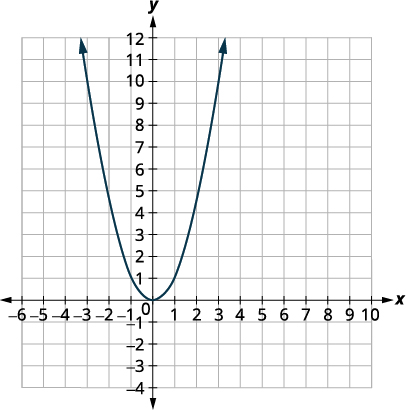 |
| تحديد\(h\). | 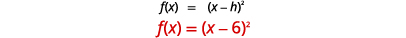 |
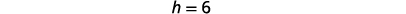 |
|
| قم بتحويل الرسم البياني\(f(x)=x^{2}\) إلى\(6\) الوحدات الصحيحة. | 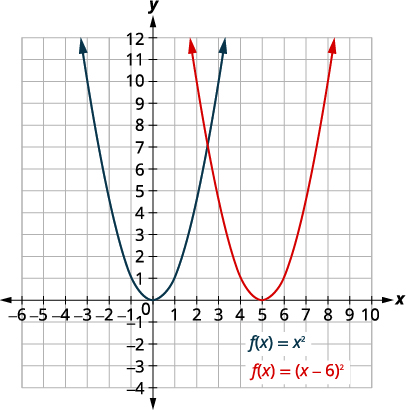 |
رسم بياني\(f(x)=(x−4)^{2}\) باستخدام التحول الأفقي.
- إجابة
-
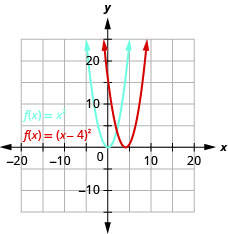
الشكل 9.7.21
رسم بياني\(f(x)=(x+6)^{2}\) باستخدام التحول الأفقي.
- إجابة
-
الشكل 9.7.22
الآن بعد أن عرفنا تأثير\(h\) الثوابت\(k\)، سنقوم برسم دالة تربيعية للنموذج\(f(x)=(x-h)^{2}+k\) عن طريق رسم المكافئ الأساسي أولاً ثم إجراء إزاحة أفقية متبوعة بتحويل رأسي. يمكننا القيام بالتحول الرأسي متبوعًا بالتحول الأفقي، لكن معظم الطلاب يفضلون التحول الأفقي متبوعًا بالرأسي.
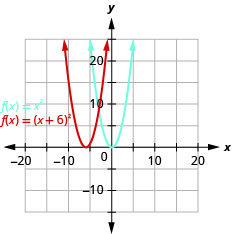
رسم بياني\(f(x)=(x+1)^{2}-2\) باستخدام التحويلات.
الحل:
ستشمل هذه الوظيفة تحولين ونحتاج إلى خطة.
دعونا أولاً نحدد الثوابت\(h, k\).
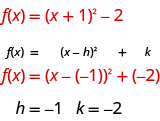
يمنحنا\(h\) الثابت تحولًا أفقيًا\(k\) ويعطينا تحولًا رأسيًا.
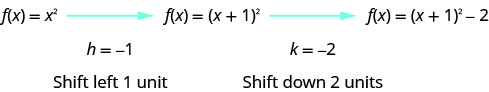
نرسم أولاً الرسم البياني\(f(x)=x^{2}\) على الشبكة.

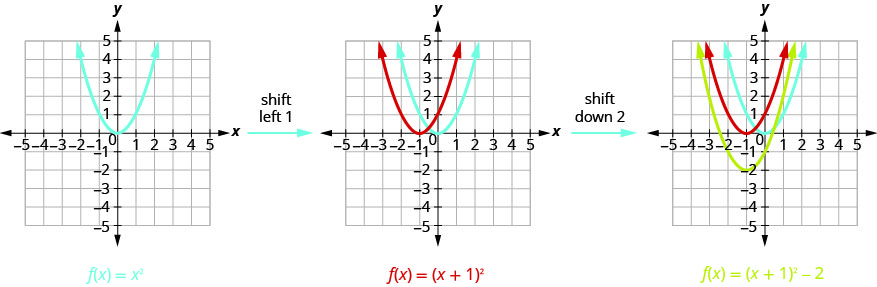
رسم بياني\(f(x)=(x+2)^{2}-3\) باستخدام التحويلات.
- إجابة
-
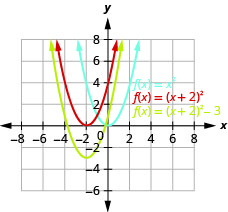
الشكل 9.7.27
رسم بياني\(f(x)=(x-3)^{2}+1\) باستخدام التحويلات.
- إجابة
-
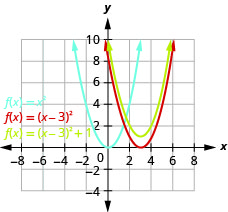
الشكل 9.7.28
تمثيل بياني للدوال التربيعية للنموذج\(f(x)=ax^{2}\)
حتى الآن، قمنا برسم الدالة\(f(x)=x^{2}\) التربيعية بيانيًا ثم رأينا تأثير تضمين ثابت\(h\) أو\(k\) في المعادلة على الرسم البياني الناتج للدالة الجديدة. سنستكشف الآن تأثير المعامل\(a\) على الرسم البياني الناتج للدالة الجديدة\(f(x)=ax^{2}\).
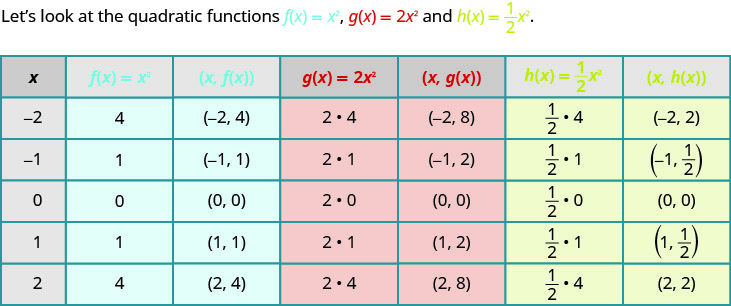
إذا رسمنا هذه الدوال بيانيًا، يمكننا أن نرى تأثير الثابت\(a\)، بافتراض\(a>0\).
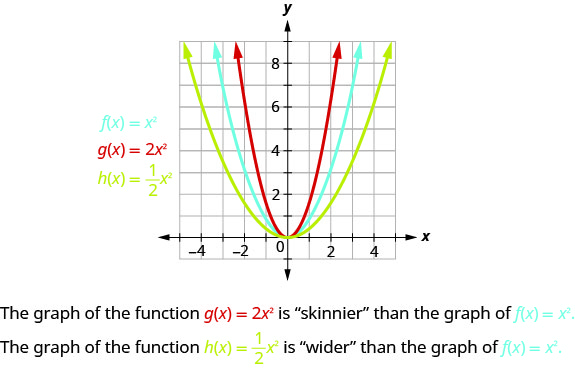
لرسم دالة ذات ثابت\(a\)، يكون من الأسهل اختيار بضع نقاط عليها\(f(x)=x^{2}\) وضربها في\(y\) القيم\(a\) -.
رسم بياني للدالة التربيعية للنموذج\(f(x)=ax^{2}\)
\(f(x)=ax^{2}\)يؤثر المعامل\(a\) في الدالة على الرسم البياني من\(f(x)=x^{2}\) خلال تمديده أو ضغطه.
- إذا كان\(0<|a|<1\) الرسم البياني\(f(x)=ax^{2}\) سيكون «أوسع» من الرسم البياني لـ\(f(x)=x^{2}\).
- إذا كان\(|a|>1\) الرسم البياني\(f(x)=ax^{2}\) سيكون «أنحف» من الرسم البياني لـ\(f(x)=x^{2}\).
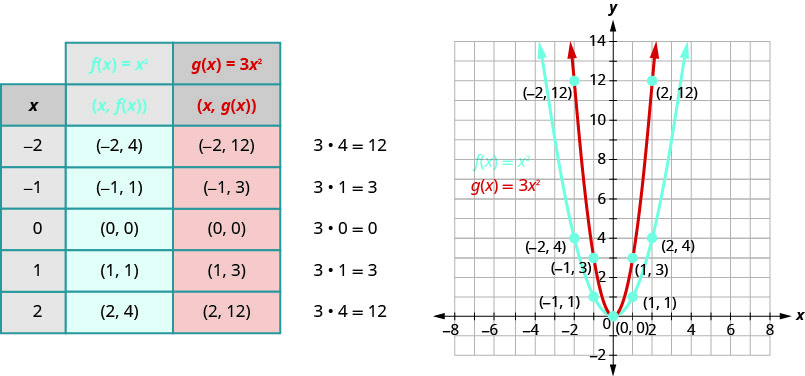
رسم بياني\(f(x)=3x^{2}\).
الحل:
سنقوم برسم الوظائف\(f(x)=x^{2}\)\(g(x)=3x^{2}\) وعلى نفس الشبكة. سنختار بضع نقاط\(f(x)=x^{2}\) ثم نضرب\(y\) قيم -في الحصول\(3\) على النقاط الخاصة بها\(g(x)=3x^{2}\).
رسم بياني\(f(x)=-3x^{2}\).
- إجابة
-
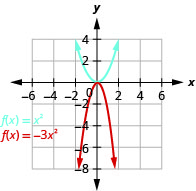
الشكل 9.7.32
رسم بياني\(f(x)=2x^{2}\).
- إجابة
-
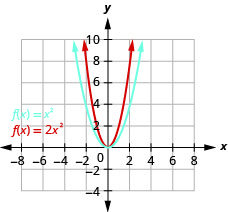
الشكل 9.7.33
تمثيل بياني للدوال التربيعية باستخدام التحويلات
لقد تعلمنا كيف\(f(x)=ax^{2}\) تؤثر الثوابت\(a, h\)،\(k\) وفي الدوال\(f(x)=x^{2}+k, f(x)=(x−h)^{2}\)، على رسوماتها البيانية. يمكننا الآن تجميع هذا معًا ورسم الدوال التربيعية\(f(x)=ax^{2}+bx+c\) عن طريق وضعها أولاً في الشكل\(f(x)=a(x−h)^{2}+k\) بإكمال المربع. يُعرف هذا النموذج أحيانًا باسم نموذج قمة الرأس أو النموذج القياسي.
يجب أن نتوخى الحذر عند جمع الرقم وطرحه على نفس الجانب من الدالة لإكمال المربع. لا يمكننا إضافة الرقم إلى كلا الطرفين كما فعلنا عندما أكملنا المربع بالمعادلات التربيعية.

عندما نكمل المربع في دالة بمعامل\(x^{2}\) ذلك ليس واحدًا، يتعين علينا حساب هذا المعامل من خلال\(x\) المصطلحات -terms فقط. نحن لا نحملها من المصطلح الثابت. غالبًا ما يكون من المفيد نقل المصطلح الثابت قليلاً إلى اليمين لتسهيل التركيز فقط على\(x\) المصطلحات.
بمجرد أن نحصل على الثابت الذي نريده لإكمال المربع، يجب أن نتذكر ضربه في هذا المعامل قبل طرحه.
أعد كتابة\(f(x)=−3x^{2}−6x−1\)\(f(x)=a(x−h)^{2}+k\) النموذج بإكمال المربع.
الحل:
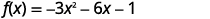 |
|
| افصل\(x\) المصطلحات عن الثابت. | 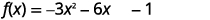 |
| عامل معامل\(x^{2}, -3\). | 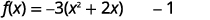 |
| استعد لإكمال المربع. | 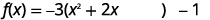 |
| خذ نصفه\(2\) ثم قم بتجميعه لإكمال المربع.\((\frac{1}{2}\cdot 2)^{2}=1\) | |
| \(1\)يُكمل الثابت المربع الموجود بين قوسين، ولكن يتم ضرب الأقواس في\(-3\). لذلك نحن نضيف حقًا\(-3\). يجب علينا بعد ذلك إضافة\(3\) عدم تغيير قيمة الدالة. | 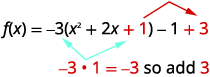 |
| أعد كتابة الثلاثية في صورة مربع واطرح الثوابت. | 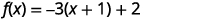 |
| الوظيفة الآن في\(f(x)=a(x-h)^{2}+k\) النموذج. | 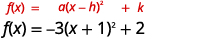 |
أعد كتابة\(f(x)=−4x^{2}−8x+1\)\(f(x)=a(x−h)^{2}+k\) النموذج بإكمال المربع.
- إجابة
-
\(f(x)=-4(x+1)^{2}+5\)
أعد كتابة\(f(x)=2x^{2}−8x+3\)\(f(x)=a(x−h)^{2}+k\) النموذج بإكمال المربع.
- إجابة
-
\(f(x)=2(x-2)^{2}-5\)
بمجرد وضع الدالة في\(f(x)=(x−h)^{2}+k\) النموذج، يمكننا بعد ذلك استخدام التحويلات كما فعلنا في المشكلات القليلة الماضية. سيوضح لنا المثال التالي كيفية القيام بذلك.
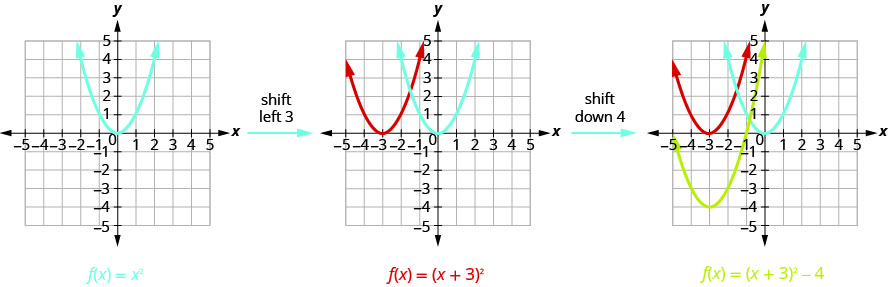
رسم بياني\(f(x)=x^{2}+6x+5\) باستخدام التحويلات.
الحل:
الخطوة 1: أعد كتابة\(f(x)=a(x-h)^{2}+k\) الدالة في شكل قمة بإكمال المربع.
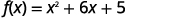 |
|
| افصل\(x\) المصطلحات عن الثابت. | 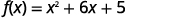 |
| خذ نصفه\(6\) ثم قم بتجميعه لإكمال المربع. \((\frac{1}{2}\cdot 6)^{2}=9\) | |
| نحن نجمع\(9\)\(9\) ونطرح معًا لعدم تغيير قيمة الدالة. | 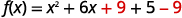 |
| أعد كتابة الثلاثية في صورة مربع واطرح الثوابت. | 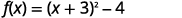 |
| الوظيفة الآن في\(f(x)=(x-h)^{2}+k\) النموذج. | 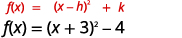 |
الخطوة 2: رسم بياني للدالة باستخدام التحويلات.
بالنظر إلى\(h, k\) القيم، نرى أن الرسم البياني سيأخذ الرسم البياني\(f(x)=x^{2}\) ويحوله إلى\(3\) الوحدات اليسرى\(4\) والوحدات السفلية.
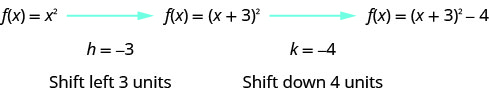
نرسم أولاً الرسم البياني\(f(x)=x^{2}\) على الشبكة.

رسم بياني\(f(x)=x^{2}+2x-3\) باستخدام التحويلات.
- إجابة
-
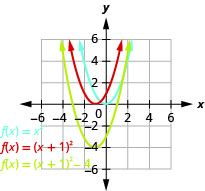
الشكل 9.7.50
رسم بياني\(f(x)=x^{2}-8x+12\) باستخدام التحويلات.
- إجابة
-
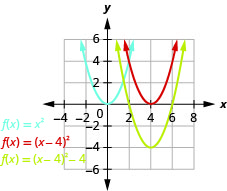
الشكل 9.7.51
نسرد خطوات رسم بياني لدالة تربيعية باستخدام التحويلات هنا.
رسم بياني لدالة تربيعية باستخدام التحويلات
- أعد كتابة الدالة في\(f(x)=a(x-h)^{2}+k\) الشكل بإكمال المربع.
- رسم بياني للدالة باستخدام التحويلات.
رسم بياني\(f(x)=-2x^{2}-4x+2\) باستخدام التحويلات.
الحل:
الخطوة 1: أعد كتابة\(f(x)=a(x-h)^{2}+k\) الدالة في شكل قمة بإكمال المربع.
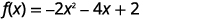 |
|
| افصل\(x\) المصطلحات عن الثابت. | 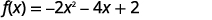 |
| نحن بحاجة\(x^{2}\) إلى معامل واحد. نحن نأخذ\(-2\) في\(x\) الاعتبار المصطلحات. | 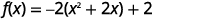 |
| خذ نصفه\(2\) ثم قم بتجميعه لإكمال المربع. \((\frac{1}{2}\cdot 2)^{2}=1\) | |
| نضيف\(1\) لإكمال المربع الموجود بين قوسين، ولكن يتم ضرب الأقواس بـ\(-2\). لذلك نحن نضيف حقًا\(-2\). لعدم تغيير قيمة الوظيفة التي نضيفها\(2\). | 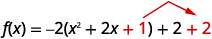 |
| أعد كتابة الثلاثية في صورة مربع واطرح الثوابت. | 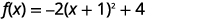 |
| الوظيفة الآن في\(f(x)=a(x-h)^{2}+k\) النموذج. | 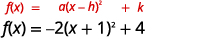 |
الخطوة 2: رسم بياني للدالة باستخدام التحويلات.
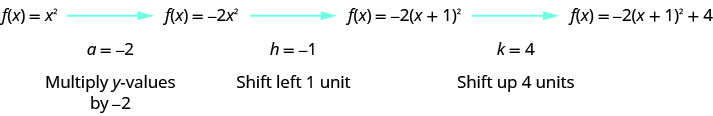
نرسم أولاً الرسم البياني\(f(x)=x^{2}\) على الشبكة.

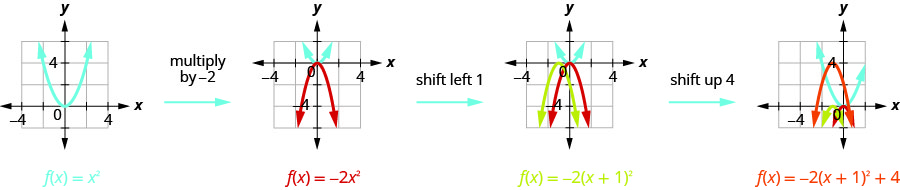
رسم بياني\(f(x)=-3x^{2}+12x-4\) باستخدام التحويلات.
- إجابة
-
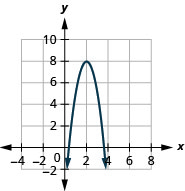
الشكل 9.7.61
رسم بياني\(f(x)=−2x^{2}+12x−9\) باستخدام التحويلات.
- إجابة
-
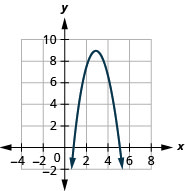
الشكل 9.7.62
الآن بعد أن أكملنا المربع لوضع دالة تربيعية في\(f(x)=a(x−h)^{2}+k\) الشكل، يمكننا أيضًا استخدام هذه التقنية لرسم الدالة بيانيًا باستخدام خصائصها كما في القسم السابق.
إذا نظرنا إلى الأمثلة القليلة الأخيرة، نرى أن قمة الرأس مرتبطة بالثوابت\(h\) و\(k\).
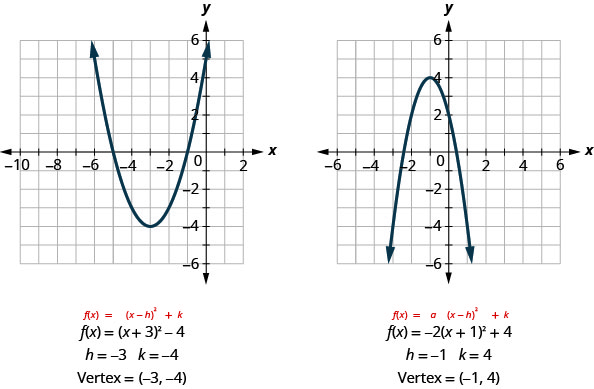
في كل حالة، تكون قمة الرأس\((h,k)\). كما أن محور التماثل هو الخط\(x=h\).
نعيد كتابة خطواتنا لتمثيل دالة تربيعية بيانيًا باستخدام خصائص عندما تكون الدالة في\(f(x)=a(x−h)^{2}+k\) الشكل.
رسم بياني لدالة تربيعية في الصورة\(f(x)=a(x-h)^{2}+k\) باستخدام الخصائص
- أعد كتابة\(f(x)=a(x-h)^{2}+k\) نموذج الدالة.
- حدِّد ما إذا كان القطع المكافئ ينفتح صعودًا أم هبوطًا\(a<0\).\(a>0\)
- أوجد محور التماثل،\(x=h\).
- ابحث عن قمة الرأس،\((h,k\).
- ابحث\(y\) عن التقاطع. ابحث عن النقطة المتماثلة للجزء\(y\) المقطوع عبر محور التماثل.
- ابحث عن\(x\) -Intercepts.
- رسم بياني القطع المكافئ.
- أعد الكتابة\(f(x)=2 x^{2}+4 x+5\) في\(f(x)=a(x-h)^{2}+k\) النموذج
- رسم بياني للدالة باستخدام الخصائص
الحل:
| أعد كتابة الدالة في\(f(x)=a(x-h)^{2}+k\) الشكل بإكمال المربع. | \(f(x)=2 x^{2}+4 x+5\) |
| \(f(x)=2\left(x^{2}+2 x\right)+5\) | |
| \(f(x)=2\left(x^{2}+2 x+1\right)+5-2\) | |
| \(f(x)=2(x+1)^{2}+3\) | |
| حدد الثوابت\(a, h, k\). | \(a=2 h=-1 k=3\) |
| منذ ذلك الحين\(a=2\)، ينفتح المكافئ لأعلى. |  |
| محور التماثل هو\(x=h\). | محور التماثل هو\(x=-1\). |
| قمة الرأس هي\((h,k)\). | قمة الرأس هي\((-1,3)\). |
| ابحث عن\(y\) التقاطع -عن طريق البحث\(f(0)\). | \(f(0)=2 \cdot 0^{2}+4 \cdot 0+5\) |
| \(f(0)=5\) | |
| \(y\)-اعتراض\((0,5)\) | |
| ابحث عن النقطة المتماثلة\((0,5)\) لعبور محور التماثل. | \((-2,5)\) |
| ابحث عن\(x\) -Intercepts. | التمييز سلبي، لذلك لا\(x\) توجد اعتراضات. رسم بياني القطع المكافئ. |
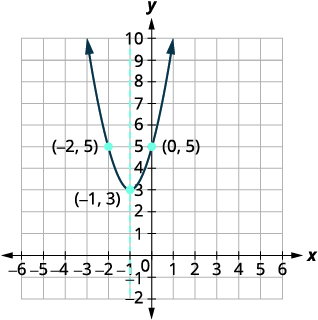 |
- أعد الكتابة\(f(x)=3 x^{2}-6 x+5\) في\(f(x)=a(x-h)^{2}+k\) النموذج
- رسم بياني للدالة باستخدام الخصائص
- إجابة
-
- \(f(x)=3(x-1)^{2}+2\)
الشكل 9.7.66
- أعد الكتابة\(f(x)=-2 x^{2}+8 x-7\) في\(f(x)=a(x-h)^{2}+k\) النموذج
- رسم بياني للدالة باستخدام الخصائص
- إجابة
-
- \(f(x)=-2(x-2)^{2}+1\)
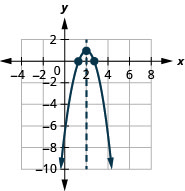
الشكل 9.7.67
ابحث عن دالة تربيعية من تمثيلها البياني
لقد بدأنا حتى الآن بدالة ثم وجدنا الرسم البياني الخاص بها.
الآن سنقوم بعكس العملية. بدءًا من الرسم البياني، سنجد الدالة.
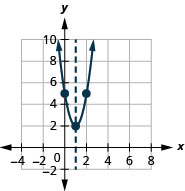
أوجد الدالة التربيعية التي يظهر تمثيلها البياني.
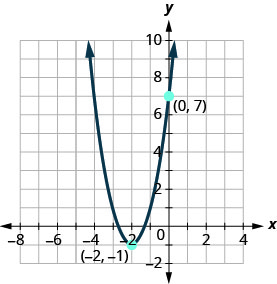
الحل:
نظرًا لأنه تربيعي، نبدأ\(f(x)=a(x−h)^{2}+k\) بالنموذج.
قمة الرأس،\((h,k)\)، هي\((−2,−1)\) هكذا\(h=−2\) و\(k=−1\).
\(f(x)=a(x-(-2))^{2}-1\)
للعثور عليه\(a\)، نستخدم\(y\) -Intercept،\((0,7)\).
لذا\(f(0)=7\).
\(7=a(0+2)^{2}-1\)
حل لـ\(a\).
\(\begin{array}{l}{7=4 a-1} \\ {8=4 a} \\ {2=a}\end{array}\)
اكتب الدالة.
\(f(x)=a(x-h)^{2}+k\)
استبدل في\(h=-2, k=-1\) و\(a=2\).
\(f(x)=2(x+2)^{2}-1\)
اكتب الدالة التربيعية في الصورة\(f(x)=a(x−h)^{2}+k\) التي يظهر الرسم البياني الخاص بها.
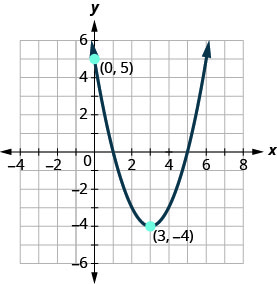
- إجابة
-
\(f(x)=(x-3)^{2}-4\)
أوجد الدالة التربيعية التي يظهر تمثيلها البياني.
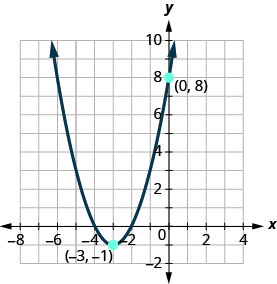
- إجابة
-
\(f(x)=(x+3)^{2}-1\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع رسم الدوال التربيعية بيانيًا باستخدام التحويلات.
المفاهيم الرئيسية
- رسم بياني للدالة التربيعية للنموذج\(f(x)=x^{2}+k\) باستخدام التحول الرأسي
- يغير الرسم\(f(x)=x^{2}+k\) البياني الرسم البياني\(k\) للوحدات\(f(x)=x^{2}\) الرأسية.
- إذا قمت\(k>0\) بتحريك القطع المكافئ رأسيًا إلى أعلى\(k\) بالوحدات.
- إذا قمت\(k<0\) بتحريك القطع المكافئ رأسيًا إلى\(|k|\) أسفل.
- يغير الرسم\(f(x)=x^{2}+k\) البياني الرسم البياني\(k\) للوحدات\(f(x)=x^{2}\) الرأسية.
- رسم بياني للدالة التربيعية للنموذج\(f(x)=(x−h)^{2}\) باستخدام التحول الأفقي
- يغير الرسم\(f(x)=(x−h)^{2}\) البياني الرسم البياني\(f(x)=x^{2}\)\(h\) للوحدات الأفقية.
- إذا\(h>0\)، قم بتحويل\(h\) وحدات القطع المكافئ أفقيًا إلى اليسار.
- إذا\(h<0\)، قم بتحويل\(|h|\) وحدات القطع المكافئ أفقيًا إلى اليمين.
- يغير الرسم\(f(x)=(x−h)^{2}\) البياني الرسم البياني\(f(x)=x^{2}\)\(h\) للوحدات الأفقية.
- رسم بياني لدالة تربيعية في النموذج\(f(x)=ax^{2}\)
- \(f(x)=ax^{2}\)يؤثر المعامل\(a\) في الدالة على الرسم البياني من\(f(x)=x^{2}\) خلال تمديده أو ضغطه.
إذا كان\(0<|a|<1\) الرسم البياني\(f(x)=ax^{2}\) سيكون «أوسع» من الرسم البياني لـ\(f(x)=x^{2}\).
إذا كان\(|a|>1\) الرسم البياني\(f(x)=ax^{2}\) سيكون «أنحف» من الرسم البياني لـ\(f(x)=x^{2}\).
- \(f(x)=ax^{2}\)يؤثر المعامل\(a\) في الدالة على الرسم البياني من\(f(x)=x^{2}\) خلال تمديده أو ضغطه.
- كيفية رسم دالة تربيعية بيانيًا باستخدام التحويلات
- أعد كتابة الدالة في\(f(x)=a(x−h)^{2}+k\) الشكل بإكمال المربع.
- رسم بياني للدالة باستخدام التحويلات.
- رسم بياني لدالة تربيعية في صورة قمة الرأس\(f(x)=a(x−h)^{2}+k\) باستخدام الخصائص
- أعد كتابة الدالة في\(f(x)=a(x−h)^{2}+k\) النموذج.
- حدِّد ما إذا كان القطع المكافئ ينفتح صعودًا أم هبوطًا\(a<0\).\(a>0\)
- أوجد محور التماثل،\(x=h\).
- ابحث عن قمة الرأس،\((h,k)\).
- ابحث\(y\) عن التقاطع. ابحث عن النقطة المتماثلة للجزء\(y\) المقطوع عبر محور التماثل.
- ابحث عن\(x\) -Intercepts، إن أمكن.
- رسم بياني القطع المكافئ.


