Skip to main content
Global

9.7E: رسم بياني للدوال التربيعية باستخدام الخصائص (تمارين)

  1. Last updated
  2. Save as PDF
  • Page ID
    201694

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    الممارسة تجعل من الكمال

    التمارين 1-4: التعرف على التمثيل البياني للدالة التربيعية

    في التمارين التالية، قم برسم الدوال من خلال رسم النقاط.

    1. \(f(x)=x^{2}+3\)

    2. \(f(x)=x^{2}-3\)

    3. \(y=-x^{2}+1\)

    4. \(f(x)=-x^{2}-1\)

    إجابة

    1.

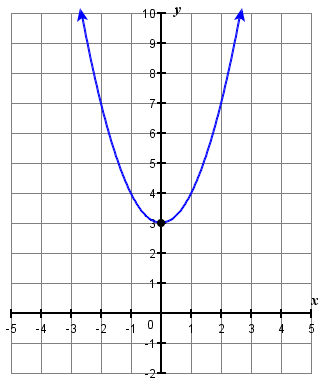
    clipboard_eb78a0f78325e7c8a9cceea709788ca1d.png

    3.

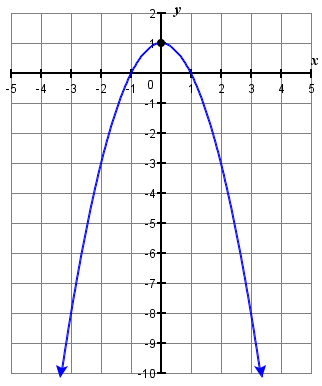
    clipboard_ef318ed788d73edacb2b69f9a778e9ce9.png

    التمارين 5-8: التعرف على التمثيل البياني للدالة التربيعية

    بالنسبة لكل من التمارين التالية، حدد ما إذا كان القطع المكافئ يفتح لأعلى أم لأسفل.

    5. أ.\(f(x)=-2 x^{2}-6 x-7\) ب.\(f(x)=6 x^{2}+2 x+3\)

    6. أ.\(f(x)=4 x^{2}+x-4\) ب.\(f(x)=-9 x^{2}-24 x-16\)

    7. أ.\(f(x)=-3 x^{2}+5 x-1\) ب.\(f(x)=2 x^{2}-4 x+5\)

    8. أ.\(f(x)=x^{2}+3 x-4\) ب.\(f(x)=-4 x^{2}-12 x-9\)

    إجابة

    5. أ. لأسفل ب. لأعلى

    7. أ. لأسفل ب. لأعلى

    التمارين 9-12: إيجاد محور التماثل ورأس المكافئ

    في الوظائف التالية، ابحث

    1. معادلة محور التماثل
    2. قمة الرسم البياني الخاص بها

    9. \(f(x)=x^{2}+8 x-1\)

    10. \(f(x)=x^{2}+10 x+25\)

    11. \(f(x)=-x^{2}+2 x+5\)

    12. \(f(x)=-2 x^{2}-8 x-3\)

    إجابة

    9- أ - محور التماثل:\(x=-4\) ب. قمة الرأس:\((-4,-17)\)

    11- أ - محور التماثل:\(x=1\) ب. قمة الرأس:\((1,2)\)

    التمارين 13 - 24: إيجاد الأجزاء المقطوعة لبارابولا

    في التمارين التالية، ابحث عن الأجزاء المقطوعة للقطع المكافئ الذي تُعطى وظيفته.

    13. \(f(x)=x^{2}+7 x+6\)

    14. \(f(x)=x^{2}+10 x-11\)

    15. \(f(x)=x^{2}+8 x+12\)

    16. \(f(x)=x^{2}+5 x+6\)

    17. \(f(x)=-x^{2}+8 x-19\)

    18. \(f(x)=-3 x^{2}+x-1\)

    19. \(f(x)=x^{2}+6 x+13\)

    20. \(f(x)=x^{2}+8 x+12\)

    21. \(f(x)=4 x^{2}-20 x+25\)

    22. \(f(x)=-x^{2}-14 x-49\)

    23. \(f(x)=-x^{2}-6 x-9\)

    24. \(f(x)=4 x^{2}+4 x+1\)

    إجابة

    13. \(y\)- الاعتراض:\((0,6)\)؛\(x\) - الاعتراض (نقاط) الاعتراض:\((-1,0), (-6,0)\)

    15. \(y\)- الاعتراض:\((0,12)\)؛\(x\) - الاعتراض (نقاط) الاعتراض:\((-2,0), (-6,0)\)

    17. \(y\)- الاعتراض:\((0,-19)\)؛\(x\) - التقاطع (نقاط) الاعتراض: لا يوجد

    19. \(y\)- الاعتراض:\((0,13)\)؛\(x\) - التقاطع (نقاط) الاعتراض: لا يوجد

    21. \(y\)- الاعتراض:\((0,-16)\)؛\(x\) - الاعتراض (نقاط) الاعتراض:\((\frac{5}{2},0)\)

    23. \(y\)- الاعتراض:\((0,9)\)؛\(x\) - الاعتراض (نقاط) الاعتراض:\((-3,0)\)

    التمارين 25 - 42: رسم بياني للدوال التربيعية باستخدام الخصائص

    في التمارين التالية، قم برسم بياني للدالة باستخدام خصائصها.

    25. \(f(x)=x^{2}+6 x+5\)

    26. \(f(x)=x^{2}+4 x-12\)

    27. \(f(x)=x^{2}+4 x+3\)

    28. \(f(x)=x^{2}-6 x+8\)

    29. \(f(x)=9 x^{2}+12 x+4\)

    30. \(f(x)=-x^{2}+8 x-16\)

    31. \(f(x)=-x^{2}+2 x-7\)

    32. \(f(x)=5 x^{2}+2\)

    33. \(f(x)=2 x^{2}-4 x+1\)

    34. \(f(x)=3 x^{2}-6 x-1\)

    35. \(f(x)=2 x^{2}-4 x+2\)

    36. \(f(x)=-4 x^{2}-6 x-2\)

    37. \(f(x)=-x^{2}-4 x+2\)

    38. \(f(x)=x^{2}+6 x+8\)

    39. \(f(x)=5 x^{2}-10 x+8\)

    40. \(f(x)=-16 x^{2}+24 x-9\)

    41. \(f(x)=3 x^{2}+18 x+20\)

    42. \(f(x)=-2 x^{2}+8 x-10\)

    إجابة

    25.

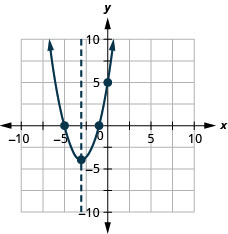
    يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. لدى المكافئ قمة عند (سالب 3، سالب 4). يتم رسم التقاطع y، النقطة (0، 5)، كما هو الحال بالنسبة للاعتراضات x، (سالب 5، 0) و (سالب 1، 0).
    الشكل 9.6.136

    27.

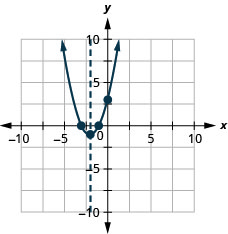
    يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. يحتوي المكافئ على قمة عند (سالب 2، سالب 1). يتم رسم التقاطع y، النقطة (0، 3)، كما هو الحال بالنسبة للاعتراضات x، (سالب 3، 0) و (سالب 1، 0).
    الشكل 9.6.137

    29.

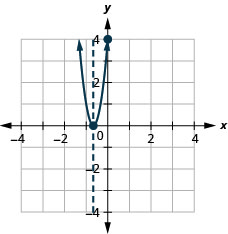
    يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 4 إلى 4. يمتد المحور y للطائرة من سالب 4 إلى 4. يحتوي المكافئ على قمة (سالب الثلثين، 0). يتم رسم التقاطع y، النقطة (0، 4). يتم رسم محور التماثل، x يساوي سالب الثلثين، كخط عمودي متقطع.
    الشكل 9.6.138

    31.

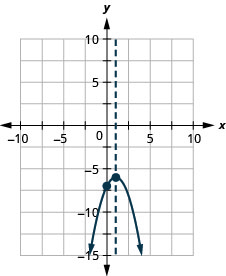
    يوضِّح هذا الشكل القطع المكافئ المتجه نحو الأسفل مُبيَّنًا بيانيًّا على مستوى الإحداثيات x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 15 إلى 10. الشكل المكافئ له قمة عند (1، سالب 6). يتم رسم التقاطع y، النقطة (0، سالب 7). يتم رسم محور التماثل، x يساوي 1، كخط عمودي متقطع.
    الشكل 9.6.139

    33.

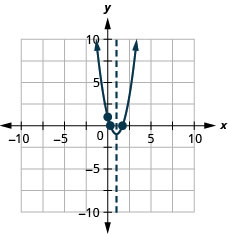
    يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. الشكل المكافئ له قمة عند (1، سالب 1). يتم رسم التقاطع y، النقطة (0، 1)، كما هو الحال بالنسبة للاعتراضات السينية، تقريبًا (0.3، 0) و (1.7، 0). محور التماثل هو الخط العمودي x يساوي 1، مرسوم كخط متقطع.
    الشكل 9.6.140

    35.

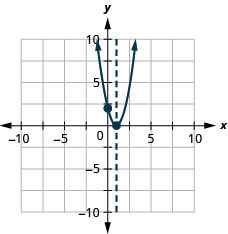
    يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. يحتوي المكافئ على قمة عند (1، 0). هذه النقطة هي التقاطع السيني الوحيد. يتم رسم التقاطع y، النقطة (0، 2). محور التماثل هو الخط العمودي x يساوي 1، مرسوم كخط متقطع.
    الشكل 9.6.141

    37.

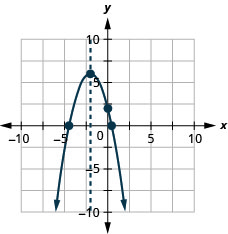
    يوضِّح هذا الشكل القطع المكافئ المتجه نحو الأسفل مُبيَّنًا بيانيًّا على مستوى الإحداثيات x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. يحتوي المكافئ على قمة عند (سالب 2، 6). يتم رسم التقاطع y، النقطة (0، 2)، كما هو الحال بالنسبة للاعتراضات x، تقريبًا (سالب 4.4، 0) و (0.4، 0). محور التماثل هو الخط العمودي x يساوي 2، مرسوم كخط متقطع.
    الشكل 9.6.142

    39.

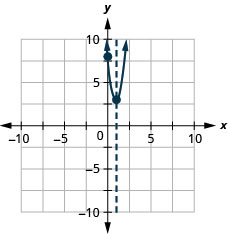
    يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. يحتوي المكافئ على قمة عند (1، 3). تم رسم نقطة التقاطع y، النقطة (0، 8)؛ لا توجد عمليات اعتراض x. محور التماثل هو الخط العمودي x يساوي 1، مرسوم كخط متقطع.
    الشكل 9.6.143

    41.

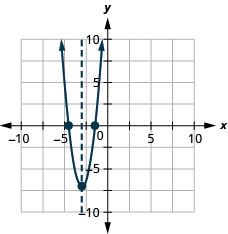
    يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. يحتوي المكافئ على قمة عند (سالب 3، سالب 7). يتم رسم التقاطعات x عند النقاط التقريبية (سالب 4.5، 0) و (سالب 1.5، 0). محور التماثل هو الخط العمودي x يساوي سالب 3، مرسوم كخط متقطع.
    الشكل 9.6.144
    التمارين 43 - 48: حل التطبيقات القصوى والدنيا

    في التمارين التالية، ابحث عن القيمة القصوى أو الدنيا لكل وظيفة.

    43. \(f(x)=2 x^{2}+x-1\)

    44. \(y=-4 x^{2}+12 x-5\)

    45. \(y=x^{2}-6 x+15\)

    46. \(y=-x^{2}+4 x-5\)

    47. \(y=-9 x^{2}+16\)

    48. \(y=4 x^{2}-49\)

    إجابة

    43. الحد الأدنى للقيمة هو\(−\frac{9}{8}\) متى\(x=−\frac{1}{4}\).

    45. القيمة القصوى هي\(6\) عندما\(x=3\).

    47. القيمة القصوى هي\(16\) عندما\(x=0\).

    التمارين 49 - 60: حل التطبيقات القصوى والدنيا

    في التمارين التالية، قم بحل. قرِّب الإجابات لأقرب جزء من عشرة.

    49. يتم إطلاق سهم رأسيًا لأعلى من ارتفاع\(45\) قدم منصة بمعدل\(168\) قدم/ثانية. استخدم الدالة التربيعية\(h(t)=-16 t^{2}+168 t+45\) للعثور على المدة التي سيستغرقها السهم للوصول إلى أقصى ارتفاع له، ثم ابحث عن الحد الأقصى للارتفاع.

    50. يُلقى حجر عموديًا لأعلى من منصة يبلغ ارتفاعها\(20\) قدمًا بمعدل\(160\) قدم/ثانية. استخدم الدالة التربيعية\(h(t)=-16 t^{2}+160 t+20\) لإيجاد المدة التي سيستغرقها الحجر للوصول إلى أقصى ارتفاع له، ثم ابحث عن الحد الأقصى للارتفاع.

    51. تُلقى كرة رأسيًّا لأعلى من الأرض بسرعة أولية قدرها\(109\) قدم/ثانية. استخدم الدالة التربيعية\(h(t)=-16 t^{2}+109 t+0\) لإيجاد المدة التي ستستغرقها الكرة للوصول إلى أقصى ارتفاع لها، ثم ابحث عن أقصى ارتفاع.

    52. تُلقى كرة رأسيًّا لأعلى من الأرض بسرعة أولية قدرها\(122\) قدم/ثانية. استخدم الدالة التربيعية\(h(t)=-16 t^{2}+122 t+0\) لإيجاد المدة التي ستستغرقها الكرة للوصول إلى أقصى ارتفاع لها، ثم ابحث عن أقصى ارتفاع.

    53. يقدر مالك متجر كمبيوتر أنه من خلال فرض\(x\) دولارات على كل جهاز كمبيوتر معين، يمكنه بيع\(40 − x\) أجهزة الكمبيوتر كل أسبوع. تُستخدم الدالة\(R(x)=-x^{2}+40 x\) التربيعية للعثور على الإيرادات\(R\)، التي يتم تلقيها عندما يكون سعر بيع الكمبيوتر\(x\)، ابحث عن سعر البيع الذي سيعطيه الحد الأقصى للإيرادات، ثم ابحث عن مبلغ الحد الأقصى للإيرادات.

    54. يقدر بائع التجزئة الذي يبيع حقائب الظهر أنه من خلال بيعها\(x\) بالدولار لكل منها، سيكون قادرًا على بيع\(100 − x\) حقائب الظهر شهريًا. \(R(x)=-x^{2}+100 x\)تُستخدم الدالة التربيعية للعثور على\(R\) السعر المستلم عند بيع حقيبة الظهر\(x\). ابحث عن سعر البيع الذي سيعطيه الحد الأقصى للإيرادات، ثم ابحث عن مبلغ الحد الأقصى للإيرادات.

    55. يقدر بائع التجزئة الذي يبيع أحذية الموضة أنه من خلال بيعها\(x\) بالدولار لكل منها، سيكون قادرًا على بيع\(70 − x\) الأحذية أسبوعيًا. استخدم الدالة التربيعية\(R(x)=-x^{2}+70 x\) للعثور على الإيرادات المستلمة عندما يكون متوسط سعر بيع زوج من أحذية الموضة\(x\). ابحث عن سعر البيع الذي سيعطيه الحد الأقصى للإيرادات، ثم ابحث عن مبلغ الحد الأقصى للإيرادات في اليوم.

    56. تقدر شركة الهواتف المحمولة أنه من خلال فرض\(x\) دولارات على كل منها مقابل هاتف محمول معين، يمكنها بيع\(8 − x\) الهواتف المحمولة يوميًا. استخدم الدالة التربيعية\(R(x)=-x^{2}+8 x\) للعثور على الإيرادات المستلمة يوميًا عندما يكون سعر بيع الهاتف الخلوي\(x\). ابحث عن سعر البيع الذي سيمنحهم الحد الأقصى للإيرادات في اليوم، ثم ابحث عن مبلغ الحد الأقصى للإيرادات.

    57. سيقوم مربي الماشية بتسييج ثلاثة جوانب من حظيرة بجوار النهر. يحتاج إلى تعظيم مساحة الحظيرة باستخدام\(240\) أقدام السياج. \(A(x)=x(240-2 x)\)تعطي المعادلة التربيعية مساحة الحظيرة\(A\)، بالنسبة لطول\(x\)، الحظيرة على طول النهر. ابحث عن طول الحظيرة على طول النهر الذي سيعطي المساحة القصوى، ثم ابحث عن أقصى مساحة للحظيرة.

    58. يقوم طبيب بيطري بإحاطة منطقة الجري الخارجية المستطيلة بمبناه للكلاب التي يعتني بها. يحتاج إلى تعظيم المساحة باستخدام\(100\) أقدام السياج. \(A(x)=x(100-2 x)\)تعطي الدالة\(A\) التربيعية مساحة ركض الكلب بطول المبنى الذي سيحيط مسار الكلب.\(x\) ابحث عن طول المبنى الذي يجب أن يحد مسار الكلب لإعطاء المساحة القصوى، ثم ابحث عن المساحة القصوى لمسار الكلب.

    59. يخطط مالك الأرض لبناء فناء مستطيل محاط بسياج خلف مرآبه، باستخدام مرآبه كأحد «الجدران». إنه يريد تعظيم المساحة باستخدام\(80\) أقدام السياج. \(A(x)=x(80-2 x)\)تعطي الدالة التربيعية مساحة الفناء، حيث\(x\) يكون عرض أحد الجانبين. ابحث عن المساحة القصوى للفناء.

    60. انتقلت عائلة مكونة من ثلاثة أطفال صغار للتو إلى منزل به ساحة غير مسيجة. أعطاهم المالك السابق\(300\) أقدامًا من السياج لاستخدامها في تطويق جزء من الفناء الخلفي الخاص بهم. استخدم الدالة التربيعية\(A(x)=x(300-2 x)\) لتحديد المساحة القصوى للسياج في الفناء.

    إجابة

    49. في\(5.3\) غضون ثوانٍ، سيصل السهم إلى أقصى ارتفاع\(486\) للقدم.

    51. في\(3.4\) غضون ثوانٍ، ستصل الكرة إلى أقصى ارتفاع\(185.6\) للأقدام.

    53. \(20\)ستعطي أجهزة الكمبيوتر الحد الأقصى البالغ $\(400\) في الإيصالات.

    55. سيكون قادرًا على بيع\(35\) أزواج من الأحذية بأقصى عائد قدره $\(1,225\).

    57. يبلغ طول الجانب على طول نهر الحظيرة\(120\) قدمًا والمساحة القصوى هي قدم\(7,200\) مربع.

    59. أقصى مساحة للفناء هي\(800\) أقدام.

    التمارين 61 - 64: تمارين الكتابة

    61. كيف\(f(x)=x^{2}−1\) تختلف الرسوم البيانية للوظائف\(f(x)=x^{2}\)؟ قمنا برسمها في بداية هذا القسم. ما الفرق بين الرسوم البيانية الخاصة بهم؟ كيف تكون الرسوم البيانية الخاصة بهم هي نفسها؟

    62. اشرح عملية إيجاد قمة القطع المكافئ.

    63. اشرح كيفية العثور على الأجزاء المقطوعة للقطع المكافئ.

    64. كيف يمكنك استخدام التمييز عندما تقوم برسم دالة تربيعية؟

    إجابة

    1. سوف تتنوع الإجابات.

    3. سوف تتنوع الإجابات.

    فحص ذاتي

    أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.

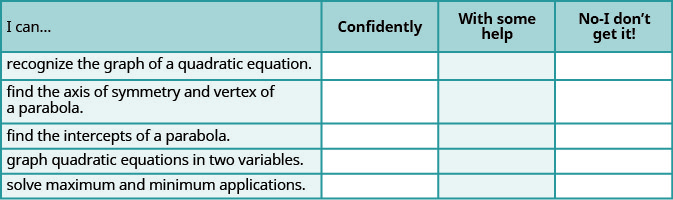
    يوفر هذا الجدول قائمة مرجعية لتقييم إتقان أهداف هذا القسم. اختر الطريقة التي سترد بها على العبارة € يمكنني التعرف على الرسم البياني للمعادلة التربيئية.†€ بثقة، †€ € ¶ ¶ مع بعض المساعدة، †أو € لا، لا أستطيع الحصول عليه.†اختر الطريقة التي سترد بها على العبارة يمكنني العثور على محور التماثل وربع المثل الأعلى.™ بعض المساعدة، †أو †لا، لا أحصل عليها.†اختر كيف سترد على العبارة € يمكنني العثور على نقاط اعتراض المظلة.†€ € بثقة، †€ مع بعض المساعدة، †أو € لا، أنا لا أحصل عليه.†اختر كيف سترد على العبارة € يمكنني رسم المعادلات التربيعية في متغيرين.††’™ بكل ثقة، †€ مع بعض المساعدة، †أو € لا، لا أستطيع الحصول عليه.†اختر كيف سترد على البيان € يمكنني حل الحد الأقصى والحد الأدنى.†€ € مع بعض المساعدة، †أو € لا، أنا لا أحصل عليه.’™
    الشكل 9.6.145

    ب- بعد الاطلاع على قائمة المراجعة، هل تعتقد أنك مستعد جيدًا للقسم التالي؟ لماذا أو لماذا لا؟