9.7: رسم بياني للدوال التربيعية باستخدام الخصائص

Last updated
Save as PDF

Page ID: 201686

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

تعرف على الرسم البياني للدالة التربيعية
أوجد محور التماثل ورأس المكافئ
ابحث عن الأجزاء المقطوعة من المكافئ
رسم بياني للدوال التربيعية باستخدام الخصائص
حل الحد الأقصى والحد الأدنى من التطبيقات

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

رسم بياني للدالة$f(x)=x^{2}$ من خلال رسم النقاط.
إذا فاتتك هذه المشكلة، راجع المثال 3.54.
حل:$2 x^{2}+3 x-2=0$.
إذا فاتتك هذه المشكلة، راجع المثال 6.45.
قم بتقييم$-\frac{b}{2 a}$ متى$a=3$ و$b=-6$.
إذا فاتتك هذه المشكلة، راجع المثال 1.21.

تعرف على التمثيل البياني للدالة التربيعية

في السابق، نظرنا بإيجاز شديد إلى الدالة$f(x)=x^{2}$، التي أطلقنا عليها اسم الدالة المربعة. كانت واحدة من أولى الوظائف غير الخطية التي نظرنا إليها. الآن سنقوم برسم وظائف النموذج$f(x)=a x^{2}+b x+c$ if$a \neq 0$. نسمي هذا النوع من الدالة الدالة الدالة التربيعية.

تعريف$\PageIndex{1}$

الدالة التربيعية$a, b$، حيث،$c$ والأعداد الحقيقية$a≠0$، هي دالة في الشكل

$f(x)=a x^{2}+b x+c$

قمنا برسم الدالة التربيعية$f(x)=x^{2}$ برسم النقاط.

يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 4 إلى 4. يمتد المحور y للطائرة من سالب 2 إلى 6. الشكل المكافئ له قمة عند (0، 0) ويمر أيضًا بالنقاط (-2، 4)، (-1، 1)، (1، 1)، (1، 1)، و (2، 4). على يمين الرسم البياني يوجد جدول قيم مكون من 3 أعمدة. الصف الأول عبارة عن صف في العنوان ويسمي كل عمود، â€xâ€، â€f من x يساوي x squaredâ€، وزوج الترتيب x، f من x.â€ في الصف 2، x يساوي سالب 3، f من x يساوي x مربع هو 9، والزوج المرتب x، f of x هو الزوج المطلوب سالب 3، 9. في الصف 3، x يساوي سالب 2، f من x يساوي x مربع هو 4، والزوج المرتب x، f of x هو الزوج المرتب سالب 2، 4. في الصف 4، x يساوي سالب 1، f من x يساوي x مربع هو 1، والزوج المرتب x، f of x هو الزوج المرتب سالب 1، 1. في الصف 5، x يساوي 0، f من x يساوي x مربع هو 0 والزوج المرتب x، f of x هو الزوج المرتب 0، 0. في الصف 6، x يساوي 1، f من x يساوي x مربع هو 1 والزوج المرتب x، f of x هو الزوج المرتب 1، 1. في الصف 7، x يساوي 2، f من x يساوي x مربع هو 4 والزوج المرتب x، f of x هو الزوج المرتب 2، 4. في الصف 8، x يساوي 3، f من x يساوي x مربع هو 9 والزوج المرتب x، f of x هو الزوج المرتب 3، 9. — الشكل 9.6.1

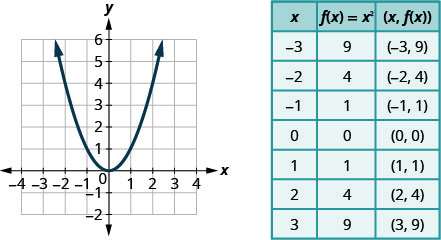
تحتوي كل دالة تربيعية على رسم بياني يشبه هذا. نسمي هذا الرقم المكافئ. دعونا نتدرب على تمثيل القطع المكافئ برسم بضع نقاط.

مثال$\PageIndex{1}$

رسم بياني:$f(x)=x^{2}-1$.

الحل:

سنقوم برسم الدالة من خلال رسم النقاط.

اختر قيمًا عددية لـ$x$، واستبدلها بالمعادلة وقم بتبسيط عملية البحث$f(x)$. سجل قيم الأزواج المرتبة في المخطط.	$.$
ارسم النقاط، ثم قم بتوصيلها بمنحنى سلس. ستكون النتيجة هي الرسم البياني للدالة$f(x)=x^{2}-1$.	$.$

التمارين الرياضية$\PageIndex{1}$

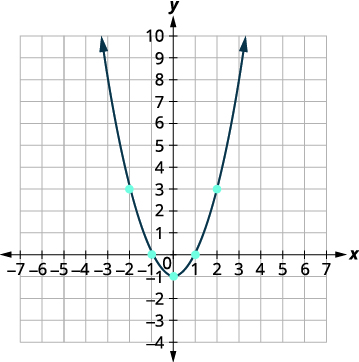رسم بياني$f(x)=-x^{2}$.

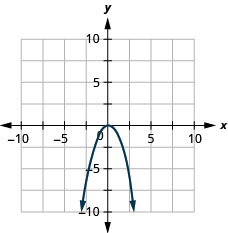
إجابة: $يوضِّح هذا الشكل القطع المكافئ المتجه نحو الأسفل مُبيَّنًا بيانيًّا على مستوى الإحداثيات x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. يحتوي المكافئ على قمة عند (0، 0).$

التمارين الرياضية$\PageIndex{2}$

رسم بياني$f(x)=x^{2}-1$.

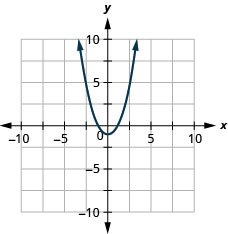
إجابة: $يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. يحتوي المكافئ على قمة عند (0, â'1).$

جميع الرسوم البيانية للدوال التربيعية للنموذج$f(x)=a x^{2}+b x+c$ عبارة عن أشكال متماثلة تفتح لأعلى أو لأسفل. انظر الشكل 9.6.6

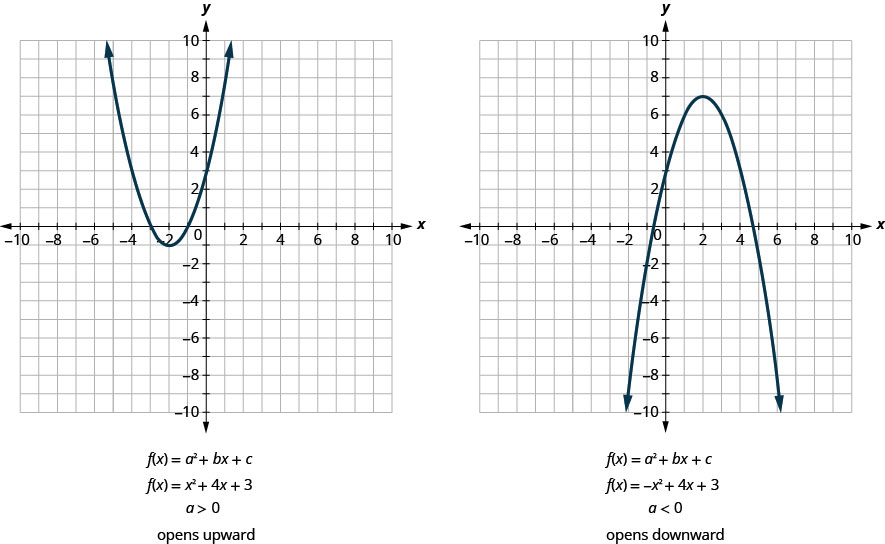
تُظهر هذه الصورة رسمين بيانيين جنبًا إلى جنب يوضِّح الرسم البياني الموجود على اليسار القطع المكافئ ذي الفتحة الصاعدة المُمثَّلة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. يحتوي المكافئ على قمة عند (سالب 2، سالب 1) ويمر عبر النقاط (سالب 4، 3) و (0، 3). الصورة العامة لمعادلة هذا الرسم البياني هي f of x يساوي x مربعًا زائد b x زائد c. معادلة هذا القطع المكافئ هي x مربع زائد 4 x زائد 3. المعامل الرئيسي، a، أكبر من 0، لذا فإن هذا المكافئ يفتح لأعلى. يُظهر الرسم البياني الموجود على اليمين المكافئ المتجه إلى الأسفل مخططًا بيانيًا على مستوى الإحداثيات x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. الشكل المكافئ له قمة عند (2، 7) ويمر بالنقاط (0، 3) و (4، 3). الصورة العامة لمعادلة هذا الرسم البياني هي f من x يساوي x مربعًا زائد b x زائد c. معادلة هذا القطع المكافئ هي سالب x مربع زائد 4 x زائد 3. المعامل الرئيسي، a، أقل من 0، لذلك يفتح هذا المكافئ لأسفل.

لاحظ أن الاختلاف الوحيد في الدالتين هو العلامة السالبة قبل الحد التربيعي ($x^{2}$في معادلة الرسم البياني في الشكل 9.6.6). عندما يكون الحد التربيعي موجبًا، ينفتح المكافئ لأعلى، وعندما يكون الحد التربيعي سالبًا، ينفتح المكافئ لأسفل.

تعريف$\PageIndex{2}$

اتجاه بارابولا

بالنسبة للرسم البياني للدالة التربيعية$f(x)=a x^{2}+b x+c$، إذا

$تعرض هذه الصور قائمة نقطية. تشير النقطة الأولى إلى أنه إذا كان a أكبر من 0، فإن القطع المكافئ يفتح لأعلى ويعرض صورة المكافئ الذي يفتح لأعلى. تشير النقطة الثانية إلى أنه إذا كان a أقل من 0، فإن المكافئ يفتح لأسفل ويعرض صورة المكافئ المفتوح لأسفل.$

مثال$\PageIndex{2}$

حدد ما إذا كان كل شكل مكافئ يفتح لأعلى أو لأسفل:

$f(x)=-3 x^{2}+2 x-4$
$f(x)=6 x^{2}+7 x-9$

الحل:

أ. ابحث عن قيمة$a$.

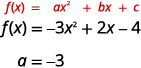
نظرًا$a$ لأن القيمة سلبية، فإن القطع المكافئ سيفتح لأسفل.

b. ابحث عن قيمة$a$.

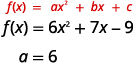
نظرًا لأن$a$ الشكل إيجابي، فإن القطع المكافئ سيفتح صعودًا.

التمارين الرياضية$\PageIndex{3}$

حدِّد هل الرسم البياني لكل دالة هو شكل مكافئ ينفتح لأعلى أو لأسفل:

$f(x)=2 x^{2}+5 x-2$
$f(x)=-3 x^{2}-4 x+7$

إجابة

أعلى
سقط

التمارين الرياضية$\PageIndex{4}$

حدِّد هل الرسم البياني لكل دالة هو شكل مكافئ ينفتح لأعلى أو لأسفل:

$f(x)=-2 x^{2}-2 x-3$
$f(x)=5 x^{2}-2 x-1$

إجابة

سقط
أعلى

أوجد محور التماثل ورأس المكافئ

انظر مرة أخرى إلى الشكل 9.6.10. هل ترى أنه يمكننا طي كل قطعة مكافئة إلى نصفين ثم وضع أحد الجانبين فوق الآخر؟ «خط الطي» هو خط التماثل. نحن نسميها محور التماثل للقطع المكافئ.

نعرض نفس الرسمين البيانيين مرة أخرى مع محور التماثل.

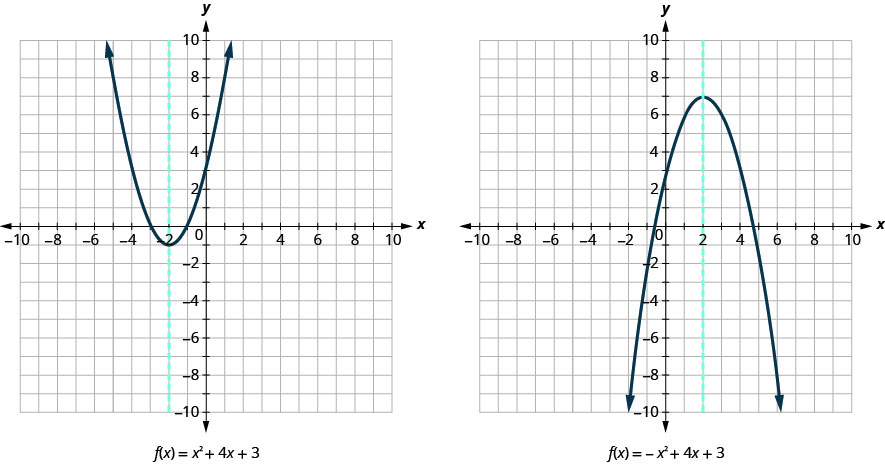
تُظهر هذه الصورة رسمين بيانيين جنبًا إلى جنب يوضِّح الرسم البياني الموجود على اليسار القطع المكافئ المتجه لأعلى والخط العمودي المتقطع المُرسَّم بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. يحتوي المكافئ على قمة عند (سالب 2، سالب 1) ويمر عبر النقاط (سالب 4، 3) و (0، 3). معادلة هذا المكافئ هي x مربع زائد 4 x زائد 3. يمر الخط العمودي بالنقطة (سالب 2، 0) وتكون المعادلة x تساوي سالب 2. يوضِّح الرسم البياني الموجود على اليمين القطع المكافئ المتجه نحو الأسفل والخط العمودي المتقطع بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. الشكل المكافئ له قمة عند (2، 7) ويمر بالنقاط (0، 3) و (4، 3). معادلة هذا المكافئ هي سالب x مربع زائد 4 x زائد 3. يمر الخط العمودي بالنقطة (2، 0) وتكون المعادلة x تساوي 2.

يمكن اشتقاق معادلة محور التماثل باستخدام الصيغة التربيعية. سنحذف الاشتقاق هنا وننتقل مباشرة إلى استخدام النتيجة. معادلة محور التماثل في الرسم البياني لـ$f(x)=a x^{2}+b x+c$ is$x=-\frac{b}{2 a}$.

لذلك لإيجاد معادلة التماثل لكل من البارابولاس التي رسمناها أعلاه، سنستبدل الصيغة$x=-\frac{b}{2 a}$.

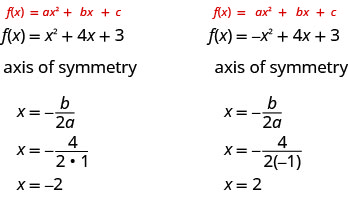
قارن الدالة f الخاصة بـ x تساوي x مربعًا زائد 4 x زائد 3 بالشكل القياسي للدالة التربيعية، f من x يساوي a x مربعًا زائد b x زائد c. محور التماثل هو الخط x يساوي سالب b مقسومًا على الناتج 2 أ. الاستبدال بـ b وa يساوي سالب 4 مقسومًا على الناتج 2 أ. 1. محور التماثل يساوي سالب 2. بعد ذلك، قارن الدالة f لـ x تساوي سالب x مربع زائد 4 x زائد 3 بالشكل القياسي للدالة التربيعية، f of x يساوي a x مربعًا زائد b x زائد c. محور التماثل هو الخط x يساوي سالب b مقسومًا على الناتج 2 a. استبدال b وa يساوي سالب 4 مقسومًا على الناتج 2 a. المنتج سلبي مرتين 1. محور التماثل يساوي 2.

لاحظ أن هذه هي معادلات الخطوط الزرقاء المتقطعة على الرسوم البيانية.

تقع النقطة الموجودة على المكافئ الأقل (يفتح القطع المكافئ)، أو الأعلى (يفتح القطع المكافئ لأسفل)، على محور التماثل. هذه النقطة تسمى قمة المكافئ.

يمكننا بسهولة العثور على إحداثيات قمة الرأس، لأننا نعلم أنها تقع على محور التماثل. هذا يعني أن
$x$ الإحداثيات الخاصة بها هي$-\frac{b}{2 a}$. لإيجاد$y$ الإحداثي -للرأس، نستبدل قيمة$x$ الإحداثي -في الدالة التربيعية.

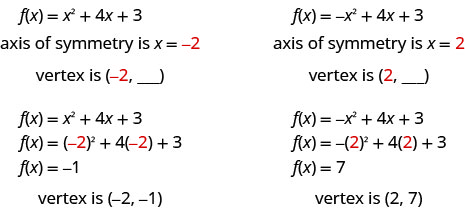
بالنسبة للدالة f من x تساوي x مربعًا زائد 4 x زائد 3، فإن محور التماثل هو x يساوي سالب 2. قمة الرأس هي النقطة الموجودة على القطع المكافئ ذات الإحداثي السيني السالب 2. البديل x يساوي سالب 2 في الدالة f لـ x يساوي x مربع زائد 4 x زائد 3. F من x يساوي مربع سالب 2 زائد 4 في سالب 2 زائد 3، لذلك f من x يساوي سالب 1. قمة الرأس هي النقطة (سالب 2، سالب 1). بالنسبة للدالة f من x تساوي سالب x مربع زائد 4 x زائد 3، فإن محور التماثل هو x يساوي 2. قمة الرأس هي النقطة الموجودة على القطع المكافئ مع الإحداثي السيني 2. البديل x يساوي 2 في الدالة f لـ x يساوي x squared زائد 4 x زائد 3. F من x يساوي 2 مربع زائد 4 في 2 زائد 3، لذلك f من x يساوي 7. قمة الرأس هي النقطة (2، 7).

محور التماثل وربع رأس البارابولا

الرسم البياني للدالة$f(x)=a x^{2}+b x+c$ هو المكافئ حيث:

محور التماثل هو الخط العمودي$x=-\frac{b}{2 a}$.
قمة الرأس هي نقطة على محور التماثل، لذا فإن$x$ إحداثياتها هي$-\frac{b}{2 a}$
يتم العثور على$y$ الإحداثيات -للرأس عن طريق الاستبدال$x=-\frac{b}{2 a}$ في المعادلة التربيعية.

مثال$\PageIndex{3}$

للحصول على الرسم البياني$f(x)=3 x^{2}-6 x+2$ للبحث:

محور التناظر
قمة الرأس

الحل:

أ.

	$.$
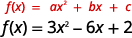محور التماثل هو الخط العمودي$x=-\frac{b}{2 a}$.
استبدل القيم$a,b$ في المعادلة.	$x=-\frac{-6}{2 \cdot 3}$
قم بالتبسيط.	$x=1$
	محور التماثل هو الخط$x=1$.

ب.

	$f(x)=3 x^{2}-6 x+2$
قمة الرأس هي نقطة على خط التماثل، لذلك ستكون$x$ إحداثياتها$x=1$. ابحث$f(1)$.	$.$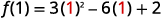
قم بالتبسيط.	$.$
والنتيجة هي$y$ الإحداثيات -conditate.	$f(1)=-1$
	قمة الرأس هي$(1,-1)$.

التمارين الرياضية$\PageIndex{5}$

للحصول على الرسم البياني$f(x)=2 x^{2}-8 x+1$ للبحث:

محور التناظر
قمة الرأس

إجابة

$x=2$
$(2,-7)$

التمارين الرياضية$\PageIndex{6}$

للحصول على الرسم البياني$f(x)=2 x^{2}-4 x-3$ للبحث:

محور التناظر
قمة الرأس

إجابة

$x=1$
$(1,-5)$

ابحث عن القطع المعترضة لبارابولا

عندما رسمنا المعادلات الخطية بيانيًا، غالبًا ما$y$ استخدمنا الأجزاء المقطوعة لمساعدتنا في رسم الخطوط.$x$ سيساعدنا العثور على إحداثيات عمليات الاعتراض على رسم البارابولاس أيضًا.

تذكر أن القيمة عند$y$ التقاطع -incept$x$ هي صفر. لذلك للعثور على$y$ التقاطع السيني،$x=0$ نستبدل الوظيفة.

دعونا نجد$y$ التقاطعات -للبارابوليين الموضحين في الشكل 9.6.20.

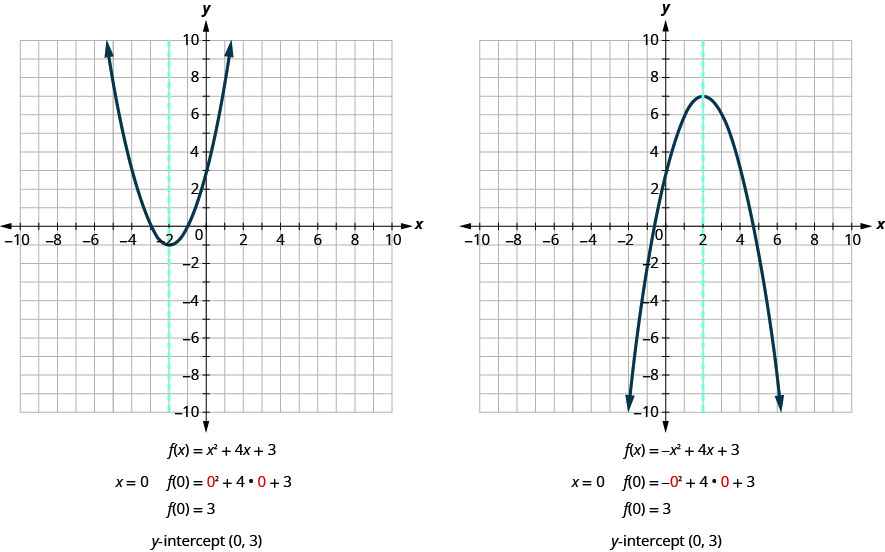
ينتج$x$ التقاطع -Intercept عندما تكون القيمة$f(x)$ صفرًا. للعثور على نقطة$x$ اعتراض، سمحنا بذلك$f(x)=0$. بمعنى آخر، سنحتاج إلى حل المعادلة$0=a x^{2}+b x+c$ لـ$x$.

$\begin{aligned} f(x) &=a x^{2}+b x+c \\ 0 &=a x^{2}+b x+c \end{aligned}$

حل المعادلات التربيعية مثل هذه هو بالضبط ما قمنا به سابقًا في هذا الفصل!

يمكننا الآن العثور$x$ على القطع الفاصلة بين المظليين اللذين نظرنا إليهما. أولاً سنجد الأجزاء$x$ المتقاطعة للقطع المكافئ الذي تكون وظيفته$f(x)=x^{2}+4 x+3$.

	$f(x)=x^{2}+4 x+3$
دعونا$f(x)=0$.	$\color{red}0\color{black}=x^{2}+4 x+3$
عامل.	$0=(x+1)(x+3)$
استخدم خاصية المنتج الصفري.	$x+1=0 \quad x+3=0$
حل.	$x=-1 \quad x=-3$
	$x$عمليات الاعتراض - هي$(-1,0)$ و$(-3,0)$.

الآن سنجد الأجزاء$x$ المتقاطعة للقطع المكافئ الذي تكون وظيفته$f(x)=-x^{2}+4 x+3$.

	$f(x)=-x^{2}+4 x+3$
دعونا$f(x)=0$.	$\color{red}0 \color{black}=-x^{2}+4 x+3$
لا تؤثر هذه الدرجة التربيعية، لذلك نستخدم الصيغة التربيعية.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
$a=-1, b=4, c=3$	$x=\frac{-4 \pm \sqrt{4^{2}-4(-1)(3)}}{2(-1)}$
قم بالتبسيط.	$x=\frac{-4 \pm \sqrt{28}}{-2}$
	$x=\frac{-4 \pm 2 \sqrt{7}}{-2}$
	$x=\frac{-2(2 \pm \sqrt{7})}{-2}$
	$x=2 \pm \sqrt{7}$
	$x$عمليات الاعتراض - هي$(2+\sqrt{7}, 0)$ و$(2-\sqrt{7}, 0)$.

سنستخدم التقديرات العشرية للقطع المقطوعة، حتى نتمكن من تحديد هذه النقاط على الرسم البياني،$x$

$(2+\sqrt{7}, 0) \approx(4.6,0) \quad(2-\sqrt{7}, 0) \approx(-0.6,0)$

هل تتفق هذه النتائج مع الرسوم البيانية الخاصة بنا؟ انظر الشكل 9.6.34

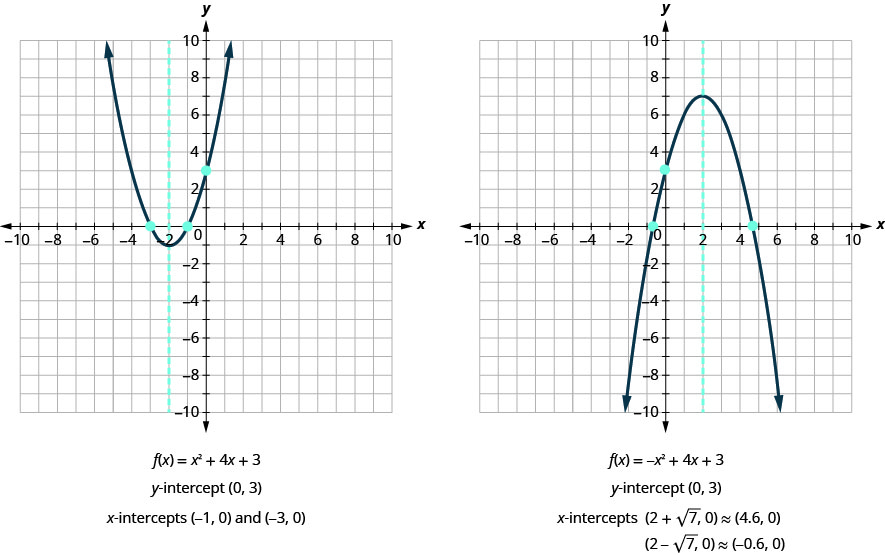
تُظهر هذه الصورة رسمين بيانيين جنبًا إلى جنب يوضِّح الرسم البياني الموجود على اليسار المكافئ الافتتاحي التصاعدي المُعرَّف بدالة f في x يساوي x مربعًا زائد 4 x زائد 3 والخط العمودي المتقطع، x يساوي سالب 2، مُبيَّنًا بيانيًّا على مستوى الإحداثيات x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. يحتوي المكافئ على قمة عند (سالب 2، سالب 1). نقطة التقاطع y هي (0، 3) وتكون التقاطعات السينية (سالبة 1، 0) و (سالبة 3، 0). يوضِّح الرسم البياني الموجود على اليمين القطع المكافئ المتجه نحو الأسفل المُعرَّف بدالة f في x يساوي سالب x مربّعًا زائد 4 x زائد 3 وخط عمودي متقطع، x يساوي 2، مُبيَّنًا بيانيًا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. يحتوي المكافئ على قمة عند (2، 7). التقاطع y هو (0، 3) وتكون التقاطعات x (2 زائد الجذر التربيعي 7، 0)، تقريبًا (4.6، 0) و (2 ناقص الجذر التربيعي، 0)، تقريبًا (سالب 0.6، 0).

ابحث عن القطع المعترضة لبارابولا

للعثور على الأجزاء المقطوعة للقطع المكافئ الذي تتمثل وظيفته في$f(x)=a x^{2}+b x+c$:

$y$-اعتراض

دعونا نحل المشكلة$x=0$ ونحلها$f(x)$.

$x$- عمليات الاعتراض

دعونا$f(x)=0$ نحل المشكلة$x$

مثال$\PageIndex{4}$

أوجد الأجزاء المقطوعة للقطع المكافئ الذي تكون وظيفته$f(x)=x^{2}-2 x-8$.

الحل:

للعثور على النقطة$y$ -Intercept$x=0$، دعنا نحلها$f(x)$.	$f(x)=x^{2}-2 x-8$
	$f(0)=\color{red}0\color{black}^{2}-2 \cdot \color{red}0 \color{black}-8$
	$f(0)=-8$
	متى$x=0$، إذن$f(0)=-8$. $y$الاعتراض -هو النقطة$(0,-8)$.
للعثور على النقطة$x$ -Intercept$f(x)=0$، دعنا نحلها$x$.	$f(x)=x^{2}-2 x-8$
	$0=x^{2}-2 x-8$
حل عن طريق التخصيم	$0=(x-4)(x+2)$
	$0=x-4 \quad 0=x+2$
	$4=x \quad-2=x$
	متى$f(x)=0$، ثم$x=4$ أو$x=-2$. نقاط$x$ الاعتراض -هي النقاط$(4,0)$ و$(-2,0)$.

التمارين الرياضية$\PageIndex{7}$

أوجد الأجزاء المقطوعة للقطع المكافئ الذي تكون وظيفته$f(x)=x^{2}+2 x-8$.

إجابة: $y$- الاعتراض:$(0,-8) x$ - عمليات الاعتراض$(-4,0),(2,0)$

التمارين الرياضية$\PageIndex{8}$

أوجد الأجزاء المقطوعة للقطع المكافئ الذي تكون وظيفته$f(x)=x^{2}-4 x-12$.

إجابة: $y$- الاعتراض:$(0,-12) x$ - عمليات الاعتراض$(-2,0),(6,0)$

في هذا الفصل، قمنا بحل المعادلات التربيعية للنموذج$a x^{2}+b x+c=0$. لقد$x$ حللنا المشكلة وكانت النتائج هي الحلول للمعادلة.

نحن نبحث الآن في الدوال التربيعية للنموذج$f(x)=a x^{2}+b x+c$. الرسوم البيانية لهذه الوظائف هي بارابولاس. يحدث$x$ - اعتراض البارابولاس في المكان الذي يحدث فيه$f(x)=0$.

على سبيل المثال:

معادلة تربيعية

$\begin{aligned}x^{2}-2 x-15 & =0\quad \text{Let}\:f(x)=0 \\ (x-5)(x+3) &=0 \\ x-5=0\:\:x+3 & =0 \\ x=5\:\:\:x&=-3\end{aligned}$

دالة تربيعية

$\begin{aligned} f(x) &=x^{2}-2 x-15 \\ 0 &=x^{2}-2 x-15 \\ 0 &=(x-5)(x+3) \\ x-5 &=0 \quad x+3=0 \\ x &=5 \quad x=-3 \\(5,0) & \text { and }(-3,0) \\& x\text { -intercepts } \end{aligned}$

حلول الدالة التربيعية هي$x$ قيم$x$ - الاعتراضات.

في وقت سابق، رأينا أن المعادلات التربيعية لها$2, 1$، أو$0$ حلول. توضح الرسوم البيانية أدناه أمثلة للبارابولاس لهذه الحالات الثلاث. نظرًا لأن حلول الوظائف تعطي$x$ الأجزاء المتقاطعة من الرسوم البيانية، فإن عدد$x$ -Intercepts هو نفس عدد الحلول.

في السابق، استخدمنا التمييز لتحديد عدد حلول الدالة التربيعية للنموذج$a x^{2}+b x+c=0$. الآن يمكننا استخدام التمييز لإخبارنا بعدد$x$ عمليات الاعتراض الموجودة على الرسم البياني.

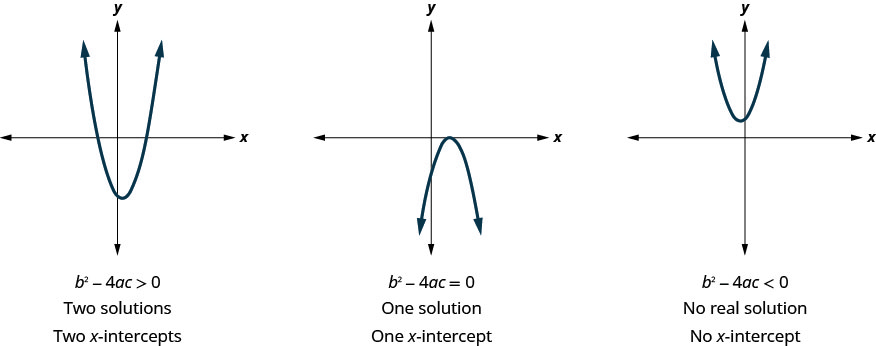
تُظهر هذه الصورة ثلاثة رسوم بيانية جنبًا إلى جنب. يوضِّح الرسم البياني الموجود على اليسار القطع المكافئ ذي الفتحة الصاعدة المُمثَّلة بيانيًّا على المستوى الإحداثي x y. تقع قمة القطع المكافئ أسفل المحور السيني ويعبر القطع المكافئ المحور السيني عند نقطتين مختلفتين. إذا كان مربع b ناقص 4 a c أكبر من 0، فإن المعادلة التربيعية a x squared زائد b x زائد c تساوي 0 لها حلان، والرسم البياني للقطع المكافئ يحتوي على قطعين x. يوضِّح الرسم البياني الموجود في المنتصف القطع المكافئ المتجه نحو الأسفل والممثَّلة بيانيًّا على المستوى الإحداثي x y. تقع قمة القطع المكافئ على المحور السيني، وهو نقطة التقاطع الوحيدة بين القطع المكافئ والمحور السيني. إذا كان مربع b ناقص 4 a c يساوي 0، فإن المعادلة التربيعية a x squared زائد b x زائد c تساوي 0 لها حل واحد، والرسم البياني للقطع المكافئ يحتوي على تقاطع x واحد. يوضِّح الرسم البياني الموجود على اليمين القطع المكافئ ذي الفتحة الصاعدة المُمثَّلة بيانيًّا على المستوى الإحداثي x y. تقع قمة المكافئ فوق المحور السيني ولا يعبر القطع المكافئ المحور السيني. إذا كان مربع b ناقص 4 a c أقل من 0، فإن المعادلة التربيعية a x squared زائد b x plus c تساوي 0 لا تحتوي على حلول، ولا يحتوي الرسم البياني للقطع المكافئ على تقاطعات x.

قبل أن تجد قيم$x$ -incepts، قد ترغب في تقييم التمييز حتى تعرف عدد الحلول المتوقعة.

مثال$\PageIndex{5}$

أوجد الأجزاء المقطوعة للقطع المكافئ للدالة$f(x)=5 x^{2}+x+4$.

الحل:

	$.$
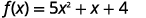للعثور على النقطة$y$ -Intercept$x=0$، دعنا نحلها$f(x)$.	$.$
	$.$
	متى$x=0$، إذن$f(0)=4$. $y$الاعتراض -هو النقطة$(0,4)$.
للعثور على النقطة$x$ -Intercept$f(x)=0$، دعنا نحلها$x$.	$.$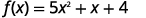
	$.$
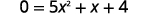ابحث عن قيمة التمييز للتنبؤ بعدد الحلول وهو أيضًا عدد$x$ عمليات الاعتراض.
$\begin{array}{c}{b^{2}-4 a c} \\ {1^{2}-4 \cdot 5 \cdot 4} \\ {1-80} \\ {-79}\end{array}$
	نظرًا لأن قيمة التمييز سالبة، فلا يوجد حل حقيقي للمعادلة. لا توجد$x$ عمليات اعتراض.

التمارين الرياضية$\PageIndex{9}$

أوجد الأجزاء المقطوعة للقطع المكافئ الذي تكون وظيفته$f(x)=3 x^{2}+4 x+4$.

إجابة: $y$- الاعتراض:$(0,4)$ عدم$x$ الاعتراض

التمارين الرياضية$\PageIndex{10}$

أوجد الأجزاء المقطوعة للقطع المكافئ الذي تكون وظيفته$f(x)=x^{2}-4 x-5$

إجابة: $y$- الاعتراض:$(0,-5)$$x$ - عمليات الاعتراض$(-1,0),(5,0)$

رسم بياني للدوال التربيعية باستخدام الخصائص

لدينا الآن جميع القطع التي نحتاجها لرسم دالة تربيعية. نحن فقط بحاجة إلى تجميعها معًا. في المثال التالي سنرى كيفية القيام بذلك.

مثال$\PageIndex{6}$ How to Graph a Quadratic Function Using Properties

رسم بياني$f(x)=x^{2}-6x+8$ باستخدام خصائصه.

الحل:

الخطوة 1: حدد ما إذا كان القطع المكافئ يفتح لأعلى أو لأسفل.	انظر$a$ في المعادلة$f(x)=x^{2}-6x+8$ نظرًا$a$ لأنه إيجابي، فإن القطع المكافئ يفتح لأعلى.	$f(x)=x^{2}-6x+8$ $\color{red}{a=1, b=-6, c=8}$ يفتح المكافئ لأعلى.
الخطوة 2: ابحث عن محور التماثل.	$f(x)=x^{2}-6x+8$ محور التماثل هو الخط$x=-\frac{b}{2 a}$.	محور التماثل $x=-\frac{b}{2 a}$ $x=-\frac{(-6)}{2 \cdot 1}$ $x=3$ محور التماثل هو الخط$x=3$.
الخطوة 3: ابحث عن قمة الرأس.	تقع قمة الرأس على محور التماثل. $x=3$استبدل الوظيفة.	فيرتكس $f(x)=x^{2}-6x+8$ $f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8$ $f(3)=-1$ قمة الرأس هي$(3,-1)$.
الخطوة 4: ابحث$y$ عن التقاطع. ابحث عن النقطة المتماثلة للجزء$y$ المقطوع عبر محور التماثل.	نجد$f(0)$. نستخدم محور التماثل لإيجاد نقطة متماثلة للجزء$y$ المقطوع. $y$التقاطع -هو$3$ الوحدات اليسرى من محور التماثل،$x=3$. $3$تحتوي الوحدات النقطية الموجودة على يمين محور التماثل على$x=6$.	$y$-اعتراض $f(x)=x^{2}-6 x+8$ $f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8$ $f(0)=8$ $y$الاعتراض الإلكتروني هو$(0,8)$. نقطة متماثلة إلى$y$ نقطة التقاطع: النقطة هي$(6,8)$.
الخطوة 5: ابحث عن$x$ -Intercepts. ابحث عن نقاط إضافية إذا لزم الأمر.	نحن نحل$f(x)=0$. يمكننا حل هذه المعادلة التربيعية عن طريق التحليل.	$x$- عمليات الاعتراض $f(x)=x^{2}-6 x+8$ $\color{red}{0}\color{black}{=}x^{2}-6x+8$ $\color{red}{0}\color{black}{=}(x-2)(x-4)$ $x=2 or x=4$ $x$عمليات الاعتراض - هي$(2,0)$ و$(4,0)$.
الخطوة 6: رسم القطع المكافئ.	نحن نرسم قمة الرأس والاعتراض والنقطة المتماثلة للنقطة المقابلة لـ$y$ -Intercept. نقوم بتوصيل هذه$5$ النقاط لرسم القطع المكافئ.	$لقطة شاشة (1) .png$

التمارين الرياضية$\PageIndex{11}$

رسم بياني$f(x)=x^{2}+2x-8$ باستخدام خصائصه.

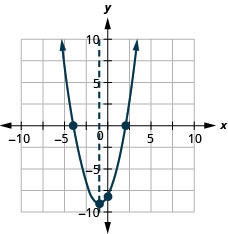
إجابة: $يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. محور التماثل، x يساوي سالب 1، تم رسمه بيانيًا كخط متقطع. يحتوي المكافئ على قمة عند (سالب 1، سالب 9). التقاطع الصادي للقطع المكافئ هو النقطة (0، سالب 8). الأجزاء المقطوعة من الأشعة السينية للقطع المكافئ هي النقاط (سالبة 4، 0) و (4، 0).$

التمارين الرياضية$\PageIndex{12}$

رسم بياني$f(x)=x^{2}-8x+12$ باستخدام خصائصه.

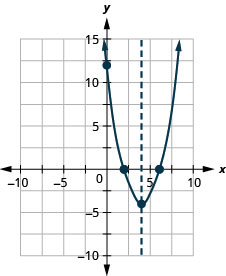
إجابة: $يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 15. محور التماثل، x يساوي 4، مرسوم بيانيًا كخط متقطع. الشكل المكافئ له قمة عند (4، سالب 4). التقاطع الصادي للقطع المكافئ هو النقطة (0، 12). الأجزاء المقطوعة من الأشعة السينية للقطع المكافئ هي النقاط (2، 0) و (6، 0).$

نسرد الخطوات التي يجب اتخاذها لرسم دالة تربيعية هنا.

تمثيل دالة تربيعية بيانيًا باستخدام الخصائص

حدِّد ما إذا كان القطع المكافئ ينفتح لأعلى أم لأسفل.
أوجد معادلة محور التماثل.
ابحث عن قمة الرأس.
ابحث$y$ عن التقاطع. ابحث عن النقطة المتماثلة للجزء$y$ المقطوع عبر محور التماثل.
ابحث عن$x$ -Intercepts. ابحث عن نقاط إضافية إذا لزم الأمر.
رسم بياني القطع المكافئ.

تمكنا من العثور على$x$ -incepts في المثال الأخير عن طريق العوملة. نجد$x$ -intercepts في المثال التالي عن طريق العوملة أيضًا.

مثال$\PageIndex{7}$

رسم بياني$f(x)=-x^{2}+6 x-9$ باستخدام خصائصه.

الحل:

	$.$
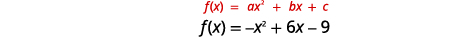منذ$a$ ذلك الحين$-1$، ينفتح المكافئ لأسفل.
	$.$
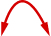للعثور على معادلة محور التماثل، استخدم$x=-\frac{b}{2 a}$.	$x=-\frac{b}{2 a}$
	$x=-\frac{6}{2(-1)}$
	$x=3$
	محور التماثل هو$x=3$. قمة الرأس على الخط$x=3$.
	$.$
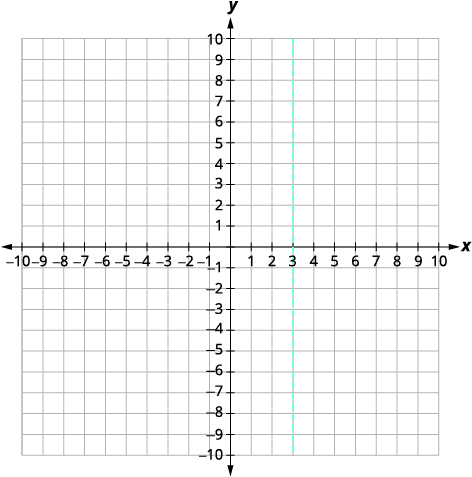ابحث$f(3)$.	$f(x)=-x^{2}+6 x-9$
	$.$
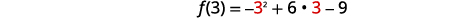	$f(3)=-9+18-9$
	$f(3)=0$
	قمة الرأس هي$(3,0)$.
	$.$
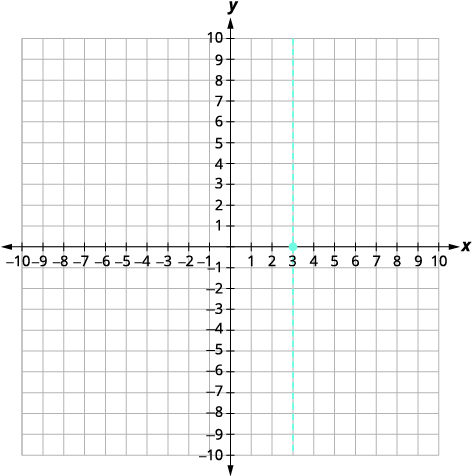يحدث$y$ التقاطع عند حدوث ذلك$x=0$. ابحث$f(0)$.	$f(x)=-x^{2}+6 x-9$
بديل$x=0$.	$.$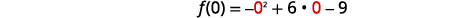
قم بالتبسيط.	$f(0)=-9$
النقطة$(0,-9)$ هي ثلاث وحدات على يسار خط التماثل. النقطة الثلاث وحدات على يمين خط التماثل هي$(6,-9)$.	$.$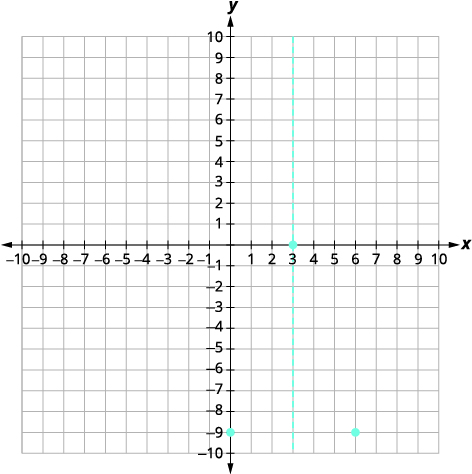
	النقطة المتماثلة في$y$ التقاطع السيني هي$(6,-9)$
يحدث$x$ التقاطع عند حدوث ذلك$f(x)=0$.	$.$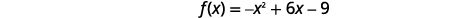
ابحث$f(x)=0$.	$.$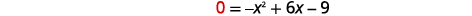
عامل عامل GCF.	$.$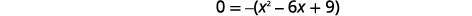
عامل الثلاثي.	$.$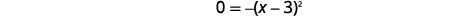
حل لـ$x$.	$.$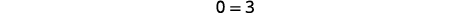
قم بتوصيل النقاط لرسم القطع المكافئ.	$.$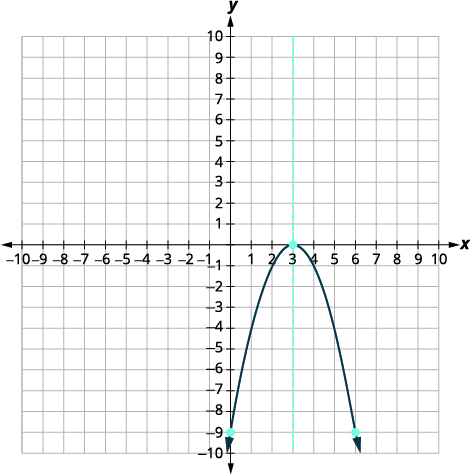

التمارين الرياضية$\PageIndex{13}$

رسم بياني$f(x)=3 x^{2}+12 x-12$ باستخدام خصائصه.

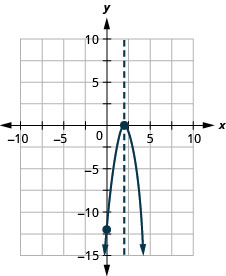
إجابة: $يوضِّح هذا الشكل القطع المكافئ المتجه نحو الأسفل مُبيَّنًا بيانيًّا على مستوى الإحداثيات x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 15 إلى 10. يحتوي المكافئ على قمة عند (2، 0). يتم رسم التقاطع y (0، سالب 12) بالإضافة إلى محور التماثل، x يساوي 2.$

التمارين الرياضية$\PageIndex{14}$

رسم بياني$f(x)=4 x^{2}+24 x+36$ باستخدام خصائصه.

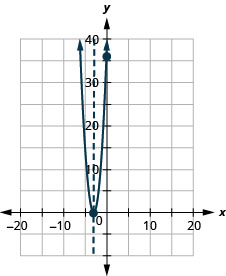
إجابة: $يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 30 إلى 20. يمتد المحور y للطائرة من سالب 10 إلى 40. يحتوي المكافئ على قمة عند (سالب 3، 0). يتم رسم التقاطع y (0، 36) بالإضافة إلى محور التماثل، x يساوي سالب 3.$

بالنسبة للرسم البياني لـ$f(x)=-x^{2}+6 x-9$، كانت قمة الرأس ونقطة$x$ التقاطع -هي نفس النقطة. تذكر كيف يحدد التمييز عدد حلول المعادلة التربيعية؟ عامل التمييز في المعادلة$0=-x^{2}+6x-9$ هو$0$، لذلك هناك حل واحد فقط. وهذا يعني أن هناك$x$ نقطة تقاطع واحدة فقط، وهي قمة المكافئ.

كم$x$ عدد عمليات الاعتراض التي تتوقع رؤيتها على الرسم البياني$f(x)=x^{2}+4 x+5$؟

مثال$\PageIndex{8}$

رسم بياني$f(x)=x^{2}+4 x+5$ باستخدام خصائصه.

الحل:

	$.$
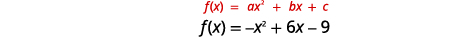منذ$a$ ذلك الحين$-1$، ينفتح المكافئ لأسفل.
	$.$
للعثور على معادلة محور التماثل، استخدم$x=-\frac{b}{2 a}$.	$.$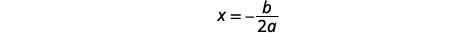
	$.$
	$.$
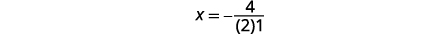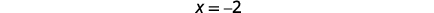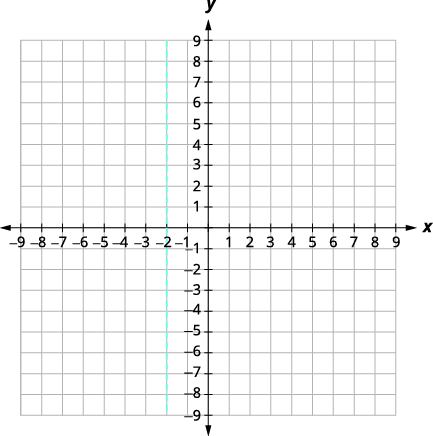
	معادلة محور التماثل هي\ (x=-2).
	$.$
قمة الرأس على الخط$x=-2$.
ابحث عن$f(x)$ متى$x=-2$.	$.$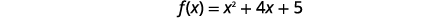
	$.$
	$.$
	$.$
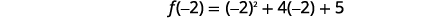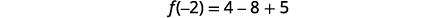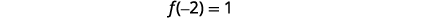	قمة الرأس هي$(-2,1)$.
	$.$
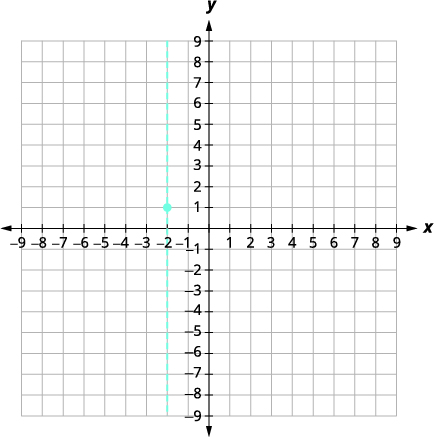يحدث$y$ التقاطع عند حدوث ذلك$x=0$.	$.$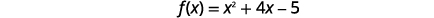
ابحث$f(0)$.	$.$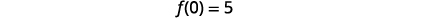
قم بالتبسيط.	$.$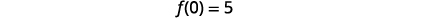
	$y$الاعتراض الإلكتروني هو$(0,5)$.
النقطة$(-4,5)$ هي وحدتان على يسار خط التماثل. النقطة إلى الوحدات الموجودة على يمين خط التماثل هي\ (0,5)\.	$.$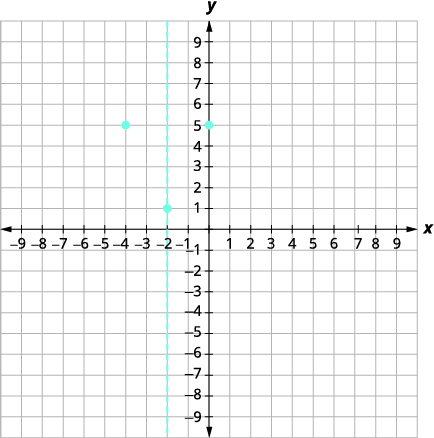
	النقطة المتماثلة في$y$ التقاطع السيني هي$(-4,5)$.
يحدث$x$ التقاطع عند حدوث ذلك$f(x)=0$.	$.$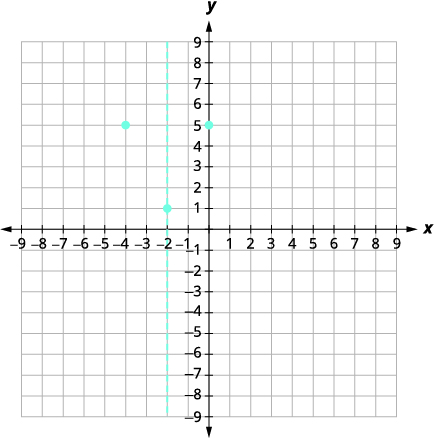
ابحث$f(x)=0$.	$.$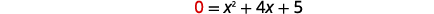
اختبر التمييز.
	$.$
	$.$
	$.$
	$.$
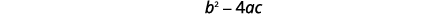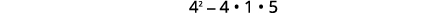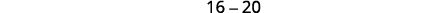نظرًا لأن قيمة التمييز سلبية، فلا يوجد حل حقيقي وبالتالي لا يوجد$x$ اعتراض.
قم بتوصيل النقاط لرسم القطع المكافئ. قد ترغب في اختيار نقطتين إضافيتين للحصول على دقة أكبر.	$.$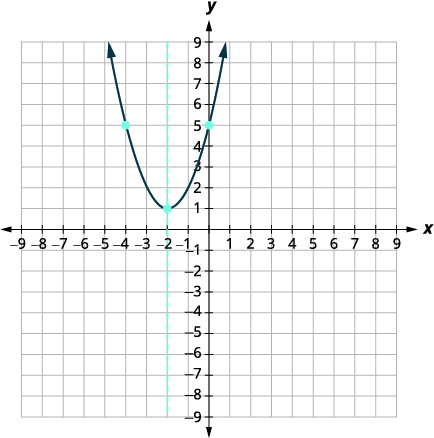

التمارين الرياضية$\PageIndex{15}$

رسم بياني$f(x)=x^{2}-2 x+3$ باستخدام خصائصه.

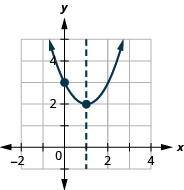
إجابة: $يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 2 إلى 4. يمتد المحور y للطائرة من سالب 1 إلى 5. يحتوي المكافئ على قمة عند (1، 2). يتم رسم التقاطع y (0، 3) كما هو خط التماثل، x يساوي 1.$

التمارين الرياضية$\PageIndex{16}$

رسم بياني$f(x)=-3x^{2}-6 x-4$ باستخدام خصائصه.

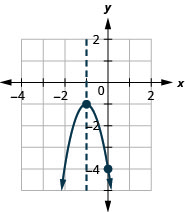
إجابة: $يوضِّح هذا الشكل القطع المكافئ المتجه نحو الأسفل مُبيَّنًا بيانيًّا على مستوى الإحداثيات x y. يمتد المحور السيني للطائرة من سالب 4 إلى 2. يمتد المحور y للطائرة من سالب 5 إلى 1. يحتوي المكافئ على قمة عند (سالب 1، سالب 2). يتم رسم التقاطع y (0، سالب 4) كما هو خط التماثل، x يساوي سالب 1.$

العثور على$y$ التقاطع من خلال البحث$f(0)$ أمر سهل، أليس كذلك؟ نحتاج أحيانًا إلى استخدام الصيغة التربيعية للعثور على$x$ نقاط التقاطع.

مثال$\PageIndex{9}$

رسم بياني$f(x)=2 x^{2}-4 x-3$ باستخدام خصائصه.

الحل:

	$.$
منذ$a$ ذلك الحين$2$، ينفتح المكافئ لأعلى.	$.$
للعثور على معادلة محور التماثل، استخدم$x=-\frac{b}{2 a}$.	$x=-\frac{b}{2 a}$
	$x=-\frac{-4}{2 \cdot 2}$
	$x=1$
	معادلة محور التماثل هي$x=1$.
قمة الرأس على الخط$x=1$.	$f(x)=2 x^{2}-4 x-3$
ابحث$f(1)$.	$.$
	$f(1)=2-4-3$
	\ (\ f (1) =-5)
	قمة الرأس هي$(1,-5)$.
يحدث$y$ التقاطع عند حدوث ذلك$x=0$.	$f(x)=2 x^{2}-4 x-3$
ابحث$f(0)$.	$.$
قم بالتبسيط.	$f(0)=-3$
	$y$الاعتراض الإلكتروني هو$(0,-3)$.
النقطة$(0,-3)$ هي وحدة واحدة على يسار خط التماثل.	النقطة المتماثلة في$y$ التقاطع السيني هي$(2,-3)$
النقطة التي تقع الوحدة الواحدة على يمين خط التماثل هي$(2,3)$.
يحدث$x$ التقاطع عند حدوث ذلك$y=0$.	$f(x)=2 x^{2}-4 x-3$
ابحث$f(x)=0$.	$.$
استخدم الصيغة التربيعية.	$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
استبدل قيم$a,b$ و$c$.	$x=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(2)(3)}}{2(2)}$
قم بالتبسيط.	$x=\frac{-4 \pm \sqrt{16+24}}{4}$
قم بالتبسيط داخل الراديكالي.	$x=\frac{4 \pm \sqrt{40}}{4}$
تبسيط الراديكالية.	$x=\frac{4 \pm 2 \sqrt{10}}{4}$
عامل عامل GCF.	$x=\frac{2(2 \pm \sqrt{10})}{4}$
قم بإزالة العوامل المشتركة.	$x=\frac{2 \pm \sqrt{10}}{2}$
اكتب كمعادلتين.	$x=\frac{2+\sqrt{10}}{2}, \quad x=\frac{2-\sqrt{10}}{2}$
قم بتقريب القيم.	$x \approx 2.5, \quad x \approx-0.6$
	القيم التقريبية لـ$x$ -Intercepts هي$(2.5,0)$ و$(-0.6,0)$.
قم برسم القطع المكافئ باستخدام النقاط التي تم العثور عليها.	$.$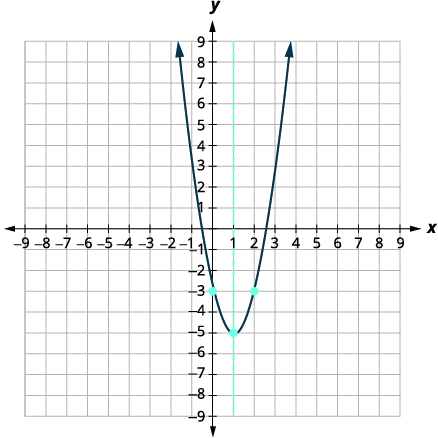

التمارين الرياضية$\PageIndex{17}$

رسم بياني$f(x)=5 x^{2}+10 x+3$ باستخدام خصائصه.

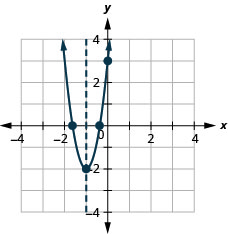
إجابة: $يوضِّح هذا الشكل المكافئ ذو الفتحة الصاعدة بيانيًّا على المستوى الإحداثي x y. يمتد المحور السيني للطائرة من سالب 4 إلى 4. يمتد المحور y للطائرة من سالب 4 إلى 4. محور التماثل، x يساوي سالب 1، تم رسمه بيانيًا كخط متقطع. يحتوي المكافئ على قمة عند (سالب 1، سالب 2). التقاطع y للقطع المكافئ هو النقطة (0، 3). تكون تقاطعات الأشعة السينية للقطع المكافئ تقريبًا (سالب 1.6، 0) و (سالب 0.4، 0).$

التمارين الرياضية$\PageIndex{18}$

رسم بياني$f(x)=-3 x^{2}-6 x+5$ باستخدام خصائصه.

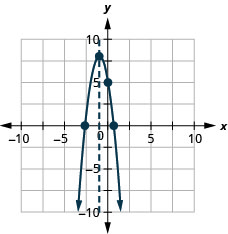
إجابة: $يوضِّح هذا الشكل القطع المكافئ المتجه نحو الأسفل مُبيَّنًا بيانيًّا على مستوى الإحداثيات x y. يمتد المحور السيني للطائرة من سالب 10 إلى 10. يمتد المحور y للطائرة من سالب 10 إلى 10. محور التماثل، x يساوي سالب 1، تم رسمه بيانيًا كخط متقطع. يحتوي المكافئ على قمة عند (سالب 1، 8). التقاطع y للقطع المكافئ هو النقطة (0، 5). تكون تقاطعات الأشعة السينية للقطع المكافئ تقريبًا (سالبة 2.6، 0) و (0.6، 0).$

حل الحد الأقصى والحد الأدنى من التطبيقات

إن معرفة أن رأس المكافئ هو أدنى أو أعلى نقطة في المكافئ يمنحنا طريقة سهلة لتحديد القيمة الدنيا أو القصوى للدالة التربيعية. الإحداثي y للرأس هو الحد الأدنى لقيمة المكافئ الذي يفتح لأعلى. إنها القيمة القصوى للقطع المكافئ الذي يفتح لأسفل. انظر الشكل 9.6.124.

يوضح هذا الشكل رسمين بيانيين جنبًا إلى جنب يُظهر الرسم البياني الأيسر المكافئ الافتتاحي الهابط المرسوم في المستوى x y. يشير السهم إلى قمة الرأس مع الحد الأقصى للتسمية. يُظهر الرسم البياني الأيمن المكافئ الافتتاحي التصاعدي المرسوم في المستوى x y. يشير السهم إلى قمة الرأس مع الحد الأدنى للتسمية. — الشكل 9.6.124

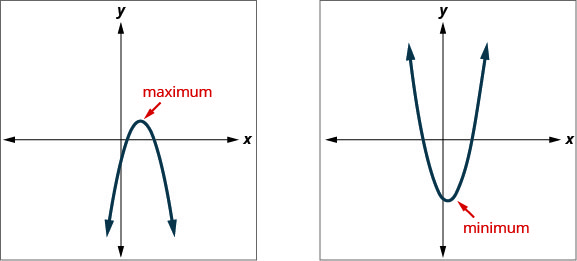
القيم الدنيا أو القصوى للدالة التربيعية

الإحداثي y لرأس الرسم البياني للدالة التربيعية هو

الحد الأدنى لقيمة المعادلة التربيعية في حالة فتح المكافئ لأعلى.
القيمة القصوى للمعادلة التربيعية إذا تم فتح القطع المكافئ لأسفل.

مثال$\PageIndex{10}$

ابحث عن القيمة الدنيا أو القصوى للدالة التربيعية$f(x)=x^{2}+2 x-8$.

الحل:

	$f(x)=x^{2}+2 x-8$
نظرًا$a$ لأنه إيجابي، فإن القطع المكافئ يفتح لأعلى. المعادلة التربيعية لها حد أدنى.
أوجد معادلة محور التماثل.	$x=-\frac{b}{2 a}$
	$x=-\frac{2}{2 \times 1}$
	$x=-1$
	معادلة محور التماثل هي$x=-1$.
قمة الرأس على الخط$x=-1$.	$f(x)=x^{2}+2 x-8$
ابحث$f(-1)$.	$.$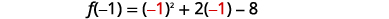
	$f(-1)=1-2-8$
	$f(-1)=-9$
	قمة الرأس هي$(-1,-9)$.
بما أن المكافئ له حد أدنى، فإن$y$ الإحداثي$y$ -للرأس هو الحد الأدنى لقيمة المعادلة التربيعية. الحد الأدنى لقيمة التربيعي هو$-9$ ويحدث عندما$x=-1$.
	$.$

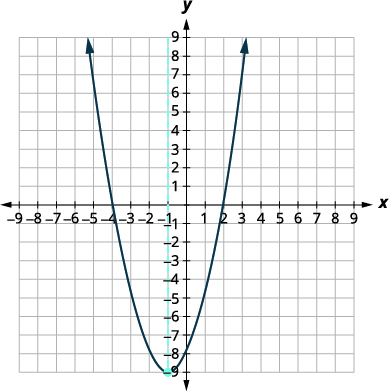اعرض الرسم البياني للتحقق من النتيجة.

التمارين الرياضية$\PageIndex{19}$

ابحث عن القيمة القصوى أو الدنيا للدالة التربيعية$f(x)=x^{2}-8 x+12$.

إجابة: الحد الأدنى لقيمة الدالة التربيعية هو$−4$ ويحدث عندما$x=4$.

التمارين الرياضية$\PageIndex{20}$

ابحث عن القيمة القصوى أو الدنيا للدالة التربيعية$f(x)=-4 x^{2}+16 x-11$.

إجابة: القيمة القصوى للدالة التربيعية هي$5$ وتحدث عندما$x=2$.

لقد استخدمنا الصيغة

$h(t)=-16 t^{2}+v_{0} t+h_{0}$

لحساب الارتفاع بالأقدام$h$، لجسم أُطلق لأعلى في الهواء بسرعة أولية$v_{0}$، بعد$t$ ثوانٍ.

هذه الصيغة عبارة عن دالة تربيعية، لذا فإن الرسم البياني الخاص بها عبارة عن مكافئ. من خلال حل إحداثيات قمة الرأس$(t,h)$، يمكننا العثور على المدة التي سيستغرقها الكائن للوصول إلى أقصى ارتفاع له. ثم يمكننا حساب الحد الأقصى للارتفاع.

مثال$\PageIndex{11}$

تُمثِّل المعادلة$h(t)=-16 t^{2}+176 t+4$ التربيعية ارتفاع الكرة الطائرة التي تضرب بشكل مستقيم لأعلى بسرعة$176$ القدمين في الثانية من ارتفاع$4$ القدمين.

ما عدد الثواني التي ستستغرقها الكرة الطائرة للوصول إلى أقصى ارتفاع لها؟
ابحث عن أقصى ارتفاع للكرة الطائرة.

الحل:

$h(t)=-16 t^{2}+176 t+4$

نظرًا$a$ لأنه سلبي، فإن المكافئ يفتح لأسفل. الدالة التربيعية لها حد أقصى.

أ. أوجد معادلة محور التماثل.

$\begin{array}{l}{t=-\frac{b}{2 a}} \\ {t=-\frac{176}{2(-16)}} \\ {t=5.5}\end{array}$

معادلة محور التماثل هي$t=5.5$.

قمة الرأس على الخط$t=5.5$.

يحدث الحد الأقصى عند$t=5.5$ الثواني.

ب. ابحث$h(5.5)$.

$\begin{array}{l}{h(t)=-16 t^{2}+176 t+4} \\ {h(t)=-16(5.5)^{2}+176(5.5)+4}\end{array}$

استخدم الآلة الحاسبة للتبسيط.

$h(t)=488$

قمة الرأس هي$(5.5,488)$.

نظرًا لأن المكافئ له حد أقصى، فإن$h$ الإحداثي -للرأس هو القيمة القصوى للدالة التربيعية.

القيمة القصوى للتربيعي هي$488$ القدمين وتحدث عند$t=5.5$ الثواني.

بعد$5.5$ ثوانٍ، ستصل الكرة الطائرة إلى أقصى ارتفاع$488$ للأقدام.

التمارين الرياضية$\PageIndex{21}$

حل، مع تقريب الإجابات لأقرب جزء من عشرة.

$h(t)=-16 t^{2}+128 t+32$تُستخدم الدالة التربيعية لإيجاد ارتفاع حجر يُلقى لأعلى من ارتفاع$32$ القدمين بمعدل$128$ قدم/ثانية. كم من الوقت سيستغرق الحجر للوصول إلى أقصى ارتفاع له؟ ما هو الحد الأقصى للارتفاع؟

إجابة: سوف يستغرق الأمر$4$ ثوانٍ حتى يصل الحجر إلى أقصى ارتفاع$288$ للقدمين.

التمارين الرياضية$\PageIndex{22}$

تم تصميم مسار صاروخ لعبة يتم إلقاؤه لأعلى من الأرض بمعدل$208$ قدم/ثانية بواسطة الدالة التربيعية لـ$h(t)=-16 t^{2}+208 t$. متى سيصل الصاروخ إلى أقصى ارتفاع له؟ ماذا سيكون الحد الأقصى للارتفاع؟

إجابة: سوف يستغرق الأمر$6.5$ ثوانٍ حتى يصل الصاروخ إلى أقصى ارتفاع$676$ للأقدام.

المفاهيم الرئيسية

اتجاه بارابولا
- بالنسبة للرسم البياني للدالة التربيعية$f(x)=a x^{2}+b x+c$، إذا
  - $a>0$، يفتح المكافئ لأعلى.
  - $a<0$، يفتح المكافئ لأسفل.
محور التماثل وربع رأس المكافئ الرسم البياني للدالة$f(x)=a x^{2}+b x+c$ هو المكافئ حيث:
- محور التماثل هو الخط العمودي$x=-\frac{b}{2 a}$.
- قمة الرأس هي نقطة على محور التماثل، لذا فإن$x$ إحداثياتها هي$-\frac{b}{2 a}$.
- يتم العثور على$y$ الإحداثيات -للرأس عن طريق الاستبدال$x=-\frac{b}{2 a}$ في المعادلة التربيعية.
ابحث عن القطع المعترضة لبارابولا
- للعثور على الأجزاء المقطوعة للقطع المكافئ الذي تتمثل وظيفته في$f(x)=a x^{2}+b x+c$:
  - $y$-اعتراض
    - دعونا نحل المشكلة$x=0$ ونحلها$f(x)$.
  - $x$- عمليات الاعتراض
    - دعونا$f(x)=0$ نحل المشكلة$x$.
كيفية رسم دالة تربيعية بيانيًا باستخدام الخصائص.
1. حدِّد ما إذا كان القطع المكافئ ينفتح لأعلى أم لأسفل.
2. أوجد معادلة محور التماثل.
3. ابحث عن قمة الرأس.
4. ابحث$y$ عن التقاطع. ابحث عن النقطة المتماثلة للجزء الصادي عبر محور التماثل.
5. ابحث عن$x$ -Intercepts. ابحث عن نقاط إضافية إذا لزم الأمر.
6. رسم بياني القطع المكافئ.
القيم الدنيا أو القصوى للمعادلة التربيعية
- $y$الإحداثي -لرأس الرسم البياني للمعادلة التربيعية هو
- الحد الأدنى لقيمة المعادلة التربيعية في حالة فتح المكافئ لأعلى.
- القيمة القصوى للمعادلة التربيعية إذا تم فتح القطع المكافئ لأسفل.

مسرد المصطلحات

دالة تربيعية: الدالة التربيعية$a, b$، حيث$c$ والأعداد الحقيقية و$a≠0$، هي دالة في الشكل$f(x)=ax^{2}+bx+c$.

	$.$
محور التماثل هو الخط العمودي\(x=-\frac{b}{2 a}\).
استبدل القيم\(a,b\) في المعادلة.	\(x=-\frac{-6}{2 \cdot 3}\)
قم بالتبسيط.	\(x=1\)
	محور التماثل هو الخط\(x=1\).

	\(f(x)=3 x^{2}-6 x+2\)
قمة الرأس هي نقطة على خط التماثل، لذلك ستكون\(x\) إحداثياتها\(x=1\). ابحث\(f(1)\).	$.$
قم بالتبسيط.	$.$
والنتيجة هي\(y\) الإحداثيات -conditate.	\(f(1)=-1\)
	قمة الرأس هي\((1,-1)\).

	\(f(x)=x^{2}+4 x+3\)
دعونا\(f(x)=0\).	\(\color{red}0\color{black}=x^{2}+4 x+3\)
عامل.	\(0=(x+1)(x+3)\)
استخدم خاصية المنتج الصفري.	\(x+1=0 \quad x+3=0\)
حل.	\(x=-1 \quad x=-3\)
	\(x\)عمليات الاعتراض - هي\((-1,0)\) و\((-3,0)\).

	\(f(x)=-x^{2}+4 x+3\)
دعونا\(f(x)=0\).	\(\color{red}0 \color{black}=-x^{2}+4 x+3\)
لا تؤثر هذه الدرجة التربيعية، لذلك نستخدم الصيغة التربيعية.	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
\(a=-1, b=4, c=3\)	\(x=\frac{-4 \pm \sqrt{4^{2}-4(-1)(3)}}{2(-1)}\)
قم بالتبسيط.	\(x=\frac{-4 \pm \sqrt{28}}{-2}\)
	\(x=\frac{-4 \pm 2 \sqrt{7}}{-2}\)
	\(x=\frac{-2(2 \pm \sqrt{7})}{-2}\)
	\(x=2 \pm \sqrt{7}\)
	\(x\)عمليات الاعتراض - هي\((2+\sqrt{7}, 0)\) و\((2-\sqrt{7}, 0)\).

للعثور على النقطة\(y\) -Intercept\(x=0\)، دعنا نحلها\(f(x)\).	\(f(x)=x^{2}-2 x-8\)
	\(f(0)=\color{red}0\color{black}^{2}-2 \cdot \color{red}0 \color{black}-8\)
	\(f(0)=-8\)
	متى\(x=0\)، إذن\(f(0)=-8\). \(y\)الاعتراض -هو النقطة\((0,-8)\).
للعثور على النقطة\(x\) -Intercept\(f(x)=0\)، دعنا نحلها\(x\).	\(f(x)=x^{2}-2 x-8\)
	\(0=x^{2}-2 x-8\)
حل عن طريق التخصيم	\(0=(x-4)(x+2)\)
	\(0=x-4 \quad 0=x+2\)
	\(4=x \quad-2=x\)
	متى\(f(x)=0\)، ثم\(x=4\) أو\(x=-2\). نقاط\(x\) الاعتراض -هي النقاط\((4,0)\) و\((-2,0)\).

تعريف\(\PageIndex{1}\)

مثال\(\PageIndex{1}\)

التمارين الرياضية\(\PageIndex{1}\)

التمارين الرياضية\(\PageIndex{2}\)

تعريف\(\PageIndex{2}\)

مثال\(\PageIndex{2}\)

التمارين الرياضية\(\PageIndex{3}\)

التمارين الرياضية\(\PageIndex{4}\)

مثال\(\PageIndex{3}\)

التمارين الرياضية\(\PageIndex{5}\)

التمارين الرياضية\(\PageIndex{6}\)

مثال\(\PageIndex{4}\)

التمارين الرياضية\(\PageIndex{7}\)

التمارين الرياضية\(\PageIndex{8}\)

مثال\(\PageIndex{5}\)

التمارين الرياضية\(\PageIndex{9}\)

التمارين الرياضية\(\PageIndex{10}\)

مثال\(\PageIndex{6}\) How to Graph a Quadratic Function Using Properties

التمارين الرياضية\(\PageIndex{11}\)

التمارين الرياضية\(\PageIndex{12}\)

مثال\(\PageIndex{7}\)

التمارين الرياضية\(\PageIndex{13}\)

التمارين الرياضية\(\PageIndex{14}\)

مثال\(\PageIndex{8}\)

التمارين الرياضية\(\PageIndex{15}\)

التمارين الرياضية\(\PageIndex{16}\)

مثال\(\PageIndex{9}\)

التمارين الرياضية\(\PageIndex{17}\)

التمارين الرياضية\(\PageIndex{18}\)

مثال\(\PageIndex{10}\)

التمارين الرياضية\(\PageIndex{19}\)

التمارين الرياضية\(\PageIndex{20}\)

مثال\(\PageIndex{11}\)

التمارين الرياضية\(\PageIndex{21}\)

التمارين الرياضية\(\PageIndex{22}\)

اختر قيمًا عددية لـ\(x\)، واستبدلها بالمعادلة وقم بتبسيط عملية البحث\(f(x)\). سجل قيم الأزواج المرتبة في المخطط.	$.$
ارسم النقاط، ثم قم بتوصيلها بمنحنى سلس. ستكون النتيجة هي الرسم البياني للدالة\(f(x)=x^{2}-1\).	$.$

	$.$
للعثور على النقطة\(y\) -Intercept\(x=0\)، دعنا نحلها\(f(x)\).	$.$
	$.$
	متى\(x=0\)، إذن\(f(0)=4\). \(y\)الاعتراض -هو النقطة\((0,4)\).
للعثور على النقطة\(x\) -Intercept\(f(x)=0\)، دعنا نحلها\(x\).	$.$
	$.$
ابحث عن قيمة التمييز للتنبؤ بعدد الحلول وهو أيضًا عدد\(x\) عمليات الاعتراض.
\(\begin{array}{c}{b^{2}-4 a c} \\ {1^{2}-4 \cdot 5 \cdot 4} \\ {1-80} \\ {-79}\end{array}\)
	نظرًا لأن قيمة التمييز سالبة، فلا يوجد حل حقيقي للمعادلة. لا توجد\(x\) عمليات اعتراض.

الخطوة 1: حدد ما إذا كان القطع المكافئ يفتح لأعلى أو لأسفل.	انظر\(a\) في المعادلة\(f(x)=x^{2}-6x+8\) نظرًا\(a\) لأنه إيجابي، فإن القطع المكافئ يفتح لأعلى.	\(f(x)=x^{2}-6x+8\) \(\color{red}{a=1, b=-6, c=8}\) يفتح المكافئ لأعلى.
الخطوة 2: ابحث عن محور التماثل.	\(f(x)=x^{2}-6x+8\) محور التماثل هو الخط\(x=-\frac{b}{2 a}\).	محور التماثل \(x=-\frac{b}{2 a}\) \(x=-\frac{(-6)}{2 \cdot 1}\) \(x=3\) محور التماثل هو الخط\(x=3\).
الخطوة 3: ابحث عن قمة الرأس.	تقع قمة الرأس على محور التماثل. \(x=3\)استبدل الوظيفة.	فيرتكس \(f(x)=x^{2}-6x+8\) \(f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8\) \(f(3)=-1\) قمة الرأس هي\((3,-1)\).
الخطوة 4: ابحث\(y\) عن التقاطع. ابحث عن النقطة المتماثلة للجزء\(y\) المقطوع عبر محور التماثل.	نجد\(f(0)\). نستخدم محور التماثل لإيجاد نقطة متماثلة للجزء\(y\) المقطوع. \(y\)التقاطع -هو\(3\) الوحدات اليسرى من محور التماثل،\(x=3\). \(3\)تحتوي الوحدات النقطية الموجودة على يمين محور التماثل على\(x=6\).	\(y\)-اعتراض \(f(x)=x^{2}-6 x+8\) \(f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8\) \(f(0)=8\) \(y\)الاعتراض الإلكتروني هو\((0,8)\). نقطة متماثلة إلى\(y\) نقطة التقاطع: النقطة هي\((6,8)\).
الخطوة 5: ابحث عن\(x\) -Intercepts. ابحث عن نقاط إضافية إذا لزم الأمر.	نحن نحل\(f(x)=0\). يمكننا حل هذه المعادلة التربيعية عن طريق التحليل.	\(x\)- عمليات الاعتراض \(f(x)=x^{2}-6 x+8\) \(\color{red}{0}\color{black}{=}x^{2}-6x+8\) \(\color{red}{0}\color{black}{=}(x-2)(x-4)\) \(x=2 or x=4\) \(x\)عمليات الاعتراض - هي\((2,0)\) و\((4,0)\).
الخطوة 6: رسم القطع المكافئ.	نحن نرسم قمة الرأس والاعتراض والنقطة المتماثلة للنقطة المقابلة لـ\(y\) -Intercept. نقوم بتوصيل هذه\(5\) النقاط لرسم القطع المكافئ.	$لقطة شاشة (1) .png$

	$.$
منذ\(a\) ذلك الحين\(-1\)، ينفتح المكافئ لأسفل.
	$.$
للعثور على معادلة محور التماثل، استخدم\(x=-\frac{b}{2 a}\).	\(x=-\frac{b}{2 a}\)
	\(x=-\frac{6}{2(-1)}\)
	\(x=3\)
	محور التماثل هو\(x=3\). قمة الرأس على الخط\(x=3\).
	$.$
ابحث\(f(3)\).	\(f(x)=-x^{2}+6 x-9\)
	$.$
	\(f(3)=-9+18-9\)
	\(f(3)=0\)
	قمة الرأس هي\((3,0)\).
	$.$
يحدث\(y\) التقاطع عند حدوث ذلك\(x=0\). ابحث\(f(0)\).	\(f(x)=-x^{2}+6 x-9\)
بديل\(x=0\).	$.$
قم بالتبسيط.	\(f(0)=-9\)
النقطة\((0,-9)\) هي ثلاث وحدات على يسار خط التماثل. النقطة الثلاث وحدات على يمين خط التماثل هي\((6,-9)\).	$.$
	النقطة المتماثلة في\(y\) التقاطع السيني هي\((6,-9)\)
يحدث\(x\) التقاطع عند حدوث ذلك\(f(x)=0\).	$.$
ابحث\(f(x)=0\).	$.$
عامل عامل GCF.	$.$
عامل الثلاثي.	$.$
حل لـ\(x\).	$.$
قم بتوصيل النقاط لرسم القطع المكافئ.	$.$

	$.$
منذ\(a\) ذلك الحين\(2\)، ينفتح المكافئ لأعلى.	$.$
للعثور على معادلة محور التماثل، استخدم\(x=-\frac{b}{2 a}\).	\(x=-\frac{b}{2 a}\)
	\(x=-\frac{-4}{2 \cdot 2}\)
	\(x=1\)
	معادلة محور التماثل هي\(x=1\).
قمة الرأس على الخط\(x=1\).	\(f(x)=2 x^{2}-4 x-3\)
ابحث\(f(1)\).	$.$
	\(f(1)=2-4-3\)
	\ (\ f (1) =-5)
	قمة الرأس هي\((1,-5)\).
يحدث\(y\) التقاطع عند حدوث ذلك\(x=0\).	\(f(x)=2 x^{2}-4 x-3\)
ابحث\(f(0)\).	$.$
قم بالتبسيط.	\(f(0)=-3\)
	\(y\)الاعتراض الإلكتروني هو\((0,-3)\).
النقطة\((0,-3)\) هي وحدة واحدة على يسار خط التماثل.	النقطة المتماثلة في\(y\) التقاطع السيني هي\((2,-3)\)
النقطة التي تقع الوحدة الواحدة على يمين خط التماثل هي\((2,3)\).
يحدث\(x\) التقاطع عند حدوث ذلك\(y=0\).	\(f(x)=2 x^{2}-4 x-3\)
ابحث\(f(x)=0\).	$.$
استخدم الصيغة التربيعية.	\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
استبدل قيم\(a,b\) و\(c\).	\(x=\frac{-(-4) \pm \sqrt{(-4)^{2}-4(2)(3)}}{2(2)}\)
قم بالتبسيط.	\(x=\frac{-4 \pm \sqrt{16+24}}{4}\)
قم بالتبسيط داخل الراديكالي.	\(x=\frac{4 \pm \sqrt{40}}{4}\)
تبسيط الراديكالية.	\(x=\frac{4 \pm 2 \sqrt{10}}{4}\)
عامل عامل GCF.	\(x=\frac{2(2 \pm \sqrt{10})}{4}\)
قم بإزالة العوامل المشتركة.	\(x=\frac{2 \pm \sqrt{10}}{2}\)
اكتب كمعادلتين.	\(x=\frac{2+\sqrt{10}}{2}, \quad x=\frac{2-\sqrt{10}}{2}\)
قم بتقريب القيم.	\(x \approx 2.5, \quad x \approx-0.6\)
	القيم التقريبية لـ\(x\) -Intercepts هي\((2.5,0)\) و\((-0.6,0)\).
قم برسم القطع المكافئ باستخدام النقاط التي تم العثور عليها.	$.$

	\(f(x)=x^{2}+2 x-8\)
نظرًا\(a\) لأنه إيجابي، فإن القطع المكافئ يفتح لأعلى. المعادلة التربيعية لها حد أدنى.
أوجد معادلة محور التماثل.	\(x=-\frac{b}{2 a}\)
	\(x=-\frac{2}{2 \times 1}\)
	\(x=-1\)
	معادلة محور التماثل هي\(x=-1\).
قمة الرأس على الخط\(x=-1\).	\(f(x)=x^{2}+2 x-8\)
ابحث\(f(-1)\).	$.$
	\(f(-1)=1-2-8\)
	\(f(-1)=-9\)
	قمة الرأس هي\((-1,-9)\).
بما أن المكافئ له حد أدنى، فإن\(y\) الإحداثي\(y\) -للرأس هو الحد الأدنى لقيمة المعادلة التربيعية. الحد الأدنى لقيمة التربيعي هو\(-9\) ويحدث عندما\(x=-1\).
	$.$