Skip to main content
Global

الفصل 9 تمارين المراجعة

  1. Last updated
  2. Save as PDF
  • Page ID
    201680

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    تمارين مراجعة الفصل

    حل المعادلات التربيعية باستخدام خاصية الجذر التربيعي

    التمارين\(\PageIndex{1}\) Solve Quadratic Equations of the Form \(ax^{2}=k\) Using the Square Root Property

    في التمارين التالية، قم بالحل باستخدام خاصية الجذر التربيعي.

    1. \(y^{2}=144\)
    2. \(n^{2}-80=0\)
    3. \(4 a^{2}=100\)
    4. \(2 b^{2}=72\)
    5. \(r^{2}+32=0\)
    6. \(t^{2}+18=0\)
    7. \(\frac{2}{3} w^{2}-20=30\)
    8. \(5 c^{2}+3=19\)
    إجابة

    1. \(y=\pm 12\)

    3. \(a=\pm 5\)

    5. \(r=\pm 4 \sqrt{2} i\)

    7. \(w=\pm 5 \sqrt{3}\)

    التمارين\(\PageIndex{2}\) Solve Quadratic Equations of the Form \(a(x-h)^{2}=k\) Using the Square Root Property

    في التمارين التالية، قم بالحل باستخدام خاصية الجذر التربيعي.

    1. \((p-5)^{2}+3=19\)
    2. \((u+1)^{2}=45\)
    3. \(\left(x-\frac{1}{4}\right)^{2}=\frac{3}{16}\)
    4. \(\left(y-\frac{2}{3}\right)^{2}=\frac{2}{9}\)
    5. \((n-4)^{2}-50=150\)
    6. \((4 c-1)^{2}=-18\)
    7. \(n^{2}+10 n+25=12\)
    8. \(64 a^{2}+48 a+9=81\)
    إجابة

    1. \(p=-1,9\)

    3. \(x=\frac{1}{4} \pm \frac{\sqrt{3}}{4}\)

    5. \(n=4 \pm 10 \sqrt{2}\)

    7. \(n=-5 \pm 2 \sqrt{3}\)

    حل المعادلات التربيعية بإكمال المربع

    التمارين\(\PageIndex{3}\) Solve Quadratic Equations Using Completing the Square

    في التمارين التالية، أكمل المربع لتكوين مربع ثلاثي الحدود مثالي. ثم اكتب النتيجة في صورة مربع ذو حدين.

    1. \(x^{2}+22 x\)
    2. \(m^{2}-8 m\)
    3. \(a^{2}-3 a\)
    4. \(b^{2}+13 b\)
    إجابة

    1. \((x+11)^{2}\)

    3. \(\left(a-\frac{3}{2}\right)^{2}\)

    التمارين\(\PageIndex{4}\) Solve Quadratic Equations Using Completing the Square

    في التمارين التالية، قم بحل المشكلة بإكمال المربع.

    1. \(d^{2}+14 d=-13\)
    2. \(y^{2}-6 y=36\)
    3. \(m^{2}+6 m=-109\)
    4. \(t^{2}-12 t=-40\)
    5. \(v^{2}-14 v=-31\)
    6. \(w^{2}-20 w=100\)
    7. \(m^{2}+10 m-4=-13\)
    8. \(n^{2}-6 n+11=34\)
    9. \(a^{2}=3 a+8\)
    10. \(b^{2}=11 b-5\)
    11. \((u+8)(u+4)=14\)
    12. \((z-10)(z+2)=28\)
    إجابة

    1. \(d=-13,-1\)

    3. \(m=-3 \pm 10 i\)

    5. \(v=7 \pm 3 \sqrt{2}\)

    7. \(m=-9,-1\)

    9. \(a=\frac{3}{2} \pm \frac{\sqrt{41}}{2}\)

    11. \(u=-6 \pm 2 \sqrt{2}\)

    حل المعادلات التربيعية\(ax^{2}+bx+c=0\) للصورة بإكمال المربع

    التمارين\(\PageIndex{5}\) Solve Quadratic Equations of the Form \(ax^{2}+bx+c=0\) by Completing the Square

    في التمارين التالية، قم بحل المشكلة بإكمال المربع.

    1. \(3 p^{2}-18 p+15=15\)
    2. \(5 q^{2}+70 q+20=0\)
    3. \(4 y^{2}-6 y=4\)
    4. \(2 x^{2}+2 x=4\)
    5. \(3 c^{2}+2 c=9\)
    6. \(4 d^{2}-2 d=8\)
    7. \(2 x^{2}+6 x=-5\)
    8. \(2 x^{2}+4 x=-5\)
    إجابة

    1. \(p=0,6\)

    3. \(y=-\frac{1}{2}, 2\)

    5. \(c=-\frac{1}{3} \pm \frac{2 \sqrt{7}}{3}\)

    7. \(x=\frac{3}{2} \pm \frac{1}{2} i\)

    التمارين\(\PageIndex{6}\) Solve Quadratic Equations Using the Quadratic Formula

    في التمارين التالية، قم بالحل باستخدام الصيغة التربيعية.

    1. \(4 x^{2}-5 x+1=0\)
    2. \(7 y^{2}+4 y-3=0\)
    3. \(r^{2}-r-42=0\)
    4. \(t^{2}+13 t+22=0\)
    5. \(4 v^{2}+v-5=0\)
    6. \(2 w^{2}+9 w+2=0\)
    7. \(3 m^{2}+8 m+2=0\)
    8. \(5 n^{2}+2 n-1=0\)
    9. \(6 a^{2}-5 a+2=0\)
    10. \(4 b^{2}-b+8=0\)
    11. \(u(u-10)+3=0\)
    12. \(5 z(z-2)=3\)
    13. \(\frac{1}{8} p^{2}-\frac{1}{5} p=-\frac{1}{20}\)
    14. \(\frac{2}{5} q^{2}+\frac{3}{10} q=\frac{1}{10}\)
    15. \(4 c^{2}+4 c+1=0\)
    16. \(9 d^{2}-12 d=-4\)
    إجابة

    1. \(x=\frac{1}{4}, 1\)

    3. \(r=-6,7\)

    5. \(v=\frac{-1 \pm \sqrt{21}}{8}\)

    7. \(m=\frac{-4 \pm \sqrt{10}}{3}\)

    9. \(a=\frac{5}{12} \pm \frac{\sqrt{23}}{12} i\)

    11. \(u=5 \pm \sqrt{21}\)

    13. \(p=\frac{4 \pm \sqrt{5}}{5}\)

    15. \(c=-\frac{1}{2}\)

    التمارين\(\PageIndex{7}\) Use the Discriminant to Predict the Number of Solutions of a Quadratic Equation

    في التمارين التالية، حدد عدد الحلول لكل معادلة تربيعية.

      1. \(9 x^{2}-6 x+1=0\)
      2. \(3 y^{2}-8 y+1=0\)
      3. \(7 m^{2}+12 m+4=0\)
      4. \(5 n^{2}-n+1=0\)
      1. \(5 x^{2}-7 x-8=0\)
      2. \(7 x^{2}-10 x+5=0\)
      3. \(25 x^{2}-90 x+81=0\)
      4. \(15 x^{2}-8 x+4=0\)
    إجابة

    1.

    1. \(1\)
    2. \(2\)
    3. \(2\)
    4. \(2\)
    التمارين\(\PageIndex{8}\) Identify the Most Appropriate Method to Use to Solve a Quadratic Equation

    في التمارين التالية، حدد الطريقة الأنسب (التحليل أو الجذر التربيعي أو الصيغة التربيعية) لاستخدامها في حل كل معادلة تربيعية. لا تحل.

      1. \(16 r^{2}-8 r+1=0\)
      2. \(5 t^{2}-8 t+3=9\)
      3. \(3(c+2)^{2}=15\)
      1. \(4 d^{2}+10 d-5=21\)
      2. \(25 x^{2}-60 x+36=0\)
      3. \(6(5 v-7)^{2}=150\)
    إجابة

    1.

    1. عامل
    2. صيغة تربيعية
    3. الجذر التربيعي

    حل المعادلات في الصورة التربيعية

    التمارين\(\PageIndex{9}\) Solve Equations in Quadratic Form

    في التمارين التالية، قم بحل.

    1. \(x^{4}-14 x^{2}+24=0\)
    2. \(x^{4}+4 x^{2}-32=0\)
    3. \(4 x^{4}-5 x^{2}+1=0\)
    4. \((2 y+3)^{2}+3(2 y+3)-28=0\)
    5. \(x+3 \sqrt{x}-28=0\)
    6. \(6 x+5 \sqrt{x}-6=0\)
    7. \(x^{\frac{2}{3}}-10 x^{\frac{1}{3}}+24=0\)
    8. \(x+7 x^{\frac{1}{2}}+6=0\)
    9. \(8 x^{-2}-2 x^{-1}-3=0\)
    إجابة

    1. \(x=\pm \sqrt{2}, x=\pm 2 \sqrt{3}\)

    3. \(x=\pm 1, x=\pm \frac{1}{2}\)

    5. \(x=16\)

    7. \(x=64, x=216\)

    9. \(x=-2, x=\frac{4}{3}\)

    حل تطبيقات المعادلات التربيعية

    التمارين\(\PageIndex{10}\) Solve Applications Modeled by Quadratic Equations

    في التمارين التالية، قم بالحل باستخدام طريقة التحليل أو مبدأ الجذر التربيعي أو الصيغة التربيعية. قرِّب إجاباتك لأقرب جزء من عشرة، إذا لزم الأمر.

    1. ابحث عن رقمين فرديين متتاليين يكون منتجهما\(323\).
    2. ابحث عن رقمين زوجيين متتاليين يكون منتجهما\(624\).
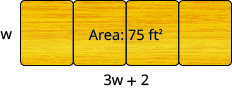
    3. تبلغ مساحة البانر الثلاثي السنتيمترات\(351\) المربعة. يبلغ طول القاعدة سنتيمترين أطول من أربعة أضعاف الارتفاع. أوجد ارتفاع القاعدة وطولها.
    4. قام جوليوس ببناء علبة عرض مثلثة لمجموعة العملات الخاصة به. يقل ارتفاع علبة العرض بست بوصات عن ضعف عرض القاعدة. مساحة الجزء الخلفي من العلبة هي بوصة\(70\) مربعة. ابحث عن ارتفاع وعرض العلبة.
    5. يتم استخدام فسيفساء البلاط على شكل مثلث قائم الزاوية كزاوية لمسار مستطيل. وتر الفسيفساء هو\(5\) القدمين. يبلغ طول أحد جانبي الفسيفساء ضعف طول الجانب الآخر. ما أطوال الأضلاع؟ قرِّب إلى أقرب جزء من عشرة.

    يظهر المستطيل على أنه مثلث قائم الزاوية. يبلغ طول وتر المثلث 5 أقدام، والساق الأطول مرتين ثانية والساق الأقصر هي s.
    الشكل 9-هاء-1

    6. قطعة مستطيلة من الخشب الرقائقي لها قطر يزيد بمقدار قدمين عن العرض. طول الخشب الرقائقي هو ضعف العرض. ما طول قطر الخشب الرقائقي؟ قرِّب إلى أقرب جزء من عشرة.

    7. تبلغ مساحة الممر الأمامي من الشارع إلى منزل بام قدمًا\(250\) مربعًا. طوله أقل مرتين من أربعة أضعاف عرضه. أوجد طول الرصيف وعرضه. قرِّب إلى أقرب جزء من عشرة.

    8. بالنسبة لحفل تخرج صوفيا، سيتم ترتيب عدة طاولات من نفس العرض من البداية إلى النهاية لتوفير طاولة تقديم بمساحة إجمالية قدرها قدم\(75\) مربع. سيكون الطول الإجمالي للجداول أكثر من ثلاثة أضعاف العرض. ابحث عن طول وعرض طاولة التقديم حتى تتمكن صوفيا من شراء مفرش المائدة بالحجم الصحيح. قرِّب الإجابة لأقرب جزء من عشرة.

    9. تُلقى كرة رأسيًّا في الهواء بسرعة\(160\) قدم/ثانية. استخدم الصيغة\(h=-16 t^{2}+v_{0} t\) لتحديد متى ستكون الكرة على\(384\) بعد أقدام من الأرض. قرِّب إلى أقرب جزء من عشرة.

    10. استقل الزوجان طائرة صغيرة في رحلة سريعة إلى بلد النبيذ لتناول عشاء رومانسي ثم عادوا إلى المنزل. حلقت الطائرة ما مجموعه\(5\) ساعات وكانت الرحلة في كل اتجاه\(360\) أميالًا. إذا كانت الطائرة تحلق\(150\) بسرعة ميل في الساعة، فما سرعة الرياح التي أثرت على الطائرة؟

    11. قام عزرا بالتجديف في النهر ثم عاد في وقت إجمالي من\(6\) الساعات. كانت الرحلة\(4\) أميالًا في كل اتجاه وكان التيار صعبًا. إذا قام روي بالتجديف بسرعة\(5\) ميل في الساعة، فما سرعة التيار؟

    12. يمكن أن يقوم اثنان من العمال المهرة بإصلاح المنزل في\(2\) غضون ساعات إذا عملوا معًا. يستغرق أحد الرجال\(3\) ساعات أكثر من الرجل الآخر لإنهاء المهمة بنفسه. كم من الوقت يستغرق كل عامل للقيام بإصلاح المنزل بشكل فردي؟

    إجابة

    2. رقمان زوجيان متتاليان\(624\) منتجهما هما\(24\)\(26\) و و\(−24\) و\(−26\).

    4. الارتفاع هو\(14\) بوصة والعرض هو\(10\) بوصة.

    6. طول القطر هو\(3.6\) القدمين.

    8. عرض طاولة التقديم هو\(4.7\) قدم وطولها\(16.1\) أقدام.

    يتم عرض أربعة جداول مرتبة من البداية إلى النهاية. تبلغ مساحتهما معًا 75 قدمًا. يقيس الجانب القصير w والجانب الطويل يقيس 3 مرات w زائد 2.
    الشكل 9-هاء-2

    10. كانت سرعة الرياح\(30\) ميلاً في الساعة.

    12. يستغرق أحد الرجال\(3\) ساعات والآخر\(6\) ساعات لإنهاء الإصلاح بمفرده.

    رسم بياني للدوال التربيعية باستخدام الخصائص

    التمارين\(\PageIndex{11}\) Recognize the Graph of a Quadratic Function

    في التمارين التالية، قم بالرسم البياني باستخدام نقطة التخطيط.

    1. رسم بياني\(y=x^{2}-2\)
    2. رسم بياني\(y=-x^{2}+3\)
    إجابة

    2.

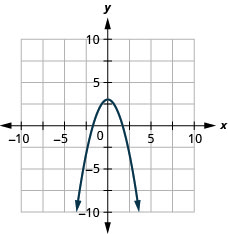
    يوضِّح هذا الشكل المكافئ المتجه نحو الأسفل على مستوى الإحداثيات x y. وله قمة (3، 0) ونقاط أخرى من (سالب 2، سالب 1) و (2، سالب 1).
    الشكل 9-هاء-3
    التمارين\(\PageIndex{12}\) Recognize the Graph of a Quadratic Function

    في التمارين التالية، حدد ما إذا كانت الأشكال المظللة التالية تنفتح لأعلى أم لأسفل.

      1. \(y=-3 x^{2}+3 x-1\)
      2. \(y=5 x^{2}+6 x+3\)
      1. \(y=x^{2}+8 x-1\)
      2. \(y=-4 x^{2}-7 x+1\)
    إجابة

    2.

    1. أعلى
    2. سقط
    التمارين\(\PageIndex{13}\) Find the Axis of Symmetry and Vertex of a Parabola

    في التمارين التالية، ابحث

    1. معادلة محور التماثل
    2. قمة الرأس
      1. \(y=-x^{2}+6 x+8\)
      2. \(y=2 x^{2}-8 x+1\)
    إجابة

    2. \(x=2\)؛\((2,-7)\)

    التمارين\(\PageIndex{14}\) Find the Intercepts of a Parabola

    في التمارين التالية، ابحث عن\(x\) - و\(y\) -Intercepts.

    1. \(y=x^{2}-4x+5\)
    2. \(y=x^{2}-8x+15\)
    3. \(y=x^{2}-4x+10\)
    4. \(y=-5x^{2}-30x-46\)
    5. \(y=16x^{2}-8x+1\)
    6. \(y=x^{2}+16x+64\)
    إجابة

    2. \(\begin{array}{l}{y :(0,15)} \\ {x :(3,0),(5,0)}\end{array}\)

    4. \(\begin{array}{l}{y :(0,-46)} \\ {x : \text { none }}\end{array}\)

    6. \(\begin{array}{l}{y :(0,-64)} \\ {x :(-8,0)}\end{array}\)

    رسم بياني للدوال التربيعية باستخدام الخصائص

    التمارين\(\PageIndex{15}\) Graph Quadratic Functions Using Properties

    في التمارين التالية، قم بالرسم البياني باستخدام خصائصه.

    1. \(y=x^{2}+8 x+15\)
    2. \(y=x^{2}-2 x-3\)
    3. \(y=-x^{2}+8 x-16\)
    4. \(y=4 x^{2}-4 x+1\)
    5. \(y=x^{2}+6 x+13\)
    6. \(y=-2 x^{2}-8 x-12\)
    إجابة

    2.

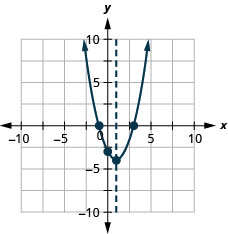
    يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على المستوى الإحداثي x y. يبلغ طول قمته (1، سالب 4) وقطعه الصادي (0، سالب 3).
    الشكل 9-هاء-4

    4.

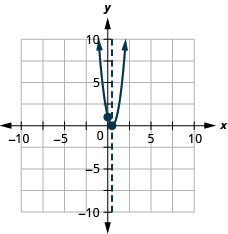
    يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على المستوى الإحداثي x y. يبلغ طول قمته (نصف واحد، 0) وقطعه الصادي (0، 1).
    الشكل 9-هاء-5

    6.

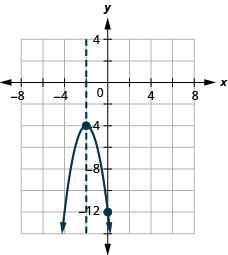
    يوضِّح هذا الشكل المكافئ المتجه نحو الأسفل على مستوى الإحداثيات x y. يبلغ طول قمته (سالب 2، سالب 4) وقطعه الصادي (0، سالب 12).
    الشكل 9-هاء-6
    التمارين\(\PageIndex{16}\) Solve Maximum and Minimum Applications

    في التمارين التالية، ابحث عن القيمة الدنيا أو القصوى.

    1. \(y=7 x^{2}+14 x+6\)
    2. \(y=-3 x^{2}+12 x-10\)
    إجابة

    2. القيمة القصوى هي\(2\) عندما\(x=2\).

    التمارين\(\PageIndex{17}\) Solve Maximum and Minimum Applications

    في التمارين التالية، قم بحل. تقريب الإجابات لأقرب جزء من عشرة.

    1. تُلقى كرة لأعلى من الأرض بسرعة أولية تبلغ\(112\) قدم/ثانية. استخدم المعادلة التربيعية\(h=-16 t^{2}+112 t\) لإيجاد المدة التي ستستغرقها الكرة للوصول إلى أقصى ارتفاع، ثم ابحث عن أقصى ارتفاع.
    2. يضم مرفق الرعاية النهارية منطقة مستطيلة على طول جانب المبنى للأطفال للعب في الهواء الطلق. إنهم بحاجة إلى تعظيم المساحة باستخدام\(180\) أقدام السياج على ثلاثة جوانب من الفناء. المعادلة التربيعية\(A=-2 x^{2}+180 x\) تعطي مساحة الفناء بالنسبة لطول المبنى الذي سيحيط الفناء.\(A\)\(x\) ابحث عن طول المبنى الذي يجب أن يحد الفناء لزيادة المساحة، ثم ابحث عن المساحة القصوى.
    يتم إعطاء شكل فردي. 3 جوانب للمستطيل متصلة بالجانب الأيمن من الشكل.
    الشكل 9-هاء-7
    إجابة

    2. الطول المجاور للمبنى هو\(90\) أقدام مما يعطي أقصى مساحة للقدم\(4,050\) المربع.

    تمثيل بياني للدوال التربيعية باستخدام التحويلات

    التمارين\(\PageIndex{18}\) Graph Quadratic Functions of the Form \(f(x)=x^{2}+k\)

    في التمارين التالية، قم برسم بياني لكل دالة باستخدام التحول الرأسي.

    1. \(g(x)=x^{2}+4\)
    2. \(h(x)=x^{2}-3\)
    إجابة

    2.

    يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على المستوى الإحداثي x y. له قمة (سالب 3، 0) ونقاط أخرى من (سالب 1، سالب 2) و (1، سالب 2).
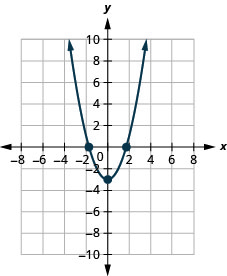
    الشكل 9-هاء-8
    التمارين\(\PageIndex{19}\) Graph Quadratic Functions of the Form \(f(x)=x^{2}+k\)

    في التمارين التالية، قم برسم بياني لكل دالة باستخدام الإزاحة الأفقية.

    1. \(f(x)=(x+1)^{2}\)
    2. \(g(x)=(x-3)^{2}\)
    إجابة

    2.

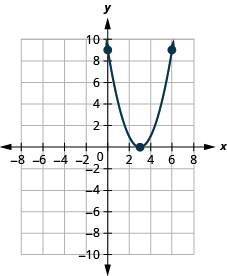
    يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على المستوى الإحداثي x y. وتتكون قمته من (3، 0) ونقاط أخرى من (2، 1) و (4,1).
    الشكل 9-هاء-9
    التمارين\(\PageIndex{20}\) Graph Quadratic Functions of the Form \(f(x)=x^{2}+k\)

    في التمارين التالية، قم برسم بياني لكل دالة باستخدام التحويلات.

    1. \(f(x)=(x+2)^{2}+3\)
    2. \(f(x)=(x+3)^{2}-2\)
    3. \(f(x)=(x-1)^{2}+4\)
    4. \(f(x)=(x-4)^{2}-3\)
    إجابة

    2.

    يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على المستوى الإحداثي x y. له قمة (سالب 3، سالب 2) ونقاط أخرى من (سالب 5، 2) و (سالب 1، 2).
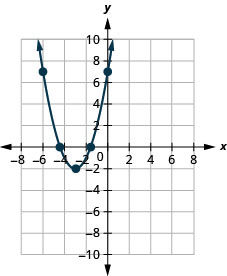
    الشكل 9-هاء-10

    4.

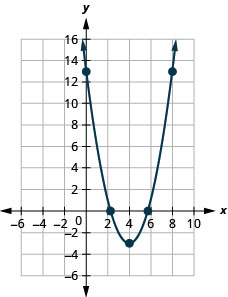
    يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على المستوى الإحداثي x y. له قمة (4، سالب 3) ونقاط أخرى من (3، سالب 2) و (5، سالب 2).
    الشكل 9-هاء-11
    التمارين\(\PageIndex{21}\) Graph Quadratic Functions of the Form \(f(x)=ax^{2}\)

    في التمارين التالية، قم برسم بياني لكل وظيفة.

    1. \(f(x)=2x^{2}\)
    2. \(f(x)=-x^{2}\)
    3. \(f(x)=\frac{1}{2} x^{2}\)
    إجابة

    2.

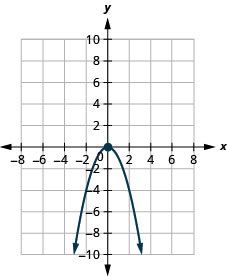
    يوضِّح هذا الشكل المكافئ المتجه نحو الأسفل على مستوى الإحداثيات x y. وله قمة (0، 0) ونقاط أخرى من (سالب 1، سالب 1) و (1، سالب 1).
    الشكل 9 هاء - 12
    التمارين\(\PageIndex{22}\) Graph Quadratic Functions Using Transformations

    في التمارين التالية، أعد كتابة كل دالة في\(f(x)=a(x-h)^{2}+k\) النموذج بإكمال المربع.

    1. \(f(x)=2 x^{2}-4 x-4\)
    2. \(f(x)=3 x^{2}+12 x+8\)
    إجابة

    1. \(f(x)=2(x-1)^{2}-6\)

    التمارين\(\PageIndex{23}\) Graph Quadratic Functions Using Transformations

    في التمارين التالية،

    1. أعد كتابة كل وظيفة في\(f(x)=a(x−h)^{2}+k\) النموذج
    2. قم برسم بياني باستخدام التحويلات
      1. \(f(x)=3 x^{2}-6 x-1\)
      2. \(f(x)=-2 x^{2}-12 x-5\)
      3. \(f(x)=2 x^{2}+4 x+6\)
      4. \(f(x)=3 x^{2}-12 x+7\)
    إجابة

    1.

    1. \(f(x)=3(x-1)^{2}-4\)

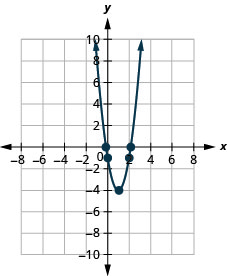
    2. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على المستوى الإحداثي x y. له قمة (1، سالب 4) ونقاط أخرى من (0، سالب 1) و (2، سالب 1).
      الشكل 9 هاء - 13

    3.

    1. \(f(x)=2(x+1)^{2}+4\)

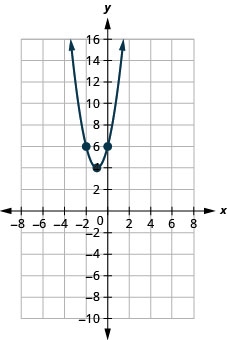
    2. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على المستوى الإحداثي x y. له قمة (سالب 1، 4) ونقاط أخرى من (سالب 2، 6) و (0، 6).
      الشكل 9 هاء - 14
    التمارين\(\PageIndex{24}\) Graph Quadratic Functions Using Transformations

    في التمارين التالية،

    1. أعد كتابة كل وظيفة في\(f(x)=a(x−h)^{2}+k\) النموذج
    2. قم برسمها باستخدام الخصائص
      1. \(f(x)=-3 x^{2}-12 x-5\)
      2. \(f(x)=2 x^{2}-12 x+7\)
    إجابة

    1.

    1. \(f(x)=-3(x+2)^{2}+7\)

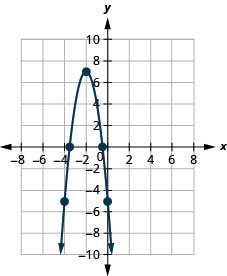
    2. يوضِّح هذا الشكل المكافئ المتجه نحو الأسفل على مستوى الإحداثيات x y. له قمة (سالب 2، 7) ونقاط أخرى من (سالب 4، سالب 5) و (0، سالب 5).
      الشكل 9 هاء - 15
    التمارين\(\PageIndex{25}\) Find a Quadratic Function From its Graph

    في التمارين التالية، اكتب الدالة التربيعية في\(f(x)=a(x−h)^{2}+k\) الشكل.


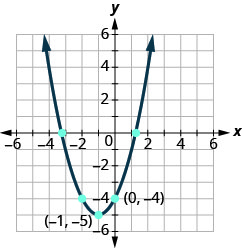
    1. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على المستوى الإحداثي x y. له قمة (سالب 1، سالب 1) ونقاط أخرى من (سالب 2، سالب 4) و (0، سالب 4).
      الشكل 9 هاء - 16

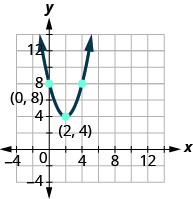
    2. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على المستوى الإحداثي x y. وتتكون قمته من (2، 4) ونقاط أخرى من (0، 8) و (4، 8).
      الشكل 9 هاء - 17
    إجابة

    1. \(f(x)=(x+1)^{2}-5\)

    حل التباينات التربيعية

    التمارين\(\PageIndex{26}\) Solve Quadratic Inequalities Graphically

    في التمارين التالية، قم بحل المشكلة بيانيًا واكتب الحل بالتدوين الفاصل الزمني.

    1. \(x^{2}-x-6>0\)
    2. \(x^{2}+4 x+3 \leq 0\)
    3. \(-x^{2}-x+2 \geq 0\)
    4. \(-x^{2}+2 x+3<0\)
    إجابة

    1.


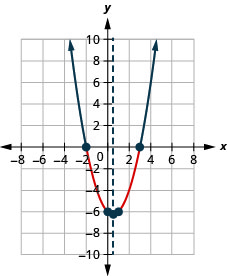
    1. يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على المستوى الإحداثي x y. وتبلغ قمته (نصف وسالب 6 وربع) ونقاط أخرى مقدارها (0، سالب 6) و (1، سالب 6).
      الشكل 9 هاء - 18
    2. \((-\infty,-2) \cup(3, \infty)\)

    3.


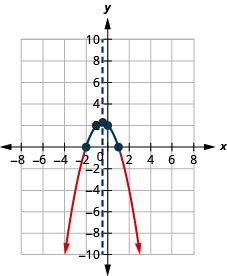
    1. يوضِّح هذا الشكل المكافئ المتجه نحو الأسفل على مستوى الإحداثيات x y. يبلغ قمته (سالب نصف، 2 وربع) ونقاط أخرى (سالب 2، 0) و (1، 0).
      الشكل 9-هاء-19
    2. \([-2,1]\)
    التمارين\(\PageIndex{27}\) Solve Quadratic Inequalities Graphically

    في التمارين التالية، قم بحل كل متباينة جبريًا واكتب أي حل في شكل فاصل زمني.

    1. \(x^{2}-6 x+8<0\)
    2. \(x^{2}+x>12\)
    3. \(x^{2}-6 x+4 \leq 0\)
    4. \(2 x^{2}+7 x-4>0\)
    5. \(-x^{2}+x-6>0\)
    6. \(x^{2}-2 x+4 \geq 0\)
    إجابة

    1. \((2,4)\)

    3. \([3-\sqrt{5}, 3+\sqrt{5}]\)

    5. لا يوجد حل

    اختبار الممارسة

    التمارين\(\PageIndex{28}\)
    1. استخدم خاصية الجذر التربيعي لحل المعادلة التربيعية\(3(w+5)^{2}=27\).
    2. استخدم إكمال المربع لحل المعادلة التربيعية\(a^{2}-8 a+7=23\).
    3. استخدم الصيغة التربيعية لحل المعادلة التربيعية\(2 m^{2}-5 m+3=0\).
    إجابة

    1. \(w=-2, w=-8\)

    3. \(m=1, m=\frac{3}{2}\)

    التمارين\(\PageIndex{29}\)

    حل المعادلات التربيعية التالية. استخدم أي طريقة.

    1. \(2 x(3 x-2)-1=0\)
    2. \(\frac{9}{4} y^{2}-3 y+1=0\)
    إجابة

    2. \(y=\frac{2}{3}\)

    التمارين\(\PageIndex{30}\)

    استخدم التمييز لتحديد عدد الحلول ونوعها لكل معادلة تربيعية.

    1. \(6 p^{2}-13 p+7=0\)
    2. \(3 q^{2}-10 q+12=0\)
    إجابة

    2. \(2\)مركب

    التمارين\(\PageIndex{31}\)

    حل كل معادلة.

    1. \(4 x^{4}-17 x^{2}+4=0\)
    2. \(y^{\frac{2}{3}}+2 y^{\frac{1}{3}}-3=0\)
    إجابة

    2. \(y=1, y=-27\)

    التمارين\(\PageIndex{32}\)

    ابحث عن كل نوع مكافئ

    1. في أي اتجاه يتم فتحه
    2. معادلة محور التماثل
    3. قمة الرأس
    4. \(x\)\(y\)عمليات الاعتراض
    5. القيمة القصوى أو الدنيا
      1. \(y=3 x^{2}+6 x+8\)
      2. \(y=-x^{2}-8 x+16\)
    إجابة

    2.

    1. سقط
    2. \(x=-4\)
    3. \((-4,0)\)
    4. \(y: (0,16); x: (-4,0)\)
    5. الحد الأدنى لقيمة\(-4\) متى\(x=0\)
    التمارين\(\PageIndex{33}\)

    ارسم بيانيًا كل دالة تربيعية باستخدام الأجزاء المقطوعة ورأس المنحنى ومعادلة محور التماثل.

    1. \(f(x)=x^{2}+6 x+9\)
    2. \(f(x)=-2 x^{2}+8 x+4\)
    إجابة

    2.

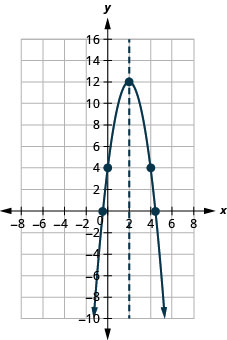
    يوضِّح هذا الشكل المكافئ المتجه نحو الأسفل على مستوى الإحداثيات x y. وتتكون قمته من (2، 12) ونقاط أخرى من (0، 4) و (4، 4).
    الشكل 9-هاء-20
    التمارين\(\PageIndex{34}\)

    في التمارين التالية، قم برسم بياني لكل دالة باستخدام التحويلات.

    1. \(f(x)=(x+3)^{2}+2\)
    2. \(f(x)=x^{2}-4 x-1\)
    إجابة

    2.

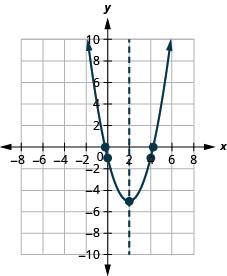
    يوضِّح هذا الشكل المكافئ الذي يفتح لأعلى على المستوى الإحداثي x y. له قمة (2، سالب 5) ونقاط أخرى من (0، سالب 1) و (4، سالب 1).
    الشكل 9 هاء - 21

    التمارين\(\PageIndex{35}\)

    في التمارين التالية، قم بحل كل متباينة جبريًا واكتب أي حل في شكل فاصل زمني.

    1. \(x^{2}-6 x-8 \leq 0\)
    2. \(2 x^{2}+x-10>0\)
    إجابة

    2. \(\left(-\infty,-\frac{5}{2}\right) \cup(2, \infty)\)

    التمارين\(\PageIndex{36}\)

    قم بتمثيل الموقف باستخدام معادلة تربيعية وحلها بأي طريقة.

    1. ابحث عن رقمين زوجيين متتاليين يكون منتجهما\(360\).
    2. يزيد طول قطر المستطيل بمقدار ثلاثة أضعاف عن العرض. طول المستطيل يساوي ثلاثة أضعاف العرض. أوجد طول القطر. (قرِّب إلى أقرب جزء من عشرة.)
    إجابة

    2. يتم إطلاق منطاد الماء لأعلى بمعدل\(86\) قدم/ثانية. باستخدام الصيغة،\(h=-16 t^{2}+86 t\) ابحث عن المدة التي سيستغرقها البالون للوصول إلى أقصى ارتفاع، ثم ابحث عن الحد الأقصى للارتفاع. قرِّب إلى أقرب جزء من عشرة.