9.6: حل تطبيقات المعادلات التربيعية

Last updated
Save as PDF

Page ID: 201665

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

حل التطبيقات التي تم تصميمها باستخدام المعادلات التربيعية

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

مجموع رقمين فرديين متتاليين هو$−100$. ابحث عن الأرقام.
إذا فاتتك هذه المشكلة، راجع المثال 2.18.
حل:$\frac{2}{x+1}+\frac{1}{x-1}=\frac{1}{x^{2}-1}$.
إذا فاتتك هذه المشكلة، راجع المثال 7.35.
أوجد طول وتر مثلث قائم الزاوية بالساقين$5$ بالبوصة$12$ والبوصة.
إذا فاتتك هذه المشكلة، راجع المثال 2.34.

حل تطبيقات على غرار المعادلات التربيعية

لقد قمنا بحل بعض التطبيقات التي تم تصميمها بواسطة المعادلات التربيعية في وقت سابق، عندما كانت الطريقة الوحيدة لحلها هي التحليل. الآن لدينا المزيد من الطرق لحل المعادلات التربيعية، سنلقي نظرة أخرى على التطبيقات.

دعونا أولاً نلخص الطرق التي لدينا الآن لحل المعادلات التربيعية.

طرق حل المعادلات التربيعية

التخص
خاصية الجذر التربيعي
إكمال المربع
صيغة تربيعية

عند حل كل معادلة، اختر الطريقة الأكثر ملاءمة لك لحل المشكلة. للتذكير، سنقوم بنسخ إستراتيجية حل المشكلات المعتادة هنا حتى نتمكن من اتباع الخطوات.

استخدم استراتيجية حل المشكلات

اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
حدد ما نبحث عنه.
اذكر ما نبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.
ترجم إلى معادلة. قد يكون من المفيد إعادة ذكر المشكلة في جملة واحدة مع جميع المعلومات المهمة. ثم ترجم الجملة الإنجليزية إلى معادلة جبرية.
حل المعادلة باستخدام تقنيات الجبر.
تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
أجب على السؤال بجملة كاملة.

لقد قمنا بحل تطبيقات الأرقام التي تتضمن أعدادًا صحيحة متتالية زوجية وفردية، من خلال نمذجة الموقف باستخدام المعادلات الخطية. تذكر أننا لاحظنا أن كل عدد صحيح زوجي$2$ يزيد عن الرقم الذي يسبقه. إذا اتصلنا بالأول$n$، فسيكون التالي هو$n+2$. سيكون التالي هو$n+2+2$ أو$n+4$. هذا صحيح أيضًا عندما نستخدم الأعداد الصحيحة الفردية. يتم عرض مجموعة واحدة من الأعداد الصحيحة الزوجية ومجموعة واحدة من الأعداد الصحيحة الفردية أدناه.

$\begin{array}{cl}{}&{\text{Consecutive even integers}}\\{}& {64,66,68}\\ {n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer }}\end{array}$

$\begin{array}{cl}{}&{\text{Consecutive odd integers}}\\{}& {77,79,81}\\ {n} & {1^{\text { st }} \text { odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer }}\end{array}$

يتم تصميم بعض تطبيقات الأعداد الصحيحة الفردية أو حتى المتتالية بواسطة المعادلات التربيعية. سيكون الترميز أعلاه مفيدًا عند تسمية المتغيرات.

مثال$\PageIndex{1}$

حاصل ضرب عددين صحيحين فرديين متتاليين هو$195$. ابحث عن الأعداد الصحيحة.

الحل:

الخطوة 1: اقرأ المشكلة

الخطوة 2: تحديد ما نبحث عنه.

نحن نبحث عن عددين صحيحين متتابعين.

الخطوة 3: قم بتسمية ما نبحث عنه.

دع$n=$ أول عدد صحيح فردي.

$n+2=$العدد الصحيح الفردي التالي.

الخطوة 4: ترجم إلى معادلة. اذكر المشكلة في جملة واحدة.

«ناتج عددين صحيحين فرديين متتاليين هو$195$.» حاصل ضرب العدد الصحيح الفردي الأول والعدد الفردي الثاني هو$195$.

ترجم إلى معادلة.

$n(n+2)=195$

الخطوة 5: حل المعادلة. قم بالتوزيع.

$n^{2}+2 n=195$

اكتب المعادلة في الصورة القياسية.

$n^{2}+2 n-195=0$

عامل.

$(n+15)(n-13)=0$

استخدم خاصية المنتج الصفري.

$n+15=0 \quad n-13=0$

حل كل معادلة.

$n=-15, \quad n=13$

هناك قيمتان$n$ لذلك وهما الحلول. سيعطينا هذا زوجين من الأعداد الصحيحة الفردية المتتالية للحل الخاص بنا.

$\begin{array}{cc}{\text { First odd integer } n=13} & {\text { First odd integer } n=-15} \\ {\text { next odd integer } n+2} & {\text { next odd integer } n+2} \\ {13+2} & {-15+2} \\ {15} & {-13}\end{array}$

الخطوة 6: تحقق من الإجابة.

هل تعمل هذه الأزواج؟ هل هي أعداد صحيحة فردية متتالية؟

$\begin{aligned} 13,15 & \text { yes } \\-13,-15 & \text { yes } \end{aligned}$

هل منتجهم$195$؟

$\begin{aligned} 13 \cdot 15 &=195 &\text{yes} \\-13(-15) &=195 & \text { yes } \end{aligned}$

الخطوة 7: أجب على السؤال.

عددان صحيحان فرديان متتاليان$195$ منتجهما هما$13,15$ و$-13,-15$.

التمارين$\PageIndex{1}$

حاصل ضرب عددين صحيحين فرديين متتاليين هو$99$. ابحث عن الأعداد الصحيحة.

إجابة: العددان الصحيحان الفرديان المتعاقدان اللذان يكون$99$ منتجهما هما$9, 11$، و$−9, −11$.

التمارين$\PageIndex{2}$

ناتج عددين صحيحين متتاليين هو$168$. ابحث عن الأعداد الصحيحة.

إجابة: العددان الصحيحان المتتابعان اللذان يكون$128$ منتجهما هما$12, 14$ و$−12, −14$.

سنستخدم صيغة منطقة المثلث لحل المثال التالي.

تعريف$\PageIndex{1}$

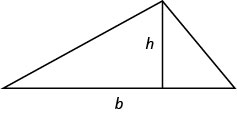
مساحة المثلث

بالنسبة للمثلث ذو القاعدة والارتفاع$b$$h$، تُعطى المساحة$A$،، بواسطة الصيغة$A=\frac{1}{2} b h$.

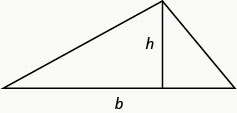
صورة مثلث. ويُسمى جانب القاعدة الأفقي b، ويكون مقطع الخط المسمى h عموديًا على القاعدة، ويربطه بالرأس المعاكس. — الشكل 9.5.1

تذكر أنه عند حل التطبيقات الهندسية، من المفيد رسم الشكل.

مثال$\PageIndex{2}$

يقوم مهندس معماري بتصميم مدخل مطعم. إنها تريد وضع نافذة مثلثة فوق المدخل. نظرًا لقيود الطاقة، يمكن أن تبلغ مساحة النافذة قدمًا$120$ مربعًا فقط ويريد المهندس المعماري أن تكون القاعدة أكثر من ضعف الارتفاع$4$ بالأقدام. ابحث عن قاعدة النافذة وارتفاعها.

الحل:

الجدول 9.5.1
الخطوة 1: اقرأ المشكلة. ارسم صورة.	$.$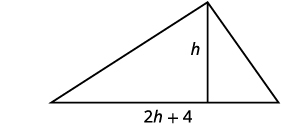
الخطوة 2: تحديد ما نبحث عنه.	نحن نبحث عن القاعدة والارتفاع.
الخطوة 3: قم بتسمية ما نبحث عنه.	$h=$دع ارتفاع المثلث. $2h+4=$قاعدة المثلث.
الخطوة 4: ترجم إلى معادلة. نحن نعرف المنطقة. اكتب صيغة مساحة المثلث.	$A=\frac{1}{2} b h$
الخطوة 5: حل المعادلة. استبدل القيم.	$120=\frac{1}{2}(2 h+4) h$
قم بالتوزيع.	$120=h^{2}+2 h$
هذه معادلة تربيعية، أعد كتابتها بالشكل القياسي.	$h^{2}+2 h-120=0$
عامل.	$(h-10)(h+12)=0$
استخدم خاصية المنتج الصفري.	$h-10=0 \quad h+12=0$
قم بالتبسيط.	$h=10, \quad \cancel{h=-12}$
$h$نظرًا لارتفاع النافذة، فإن القيمة$h=-12$ لا معنى لها.
ارتفاع المثلث$h=10$.
قاعدة المثلث$2h+4$. $2 \cdot 10+4$ $24$
الخطوة 6: تحقق من الإجابة. هل يحتوي المثلث ذو الارتفاع$10$ والقاعدة$24$ على مساحة$120$؟ نعم.
الخطوة 7: أجب على السؤال.	ارتفاع النافذة المثلثة هو$10$ القدمين والقاعدة هي$24$ القدمين.

التمارين$\PageIndex{3}$

أوجد قاعدة المثلث وارتفاعه، الذي تزيد قاعدته بأربع بوصات عن ستة أضعاف ارتفاعه، ومساحته بوصات$456$ مربعة.

إجابة: ارتفاع المثلث هو$12$ بوصة والقاعدة هي$76$ بوصة.

التمارين$\PageIndex{4}$

إذا كانت قاعدة المثلث الذي تبلغ مساحته قدمًا$110$ مربعًا أقل بمقدار قدمين من ضعف الارتفاع، فما طول قاعدته وارتفاعه؟

إجابة: ارتفاع المثلث هو$11$ القدمين والقاعدة هي$20$ القدمين.

في المثالين السابقين، كان الرقم في الجذر في الصيغة التربيعية مربعًا مثاليًا وبالتالي كانت الحلول عبارة عن أرقام منطقية. إذا حصلنا على رقم غير منطقي كحل لمشكلة التطبيق، فسنستخدم الآلة الحاسبة للحصول على قيمة تقريبية.

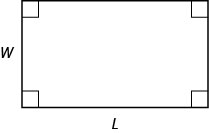
سنستخدم صيغة مساحة المستطيل لحل المثال التالي.

تعريف$\PageIndex{2}$

مساحة المستطيل

بالنسبة للمستطيل ذي الطول والعرض$L$$W$، تُعطى المساحة$A$،، بواسطة الصيغة$A=LW$.

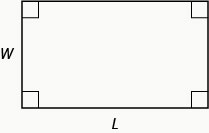
تظهر الصورة مستطيلاً. يتم تمييز جميع الزوايا الأربع كزوايا قائمة. أما الجانب الأفقي الأطول فيسمى L والجانب الرأسي الأقصر بـ w. — الشكل 9.5.3

مثال$\PageIndex{3}$

يريد مايك وضع قدم$150$ مربع من العشب الصناعي في فناء منزله الأمامي. هذه هي المساحة القصوى للعشب الصناعي التي تسمح بها جمعية أصحاب المنازل. يريد أن يكون لديه مساحة مستطيلة من العشب بطول قدم أقل من$3$ ضعف العرض. ابحث عن الطول والعرض. قرِّب حتى أقرب عُشر قدم.

الحل:

الجدول 9.5.2
الخطوة 1: اقرأ المشكلة. ارسم صورة.	$.$
الخطوة 2: تحديد ما نبحث عنه.	نحن نبحث عن الطول والعرض.
الخطوة 3: قم بتسمية ما نبحث عنه.	$w=$دع عرض المستطيل. $3w-1=$طول المستطيل
الخطوة 4: ترجم إلى معادلة. نحن نعرف المنطقة. اكتب صيغة مساحة المستطيل.	$.$
الخطوة 5: حل المعادلة. استبدل القيم.	$.$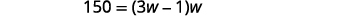
قم بالتوزيع.	$.$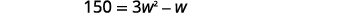
هذه معادلة تربيعية؛ أعد كتابتها بالشكل القياسي. حل المعادلة باستخدام الصيغة التربيعية.	$.$
حدد$a,b,c$ القيم.	$.$
اكتب الصيغة التربيعية.	$.$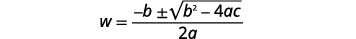
ثم استبدل قيم$a,b,c$.	$.$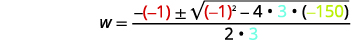
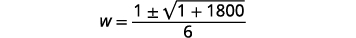
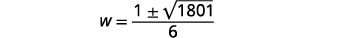
قم بالتبسيط.	$.$ $.$ الشكل 9.5.13
أعد الكتابة لإظهار حلين.	$.$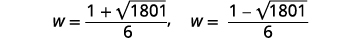
قم بتقريب الإجابات باستخدام الآلة الحاسبة. نحن نزيل الحل السلبي للعرض.	$.$
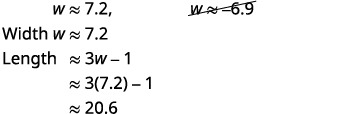الخطوة 6: تحقق من الإجابة. تأكد من أن الإجابات منطقية. نظرًا لأن الإجابات تقريبية، فلن تخرج المنطقة تمامًا$150$.
الخطوة 7: أجب على السؤال.	يبلغ عرض المستطيل$7.2$ قدمًا تقريبًا والطول$20.6$ قدمًا تقريبًا.

التمارين$\PageIndex{5}$

يبلغ طول حديقة الخضروات المستطيلة التي$200$ تبلغ مساحتها أربعة أقدام أقل من ضعف العرض. أوجد طول وعرض الحديقة لأقرب عُشر قدم.

إجابة: يبلغ طول الحديقة حوالي$18$ قدم وعرض$11$ القدمين.

التمارين$\PageIndex{6}$

مفرش طاولة مستطيل بمساحة قدم$80$ مربع. العرض أقصر$5$ بالأقدام من الطول. ما طول وعرض مفرش المائدة لأقرب عُشر قدم؟

إجابة: يبلغ طول مفرش المائدة حوالي$11.8$ القدمين وعرض$6.8$ القدمين.

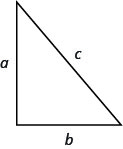
توضح نظرية فيثاغورس العلاقة بين الساقين والوتر في مثلث قائم الزاوية. سنستخدم نظرية فيثاغورس لحل المثال التالي.

تعريف$\PageIndex{3}$

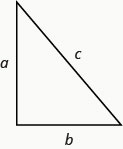
نظرية فيثاغورس

في أي مثلث قائم الزاوية، أين$a$$b$ توجد أطوال الأرجل،$c$ ويكون طول الوتر،$a^{2}+b^{2}=c^{2}$.

تُظهر الصورة مثلثًا قائمًا بأرجل أفقية وعمودية. يُطلق على الساق الرأسية أ. أما الجانب الأفقي فيسمى ب. والوتر يسمى c. — الشكل 9.5.16

مثال$\PageIndex{4}$

يقوم رينيه بإعداد شاشة عرض ضوء العطلات. يريد أن يصنع «شجرة» على شكل مثلثين قائمين، كما هو موضح أدناه، ولديه سلاسل من الأضواء$10$ بطول قدمين لاستخدامها في الجوانب. سوف يعلق الأضواء على الجزء العلوي من العمود وعلى ورقتين على الأرض. يريد أن يكون ارتفاع القطب هو نفس المسافة من قاعدة القطب إلى كل حصة. كم يجب أن يكون طول القطب؟

الحل:

الجدول 9-5-3
الخطوة 1: اقرأ المشكلة. ارسم صورة.	$.$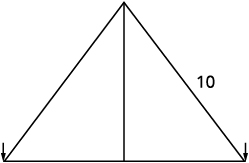
الخطوة 2: تحديد ما نبحث عنه.	نحن نبحث عن ارتفاع القطب.
الخطوة 3: قم بتسمية ما نبحث عنه.	المسافة من قاعدة القطب إلى أي من الوتد هي نفس ارتفاع القطب. $x=$دع ارتفاع القطب. $x=$المسافة من القطب إلى الحصة كل جانب هو مثلث قائم. نرسم صورة لأحدهم. 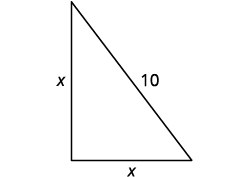$.$ الشكل 9.5.18
الخطوة 4: ترجم إلى معادلة. يمكننا استخدام نظرية فيثاغورس لحل المشكلة$x$. اكتب نظرية فيثاغورس.	$a^{2}+b^{2}=c^{2}$
الخطوة 5: حل المعادلة. بديل.	$x^{2}+x^{2}=10^{2}$
قم بالتبسيط.	$2 x^{2}=100$
قم$2$ بالقسمة لعزل المتغير.	$\frac{2 x^{2}}{2}=\frac{100}{2}$
قم بالتبسيط.	$x^{2}=50$
استخدم خاصية الجذر التربيعي.	$x=\pm \sqrt{50}$
قم بتبسيط الراديكالية.	$x=\pm 5 \sqrt{2}$
أعد الكتابة لإظهار حلين.	$x=5 \sqrt{2}, \quad \cancel{x=-5 \sqrt{2}}$
	إذا قمنا بتقريب هذا الرقم إلى أقرب جزء من عشرة باستخدام الآلة الحاسبة، نجد$x≈7.1$.
الخطوة 6: تحقق من الإجابة. تحقق بنفسك في نظرية فيثاغورس.
الخطوة 7: أجب على السؤال.	يجب أن يكون طول العمود حوالي$7.1$ قدم.

التمارين$\PageIndex{7}$

تلقي الشمس بظلالها من عمود العلم. يبلغ ارتفاع عمود العلم ثلاثة أضعاف طول ظله. المسافة بين نهاية الظل وأعلى عمود العلم هي$20$ الأقدام. أوجد طول الظل وطول عمود العلم. قرِّب إلى أقرب جزء من عشرة.

إجابة: يبلغ طول ظل عمود العلم$6.3$ قدمًا تقريبًا وارتفاع عمود العلم$18.9$ أقدام.

التمارين$\PageIndex{8}$

تزيد المسافة بين الزوايا المتقابلة لحقل مستطيل بمقدار أربعة أضعاف عن عرض الحقل. يبلغ طول الحقل ضعف عرضه. أوجد المسافة بين الزوايا المقابلة. قرِّب إلى أقرب جزء من عشرة.

إجابة: المسافة بين الزوايا المقابلة هي$7.2$ قدم تقريبًا.

تم تصميم ارتفاع المقذوف الذي تم إطلاقه لأعلى من الأرض بمعادلة تربيعية. السرعة الأولية$v_{0}$، تدفع الجسم لأعلى حتى تتسبب الجاذبية في تراجع الجسم إلى الأسفل.

تعريف$\PageIndex{4}$

تُحدد الصيغة الارتفاع بالأقدام لجسم يُطلَق لأعلى في الهواء بسرعة أولية$v_{0}$، بعد$t$ ثوانٍ$h$

$h=-16 t^{2}+v_{0} t$

يمكننا استخدام هذه الصيغة للعثور على عدد الثواني التي ستستغرقها الألعاب النارية للوصول إلى ارتفاع معين.

مثال$\PageIndex{5}$

يتم إطلاق الألعاب النارية لأعلى بسرعة أولية$130$ بأقدام في الثانية. كم عدد الثواني التي سيستغرقها الوصول إلى ارتفاع$260$ القدمين؟ قرِّب لأقرب جزء من عُشر من الثانية.

الحل:

الجدول 9-5-4
الخطوة 1: اقرأ المشكلة.
الخطوة 2: تحديد ما نبحث عنه.	نحن نبحث عن عدد الثواني، وهو الوقت.
الخطوة 3: قم بتسمية ما نبحث عنه.	$t=$دع عدد الثواني.
الخطوة 4: ترجم إلى معادلة. استخدم الصيغة.	$.$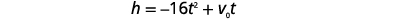
الخطوة 5: حل المعادلة. نحن نعلم أن السرعة$v_{0}$ هي$130$ قدم في الثانية. الارتفاع هو$260$ القدمين. استبدل القيم.	$.$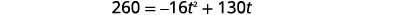
هذه معادلة تربيعية، أعد كتابتها بالشكل القياسي. حل المعادلة باستخدام الصيغة التربيعية.	$.$
حدد قيم$a, b, c$.	$.$
اكتب الصيغة التربيعية.	$.$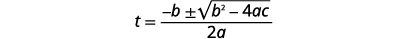
ثم استبدل قيم$a,b,c$.	$.$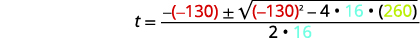
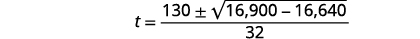
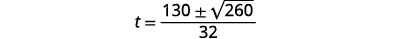
قم بالتبسيط.	$.$ $.$ الشكل 9.5.26
أعد الكتابة لإظهار حلين.	$.$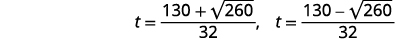
قم بتقريب الإجابة باستخدام الآلة الحاسبة.	$.$
الخطوة 6: تحقق من الإجابة. الشيك متروك لك.
الخطوة 7: أجب على السؤال.	سوف ترتفع الألعاب النارية ثم تسقط مرة أخرى. مع ارتفاع الألعاب النارية، ستصل إلى$260$ القدمين بعد$3.6$ ثوانٍ تقريبًا. سيتجاوز هذا الارتفاع أيضًا في طريقه إلى الأسفل في$4.6$ ثوانٍ.

التمارين$\PageIndex{9}$

يتم إطلاق سهم من الأرض إلى الهواء بسرعة أولية تبلغ$108$ قدم/ثانية. استخدم الصيغة$h=-16 t^{2}+v_{0} t$ لتحديد متى سيكون السهم على$180$ بعد أقدام من الأرض. قرِّب أقرب جزء من عشرة.

إجابة: سيصل السهم إلى$180$ القدمين في طريقه لأعلى بعد$3$ ثوانٍ ومرة أخرى في طريقه لأسفل بعد$3.8$ ثوانٍ تقريبًا.

التمارين$\PageIndex{10}$

رجل يرمي كرة في الهواء بسرعة$96$ قدم/ث، استخدم الصيغة$h=-16 t^{2}+v_{0} t$ لتحديد متى سيكون ارتفاع الكرة$48$ قدمًا. قرِّب إلى أقرب جزء من عشرة.

إجابة: ستصل الكرة إلى$48$ القدمين في طريقها لأعلى بعد حوالي$.6$ ثانية ومرة أخرى في طريقها لأسفل بعد$5.4$ ثوانٍ تقريبًا.

لقد قمنا بحل مشاكل الحركة المنتظمة باستخدام الصيغة$D=rt$ في الفصول السابقة. استخدمنا جدولًا مثل الجدول أدناه لتنظيم المعلومات وقيادتنا إلى المعادلة.

تعرض الصورة قالب جدول يحتوي على ثلاثة صفوف وأربعة أعمدة. العمود الأول فارغ. العمود الثاني يسمى â€rate.â€ العمود الثالث يسمى €time.â€ العمود الرابع يسمى €distance.â€ التسميات مكتوبة في المعادلة معدل مرات الوقت يساوي المسافة. توجد خلية إضافية في أسفل العمود الرابع. — الشكل 9.5.29

$D=rt$تفترض الصيغة أننا نعرفها$r$$t$ ونستخدمها للبحث عنها$D$. إذا كنا نعرف$D$ $r$ونحتاج إلى البحث$t$، فسنحل المعادلة$t$ ونحصل على الصيغة$t=\frac{D}{r}$.

يتم أيضًا تصميم بعض مشاكل الحركة المنتظمة بواسطة المعادلات التربيعية.

مثال$\PageIndex{6}$

عاد البروفيسور سميث للتو من مؤتمر كان$2,000$ على بعد أميال شرق منزله. كان إجمالي الوقت الذي قضاه في الطائرة للرحلة ذهابًا وإيابًا$9$ ساعات. إذا كانت الطائرة تحلق بمعدل$450$ أميال في الساعة، فما سرعة التيار النفاث؟

الحل:

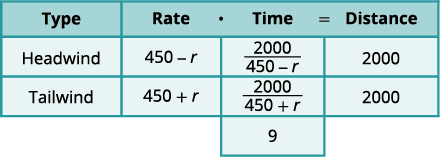
هذه حالة حركة موحدة. سيساعدنا الرسم التخطيطي على تصور الموقف.

يوضِّح الرسم التخطيطي أولاً حركة الطائرة بسرعة ٤٥٠ ميلًا في الساعة مع وجود سهم إلى اليمين. تسير الطائرة مسافة 2000 ميل مع الريح، ممثلة بالعبارة 450 زائد r. وحركة التيار النفاث على اليمين. تستغرق الرحلة ذهابًا وإيابًا 9 ساعات. في الجزء السفلي من الرسم التخطيطي، يوجد سهم إلى اليسار يمثل حركة عودة الطائرة. تبلغ سرعة الكوكب™ 450 ميلاً في الساعة، والحركة هي 2000 ميل مقابل الريح على غرار التعبير 450 â€ «r. — الشكل 9.5.30

نقوم بملء المخطط لتنظيم المعلومات.

نحن نبحث عن سرعة التيار النفاث. $r=$دع سرعة التيار النفاث.

عندما تطير الطائرة مع الريح، تزيد الرياح من سرعتها وبالتالي يكون المعدل$450 + r$.

عندما تطير الطائرة ضد الريح، تقلل الرياح من سرعتها ويكون المعدل كذلك$450 − r$.

الجدول 9-5-5
اكتب في الأسعار. اكتب في المسافات. منذ ذلك الحين$D=r⋅t$، نحل المشكلة $t$ ونحصل عليها$t=\frac{D}{r}$. نقسم المسافة على المعدل في كل صف، ونضع التعبير في عمود الوقت.	$.$
نحن نعلم أن الأوقات تضاف إلى$9$ وهكذا نكتب المعادلة.	$\frac{2000}{450-r}+\frac{2000}{450+r}=9$
نضرب كلا الجانبين بواسطة شاشة LCD.	$(450-r)(450+r)\left(\frac{2000}{450-r}+\frac{2000}{450+r}\right)=9(450-r)(450+r)$
قم بالتبسيط.	$2000(450+r)+2000(450-r)=9(450-r)(450+r)$
عامل ال$2,000$.	$2000(450+r+450-r)=9\left(450^{2}-r^{2}\right)$
حل.	$2000(900)=9\left(450^{2}-r^{2}\right)$
اقسم على$9$.	$2000(100)=450^{2}-r^{2}$
قم بالتبسيط.	$\begin{aligned}200000&=202500-r^{2} \\ -2500&=-r^{2}\\ 50&=r\end{aligned}$\ سرعة التيار النفاث هي$50$ ميل في الساعة.
تحقق من: هل$50$ ميل في الساعة هي سرعة معقولة للتيار النفاث؟ نعم. إذا كانت الطائرة تسير$450$ ميلاً في الساعة وكانت الرياح$50$ ميلاً في الساعة، الرياح الخلفية $450+50=500 \mathrm{mph} \quad \frac{2000}{500}=4$ساعات الرياح المعاكسة $450-50=400 \mathrm{mph} \quad \frac{2000}{400}=5$ساعات تضيف الأوقات إلى$9$ ساعات، لذلك يتم التحقق.

كانت سرعة التيار النفاث$50$ ميلاً في الساعة.

التمارين$\PageIndex{11}$

عادت ماري آن للتو من زيارة مع أحفادها في الشرق. كانت الرحلة$2400$ على بعد أميال من منزلها وكان إجمالي الوقت الذي قضته في الطائرة للرحلة ذهابًا وإيابًا$10$ ساعات. إذا كانت الطائرة تحلق بمعدل$500$ أميال في الساعة، فما سرعة التيار النفاث؟

إجابة: كانت سرعة التيار النفاث$100$ ميلاً في الساعة.

التمارين$\PageIndex{12}$

عاد جيري للتو من رحلة عبر البلاد. كانت الرحلة$3000$ على بعد أميال من منزله وكان إجمالي الوقت الذي قضاه في الطائرة للرحلة ذهابًا وإيابًا$11$ ساعات. إذا كانت الطائرة تحلق بمعدل$550$ أميال في الساعة، فما سرعة التيار النفاث؟

إجابة: كانت سرعة التيار النفاث$50$ ميلاً في الساعة.

يمكن أيضًا تصميم تطبيقات العمل من خلال المعادلات التربيعية. سنقوم بإعدادها باستخدام نفس الطرق التي استخدمناها عندما قمنا بحلها بالمعادلات النسبية. سنستخدم سيناريو مماثل الآن.

مثال$\PageIndex{7}$

تحتوي مجلة gossip الأسبوعية على قصة كبيرة عن الانتخابات الرئاسية ويريد المحرر طباعة المجلة في أقرب وقت ممكن. لقد طلبت من الطابعة تشغيل مطبعة إضافية لإنجاز الطباعة بسرعة أكبر. يستغرق الضغط على #1$12$ ساعات أكثر من الضغط على #2 للقيام بهذه المهمة، وعند تشغيل المطبعتين، يمكنهما طباعة المهمة في$8$ ساعات. ما المدة التي تستغرقها كل مطبعة لطباعة المهمة بمفردها؟

الحل:

هذه مشكلة عمل. سيساعدنا المخطط على تنظيم المعلومات.

نحن نبحث عن عدد الساعات التي ستستغرقها كل ضغطة على حدة لإكمال المهمة.

الجدول 9-5-6
$x=$حدد عدد ساعات الضغط #2 لإكمال المهمة. أدخل الساعات لكل مهمة للضغط #1، ثم اضغط #2، والوقت الذي يعملون فيه معًا.	$.$
الجزء المكتمل بواسطة Press #1 بالإضافة إلى الجزء المكتمل بواسطة Press #2 يساوي المبلغ المكتمل معًا. ترجم إلى معادلة.	$.$
حل.	$.$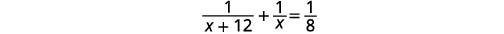
اضرب في شاشة LCD، 8$x(x+12)$.	$.$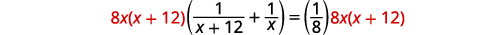
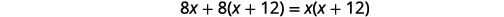
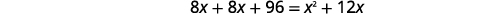
قم بالتبسيط.	$.$ $.$ الشكل 9.5.37 $.$ الشكل 9.5.38
حل.	$.$ $.$ الشكل 9.5.40 $.$ الشكل 9.5.41
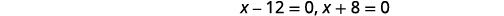
نظرًا لأن فكرة الساعات السلبية لا معنى لها، فإننا نستخدم القيم$x=12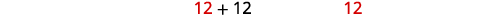$.	$.$ $.$ الشكل 9.5.43
اكتب إجابة الجملة الخاصة بنا.	قد يستغرق الضغط على #1$24$ ساعات والضغط على #2 سيستغرق$12$ ساعات للقيام بهذه المهمة بمفرده.

التمارين$\PageIndex{13}$

تحتوي المجلة الإخبارية الأسبوعية على قصة كبيرة تحمل اسم شخص العام ويريد المحرر طباعة المجلة في أقرب وقت ممكن. لقد طلبت من الطابعة تشغيل مطبعة إضافية لإنجاز الطباعة بسرعة أكبر. يستغرق الضغط على #1$6$ ساعات أكثر من الضغط على #2 للقيام بهذه المهمة، وعند تشغيل المطبعتين، يمكنهما طباعة المهمة في$4$ ساعات. ما المدة التي تستغرقها كل مطبعة لطباعة المهمة بمفردها؟

إجابة: قد يستغرق الضغط على #1$12$ ساعات، وسوف يستغرق الضغط على #2$6$ ساعات للقيام بهذه المهمة بمفرده.

التمارين$\PageIndex{14}$

تقيم Erlinda حفلة وتريد ملء حوض الاستحمام الساخن الخاص بها. إذا كانت تستخدم الخرطوم الأحمر فقط، فإن الأمر يستغرق$3$ ساعات أكثر مما لو كانت تستخدم الخرطوم الأخضر فقط. إذا استخدمت كلا الخراطيم معًا، يمتلئ حوض الاستحمام الساخن$2$ بساعات. كم من الوقت يستغرق كل خرطوم لملء حوض الاستحمام الساخن؟

إجابة: يستغرق الخرطوم الأحمر$6$ ساعات والخراطيم الخضراء تستغرق$3$ ساعات بمفردها.

يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات إضافية وممارسة حل التطبيقات التي تم تصميمها بواسطة المعادلات التربيعية.

المفاهيم الرئيسية

طرق حل المعادلات التربيعية
- التخص
- خاصية الجذر التربيعي
- إكمال المربع
- صيغة تربيعية
كيفية استخدام استراتيجية حل المشكلات.
1. اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
2. حدد ما نبحث عنه.
3. اذكر ما نبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.
4. ترجم إلى معادلة. قد يكون من المفيد إعادة ذكر المشكلة في جملة واحدة مع جميع المعلومات المهمة. ثم ترجم الجملة الإنجليزية إلى معادلة الجبر.
5. حل المعادلة باستخدام تقنيات الجبر الجيدة.
6. تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
7. أجب على السؤال بجملة كاملة.
مساحة المثلث
- بالنسبة للمثلث ذو القاعدة والارتفاع$b$$h$، تُعطى المساحة$A$،، بواسطة الصيغة$A=\frac{1}{2}bh$.

مساحة المستطيل
- بالنسبة للمستطيل ذي الطول والعرض$L$$W$، تُعطى المساحة$A$،، بواسطة الصيغة$A=LW$.

نظرية فيثاغورس
- في أي مثلث قائم الزاوية، أين$a$$b$ توجد أطوال الأرجل،$c$ ويكون طول الوتر،$a^{2}+b^{2}=c^{2}$.

حركة القذيفة
- تُحدد الصيغة الارتفاع بالأقدام لجسم أُطلق صعودًا في الهواء بسرعة أولية$v_{0}$، بعد$t$ ثوانٍ$h=-16 t^{2}+v_{0} t$.$h$

اكتب في الأسعار. اكتب في المسافات. منذ ذلك الحين\(D=r⋅t\)، نحل المشكلة \(t\) ونحصل عليها\(t=\frac{D}{r}\). نقسم المسافة على المعدل في كل صف، ونضع التعبير في عمود الوقت.	$.$
نحن نعلم أن الأوقات تضاف إلى\(9\) وهكذا نكتب المعادلة.	\(\frac{2000}{450-r}+\frac{2000}{450+r}=9\)
نضرب كلا الجانبين بواسطة شاشة LCD.	\((450-r)(450+r)\left(\frac{2000}{450-r}+\frac{2000}{450+r}\right)=9(450-r)(450+r)\)
قم بالتبسيط.	\(2000(450+r)+2000(450-r)=9(450-r)(450+r)\)
عامل ال\(2,000\).	\(2000(450+r+450-r)=9\left(450^{2}-r^{2}\right)\)
حل.	\(2000(900)=9\left(450^{2}-r^{2}\right)\)
اقسم على\(9\).	\(2000(100)=450^{2}-r^{2}\)
قم بالتبسيط.	\(\begin{aligned}200000&=202500-r^{2} \\ -2500&=-r^{2}\\ 50&=r\end{aligned}\)\ سرعة التيار النفاث هي\(50\) ميل في الساعة.
تحقق من: هل\(50\) ميل في الساعة هي سرعة معقولة للتيار النفاث؟ نعم. إذا كانت الطائرة تسير\(450\) ميلاً في الساعة وكانت الرياح\(50\) ميلاً في الساعة، الرياح الخلفية \(450+50=500 \mathrm{mph} \quad \frac{2000}{500}=4\)ساعات الرياح المعاكسة \(450-50=400 \mathrm{mph} \quad \frac{2000}{400}=5\)ساعات تضيف الأوقات إلى\(9\) ساعات، لذلك يتم التحقق.

مثال\(\PageIndex{1}\)

التمارين\(\PageIndex{1}\)

التمارين\(\PageIndex{2}\)

تعريف\(\PageIndex{1}\)

مثال\(\PageIndex{2}\)

التمارين\(\PageIndex{3}\)

التمارين\(\PageIndex{4}\)

تعريف\(\PageIndex{2}\)

مثال\(\PageIndex{3}\)

التمارين\(\PageIndex{5}\)

التمارين\(\PageIndex{6}\)

تعريف\(\PageIndex{3}\)

مثال\(\PageIndex{4}\)

التمارين\(\PageIndex{7}\)

التمارين\(\PageIndex{8}\)

تعريف\(\PageIndex{4}\)

مثال\(\PageIndex{5}\)

التمارين\(\PageIndex{9}\)

التمارين\(\PageIndex{10}\)

مثال\(\PageIndex{6}\)

التمارين\(\PageIndex{11}\)

التمارين\(\PageIndex{12}\)

مثال\(\PageIndex{7}\)

التمارين\(\PageIndex{13}\)

التمارين\(\PageIndex{14}\)

\(x=\)حدد عدد ساعات الضغط #2 لإكمال المهمة. أدخل الساعات لكل مهمة للضغط #1، ثم اضغط #2، والوقت الذي يعملون فيه معًا.	$.$
الجزء المكتمل بواسطة Press #1 بالإضافة إلى الجزء المكتمل بواسطة Press #2 يساوي المبلغ المكتمل معًا. ترجم إلى معادلة.	$.$
حل.	$.$
اضرب في شاشة LCD، 8\(x(x+12)\).	$.$
قم بالتبسيط.	$.$ $.$ الشكل 9.5.37 $.$ الشكل 9.5.38
حل.	$.$ $.$ الشكل 9.5.40 $.$ الشكل 9.5.41
نظرًا لأن فكرة الساعات السلبية لا معنى لها، فإننا نستخدم القيم\(x=12\).	$.$ $.$ الشكل 9.5.43
اكتب إجابة الجملة الخاصة بنا.	قد يستغرق الضغط على #1\(24\) ساعات والضغط على #2 سيستغرق\(12\) ساعات للقيام بهذه المهمة بمفرده.