9.5: حل المعادلات التربيعية في الصورة التربيعية

Last updated
Save as PDF

Page ID: 201652

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

حل المعادلات في الصورة التربيعية

قبل أن تبدأ

... خذ اختبار الاستعداد هذا.

عامل عن طريق الاستبدال:$y^{4}-y^{2}-20$.
عامل عن طريق الاستبدال:$(y-4)^{2}+8(y-4)+15$.
تبسيط
1. $x^{\frac{1}{2}} \cdot x^{\frac{1}{4}}$
2. $\left(x^{\frac{1}{3}}\right)^{2}$
3. $\left(x^{-1}\right)^{2}$

حل المعادلات في الصورة التربيعية

في بعض الأحيان عندما نأخذ في الاعتبار التثليث، لا يبدو أن الثلاثية في$ax^{2}+bx+c$ الشكل. لذلك قمنا بأخذ الاستبدال بعين الاعتبار مما يسمح لنا بجعله مناسبًا$ax^{2}+bx+c$ للنموذج. استخدمنا$u$ معيار الاستبدال.

لتحليل التعبير$x^{4}-4 x^{2}-5$، لاحظنا أن الجزء المتغير من الحد الأوسط هو$x^{2}$ ومربعه$x^{4}$، هو الجزء المتغير من الحد الأول. (نحن نعلم$\left(x^{2}\right)^{2}=x^{4}$.) لذلك سمحنا$u=x^{2}$ وأخذنا في الاعتبار.

	$x^{4}-4 x^{2}-5$
	$\left(\color{red}x^2 \color{black} \right)^{2}-4\left( \color{red}x^{2} \color{black}\right)-5$
دع$u=x^{2}$ واستبدل.	$\color{red}u \color{black}^{2}-4 \color{red}u \color{black}-5$
عامل ثلاثي الحدود.	$(u+1)(u-5)$
استبدل$u$ بـ$x^{2}$.	$\left( \color{red}x^{2} \color{black} + 1\right)\left( \color{red}x^2 \color{black}-5\right)$

وبالمثل، في بعض الأحيان لا تكون المعادلة في$ax^{2}+bx+c=0$ الشكل ولكنها تشبه إلى حد كبير المعادلة التربيعية. بعد ذلك، يمكننا غالبًا إجراء استبدال مدروس يسمح لنا بجعله مناسبًا$ax^{2}+bx+c=0$ للنموذج. إذا تمكنا من جعله مناسبًا للشكل، فيمكننا بعد ذلك استخدام جميع طرقنا لحل المعادلات التربيعية.

لاحظ أنه في المعادلة التربيعية$ax^{2}+bx+c=0$، يحتوي الحد الأوسط على متغير$x$$x^{2}$، ومربعه هو الجزء المتغير من الحد الأول. ابحث عن هذه العلاقة أثناء محاولتك العثور على بديل.

مرة أخرى، سنستخدم المعيار$u$ لإجراء الاستبدال الذي سيضع المعادلة في الصورة التربيعية. إذا كان الاستبدال يعطينا معادلة للنموذج$ax^{2}+bx+c=0$، فإننا نقول أن المعادلة الأصلية كانت في الصورة التربيعية.

يوضح المثال التالي خطوات حل معادلة في الصورة التربيعية.

مثال$\PageIndex{1}$ How to Solve Equations in Quadratic Form

حل:$6 x^{4}-7 x^{2}+2=0$

الحل:

الخطوة 1: تحديد الاستبدال الذي سيضع المعادلة في صورة تربيعية.	منذ ذلك الحين$\left(x^{2}\right)^{2}=x^{4}$، سمحنا$u=x^{2}$.	$6 x^{4}-7 x^{2}+2=0$
الخطوة 2: أعد كتابة المعادلة مع الاستبدال لوضعها في الصورة التربيعية.	أعد الكتابة للتحضير للاستبدال. بديل$u=x^{2}$.	$\begin{aligned}6\color{black}{\left(\color{red}{x^{2}}\right)}^{2}-7\color{red}{ x^{2}}\color{black}{+}2&=0 \\ \color{black}{6 \color{red}{u}^{2}}-7 \color{red}{u}\color{black}{+}2&=0\end{aligned}$
الخطوة 3: حل المعادلة التربيعية لـ$u$.	يمكننا حلها عن طريق التخصيم. استخدم خاصية المنتج الصفري.	$\begin{aligned}(2 u-1)(3 u-2) &=0 \\ 2 u-1=0, 3 u-2&=0 \\ 2 u =1,3 u&=2 \\ u =\frac{1}{2} u&=\frac{2}{3} \end{aligned}$
الخطوة 4: استبدل المتغير الأصلي مرة أخرى في النتائج باستخدام الاستبدال.	استبدل$u$ بـ$x^{2}$.	$x^{2}=\frac{1}{2} \quad x^{2}=\frac{2}{3}$
الخطوة 5: حل المتغير الأصلي.	قم بحل المشكلة باستخدام خاصية الجذر التربيعي.$x$	$\begin{array}{ll}{x=\pm \sqrt{\frac{1}{2}}} & {x=\pm \sqrt{\frac{2}{3}}} \\ {x=\pm \frac{\sqrt{2}}{2}} & {x=\pm \frac{\sqrt{6}}{3}}\end{array}$ هناك أربعة حلول. $\begin{array}{ll}{x=\frac{\sqrt{2}}{2}} & {x=\frac{\sqrt{6}}{3}} \\ {x=-\frac{\sqrt{2}}{2}} & {x=-\frac{\sqrt{6}}{3}}\end{array}$
الخطوة 6: تحقق من الحلول.	تحقق من جميع الحلول الأربعة. سنعرض شيكًا واحدًا هنا.	$\begin{aligned}x&=\frac{\sqrt{2}}{2} \\ 6 x^{4}-7 x^{2}+2&=0 \\ 6\left(\frac{\sqrt{2}}{2}\right)^{4}-7\left(\frac{\sqrt{2}}{2}\right)^{2}+2 &\stackrel{?}{=} 0\\ 6\left(\frac{4}{16} \right)-7\left(\frac{2}{4} \right)^{2}+2&\stackrel{?}{=}0 \\ \frac{3}{2}-\frac{7}{2}+\frac{4}{2}&\stackrel{?}{=}0 \\ 0&=0 \end{aligned}$ نترك الشيكات الأخرى لك!

التمارين$\PageIndex{1}$

حل:$x^{4}-6 x^{2}+8=0$.

إجابة: $x=\sqrt{2}, x=-\sqrt{2}, x=2, x=-2$

التمارين$\PageIndex{2}$

حل:$x^{4}-11 x^{2}+28=0$.

إجابة: $x=\sqrt{7}, x=-\sqrt{7}, x=2, x=-2$

نلخص خطوات حل المعادلة في الصورة التربيعية.

حل المعادلات في الصورة التربيعية

حدد الاستبدال الذي سيضع المعادلة في صورة تربيعية.
أعد كتابة المعادلة مع الاستبدال لوضعها في الصورة التربيعية.
حل المعادلة التربيعية لـ$u$.
استبدل المتغير الأصلي مرة أخرى في النتائج باستخدام الاستبدال.
حل للمتغير الأصلي.
تحقق من الحلول.

في المثال التالي، يتم تربيع المعادلة ذات الحدين في المدى المتوسط في الفصل الأول.$(x-2)$ إذا سمحنا$u=x-2$ واستبدلنا، ستكون معادلتنا الثلاثية في$a x^{2}+b x+c$ الشكل.

مثال$\PageIndex{2}$

حل:$(x-2)^{2}+7(x-2)+12=0$.

الحل:

	$(x-2)^{2}+7(x-2)+12=0$
استعد للاستبدال.	$\color{red}(x-2)\color{black}^{2}+7\color{red}(x-2) \color{black} +12=0$
دع$u=x-2$ واستبدل.	$\color{red}u^{\color{black}2} \color{black}+ 7 \color{red}u \color{black}+12=0$
حل عن طريق التخصيم	$(u+3)(u+4)=0$ \ (\ ابدأ {بالتجميع} u+3=0،\ رباعي u+4=0\\ u=-3،\ رباعي u=-4 \ النهاية {تم تجميعها}\)
استبدل$u$ بـ$x-2$.	$x-2=-3, \quad x-2=-4$
حل لـ$x$.	$x=-1, \quad x=-2$
تحقق من: 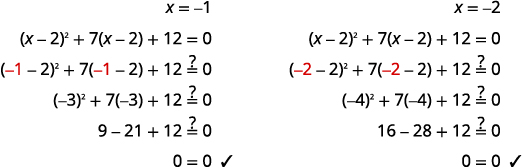$.$ الشكل 9.4.14

التمارين$\PageIndex{3}$

حل:$(x-5)^{2}+6(x-5)+8=0$.

إجابة: $x=3, x=1$

التمارين$\PageIndex{4}$

حل:$(y-4)^{2}+8(y-4)+15=0$.

إجابة: $y=-1, y=1$

في المثال التالي، نلاحظ ذلك$(\sqrt{x})^{2}=x$. تذكر أيضًا أنه عندما نرتب طرفي المعادلة، قد ندخل جذورًا غريبة. تأكد من التحقق من إجاباتك!

مثال$\PageIndex{3}$

حل:$x-3 \sqrt{x}+2=0$.

الحل:

$\sqrt{x}$في المدى المتوسط، يتم تربيعه في الفصل الأول$(\sqrt{x})^{2}=x$. إذا سمحنا$u=\sqrt{x}$ واستبدلنا، ستكون معادلتنا الثلاثية في$a x^{2}+b x+c=0$ الشكل.

	$x-3 \sqrt{x}+2=0$
أعد كتابة الثلاثية للتحضير للاستبدال.	$.$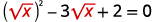
دع$u=\sqrt{x}$ واستبدل.	$.$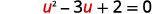
حل عن طريق التخصيم	$(u-2)(u-1)=0$ $u-2=0, \quad u-1=0$ $u=2, \quad u=1$\)
استبدل$u$ بـ$\sqrt{x}$.	$\sqrt{x}=2, \quad \sqrt{x}=1$
حل المشكلة$x$، من خلال تسوية كلا الجانبين.	$x=4, \quad x=1$
تحقق من: $.$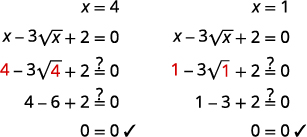

التمارين$\PageIndex{5}$

حل:$x-7 \sqrt{x}+12=0$.

إجابة: $x=9, x=16$

التمارين$\PageIndex{6}$

حل:$x-6 \sqrt{x}+8=0$.

إجابة: $x=4, x=16$

يمكن أن تساعدنا بدائل الأسس النسبية أيضًا في حل معادلة في الصورة التربيعية. فكر في خصائص الأسس عندما تبدأ المثال التالي.

مثال$\PageIndex{4}$

حل:$x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0$.

الحل:

يتم تربيع الرقم$x^{\frac{1}{3}}$ في المدى المتوسط في الفصل الأول$\left(x^{\frac{1}{3}}\right)^{2}=x^{\frac{2}{3}}$. إذا سمحنا$u=x^{\frac{1}{3}}$ واستبدلنا، ستكون معادلتنا الثلاثية في$a x^{2}+b x+c=0$ الشكل.

	$x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0$
أعد كتابة الثلاثية للتحضير للاستبدال.	$.$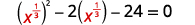
دع$u=x^{\frac{1}{3}}$	$.$
حل عن طريق التخصيم	$(u-6)(u+4)=0$ $u-6=0, \quad u+4=0$ $u=6, \quad u=-4$
استبدل$u$ بـ$x^{\frac{1}{3}}$.	$x^{\frac{1}{3}}=6, \quad x^{\frac{1}{3}}=-4$
حل المشكلة عن$x$ طريق تكعيب كلا الجانبين.	$\left(x^{\frac{1}{3}}\right)^{3}=(6)^{3}, \quad\left(x^{\frac{1}{3}}\right)^{3}=(-4)^{3}$ $x=216, \quad x=-64$
تحقق من: 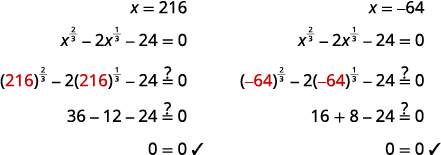$.$ الشكل 9.4.33

التمارين$\PageIndex{7}$

حل:$x^{\frac{2}{3}}-5 x^{\frac{1}{3}}-14=0$.

إجابة: $x=-8, x=343$

التمارين$\PageIndex{8}$

حل:$x^{\frac{1}{2}}+8 x^{\frac{1}{4}}+15=0$.

إجابة: $x=81, x=625$

في المثال التالي، يجب أن نضع في الاعتبار تعريف الأس السالب بالإضافة إلى خصائص الأسس.

مثال$\PageIndex{5}$

حل:$3 x^{-2}-7 x^{-1}+2=0$.

الحل:

يتم تربيع الرقم$x^{−1}$ في المدى المتوسط في الفصل الأول$\left(x^{-1}\right)^{2}=x^{-2}$. إذا سمحنا$u=x^{−1}$ واستبدلنا، ستكون معادلتنا الثلاثية في$a x^{2}+b x+c=0$ الشكل.

	$3 x^{-2}-7 x^{-1}+2=0$
أعد كتابة الثلاثية للتحضير للاستبدال.	$.$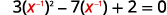
دع$u=x^{-1}$ واستبدل.	$.$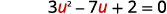
حل عن طريق التخصيم	$(3 u-1)(u-2)=0$
	$3 u-1=0, \quad u-2=0$
	$u=\frac{1}{3}, \quad u=2$
استبدل$u$ بـ$x^{-1}$.	$x^{-1}=\frac{1}{3}, \quad x^{-1}=2$
حل المشكلة$x$ بأخذ المعاملة بالمثل منذ ذلك الحين$x^{-1}=\frac{1}{x}$.	$x=3, \quad x=\frac{1}{2}$
تحقق من: 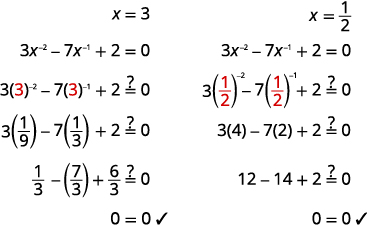$.$ الشكل 9.4.42

التمارين$\PageIndex{9}$

حل:$8 x^{-2}-10 x^{-1}+3=0$.

إجابة: $x=\frac{4}{3}, x=2$

التمارين$\PageIndex{10}$

حل:$6 x^{-2}-23 x^{-1}+20=0$.

إجابة: $x=\frac{2}{5}, x=\frac{3}{4}$

يمكنك الوصول إلى هذا الفيديو عبر الإنترنت للحصول على تعليمات إضافية وممارسة حل المعادلات التربيعية: https://www.youtube.com/watch?v=7X-CZMbpxuw

المفاهيم الرئيسية

كيفية حل المعادلات في الصورة التربيعية.
1. حدد الاستبدال الذي سيضع المعادلة في صورة تربيعية.
2. أعد كتابة المعادلة مع الاستبدال لوضعها في الصورة التربيعية.
3. حل المعادلة التربيعية لـ$u$.
4. استبدل المتغير الأصلي مرة أخرى في النتائج باستخدام الاستبدال.
5. حل للمتغير الأصلي.
6. تحقق من الحلول.

	\(x^{4}-4 x^{2}-5\)
	\(\left(\color{red}x^2 \color{black} \right)^{2}-4\left( \color{red}x^{2} \color{black}\right)-5\)
دع\(u=x^{2}\) واستبدل.	\(\color{red}u \color{black}^{2}-4 \color{red}u \color{black}-5\)
عامل ثلاثي الحدود.	\((u+1)(u-5)\)
استبدل\(u\) بـ\(x^{2}\).	\(\left( \color{red}x^{2} \color{black} + 1\right)\left( \color{red}x^2 \color{black}-5\right)\)

الخطوة 1: تحديد الاستبدال الذي سيضع المعادلة في صورة تربيعية.	منذ ذلك الحين\(\left(x^{2}\right)^{2}=x^{4}\)، سمحنا\(u=x^{2}\).	\(6 x^{4}-7 x^{2}+2=0\)
الخطوة 2: أعد كتابة المعادلة مع الاستبدال لوضعها في الصورة التربيعية.	أعد الكتابة للتحضير للاستبدال. بديل\(u=x^{2}\).	\(\begin{aligned}6\color{black}{\left(\color{red}{x^{2}}\right)}^{2}-7\color{red}{ x^{2}}\color{black}{+}2&=0 \\ \color{black}{6 \color{red}{u}^{2}}-7 \color{red}{u}\color{black}{+}2&=0\end{aligned}\)
الخطوة 3: حل المعادلة التربيعية لـ\(u\).	يمكننا حلها عن طريق التخصيم. استخدم خاصية المنتج الصفري.	\(\begin{aligned}(2 u-1)(3 u-2) &=0 \\ 2 u-1=0, 3 u-2&=0 \\ 2 u =1,3 u&=2 \\ u =\frac{1}{2} u&=\frac{2}{3} \end{aligned}\)
الخطوة 4: استبدل المتغير الأصلي مرة أخرى في النتائج باستخدام الاستبدال.	استبدل\(u\) بـ\(x^{2}\).	\(x^{2}=\frac{1}{2} \quad x^{2}=\frac{2}{3}\)
الخطوة 5: حل المتغير الأصلي.	قم بحل المشكلة باستخدام خاصية الجذر التربيعي.\(x\)	\(\begin{array}{ll}{x=\pm \sqrt{\frac{1}{2}}} & {x=\pm \sqrt{\frac{2}{3}}} \\ {x=\pm \frac{\sqrt{2}}{2}} & {x=\pm \frac{\sqrt{6}}{3}}\end{array}\) هناك أربعة حلول. \(\begin{array}{ll}{x=\frac{\sqrt{2}}{2}} & {x=\frac{\sqrt{6}}{3}} \\ {x=-\frac{\sqrt{2}}{2}} & {x=-\frac{\sqrt{6}}{3}}\end{array}\)
الخطوة 6: تحقق من الحلول.	تحقق من جميع الحلول الأربعة. سنعرض شيكًا واحدًا هنا.	\(\begin{aligned}x&=\frac{\sqrt{2}}{2} \\ 6 x^{4}-7 x^{2}+2&=0 \\ 6\left(\frac{\sqrt{2}}{2}\right)^{4}-7\left(\frac{\sqrt{2}}{2}\right)^{2}+2 &\stackrel{?}{=} 0\\ 6\left(\frac{4}{16} \right)-7\left(\frac{2}{4} \right)^{2}+2&\stackrel{?}{=}0 \\ \frac{3}{2}-\frac{7}{2}+\frac{4}{2}&\stackrel{?}{=}0 \\ 0&=0 \end{aligned}\) نترك الشيكات الأخرى لك!

	\((x-2)^{2}+7(x-2)+12=0\)
استعد للاستبدال.	\(\color{red}(x-2)\color{black}^{2}+7\color{red}(x-2) \color{black} +12=0\)
دع\(u=x-2\) واستبدل.	\(\color{red}u^{\color{black}2} \color{black}+ 7 \color{red}u \color{black}+12=0\)
حل عن طريق التخصيم	\((u+3)(u+4)=0\) \ (\ ابدأ {بالتجميع} u+3=0،\ رباعي u+4=0\\ u=-3،\ رباعي u=-4 \ النهاية {تم تجميعها}\)
استبدل\(u\) بـ\(x-2\).	\(x-2=-3, \quad x-2=-4\)
حل لـ\(x\).	\(x=-1, \quad x=-2\)
تحقق من: $.$ الشكل 9.4.14

	\(x-3 \sqrt{x}+2=0\)
أعد كتابة الثلاثية للتحضير للاستبدال.	$.$
دع\(u=\sqrt{x}\) واستبدل.	$.$
حل عن طريق التخصيم	\((u-2)(u-1)=0\) \(u-2=0, \quad u-1=0\) \(u=2, \quad u=1\)\)
استبدل\(u\) بـ\(\sqrt{x}\).	\(\sqrt{x}=2, \quad \sqrt{x}=1\)
حل المشكلة\(x\)، من خلال تسوية كلا الجانبين.	\(x=4, \quad x=1\)
تحقق من: $.$

	\(x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0\)
أعد كتابة الثلاثية للتحضير للاستبدال.	$.$
دع\(u=x^{\frac{1}{3}}\)	$.$
حل عن طريق التخصيم	\((u-6)(u+4)=0\) \(u-6=0, \quad u+4=0\) \(u=6, \quad u=-4\)
استبدل\(u\) بـ\(x^{\frac{1}{3}}\).	\(x^{\frac{1}{3}}=6, \quad x^{\frac{1}{3}}=-4\)
حل المشكلة عن\(x\) طريق تكعيب كلا الجانبين.	\(\left(x^{\frac{1}{3}}\right)^{3}=(6)^{3}, \quad\left(x^{\frac{1}{3}}\right)^{3}=(-4)^{3}\) \(x=216, \quad x=-64\)
تحقق من: $.$ الشكل 9.4.33

مثال\(\PageIndex{1}\) How to Solve Equations in Quadratic Form

التمارين\(\PageIndex{1}\)

التمارين\(\PageIndex{2}\)

حل المعادلات في الصورة التربيعية

مثال\(\PageIndex{2}\)

التمارين\(\PageIndex{3}\)

التمارين\(\PageIndex{4}\)

مثال\(\PageIndex{3}\)

التمارين\(\PageIndex{5}\)

التمارين\(\PageIndex{6}\)

مثال\(\PageIndex{4}\)

التمارين\(\PageIndex{7}\)

التمارين\(\PageIndex{8}\)

مثال\(\PageIndex{5}\)

التمارين\(\PageIndex{9}\)

التمارين\(\PageIndex{10}\)

	\(3 x^{-2}-7 x^{-1}+2=0\)
أعد كتابة الثلاثية للتحضير للاستبدال.	$.$
دع\(u=x^{-1}\) واستبدل.	$.$
حل عن طريق التخصيم	\((3 u-1)(u-2)=0\)
	\(3 u-1=0, \quad u-2=0\)
	\(u=\frac{1}{3}, \quad u=2\)
استبدل\(u\) بـ\(x^{-1}\).	\(x^{-1}=\frac{1}{3}, \quad x^{-1}=2\)
حل المشكلة\(x\) بأخذ المعاملة بالمثل منذ ذلك الحين\(x^{-1}=\frac{1}{x}\).	\(x=3, \quad x=\frac{1}{2}\)
تحقق من: $.$ الشكل 9.4.42