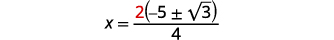9.4: حل المعادلات التربيعية باستخدام الصيغة التربيعية
- Page ID
- 201664
في نهاية هذا القسم، ستكون قادرًا على:
- حل المعادلات التربيعية باستخدام الصيغة التربيعية
- استخدم التمييز للتنبؤ بعدد ونوع حلول المعادلة التربيعية
- حدد الطريقة الأنسب التي يجب استخدامها لحل المعادلة التربيعية
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- قم بتقييم\(b^{2}-4 a b\) متى\(a=3\) و\(b=−2\).
- قم بالتبسيط\(\sqrt{108}\).
- قم بالتبسيط\(\sqrt{50}\).
حل المعادلات التربيعية باستخدام الصيغة التربيعية
عندما قمنا بحل المعادلات التربيعية في القسم الأخير بإكمال المربع، اتخذنا نفس الخطوات في كل مرة. في نهاية مجموعة التمارين، ربما كنت تتساءل «أليس هناك طريقة أسهل للقيام بذلك؟» الجواب هو «نعم». يبحث علماء الرياضيات عن الأنماط عندما يقومون بالأشياء مرارًا وتكرارًا من أجل تسهيل عملهم. في هذا القسم، سنشتق صيغة ونستخدمها لإيجاد حل المعادلة التربيعية.
لقد رأينا بالفعل كيفية حل صيغة لمتغير معين «بشكل عام»، بحيث نقوم بالخطوات الجبرية مرة واحدة فقط، ثم نستخدم الصيغة الجديدة للعثور على قيمة المتغير المحدد. سننتقل الآن إلى خطوات إكمال المربع باستخدام الشكل العام للمعادلة التربيعية لحل المعادلة التربيعية لـ\(x\).
نبدأ بالشكل القياسي للمعادلة التربيعية ونحلها\(x\) بإكمال المربع.
| \(ax^2 + bx + c = 0, \quad a \ne 0\) | |
| اعزل مصطلحات المتغير على جانب واحد. | \(ax^2 + bx \quad = -c\) |
| اجعل معامل\(x^{2}\) يساوي\(1\)، بالقسمة على\(a\). | \(\dfrac{ax^2}{a} + \dfrac{b}{a}x \quad = -\dfrac{c}{a}\) |
| قم بالتبسيط. | \(x^2+ \dfrac{b}{a}x \quad = -\dfrac{c}{a}\) |
| لإكمال المربع، ابحث\(\left(\dfrac{1}{2} \cdot \dfrac{b}{a}\right)^{2}\) عنه وأضفه إلى كلا طرفي المعادلة. | |
| \(\left(\dfrac{1}{2} \dfrac{b}{a}\right)^{2}=\dfrac{b^{2}}{4 a^{2}}\) | \(x^2 + \dfrac{b}{a}x +{\color{red}{\dfrac{b^2}{4a^2}}}{\color{black}{ = -\dfrac{c}{a}\,+\,}}{\color{red}{\dfrac{b^2}{4a^2}}}\) |
| الجانب الأيسر هو مربع مثالي، ضعه في الاعتبار. | \(\left( x + \dfrac{b}{2a}\right)^2 = -\dfrac{c}{a}+\dfrac{b^2}{4a^2}\) |
| ابحث عن المقام المشترك للجانب الأيمن واكتب الكسور المتكافئة ذات المقام المشترك. | \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2}{4a^2}-\dfrac{c\cdot\color{red}{4a}}{a\cdot\color{red}{4a}}\) |
| قم بالتبسيط. | \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2}{4a^2}-\dfrac{4ac}{4a^2}\) |
| ادمج في كسر واحد. | \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2-4ac}{4a^2}\) |
| استخدم خاصية الجذر التربيعي. | \(x + \dfrac{b}{2a}= \pm\sqrt{\dfrac{b^2-4ac}{4a^2}}\) |
| قم بتبسيط الراديكالية. | \(x + \dfrac{b}{2a}= \pm\dfrac{\sqrt{b^2-4ac}}{2a}\) |
| أضف\(-\dfrac{b}{2a}\) إلى كلا طرفي المعادلة. | \(x = -\dfrac{b}{2a} \pm\dfrac{\sqrt{b^2-4ac}}{2a}\) |
| ادمج المصطلحات الموجودة على الجانب الأيمن. | \(x = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\) |
تسمى المعادلة النهائية «الصيغة التربيعية».
حلول المعادلة التربيعية للنموذج\(a x^{2}+b x+c=0\)، حيث\(a≠0\) يتم تقديمها بواسطة الصيغة:
\[x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \label{quad}\]
لاستخدام الصيغة التربيعية، نستبدل قيم النموذج القياسي\(c\) ومنه إلى التعبير الموجود على الجانب الأيمن من الصيغة.\(a,b\) ثم نقوم بتبسيط التعبير. والنتيجة هي زوج من الحلول للمعادلة التربيعية.
لاحظ أن الصيغة التربيعية (المعادلة\ ref {quad}) هي معادلة. تأكد من استخدام كلا جانبي المعادلة.
حل باستخدام الصيغة التربيعية:\(2 x^{2}+9 x-5=0\).
الحل:
| الخطوة 1: اكتب المعادلة التربيعية في الصورة القياسية. حدد\(a,b,c\) القيم. | هذه المعادلة في الشكل القياسي. | \(\begin{aligned} \color{red}{a x^{2}+b x+c =0} \\ 2 x^{2}+9 x-5 =0 \\ a=2, b =9, c=-5 \end{aligned}\) |
| الخطوة 2: اكتب الصيغة التربيعية. ثم استبدل قيم\(a,b,c\). | استبدل في\(a=2, b=9, c=-5\) | \(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) \(x=\dfrac{-9 \pm \sqrt{9^{2}-4 \cdot 2 \cdot(-5)}}{2 \cdot 2}\) |
| الخطوة 3: تبسيط الكسر وحله\(x\). | \(\begin{array}{l}{x=\dfrac{-9 \pm \sqrt{81-(-40)}}{4}} \\ {x=\dfrac{-9 \pm \sqrt{121}}{4}} \\ {x=\dfrac{-9 \pm 11}{4}} \\ {x=\dfrac{-9+11}{4}}\quad x=\dfrac{-9-11}{4} \\ {x=\dfrac{2}{4} \quad \quad\:\:\: x=\dfrac{-20}{4}}\\ {x=\dfrac{1}{2} \quad\quad\:\:\: x=-5}\end{array}\) | |
| الخطوة 4: تحقق من الحلول. | ضع كل إجابة في المعادلة الأصلية للتحقق منها. بديل\(x=\color{red}{\dfrac{1}{2}}\) و\(x=\color{red}{-5}\). |
\(\begin{aligned}2 x^{2}+9 x-5&=0 \\ 2\color{black}{\left(\color{red}{\dfrac{1}{2}}\right)}^{2}+9 \cdot \color{red}{\dfrac{1}{2}}\color{black}{-}5 &\stackrel{?}{=} 0 \\ 2\cdot\dfrac{1}{4}+0\cdot\dfrac{1}{2}-5&\stackrel{?}{=}0 \\ 2\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{2}-5&\stackrel{?}{=}0 \\ \dfrac{1}{2}+\dfrac{9}{2}-5&\stackrel{?}{=}0 \\ \dfrac{10}{2}-5&\stackrel{?}{=}0 \\5-5&\stackrel{?}{=}0\\0&=0\end{aligned}\) \(\begin{array}{r}{2 x^{2}+9 x-5=0} \\ {2(\color{red}{-5}\color{black}{)}^{2}+9(\color{red}{-5}\color{black}{)}-5\stackrel{?}{=}0} \\ {2 \cdot 25-45-5\stackrel{?}{=}0} \\ {50-45-5\stackrel{?}{=}0} \\ {0=0}\end{array}\) |
حل باستخدام الصيغة التربيعية:\(3 y^{2}-5 y+2=0\).
- إجابة
-
\(y=1, y=\dfrac{2}{3}\)
حل باستخدام الصيغة التربيعية:\(4 z^{2}+2 z-6=0\).
- إجابة
-
\(z=1, z=-\dfrac{3}{2}\)
- اكتب المعادلة التربيعية في الصورة القياسية،\(a x^{2}+b x+c=0\). حدد قيم\(a,b\) و\(c\).
- اكتب الصيغة التربيعية. ثم استبدل قيم\(a,b\) و\(c\).
- قم بالتبسيط.
- تحقق من الحلول.
إذا قلت الصيغة أثناء كتابتها في كل مشكلة، فسوف يتم حفظها في أي وقت من الأوقات! وتذكر أن الصيغة التربيعية هي معادلة. تأكد من البدء بـ «\(x=\)».
حل باستخدام الصيغة التربيعية:\(x^{2}-6 x=-5\).
الحل:
|
\(x^{2}-6 x=-5\) |
|
| اكتب المعادلة في الصورة القياسية عن طريق الإضافة\(5\) إلى كل جانب. |
\(x^{2}-6 x+5=0\) |
| هذه المعادلة الآن في الشكل القياسي. |
\({\color{red}{\small{ax^2+bx + c} = \small{0}}}\) |
| تحديد قيم\(\color{cyan}a\)،\(\color{red}b\)،\(\color{limegreen}c\). | \({\color{cyan}a=1}\)،\({\color{red}b=-6}\)،\({\color{limegreen}c=5}\) |
| اكتب الصيغة التربيعية. |
\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) |
| ثم استبدل قيم\(a, b, c\). |
\(x=\dfrac{-\color{red} (-6 ) \color{black} \pm \sqrt{\color{red}(-6) \color{black}^{2}-4 \cdot \color{cyan}1 \color{black} \cdot ( \color{limegreen}5 \color{black})}}{2 \cdot \color{cyan} 1} \) |
| قم بالتبسيط. |
\(x=\dfrac{6 \pm \sqrt{36-20}}{2}\) \(x=\dfrac{6 \pm \sqrt{16}}{2}\) \(x=\dfrac{6 \pm 4}{2}\) |
| أعد الكتابة لإظهار حلين. |
\(x=\frac{6+4}{2}, \quad x=\frac{6-4}{2}\) |
| قم بالتبسيط. |
\(x=\frac{10}{2}, \quad x=\frac{2}{2}\) |
| \(x=5, \quad x=1\) | |
|
تحقق من: 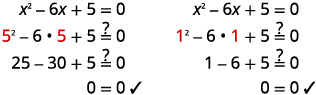 |
حل باستخدام الصيغة التربيعية:\(a^{2}-2 a=15\).
- إجابة
-
\(a=-3, a=5\)
حل باستخدام الصيغة التربيعية:\(b^{2}+24=-10 b\).
- إجابة
-
\(b=-6, b=-4\)
عندما قمنا بحل المعادلات التربيعية باستخدام خاصية الجذر التربيعي، نحصل أحيانًا على إجابات تحتوي على جذور. يمكن أن يحدث ذلك أيضًا عند استخدام الصيغة التربيعية. إذا حصلنا على حل جذري، يجب أن تحتوي الإجابة النهائية على الراديكالية في شكلها المبسط.
حل باستخدام الصيغة التربيعية:\(2 x^{2}+10 x+11=0\).
الحل:
 |
|
| هذه المعادلة في الشكل القياسي. |  |
| حدد قيم\(a,b\) و\(c\). |  |
| اكتب الصيغة التربيعية. |
\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) |
| ثم استبدل قيم\(a, b\) و\(c\). | 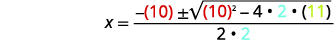 |
| قم بالتبسيط. |
\(x=\dfrac{-10 \pm \sqrt{100-88}}{4}\) |
|
\(x=\dfrac{-10 \pm \sqrt{12}}{4}\) |
|
| قم بتبسيط الراديكالية. |
\(x=\dfrac{-10 \pm 2 \sqrt{3}}{4}\) |
| ضع العامل المشترك في البسط في الاعتبار. |
\(x=\dfrac{\color{red}{2}(-5 \pm \sqrt{3})}{4}\) |
| قم بإزالة العوامل المشتركة. |
\(x=\dfrac{-5 \pm \sqrt{3}}{2}\) |
| أعد الكتابة لإظهار حلين. |
\(x=\dfrac{-5+\sqrt{3}}{2}, \quad x=\dfrac{-5-\sqrt{3}}{2}\) |
|
تحقق من: نترك الشيك لك! |
حل باستخدام الصيغة التربيعية:\(3 m^{2}+12 m+7=0\).
- إجابة
-
\(m=\dfrac{-6+\sqrt{15}}{3}, m=\dfrac{-6-\sqrt{15}}{3}\)
حل باستخدام الصيغة التربيعية:\(5 n^{2}+4 n-4=0\).
- إجابة
-
\(n=\dfrac{-2+2 \sqrt{6}}{5}, n=\dfrac{-2-2 \sqrt{6}}{5}\)
عندما نستبدل\(a, b\)، وفي\(c\) الصيغة التربيعية ويصبح الجذر سالبًا، ستحتوي المعادلة التربيعية على حلول خيالية أو معقدة. سنرى هذا في المثال التالي.
حل باستخدام الصيغة التربيعية:\(3 p^{2}+2 p+9=0\).
الحل:
 |
|
| هذه المعادلة في الشكل القياسي. |  |
| حدد قيم\(a,b,c\). |  |
| اكتب الصيغة التربيعية. | 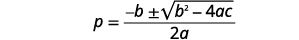 |
| ثم استبدل قيم\(a,b,c\). | 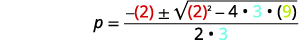 |
| قم بالتبسيط. | 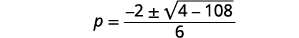 |
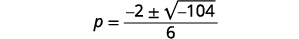 |
|
| قم بتبسيط الجذور باستخدام الأرقام المعقدة. | 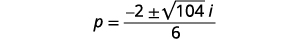 |
| قم بتبسيط الراديكالية. | 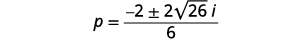 |
| ضع في اعتبارك العامل المشترك في البسط. | 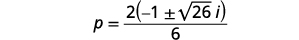 |
| قم بإزالة العوامل المشتركة. | 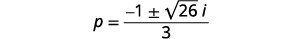 |
| أعد الكتابة في\(a+bi\) النموذج القياسي. | 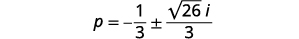 |
| اكتب كحلين. | 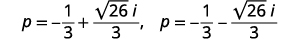 |
حل باستخدام الصيغة التربيعية:\(4 a^{2}-2 a+8=0\).
- إجابة
-
\(a=\dfrac{1}{4}+\dfrac{\sqrt{31}}{4} i, \quad a=\dfrac{1}{4}-\dfrac{\sqrt{31}}{4} i\)
حل باستخدام الصيغة التربيعية:\(5 b^{2}+2 b+4=0\).
- إجابة
-
\(b=-\dfrac{1}{5}+\dfrac{\sqrt{19}}{5} i, \quad b=-\dfrac{1}{5}-\dfrac{\sqrt{19}}{5} i\)
تذكر، لاستخدام الصيغة التربيعية، يجب كتابة المعادلة في شكل قياسي،\(a x^{2}+b x+c=0\). في بعض الأحيان، سنحتاج إلى إجراء بعض الجبر للحصول على المعادلة في الشكل القياسي قبل أن نتمكن من استخدام الصيغة التربيعية.
حل باستخدام الصيغة التربيعية:\(x(x+6)+4=0\).
الحل:
خطوتنا الأولى هي الحصول على المعادلة في النموذج القياسي.
 |
|
| قم بالتوزيع للحصول على المعادلة في النموذج القياسي. |  |
| هذه المعادلة الآن في الشكل القياسي. |  |
| حدد قيم\(a,b,c\). |  |
| اكتب الصيغة التربيعية. | 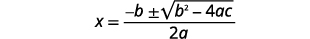 |
| ثم استبدل قيم\(a,b,c\). | 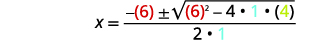 |
| قم بالتبسيط. | 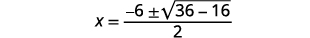 |
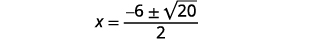 |
|
| قم بتبسيط الراديكالية. | 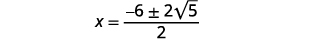 |
| ضع في اعتبارك العامل المشترك في البسط. | 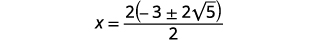 |
| قم بإزالة العوامل المشتركة. | 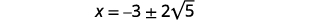 |
| اكتب كحلين. | 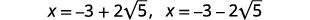 |
|
تحقق من: نترك الشيك لك! |
حل باستخدام الصيغة التربيعية:\(x(x+2)−5=0\).
- إجابة
-
\(x=-1+\sqrt{6}, x=-1-\sqrt{6}\)
حل باستخدام الصيغة التربيعية:\(3y(y−2)−3=0\).
- إجابة
-
\(y=1+\sqrt{2}, y=1-\sqrt{2}\)
عندما قمنا بحل المعادلات الخطية، إذا كانت المعادلة تحتوي على عدد كبير جدًا من الكسور، قمنا بمسح الكسور بضرب كلا طرفي المعادلة في شاشة LCD. أعطانا هذا معادلة مكافئة - بدون كسور - لحلها. يمكننا استخدام نفس الإستراتيجية مع المعادلات التربيعية.
حل باستخدام الصيغة التربيعية:\(\dfrac{1}{2} u^{2}+\dfrac{2}{3} u=\dfrac{1}{3}\).
الحل:
خطوتنا الأولى هي مسح الكسور.
 |
|
| اضرب كلا الجانبين في شاشة LCD لمسح الكسور.\(6\) | 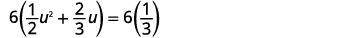 |
| اضرب. |  |
| اطرح\(2\) للحصول على المعادلة في الصورة القياسية. |  |
| حدد قيم\(a, b\) و\(c\). |  |
| اكتب الصيغة التربيعية. | 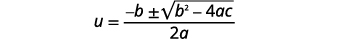 |
| ثم استبدل قيم\(a, b,\) و\(c\). | 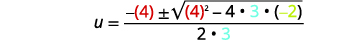 |
| قم بالتبسيط. | 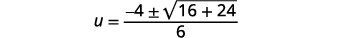 |
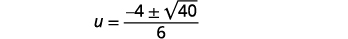 |
|
| قم بتبسيط الراديكالية. | 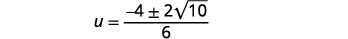 |
| ضع في اعتبارك العامل المشترك في البسط. | 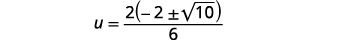 |
| قم بإزالة العوامل المشتركة. | 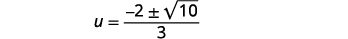 |
| أعد الكتابة لإظهار حلين. | 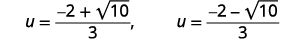 |
|
تحقق من: نترك الشيك لك! |
حل باستخدام الصيغة التربيعية:\(\dfrac{1}{4} c^{2}-\dfrac{1}{3} c=\dfrac{1}{12}\).
- إجابة
-
\(c=\dfrac{2+\sqrt{7}}{3}, \quad c=\dfrac{2-\sqrt{7}}{3}\)
حل باستخدام الصيغة التربيعية:\(\dfrac{1}{9} d^{2}-\dfrac{1}{2} d=-\dfrac{1}{3}\).
- إجابة
-
\(d=\dfrac{9+\sqrt{33}}{4}, d=\dfrac{9-\sqrt{33}}{4}\)
فكر في المعادلة\((x-3)^{2}=0\). نعلم من خاصية Zero Product أن هذه المعادلة لها حل واحد فقط،\(x=3\).
سنرى في المثال التالي كيفية استخدام الصيغة التربيعية لحل معادلة يكون شكلها القياسي مربعًا مثاليًا يساوي ثلاثي الحدود يساوي\(0\) حلًا واحدًا فقط. لاحظ أنه بمجرد تبسيط الجذور\(0\)، يصبح الأمر الذي يؤدي إلى حل واحد فقط.
حل باستخدام الصيغة التربيعية:\(4 x^{2}-20 x=-25\).
الحل:
 |
|
| أضف\(25\) للحصول على المعادلة في النموذج القياسي. |  |
| حدد قيم\(a, b\) و\(c\). |  |
| اكتب الصيغة التربيعية. | 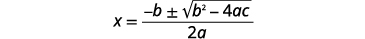 |
| ثم استبدل قيم\(a, b\) و\(c\). |  |
| قم بالتبسيط. | 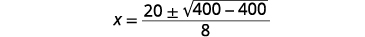 |
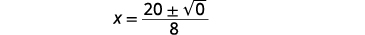 |
|
| قم بتبسيط الراديكالية. |  |
| قم بتبسيط الكسر. |  |
|
تحقق من: نترك الشيك لك! |
هل أدركت أن هذه\(4 x^{2}-20 x+25\) عبارة عن ثلاثية مربعة مثالية. وهو ما يعادل\((2 x-5)^{2}\)؟ إذا قمت بالحل\(4 x^{2}-20 x+25=0\) عن طريق العوملة ثم استخدام خاصية Square Root، فهل تحصل على نفس النتيجة؟
حل باستخدام الصيغة التربيعية:\(r^{2}+10 r+25=0\).
- إجابة
-
\(r=-5\)
حل باستخدام الصيغة التربيعية:\(25 t^{2}-40 t=-16\).
- إجابة
-
\(t=\dfrac{4}{5}\)
استخدم التمييز للتنبؤ بعدد ونوع حلول المعادلة التربيعية
عندما قمنا بحل المعادلات التربيعية في الأمثلة السابقة، أحيانًا نحصل على حلين حقيقيين، حل حقيقي واحد، وأحيانًا حلين معقدين. هل هناك طريقة للتنبؤ بعدد ونوع الحلول للمعادلة التربيعية دون حل المعادلة فعليًا؟
نعم، إن التعبير تحت جذر الصيغة التربيعية يجعل من السهل علينا تحديد عدد الحلول ونوعها. هذا التعبير يسمى التمييزي.
تمييزي

دعونا ننظر إلى تمييز المعادلات في بعض الأمثلة وعدد ونوع الحلول لتلك المعادلات التربيعية.
| المعادلة التربيعية (في الشكل القياسي) | تمييزي\(b^{2}-4ac\) | قيمة التمييز | عدد الحلول ونوعها |
|---|---|---|---|
| \(2 x^{2}+9 x-5=0\) | \ (b^ {2} -4ac\) ">\(\begin{aligned} 9^{2}-& 4 \cdot 2(-5) \\ & 121 \end{aligned}\) | \(+\) | \(2\)حقيقي |
| \(4 x^{2}-20 x+25=0\) | \ (b^ {2} -4ac\) ">\((-20)^{2}-4 \cdot 4 \cdot 25\) \(0\) |
\(0\) | \(1\)حقيقي |
| \(3 p^{2}+2 p+9=0\) | \ (b^ {2} -4ac\) ">\(2^{2}-4 \cdot 3 \cdot 9\) \(-104\) |
\(-\) | \(2\)مركب |

استخدام التمييز لتحديد\(b^{2}-4ac\) عدد الحلول ونوعها للمعادلة التربيعية
للمعادلة التربيعية للنموذج\(ax^{2}+bx+c=0\)،\(a \neq 0\)،
- إذا كانت\(b^{2}-4 a c>0\) المعادلة تحتوي على حلول\(2\) حقيقية.
- إذا كان\(b^{2}-4 a c=0\) للمعادلة حل\(1\) حقيقي.
- إذا كانت\(b^{2}-4 a c<0\) المعادلة تحتوي على حلول\(2\) معقدة.
أوجد عدد الحلول لكل معادلة تربيعية.
- \(3 x^{2}+7 x-9=0\)
- \(5 n^{2}+n+4=0\)
- \(9 y^{2}-6 y+1=0\)
الحل:
لتحديد عدد حلول كل معادلة تربيعية، سننظر إلى التمييز الخاص بها.
أ.
\(3 x^{2}+7 x-9=0\)
تكون المعادلة في الشكل القياسي، حدد\(a, b\)، و\(c\).
\(a=3, \quad b=7, \quad c=-9\)
اكتب التمييز.
\(b^{2}-4 a c\)
استبدل قيم\(a, b\) و\(c\).
\((7)^{2}-4 \cdot 3 \cdot(-9)\)
قم بالتبسيط.
\(49+108\)
\(157\)
نظرًا لأن التمييز إيجابي، فهناك حلول\(2\) حقيقية للمعادلة.
ب.
\(5 n^{2}+n+4=0\)
تكون المعادلة في الشكل القياسي، حدد\(a, b\)، و\(c\).
\(a=5, \quad b=1, \quad c=4\)
اكتب التمييز.
\(b^{2}-4 a c\)
استبدل قيم\(a, b\) و\(c\).
\((1)^{2}-4 \cdot 5 \cdot 4\)
قم بالتبسيط.
\(1-80\)
\(-79\)
نظرًا لأن التمييز سلبي، فهناك حلول\(2\) معقدة للمعادلة.
ج.
\(9 y^{2}-6 y+1=0\)
تكون المعادلة في الشكل القياسي، حدد\(a, b\)، و\(c\).
\(a=9, \quad b=-6, \quad c=1\)
اكتب التمييز.
\(b^{2}-4 a c\)
استبدل قيم\(a, b\) و\(c\).
\((-6)^{2}-4 \cdot 9 \cdot 1\)
قم بالتبسيط.
\(36-36\)
\(0\)
بما أن التمييز هو\(0\)، فهناك حل\(1\) حقيقي للمعادلة.
حدد عدد الحلول لكل معادلة تربيعية ونوعها.
- \(8 m^{2}-3 m+6=0\)
- \(5 z^{2}+6 z-2=0\)
- \(9 w^{2}+24 w+16=0\)
- إجابة
-
- \(2\)حلول معقدة
- \(2\)حلول حقيقية
- \(1\)حل حقيقي
حدد عدد الحلول لكل معادلة تربيعية ونوعها.
- \(b^{2}+7 b-13=0\)
- \(5 a^{2}-6 a+10=0\)
- \(4 r^{2}-20 r+25=0\)
- إجابة
-
- \(2\)حلول حقيقية
- \(2\)حلول معقدة
- \(1\)حل حقيقي
حدد الطريقة الأنسب لحل المعادلة التربيعية
نلخص الطرق الأربعة التي استخدمناها لحل المعادلات التربيعية أدناه.
طرق حل المعادلات التربيعية
- التخص
- خاصية الجذر التربيعي
- إكمال المربع
- صيغة تربيعية
بالنظر إلى أن لدينا أربع طرق لاستخدامها لحل المعادلة التربيعية، كيف يمكنك تحديد الطريقة التي يجب استخدامها؟ غالبًا ما يكون التخصيم هو أسرع طريقة ولذا نجربها أولاً. إذا كانت المعادلة هي\(ax^{2}=k\) أو\(a(x−h)^{2}=k\) نستخدم خاصية الجذر التربيعي. بالنسبة لأي معادلة أخرى، ربما يكون من الأفضل استخدام الصيغة التربيعية. تذكر أنه يمكنك حل أي معادلة تربيعية باستخدام الصيغة التربيعية، ولكن هذه ليست دائمًا الطريقة الأسهل.
ماذا عن طريقة إكمال المربع؟ يجد معظم الناس هذه الطريقة مرهقة ويفضلون عدم استخدامها. كنا بحاجة إلى تضمينه في قائمة الطرق لأننا أكملنا المربع بشكل عام لاشتقاق الصيغة التربيعية. ستستخدم أيضًا عملية إكمال المربع في مناطق الجبر الأخرى.
حدد الطريقة الأنسب لحل المعادلة التربيعية
- جرب التخصيم أولاً. إذا كانت العوامل التربيعية سهلة، فإن هذه الطريقة سريعة جدًا.
- جرب خاصية الجذر التربيعي بعد ذلك. إذا كانت المعادلة تناسب النموذج\(ax^{2}=k\)\(a(x−h)^{2}=k\) أو يمكن حلها بسهولة باستخدام خاصية الجذر التربيعي.
- استخدم الصيغة التربيعية. من الأفضل حل أي معادلة تربيعية أخرى باستخدام الصيغة التربيعية.
يستخدم المثال التالي هذه الإستراتيجية لتحديد كيفية حل كل معادلة تربيعية.
حدد الطريقة الأنسب لحل كل معادلة تربيعية.
- \(5 z^{2}=17\)
- \(4 x^{2}-12 x+9=0\)
- \(8 u^{2}+6 u=11\)
الحل:
أ.
\(5z^{2}=17\)
نظرًا لوجود المعادلة في\(ax^{2}=k\)، فإن الطريقة الأكثر ملاءمة هي استخدام خاصية الجذر التربيعي.
ب.
\(4 x^{2}-12 x+9=0\)
نحن ندرك أن الجانب الأيسر من المعادلة هو مربع كامل ثلاثي الحدود، وبالتالي فإن التحليل سيكون الطريقة الأنسب.
ج.
\(8 u^{2}+6 u=11\)
ضع المعادلة في النموذج القياسي.
\(8 u^{2}+6 u-11=0\)
في حين أن فكرتنا الأولى قد تكون محاولة العوملة، فإن التفكير في جميع إمكانيات طريقة التجربة والخطأ يقودنا إلى اختيار الصيغة التربيعية باعتبارها الطريقة الأنسب.
حدد الطريقة الأنسب لحل كل معادلة تربيعية.
- \(x^{2}+6 x+8=0\)
- \((n-3)^{2}=16\)
- \(5 p^{2}-6 p=9\)
- إجابة
-
- التخص
- خاصية الجذر التربيعي
- صيغة تربيعية
حدد الطريقة الأنسب لحل كل معادلة تربيعية.
- \(8 a^{2}+3 a-9=0\)
- \(4 b^{2}+4 b+1=0\)
- \(5 c^{2}=125\)
- إجابة
-
- صيغة تربيعية
- التخصيم أو خاصية الجذر المربع
- خاصية الجذر التربيعي
قم بالوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية باستخدام الصيغة التربيعية.
المفاهيم الرئيسية
- صيغة تربيعية
- يتم إعطاء حلول المعادلة\(a x^{2}+b x+c=0, a \neq 0\) التربيعية للنموذج بواسطة الصيغة:
\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
- يتم إعطاء حلول المعادلة\(a x^{2}+b x+c=0, a \neq 0\) التربيعية للنموذج بواسطة الصيغة:
- كيفية حل المعادلة التربيعية باستخدام الصيغة التربيعية.
- اكتب المعادلة التربيعية في الصورة القياسية،\(a x^{2}+b x+c=0\). حدد قيم\(a, b, c\).
- اكتب الصيغة التربيعية. ثم استبدل قيم\(a, b, c\).
- قم بالتبسيط.
- تحقق من الحلول.
- استخدام التمييز لتحديد عدد حلول المعادلة التربيعية ونوعها\(b^{2}-4 a c\)
- للمعادلة التربيعية للنموذج\(a x^{2}+b x+c=0, a \neq 0\)،
- إذا كانت\(b^{2}-4 a c>0\) المعادلة تحتوي على حلول\(2\) حقيقية.
- إذا كان\(b^{2}-4 a c=0\) للمعادلة حل\(1\) حقيقي.
- إذا كانت\(b^{2}-4 a c<0\) المعادلة تحتوي على حلول\(2\) معقدة.
- للمعادلة التربيعية للنموذج\(a x^{2}+b x+c=0, a \neq 0\)،
- طرق حل المعادلات التربيعية:
- التخص
- خاصية الجذر التربيعي
- إكمال المربع
- صيغة تربيعية
- كيفية تحديد الطريقة الأنسب لحل المعادلة التربيعية.
- جرب التخصيم أولاً. إذا كانت العوامل التربيعية سهلة، فإن هذه الطريقة سريعة جدًا.
- جرب خاصية الجذر التربيعي بعد ذلك. إذا كانت المعادلة تناسب النموذج\(a x^{2}=k\)\(a(x-h)^{2}=k\) أو يمكن حلها بسهولة باستخدام خاصية الجذر التربيعي.
- استخدم الصيغة التربيعية. من الأفضل حل أي معادلة تربيعية أخرى باستخدام الصيغة التربيعية.
مسرد المصطلحات
- تمييزي
- في الصيغة التربيعية\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)،\(b^{2}-4 a c\) تُسمى الكمية بالتمييز.