Skip to main content
Global

9.3: حل المعادلات التربيعية بإكمال المربع

  1. Last updated
  2. Save as PDF
  • Page ID
    201679

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • أكمل مربع التعبير ذي الحدين
    • حل المعادلات التربيعية\(x^{2}+bx+c=0\) للنموذج بإكمال المربع
    • حل المعادلات التربيعية\(ax^{2}+bx+c=0\) للنموذج بإكمال المربع

    قبل البدء، قم بإجراء اختبار الاستعداد هذا.

    1. قم بتوسيع:\((x+9)^{2}\).
      إذا فاتتك هذه المشكلة، راجع مثال 5.32.
    2. عامل\(y^{2}-14 y+49\).
      إذا فاتتك هذه المشكلة، راجع المثال 6.9.
    3. عامل\(5 n^{2}+40 n+80\).
      إذا فاتتك هذه المشكلة، راجع المثال 6.14.

    لقد قمنا حتى الآن بحل المعادلات التربيعية عن طريق تحليل واستخدام خاصية الجذر التربيعي. في هذا القسم، سوف نحل المعادلات التربيعية من خلال عملية تسمى إكمال المربع، وهو أمر مهم لعملنا على المخروط لاحقًا.

    أكمل مربع التعبير ذي الحدين

    في القسم الأخير، تمكنا من استخدام خاصية الجذر التربيعي لحل المعادلة\((y-7)^{2}=12\) لأن الجانب الأيسر كان مربعًا مثاليًا.

    \(\begin{aligned}(y-7)^{2} &=12 \\ y-7 &=\pm \sqrt{12} \\ y-7 &=\pm 2 \sqrt{3} \\ y &=7 \pm 2 \sqrt{3} \end{aligned}\)

    لقد حللنا أيضًا معادلة يكون فيها الجانب الأيسر عبارة عن مربع ثلاثي كامل، ولكن كان علينا إعادة كتابته بالشكل من\((x−k)^{2}\) أجل استخدام خاصية الجذر التربيعي.

    \(\begin{aligned} x^{2}-10 x+25 &=18 \\(x-5)^{2} &=18 \end{aligned}\)

    ماذا يحدث إذا لم يكن المتغير جزءًا من مربع مثالي؟ هل يمكننا استخدام الجبر لإنشاء مربع مثالي؟

    دعونا نلقي نظرة على مثالين لمساعدتنا في التعرف على الأنماط.

    \(\begin{array}{cc}{(x+9)^{2}} & {(y-7)^{2}} \\ {(x+9 )(x+9)} & {(y-7)(y-7)} \\ {x^{2}+9 x+9 x+81} & {y^{2}-7 y-7 y+49} \\ {x^{2}+18 x+81} & {y^{2}-14 y+49}\end{array}\)

    نعيد ذكر الأنماط هنا كمرجع.

    تعريف\(\PageIndex{1}\): Binomial Squares Pattern

    إذا كانت\(a\)\(b\) الأرقام حقيقية،

    الكمية a زائد b squared تساوي مربعًا زائد 2 a b زائد b2 حيث يساوي المربع ذو الحدين مربع الحد الأول زائد 2 أضعاف حاصل ضرب المصطلحات بالإضافة إلى مربع المصطلح الثاني. الكمية a ناقص b squared تساوي مربع ناقص 2 a b زائد b2 حيث يساوي المربع ذو الحدين الحد الأول التربيعي ناقص 2 في حاصل ضرب المصطلحات بالإضافة إلى مربع الحد الثاني.

    يمكننا استخدام هذا النمط «لصنع» مربع مثالي.

    سنبدأ بالتعبير\(x^{2}+6 x\). نظرًا لوجود علامة الجمع بين المصطلحين، سنستخدم\((a+b)^{2}\) النمط،\(a^{2}+2 a b+b^{2}=(a+b)^{2}\).

    يظهر التعبير المربع المثالي a squared زائد 2 a b plus b squared فوق التعبير x squared بالإضافة إلى 6x بالإضافة إلى المجهول للسماح بمقارنة المصطلحات المقابلة للتعبيرات.

    نحتاج في النهاية إلى إيجاد المصطلح الأخير من هذا الثلاثي الذي سيجعله مربعًا ثلاثيًا مثاليًا. للقيام بذلك سنحتاج إلى العثور عليها\(b\). لكن أولاً نبدأ بالتحديد\(a\). لاحظ أن المصطلح الأول\(x^{2}+6x\) هو مربع,\(x^{2}\). هذا يخبرنا بذلك\(a=x\).

    يظهر التعبير المربع المثالي a squared زائد 2 a b زائد b squared فوق التعبير x squared زائد 2 x b + b squared. لاحظ أنه تم استبدال x بـ a في المعادلة الثانية وقارن المصطلحات المقابلة.

    ما العدد\(b\)، عند ضربه\(2x\) بالعطاء\(6x\)؟ يجب أن يكون\(3\)، وهو\(\frac{1}{2}(6)\). لذا\(b=3\).

    يظهر التعبير المربع المثالي a squared زائد 2 a b plus b squared فوق التعبير x squared بالإضافة إلى 2 في 3 مرات x بالإضافة إلى قيمة غير معروفة للمساعدة في مقارنة المصطلحات.

    الآن لإكمال المعادلة الثلاثية المربعة المثالية، سنجد الحد الأخير عن طريق التربيع\(b\)، وهو\(3^{2}=9\).

    يظهر التعبير المربع المثالي a squared زائد 2 a b زائد b squared فوق التعبير x squared زائد 6 x plus 9.

    يمكننا الآن أن نأخذ في الاعتبار.

    يظهر التعبير المعامل، مربع a plus b، فوق مربع التعبير x + 3.

    لذلك وجدنا أن الإضافة\(9\) إلى\(x^{2}+6 x\) «تكمل المربع»، ونكتبها كـ\((x+3)^{2}\).

    كيفية: أكمل مربعًا بـ\(x^{2}+bx\)
    1. حدد\(b\) معامل\(x\).
    2. ابحث\(\left(\frac{1}{2} b\right)^{2}\) عن الرقم المطلوب لإكمال المربع.
    3. أضف\(\left(\frac{1}{2} b\right)^{2}\) إلى\(x^{2}+bx\).
    4. ضع المعادلة الثلاثية المربعة المثالية بعين الاعتبار، واكتبها في صورة مربع ذو حدين.
    مثال\(\PageIndex{1}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. ثم اكتب النتيجة في صورة مربع ذو حدين.

    1. \(x^{2}-26 x\)
    2. \(y^{2}-9 y\)
    3. \(n^{2}+\frac{1}{2} n\)

    الحل:

    أ.

      .
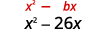    المعامل\(x\) هو -26.  

    ابحث\(\left(\frac{1}{2} b\right)^{2}\).

    \(\left(\frac{1}{2} \cdot(-26)\right)^{2}\)
    \((13)^{2}\)
    169

    		  
    أضف\(169\) إلى المعادلة ذات الحدين لإكمال المربع.

    \(x^{2}-26 x+169\)
    ضع المعادلة الثلاثية المربعة المثالية بعين الاعتبار، واكتبها في صورة مربع ذو حدين.

    \((x-13)^{2}\)

    ب.

      .
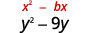    معامل\(y\) هو\(-9\).  

    ابحث\(\left(\frac{1}{2} b\right)^{2}\).

    \(\left(\frac{1}{2} \cdot(-9)\right)^{2}\)
    \(\left(-\frac{9}{2}\right)^{2}\)
    \(\frac{81}{4}\)

    		  
    أضف\(\frac{81}{4}\) إلى المعادلة ذات الحدين لإكمال المربع.

    \(y^{2}-9 y+\frac{81}{4}\)
    ضع المعادلة الثلاثية المربعة المثالية بعين الاعتبار، واكتبها في صورة مربع ذو حدين.

    \(\left(y-\frac{9}{2}\right)^{2}\)

    ج.

      .
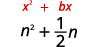    معامل\(n\) هو\(\frac{1}{2}\).  

    ابحث\(\left(\frac{1}{2} b\right)^{2}\).

    \(\left(\frac{1}{2} \cdot \frac{1}{2}\right)^{2}\)
    \(\left(\frac{1}{4}\right)^{2}\)
    \(\frac{1}{16}\)

    		  
    أضف\(\frac{1}{16}\) إلى المعادلة ذات الحدين لإكمال المربع. \(n^{2}+\frac{1}{2} n+\frac{1}{16}\)
    أعد الكتابة كمربع ذو حدين. \(\left(n+\frac{1}{4}\right)^{2}\)
    التمارين الرياضية\(\PageIndex{1}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. ثم اكتب النتيجة في صورة مربع ذو حدين.

    1. \(a^{2}-20 a\)
    2. \(m^{2}-5 m\)
    3. \(p^{2}+\frac{1}{4} p\)
    إجابة
    1. \((a-10)^{2}\)
    2. \(\left(b-\frac{5}{2}\right)^{2}\)
    3. \(\left(p+\frac{1}{8}\right)^{2}\)
    التمارين الرياضية\(\PageIndex{2}\)

    أكمل المربع لإنشاء مربع ثلاثي الحدود مثالي. ثم اكتب النتيجة في صورة مربع ذو حدين.

    1. \(b^{2}-4 b\)
    2. \(n^{2}+13 n\)
    3. \(q^{2}-\frac{2}{3} q\)
    إجابة
    1. \((b-2)^{2}\)
    2. \(\left(n+\frac{13}{2}\right)^{2}\)
    3. \(\left(q-\frac{1}{3}\right)^{2}\)

    حل المعادلات التربيعية\(x^{2}+bx+c=0\) للنموذج بإكمال المربع

    في حل المعادلات، يجب أن نفعل دائمًا نفس الشيء لكلا طرفي المعادلة. هذا صحيح بالطبع عندما نحل المعادلة التربيعية بإكمال المربع أيضًا. عندما نضيف حدًا إلى أحد طرفي المعادلة لتكوين مربع كامل ثلاثي الحدود، يجب علينا أيضًا إضافة نفس الحد إلى الجانب الآخر من المعادلة.

    على سبيل المثال، إذا بدأنا بالمعادلة\(x^{2}+6x=40\)، وأردنا إكمال المربع الموجود على اليسار، فسنضيف 9 إلى كلا طرفي المعادلة.

      .
      .
      .
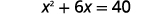    أضف\(9\) إلى كلا الجانبين لإكمال المربع. .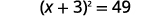

    الآن المعادلة في شكل الحل باستخدام خاصية الجذر التربيعي! يعد إكمال المربع طريقة لتحويل المعادلة إلى النموذج الذي نحتاجه حتى نتمكن من استخدام خاصية الجذر التربيعي.

    مثال\(\PageIndex{2}\) How to Solve a Quadratic Equation of the Form \(x^{2}+bx+x=0\) by Completing the Square

    حل عن طريق إكمال المربع:\(x^{2}+8x=48\).

    الحل:

    الخطوة 1: اعزل مصطلحات المتغير من جهة والشروط الثابتة من جهة أخرى. تحتوي هذه المعادلة على جميع المتغيرات على اليسار. \(\begin{array}{l}{\color{red}{x^{2}+b x\quad\:\:\: c }} \\ {x^{2}+8 x=48}\end{array}\)
    الخطوة 2: ابحث\(\left(\frac{1}{2} \cdot b\right)^{2}\) عن الرقم لإكمال المربع. أضفه إلى كلا طرفي المعادلة.

    خذ نصفها\(8\) وقم بترتيبها.

    \(4^{2}=16\)

    أضف\(16\) إلى كلا طرفي المعادلة.

    \(x^{2}+8 x+\frac{}{\color{red}{\left(\frac{1}{2} \cdot 8\right)^{2}}}\color{black}{=}48 \)

    \(x^{2}+8 x\color{red}{+16}\color{black}{=}48\color{red}{+16}\)
    الخطوة 3: ضع مربع ثلاثي الحدود المثالي كمربع ذو حدين.

    \(x^{2}+8 x+16=(x+4)^{2}\)

    أضف المصطلحات الموجودة على اليمين.

    		 \((x+4)^{2}=64\)
    الخطوة 4: استخدم خاصية الجذر التربيعي.   \(x+4=\pm \sqrt{64}\)
    الخطوة 5: تبسيط الجذر ثم حل المعادلتين الناتجتين.  

    \(x+4=\pm 8\)

    \(\begin{aligned} x+4 &=8 \quad x+4=-8 \\ x &=4 \quad\quad\:\:\: x=-12 \end{aligned}\)
    الخطوة 6: تحقق من الحلول. ضع كل إجابة في المعادلة الأصلية للتحقق منها. بديل\(x=4\) و\(x=-12\).

    \(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{4}\color{black}{)}^{2}+8(\color{red}{4}\color{black}{)} \stackrel{?}{=} 48} \\ {16+32\stackrel{?}{=}48} \\ {48=48}\end{array}\)

    \(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{-12}\color{black}{)}^{2}+8(\color{red}{-12}\color{black}{)}\stackrel{?}{=} 48} \\ {144-96 \stackrel{?}{=} 48} \\ {48=48}\end{array}\)
    التمارين الرياضية\(\PageIndex{3}\)

    حل عن طريق إكمال المربع:\(x^{2}+4 x=5\).

    إجابة

    \(x=-5, x=-1\)

    التمارين الرياضية\(\PageIndex{4}\)

    حل عن طريق إكمال المربع:\(y^{2}−10y=−9\).

    إجابة

    \(y=1, y=9\)

    يتم سرد خطوات حل المعادلة التربيعية بإكمال المربع هنا.

    حل المعادلة التربيعية\(x^{2}+bx+c=0\) للنموذج بإكمال المربع

    1. اعزل المصطلحات المتغيرة على أحد الجانبين والشروط الثابتة على الجانب الآخر.
    2. ابحث\(\left(\frac{1}{2} \cdot b\right)^{2}\) عن الرقم المطلوب لإكمال المربع. أضفه إلى كلا طرفي المعادلة.
    3. قم بتحليل المعادلة الثلاثية المثالية للمربع، واكتبها كمربع ذو حدين على اليسار وقم بالتبسيط عن طريق إضافة المصطلحات الموجودة على اليمين
    4. استخدم خاصية الجذر التربيعي.
    5. قم بتبسيط الجذر ثم حل المعادلتين الناتجتين.
    6. تحقق من الحلول.

    عندما نحل معادلة بإكمال المربع، لن تكون الإجابات دائمًا أعدادًا صحيحة.

    مثال\(\PageIndex{3}\)

    حل عن طريق إكمال المربع:\(x^{2}+4 x=-21\).

    الحل:

      .

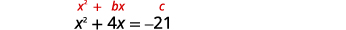    توجد المصطلحات المتغيرة على الجانب الأيسر.

    خذ نصفها\(4\) وقم بترتيبها.

    		 .
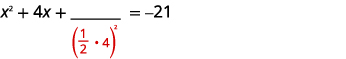    \(\left(\frac{1}{2}(4)\right)^{2}=4\)  
    أضف\(4\) إلى كلا الجانبين. .
    ضع المعادلة الثلاثية المربعة المثالية بعين الاعتبار، واكتبها في صورة مربع ذو حدين. .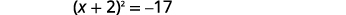
    استخدم خاصية الجذر التربيعي. .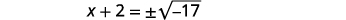
    تبسيط استخدام الأرقام المركبة. .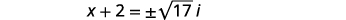
    اطرح\(2\) من كل جانب. .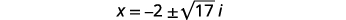
    أعد الكتابة لإظهار حلين. .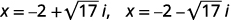
    نترك الشيك لك.  
    التمارين الرياضية\(\PageIndex{5}\)

    حل عن طريق إكمال المربع:\(y^{2}-10 y=-35\).

    إجابة

    \(y=5+\sqrt{15} i, y=5-\sqrt{15 i}\)

    التمارين الرياضية\(\PageIndex{6}\)

    حل عن طريق إكمال المربع:\(z^{2}+8 z=-19\).

    إجابة

    \(z=-4+\sqrt{3} i, z=-4-\sqrt{3} i\)

    في المثال السابق، كانت حلولنا عبارة عن أرقام معقدة. في المثال التالي، ستكون الحلول عبارة عن أرقام غير منطقية.

    مثال\(\PageIndex{4}\)

    حل عن طريق إكمال المربع:\(y^{2}-18 y=-6\).

    الحل:

      .
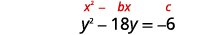    توجد المصطلحات المتغيرة على الجانب الأيسر. خذ نصفها\(-18\) وقم بترتيبها.
    \(\left(\frac{1}{2}(-18)\right)^{2}=81\) .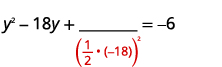
    أضف\(81\) إلى كلا الجانبين. .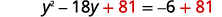
    ضع المعادلة الثلاثية المربعة المثالية بعين الاعتبار، واكتبها في صورة مربع ذو حدين. .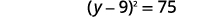
    استخدم خاصية الجذر التربيعي. .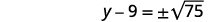
    تبسيط الراديكالية. .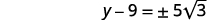
    حل لـ\(y\). .

    تحقق.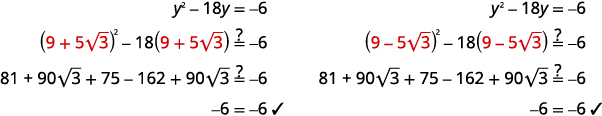

    .
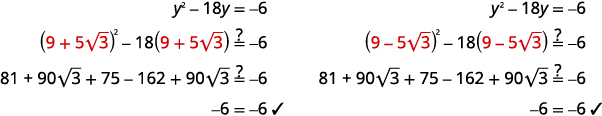    الشكل 9.2.35
    		 .

    هناك طريقة أخرى للتحقق من ذلك وهي استخدام الآلة الحاسبة. قم بتقييم\(y^{2}−18y\) كلا الحلين. يجب أن تكون الإجابة\(−6\).

    التمارين الرياضية\(\PageIndex{7}\)

    حل عن طريق إكمال المربع:\(x^{2}-16 x=-16\).

    إجابة

    \(x=8+4 \sqrt{3}, x=8-4 \sqrt{3}\)

    التمارين الرياضية\(\PageIndex{8}\)

    حل عن طريق إكمال المربع:\(y^{2}+8 y=11\).

    إجابة

    \(y=-4+3 \sqrt{3}, y=-4-3 \sqrt{3}\)

    سنبدأ المثال التالي بعزل مصطلحات المتغير على الجانب الأيسر من المعادلة.

    مثال\(\PageIndex{5}\)

    حل عن طريق إكمال المربع:\(x^{2}+10 x+4=15\).

    الحل:

      .
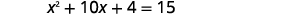    اعزل مصطلحات المتغير على الجانب الأيسر. اطرح\(4\) للحصول على الشروط الثابتة على الجانب الأيمن. .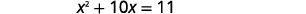
    خذ نصفها\(10\) وقم بترتيبها.  
    \(\left(\frac{1}{2}(10)\right)^{2}=25\) .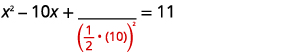
    أضف\(25\) إلى كلا الجانبين. .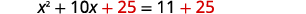
    ضع المعادلة الثلاثية المربعة المثالية بعين الاعتبار، واكتبها في صورة مربع ذو حدين. .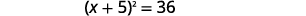
    استخدم خاصية الجذر التربيعي. .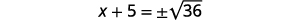
    تبسيط الراديكالية. .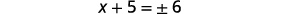
    حل لـ\(x\). .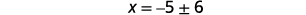
    أعد الكتابة لإظهار حلين. .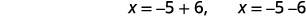
    حل المعادلات. .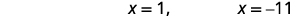

    تحقق من: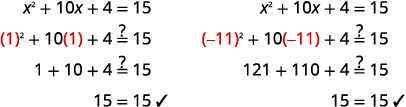

    .
    الشكل 9.2.47
    		  
    التمارين الرياضية\(\PageIndex{9}\)

    حل عن طريق إكمال المربع:\(a^{2}+4 a+9=30\).

    إجابة

    \(a=-7, a=3\)

    التمارين الرياضية\(\PageIndex{10}\)

    حل عن طريق إكمال المربع:\(b^{2}+8 b-4=16\).

    إجابة

    \(b=-10, b=2\)

    لحل المعادلة التالية، يجب علينا أولاً جمع كل مصطلحات المتغيرات على الجانب الأيسر من المعادلة. ثم نمضي كما فعلنا في الأمثلة السابقة.

    مثال\(\PageIndex{6}\)

    حل عن طريق إكمال المربع:\(n^{2}=3 n+11\).

    الحل:

      .
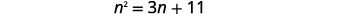    اطرح\(3n\) للحصول على الشروط المتغيرة على الجانب الأيسر. .
    خذ نصفها\(-3\) وقم بترتيبها.  
    \(\left(\frac{1}{2}(-3)\right)^{2}=\frac{9}{4}\) .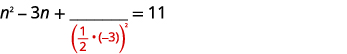
    أضف\(\frac{9}{4}\) إلى كلا الجانبين. .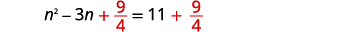
    ضع المعادلة الثلاثية المربعة المثالية بعين الاعتبار، واكتبها في صورة مربع ذو حدين. .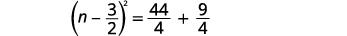
    أضف الكسور الموجودة على الجانب الأيمن. .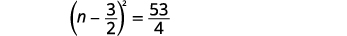
    استخدم خاصية الجذر التربيعي. .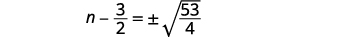
    تبسيط الراديكالية. .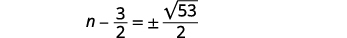
    حل لـ\(n\). .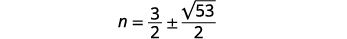
    أعد الكتابة لإظهار حلين. .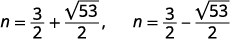

    تحقق من:

    نترك الشيك لك!

    		  
    التمارين الرياضية\(\PageIndex{11}\)

    حل عن طريق إكمال المربع:\(p^{2}=5 p+9\).

    إجابة

    \(p=\frac{5}{2}+\frac{\sqrt{61}}{2}, p=\frac{5}{2}-\frac{\sqrt{61}}{2}\)

    التمارين الرياضية\(\PageIndex{12}\)

    حل عن طريق إكمال المربع:\(q^{2}=7 q-3\).

    إجابة

    \(q=\frac{7}{2}+\frac{\sqrt{37}}{2}, q=\frac{7}{2}-\frac{\sqrt{37}}{2}\)

    لاحظ أن الجانب الأيسر من المعادلة التالية هو في شكل عامل. لكن الجانب الأيمن ليس صفرًا. لذلك، لا يمكننا استخدام خاصية Zero Product لأنها تقول «If\(a⋅b=0\)، then\(a=0\) أو»\(b=0\). بدلاً من ذلك، نضرب العوامل ثم نضع المعادلة في الصورة القياسية لحلها بإكمال المربع.

    مثال\(\PageIndex{7}\)

    حل عن طريق إكمال المربع:\((x-3)(x+5)=9\).

    الحل:

      .
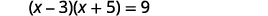    نضرب المقادير ذات الحدين على اليسار. .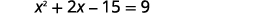
    أضف\(15\) لعزل المصطلحات الثابتة على اليمين. .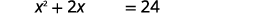
    خذ نصفها\(2\) وقم بترتيبها.  
    \(\left(\frac{1}{2} \cdot(2)\right)^{2}=1\) .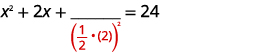
    أضف\(1\) إلى كلا الجانبين. .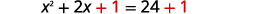
    ضع المعادلة الثلاثية المربعة المثالية بعين الاعتبار، واكتبها في صورة مربع ذو حدين. .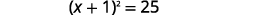
    استخدم خاصية الجذر التربيعي. .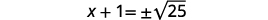
    حل لـ\(x\). .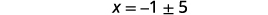
    أعد الكتابة لإظهار حلين. .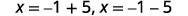
    قم بالتبسيط. .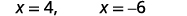

    تحقق من:

    نترك الشيك لك!

    		  
    التمارين الرياضية\(\PageIndex{13}\)

    حل عن طريق إكمال المربع:\((c-2)(c+8)=11\).

    إجابة

    \(c=-9, c=3\)

    التمارين الرياضية\(\PageIndex{14}\)

    حل عن طريق إكمال المربع:\((d-7)(d+3)=56\).

    إجابة

    \(d=11, d=-7\)

    حل المعادلات التربيعية\(ax^{2}+bx+c=0\) للنموذج بإكمال المربع

    تعمل عملية إكمال المربع بشكل أفضل عندما يكون المعامل\(x^{2}\) هو\(1\)، لذلك يكون الجانب الأيسر من المعادلة من الشكل\(x^{2}+bx+c\). إذا كان\(x^{2}\) المصطلح يحتوي على معامل آخر غير\(1\) ذلك، فإننا نتخذ بعض الخطوات الأولية لجعل المعامل مساويًا لـ\(1\).

    في بعض الأحيان يمكن حساب المعامل من جميع المصطلحات الثلاثة للثلاثية. ستكون هذه استراتيجيتنا في المثال التالي.

    مثال\(\PageIndex{8}\)

    حل عن طريق إكمال المربع:\(3 x^{2}-12 x-15=0\).

    الحل:

    لإكمال المربع، نحتاج\(x^{2}\) إلى معامل واحد. إذا قمنا بحساب المعامل\(x^{2}\) كعامل مشترك، يمكننا الاستمرار في حل المعادلة بإكمال المربع.

      .
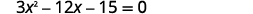    ضع العامل المشترك الأكبر في الاعتبار. .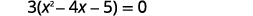
    قسّم كلا الجانبين\(3\) لعزل الثلاثي باستخدام المعامل\(1\). .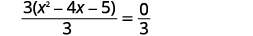
    قم بالتبسيط. .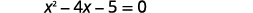
    أضف\(5\) للحصول على الشروط الثابتة على الجانب الأيمن. .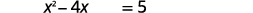
    خذ نصفها\(4\) وقم بتجميعها.  
    \(\left(\frac{1}{2}(-4)\right)^{2}=4\) .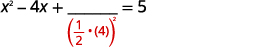
    أضف\(4\) إلى كلا الجانبين. .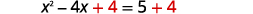
    ضع المعادلة الثلاثية المربعة المثالية بعين الاعتبار، واكتبها في صورة مربع ذو حدين. .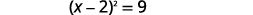
    استخدم خاصية الجذر التربيعي. .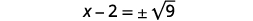
    حل لـ\(x\). .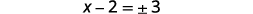
    أعد الكتابة لإظهار حلين. .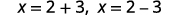
    قم بالتبسيط. .

    تحقق من: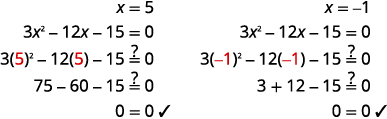

    .
    الشكل 9.2.80
    		  
    التمارين الرياضية\(\PageIndex{15}\)

    حل عن طريق إكمال المربع:\(2 m^{2}+16 m+14=0\).

    إجابة

    \(m=-7, m=-1\)

    التمارين الرياضية\(\PageIndex{16}\)

    حل عن طريق إكمال المربع:\(4 n^{2}-24 n-56=8\).

    إجابة

    \(n=-2, n=8\)

    لإكمال المربع،\(x^{2}\) يجب أن يكون معامل القيمة\(1\). عندما لا يكون المعامل الرئيسي عاملاً لجميع المصطلحات، سنقسم كلا جانبي المعادلة بالمعامل الرئيسي! سيعطينا هذا جزءًا من المعامل الثاني. لقد رأينا بالفعل كيفية إكمال المربع بالكسور في هذا القسم.

    مثال\(\PageIndex{9}\)

    حل عن طريق إكمال المربع:\(2 x^{2}-3 x=20\).

    الحل:

    لإكمال المربع، نحتاج\(x^{2}\) إلى معامل واحد. سنقسم طرفي المعادلة بمعامل\(x^{2}\). ثم يمكننا متابعة حل المعادلة بإكمال المربع.

      .
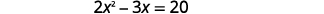    قسّم كلا الجانبين\(2\) للحصول على معامل\(x^{2}\) أن يكون\(1\). .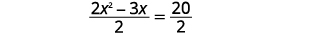
    قم بالتبسيط. .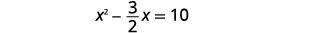
    خذ نصفها\(-\frac{3}{2}\) وقم بتجميعها.  
    \(\left(\frac{1}{2}\left(-\frac{3}{2}\right)\right)^{2}=\frac{9}{16}\) .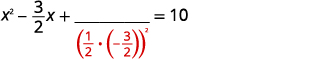
    أضف\(\frac{9}{16}\) إلى كلا الجانبين. .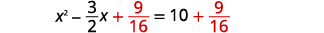
    ضع المعادلة الثلاثية المربعة المثالية بعين الاعتبار، واكتبها في صورة مربع ذو حدين. .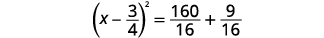
    أضف الكسور الموجودة على الجانب الأيمن. .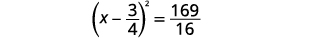
    استخدم خاصية الجذر التربيعي. .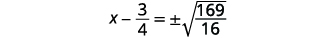
    تبسيط الراديكالية. .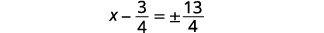
    حل لـ\(x\). .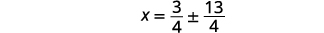
    أعد الكتابة لإظهار حلين. .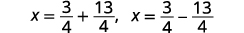
    قم بالتبسيط. .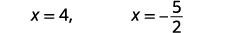

    تحقق من:

    نترك الشيك لك!

    		  
    التمارين الرياضية\(\PageIndex{17}\)

    حل عن طريق إكمال المربع:\(3 r^{2}-2 r=21\).

    إجابة

    \(r=-\frac{7}{3}, r=3\)

    التمارين الرياضية\(\PageIndex{18}\)

    حل عن طريق إكمال المربع:\(4 t^{2}+2 t=20\).

    إجابة

    \(t=-\frac{5}{2}, t=2\)

    الآن بعد أن رأينا أن المعامل\(x^{2}\) يجب أن يكون\(1\) لنا لإكمال المربع، نقوم بتحديث الإجراء الخاص بنا لحل المعادلة التربيعية بإكمال المربع ليشمل معادلات الشكل\(a x^{2}+b x+c=0\).

    كيفية: حل المعادلة التربيعية للنموذج\(a x^{2}+b x+c=0\) by Completing the Square
    1. اقسم على aa لعمل معامل\(x^{2}\) المصطلح\(1\).
    2. اعزل المصطلحات المتغيرة على أحد الجانبين والشروط الثابتة على الجانب الآخر.
    3. ابحث\(\left(\frac{1}{2} \cdot b\right)^{2}\) عن الرقم المطلوب لإكمال المربع. أضفه إلى كلا طرفي المعادلة.
    4. قم بتحليل المعادلة الثلاثية المثالية للمربع، واكتبها كمربع ذو حدين على اليسار وقم بالتبسيط عن طريق إضافة المصطلحات الموجودة على اليمين
    5. استخدم خاصية الجذر التربيعي.
    6. قم بتبسيط الجذر ثم حل المعادلتين الناتجتين.
    7. تحقق من الحلول.
    مثال\(\PageIndex{10}\)

    حل عن طريق إكمال المربع:\(3 x^{2}+2 x=4\).

    الحل:

    مرة أخرى، ستكون خطوتنا الأولى هي جعل معامل\(x^{2}\) واحد. بقسمة طرفي المعادلة على المعامل\(x^{2}\)، يمكننا عندئذٍ متابعة حل المعادلة بإكمال المربع.

      .
    قسّم كلا الجانبين\(3\) لجعل المعامل\(x^{2}\) متساويًا\(1\). .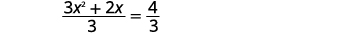
    قم بالتبسيط. .
    خذ نصفها\(\frac{2}{3}\) وقم بتجميعها.  
    \(\left(\frac{1}{2} \cdot \frac{2}{3}\right)^{2}=\frac{1}{9}\) .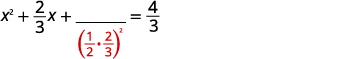
    أضف\(\frac{1}{9}\) إلى كلا الجانبين. .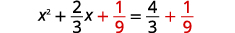
    ضع المعادلة الثلاثية المربعة المثالية بعين الاعتبار، واكتبها في صورة مربع ذو حدين. .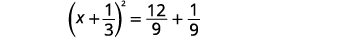
    استخدم خاصية الجذر التربيعي. .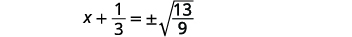
    تبسيط الراديكالية. .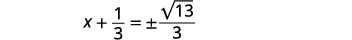
    حل لـ\(x\). .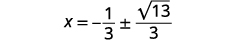
    أعد الكتابة لإظهار حلين. .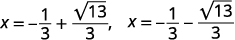

    تحقق من:

    نترك الشيك لك!

    		  
    التمارين الرياضية\(\PageIndex{19}\)

    حل عن طريق إكمال المربع:\(4 x^{2}+3 x=2\).

    إجابة

    \(x=-\frac{3}{8}+\frac{\sqrt{41}}{8}, x=-\frac{3}{8}-\frac{\sqrt{41}}{8}\)

    التمارين الرياضية\(\PageIndex{20}\)

    حل عن طريق إكمال المربع:\(3 y^{2}-10 y=-5\).

    إجابة

    \(y=\frac{5}{3}+\frac{\sqrt{10}}{3}, y=\frac{5}{3}-\frac{\sqrt{10}}{3}\)

    يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع إكمال المربع.

    المفاهيم الرئيسية

    • نمط المربعات ذات الحدين
      إذا كانت\(a\) أعدادًا حقيقية،\(b\)
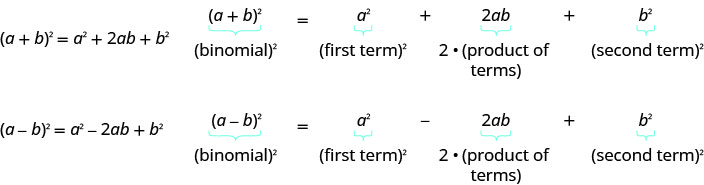
    الكمية a زائد b squared تساوي مربعًا زائد 2 a b زائد b2 حيث يساوي المربع ذو الحدين مربع الحد الأول زائد 2 أضعاف حاصل ضرب المصطلحات بالإضافة إلى مربع المصطلح الثاني. الكمية a ناقص b squared تساوي مربع ناقص 2 a b زائد b2 حيث يساوي المربع ذو الحدين الحد الأول التربيعي ناقص 2 في حاصل ضرب المصطلحات بالإضافة إلى مربع الحد الثاني.
    • كيفية إكمال المربع
      1. حدد\(b\) معامل\(x\).
      2. ابحث\(\left(\frac{1}{2} b\right)^{2}\) عن الرقم المطلوب لإكمال المربع.
      3. أضف\(\left(\frac{1}{2} b\right)^{2}\) إلى\(x^{2}+bx\)
      4. أعد كتابة المعادلة الثلاثية في صورة مربع ذي حدين
    • كيفية حل المعادلة التربيعية للنموذج \(a x^{2}+b x+c=0\)بإكمال المربع.
      1. اقسم\(a\) على حساب معامل\(x^{2}\) المصطلح\(1\).
      2. اعزل المصطلحات المتغيرة على أحد الجانبين والشروط الثابتة على الجانب الآخر.
      3. ابحث\(\left(\frac{1}{2} \cdot b\right)^{2}\) عن الرقم المطلوب لإكمال المربع. أضفه إلى كلا طرفي المعادلة.
      4. قم بتحليل المعادلة الثلاثية المثالية للمربع، واكتبها كمربع ذو حدين على اليسار وقم بالتبسيط عن طريق إضافة المصطلحات الموجودة على اليمين.
      5. استخدم خاصية الجذر التربيعي.
      6. قم بتبسيط الجذر ثم حل المعادلتين الناتجتين.
      7. تحقق من الحلول.