Skip to main content
Global

الفصل 8 تمارين المراجعة

  1. Last updated
  2. Save as PDF
  • Page ID
    201629

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    تمارين مراجعة الفصل

    تبسيط التعبيرات باستخدام الجذور

    التمارين\(\PageIndex{1}\) Simplify Expressions with Roots

    في التمارين التالية، قم بالتبسيط.

      1. \(\sqrt{225}\)
      2. \(-\sqrt{16}\)
      1. \(-\sqrt{169}\)
      2. \(\sqrt{-8}\)
      1. \(\sqrt[3]{8}\)
      2. \(\sqrt[4]{81}\)
      3. \(\sqrt[5]{243}\)
      1. \(\sqrt[3]{-512}\)
      2. \(\sqrt[4]{-81}\)
      3. \(\sqrt[5]{-1}\)
    إجابة

    1.

    1. \(15\)
    2. \(-4\)

    3.

    1. \(2\)
    2. \(3\)
    3. \(3\)
    التمارين\(\PageIndex{2}\) Estimate and Approximate Roots

    في التمارين التالية، قم بتقدير كل جذر بين عددين صحيحين متتاليين.

      1. \(\sqrt{68}\)
      2. \(\sqrt[3]{84}\)
    إجابة

    1.

    1. \(8<\sqrt{68}<9\)
    2. \(4<\sqrt[3]{84}<5\)
    التمارين\(\PageIndex{3}\) Estimate and Approximate Roots

    في التمارين التالية، قم بتقريب كل جذر وتقريبه إلى منزلتين عشريتين.

      1. \(\sqrt{37}\)
      2. \(\sqrt[3]{84}\)
      3. \(\sqrt[4]{125}\)
    إجابة

    1. قم بحل المشكلة بنفسك

    التمارين\(\PageIndex{4}\) Simplify Variable Expressions with Roots

    في التمارين التالية، قم بتبسيط استخدام القيم المطلقة حسب الضرورة.

      1. \(\sqrt[3]{a^{3}}\)
      2. \(\sqrt[7]{b^{7}}\)
      1. \(\sqrt{a^{14}}\)
      2. \(\sqrt{w^{24}}\)
      1. \(\sqrt[4]{m^{8}}\)
      2. \(\sqrt[5]{n^{20}}\)
      1. \(\sqrt{121 m^{20}}\)
      2. \(-\sqrt{64 a^{2}}\)
      1. \(\sqrt[3]{216 a^{6}}\)
      2. \(\sqrt[5]{32 b^{20}}\)
      1. \(\sqrt{144 x^{2} y^{2}}\)
      2. \(\sqrt{169 w^{8} y^{10}}\)
      3. \(\sqrt[3]{8 a^{51} b^{6}}\)
    إجابة

    1.

    1. \(a\)
    2. \(|b|\)

    3.

    1. \(m^{2}\)
    2. \(n^{4}\)

    5.

    1. \(6a^{2}\)
    2. \(2b^{4}\)

    تبسيط التعبيرات الراديكالية

    التمارين\(\PageIndex{5}\) Use the Product Property to Simplify Radical Expressions

    في التمارين التالية، استخدم خاصية المنتج لتبسيط التعبيرات الجذرية.

    1. \(\sqrt{125}\)
    2. \(\sqrt{675}\)
      1. \(\sqrt[3]{625}\)
      2. \(\sqrt[6]{128}\)
    إجابة

    1. \(5\sqrt{5}\)

    3.

    1. \(5 \sqrt[3]{5}\)
    2. \(2 \sqrt[6]{2}\)
    التمارين\(\PageIndex{6}\) Use the Product Property to Simplify Radical Expressions

    في التمارين التالية، قم بتبسيط استخدام علامات القيمة المطلقة حسب الحاجة.

      1. \(\sqrt{a^{23}}\)
      2. \(\sqrt[3]{b^{8}}\)
      3. \(\sqrt[8]{c^{13}}\)
      1. \(\sqrt{80 s^{15}}\)
      2. \(\sqrt[5]{96 a^{7}}\)
      3. \(\sqrt[6]{128 b^{7}}\)
      1. \(\sqrt{96 r^{3} s^{3}}\)
      2. \(\sqrt[3]{80 x^{7} y^{6}}\)
      3. \(\sqrt[4]{80 x^{8} y^{9}}\)
      1. \(\sqrt[5]{-32}\)
      2. \(\sqrt[8]{-1}\)
      1. \(8+\sqrt{96}\)
      2. \(\frac{2+\sqrt{40}}{2}\)
    إجابة

    2.

    1. \(4\left|s^{7}\right| \sqrt{5 s}\)
    2. \(2 a \sqrt[5]{3 a^{2}}\)
    3. \(2|b| \sqrt[6]{2 b}\)

    4.

    1. \(-2\)
    2. غير حقيقي
    التمارين\(\PageIndex{7}\) Use the Quotient Property to Simplify Radical Expressions

    في التمارين التالية، استخدم خاصية Quotient لتبسيط الجذور التربيعية.

      1. \(\sqrt{\frac{72}{98}}\)
      2. \(\sqrt[3]{\frac{24}{81}}\)
      3. \(\sqrt[4]{\frac{6}{96}}\)
      1. \(\sqrt{\frac{y^{4}}{y^{8}}}\)
      2. \(\sqrt[5]{\frac{u^{21}}{u^{11}}}\)
      3. \(\sqrt[6]{\frac{v^{30}}{v^{12}}}\)
    3. \(\sqrt{\frac{300 m^{5}}{64}}\)
      1. \(\sqrt{\frac{28 p^{7}}{q^{2}}}\)
      2. \(\sqrt[3]{\frac{81 s^{8}}{t^{3}}}\)
      3. \(\sqrt[4]{\frac{64 p^{15}}{q^{12}}}\)
      1. \(\sqrt{\frac{27 p^{2} q}{108 p^{4} q^{3}}}\)
      2. \(\sqrt[3]{\frac{16 c^{5} d^{7}}{250 c^{2} d^{2}}}\)
      3. \(\sqrt[6]{\frac{2 m^{9} n^{7}}{128 m^{3} n}}\)
      1. \(\frac{\sqrt{80 q^{5}}}{\sqrt{5 q}}\)
      2. \(\frac{\sqrt[3]{-625}}{\sqrt[3]{5}}\)
      3. \(\frac{\sqrt[4]{80 m^{7}}}{\sqrt[4]{5 m}}\)
    إجابة

    1.

    1. \(\frac{6}{7}\)
    2. \(\frac{2}{3}\)
    3. \(\frac{1}{2}\)

    3. \(\frac{10 m^{2} \sqrt{3 m}}{8}\)

    5.

    1. \(\frac{1}{2|p q|}\)
    2. \(\frac{2 c d \sqrt[5]{2 d^{2}}}{5}\)
    3. \(\frac{|m n| \sqrt[6]{2}}{2}\)

    تبسيط الأسس النسبية

    التمارين\(\PageIndex{8}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    في التمارين التالية، اكتب كتعبير جذري.

      1. \(r^{\frac{1}{2}}\)
      2. \(s^{\frac{1}{3}}\)
      3. \(t^{\frac{1}{4}}\)
    إجابة

    1.

    1. \(\sqrt{r}\)
    2. \(\sqrt[3]{s}\)
    3. \(\sqrt[4]{t}\)
    التمارين\(\PageIndex{9}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    في التمارين التالية، اكتب باستخدام الأس النسبي.

      1. \(\sqrt{21p}\)
      2. \(\sqrt[4]{8q}\)
      3. \(4\sqrt[6]{36r}\)
    إجابة

    1. قم بحل المشكلة بنفسك

    التمارين\(\PageIndex{10}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    في التمارين التالية، قم بالتبسيط.

      1. \(625^{\frac{1}{4}}\)
      2. \(243^{\frac{1}{5}}\)
      3. \(32^{\frac{1}{5}}\)
      1. \((-1,000)^{\frac{1}{3}}\)
      2. \(-1,000^{\frac{1}{3}}\)
      3. \((1,000)^{-\frac{1}{3}}\)
      1. \((-32)^{\frac{1}{5}}\)
      2. \((243)^{-\frac{1}{5}}\)
      3. \(-125^{\frac{1}{3}}\)
    إجابة

    1.

    1. \(5\)
    2. \(3\)
    3. \(2\)

    3.

    1. \(-2\)
    2. \(\frac{1}{3}\)
    3. \(-5\)
    التمارين\(\PageIndex{11}\) Simplify Expressions with \(a^{\frac{m}{n}}\)

    في التمارين التالية، اكتب باستخدام الأس النسبي.

      1. \(\sqrt[4]{r^{7}}\)
      2. \((\sqrt[5]{2 p q})^{3}\)
      3. \(\sqrt[4]{\left(\frac{12 m}{7 n}\right)^{3}}\)
    إجابة

    1. قم بحل المشكلة بنفسك

    التمارين\(\PageIndex{12}\) Simplify Expressions with \(a^{\frac{m}{n}}\)

    في التمارين التالية، قم بالتبسيط.

      1. \(25^{\frac{3}{2}}\)
      2. \(9^{-\frac{3}{2}}\)
      3. \((-64)^{\frac{2}{3}}\)
      1. \(-64^{\frac{3}{2}}\)
      2. \(-64^{-\frac{3}{2}}\)
      3. \((-64)^{\frac{3}{2}}\)
    إجابة

    1.

    1. \(125\)
    2. \(\frac{1}{27}\)
    3. \(16\)
    التمارين\(\PageIndex{13}\) Use the Laws of Exponents to Simplify Expressions with Rational Exponents

    في التمارين التالية، قم بالتبسيط.

      1. \(6^{\frac{5}{2}} \cdot 6^{\frac{1}{2}}\)
      2. \(\left(b^{15}\right)^{\frac{3}{5}}\)
      3. \(\frac{w^{\frac{2}{7}}}{w^{\frac{9}{7}}}\)
      1. \(\frac{a^{\frac{3}{4}} \cdot a^{-\frac{1}{4}}}{a^{-\frac{10}{4}}}\)
      2. \(\left(\frac{27 b^{\frac{2}{3}} c^{-\frac{5}{2}}}{b^{-\frac{7}{3}} c^{\frac{1}{2}}}\right)^{\frac{1}{3}}\)
    إجابة

    1.

    1. \(6^{3}\)
    2. \(b^{9}\)
    3. \(\frac{1}{w}\)

    جمع التعبيرات الجذرية وطرحها وضربها

    التمارين\(\PageIndex{14}\) add and Subtract Radical Expressions

    في التمارين التالية، قم بالتبسيط.

      1. \(7 \sqrt{2}-3 \sqrt{2}\)
      2. \(7 \sqrt[3]{p}+2 \sqrt[3]{p}\)
      3. \(5 \sqrt[3]{x}-3 \sqrt[3]{x}\)
      1. \(\sqrt{11 b}-5 \sqrt{11 b}+3 \sqrt{11 b}\)
      2. \(8 \sqrt[4]{11 c d}+5 \sqrt[4]{11 c d}-9 \sqrt[4]{11 c d}\)
      1. \(\sqrt{48}+\sqrt{27}\)
      2. \(\sqrt[3]{54}+\sqrt[3]{128}\)
      3. \(6 \sqrt[4]{5}-\frac{3}{2} \sqrt[4]{320}\)
      1. \(\sqrt{80 c^{7}}-\sqrt{20 c^{7}}\)
      2. \(2 \sqrt[4]{162 r^{10}}+4 \sqrt[4]{32 r^{10}}\)
    5. \(3 \sqrt{75 y^{2}}+8 y \sqrt{48}-\sqrt{300 y^{2}}\)
    إجابة

    1.

    1. \(4\sqrt{2}\)
    2. \(9\sqrt[3]{p}\)
    3. \(2\sqrt[3]{x}\)

    3.

    1. \(7\sqrt{3}\)
    2. \(7\sqrt[3]{2}\)
    3. \(3\sqrt[4]{5}\)

    5. \(37 y \sqrt{3}\)

    التمارين\(\PageIndex{15}\) Multiply Radical Expressions

    في التمارين التالية، قم بالتبسيط.

      1. \((5 \sqrt{6})(-\sqrt{12})\)
      2. \((-2 \sqrt[4]{18})(-\sqrt[4]{9})\)
      1. \(\left(3 \sqrt{2 x^{3}}\right)\left(7 \sqrt{18 x^{2}}\right)\)
      2. \(\left(-6 \sqrt[3]{20 a^{2}}\right)\left(-2 \sqrt[3]{16 a^{3}}\right)\)
    إجابة

    2.

    1. \(126 x^{2} \sqrt{2}\)
    2. \(48 a \sqrt[3]{a^{2}}\)
    التمارين\(\PageIndex{16}\) Use Polynomial Multiplication to Multiply Radical Expressions

    في التمارين التالية، اضرب.

      1. \(\sqrt{11}(8+4 \sqrt{11})\)
      2. \(\sqrt[3]{3}(\sqrt[3]{9}+\sqrt[3]{18})\)
      1. \((3-2 \sqrt{7})(5-4 \sqrt{7})\)
      2. \((\sqrt[3]{x}-5)(\sqrt[3]{x}-3)\)
    3. \((2 \sqrt{7}-5 \sqrt{11})(4 \sqrt{7}+9 \sqrt{11})\)
      1. \((4+\sqrt{11})^{2}\)
      2. \((3-2 \sqrt{5})^{2}\)
    5. \((7+\sqrt{10})(7-\sqrt{10})\)
    6. \((\sqrt[3]{3 x}+2)(\sqrt[3]{3 x}-2)\)
    إجابة

    2.

    1. \(71-22 \sqrt{7}\)
    2. \(\sqrt[3]{x^{2}}-8 \sqrt[3]{x}+15\)

    4.

    1. \(27+8 \sqrt{11}\)
    2. \(29-12 \sqrt{5}\)

    6. \(\sqrt[3]{9 x^{2}}-4\)

    اقسم التعبيرات الراديكالية

    التمارين\(\PageIndex{17}\) Divide Square Roots

    في التمارين التالية، قم بالتبسيط.

      1. \(\frac{\sqrt{48}}{\sqrt{75}}\)
      2. \(\frac{\sqrt[3]{81}}{\sqrt[3]{24}}\)
      1. \(\frac{\sqrt{320 m n^{-5}}}{\sqrt{45 m^{-7} n^{3}}}\)
      2. \(\frac{\sqrt[3]{16 x^{4} y^{-2}}}{\sqrt[3]{-54 x^{-2} y^{4}}}\)
    إجابة

    2.

    1. \(\frac{8 m^{4}}{3 n^{4}}\)
    2. \(-\frac{x^{2}}{2 y^{2}}\)
    التمارين\(\PageIndex{18}\) rationalize a One Term Denominator

    في التمارين التالية، قم بترشيد المقام.

      1. \(\frac{8}{\sqrt{3}}\)
      2. \(\sqrt{\frac{7}{40}}\)
      3. \(\frac{8}{\sqrt{2 y}}\)
      1. \(\frac{1}{\sqrt[3]{11}}\)
      2. \(\sqrt[3]{\frac{7}{54}}\)
      3. \(\frac{3}{\sqrt[3]{3 x^{2}}}\)
      1. \(\frac{1}{\sqrt[4]{4}}\)
      2. \(\sqrt[4]{\frac{9}{32}}\)
      3. \(\frac{6}{\sqrt[4]{9 x^{3}}}\)
    إجابة

    2.

    1. \(\frac{\sqrt[3]{121}}{11}\)
    2. \(\frac{\sqrt[3]{28}}{6}\)
    3. \(\frac{\sqrt[3]{9 x}}{x}\)
    التمارين\(\PageIndex{19}\) Rationalize a Two Term Denominator

    في التمارين التالية، قم بالتبسيط.

    1. \(\frac{7}{2-\sqrt{6}}\)
    2. \(\frac{\sqrt{5}}{\sqrt{n}-\sqrt{7}}\)
    3. \(\frac{\sqrt{x}+\sqrt{8}}{\sqrt{x}-\sqrt{8}}\)
    إجابة

    1. \(-\frac{7(2+\sqrt{6})}{2}\)

    3. \(\frac{(\sqrt{x}+2 \sqrt{2})^{2}}{x-8}\)

    حل المعادلات الجذرية

    التمارين الرياضية\(\PageIndex{20}\) Solve Radical Equations

    في التمارين التالية، قم بحل.

    1. \(\sqrt{4 x-3}=7\)
    2. \(\sqrt{5 x+1}=-3\)
    3. \(\sqrt[3]{4 x-1}=3\)
    4. \(\sqrt{u-3}+3=u\)
    5. \(\sqrt[3]{4 x+5}-2=-5\)
    6. \((8 x+5)^{\frac{1}{3}}+2=-1\)
    7. \(\sqrt{y+4}-y+2=0\)
    8. \(2 \sqrt{8 r+1}-8=2\)
    إجابة

    2. لا يوجد حل

    4. \(u=3, u=4\)

    6. \(x=-4\)

    8. \(r=3\)

    التمارين الرياضية\(\PageIndex{21}\) Solve Radical Equations with Two Radicals

    في التمارين التالية، قم بحل.

    1. \(\sqrt{10+2 c}=\sqrt{4 c+16}\)
    2. \(\sqrt[3]{2 x^{2}+9 x-18}=\sqrt[3]{x^{2}+3 x-2}\)
    3. \(\sqrt{r}+6=\sqrt{r+8}\)
    4. \(\sqrt{x+1}-\sqrt{x-2}=1\)
    إجابة

    2. \(x=-8, x=2\)

    4. \(x=3\)

    التمارين الرياضية\(\PageIndex{22}\) Use Radicals in Applications

    في التمارين التالية، قم بحل. تقريب التقديرات إلى منزلة عشرية واحدة.

    1. يريد Landscanding Reed الحصول على قطعة أرض مربعة في الفناء الخلفي لمنزله. لديه ما يكفي من السماد لتغطية مساحة قدم\(75\) مربع. استخدم الصيغة\(s=\sqrt{A}\) لإيجاد طول كل جانب من حديقته. قرِّب إجاباتك لأقرب عُشر قدم.
    2. التحقيق في الحوادث قام محقق الحوادث بقياس علامات الانزلاق لإحدى المركبات المتورطة في حادث. كان طول علامات الانزلاق هو\(175\) القدمين. استخدم الصيغة\(s=\sqrt{24d}\) للعثور على سرعة السيارة قبل استخدام الفرامل. قرِّب إجابتك لأقرب جزء من عشرة.
    إجابة

    2. \(64.8\)أقدام

    استخدم الجذور في الوظائف

    التمارين الرياضية\(\PageIndex{23}\) Evaluate a Radical Function

    في التمارين التالية، قم بتقييم كل وظيفة.

    1. \(g(x)=\sqrt{6 x+1}\)، ابحث
      1. \(g(4)\)
      2. \(g(8)\)
    2. \(G(x)=\sqrt{5 x-1}\)، ابحث
      1. \(G(5)\)
      2. \(G(2)\)
    3. \(h(x)=\sqrt[3]{x^{2}-4}\)، ابحث
      1. \(h(-2)\)
      2. \(h(6)\)
    4. للحصول على الوظيفة\(g(x)=\sqrt[4]{4-4 x}\)، ابحث
      1. \(g(1)\)
      2. \(g(-3)\)
    إجابة

    2.

    1. \(G(5)=2 \sqrt{6}\)
    2. \(G(2)=3\)

    4.

    1. \(g(1)=0\)
    2. \(g(-3)=2\)
    التمارين الرياضية\(\PageIndex{24}\) Find the Domain of a Radical Function

    في التمارين التالية، ابحث عن مجال الدالة واكتب المجال بالتدوين الفاصل الزمني.

    1. \(g(x)=\sqrt{2-3 x}\)
    2. \(F(x)=\sqrt{\frac{x+3}{x-2}}\)
    3. \(f(x)=\sqrt[3]{4 x^{2}-16}\)
    4. \(F(x)=\sqrt[4]{10-7 x}\)
    إجابة

    2. \((2, \infty)\)

    4. \(\left[\frac{7}{10}, \infty\right)\)

    التمارين الرياضية\(\PageIndex{25}\) graph Radical Functions

    في التمارين التالية،

    1. ابحث عن مجال الدالة
    2. رسم بياني للدالة
    3. استخدم الرسم البياني لتحديد النطاق
    1. \(g(x)=\sqrt{x+4}\)
    2. \(g(x)=2 \sqrt{x}\)
    3. \(f(x)=\sqrt[3]{x-1}\)
    4. \(f(x)=\sqrt[3]{x}+3\)
    إجابة

    2.

    1. اسم النطاق:\([0, \infty)\)

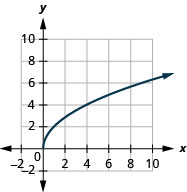
    2. يوضِّح الشكل رسمًا بيانيًا لدالة الجذر التربيعي على مستوى الإحداثيات x y. يمتد المحور السيني للطائرة من 0 إلى 8. يمتد المحور y من 0 إلى 8. تحتوي الدالة على نقطة بداية عند (0، 0) وتمر بالنقاط (1، 2) و (4، 4).
      الشكل 8-هاء-1
    3. النطاق:\([0, \infty)\)

    4.

    1. اسم النطاق:\((-\infty, \infty)\)

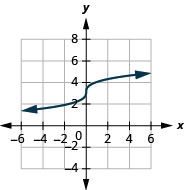
    2. يوضِّح الشكل رسمًا بيانيًا لدالة الجذر التكعيبي على مستوى الإحداثيات x y. يمتد المحور السيني للطائرة من سالب 4 إلى 4. يمتد المحور y من سالب 2 إلى 6. تحتوي الدالة على نقطة مركزية عند (0، 3) وتمر بالنقاط (سالب 1، 2) و (1، 4).
      الشكل 8-هاء-2
    3. النطاق:\((-\infty, \infty)\)

    استخدم نظام الأرقام المعقدة

    التمارين الرياضية\(\PageIndex{26}\) evaluate the Square Root of a Negative Number

    في التمارين التالية، اكتب كل تعبير بعبارات\(i\) وقم بتبسيطه إن أمكن.

      1. \(\sqrt{-100}\)
      2. \(\sqrt{-13}\)
      3. \(\sqrt{-45}\)
    إجابة

    قم بحل المشكلة بنفسك

    التمارين الرياضية\(\PageIndex{27}\) Add or Subtract Complex Numbers

    في التمارين التالية، قم بالجمع أو الطرح.

    1. \(\sqrt{-50}+\sqrt{-18}\)
    2. \((8-i)+(6+3 i)\)
    3. \((6+i)-(-2-4 i)\)
    4. \((-7-\sqrt{-50})-(-32-\sqrt{-18})\)
    إجابة

    1. \(8 \sqrt{2} i\)

    3. \(8+5 i\)

    التمارين الرياضية\(\PageIndex{28}\) Multiply Complex Numbers

    في التمارين التالية، اضرب.

    1. \((-2-5 i)(-4+3 i)\)
    2. \(-6 i(-3-2 i)\)
    3. \(\sqrt{-4} \cdot \sqrt{-16}\)
    4. \((5-\sqrt{-12})(-3+\sqrt{-75})\)
    إجابة

    1. \(23+14 i\)

    3. \(-6\)

    التمارين الرياضية\(\PageIndex{29}\) Multiply Complex Numbers

    في التمارين التالية، قم بالضرب باستخدام حاصل ضرب نمط المربعات ذات الحدين.

    1. \((-2-3 i)^{2}\)
    إجابة

    1. \(-5-12 i\)

    التمارين الرياضية\(\PageIndex{30}\) Multiply Complex Numbers

    في التمارين التالية، اضرب باستخدام حاصل ضرب نمط الاقتران المركب.

    1. \((9-2 i)(9+2 i)\)
    إجابة

    قم بحل المشكلة بنفسك

    التمارين الرياضية\(\PageIndex{31}\) divide Complex Numbers

    في التمارين التالية، قسّم.

    1. \(\frac{2+i}{3-4 i}\)
    2. \(\frac{-4}{3-2 i}\)
    إجابة

    1. \(\frac{2}{25}+\frac{11}{25} i\)

    التمارين الرياضية\(\PageIndex{32}\) Simplify Powers of \(i\)

    في التمارين التالية، قم بالتبسيط.

    1. \(i^{48}\)
    2. \(i^{255}\)
    إجابة

    1. \(1\)

    اختبار الممارسة

    التمارين الرياضية\(\PageIndex{33}\)

    في التمارين التالية، قم بتبسيط استخدام القيم المطلقة حسب الضرورة.

    1. \(\sqrt[3]{125 x^{9}}\)
    2. \(\sqrt{169 x^{8} y^{6}}\)
    3. \(\sqrt[3]{72 x^{8} y^{4}}\)
    4. \(\sqrt{\frac{45 x^{3} y^{4}}{180 x^{5} y^{2}}}\)
    إجابة

    1. \(5x^{3}\)

    3. \(2 x^{2} y \sqrt[3]{9 x^{2} y}\)

    التمارين الرياضية\(\PageIndex{34}\)

    في التمارين التالية، قم بالتبسيط. افترض أن جميع المتغيرات إيجابية.

      1. \(216^{-\frac{1}{4}}\)
      2. \(-49^{\frac{3}{2}}\)
    2. \(\sqrt{-45}\)
    3. \(\frac{x^{-\frac{1}{4}} \cdot x^{\frac{5}{4}}}{x^{-\frac{3}{4}}}\)
    4. \(\left(\frac{8 x^{\frac{2}{3}} y^{-\frac{5}{2}}}{x^{-\frac{7}{3}} y^{\frac{1}{2}}}\right)^{\frac{1}{3}}\)
    5. \(\sqrt{48 x^{5}}-\sqrt{75 x^{5}}\)
    6. \(\sqrt{27 x^{2}}-4 x \sqrt{12}+\sqrt{108 x^{2}}\)
    7. \(2 \sqrt{12 x^{5}} \cdot 3 \sqrt{6 x^{3}}\)
    8. \(\sqrt[3]{4}(\sqrt[3]{16}-\sqrt[3]{6})\)
    9. \((4-3 \sqrt{3})(5+2 \sqrt{3})\)
    10. \(\frac{\sqrt[3]{128}}{\sqrt[3]{54}}\)
    11. \(\frac{\sqrt{245 x y^{-4}}}{\sqrt{45 x^{4} y^{3}}}\)
    12. \(\frac{1}{\sqrt[3]{5}}\)
    13. \(\frac{3}{2+\sqrt{3}}\)
    14. \(\sqrt{-4} \cdot \sqrt{-9}\)
    15. \(-4 i(-2-3 i)\)
    16. \(\frac{4+i}{3-2 i}\)
    17. \(i^{172}\)
    إجابة

    1.

    1. \(\frac{1}{4}\)
    2. \(-343\)

    3. \(x^{\frac{7}{4}}\)

    5. \(-x^{2} \sqrt{3 x}\)

    7. \(36 x^{4} \sqrt{2}\)

    9. \(2-7 \sqrt{3}\)

    11. \(\frac{7 x^{5}}{3 y^{7}}\)

    13. \(3(2-\sqrt{3})\)

    15. \(-12+8i\)

    17. \(-i\)

    التمارين الرياضية\(\PageIndex{35}\)

    في التمارين التالية، قم بحل.

    1. \(\sqrt{2 x+5}+8=6\)
    2. \(\sqrt{x+5}+1=x\)
    3. \(\sqrt[3]{2 x^{2}-6 x-23}=\sqrt[3]{x^{2}-3 x+5}\)
    إجابة

    2. \(x=4\)

    التمارين الرياضية\(\PageIndex{36}\)

    في التمرين التالي،

    1. ابحث عن مجال الدالة
    2. رسم بياني للدالة
    3. استخدم الرسم البياني لتحديد النطاق
    1. \(g(x)=\sqrt{x+2}\)
    إجابة

    1.

    1. اسم النطاق:\([-2, \infty)\)

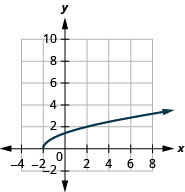
    2. يوضِّح الشكل رسمًا بيانيًا لدالة الجذر التربيعي على مستوى الإحداثيات x y. يمتد المحور السيني للطائرة من سالب 2 إلى 6. يمتد المحور y من 0 إلى 8. تحتوي الدالة على نقطة بداية عند (سالب 2، 0) وتمر بالنقاط (سالب 1، 1) و (2، 2).
      الشكل 8-هاء-3
    3. النطاق:\([0, \infty)\)