8.9E: تمارين
- Page ID
- 201613
الممارسة تجعل من الكمال
في التمارين التالية، اكتب كل تعبير بعبارات\(i\) وقم بتبسيطه إن أمكن.
- أ.\(\sqrt{-16}\) ب.\(\sqrt{-11}\) ج.\(\sqrt{-8}\)
- أ.\(\sqrt{-121}\) ب.\(\sqrt{-1}\) ج.\(\sqrt{-20}\)
- أ.\(\sqrt{-100}\) ب.\(\sqrt{-13}\) ج.\(\sqrt{-45}\)
- أ.\(\sqrt{-49}\) ب.\(\sqrt{-15}\) ج.\(\sqrt{-75}\)
- إجابة
-
1. أ.\(4i\) ب.\(i\sqrt{11}\) ج.\(2i\sqrt{2}\)
3. أ.\(10i\) ب.\(i\sqrt{13}\) ج.\(3i\sqrt{5}\)
في التمارين التالية، قم بالجمع أو الطرح، مع وضع الإجابة في\(a + bi\) الشكل.
5. \(\sqrt{-75}+\sqrt{-48}\)
6. \(\sqrt{-12}+\sqrt{-75}\)
7. \(\sqrt{-50}+\sqrt{-18}\)
8. \(\sqrt{-72}+\sqrt{-8}\)
9. \((1+3 i)+(7+4 i)\)
10. \((6+2 i)+(3-4 i)\)
11. \((8-i)+(6+3 i)\)
12. \((7-4 i)+(-2-6 i)\)
13. \((1-4 i)-(3-6 i)\)
14. \((8-4 i)-(3+7 i)\)
15. \((6+i)-(-2-4 i)\)
16. \((-2+5 i)-(-5+6 i)\)
17. \((5-\sqrt{-36})+(2-\sqrt{-49})\)
18. \((-3+\sqrt{-64})+(5-\sqrt{-16})\)
19. \((-7-\sqrt{-50})-(-32-\sqrt{-18})\)
20. \((-5+\sqrt{-27})-(-4-\sqrt{-48})\)
- إجابة
-
5. \(0+\left(9\sqrt{3}\right)i\)
7. \(0+\left(8\sqrt{2}\right)i\)
9. \(8+7i\)
11. \(14+2i\)
13. \(-2+2i\)
15. \(8+5i\)
17. \(7-13i\)
19. \(25-\left(2 \sqrt{2}\right) i\)
في التمارين التالية، اضرب، ضع الإجابة في\(a+bi\) الشكل.
21. \(4 i(5-3 i)\)
22. \(2 i(-3+4 i)\)
23. \(-6 i(-3-2 i)\)
24. \(-i(6+5 i)\)
25. \((4+3 i)(-5+6 i)\)
26. \((-2-5 i)(-4+3 i)\)
27. \((-3+3 i)(-2-7 i)\)
28. \((-6-2 i)(-3-5 i)\)
- إجابة
-
21. \(12+20i\)
23. \(-12+18i\)
25. \(-38+9 i\)
27. \(27+15i\)
في التمارين التالية، اضرب باستخدام حاصل ضرب نمط المربعات ذات الحدين، مع وضع الإجابة في\(a+bi\) الشكل.
29. \((3+4 i)^{2}\)
30. \((-1+5 i)^{2}\)
31. \((-2-3 i)^{2}\)
32. \((-6-5 i)^{2}\)
- إجابة
-
29. \(-7+24i\)
31. \(-5-12i\)
في التمارين التالية، اضرب، ضع الإجابة في\(a+bi\) الشكل.
33. \(\sqrt{-25} \cdot \sqrt{-36}\)
34. \(\sqrt{-4} \cdot \sqrt{-16}\)
35. \(\sqrt{-9} \cdot \sqrt{-100}\)
36. \(\sqrt{-64} \cdot \sqrt{-9}\)
37. \((-2-\sqrt{-27})(4-\sqrt{-48})\)
38. \((5-\sqrt{-12})(-3+\sqrt{-75})\)
39. \((2+\sqrt{-8})(-4+\sqrt{-18})\)
40. \((5+\sqrt{-18})(-2-\sqrt{-50})\)
41. \((2-i)(2+i)\)
42. \((4-5 i)(4+5 i)\)
43. \((7-2 i)(7+2 i)\)
44. \((-3-8 i)(-3+8 i)\)
- إجابة
-
33. \(30i = 0 + 30i\)
35. \(-30 = -30 + 0i\)
37. \(-44+\left(4 \sqrt{3}\right) i\)
39. \(-20-\left(2 \sqrt{2}\right) i\)
41. \(5 = 5 + 0i\)
43. \(53 = 53 + 0i\)
في التمارين التالية، اضرب باستخدام حاصل ضرب نمط الاقتران المركب.
45. \((7-i)(7+i)\)
46. \((6-5 i)(6+5 i)\)
47. \((9-2 i)(9+2 i)\)
48. \((-3-4 i)(-3+4 i)\)
- إجابة
-
45. \(50\)
47. \(85\)
في التمارين التالية، قم بالقسمة ووضع الإجابة في\(a+bi\) الشكل.
49. \(\dfrac{3+4 i}{4-3 i}\)
50. \(\dfrac{5-2 i}{2+5 i}\)
51. \(\dfrac{2+i}{3-4 i}\)
52. \(\dfrac{3-2 i}{6+i}\)
53. \(\dfrac{3}{2-3 i}\)
54. \(\dfrac{2}{4-5 i}\)
55. \(\dfrac{-4}{3-2 i}\)
56. \(\dfrac{-1}{3+2 i}\)
57. \(\dfrac{1+4 i}{3 i}\)
58. \(\dfrac{4+3 i}{7 i}\)
59. \(\dfrac{-2-3 i}{4 i}\)
60. \(\dfrac{-3-5 i}{2 i}\)
- إجابة
-
49. \(i = 0 + i\)
51. \(\frac{2}{25}+\frac{11}{25} i\)
53. \(\frac{6}{13}+\frac{9}{13} i\)
55. \(-\frac{12}{13}-\frac{8}{13} i\)
57. \(\frac{4}{3}-\frac{1}{3} i\)
59. \(-\frac{3}{4}+\frac{1}{2} i\)
في التمارين التالية، قم بالتبسيط.
61. \(i^{41}\)
62. \(i^{39}\)
63. \(i^{66}\)
64. \(i^{48}\)
65. \(i^{128}\)
66. \(i^{162}\)
67. \(i^{137}\)
68. \(i^{255}\)
- إجابة
-
61. \(i^{41} = i^{40}\cdot i = \left(i^{4}\right)^{10}\cdot i= i\)
63. \(i^{66} = i^{64}\cdot i^{2} = \left(i^{4}\right)^{16}\cdot (-1)= -1\)
65. \(i^{128} = \left(i^{4}\right)^{32} = 1\)
67. \(i^{137} = i^{136}\cdot i = \left(i^{4}\right)^{34}\cdot i = 1 \cdot i = i\)
69. اشرح العلاقة بين الأعداد الحقيقية والأرقام المركبة.
70. تضاعف Aniket على النحو التالي وحصل على إجابة خاطئة. ما هو الخطأ في منطقه؟
\(\begin{array}{c}{\sqrt{-7} \cdot \sqrt{-7}} \\ {\sqrt{49}} \\ {7}\end{array}\)
71. لماذا\(\sqrt{-64}=8 i\) ولكن\(\sqrt[3]{-64}=-4\).
72. اشرح كيف أن قسمة الأعداد المركبة تشبه ترشيد المقام.
- إجابة
-
69. قد تختلف الإجابات
71. قد تختلف الإجابات
فحص ذاتي
أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.
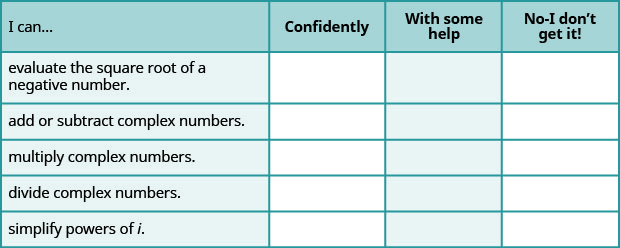
ب- على مقياس من 1 إلى 10، كيف تقيم إتقانك لهذا القسم في ضوء إجاباتك على قائمة التحقق؟ كيف يمكنك تحسين هذا؟


