8.9: استخدم نظام الأرقام المركبة
- Page ID
- 201606
في نهاية هذا القسم، ستكون قادرًا على:
- قم بتقييم الجذر التربيعي لرقم سالب
- جمع الأعداد المركبة وطرحها
- اضرب الأرقام المركبة
- اقسم الأرقام المعقدة
- تبسيط صلاحيات\(i\)
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- بالنظر إلى الأرقام\(-4,-\sqrt{7}, 0 . \overline{5}, \frac{7}{3}, 3, \sqrt{81}\)، ضع قائمة بـ
- أرقام عقلانية
- أرقام غير منطقية
- الأرقام الحقيقية
إذا فاتتك هذه المشكلة، راجع مثال 1.42.
- اضرب:\((x−3)(2x+5)\).
إذا فاتتك هذه المشكلة، راجع المثال 5.28. - قم بترشيد المقام:\(\frac{\sqrt{5}}{\sqrt{5}-\sqrt{3}}\)
إذا فاتتك هذه المشكلة، راجع مثال 5.32.
إيجاد الجذر التربيعي لعدد سالب
عندما يكون لدينا موقف يكون فيه الجذر التربيعي لعدد سالب نقول أنه لا يوجد رقم حقيقي يساوي هذا الجذر التربيعي. على سبيل المثال\(\sqrt{-1}\)، للتبسيط، نبحث عن رقم حقيقي\(x\) لذلك\(x^{2}=-1\). نظرًا لأن جميع الأرقام الحقيقية المربعة هي أرقام موجبة، فلا يوجد عدد حقيقي يساوي\(–1\) عند تربيعه.
غالبًا ما قام علماء الرياضيات بتوسيع أنظمة الأرقام الخاصة بهم حسب الحاجة. أضافوا\(0\) إلى أرقام العد للحصول على الأرقام الصحيحة. عندما احتاجوا إلى أرصدة سلبية، أضافوا أرقامًا سالبة للحصول على الأعداد الصحيحة. عندما احتاجوا إلى فكرة أجزاء من الكل، قاموا بإضافة الكسور وحصلوا على الأرقام المنطقية. تسمح إضافة الأرقام غير المنطقية بالأرقام مثل\(\sqrt{5}\). كل هذه الأشياء مجتمعة أعطتنا الأرقام الحقيقية وحتى الآن في دراستك للرياضيات، كان ذلك كافياً.
ولكن الآن سنقوم بتوسيع الأرقام الحقيقية لتشمل الجذور التربيعية للأرقام السالبة. نبدأ بتعريف الوحدة التخيلية على\(i\) أنها الرقم الذي يكون مربعه\(–1\).
تعريف\(\PageIndex{1}\)
الوحدة التخيلية\(i\) هي الرقم الذي يكون مربعه\(-1\).
\(i^{2}=-1 \text { or } i=\sqrt{-1}\)
سنستخدم الوحدة التخيلية لتبسيط الجذور التربيعية للأرقام السالبة.
تعريف\(\PageIndex{2}\)
الجذر التربيعي لعدد سالب
\(b\)إذا كان الرقم الحقيقي موجبًا، إذن
\(\sqrt{-b}=\sqrt{b} i\)
سنستخدم هذا التعريف في المثال التالي. كن حذرًا من أنه من الواضح أنه\(i\) ليس تحت التطرف. في بعض الأحيان سترى هذا مكتوبًا\(\sqrt{-b}=i \sqrt{b}\) للتأكيد على\(i\) أنه ليس تحت التطرف. ولكن\(\sqrt{-b}=\sqrt{b} i\) هذا يعتبر النموذج القياسي.
اكتب كل تعبير بالمصطلحات\(i\) والتبسيط ممكن:
- \(\sqrt{-25}\)
- \(\sqrt{-7}\)
- \(\sqrt{-12}\)
الحل:
أ.
\(\sqrt{-25}\)
استخدم تعريف الجذر التربيعي للأرقام السالبة.
\(\sqrt{25} i\)
قم بالتبسيط.
\(5i\)
ب.
\(\sqrt{-7}\)
استخدم تعريف الجذر التربيعي للأرقام السالبة.
\(\sqrt{7} i\)
قم بالتبسيط.
كن حذرًا من أنه من الواضح أنه\(i\) ليس تحت العلامة الراديكالية.
ج.
\(\sqrt{-12}\)
استخدم تعريف الجذر التربيعي للأرقام السالبة.
\(\sqrt{12} i\)
قم بالتبسيط\(\sqrt{12}\).
\(2 \sqrt{3} i\)
اكتب كل تعبير بعبارات\(i\) وقم بتبسيطه إن أمكن:
- \(\sqrt{-81}\)
- \(\sqrt{-5}\)
- \(\sqrt{-18}\)
- إجابة
-
- \(9i\)
- \(\sqrt{5} i\)
- \(3 \sqrt{2} i\)
اكتب كل تعبير بعبارات\(i\) وقم بتبسيطه إن أمكن:
- \(\sqrt{-36}\)
- \(\sqrt{-3}\)
- \(\sqrt{-27}\)
- إجابة
-
- \(6i\)
- \(\sqrt{3} i\)
- \(3\sqrt{3} i\)
الآن بعد أن أصبحنا على دراية بالرقم التخيلي\(i\)، يمكننا توسيع الأرقام الحقيقية لتشمل الأرقام التخيلية. يتضمن نظام الأرقام المركب الأرقام الحقيقية والأرقام التخيلية. الرقم المركب هو من النموذج\(a+bi\)، حيث\(a, b\) توجد الأرقام الحقيقية. نسمي\(a\) الجزء الحقيقي\(b\) والجزء الخيالي.
تعريف\(\PageIndex{3}\)
الرقم المركب هو من النموذج\(a+bi\)\(a\) وأين\(b\) والأرقام الحقيقية.
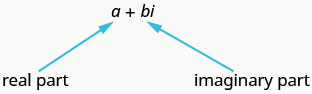
يكون الرقم المركب في شكل قياسي عند كتابته\(a+bi\) كأرقام حقيقية\(a\) وأين\(b\) تكون.
إذا أصبح\(b=0\)، ثم\(a+bi\) أصبح\(a+0⋅i=a\)، وهو رقم حقيقي.
إذا كان\(b≠0\)، إذن\(a+bi\) هو رقم وهمي.
إذا\(a+bi\) أصبح\(a=0\)، ثم\(0+bi=bi\)، ويسمى عددًا خياليًا خالصًا.
نحن نلخص هذا هنا.
| \(a+bi\) | ||
| \(b=0\) |
\(a+0 \cdot i\) \(a\) |
رقم حقيقي |
| \(b\neq 0\) | \(a+bi\) | رقم وهمي |
| \(a=0\)R |
\(0+bi\) \(bi\) |
رقم خيالي خالص 4 |
الشكل القياسي للرقم المركب هو\(a+bi\)، لذلك يفسر هذا سبب كون النموذج المفضل هو\(\sqrt{-b}=\sqrt{b} i\) متى\(b>0\).
يساعدنا الرسم التخطيطي على تصور نظام الأرقام المعقدة. وتتكون من كل من الأرقام الحقيقية والأرقام التخيلية.
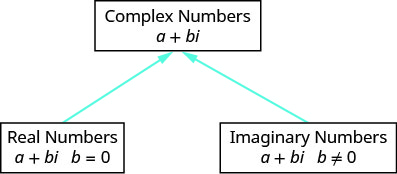
جمع الأعداد المركبة أو طرحها
نحن الآن جاهزون لإجراء عمليات الجمع والطرح والضرب والقسمة على الأعداد المركبة - تمامًا كما فعلنا مع الأعداد الحقيقية.
إن جمع الأعداد المركبة وطرحها يشبه إلى حد كبير جمع أو طرح مصطلحات متشابهة. نضيف أو نطرح الأجزاء الحقيقية ثم نضيف أو نطرح الأجزاء التخيلية. يجب أن تكون النتيجة النهائية في شكل قياسي.
إضافة:\(\sqrt{-12}+\sqrt{-27}\).
الحل:
\(\sqrt{-12}+\sqrt{-27}\)
استخدم تعريف الجذر التربيعي للأرقام السالبة.
\(\sqrt{12} i+\sqrt{27} i\)
قم بتبسيط الجذور التربيعية.
\(2 \sqrt{3} i+3 \sqrt{3} i\)
أضف.
\(5 \sqrt{3} i\)
إضافة:\(\sqrt{-8}+\sqrt{-32}\).
- إجابة
-
\(6 \sqrt{2} i\)
إضافة:\(\sqrt{-27}+\sqrt{-48}\)
- إجابة
-
\(7 \sqrt{3} i\)
تذكر إضافة كل من الأجزاء الحقيقية والأجزاء التخيلية في هذا المثال التالي.
قم بالتبسيط:
- \((4-3 i)+(5+6 i)\)
- \((2-5 i)-(5-2 i)\)
الحل:
أ.
\((4-3 i)+(5+6 i)\)
استخدم الخاصية الترابطية لتجميع الأجزاء الحقيقية والأجزاء التخيلية معًا.
\((4+5)+(-3 i+6 i)\)
قم بالتبسيط.
\(9+3i\)
ب.
\((2-5 i)-(5-2 i)\)
قم بالتوزيع.
\(2-5 i-5+2 i\)
استخدم الخاصية الترابطية لتجميع الأجزاء الحقيقية والأجزاء التخيلية معًا.
\(2-5-5 i+2 i\)
قم بالتبسيط.
\(-3-3 i\)
قم بالتبسيط:
- \((2+7 i)+(4-2 i)\)
- \((8-4 i)-(2-i)\)
- إجابة
-
- \(6+5i\)
- \(6-3i\)
قم بالتبسيط:
- \((3-2 i)+(-5-4 i)\)
- \((4+3 i)-(2-6 i)\)
- إجابة
-
- \(-2-6i\)
- \(2+9i\)
اضرب الأعداد المركبة
ضرب الأرقام المركبة يشبه أيضًا ضرب التعبيرات باستخدام المعاملات والمتغيرات. هناك حالة خاصة واحدة فقط نحتاج إلى أخذها في الاعتبار. سننظر إلى ذلك بعد أن نتدرب في المثالين التاليين.
اضرب:\(2 i(7-5 i)\)
الحل:
\(2 i(7-5 i)\)
قم بالتوزيع.
\(14 i-10 i^{2}\)
قم بالتبسيط\(i^{2}\).
\(14 i-10(-1)\)
اضرب.
\(14 i+10\)
اكتب في النموذج القياسي.
\(10+14i\)
اضرب:\(4 i(5-3 i)\).
- إجابة
-
\(12+20i\)
اضرب:\(-3 i(2+4 i)\).
- إجابة
-
\(12-6i\)
في المثال التالي، نضرب المقادير ذات الحدين باستخدام خاصية التوزيع أو FOIL.
اضرب:\((3+2 i)(4-3 i)\).
الحل:
\((3+2 i)(4-3 i)\)
استخدم FOIL.
\(12-9 i+8 i-6 i^{2}\)
قم\(i^{2}\) بتبسيط المصطلحات المتشابهة ودمجها.
\(12-i-6(-1)\)
اضرب.
\(12-i+6\)
اجمع بين الأجزاء الحقيقية.
\(18-i\)
متعدد:\((5-3 i)(-1-2 i)\).
- إجابة
-
\(-11-7i\)
متعدد:\((-4-3 i)(2+i)\).
- إجابة
-
\(-5-10i\)
في المثال التالي، يمكننا استخدام FOIL أو منتج نمط المربعات ذات الحدين.
اضرب:\((3+2 i)^{2}\)
الحل:
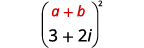 |
|
| استخدم حاصل ضرب نمط المربعات ذات الحدين،\((a+b)^{2}=a^{2}+2 a b+b^{2}\). |  |
| قم بالتبسيط. | 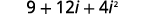 |
| قم بالتبسيط\(i^{2}\). | 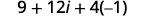 |
| قم بالتبسيط. | 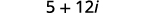 |
اضرب باستخدام نمط المربعات ذات الحدين:\((-2-5 i)^{2}\).
- إجابة
-
\(-21+20 i\)
اضرب باستخدام نمط المربعات ذات الحدين:\((-5+4 i)^{2}\).
- إجابة
-
\(9-40i\)
نظرًا لأن الجذر التربيعي لرقم سالب ليس رقمًا حقيقيًا، فلا يمكننا استخدام خاصية المنتج للجذور. من أجل ضرب الجذور التربيعية للأرقام السالبة، يجب أن نكتبها أولاً كأرقام مركبة، باستخدام\(\sqrt{-b}=\sqrt{b}i\) هذا المكان الذي يميل فيه الطلاب إلى ارتكاب الأخطاء، لذا كن حذرًا عندما ترى الضرب بجذر تربيعي سالب.
اضرب:\(\sqrt{-36} \cdot \sqrt{-4}\).
الحل:
لضرب الجذور التربيعية للأرقام السالبة، نكتبها أولاً كأرقام مركبة.
\(\sqrt{-36} \cdot \sqrt{-4}\)
اكتب كأرقام مركبة باستخدام\(\sqrt{-b}=\sqrt{b}i\).
\(\sqrt{36} i \cdot \sqrt{4} i\)
قم بالتبسيط.
\(6 i \cdot 2 i\)
اضرب.
\(12i^{2}\)
قم بالتبسيط\(i^{2}\) والتضاعف.
\(-12\)
اضرب:\(\sqrt{-49} \cdot \sqrt{-4}\).
- إجابة
-
\(-14\)
اضرب:\(\sqrt{-36} \cdot \sqrt{-81}\).
- إجابة
-
\(-54\)
في المثال التالي، يحتوي كل مكون من حدين على جذر تربيعي لعدد سالب. قبل الضرب، يجب كتابة كل جذر تربيعي لرقم سالب كرقم مركب.
اضرب:\((3-\sqrt{-12})(5+\sqrt{-27})\).
الحل:
لضرب الجذور التربيعية للأرقام السالبة، نكتبها أولاً كأرقام مركبة.
\((3-\sqrt{-12})(5+\sqrt{-27})\)
اكتب كأرقام مركبة باستخدام\(\sqrt{-b}=\sqrt{b}i\).
\((3-2 \sqrt{3} i)(5+3 \sqrt{3} i)\)
استخدم FOIL.
\(15+9 \sqrt{3} i-10 \sqrt{3} i-6 \cdot 3 i^{2}\)
اجمع بين المصطلحات المتشابهة وقم بتبسيطها\(i^{2}\).
\(15-\sqrt{3} i-6 \cdot(-3)\)
اضرب وادمج المصطلحات المتشابهة.
\(33-\sqrt{3} i\)
اضرب:\((4-\sqrt{-12})(3-\sqrt{-48})\).
- إجابة
-
\(-12-22 \sqrt{3} i\)
اضرب:\((-2+\sqrt{-8})(3-\sqrt{-18})\).
- إجابة
-
\(6+12 \sqrt{2} i\)
نظرنا أولاً إلى الأزواج المترافقة عندما درسنا كثيرات الحدود. قلنا أن زوجًا من الحدين لكل منهما نفس الحد الأول ونفس الحد الأخير، ولكن الواحد هو المجموع والآخر هو الفرق يسمى الزوج المترافق وهو من الشكل\((a−b),(a+b)\).
الزوج المترافق المعقد مشابه جدًا. بالنسبة لعدد مركب من النموذج\(a+bi\)، يكون مترافق الشكل\(a−bi\). لاحظ أن لديهم نفس الفصل الأول ونفس الفصل الأخير، لكن الواحد هو المجموع والآخر هو الفرق.
تعريف\(\PageIndex{4}\)
الزوج المترافق المعقد هو من الشكل\(a+bi,a-bi\).
سنضرب زوجًا مترافقًا معقدًا في المثال التالي.
اضرب:\((3-2 i)(3+2 i)\).
الحل:
\((3-2 i)(3+2 i)\)
استخدم الفويل
\(9+6 i-6 i-4 i^{2}\)
اجمع بين المصطلحات المتشابهة وقم بتبسيطها\(i^{2}\).
\(9-4(-1)\)
اضرب وادمج المصطلحات المتشابهة.
\(13\)
اضرب:\((4-3 i) \cdot(4+3 i)\).
- إجابة
-
\(25\)
اضرب:\((-2+5 i) \cdot(-2-5 i)\).
- إجابة
-
\(29\)
من خلال دراستنا لكثيرات الحدود، نعلم أن ناتج الاقتران دائمًا ما يكون\((a-b)(a+b)=a^{2}-b^{2}\) بالشكل. والنتيجة تسمى فرق المربعات. يمكننا ضرب زوج مترافق معقد باستخدام هذا النمط.
المثال الأخير الذي استخدمناه FOIL. الآن سوف نستخدم منتج نمط الاقتران.
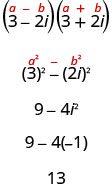
لاحظ أن هذه هي نفس النتيجة التي وجدناها في المثال 8.8.9.
عندما نضاعف المترابطات المعقدة، فإن منتج المصطلحات الأخيرة سيكون دائمًا\(i^{2}\) ما يبسط إلى\(−1\).
\(\begin{array}{c}{(a-b i)(a+b i)} \\ {a^{2}-(b i)^{2}} \\ {a^{2}-b^{2} i^{2}} \\ {a^{2}-b^{2}(-1)} \\ {a^{2}+b^{2}}\end{array}\)
هذا يقودنا إلى منتج نمط المترافقات المعقدة:\((a-b i)(a+b i)=a^{2}+b^{2}\)
تعريف\(\PageIndex{5}\)
منتج من منتجات المترافقات المعقدة
إذا كانت\(a\)\(b\) الأرقام حقيقية، إذن
\((a-b i)(a+b i)=a^{2}+b^{2}\)
اضرب باستخدام حاصل ضرب نمط الاقتران المعقد:\((8-2 i)(8+2 i)\).
الحل:
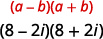 |
|
| استخدم حاصل ضرب نمط المترادفات المعقدة،\((a-b i)(a+b i)=a^{2}+b^{2}\). | 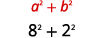 |
| قم بتبسيط المربعات. | 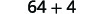 |
| أضف. | 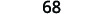 |
اضرب باستخدام حاصل ضرب نمط الاقتران المعقد:\((3-10 i)(3+10 i)\).
- إجابة
-
\(109\)
اضرب باستخدام حاصل ضرب نمط الاقتران المعقد:\((-5+4 i)(-5-4 i)\).
- إجابة
-
\(41\)
قسمة الأعداد المركبة
إن تقسيم الأرقام المركبة يشبه إلى حد كبير ترشيد المقام. نريد أن تكون النتيجة في الصورة القياسية مع عدم وجود أرقام خيالية في المقام.
قسّم:\(\frac{4+3 i}{3-4 i}\).
الحل:
| الخطوة 1: اكتب كلا من البسط والمقام في الصورة القياسية. | كلاهما في شكل قياسي. | \(\frac{4+3 i}{3-4 i}\) |
| الخطوة 2: اضرب البسط والمقام في المترافق المركب للقاسم. | المترافق المعقد لـ\(3-4i\) هو\(3+4i\). | \(\frac{(4+3 i)\color{red}{(3+4 i)}}{(3-4 i)\color{red}{(3+4 i)}}\) |
| الخطوة 3: تبسيط النتيجة وكتابتها في النموذج القياسي. |
استخدم النمط الموجود\((a-b i)(a+b i)=a^{2}+b^{2}\) في المقام. اجمع بين المصطلحات المتشابهة. قم بالتبسيط. اكتب النتيجة في النموذج القياسي. |
\(\begin{array}{c}{\frac{12+16 i+9 i+12 i^{2}}{9+16}} \\ {\frac{12+25 i-12}{25}} \\ {\frac{25 i}{25}} \\ {i}\end{array}\) |
قسّم:\(\frac{2+5 i}{5-2 i}\).
- إجابة
-
\(i\)
قسّم:\(\frac{1+6 i}{6-i}\).
- إجابة
-
\(i\)
نحن نلخص الخطوات هنا.
كيفية تقسيم الأرقام المركبة
- اكتب كلا من البسط والمقام في الصورة القياسية.
- اضرب كلا من البسط والمقام في المترافق المركب للقاسم.
- قم بتبسيط النتيجة وكتابتها في النموذج القياسي.
قسّم، اكتب الإجابات في النموذج القياسي:\(\frac{-3}{5+2 i}\).
الحل:
\(\frac{-3}{5+2 i}\)
اضرب البسط والمقام في المترافق المركب للقاسم.
\(\frac{-3(5-2 i)}{(5+2 i)(5-2 i)}\)
اضرب في البسط واستخدم حاصل ضرب نمط الاقتران المركب في المقام.
\(\frac{-15+6 i}{5^{2}+2^{2}}\)
قم بالتبسيط.
\(\frac{-15+6 i}{29}\)
اكتب في النموذج القياسي.
\(-\frac{15}{29}+\frac{6}{29} i\)
قسّم، اكتب الإجابة في النموذج القياسي:\(\frac{4}{1-4 i}\).
- إجابة
-
\(\frac{4}{17}+\frac{16}{17} i\)
قسّم، اكتب الإجابة في النموذج القياسي:\(\frac{-2}{-1+2 i}\).
- إجابة
-
\(\frac{2}{5}+\frac{4}{5} i\)
كن حذرًا عندما تجد مترافق المقام.
قسّم:\(\frac{5+3 i}{4 i}\).
الحل:
\(\frac{5+3 i}{4 i}\)
اكتب المقام في الصورة القياسية.
\(\frac{5+3 i}{0+4 i}\)
اضرب البسط والمقام في المترافق المركب للقاسم.
\(\frac{(5+3 i)(0-4 i)}{(0+4 i)(0-4 i)}\)
قم بالتبسيط.
\(\frac{(5+3 i)(-4 i)}{(4 i)(-4 i)}\)
اضرب.
\(\frac{-20 i-12 i^{2}}{-16 i^{2}}\).
قم بتبسيط ملف\(i^{2}\).
\(\frac{-20 i+12}{16}\)
أعد الكتابة في النموذج القياسي.
\(\frac{12}{16}-\frac{20}{16} i\)
قم بتبسيط الكسور.
\(\frac{3}{4}-\frac{5}{4} i\)
قسّم:\(\frac{3+3 i}{2 i}\).
- إجابة
-
\(\frac{3}{2}-\frac{3}{2} i\)
قسّم:\(\frac{2+4 i}{5 i}\).
- إجابة
-
\(\frac{4}{5}-\frac{2}{5} i\)
تبسيط صلاحيات\(i\)
إن قوى\(i\) صنع نمط مثير للاهتمام سيساعدنا على تبسيط القوى العليا لـ\(i\). دعونا نقيم صلاحيات\(i\) رؤية النمط.
\(\begin{array}{ccc}{i^{1}} & {i^{2}} & {i^{3}} & {i^{4}} \\ {i} & {-1} & {i^{2}\cdot i} & {i^{2}\cdot i^{2}}\\ {}&{}&{-1\cdot i}&{(-1)(-1)}\\ {}&{}&{-i}&{1}\end{array}\)
\(\begin{array}{cccc}{i^{5}} & {i^{6}} & {i^{7}} & {i^{8}} \\ {i^{4} \cdot i} & {i^{4} \cdot i^{2}} & {i^{4} \cdot i^{3}} & {i^{4} \cdot i^{4}} \\ {1 \cdot i} & {1 \cdot i^{2}} & {1 \cdot i^{3}} & {1 \cdot 1} \\ {i} & {i^{2}} & {i^{3}} & {1} \\ {}&{-1} & {-i}\end{array}\)
نحن نلخص هذا الآن.
\(\begin{array}{ll}{i^{1}=i} & {i^{5}=i} \\ {i^{2}=-1} & {i^{6}=-1} \\ {i^{3}=-i} & {i^{7}=-i} \\ {i^{4}=1} & {i^{8}=1}\end{array}\)
إذا واصلنا، سيستمر النمط في التكرار في كتل من أربعة. يمكننا استخدام هذا النمط لمساعدتنا على تبسيط سلطات\(i\). نظرًا\(i^{4}=1\) لأننا نعيد كتابة كل قوة\(i^{n}\)، كمنتج يستخدم\(i^{4}\) قوة وقوة أخرى\(i\).
نعيد كتابته بالشكل\(i^{n}=\left(i^{4}\right)^{q} \cdot i^{r}\)، حيث الأس\(q\)، هو حاصل القسمة على والأس\(r\)، هو الباقي من هذه القسمة.\(n\)\(4\) على سبيل المثال\(i^{57}\)، للتبسيط، نقسم\(57\)\(4\) ونحصل\(14\) على ما تبقى من\(1\). وبعبارة أخرى،\(57=4⋅14+1\). لذلك نكتب\(i^{57}=\left(1^{4}\right)^{14} \cdot i^{1}\) ثم نبسط من هناك.
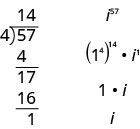
قم بالتبسيط:\(i^{86}\).
الحل:
\(i^{86}\)
قم\(86\) بالقسمة\(4\) وإعادة الكتابة\(i^{86}\) في\(i^{n}=\left(i^{4}\right)^{q} \cdot i^{r}\) النموذج.
\(\left(1^{4}\right)^{21} \cdot i^{2}\)
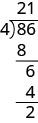
قم بالتبسيط.
\((1)^{21} \cdot(-1)\)
قم بالتبسيط.
\(-1\)
قم بالتبسيط:\(i^{74}\).
- إجابة
-
\(-1\)
قم بالتبسيط:\(i^{92}\).
- إجابة
-
\(1\)
يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية باستخدام نظام الأرقام المعقدة.
- التعبير عن الجذور التربيعية للأعداد السالبة باستخدام i
- طرح الأعداد المركبة وضربها
- قسمة الأعداد المركبة
- إعادة كتابة قوى i
المفاهيم الرئيسية
- الجذر التربيعي لعدد سالب
- \(b\)إذا كان الرقم الحقيقي موجبًا، فعندئذٍ\ (\ sqrt {-b} =\ sqrt {b} i\
| \(a+bi\) | ||
| \(b=0\) |
\(a+0\cdot i\) \(a\) |
رقم حقيقي |
| \(b\neq 0\) | \(a+bi\) | رقم وهمي |
| \(a=0\) |
\(0+bi\) \(bi\) |
رقم وهمي خالص |
-
- يكون الرقم المركب في شكل قياسي عند كتابته كـ a + bi، حيث a و b هي أرقام حقيقية.
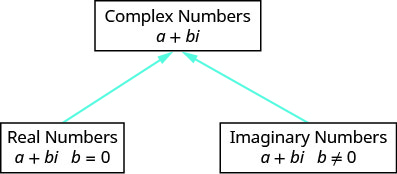
الشكل 8.8.2
- يكون الرقم المركب في شكل قياسي عند كتابته كـ a + bi، حيث a و b هي أرقام حقيقية.
- منتج من منتجات المترافقة المعقدة
- إذا كانت\(a, b\) الأرقام حقيقية، إذن
\((a−bi)(a+bi)=a^{2}+b^{2}\)
- إذا كانت\(a, b\) الأرقام حقيقية، إذن
- كيفية تقسيم الأرقام المركبة
- اكتب كلا من البسط والمقام في الصورة القياسية.
- اضرب البسط والمقام في المترافق المركب للقاسم.
- قم بتبسيط النتيجة وكتابتها في النموذج القياسي.
مسرد المصطلحات
- زوج مترافق معقد
- الزوج المترافق المعقد هو من الشكل\(a+bi, a-bi\).
- رقم مركب
- الرقم المركب هو من النموذج\(a+bi\)\(a\) وأين\(b\) والأرقام الحقيقية. نسمي\(a\) الجزء الحقيقي\(b\) والجزء الخيالي.
- نظام الأرقام المعقدة
- يتكون نظام الأرقام المركب من كل من الأرقام الحقيقية والأرقام التخيلية.
- وحدة خيالية
- الوحدة التخيلية\(i\) هي الرقم الذي يكون مربعه\(–1\). \(i^{2}=-1\)أو\(i=\sqrt{−1}\).
- نموذج قياسي
- يكون الرقم المركب في شكل قياسي عند كتابته كـ\(a+bi\)، أين\(a, b\) توجد أرقام حقيقية.


