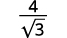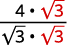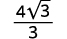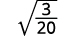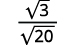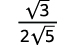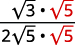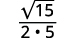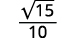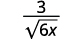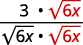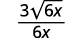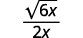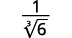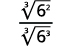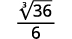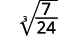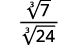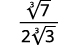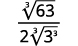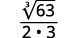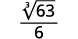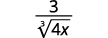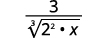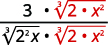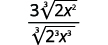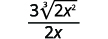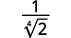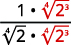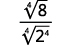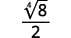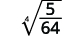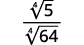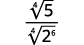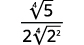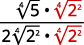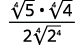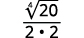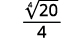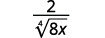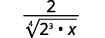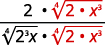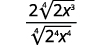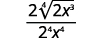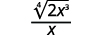Skip to main content
Global

8.6: تقسيم التعبيرات الراديكالية

  1. Last updated
  2. Save as PDF
  • Page ID
    201601

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • اقسم التعبيرات الراديكالية
    • ترشيد قاسم مصطلح واحد
    • ترشيد قاسم فترتين

    قبل البدء، قم بإجراء اختبار الاستعداد هذا.

    1. قم بالتبسيط:\(\dfrac{30}{48}\).
      إذا فاتتك هذه المشكلة، راجع المثال 1.24.
    2. قم بالتبسيط:\(x^{2}⋅x^{4}\).
      إذا فاتتك هذه المشكلة، راجع المثال 5.12.
    3. اضرب:\((7+3x)(7−3x)\).
      إذا فاتتك هذه المشكلة، راجع مثال 5.32.

    اقسم التعبيرات الراديكالية

    لقد استخدمنا خاصية حاصل القسمة في التعبيرات الجذرية لتبسيط جذور الكسور. سنحتاج إلى استخدام هذه الخاصية «في الاتجاه المعاكس» لتبسيط الكسر باستخدام الجذور. نعطي خاصية حاصل القسمة للتعبيرات الراديكالية مرة أخرى لسهولة الرجوع إليها. تذكر أننا نفترض أن جميع المتغيرات أكبر من أو تساوي الصفر بحيث لا تكون هناك حاجة إلى أشرطة القيم المطلقة.

    تعريف\(\PageIndex{1}\): Quotient Property of Radical Expressions

    إذا كانت\(\sqrt[n]{a}\)\(\sqrt[n]{b}\) الأرقام حقيقية\(b≠0\)، ولأي عدد صحيح\(n≥2\) إذن،

    \(\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} \quad \text { and } \quad \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\)

    سنستخدم خاصية حاصل القسمة للتعبيرات الجذرية عندما يكون الكسر الذي نبدأ به هو حاصل قسمة جذرين، ولا يمثل أي من الراديكوند قوة مثالية للمؤشر. عندما نكتب الكسر في جذر واحد، قد نجد عوامل مشتركة في البسط والمقام.

    مثال\(\PageIndex{1}\)

    قم بالتبسيط:

    1. \(\dfrac{\sqrt{72 x^{3}}}{\sqrt{162 x}}\)
    2. \(\dfrac{\sqrt[3]{32 x^{2}}}{\sqrt[3]{4 x^{5}}}\)

    الحل:

    أ.

    \(\dfrac{\sqrt{72 x^{3}}}{\sqrt{162 x}}\)

    أعد الكتابة باستخدام خاصية حاصل القسمة،

    \(\sqrt{\dfrac{72 x^{3}}{162 x}}\)

    قم بإزالة العوامل المشتركة.

    \(\sqrt{\dfrac{\cancel{18} \cdot 4 \cdot x^{2} \cdot \cancel{x}}{\cancel{18} \cdot 9 \cdot \cancel{x}}}\)

    قم بالتبسيط.

    \(\sqrt{\dfrac{4 x^{2}}{9}}\)

    قم بتبسيط الراديكالية.

    \(\dfrac{2 x}{3}\)

    ب.

    \(\dfrac{\sqrt[3]{32 x^{2}}}{\sqrt[3]{4 x^{5}}}\)

    أعد الكتابة باستخدام خاصية حاصل القسمة،\(\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\).

    \(\sqrt[3]{\dfrac{32 x^{2}}{4 x^{5}}}\)

    قم بتبسيط الكسر تحت الجذر.

    \(\sqrt[3]{\dfrac{8}{x^{3}}}\)

    قم بتبسيط الراديكالية.

    \(\dfrac{2}{x}\)

    التمارين\(\PageIndex{1}\)

    قم بالتبسيط:

    1. \(\dfrac{\sqrt{50 s^{3}}}{\sqrt{128 s}}\)
    2. \(\dfrac{\sqrt[3]{56 a}}{\sqrt[3]{7 a^{4}}}\)
    إجابة
    1. \(\dfrac{5s}{8}\)
    2. \(\dfrac{2}{a}\)
    التمارين\(\PageIndex{2}\)

    قم بالتبسيط:

    1. \(\dfrac{\sqrt{75 q^{5}}}{\sqrt{108 q}}\)
    2. \(\dfrac{\sqrt[3]{72 b^{2}}}{\sqrt[3]{9 b^{5}}}\)
    إجابة
    1. \(\dfrac{5 q^{2}}{6}\)
    2. \(\dfrac{2}{b}\)
    مثال\(\PageIndex{2}\)

    قم بالتبسيط:

    1. \(\dfrac{\sqrt{147 a b^{8}}}{\sqrt{3 a^{3} b^{4}}}\)
    2. \(\dfrac{\sqrt[3]{-250 m n^{-2}}}{\sqrt[3]{2 m^{-2} n^{4}}}\)

    الحل:

    أ.

    \(\dfrac{\sqrt{147 a b^{8}}}{\sqrt{3 a^{3} b^{4}}}\)

    أعد الكتابة باستخدام خاصية حاصل القسمة.

    \(\sqrt{\dfrac{147 a b^{8}}{3 a^{3} b^{4}}}\)

    قم بإزالة العوامل الشائعة في الكسر.

    \(\sqrt{\dfrac{49 b^{4}}{a^{2}}}\)

    قم بتبسيط الراديكالية.

    \(\dfrac{7 b^{2}}{a}\)

    ب.

    \(\dfrac{\sqrt[3]{-250 m n^{-2}}}{\sqrt[3]{2 m^{-2} n^{4}}}\)

    أعد الكتابة باستخدام خاصية حاصل القسمة.

    \(\sqrt[3]{\dfrac{-250 m n^{-2}}{2 m^{-2} n^{4}}}\)

    قم بتبسيط الكسر تحت الجذر.

    \(\sqrt[3]{\dfrac{-125 m^{3}}{n^{6}}}\)

    قم بتبسيط الراديكالية.

    \(-\dfrac{5 m}{n^{2}}\)

    التمارين\(\PageIndex{3}\)

    قم بالتبسيط:

    1. \(\dfrac{\sqrt{162 x^{10} y^{2}}}{\sqrt{2 x^{6} y^{6}}}\)
    2. \(\dfrac{\sqrt[3]{-128 x^{2} y^{-1}}}{\sqrt[3]{2 x^{-1} y^{2}}}\)
    إجابة
    1. \(\dfrac{9 x^{2}}{y^{2}}\)
    2. \(\dfrac{-4 x}{y}\)
    التمارين\(\PageIndex{4}\)

    قم بالتبسيط:

    1. \(\dfrac{\sqrt{300 m^{3} n^{7}}}{\sqrt{3 m^{5} n}}\)
    2. \(\dfrac{\sqrt[3]{-81 p q^{-1}}}{\sqrt[3]{3 p^{-2} q^{5}}}\)
    إجابة
    1. \(\dfrac{10 n^{3}}{m}\)
    2. \(\dfrac{-3 p}{q^{2}}\)
    مثال\(\PageIndex{3}\)

    قم بالتبسيط:\(\dfrac{\sqrt{54 x^{5} y^{3}}}{\sqrt{3 x^{2} y}}\)

    الحل:

    \(\dfrac{\sqrt{54 x^{5} y^{3}}}{\sqrt{3 x^{2} y}}\)

    أعد الكتابة باستخدام خاصية حاصل القسمة.

    \(\sqrt{\dfrac{54 x^{5} y^{3}}{3 x^{2} y}}\)

    قم بإزالة العوامل الشائعة في الكسر.

    \(\sqrt{18 x^{3} y^{2}}\)

    أعد كتابة الراديكاند كمنتج باستخدام أكبر عامل مربع مثالي.

    \(\sqrt{9 x^{2} y^{2} \cdot 2 x}\)

    أعد كتابة الراديكالية على أنها نتاج جذريين.

    \(\sqrt{9 x^{2} y^{2}} \cdot \sqrt{2 x}\)

    قم بالتبسيط.

    \(3 x y \sqrt{2 x}\)

    التمارين\(\PageIndex{5}\)

    قم بالتبسيط:\(\dfrac{\sqrt{64 x^{4} y^{5}}}{\sqrt{2 x y^{3}}}\)

    إجابة

    \(4 x y \sqrt{2 x}\)

    التمارين\(\PageIndex{6}\)

    قم بالتبسيط:\(\dfrac{\sqrt{96 a^{5} b^{4}}}{\sqrt{2 a^{3} b}}\)

    إجابة

    \(4 a b \sqrt{3 b}\)

    ترشيد قاسم مصطلح واحد

    قبل أن تصبح الآلة الحاسبة أداة للحياة اليومية، كان تقريب قيمة الكسر مع وجود جذر في المقام عملية مرهقة للغاية!

    لهذا السبب، تم تطوير عملية تسمى ترشيد المقام. يتم تحويل الكسر الذي يحتوي على جذر في المقام إلى كسر مكافئ مقامه عدد صحيح. الجذور التربيعية للأرقام التي ليست مربعات مثالية هي أرقام غير منطقية. عندما نقوم بترشيد المقام، نكتب كسرًا مكافئًا برقم نسبي في المقام. لا تزال هذه العملية مستخدمة حتى اليوم، وهي مفيدة في مجالات الرياضيات الأخرى أيضًا.

    تعريف\(\PageIndex{2}\): Rationalizing the Denominator

    ترشيد المقام هو عملية تحويل كسر ذي جذر في المقام إلى كسر مكافئ مقامه عدد صحيح.

    على الرغم من توفر الآلات الحاسبة في كل مكان تقريبًا، لا يزال يتعين ترشيد الكسر الذي يحتوي على جذر في المقام. لا يعتبر الأمر مبسطًا إذا كان القاسم يحتوي على جذر.

    وبالمثل، لا يعتبر التعبير الراديكالي مبسطًا إذا كان الجذر يحتوي على كسر.

    التعبيرات الراديكالية المبسطة

    يعتبر التعبير الراديكالي مبسطًا إذا كان هناك

    • لا توجد عوامل في التطرف ولديها قوى كاملة للمؤشر
    • لا توجد كسور في الراديكواند
    • لا توجد جذور في مقام الكسر

    لترشيد المقام بجذر تربيعي، نستخدم الخاصية التي\((\sqrt{a})^{2}=a\). إذا قمنا بتربيع جذر تربيعي غير منطقي، نحصل على عدد نسبي.

    سنستخدم هذه الخاصية لترشيد المقام في المثال التالي.

    مثال\(\PageIndex{4}\)

    قم بالتبسيط:

    1. \(\dfrac{4}{\sqrt{3}}\)
    2. \(\sqrt{\dfrac{3}{20}}\)
    3. \(\dfrac{3}{\sqrt{6 x}}\)

    الحل:

    لترشيد المقام بمصطلح واحد، يمكننا ضرب الجذر التربيعي في حد ذاته. للحفاظ على مكافئ الكسر، نضرب كلا من البسط والمقام بنفس العامل.

    أ.

     

    .
    اضرب كل من البسط والمقام في\(\sqrt{3}\).

    .
    قم بالتبسيط.

    .
    الجدول 8.5.1

    ب- نقوم دائمًا بتبسيط الراديكالية في المقام أولاً قبل ترشيدها. بهذه الطريقة تظل الأرقام أصغر ويسهل التعامل معها.

     

    .
    الكسر ليس مربعًا مثاليًا، لذا أعد الكتابة باستخدام خاصية Quotient.

    .
    قم بتبسيط المقام.

    .
    اضرب البسط والمقام في\(\sqrt{5}\).

    .
    قم بالتبسيط.

    .
    قم بالتبسيط.

    .
    الجدول 8.5.2

    ج.

     

    .
    اضرب البسط والمقام في\(\sqrt{6x}\).

    .
    قم بالتبسيط.

    .
    قم بالتبسيط.

    .
    الجدول 8-5-3
    التمارين\(\PageIndex{7}\)

    قم بالتبسيط:

    1. \(\dfrac{5}{\sqrt{3}}\)
    2. \(\sqrt{\dfrac{3}{32}}\)
    3. \(\dfrac{2}{\sqrt{2 x}}\)
    إجابة
    1. \(\dfrac{5 \sqrt{3}}{3}\)
    2. \(\dfrac{\sqrt{6}}{8}\)
    3. \(\dfrac{\sqrt{2 x}}{x}\)
    التمارين\(\PageIndex{8}\)

    قم بالتبسيط:

    1. \(\dfrac{6}{\sqrt{5}}\)
    2. \(\sqrt{\dfrac{7}{18}}\)
    3. \(\dfrac{5}{\sqrt{5 x}}\)
    إجابة
    1. \(\dfrac{6 \sqrt{5}}{5}\)
    2. \(\dfrac{\sqrt{14}}{6}\)
    3. \(\dfrac{\sqrt{5 x}}{x}\)

    عندما قمنا بترشيد الجذر التربيعي، قمنا بضرب البسط والمقام في الجذر التربيعي الذي يعطينا مربعًا كاملاً تحت الجذر في المقام. عندما أخذنا الجذر التربيعي، لم يعد القاسم جذريًا.

    سوف نتبع عملية مماثلة لترشيد الجذور العليا. ولتبرير قاسم ذي مؤشر جذري أعلى، نضرب البسط والمقام في جذر من شأنه أن يعطينا جذريًا يمثل قوة مثالية للمؤشر. عندما نقوم بتبسيط الراديكالية الجديدة، لن يكون القاسم راديكالي بعد الآن.

    على سبيل المثال،

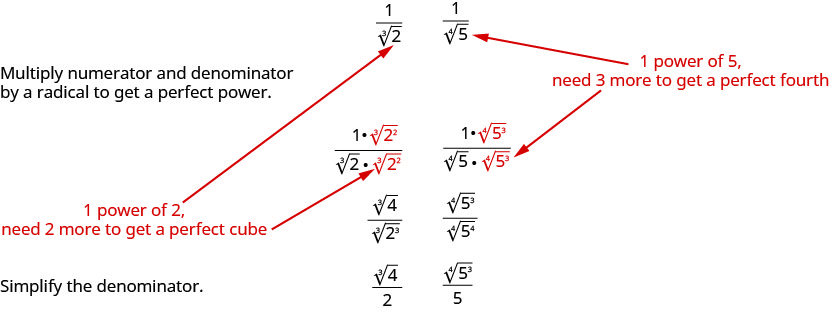
    يتم عرض مثالين لترشيد القواسم. المثال الأول هو 1 مقسومًا على الجذر التكعيبي 2. تجدر الإشارة إلى أن الراديكاند في المقام يساوي قوة واحدة من 2 وأننا بحاجة إلى 2 آخرين للحصول على مكعب مثالي. نضرب البسط والمقام في الجذر التكعيبي للكمية 2 المربعة. والنتيجة هي الجذر التكعيبي 4 مقسومًا على الجذر التكعيبي للكمية 2 المكعبة. هذا يبسط إلى الجذر التكعيبي 4 مقسومًا على 2. المثال الثاني هو 1 مقسومًا على الجذر الرابع 5. تجدر الإشارة إلى أن الراديكاند في المقام هو قوة واحدة من 5 وأننا بحاجة إلى 3 آخرين للحصول على رابع مثالي. نضرب البسط والمقام في الجذر الرابع للكمية 5 المكعبة. والنتيجة هي الجذر الرابع لـ 125 مقسومًا على الجذر الرابع للكمية 5 إلى الرابعة. هذا يبسط إلى الجذر الرابع 125 مقسومًا على 5.
    الشكل 8.5.14

    سنستخدم هذه التقنية في الأمثلة التالية.

    مثال\(\PageIndex{5}\)

    قم بالتبسيط:

    1. \(\dfrac{1}{\sqrt[3]{6}}\)
    2. \(\sqrt[3]{\dfrac{7}{24}}\)
    3. \(\dfrac{3}{\sqrt[3]{4 x}}\)

    الحل:

    لترشيد المقام بالجذر التكعيبي، يمكننا الضرب في الجذر التكعيبي الذي سيعطينا مكعبًا مثاليًا في الجذر في المقام. للحفاظ على مكافئ الكسر، نضرب كلا من البسط والمقام بنفس العامل.

    أ.

     

    .
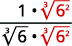
    والراديكالي في المقام له عامل واحد هو\(6\). اضرب كل من البسط والمقام في\(\sqrt[3]{6^{2}}\)، مما يعطينا\(2\) المزيد من العوامل\(6\).

    .
    اضرب. لاحظ أن الراديكوند الموجود في المقام له\(3\) قوى\(6\).

    .
    قم بتبسيط الجذر التكعيبي في المقام.

    .
    الجدول 8-5-4

    ب- نقوم دائمًا بتبسيط الراديكالية في المقام أولاً قبل ترشيدها. بهذه الطريقة تظل الأرقام أصغر ويسهل التعامل معها.

     

    .
    الكسر ليس مكعبًا مثاليًا، لذا أعد الكتابة باستخدام خاصية Quotient.

    .
    قم بتبسيط المقام.

    .
    اضرب البسط والمقام في\(\sqrt[3]{3^{2}}\). سيعطينا هذا\(3\) عوامل\(3\).

    .
    قم بالتبسيط.

    .
    تذكر،\(\sqrt[3]{3^{3}}=3\).

    .
    قم بالتبسيط.

    .
    الجدول 8-5-5

    ج.

     

    .
    أعد كتابة الجذر لإظهار العوامل.

    .
    اضرب البسط والمقام في\(\sqrt[3]{2 \cdot x^{2}}\). سيوفر لنا هذا\(3\)\(3\) عوامل\(2\) وعوامل\(x\).

    .
    قم بالتبسيط.

    .
    قم بتبسيط الراديكالية في المقام.

    .
    الجدول 8-5-6
    التمارين\(\PageIndex{9}\)

    قم بالتبسيط:

    1. \(\dfrac{1}{\sqrt[3]{7}}\)
    2. \(\sqrt[3]{\dfrac{5}{12}}\)
    3. \(\dfrac{5}{\sqrt[3]{9 y}}\)
    إجابة
    1. \(\dfrac{\sqrt[3]{49}}{7}\)
    2. \(\dfrac{\sqrt[3]{90}}{6}\)
    3. \(\dfrac{5 \sqrt[3]{3 y^{2}}}{3 y}\)
    التمارين\(\PageIndex{10}\)

    قم بالتبسيط:

    1. \(\dfrac{1}{\sqrt[3]{2}}\)
    2. \(\sqrt[3]{\dfrac{3}{20}}\)
    3. \(\dfrac{2}{\sqrt[3]{25 n}}\)
    إجابة
    1. \(\dfrac{\sqrt[3]{4}}{2}\)
    2. \(\dfrac{\sqrt[3]{150}}{10}\)
    3. \(\dfrac{2 \sqrt[3]{5 n^{2}}}{5 n}\)
    مثال\(\PageIndex{6}\)

    قم بالتبسيط:

    1. \(\dfrac{1}{\sqrt[4]{2}}\)
    2. \(\sqrt[4]{\dfrac{5}{64}}\)
    3. \(\dfrac{2}{\sqrt[4]{8 x}}\)

    الحل:

    لترشيد المقام بجذر رابع، يمكننا الضرب في الجذر الرابع الذي سيعطينا قوة رابعة مثالية في الجذر وفي المقام. للحفاظ على مكافئ الكسر، نضرب كلا من البسط والمقام بنفس العامل.

    أ.

     

    .
    والراديكالي في المقام له عامل واحد هو\(2\).
    اضرب كل من البسط والمقام في\(\sqrt[4]{2^{3}}\)، مما يعطينا\(3\) المزيد من العوامل\(2\).

    .
    اضرب. لاحظ أن الراديكوند الموجود في المقام له\(4\) قوى\(2\).

    .
    قم بتبسيط الجذر الرابع في المقام.

    .
    الجدول 8.5.7

    ب- نقوم دائمًا بتبسيط الراديكالية في المقام أولاً قبل ترشيدها. بهذه الطريقة تظل الأرقام أصغر ويسهل التعامل معها.

     

    .
    لا يمثل الكسر قوة رابعة مثالية، لذا أعد الكتابة باستخدام خاصية Quotient.

    .
    أعد كتابة الجذر في المقام لإظهار العوامل.

    .
    قم بتبسيط المقام.

    .
    اضرب البسط والمقام في\(\sqrt[4]{2^{2}}\). سيعطينا هذا\(4\) عوامل\(2\).

    .
    قم بالتبسيط.

    .
    تذكر،\(\sqrt[4]{2^{4}}=2\).

    .
    قم بالتبسيط.

    .
    الجدول 8-5-8

    ج.

     

    .
    أعد كتابة الجذر لإظهار العوامل.

    .
    اضرب البسط والمقام في\(\sqrt[4]{2 \cdot x^{3}}\). سيوفر لنا هذا\(4\)\(4\) عوامل\(2\) وعوامل\(x\).

    .
    قم بالتبسيط.

    .
    قم بتبسيط الراديكالية في المقام.

    .
    قم بتبسيط الكسر.

    .
    الجدول 8-5-9
    التمارين\(\PageIndex{11}\)

    قم بالتبسيط:

    1. \(\dfrac{1}{\sqrt[4]{3}}\)
    2. \(\sqrt[4]{\dfrac{3}{64}}\)
    3. \(\dfrac{3}{\sqrt[4]{125 x}}\)
    إجابة
    1. \(\dfrac{\sqrt[4]{27}}{3}\)
    2. \(\dfrac{\sqrt[4]{12}}{4}\)
    3. \(\dfrac{3 \sqrt[4]{5 x^{3}}}{5 x}\)
    التمارين\(\PageIndex{12}\)

    قم بالتبسيط:

    1. \(\dfrac{1}{\sqrt[4]{5}}\)
    2. \(\sqrt[4]{\dfrac{7}{128}}\)
    3. \(\dfrac{4}{\sqrt[4]{4 x}}\)
    إجابة
    1. \(\dfrac{\sqrt[4]{125}}{5}\)
    2. \(\dfrac{\sqrt[4]{224}}{8}\)
    3. \(\dfrac{\sqrt[4]{64 x^{3}}}{x}\)

    ترشيد قاسم فترتين

    عندما يكون مقام الكسر عبارة عن مجموع أو فرق ذي جذور مربعة، فإننا نستخدم حاصل ضرب النمط المترافق لترشيد المقام.

    \(\begin{array}{c c}{(a-b)(a+b)} & {(2-\sqrt{5})(2+\sqrt{5})} \\ {a^{2}-b^{2}} &{ 2^{2}-(\sqrt{5})^{2}} \\ {}&{4-5} \\ {}&{-1}\end{array}\)

    عندما نضرب مقياسًا ذا حدين يتضمن جذرًا تربيعيًا بمترافقه، فإن المنتج ليس له جذور مربعة.

    مثال\(\PageIndex{7}\)

    قم بالتبسيط:\(\dfrac{5}{2-\sqrt{3}}\)

    الحل:

      .
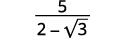    اضرب البسط والمقام في مترافق المقام. .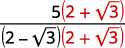
    اضرب المترادفات في المقام. .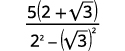
    قم بتبسيط المقام. .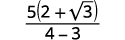
    قم بتبسيط المقام. .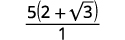
    قم بالتبسيط. .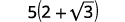
    الجدول 8-5-10
    التمارين\(\PageIndex{13}\)

    قم بالتبسيط:\(\dfrac{3}{1-\sqrt{5}}\).

    إجابة

    \(-\dfrac{3(1+\sqrt{5})}{4}\)

    التمارين\(\PageIndex{14}\)

    قم بالتبسيط:\(\dfrac{2}{4-\sqrt{6}}\).

    إجابة

    \(\dfrac{4+\sqrt{6}}{5}\)

    لاحظ أننا لم نوزع الإجابة\(5\) في المثال الأخير. من خلال ترك النتيجة في الاعتبار، يمكننا معرفة ما إذا كانت هناك أي عوامل قد تكون مشتركة بين كل من البسط والمقام.

    مثال\(\PageIndex{8}\)

    قم بالتبسيط:\(\dfrac{\sqrt{3}}{\sqrt{u}-\sqrt{6}}\).

    الحل:

      .
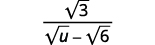    اضرب البسط والمقام في مترافق المقام. .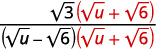
    اضرب المترادفات في المقام. .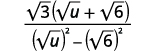
    قم بتبسيط المقام. .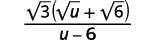
    الجدول 8-5-11
    التمارين\(\PageIndex{15}\)

    قم بالتبسيط:\(\dfrac{\sqrt{5}}{\sqrt{x}+\sqrt{2}}\).

    إجابة

    \(\dfrac{\sqrt{5}(\sqrt{x}-\sqrt{2})}{x-2}\)

    التمارين\(\PageIndex{16}\)

    قم بالتبسيط:\(\dfrac{\sqrt{10}}{\sqrt{y}-\sqrt{3}}\)

    إجابة

    \(\dfrac{\sqrt{10}(\sqrt{y}+\sqrt{3})}{y-3}\)

    احذر من العلامات عند الضرب. يبدو البسط والمقام متشابهين جدًا عند الضرب في المترافق.

    مثال\(\PageIndex{9}\)

    قم بالتبسيط:\(\dfrac{\sqrt{x}+\sqrt{7}}{\sqrt{x}-\sqrt{7}}\).

    الحل:

      .
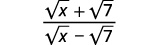    اضرب البسط والمقام في مترافق المقام. .
    اضرب المترادفات في المقام. .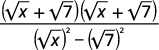
    قم بتبسيط المقام. .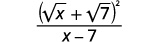
    الجدول 8-5-12

    نحن لا نعادل البسط. وبتركه في صورة معمول به، يمكننا أن نرى أنه لا توجد عوامل مشتركة يمكن إزالتها من البسط والمقام.

    التمارين\(\PageIndex{17}\)

    قم بالتبسيط:\(\dfrac{\sqrt{p}+\sqrt{2}}{\sqrt{p}-\sqrt{2}}\).

    إجابة

    \(\dfrac{(\sqrt{p}+\sqrt{2})^{2}}{p-2}\)

    التمارين\(\PageIndex{18}\)

    قم بالتبسيط:\(\dfrac{\sqrt{q}-\sqrt{10}}{\sqrt{q}+\sqrt{10}}\)

    إجابة

    \(\dfrac{(\sqrt{q}-\sqrt{10})^{2}}{q-10}\)

    المفاهيم الرئيسية

    • خاصية خارج القسمة للتعبيرات الجذرية
      • إذا كانت\(\sqrt[n]{a}\)\(\sqrt[n]{b}\) الأرقام حقيقية\(b≠0\)، ولأي عدد صحيح\(n≥2\) إذن،\(\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\) و\(\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\)
    • التعبيرات الراديكالية المبسطة
      • يعتبر التعبير الراديكالي مبسطًا إذا كان هناك:
        • لا توجد عوامل في الراديكوند التي تتمتع بالقوى الكاملة للمؤشر
        • لا توجد كسور في الراديكواند
        • لا توجد جذور في مقام الكسر

    مسرد المصطلحات

    ترشيد المقام
    ترشيد المقام هو عملية تحويل كسر ذي جذر في المقام إلى كسر مكافئ مقامه عدد صحيح.