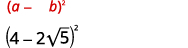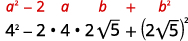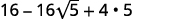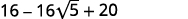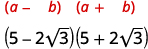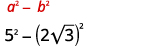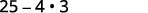Home
اللغة العربية
الجبر المتوسط (OpenStax)
8: الجذور والجذور
8.5: جمع التعبيرات الجذرية وطرحها وضربها

8.5: جمع التعبيرات الجذرية وطرحها وضربها

Last updated

Nov 1, 2022
Page ID
201614
Save as PDF
- 8.4E: تمارين
- 8.5E: تمارين

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

جمع وطرح التعبيرات الجذرية
اضرب التعبيرات الراديكالية
استخدم الضرب متعدد الحدود لضرب التعبيرات الجذرية

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

إضافة: $3x^{2}+9x−5−(x^{2}−2x+3)$ .
إذا فاتتك هذه المشكلة، راجع المثال 5.5.
قم بالتبسيط: $(2+a)(4−a)$ .
إذا فاتتك هذه المشكلة، راجع المثال 5.28.
قم بالتبسيط: $(9−5y)^{2}$ .
إذا فاتتك هذه المشكلة، راجع مثال 5.31.

جمع وطرح التعبيرات الجذرية

إن إضافة تعبيرات جذرية بنفس الفهرس ونفس الجذر يشبه تمامًا إضافة مصطلحات متشابهة. نسمي الراديكاليين بنفس المؤشر ونفس الراديكاليون مثل الراديكاليين لتذكيرنا بأنهم يعملون بنفس المصطلحات المتشابهة.

تعريف $\PageIndex{1}$ : Like Radicals

مثل الجذور هي التعبيرات الجذرية بنفس المؤشر ونفس الجذور.

نجمع ونطرح الجذور المتشابهة بنفس الطريقة التي نجمع بها ونطرح المصطلحات المتشابهة. نحن نعلم أن هذا $3x+8x$ هو $11x$ .وبالمثل نضيف $3 \sqrt{x}+8 \sqrt{x}$ والنتيجة هي $11 \sqrt{x}$ .

فكر في إضافة مصطلحات مماثلة مع المتغيرات كما تفعل في الأمثلة القليلة التالية. عندما يكون لديك مثل الجذور، يمكنك فقط إضافة المعاملات أو طرحها. عندما لا يكون الراديكاليون متشابهين، لا يمكنك الجمع بين المصطلحات.

مثال $\PageIndex{1}$

قم بالتبسيط:

$2 \sqrt{2}-7 \sqrt{2}$
$5 \sqrt[3]{y}+4 \sqrt[3]{y}$
$7 \sqrt[4]{x}-2 \sqrt[4]{y}$

الحل:

أ.

$2 \sqrt{2}-7 \sqrt{2}$

بما أن الجذور متشابهة، فإننا نطرح المعاملات.

$-5 \sqrt{2}$

ب.

$5 \sqrt[3]{y}+4 \sqrt[3]{y}$

بما أن الجذور متشابهة، نضيف المعاملات.

$9 \sqrt[3]{y}$

ج.

$7 \sqrt[4]{x}-2 \sqrt[4]{y}$

المؤشرات هي نفسها ولكن الجذور مختلفة. هؤلاء ليسوا مثل الراديكاليين. نظرًا لأن الجذور ليست متشابهة، فلا يمكننا طرحها.

التمارين $\PageIndex{1}$

قم بالتبسيط:

$8 \sqrt{2}-9 \sqrt{2}$
$4 \sqrt[3]{x}+7 \sqrt[3]{x}$
$3 \sqrt[4]{x}-5 \sqrt[4]{y}$

إجابة

$-\sqrt{2}$
$11 \sqrt[3]{x}$
$3 \sqrt[4]{x}-5 \sqrt[4]{y}$

التمارين $\PageIndex{2}$

قم بالتبسيط:

$5 \sqrt{3}-9 \sqrt{3}$
$5 \sqrt[3]{y}+3 \sqrt[3]{y}$
$5 \sqrt[4]{m}-2 \sqrt[3]{m}$

إجابة

$-4 \sqrt{3}$
$8 \sqrt[3]{y}$
$5 \sqrt[4]{m}-2 \sqrt[3]{m}$

لكي يتشابه الراديكاليون، يجب أن يكون لديهم نفس المؤشر والراديكالية. عندما تحتوي الجذور على أكثر من متغير واحد، طالما أن جميع المتغيرات وأسسها متطابقة، فإن الجذور هي نفسها.

مثال $\PageIndex{2}$

قم بالتبسيط:

$2 \sqrt{5 n}-6 \sqrt{5 n}+4 \sqrt{5 n}$
$\sqrt[4]{3 x y}+5 \sqrt[4]{3 x y}-4 \sqrt[4]{3 x y}$

الحل:

أ.

$2 \sqrt{5 n}-6 \sqrt{5 n}+4 \sqrt{5 n}$

بما أن الراديكاليين متشابهون، فإننا ندمجهم.

$0 \sqrt{5 n}$

قم بالتبسيط.

$0$

ب.

$\sqrt[4]{3 x y}+5 \sqrt[4]{3 x y}-4 \sqrt[4]{3 x y}$

بما أن الراديكاليين متشابهون، فإننا ندمجهم.

$2 \sqrt[4]{3 x y}$

التمارين $\PageIndex{3}$

قم بالتبسيط:

$\sqrt{7 x}-7 \sqrt{7 x}+4 \sqrt{7 x}$
$4 \sqrt[4]{5 x y}+2 \sqrt[4]{5 x y}-7 \sqrt[4]{5 x y}$

إجابة

$-2 \sqrt{7 x}$
$-\sqrt[4]{5 x y}$

التمارين $\PageIndex{4}$

قم بالتبسيط:

$4 \sqrt{3 y}-7 \sqrt{3 y}+2 \sqrt{3 y}$
$6 \sqrt[3]{7 m n}+\sqrt[3]{7 m n}-4 \sqrt[3]{7 m n}$

إجابة

$-\sqrt{3 y}$
$3 \sqrt[3]{7 m n}$

تذكر أننا نقوم دائمًا بتبسيط الجذور عن طريق إزالة العامل الأكبر من الجذر وهو قوة المؤشر. بمجرد تبسيط كل راديكالي، يمكننا بعد ذلك أن نقرر ما إذا كانوا مثل الراديكاليين.

مثال $\PageIndex{3}$

قم بالتبسيط:

$\sqrt{20}+3 \sqrt{5}$
$\sqrt[3]{24}-\sqrt[3]{375}$
$\frac{1}{2} \sqrt[4]{48}-\frac{2}{3} \sqrt[4]{243}$

الحل:

أ.

$\sqrt{20}+3 \sqrt{5}$

قم بتبسيط الجذور، عندما يكون ذلك ممكنًا.

$\sqrt{4} \cdot \sqrt{5}+3 \sqrt{5}$

$2 \sqrt{5}+3 \sqrt{5}$

اجمع بين الجذور المتشابهة.

$5 \sqrt{5}$

ب.

$\sqrt[3]{24}-\sqrt[3]{375}$

قم بتبسيط الجذور.

$\sqrt[3]{8} \cdot \sqrt[3]{3}-\sqrt[3]{125} \cdot \sqrt[3]{3}$

$2 \sqrt[3]{3}-5 \sqrt[3]{3}$

اجمع بين الجذور المتشابهة.

$-3 \sqrt[3]{3}$

ج.

$\frac{1}{2} \sqrt[4]{48}-\frac{2}{3} \sqrt[4]{243}$

قم بتبسيط الجذور.

$\frac{1}{2} \sqrt[4]{16} \cdot \sqrt[4]{3}-\frac{2}{3} \sqrt[4]{81} \cdot \sqrt[4]{3}$

$\frac{1}{2} \cdot 2 \cdot \sqrt[4]{3}-\frac{2}{3} \cdot 3 \cdot \sqrt[4]{3}$

$\sqrt[4]{3}-2 \sqrt[4]{3}$

اجمع بين الجذور المتشابهة.

$-\sqrt[4]{3}$

التمارين $\PageIndex{5}$

قم بالتبسيط:

$\sqrt{18}+6 \sqrt{2}$
$6 \sqrt[3]{16}-2 \sqrt[3]{250}$
$\frac{2}{3} \sqrt[3]{81}-\frac{1}{2} \sqrt[3]{24}$

إجابة

$9 \sqrt{2}$
$2 \sqrt[3]{2}$
$\sqrt[3]{3}$

التمارين $\PageIndex{6}$

قم بالتبسيط:

$\sqrt{27}+4 \sqrt{3}$
$4 \sqrt[3]{5}-7 \sqrt[3]{40}$
$\frac{1}{2} \sqrt[3]{128}-\frac{5}{3} \sqrt[3]{54}$

إجابة

$7 \sqrt{3}$
$-10 \sqrt[3]{5}$
$-3 \sqrt[3]{2}$

في المثال التالي، سنزيل العوامل الثابتة والمتغيرة من الجذور. الآن وقد تدربنا على أخذ الجذور الزوجية والفردية للمتغيرات، فمن الشائع في هذه المرحلة أن نفترض أن جميع المتغيرات أكبر من أو تساوي الصفر بحيث لا تكون القيم المطلقة مطلوبة. سنستخدم هذا الافتراض في بقية هذا الفصل.

مثال $\PageIndex{4}$

قم بالتبسيط:

$9 \sqrt{50 m^{2}}-6 \sqrt{48 m^{2}}$
$\sqrt[3]{54 n^{5}}-\sqrt[3]{16 n^{5}}$

الحل:

أ.

$9 \sqrt{50 m^{2}}-6 \sqrt{48 m^{2}}$

قم بتبسيط الجذور.

$9 \sqrt{25 m^{2}} \cdot \sqrt{2}-6 \sqrt{16 m^{2}} \cdot \sqrt{3}$

$9 \cdot 5 m \cdot \sqrt{2}-6 \cdot 4 m \cdot \sqrt{3}$

$45 m \sqrt{2}-24 m \sqrt{3}$

الراديكاليون ليسوا متشابهين وبالتالي لا يمكن دمجهم.

ب.

$\sqrt[3]{54 n^{5}}-\sqrt[3]{16 n^{5}}$

قم بتبسيط الجذور.

$\sqrt[3]{27 n^{3}} \cdot \sqrt[3]{2 n^{2}}-\sqrt[3]{8 n^{3}} \cdot \sqrt[3]{2 n^{2}}$

$3 n \sqrt[3]{2 n^{2}}-2 n \sqrt[3]{2 n^{2}}$

اجمع بين الجذور المتشابهة.

$n \sqrt[3]{2 n^{2}}$

التمارين $\PageIndex{7}$

قم بالتبسيط:

$\sqrt{32 m^{7}}-\sqrt{50 m^{7}}$
$\sqrt[3]{135 x^{7}}-\sqrt[3]{40 x^{7}}$

إجابة

$-m^{3} \sqrt{2 m}$
$x^{2} \sqrt[3]{5 x}$

التمارين $\PageIndex{8}$

قم بالتبسيط:

$\sqrt{27 p^{3}}-\sqrt{48 p^{3}}$
$\sqrt[3]{256 y^{5}}-\sqrt[3]{32 n^{5}}$

إجابة

$-p \sqrt{3 p}$
$4 y \sqrt[3]{4 y^{2}}-2 n \sqrt[3]{4 n^{2}}$

اضرب التعبيرات الراديكالية

لقد استخدمنا خاصية منتج الجذور لتبسيط الجذور التربيعية عن طريق إزالة العوامل المربعة المثالية. يمكننا استخدام خاصية منتج الجذور «في الاتجاه المعاكس» لمضاعفة الجذور التربيعية. تذكر أننا نفترض أن جميع المتغيرات أكبر من أو تساوي الصفر.

سنعيد كتابة خاصية منتج الجذور حتى نرى كلا الطريقتين معًا.

تعريف $\PageIndex{2}$ : Product Property of Roots

لأي أرقام حقيقية $\sqrt[b]{n}$ ، $\sqrt[n]{a}$ ولأي عدد صحيح $n≥2$

$\sqrt[n]{a b}=\sqrt[n]{a} \cdot \sqrt[n]{b} \quad \text { and } \quad \sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a b}$

عندما نضرب جذريين يجب أن يكون لهما نفس المؤشر. بمجرد ضرب الجذور، نبحث بعد ذلك عن العوامل التي تمثل قوة المؤشر ونبسط الراديكالية كلما أمكن ذلك.

ضرب الجذور بمعاملات يشبه إلى حد كبير ضرب المتغيرات بمعاملات. للضرب، $4x⋅3y$ نضرب المعاملات معًا ثم المتغيرات. النتيجة هي $12xy$ . ضع ذلك في الاعتبار أثناء قيامك بهذه الأمثلة.

مثال $\PageIndex{5}$

قم بالتبسيط:

$(6 \sqrt{2})(3 \sqrt{10})$
$(-5 \sqrt[3]{4})(-4 \sqrt[3]{6})$

الحل:

أ.

$(6 \sqrt{2})(3 \sqrt{10})$

اضرب باستخدام خاصية المنتج.

$18\sqrt{20}$

قم بتبسيط الراديكالية.

$18 \sqrt{4} \cdot \sqrt{5}$

قم بالتبسيط.

$18 \cdot 2 \cdot \sqrt{5}$

$36 \sqrt{5}$

ب.

$(-5 \sqrt[3]{4})(-4 \sqrt[3]{6})$

اضرب باستخدام خاصية المنتج.

$20 \sqrt[3]{24}$

قم بتبسيط الراديكالية.

$20 \sqrt[3]{8} \cdot \sqrt[3]{3}$

قم بالتبسيط.

$20 \cdot 2 \cdot \sqrt[3]{3}$

$40 \sqrt[3]{3}$

التمارين $\PageIndex{9}$

قم بالتبسيط:

$(3 \sqrt{2})(2 \sqrt{30})$
$(2 \sqrt[3]{18})(-3 \sqrt[3]{6})$

إجابة

$12 \sqrt{15}$
$-18 \sqrt[3]{2}$

التمارين $\PageIndex{10}$

قم بالتبسيط:

$(3 \sqrt{3})(3 \sqrt{6})$
$(-4 \sqrt[3]{9})(3 \sqrt[3]{6})$

إجابة

$27 \sqrt{2}$
$-36 \sqrt[3]{2}$

نحن نتبع نفس الإجراءات عندما تكون هناك متغيرات في الجذور.

مثال $\PageIndex{6}$

قم بالتبسيط:

$\left(10 \sqrt{6 p^{3}}\right)(4 \sqrt{3 p})$
$\left(2 \sqrt[4]{20 y^{2}}\right)\left(3 \sqrt[4]{28 y^{3}}\right)$

الحل:

أ.

$\left(10 \sqrt{6 p^{3}}\right)(4 \sqrt{3 p})$

اضرب.

$40 \sqrt{18 p^{4}}$

قم بتبسيط الراديكالية.

$40 \sqrt{9 p^{4}} \cdot \sqrt{2}$

قم بالتبسيط.

$40 \cdot 3 p^{2} \cdot \sqrt{3}$

$120 p^{2} \sqrt{3}$

(ب) عندما يشمل المتطرفون أعدادًا كبيرة، غالبًا ما يكون من المفيد أخذها في الاعتبار من أجل العثور على القوى المثالية.

$\left(2 \sqrt[4]{20 y^{2}}\right)\left(3 \sqrt[4]{28 y^{3}}\right)$

اضرب.

$6 \sqrt[4]{4 \cdot 5 \cdot 4 \cdot 7 y^{5}}$

قم بتبسيط الراديكالية.

$6 \sqrt[4]{16 y^{4}} \cdot \sqrt[4]{35 y}$

قم بالتبسيط.

$6 \cdot 2 y \sqrt[4]{35 y}$

اضرب.

$12 y \sqrt[4]{35 y}$

التمارين $\PageIndex{11}$

قم بالتبسيط:

$\left(6 \sqrt{6 x^{2}}\right)\left(8 \sqrt{30 x^{4}}\right)$
$\left(-4 \sqrt[4]{12 y^{3}}\right)\left(-\sqrt[4]{8 y^{3}}\right)$

إجابة

$36 x^{3} \sqrt{5}$
$8 y \sqrt[4]{3 y^{2}}$

التمارين $\PageIndex{12}$

قم بالتبسيط:

$\left(2 \sqrt{6 y^{4}}\right)(12 \sqrt{30 y})$
$\left(-4 \sqrt[4]{9 a^{3}}\right)\left(3 \sqrt[4]{27 a^{2}}\right)$

إجابة

$144 y^{2} \sqrt{5 y}$
$-36 \sqrt[4]{3 a}$

استخدم الضرب متعدد الحدود لضرب التعبيرات الجذرية

في الأمثلة القليلة التالية، سنستخدم خاصية التوزيع لضرب التعبيرات ذات الجذور. سنقوم أولاً بتوزيع الجذور ثم تبسيطها عندما يكون ذلك ممكنًا.

مثال $\PageIndex{7}$

قم بالتبسيط:

$\sqrt{6}(\sqrt{2}+\sqrt{18})$
$\sqrt[3]{9}(5-\sqrt[3]{18})$

الحل:

أ.

$\sqrt{6}(\sqrt{2}+\sqrt{18})$

اضرب.

$\sqrt{12}+\sqrt{108}$

قم بالتبسيط.

$\sqrt{4} \cdot \sqrt{3}+\sqrt{36} \cdot \sqrt{3}$

قم بالتبسيط.

$2 \sqrt{3}+6 \sqrt{3}$

اجمع مثل الراديكاليين.

$8\sqrt{3}$

ب.

$\sqrt[3]{9}(5-\sqrt[3]{18})$

توزيع.

$5 \sqrt[3]{9}-\sqrt[3]{162}$

قم بالتبسيط.

$5 \sqrt[3]{9}-\sqrt[3]{27} \cdot \sqrt[3]{6}$

قم بالتبسيط.

$5 \sqrt[3]{9}-3 \sqrt[3]{6}$

التمارين $\PageIndex{13}$

قم بالتبسيط:

$\sqrt{6}(1+3 \sqrt{6})$
$\sqrt[3]{4}(-2-\sqrt[3]{6})$

إجابة

$18+\sqrt{6}$
$-2 \sqrt[3]{4}-2 \sqrt[3]{3}$

التمارين $\PageIndex{14}$

قم بالتبسيط:

$\sqrt{8}(2-5 \sqrt{8})$
$\sqrt[3]{3}(-\sqrt[3]{9}-\sqrt[3]{6})$

إجابة

$-40+4 \sqrt{2}$
$-3-\sqrt[3]{18}$

عندما تعاملنا مع كثيرات الحدود، قمنا بضرب المقادير ذات الحدين في الحدود الثنائية. تذكر أن هذا أعطانا أربعة منتجات قبل أن نجمع أي شروط مماثلة. للتأكد من الحصول على جميع المنتجات الأربعة، قمنا بتنظيم عملنا - عادةً بطريقة FOIL.

مثال $\PageIndex{8}$

قم بالتبسيط:

$(3-2 \sqrt{7})(4-2 \sqrt{7})$
$(\sqrt[3]{x}-2)(\sqrt[3]{x}+4)$

الحل:

أ.

$(3-2 \sqrt{7})(4-2 \sqrt{7})$

اضرب.

$12-6 \sqrt{7}-8 \sqrt{7}+4 \cdot 7$

قم بالتبسيط.

$12-6 \sqrt{7}-8 \sqrt{7}+28$

اجمع بين المصطلحات المتشابهة.

$40-14 \sqrt{7}$

ب.

$(\sqrt[3]{x}-2)(\sqrt[3]{x}+4)$

اضرب.

$\sqrt[3]{x^{2}}+4 \sqrt[3]{x}-2 \sqrt[3]{x}-8$

اجمع بين المصطلحات المتشابهة.

$\sqrt[3]{x^{2}}+2 \sqrt[3]{x}-8$

التمارين $\PageIndex{15}$

قم بالتبسيط:

$(6-3 \sqrt{7})(3+4 \sqrt{7})$
$(\sqrt[3]{x}-2)(\sqrt[3]{x}-3)$

إجابة

$-66+15 \sqrt{7}$
$\sqrt[3]{x^{2}}-5 \sqrt[3]{x}+6$

التمارين $\PageIndex{16}$

قم بالتبسيط:

$(2-3 \sqrt{11})(4-\sqrt{11})$
$(\sqrt[3]{x}+1)(\sqrt[3]{x}+3)$

إجابة

$41-14 \sqrt{11}$
$\sqrt[3]{x^{2}}+4 \sqrt[3]{x}+3$

مثال $\PageIndex{9}$

قم بالتبسيط: $(3 \sqrt{2}-\sqrt{5})(\sqrt{2}+4 \sqrt{5})$

الحل:

$(3 \sqrt{2}-\sqrt{5})(\sqrt{2}+4 \sqrt{5})$

اضرب.

$3 \cdot 2+12 \sqrt{10}-\sqrt{10}-4 \cdot 5$

قم بالتبسيط.

$6+12 \sqrt{10}-\sqrt{10}-20$

اجمع بين المصطلحات المتشابهة.

$-14+11 \sqrt{10}$

التمارين $\PageIndex{17}$

قم بالتبسيط: $(5 \sqrt{3}-\sqrt{7})(\sqrt{3}+2 \sqrt{7})$

إجابة: $1+9 \sqrt{21}$

التمارين $\PageIndex{18}$

قم بالتبسيط: $(\sqrt{6}-3 \sqrt{8})(2 \sqrt{6}+\sqrt{8})$

إجابة: $-12-20 \sqrt{3}$

إن التعرف على بعض المنتجات الخاصة جعل عملنا أسهل عندما قمنا بضرب الحدين في وقت سابق. هذا صحيح عندما نضاعف الراديكاليين أيضًا. يتم عرض صيغ المنتجات الخاصة التي استخدمناها هنا.

منتجات خاصة

مربعات ذات حدين

$\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}$

منتج من منتجات المترافقة

$(a+b)(a-b)=a^{2}-b^{2}$

سنستخدم صيغ المنتجات الخاصة في الأمثلة القليلة التالية. سنبدأ بمنتج نمط المربعات ذات الحدين.

مثال $\PageIndex{10}$

قم بالتبسيط:

$2+\sqrt{3})^{2}$
$(4-2 \sqrt{5})^{2}$

الحل:

أ.

الجدول 8.4.1
	$.$
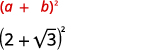اضرب باستخدام حاصل ضرب نمط المربعات ذات الحدين.	$.$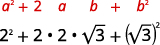
قم بالتبسيط.	$.$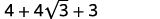
اجمع بين المصطلحات المتشابهة.	$.$

ب.

الجدول 8.4.2
	$.$
متعدد، باستخدام حاصل ضرب نمط المربعات ذات الحدين.	$.$
قم بالتبسيط.	$.$
	$.$
اجمع بين المصطلحات المتشابهة.	$.$

التمارين $\PageIndex{19}$

قم بالتبسيط:

$(10+\sqrt{2})^{2}$
$(1+3 \sqrt{6})^{2}$

إجابة

$102+20 \sqrt{2}$
$55+6 \sqrt{6}$

التمارين $\PageIndex{20}$

قم بالتبسيط:

$(6-\sqrt{5})^{2}$
$(9-2 \sqrt{10})^{2}$

إجابة

$41-12 \sqrt{5}$
$121-36 \sqrt{10}$

في المثال التالي، سنستخدم نمط منتج الاقتران. لاحظ أن المنتج النهائي ليس له جذور جذرية.

مثال $\PageIndex{11}$

قم بالتبسيط: $(5-2 \sqrt{3})(5+2 \sqrt{3})$

الحل:

الجدول 8.4.3
	$.$
اضرب باستخدام حاصل ضرب النمط المترافق.	$.$
قم بالتبسيط.	$.$
	$.$

التمارين $\PageIndex{21}$

قم بالتبسيط: $(3-2 \sqrt{5})(3+2 \sqrt{5})$

إجابة: $-11$

التمارين $\PageIndex{22}$

قم بالتبسيط: $(4+5 \sqrt{7})(4-5 \sqrt{7})$

إجابة: $-159$

يمكنك الوصول إلى هذه الموارد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع إضافة التعبيرات الجذرية وطرحها وضربها.

ضرب جمع الجذور المطروحة
ضرب المنتجات الخاصة: ثنائيات مربعة ذات حدين تحتوي على جذور مربعة
ضرب المترادفات

المفاهيم الرئيسية

خاصية المنتج للجذور
- لأي أرقام حقيقية $\sqrt[n]{b}$ ، $\sqrt[n]{a}$ ولأي عدد صحيح $n≥2$ $\sqrt[n]{a b}=\sqrt[n]{a} \cdot \sqrt[n]{b}$ و $\sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a b}$
منتجات خاصة

$\begin{array}{c c}{\text { Binomial Squares }}& {\text{Product of Conjugates}} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a+b)(a-b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}$

مسرد المصطلحات

مثل الراديكاليين: مثل الجذور هي التعبيرات الجذرية بنفس المؤشر ونفس الجذور.

أهداف التعلم

جمع وطرح التعبيرات الجذرية

تعريف8.5.1\PageIndex{1}: Like Radicals

مثال8.5.1\PageIndex{1}

التمارين8.5.1\PageIndex{1}

التمارين8.5.2\PageIndex{2}

مثال8.5.2\PageIndex{2}

التمارين8.5.3\PageIndex{3}

التمارين8.5.4\PageIndex{4}

مثال8.5.3\PageIndex{3}

التمارين8.5.5\PageIndex{5}

التمارين8.5.6\PageIndex{6}

مثال8.5.4\PageIndex{4}

التمارين8.5.7\PageIndex{7}

التمارين8.5.8\PageIndex{8}

اضرب التعبيرات الراديكالية

مثال8.5.5\PageIndex{5}

التمارين8.5.9\PageIndex{9}

التمارين8.5.10\PageIndex{10}

مثال8.5.6\PageIndex{6}

التمارين8.5.11\PageIndex{11}

التمارين8.5.12\PageIndex{12}

استخدم الضرب متعدد الحدود لضرب التعبيرات الجذرية

مثال8.5.7\PageIndex{7}

التمارين8.5.13\PageIndex{13}

التمارين8.5.14\PageIndex{14}

مثال8.5.8\PageIndex{8}

التمارين8.5.15\PageIndex{15}

التمارين8.5.16\PageIndex{16}

مثال8.5.9\PageIndex{9}

التمارين8.5.17\PageIndex{17}

التمارين8.5.18\PageIndex{18}

منتجات خاصة

مثال8.5.10\PageIndex{10}

التمارين8.5.19\PageIndex{19}

التمارين8.5.20\PageIndex{20}

مثال8.5.11\PageIndex{11}

التمارين8.5.21\PageIndex{21}

التمارين8.5.22\PageIndex{22}

المفاهيم الرئيسية

مسرد المصطلحات

تعريف $\PageIndex{1}$ : Like Radicals

مثال $\PageIndex{1}$

التمارين $\PageIndex{1}$

التمارين $\PageIndex{2}$

مثال $\PageIndex{2}$

التمارين $\PageIndex{3}$

التمارين $\PageIndex{4}$

مثال $\PageIndex{3}$

التمارين $\PageIndex{5}$

التمارين $\PageIndex{6}$

مثال $\PageIndex{4}$

التمارين $\PageIndex{7}$

التمارين $\PageIndex{8}$

مثال $\PageIndex{5}$

التمارين $\PageIndex{9}$

التمارين $\PageIndex{10}$

مثال $\PageIndex{6}$

التمارين $\PageIndex{11}$

التمارين $\PageIndex{12}$

مثال $\PageIndex{7}$

التمارين $\PageIndex{13}$

التمارين $\PageIndex{14}$

مثال $\PageIndex{8}$

التمارين $\PageIndex{15}$

التمارين $\PageIndex{16}$

مثال $\PageIndex{9}$

التمارين $\PageIndex{17}$

التمارين $\PageIndex{18}$

مثال $\PageIndex{10}$

التمارين $\PageIndex{19}$

التمارين $\PageIndex{20}$

مثال $\PageIndex{11}$

التمارين $\PageIndex{21}$

التمارين $\PageIndex{22}$