Skip to main content
Global

8.4E: تمارين

  1. Last updated
  2. Save as PDF
  • Page ID
    201628

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    الممارسة تجعل من الكمال

    مجموعة التمرين A: تبسيط التعبيرات باستخدام\(a^{\frac{1}{n}}\)

    في التمارين التالية، اكتب كتعبير جذري.

    1. أ.\(x^{\frac{1}{2}}\) ب.\(y^{\frac{1}{3}}\) ج.\(z^{\frac{1}{4}}\)
    2. أ.\(r^{\frac{1}{2}}\) ب.\(s^{\frac{1}{3}}\) ج.\(t^{\frac{1}{4}}\)
    3. أ.\(u^{\frac{1}{5}}\) ب.\(v^{\frac{1}{9}}\) ج.\(w^{\frac{1}{20}}\)
    4. أ.\(g^{\frac{1}{7}}\) ب.\(h^{\frac{1}{5}}\) ج.\(j^{\frac{1}{25}}\)
    إجابة

    1. أ.\(\sqrt{x}\) ب.\(\sqrt[3]{y}\) ج.\(\sqrt[4]{z}\)

    3. أ.\(\sqrt[5]{u}\) ب.\(\sqrt[9]{v}\) ج.\(\sqrt[20]{w}\)

    مجموعة التمارين B: تبسيط التعبيرات باستخدام\(a^{\frac{1}{n}}\)

    في التمارين التالية، اكتب باستخدام الأس النسبي.

    1. أ.\(\sqrt[7]{x}\) ب.\(\sqrt[9]{y}\) ج.\(\sqrt[5]{f}\)
    2. أ.\(\sqrt[8]{4}\) ب.\(\sqrt[10]{s}\) ج.\(\sqrt[4]{t}\)
    3. أ.\(\sqrt[3]{7c}\) ب.\(\sqrt[7]{12d}\) ج.\(2\sqrt[4]{6b}\)
    4. أ.\(\sqrt[4]{5x}\) ب.\(\sqrt[8]{9y}\) ج.\(7\sqrt[5]{3z}\)
    5. أ.\(\sqrt{21p}\) ب.\(\sqrt[4]{8q}\) ج.\(4\sqrt[6]{36r}\)
    6. أ.\(\sqrt[3]{25a}\) ب.\(\sqrt{3b}\) ج.\(\sqrt[8]{40c}\)
    إجابة

    1. أ.\(x^{\frac{1}{7}}\) ب.\(y^{\frac{1}{9}}\) ج.\(f^{\frac{1}{5}}\)

    3. أ.\((7 c)^{\frac{1}{4}}\) ب.\((12 d)^{\frac{1}{7}}\) ج.\(2(6 b)^{\frac{1}{4}}\)

    5. أ.\((21 p)^{\frac{1}{2}}\) ب.\((8 q)^{\frac{1}{4}}\) ج.\(4(36 r)^{\frac{1}{6}}\)

    مجموعة التمرين C: تبسيط التعبيرات باستخدام\(a^{\frac{1}{n}}\)

    في التمارين التالية، قم بالتبسيط.

    1. أ.\(81^{\frac{1}{2}}\) ب.\(125^{\frac{1}{3}}\) ج.\(64^{\frac{1}{2}}\)
    2. أ.\(625^{\frac{1}{4}}\) ب.\(243^{\frac{1}{5}}\) ج.\(32^{\frac{1}{5}}\)
    3. أ.\(16^{\frac{1}{4}}\) ب.\(16^{\frac{1}{2}}\) ج.\(625^{\frac{1}{4}}\)
    4. أ.\(64^{\frac{1}{3}}\) ب.\(32^{\frac{1}{5}}\) ج.\(81^{\frac{1}{4}}\)
    5. أ.\((-216)^{\frac{1}{3}}\) ب.\(-216^{\frac{1}{3}}\) ج.\((216)^{-\frac{1}{3}}\)
    6. أ.\((-1000)^{\frac{1}{3}}\) ب.\(-1000^{\frac{1}{3}}\) ج.\((1000)^{-\frac{1}{3}}\)
    7. أ.\((-81)^{\frac{1}{4}}\) ب.\(-81^{\frac{1}{4}}\) ج.\((81)^{-\frac{1}{4}}\)
    8. أ.\((-49)^{\frac{1}{2}}\) ب.\(-49^{\frac{1}{2}}\) ج.\((49)^{-\frac{1}{2}}\)
    9. أ.\((-36)^{\frac{1}{2}}\) ب.\(-36^{\frac{1}{2}}\) ج.\((36)^{-\frac{1}{2}}\)
    10. أ.\((-16)^{\frac{1}{4}}\) ب.\(-16^{\frac{1}{4}}\) ج.\(16^{-\frac{1}{4}}\)
    11. أ.\((-100)^{\frac{1}{2}}\) ب.\(-100^{\frac{1}{2}}\) ج.\((100)^{-\frac{1}{2}}\)
    12. أ.\((-32)^{\frac{1}{5}}\) ب.\((243)^{-\frac{1}{5}}\) ج.\(-125^{\frac{1}{3}}\)
    إجابة

    1. أ.\(9\) ب.\(5\) ج.\(8\)

    3. أ.\(2\) ب.\(4\) ج.\(5\)

    5. أ.\(-6\) ب.\(-6\) ج.\(\frac{1}{6}\)

    7. أ. غير حقيقي ب.\(-3\) ج.\(\frac{1}{3}\)

    9. أ. غير حقيقي ب.\(-6\) ج.\(\frac{1}{6}\)

    11. أ. غير حقيقي ب.\(-10\) ج.\(\frac{1}{10}\)

    مجموعة التمرين D: تبسيط التعبيرات باستخدام\(a^{\frac{m}{n}}\)

    في التمارين التالية، اكتب باستخدام الأس النسبي.

    1. أ.\(\sqrt{m^{5}}\) ب.\((\sqrt[3]{3 y})^{7}\) ج.\(\sqrt[5]{\left(\dfrac{4 x}{5 y}\right)^{3}}\)
    2. أ.\(\sqrt[4]{r^{7}}\) ب.\((\sqrt[5]{2 p q})^{3}\) ج.\(\sqrt[4]{\left(\dfrac{12 m}{7 n}\right)^{3}}\)
    3. أ.\(\sqrt[5]{u^{2}}\) ب.\((\sqrt[3]{6 x})^{5}\) ج.\(\sqrt[4]{\left(\dfrac{18 a}{5 b}\right)^{7}}\)
    4. أ.\(\sqrt[3]{a}\) ب.\((\sqrt[4]{21 v})^{3}\) ج.\(\sqrt[4]{\left(\dfrac{2 x y}{5 z}\right)^{2}}\)
    إجابة

    1. أ.\(m^{\frac{5}{2}}\) ب.\((3 y)^{\frac{7}{3}}\) ج.\(\left(\dfrac{4 x}{5 y}\right)^{\frac{3}{5}}\)

    3. أ.\(u^{\frac{2}{5}}\) ب.\((6 x)^{\frac{5}{3}}\) ج.\(\left(\dfrac{18 a}{5 b}\right)^{\frac{7}{4}}\)

    مجموعة التمرين E: تبسيط التعبيرات باستخدام\(a^{\frac{m}{n}}\)

    في التمارين التالية، قم بالتبسيط.

    1. أ.\(64^{\frac{5}{2}}\) ب.\(81^{\frac{-3}{2}}\) ج.\((-27)^{\frac{2}{3}}\)
    2. أ.\(25^{\frac{3}{2}}\) ب.\(9^{-\frac{3}{2}}\) ج.\((-64)^{\frac{2}{3}}\)
    3. أ.\(32^{\frac{2}{5}}\) ب.\(27^{-\frac{2}{3}}\) ج.\((-25)^{\frac{1}{2}}\)
    4. أ.\(100^{\frac{3}{2}}\) ب.\(49^{-\frac{5}{2}}\) ج.\((-100)^{\frac{3}{2}}\)
    5. أ.\(-9^{\frac{3}{2}}\) ب.\(-9^{-\frac{3}{2}}\) ج.\((-9)^{\frac{3}{2}}\)
    6. أ.\(-64^{\frac{3}{2}}\) ب.\(-64^{-\frac{3}{2}}\) ج.\((-64)^{\frac{3}{2}}\)
    إجابة

    1. أ.\(32,768\) ب.\(\frac{1}{729}\) ج.\(9\)

    3. أ.\(4\) ب.\(\frac{1}{9}\) ج. غير حقيقي

    5. أ.\(-27\) ب.\(-\frac{1}{27}\) ج. غير حقيقي

    مجموعة التمرين F: استخدم قوانين الأسس لتبسيط التعبيرات ذات الأسس النسبية

    في التمارين التالية، قم بالتبسيط. افترض أن جميع المتغيرات إيجابية.

    1. أ.\(c^{\frac{1}{4}} \cdot c^{\frac{5}{8}}\) ب.\(\left(p^{12}\right)^{\frac{3}{4}}\) ج.\(\dfrac{r^{\frac{4}{5}}}{r^{\frac{9}{5}}}\)
    2. أ.\(6^{\frac{5}{2}} \cdot 6^{\frac{1}{2}}\) ب.\(\left(b^{15}\right)^{\frac{3}{5}}\) ج.\(\dfrac{w^{\frac{2}{7}}}{w^{\frac{9}{7}}}\)
    3. أ.\(y^{\frac{1}{2}} \cdot y^{\frac{3}{4}}\) ب.\(\left(x^{12}\right)^{\frac{2}{3}}\) ج.\(\dfrac{m^{\frac{5}{8}}}{m^{\frac{13}{8}}}\)
    4. أ.\(q^{\frac{2}{3}} \cdot q^{\frac{5}{6}}\) ب.\(\left(h^{6}\right)^{\frac{4}{3}}\) ج.\(\dfrac{n^{\frac{3}{5}}}{n^{\frac{8}{5}}}\)
    5. أ.\(\left(27 q^{\frac{3}{2}}\right)^{\frac{4}{3}}\) ب.\(\left(a^{\frac{1}{3}} b^{\frac{2}{3}}\right)^{\frac{3}{2}}\)
    6. أ.\(\left(64 s^{\frac{3}{7}}\right)^{\frac{1}{6}}\) ب.\(\left(m^{\frac{4}{3}} n^{\frac{1}{2}}\right)^{\frac{3}{4}}\)
    7. أ.\(\left(16 u^{\frac{1}{3}}\right)^{\frac{3}{4}}\) ب.\(\left(4 p^{\frac{1}{3}} q^{\frac{1}{2}}\right)^{\frac{3}{2}}\)
    8. أ.\(\left(625 n^{\frac{8}{3}}\right)^{\frac{3}{4}}\) ب.\(\left(9 x^{\frac{2}{5}} y^{\frac{3}{5}}\right)^{\frac{5}{2}}\)
    9. أ.\(\dfrac{r^{\frac{5}{2}} \cdot r^{-\frac{1}{2}}}{r^{-\frac{3}{2}}}\) ب.\(\left(\dfrac{36 s^{\frac{1}{5}} t^{-\frac{3}{2}}}{s^{-\frac{9}{5}} t^{\frac{1}{2}}}\right)^{\frac{1}{2}}\)
    10. أ.\(\dfrac{a^{\frac{3}{4}} \cdot a^{-\frac{1}{4}}}{a^{-\frac{10}{4}}}\) ب.\(\left(\dfrac{27 b^{\frac{2}{3}} c^{-\frac{5}{2}}}{b^{-\frac{7}{3}} c^{\frac{1}{2}}}\right)^{\frac{1}{3}}\)
    11. أ.\(\dfrac{c^{\frac{5}{3}} \cdot c^{-\frac{1}{3}}}{c^{-\frac{2}{3}}}\) ب.\(\left(\dfrac{8 x^{\frac{5}{3}} y^{-\frac{1}{2}}}{27 x^{-\frac{4}{3}} y^{\frac{5}{2}}}\right)^{\frac{1}{3}}\)
    12. أ.\(\dfrac{m^{\frac{7}{4}} \cdot m^{-\frac{5}{4}}}{m^{-\frac{2}{4}}}\) ب.\(\left(\dfrac{16 m^{\frac{1}{5}} n^{\frac{3}{2}}}{81 m^{\frac{9}{5}} n^{-\frac{1}{2}}}\right)^{\frac{1}{4}}\)
    إجابة

    1. أ.\(c^{\frac{7}{8}}\) ب.\(p^{9}\) ج.\(\frac{1}{r}\)

    3. أ.\(y^{\frac{5}{4}}\) ب.\(x^{8}\) ج.\(\dfrac{1}{m}\)

    5. أ.\(81 q^{2}\) ب.\(a^{\frac{1}{2}} b\)

    7. أ.\(8 u^{\frac{1}{4}}\) ب.\(8 p^{\frac{1}{2}} q^{\frac{3}{4}}\)

    9. أ.\(r^{\frac{7}{2}}\) ب.\(\dfrac{6 s}{t}\)

    11. أ.\(c^{2}\) ب.\(\dfrac{2x}{3y}\)

    مجموعة التمارين G: تمارين الكتابة
    1. اعرض طريقتين جبريتين مختلفتين للتبسيط\(4^{\frac{3}{2}}\). اشرح جميع خطواتك.
    2. اشرح لماذا\((-16)^{\frac{3}{2}}\) لا يمكن تقييم التعبير.
    إجابة

    1. سوف تتنوع الإجابات.

    فحص ذاتي

    أ- بعد الانتهاء من التمارين، استخدم قائمة التحقق هذه لتقييم مدى إتقانك لأهداف هذا القسم.

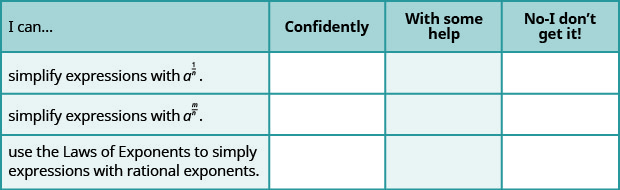
    يحتوي هذا الجدول على 4 صفوف و4 أعمدة. الصف الأول عبارة عن صف العنوان ويقوم بتسمية كل عمود. عنوان العمود الأول هو €canâ€â€، والثاني هو €بثقة، والثالث هو € مع بعض المساعدةâ€، والرابع هو €لا، أنا لا أحصل عليه.™ تحت العمود الأول توجد العبارات †تبسيط التعبيرات بقسمة a إلى قوة 1 مقسومًا على nâ€، تبسيط التعبير بـ a إلى قوة m مقسومًا على nâ€، و € استخدم قوانين الأسس لتبسيط التعبير باستخدام الأسس المنطقية â€. يتم ترك الأعمدة الأخرى فارغة حتى يتمكن المتعلم من تحديد مستوى إتقانه لكل موضوع.
    الشكل 8.3.4

    ب- ماذا تخبرك قائمة التحقق هذه عن إتقانك لهذا القسم؟ ما الخطوات التي ستتخذها للتحسين؟