8.2: تبسيط التعبيرات باستخدام الجذور

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• تبسيط التعبيرات باستخدام الجذور
• تقدير وجذور تقريبية
• قم بتبسيط التعبيرات المتغيرة باستخدام الجذور

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

1. قم بالتبسيط: a.$(−9)^{2}$ b.$-9^{2}$ c.$(−9)^{3}$
   إذا فاتتك هذه المشكلة، راجع المثال 2.21.
2. $3.846$قرِّب لأقرب جزء من مائة.
   إذا فاتتك هذه المشكلة، راجع المثال 1.34.
3. قم بالتبسيط: a.$x^{3} \cdot x^{3}$ b.$y^{2} \cdot y^{2} \cdot y^{2}$ c.$z^{3} \cdot z^{3} \cdot z^{3} \cdot z^{3}$
   إذا فاتتك هذه المشكلة، راجع المثال 5.12.

تبسيط التعبيرات باستخدام الجذور

في المؤسسات، نظرنا بإيجاز إلى الجذور التربيعية. تذكر أنه عندما$n$ يتم ضرب الرقم الحقيقي في حد ذاته، فإننا نكتبه$n^{2}$ ونقرأه «$n^{2}$مربّع». هذا الرقم يسمى مربع$n$،$n$ ويسمى الجذر التربيعي. على سبيل المثال،

$13^{2}$مكتوب عليه «$13$مربع»

$169$يسمى مربع$13$، منذ$13^{2}=169$

$13$هو الجذر التربيعي لـ$169$

تعريف$\PageIndex{1}$: Square and Square Root of a Number

مربع

إذا كان$n^{2}=m$، إذن،$m$ هو مربع$n$.

الجذر التربيعي

إذا كان$n^{2}=m$، إذن$n$ هو الجذر التربيعي لـ$m$.

لاحظ$(−13)^{2} = 169$ أيضًا$−13$ أن الجذر التربيعي لـ$169$. لذلك،$−13$ كلاهما$13$ لهما جذور مربعة لـ$169$.

لذلك، كل عدد موجب له جذران مربعان - أحدهما موجب والآخر سالب. ماذا لو أردنا فقط الجذر التربيعي الموجب لعدد موجب؟ نستخدم علامة جذرية ونكتب تشير إلى الجذر التربيعي الإيجابي لـ$m$.$\sqrt{m}$ يُطلق على الجذر التربيعي الموجب أيضًا الجذر التربيعي الرئيسي.

نستخدم أيضًا العلامة الجذرية للجذر التربيعي للصفر. بسبب$0^{2}=0, \sqrt{0}=0$. لاحظ أن الصفر يحتوي على جذر مربع واحد فقط.

تعريف$\PageIndex{2}$: Square Root Notation

$\sqrt{m}$يُقرأ «الجذر التربيعي لـ»$m$.

إذا$n^{2}=m$، إذن$n=\sqrt{m}$، من أجل$n\geq 0$.

$$\color{cyan} \text{radical sign} \longrightarrow \color{black} \sqrt{m} \color{cyan} \longleftarrow \text{radicand} \nonumber$$

الشكل 8.1.1

نحن نعلم أن كل رقم موجب له جذران تربيعيان وأن العلامة الجذرية تشير إلى الموجب. نحن نكتب$\sqrt{169}=13$. إذا أردنا إيجاد الجذر التربيعي السالب لعدد ما، فإننا نضع القيمة السالبة أمام العلامة الجذرية. على سبيل المثال،$-\sqrt{169}=-13$.

مثال$\PageIndex{1}$

قم بالتبسيط:

1. $\sqrt{144}$
2. $-\sqrt{289}$

الحل:

أ.

$\sqrt{144}$

منذ$12^{2}=144$.

$12$

ب.

$-\sqrt{289}$

منذ ذلك الحين$17^{2}=289$ والسلبية أمام العلامة الراديكالية.

$-17$

التمارين$\PageIndex{1}$

قم بالتبسيط:

1. $-\sqrt{64}$
2. $\sqrt{225}$

إجابة

1. $-8$
2. $15$

التمارين$\PageIndex{2}$

قم بالتبسيط:

1. $\sqrt{100}$
2. $-\sqrt{121}$

إجابة

1. $10$
2. $-11$

هل يمكننا التبسيط$-\sqrt{49}$؟ هل هناك رقم مربعه$-49$؟

$($___$)^{2}=-49$

أي رقم موجب مربع يكون موجبًا. أي رقم سالب مربّع يكون موجبًا. لا يوجد رقم حقيقي يساوي$\sqrt{-49}$. الجذر التربيعي للرقم السالب ليس رقمًا حقيقيًا.

مثال$\PageIndex{2}$

قم بالتبسيط:

1. $\sqrt{-196}$
2. $-\sqrt{64}$

الحل:

أ.

$\sqrt{-196}$

لا يوجد رقم حقيقي مربعه$-196$.

$\sqrt{-196}$ليس رقمًا حقيقيًا.

ب.

$-\sqrt{64}$

السلبية أمام الراديكالية.

$-8$

التمارين$\PageIndex{3}$

قم بالتبسيط:

1. $\sqrt{-169}$
2. $-\sqrt{81}$

إجابة

1. ليس رقمًا حقيقيًا
2. $-9$

التمارين$\PageIndex{4}$

قم بالتبسيط:

1. $-\sqrt{49}$
2. $\sqrt{-121}$

إجابة

1. $-7$
2. ليس رقمًا حقيقيًا

حتى الآن تحدثنا فقط عن المربعات والجذور التربيعية. دعونا الآن نوسع نطاق عملنا ليشمل قوى أعلى وجذور أعلى.

دعونا نراجع بعض المفردات أولاً.

$\begin{array}{ll}{\text { We write: }} & {\text { We say: }} \\ {n^{2}} & {n \text { squared }} \\ {n^{3}} & {n \text { cubed }} \\ {n^{4}} & {n \text { to the fourth power }} \\ {n^{5}} & {n \text { to the fifth power }}\end{array}$

يأتي المصطلحان «مربع» و «مكعب» من معادلات مساحة المربع وحجم المكعب.

سيكون من المفيد الحصول على جدول لقوى الأعداد الصحيحة من$−5$ إلى$5$. انظر الشكل 8.1.2

الشكل 8.1.2

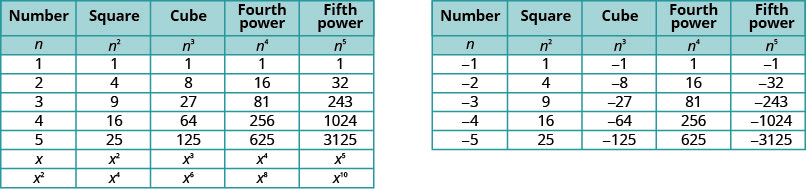
لاحظ العلامات الموجودة في الجدول. جميع قوى الأرقام الموجبة إيجابية بالطبع. ولكن عندما يكون لدينا رقم سالب، تكون القوى الزوجية إيجابية والقوى الفردية سلبية. سنقوم بنسخ الصف بصلاحيات$−2$ لمساعدتك على رؤية ذلك.

الشكل 8.1.3

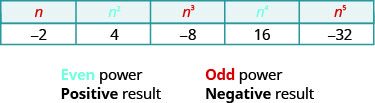
سنقوم الآن بتوسيع تعريف الجذر التربيعي إلى الجذور العليا.

تعريف$\PageIndex{3}$: N^th Root of a Number

إذا كان$b^{n}=a$، إذن$b$ هو$n^{th}$ جذر$a$.

يتم كتابة$n^{th}$ الجذر$a$ الرئيسي لـ$\sqrt[n]{a}$.

$n$وهذا ما يسمى مؤشر الراديكالي.

تمامًا مثلما نستخدم كلمة «مكعبة» لـ$b^{3}$، نستخدم مصطلح «الجذر المكعب» لـ$\sqrt[3]{a}$.

يمكننا الرجوع إلى الشكل 8.1.2 للمساعدة في العثور على جذور أعلى.

$\begin{aligned} 4^{3} &=64 & \sqrt[3]{64}&=4 \\ 3^{4} &=81 & \sqrt[4]{81}&=3 \\(-2)^{5} &=-32 & \sqrt[5]{-32}&=-2 \end{aligned}$

هل يمكن أن يكون لدينا جذر زوجي لرقم سالب؟ نحن نعلم أن الجذر التربيعي لعدد سالب ليس رقمًا حقيقيًا. وينطبق الشيء نفسه على أي جذر متساوٍ. حتى جذور الأرقام السالبة ليست أرقامًا حقيقية. الجذور الفردية للأرقام السالبة هي أرقام حقيقية.

خصائص لـ$\sqrt[n]{a}$

متى$n$ يكون الرقم الزوجي و

• $a \geq 0$، إذن$\sqrt[n]{a}$ هو رقم حقيقي.
• $a<0$، إذن$\sqrt[n]{a}$ ليس رقمًا حقيقيًا.

عندما$n$ يكون رقمًا فرديًا،$\sqrt[n]{a}$ يكون رقمًا حقيقيًا لجميع قيم$a$.

سنقوم بتطبيق هذه الخصائص في المثالين التاليين.

مثال$\PageIndex{3}$

قم بالتبسيط:

1. $\sqrt[3]{64}$
2. $\sqrt[4]{81}$
3. $\sqrt[5]{32}$

الحل:

أ.

$\sqrt[3]{64}$

منذ$4^{3}=64$.

$4$

ب.

$\sqrt[4]{81}$

منذ$(3)^{4}=81$.

$3$

ج.

$\sqrt[5]{32}$

منذ$(2)^{5}=32$.

$2$

التمارين$\PageIndex{5}$

قم بالتبسيط:

1. $\sqrt[3]{27}$
2. $\sqrt[4]{256}$
3. $\sqrt[5]{243}$

إجابة

1. $3$
2. $4$
3. $3$

التمارين$\PageIndex{6}$

قم بالتبسيط:

1. $\sqrt[3]{1000}$
2. $\sqrt[4]{16}$
3. $\sqrt[5]{243}$

إجابة

1. $10$
2. $2$
3. $3$

في هذا المثال، انتبه للعلامات السلبية وكذلك القوى الزوجية والغريبة.

مثال$\PageIndex{4}$

قم بالتبسيط:

1. $\sqrt[3]{-125}$
2. $\sqrt[4]{16}$
3. $\sqrt[5]{-243}$

الحل:

أ.

$\sqrt[3]{-125}$

منذ$(-5)^{3}=-125$.

$-5$

ب.

$\sqrt[4]{16}$

فكر،$(?)^{4}=-16$. لا يوجد رقم حقيقي تم رفعه إلى القوة الرابعة يكون سالبًا.

ليس رقمًا حقيقيًا.

ج.

$\sqrt[5]{-243}$

منذ$(-3)^{5}=-243$.

$-3$

التمارين$\PageIndex{7}$

قم بالتبسيط:

1. $\sqrt[3]{-27}$
2. $\sqrt[4]{-256}$
3. $\sqrt[5]{-32}$

إجابة

1. $-3$
2. غير حقيقي
3. $-2$

التمارين$\PageIndex{8}$

قم بالتبسيط:

1. $\sqrt[3]{-216}$
2. $\sqrt[4]{-81}$
3. $\sqrt[5]{-1024}$

إجابة

1. $-6$
2. غير حقيقي
3. $-4$

تقدير وجذور تقريبية

عندما نرى رقمًا بعلامة جذرية، فإننا غالبًا لا نفكر في قيمته العددية. في حين أننا ربما نعرف أن$\sqrt{4}=2$، ما هي قيمة$\sqrt{21}$ أو$\sqrt[3]{50}$؟ في بعض الحالات، يكون التقدير السريع مفيدًا وفي حالات أخرى يكون من الملائم الحصول على تقريب عشري.

للحصول على تقدير عددي للجذر التربيعي، نبحث عن الأعداد المربعة المثالية الأقرب إلى الجذر. للعثور على تقدير لـ$\sqrt{11}$، نرى$11$ أنه يقع بين الأعداد المربعة المثالية$9$$16$ والأقرب إلى$9$. عندها سيكون جذره التربيعي بين$3$ و$4$، ولكن أقرب إلى$3$.

الشكل 8.1.4

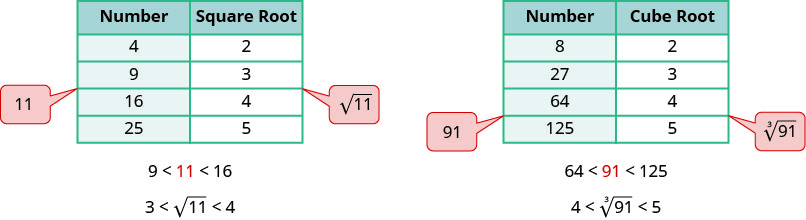
وبالمثل، للتقدير$\sqrt[3]{91}$، نرى$91$ ما بين الأرقام المكعبة المثالية$64$ و$125$. سيكون الجذر التكعيبي بعد ذلك بين$4$ و$5$.

مثال$\PageIndex{5}$

قم بتقدير كل جذر بين رقمين صحيحين متتاليين:

1. $\sqrt{105}$
2. $\sqrt[3]{43}$

الحل:

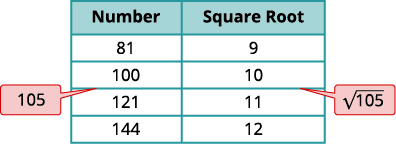
أ- فكر في الأعداد المربعة المثالية الأقرب إلى$105$. اصنع جدولًا صغيرًا من هذه المربعات المثالية وجذورها المربعة.

الجدول 8.1.1

	$\sqrt{105}$
حدد الموقع$105$ بين مربعين مثاليين متتاليين.	$100<\color{red}105 \color{black} <121$
$\sqrt{105}$تقع بين جذورها المربعة.	$10< \color{red}\sqrt{105}< \color{black}11$

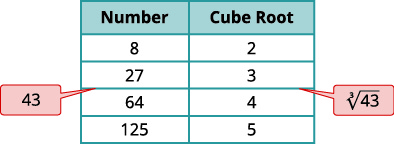
ب- وبالمثل، فإننا نحدد$43$ بين رقمين مكعبين مثاليين.

الجدول 8.1.2

	$\sqrt[3]{43}$
حدد موقعه$43$ بين مكعبين مثاليين متتاليين.
$\sqrt[3]{43}$تقع بين جذورها المكعبة.

التمارين$\PageIndex{9}$

قم بتقدير كل جذر بين رقمين صحيحين متتاليين:

1. $\sqrt{38}$
2. $\sqrt[3]{93}$

إجابة

1. $6<\sqrt{38}<7$
2. $4<\sqrt[3]{93}<5$

التمارين$\PageIndex{10}$

قم بتقدير كل جذر بين رقمين صحيحين متتاليين:

1. $\sqrt{84}$
2. $\sqrt[3]{152}$

إجابة

1. $9<\sqrt{84}<10$
2. $5<\sqrt[3]{152}<6$

هناك طرق رياضية لتقريب الجذور التربيعية، ولكن في الوقت الحاضر يستخدم معظم الناس الآلة الحاسبة للعثور على الجذور التربيعية. للعثور على الجذر التربيعي، ستستخدم$\sqrt{x}$ المفتاح الموجود في الآلة الحاسبة. للعثور على جذر مكعب، أو أي جذر بمؤشر أعلى، ستستخدم$\sqrt[y]{x}$ المفتاح.

عند استخدام هذه المفاتيح، تحصل على قيمة تقريبية. إنه تقدير تقريبي ودقيق لعدد الأرقام المعروضة على شاشة الآلة الحاسبة. رمز التقريب هو$≈$ ويُقرأ «تقريبًا».

لنفترض أن الآلة الحاسبة الخاصة بك تحتوي$10$ على شاشة رقمية. سوف ترى ذلك

$\sqrt{5} \approx 2.236067978$مقرّبة إلى منزلتين عشريتين هي$\sqrt{5} \approx 2.24$

$\sqrt[4]{93} \approx 3.105422799$مقرّبة إلى منزلتين عشريتين هي$\sqrt[4]{93} \approx 3.11$

كيف نعرف أن هذه القيم تقريبية وليست القيم الدقيقة؟ انظر إلى ما يحدث عندما نربحها:

$\begin{aligned}(2.236067978)^{2} &=5.000000002 &(3.105422799)^{4}&=92.999999991 \\(2.24)^{2} &=5.0176 & (3.11)^{4}&=93.54951841 \end{aligned}$

مربعاتها قريبة من$5$، ولكنها لا تساوي تمامًا$5$. القوى الرابعة قريبة من$93$، لكنها لا تساوي$93$.

مثال$\PageIndex{6}$

تقريبه إلى منزلتين عشريتين:

1. $\sqrt{17}$
2. $\sqrt[3]{49}$
3. $\sqrt[4]{51}$

الحل:

أ.

$\sqrt{17}$

استخدم مفتاح الجذر التربيعي للآلة الحاسبة.

$4.123105626 \dots$

قرِّب إلى منزلتين عشريتين.

$4.12$

$\sqrt{17} \approx 4.12$

ب.

$\sqrt[3]{49}$

استخدم$\sqrt[y]{x}$ مفتاح الآلة الحاسبة.

$3.659305710 \ldots$

قرِّب إلى منزلتين عشريتين.

$3.66$

$\sqrt[3]{49} \approx 3.66$

ج.

$\sqrt[4]{51}$

استخدم$\sqrt[y]{x}$ مفتاح الآلة الحاسبة.

$2.6723451177 \ldots$

قرِّب إلى منزلتين عشريتين.

$2.67$

$\sqrt[4]{51} \approx 2.67$

التمارين$\PageIndex{11}$

تقريبه إلى منزلتين عشريتين:

1. $\sqrt{11}$
2. $\sqrt[3]{71}$
3. $\sqrt[4]{127}$

إجابة

1. $\approx 3.32$
2. $\approx 4.14$
3. $\approx 3.36$

التمارين$\PageIndex{12}$

تقريبه إلى منزلتين عشريتين:

1. $\sqrt{13}$
2. $\sqrt[3]{84}$
3. $\sqrt[4]{98}$

إجابة

1. $\approx 3.61$
2. $\approx 4.38$
3. $\approx 3.15$

قم بتبسيط التعبيرات المتغيرة باستخدام الجذور

يمكن أن يكون الجذر الفردي للرقم موجبًا أو سلبيًا. على سبيل المثال،

الشكل 8.1.13

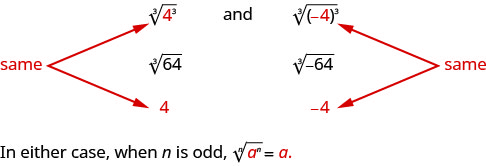
ولكن ماذا عن الجذر المتساوي؟ نريد الجذر الرئيسي، لذلك$\sqrt[4]{625}=5$.

لكن لاحظ،

الشكل 8.1.14

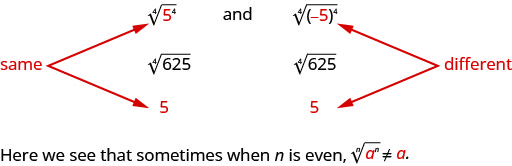
كيف يمكننا التأكد من أن الجذر الرابع$−5$ للرفع إلى القوة الرابعة هو$5$؟ يمكننا استخدام القيمة المطلقة. $|−5|=5$. لذلك نقول ذلك عندما$n$ يكون الوقت متساويًا$\sqrt[n]{a^{n}}=|a|$. هذا يضمن أن الجذر الرئيسي إيجابي.

تعريف$\PageIndex{4}$: Simplifying Odd and Even Roots

لأي عدد صحيح$n\geq 2$،

عندما$n$ يكون الفهرس غريبًا$\sqrt[n]{a^{n}}=a$

عندما يكون المؤشر$n$ متساويًا$\sqrt[n]{a^{n}}=|a|$

يجب أن نستخدم علامات القيمة المطلقة عندما نأخذ جذرًا متساويًا للتعبير مع متغير في الجذر.

مثال$\PageIndex{7}$

قم بالتبسيط:

1. $\sqrt{x^{2}}$
2. $\sqrt[3]{n^{3}}$
3. $\sqrt[4]{p^{4}}$
4. $\sqrt[5]{y^{5}}$

الحل:

أ- نستخدم القيمة المطلقة للتأكد من الحصول على الجذر الإيجابي.

$\sqrt{x^{2}}$

بما أن$n$ المؤشر متساوٍ،$\sqrt[n]{a^{n}}=|a|$.

b. هذا جذر مفهرس فردي لذا ليست هناك حاجة لعلامة القيمة المطلقة.

$\sqrt[3]{m^{3}}$

نظرًا لأن الفهرس$n$ غريب،$\sqrt[n]{a^{n}}=a$.

$m$

ج.

$\sqrt[4]{p^{4}}$

نظرًا$n$ لأن الفهرس متساوٍ$\sqrt[n]{a^{n}}=|a|$.

$|p|$

د.

$\sqrt[5]{y^{5}}$

نظرًا$n$ لأن الفهرس غريب،$\sqrt[n]{a^{n}}=a$.

$y$

التمارين$\PageIndex{13}$

قم بالتبسيط:

1. $\sqrt{b^{2}}$
2. $\sqrt[3]{w^{3}}$
3. $\sqrt[4]{m^{4}}$
4. $\sqrt[5]{q^{5}}$

إجابة

1. $|b|$
2. $w$
3. $|m|$
4. $q$

التمارين$\PageIndex{14}$

قم بالتبسيط:

1. $\sqrt{y^{2}}$
2. $\sqrt[3]{p^{3}}$
3. $\sqrt[4]{z^{4}}$
4. $\sqrt[5]{q^{5}}$

إجابة

1. $|y|$
2. $p$
3. $|z|$
4. $q$

ماذا عن الجذور التربيعية للقوى العليا للمتغيرات؟ تقول خاصية القوة الخاصة بالأسس$\left(a^{m}\right)^{n}=a^{m \cdot n}$. لذلك إذا قمنا بالتعادل$a^{m}$، سيصبح الأس$2m$.

$\left(a^{m}\right)^{2}=a^{2 m}$

ننظر الآن إلى الجذر التربيعي.

$\sqrt{a^{2 m}}$

منذ$\left(a^{m}\right)^{2}=a^{2 m}$.

$\sqrt{\left(a^{m}\right)^{2}}$

منذ$n$ ذلك الحين$\sqrt[n]{a^{n}}=|a|$.

$\left|a^{m}\right|$

لذا$\sqrt{a^{2 m}}=\left|a^{m}\right|$.

نطبق هذا المفهوم في المثال التالي.

مثال$\PageIndex{8}$

قم بالتبسيط:

1. $\sqrt{x^{6}}$
2. $\sqrt{y^{16}}$

الحل:

أ.

$\sqrt{x^{6}}$

منذ$\left(x^{3}\right)^{2}=x^{6}$.

$\sqrt{\left(x^{3}\right)^{2}}$

نظرًا$n$ لأن الفهرس متساوٍ$\sqrt{a^{n}}=|a|$.

$\left|x^{3}\right|$

ب.

$\sqrt{y^{16}}$

منذ$\left(y^{8}\right)^{2}=y^{16}$.

$\sqrt{\left(y^{8}\right)^{2}}$

نظرًا$n$ لأن الفهرس متساوٍ$\sqrt[n]{a^{n}}=|a|$.

$y^{8}$

في هذه الحالة، لا تكون علامة القيمة المطلقة$y^{8}$ مطلوبة لأنها إيجابية.

التمارين$\PageIndex{15}$

قم بالتبسيط:

1. $\sqrt{y^{18}}$
2. $\sqrt{z^{12}}$

إجابة

1. $|y^{9}|$
2. $z^{6}$

التمارين$\PageIndex{16}$

قم بالتبسيط:

1. $\sqrt{m^{4}}$
2. $\sqrt{b^{10}}$

إجابة

1. $m^{2}$
2. $|b^{5}|$

يستخدم المثال التالي نفس الفكرة للجذور العليا.

مثال$\PageIndex{9}$

قم بالتبسيط:

1. $\sqrt[3]{y^{18}}$
2. $\sqrt[4]{z^{8}}$

الحل:

أ.

$\sqrt[3]{y^{18}}$

منذ$\left(y^{6}\right)^{3}=y^{18}$.

$\sqrt[3]{\left(y^{6}\right)^{3}}$

لأنه$n$ أمر غريب,$\sqrt[n]{a^{n}}=a$.

$y^{6}$

ب.

$\sqrt[4]{z^{8}}$

منذ$\left(z^{2}\right)^{4}=z^{8}$.

$\sqrt[4]{\left(z^{2}\right)^{4}}$

نظرًا$z^{2}$ لأنه إيجابي، فإننا لا نحتاج إلى علامة القيمة المطلقة.

$z^{2}$

التمارين$\PageIndex{17}$

قم بالتبسيط:

1. $\sqrt[4]{u^{12}}$
2. $\sqrt[3]{v^{15}}$

إجابة

1. $|u^{3}|$
2. $v^{5}$

التمارين$\PageIndex{18}$

قم بالتبسيط:

1. $\sqrt[5]{c^{20}}$
2. $\sqrt[6]{d^{24}}$

إجابة

1. $c^{4}$
2. $d^{4}$

في المثال التالي، لدينا الآن معامل أمام المتغير. $\sqrt{a^{2 m}}=\left|a^{m}\right|$يعمل المفهوم بنفس الطريقة تقريبًا.

$\sqrt{16 r^{22}}=4\left|r^{11}\right|$بسبب$\left(4 r^{11}\right)^{2}=16 r^{22}$.

لكن لاحظ$\sqrt{25 u^{8}}=5 u^{4}$ ولا توجد حاجة إلى علامة القيمة المطلقة كما$u^{4}$ هو الحال دائمًا.

مثال$\PageIndex{10}$

قم بالتبسيط:

1. $\sqrt{16 n^{2}}$
2. $-\sqrt{81 c^{2}}$

الحل:

أ.

$\sqrt{16 n^{2}}$

منذ$(4 n)^{2}=16 n^{2}$.

$\sqrt{(4 n)^{2}}$

نظرًا$n$ لأن الفهرس متساوٍ$\sqrt[n]{a^{n}}=|a|$.

$4|n|$

ب.

$-\sqrt{81 c^{2}}$

منذ$(9 c)^{2}=81 c^{2}$.

$-\sqrt{(9 c)^{2}}$

نظرًا$n$ لأن الفهرس متساوٍ$\sqrt[n]{a^{n}}=|a|$.

$-9|c|$

التمارين$\PageIndex{19}$

قم بالتبسيط:

1. $\sqrt{64 x^{2}}$
2. $-\sqrt{100 p^{2}}$

إجابة

1. $8|x|$
2. $-10|p|$

التمارين$\PageIndex{20}$

قم بالتبسيط:

1. $\sqrt{169 y^{2}}$
2. $-\sqrt{121 y^{2}}$

إجابة

1. $13|y|$
2. $-11|y|$

يأخذ هذا المثال الفكرة إلى أبعد من ذلك لأنه يحتوي على جذور مؤشر أعلى.

مثال$\PageIndex{11}$

قم بالتبسيط:

1. $\sqrt[3]{64 p^{6}}$
2. $\sqrt[4]{16 q^{12}}$

الحل:

أ.

$\sqrt[3]{64 p^{6}}$

أعد الكتابة$64p^{6}$ باسم$\left(4 p^{2}\right)^{3}$.

$\sqrt[3]{\left(4 p^{2}\right)^{3}}$

خذ الجذر التكعيبي.

$4p^{2}$

ب.

$\sqrt[4]{16 q^{12}}$

أعد كتابة الراديكاند كقوة رابعة.

$\sqrt[4]{\left(2 q^{3}\right)^{4}}$

خذ الجذر الرابع.

$2|q^{3}|$

التمارين$\PageIndex{21}$

قم بالتبسيط:

1. $\sqrt[3]{27 x^{27}}$
2. $\sqrt[4]{81 q^{28}}$

إجابة

1. $3x^{9}$
2. $3|q^{7}|$

التمارين$\PageIndex{22}$

قم بالتبسيط:

1. $\sqrt[3]{125 q^{9}}$
2. $\sqrt[5]{243 q^{25}}$

إجابة

1. $5p^{3}$
2. $3q^{5}$

تحتوي الأمثلة التالية على متغيرين.

مثال$\PageIndex{12}$

قم بالتبسيط:

1. $\sqrt{36 x^{2} y^{2}}$
2. $\sqrt{121 a^{6} b^{8}}$
3. $\sqrt[3]{64 p^{63} q^{9}}$

الحل:

أ.

$\sqrt{36 x^{2} y^{2}}$

منذ$(6 x y)^{2}=36 x^{2} y^{2}$

$\sqrt{(6 x y)^{2}}$

خذ الجذر التربيعي.

$6|xy|$

ب.

$\sqrt{121 a^{6} b^{8}}$

منذ$\left(11 a^{3} b^{4}\right)^{2}=121 a^{6} b^{8}$

$\sqrt{\left(11 a^{3} b^{4}\right)^{2}}$

خذ الجذر التربيعي.

$11\left|a^{3}\right| b^{4}$

ج.

$\sqrt[3]{64 p^{63} q^{9}}$

منذ$\left(4 p^{21} q^{3}\right)^{3}=64 p^{63} q^{9}$

$\sqrt[3]{\left(4 p^{21} q^{3}\right)^{3}}$

خذ الجذر التكعيبي.

$4p^{21}q^{3}$

التمارين$\PageIndex{23}$

قم بتبسيط:

1. $\sqrt{100 a^{2} b^{2}}$
2. $\sqrt{144 p^{12} q^{20}}$
3. $\sqrt[3]{8 x^{30} y^{12}}$

إجابة

1. $10|ab|$
2. $12p^{6}q^{10}$
3. $2x^{10}y^{4}$

التمارين$\PageIndex{24}$

قم بتبسيط:

1. $\sqrt{225 m^{2} n^{2}}$
2. $\sqrt{169 x^{10} y^{14}}$
3. $\sqrt[3]{27 w^{36} z^{15}}$

إجابة

1. $15|mn|$
2. $13\left|x^{5} y^{7}\right|$
3. $3w^{12}z^{5}$

قم بالوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات وممارسة إضافية مع تبسيط التعبيرات باستخدام الجذور.

• تبسيط أسس المتغيرات باستخدام الجذور باستخدام القيم المطلقة

المفاهيم الرئيسية

• ترميز الجذر التربيعي
  • $\sqrt{m}$يُقرأ «الجذر التربيعي لـ$m$»
  • إذا$n^{2}=m$، إذن$n=\sqrt{m}$، من أجل$n≥0$.
    
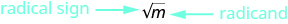
    الشكل 8.1.1
  • الجذر التربيعي$m$ لـ$\sqrt{m}$،، هو رقم موجب مربعه هو$m$.
• ^في جذر رقم
  • إذا كان$b^{n}=a$، إذن$b$ هو$n^{th}$ جذر$a$.
  • يتم كتابة$n^{th}$ الجذر$a$ الرئيسي لـ$\sqrt[n]{a}$.
  • $n$يسمى مؤشر الراديكالي.
• خصائص لـ$\sqrt[n]{a}$
  • متى$n$ يكون الرقم الزوجي و
    • $a≥0$، إذن$\sqrt[n]{a}$ هو رقم حقيقي
    • $a<0$، إذن$\sqrt[n]{a}$ ليس رقمًا حقيقيًا
  • عندما$n$ يكون رقمًا فرديًا،$\sqrt[n]{a}$ يكون رقمًا حقيقيًا لجميع قيم$a$.
• تبسيط الجذور الفردية والزوجية
  • لأي عدد صحيح$n≥2$،
    • عندما$n$ يكون غريبًا$\sqrt[n]{a^{n}}=a$
    • عندما$n$ يكون متساويًا$\sqrt[n]{a^{n}}=|a|$
  • يجب أن نستخدم علامات القيمة المطلقة عندما نأخذ جذرًا متساويًا للتعبير مع متغير في الجذر.

مسرد المصطلحات

مربع الرقم

إذا كان$n^{2}=m$، إذن،$m$ هو مربع$n$.

الجذر التربيعي لعدد

إذا كان$n^{2}=m$، إذن$n$ هو الجذر التربيعي لـ$m$.