7.E: تمارين مراجعة الفصل 7

تبسيط التعبيرات الكسرية وضربها وقسمتها

حدد القيم التي لا يتم تعريف التعبير العقلاني لها

في التمارين التالية، حدد القيم التي لم يتم تعريف التعبير العقلاني لها.

1. $\dfrac{5 a+3}{3 a-2}$

إجابة

$a \neq \dfrac{2}{3}$

2. $\dfrac{b-7}{b^{2}-25}$

3. $\dfrac{5 x^{2} y^{2}}{8 y}$

إجابة

$y \neq 0$

4. $\dfrac{x-3}{x^{2}-x-30}$

تبسيط التعبيرات الكسرية

في التمارين التالية، قم بالتبسيط.

5. $\dfrac{18}{24}$

إجابة

$\dfrac{3}{4}$

6. $\dfrac{9 m^{4}}{18 m n^{3}}$

7. $\dfrac{x^{2}+7 x+12}{x^{2}+8 x+16}$

إجابة

$\dfrac{x+3}{x+4}$

8. $\dfrac{7 v-35}{25-v^{2}}$

ضرب التعبيرات الكسرية

في التمارين التالية، اضرب.

9. $\dfrac{5}{8} \cdot \dfrac{4}{15}$

إجابة

$\dfrac{1}{6}$

10. $\dfrac{3 x y^{2}}{8 y^{3}} \cdot \dfrac{16 y^{2}}{24 x}$

11. $\dfrac{72 x-12 x^{2}}{8 x+32} \cdot \dfrac{x^{2}+10 x+24}{x^{2}-36}$

إجابة

$\dfrac{-3 x}{2}$

12. $\dfrac{6 y^{2}-2 y-10}{9-y^{2}} \cdot \dfrac{y^{2}-6 y+9}{6 y^{2}+29 y-20}$

قسمة التعبيرات الكسرية

في التمارين التالية، قسّم.

13. $\dfrac{x^{2}-4 x-12}{x^{2}+8 x+12} \div \dfrac{x^{2}-36}{3 x}$

إجابة

$\dfrac{3 x}{(x+6)(x+6)}$

14. $\dfrac{y^{2}-16}{4} \div \dfrac{y^{3}-64}{2 y^{2}+8 y+32}$

15. $\dfrac{11+w}{w-9} \div \dfrac{121-w^{2}}{9-w}$

إجابة

$\dfrac{1}{11+w}$

16. $\dfrac{3 y^{2}-12 y-63}{4 y+3} \div\left(6 y^{2}-42 y\right)$

17. $\dfrac{\dfrac{c^{2}-64}{3 c^{2}+26 c+16}}{\dfrac{c^{2}-4 c-32}{15 c+10}}$

إجابة

$\dfrac{5}{c+4}$

18. $\dfrac{8 a^{2}+16 a}{a-4} \cdot \dfrac{a^{2}+2 a-24}{a^{2}+7 a+10} \div \dfrac{2 a^{2}-6 a}{a+5}$

ضرب الدوال الكسرية وقسمتها

19. ابحث عن$R(x)=f(x) \cdot g(x)$ المكان$f(x)=\dfrac{9 x^{2}+9 x}{x^{2}-3 x-4}$ و$g(x)=\dfrac{x^{2}-16}{3 x^{2}+12 x}$.

إجابة

$R(x)=3$

20. ابحث عن$R(x)=\dfrac{f(x)}{g(x)}$ المكان$f(x)=\dfrac{27 x^{2}}{3 x-21}$ و$g(x)=\dfrac{9 x^{2}+54 x}{x^{2}-x-42}$.

جمع وطرح التعبيرات النسبية

جمع وطرح التعبيرات الكسرية ذات المقام المشترك

في التمارين التالية، قم بإجراء العمليات المشار إليها.

21. $\dfrac{7}{15}+\dfrac{8}{15}$

إجابة

$1$

22. $\dfrac{4 a^{2}}{2 a-1}-\dfrac{1}{2 a-1}$

23. $\dfrac{y^{2}+10 y}{y+5}+\dfrac{25}{y+5}$

إجابة

$y+5$

24. $\dfrac{7 x^{2}}{x^{2}-9}+\dfrac{21 x}{x^{2}-9}$

25. $\dfrac{x^{2}}{x-7}-\dfrac{3 x+28}{x-7}$

إجابة

$x+4$

26. $\dfrac{y^{2}}{y+11}-\dfrac{121}{y+11}$

27. $\dfrac{4 q^{2}-q+3}{q^{2}+6 q+5}-\dfrac{3 q^{2}-q-6}{q^{2}+6 q+5}$

إجابة

$\dfrac{q-3}{q+5}$

28. $\dfrac{5 t+4 t+3}{t^{2}-25}-\dfrac{4 t^{2}-8 t-32}{t^{2}-25}$

جمع وطرح التعبيرات الكسرية التي مقاماتها أضداد

في التمارين التالية، قم بالجمع والطرح.

29. $\dfrac{18 w}{6 w-1}+\dfrac{3 w-2}{1-6 w}$

إجابة

$\dfrac{15 w+2}{6 w-1}$

30. $\dfrac{a^{2}+3 a}{a^{2}-4}-\dfrac{3 a-8}{4-a^{2}}$

31. $\dfrac{2 b^{2}+3 b-15}{b^{2}-49}-\dfrac{b^{2}+16 b-1}{49-b^{2}}$

إجابة

$\dfrac{3 b-2}{b+7}$

32. $\dfrac{8 y^{2}-10 y+7}{2 y-5}+\dfrac{2 y^{2}+7 y+2}{5-2 y}$

أوجد المقام المشترك الأصغر للمقادير الكسرية

في التمارين التالية، ابحث عن شاشة LCD.

33. $\dfrac{7}{a^{2}-3 a-10}, \dfrac{3 a}{a^{2}-a-20}$

إجابة

$(a+2)(a-5)(a+4)$

34. $\dfrac{6}{n^{2}-4}, \dfrac{2 n}{n^{2}-4 n+4}$

35. $\dfrac{5}{3 p^{2}+17 p-6}, \dfrac{2 m}{3 p^{2}-23 p-8}$

إجابة

$(3 p+1)(p+6)(p+8)$

جمع وطرح التعبيرات الكسرية ذات المقامات المختلفة

في التمارين التالية، قم بإجراء العمليات المشار إليها.

36. $\dfrac{7}{5 a}+\dfrac{3}{2 b}$

37. $\dfrac{2}{c-2}+\dfrac{9}{c+3}$

إجابة

$\dfrac{11 c-12}{(c-2)(c+3)}$

38. $\dfrac{3 x}{x^{2}-9}+\dfrac{5}{x^{2}+6 x+9}$

39. $\dfrac{2 x}{x^{2}+10 x+24}+\dfrac{3 x}{x^{2}+8 x+16}$

إجابة

$\dfrac{5 x^{2}+26 x}{(x+4)(x+4)(x+6)}$

40. $\dfrac{5 q}{p^{2} q-p^{2}}+\dfrac{4 q}{q^{2}-1}$

41. $\dfrac{3 y}{y+2}-\dfrac{y+2}{y+8}$

إجابة

$\dfrac{2\left(y^{2}+10 y-2\right)}{(y+2)(y+8)}$

42. $\dfrac{-3 w-15}{w^{2}+w-20}-\dfrac{w+2}{4-w}$

43. $\dfrac{7 m+3}{m+2}-5$

إجابة

$\dfrac{2 m-7}{m+2}$

44. $\dfrac{n}{n+3}+\dfrac{2}{n-3}-\dfrac{n-9}{n^{2}-9}$

45. $\dfrac{8 a}{a^{2}-64}-\dfrac{4}{a+8}$

إجابة

$\dfrac{4}{a-8}$

46. $\dfrac{5}{12 x^{2} y}+\dfrac{7}{20 x y^{3}}$

جمع وطرح الدوال الكسرية

في التمارين التالية، ابحث عن$R(x)=f(x)+g(x)$ المكان الذي$f(x)$$g(x)$ يتم تقديمه.

47. $f(x)=\dfrac{2 x^{2}+12 x-11}{x^{2}+3 x-10}, g(x)=\dfrac{x+1}{2-x}$

إجابة

$R(x)=\dfrac{x+8}{x+5}$

48. $f(x)=\dfrac{-4 x+31}{x^{2}+x-30}, g(x)=\dfrac{5}{x+6}$

في التمارين التالية، ابحث عن$R(x)=f(x)-g(x)$ المكان الذي$f(x)$$g(x)$ يتم تقديمه.

49. $f(x)=\dfrac{4 x}{x^{2}-121}, g(x)=\dfrac{2}{x-11}$

إجابة

$R(x)=\dfrac{2}{x+11}$

50. $f(x)=\dfrac{7}{x+6}, g(x)=\dfrac{14 x}{x^{2}-36}$

تبسيط التعبيرات الكسرية المعقدة

بسِّط مقدارًا كسريًا معقدًا بكتابته في صورة قسمة

في التمارين التالية، قم بالتبسيط.

51. $\dfrac{\dfrac{7 x}{x+2}}{\dfrac{14 x^{2}}{x^{2}-4}}$

إجابة

$\dfrac{x-2}{2 x}$

52. $\dfrac{\dfrac{2}{5}+\dfrac{5}{6}}{\dfrac{1}{3}+\dfrac{1}{4}}$

53. $\dfrac{x-\dfrac{3 x}{x+5}}{\dfrac{1}{x+5}+\dfrac{1}{x-5}}$

إجابة

$\dfrac{(x-8)(x-5)}{2}$

54. $\dfrac{\dfrac{2}{m}+\dfrac{m}{n}}{\dfrac{n}{m}-\dfrac{1}{n}}$

قم بتبسيط التعبير العقلاني المعقد باستخدام شاشة LCD

في التمارين التالية، قم بالتبسيط.

55. $\dfrac{\dfrac{1}{3}+\dfrac{1}{8}}{\dfrac{1}{4}+\dfrac{1}{12}}$

إجابة

$\dfrac{11}{8}$

56. $\dfrac{\dfrac{3}{a^{2}}-\dfrac{1}{b}}{\dfrac{1}{a}+\dfrac{1}{b^{2}}}$

57. $\dfrac{\dfrac{2}{z^{2}-49}+\dfrac{1}{z+7}}{\dfrac{9}{z+7}+\dfrac{12}{z-7}}$

إجابة

$\dfrac{z-5}{21 z+21}$

58. $\dfrac{\dfrac{3}{y^{2}-4 y-32}}{\dfrac{2}{y-8}+\dfrac{1}{y+4}}$

حل المعادلات الكسرية

حل المعادلات الكسرية

في التمارين التالية، قم بحل.

59. $\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{1}{x}$

إجابة

$x=\dfrac{6}{7}$

60. $1-\dfrac{2}{m}=\dfrac{8}{m^{2}}$

61. $\dfrac{1}{b-2}+\dfrac{1}{b+2}=\dfrac{3}{b^{2}-4}$

إجابة

$b=\dfrac{3}{2}$

62. $\dfrac{3}{q+8}-\dfrac{2}{q-2}=1$

63. $\dfrac{v-15}{v^{2}-9 v+18}=\dfrac{4}{v-3}+\dfrac{2}{v-6}$

إجابة

لا يوجد حل

64. $\dfrac{z}{12}+\dfrac{z+3}{3 z}=\dfrac{1}{z}$

حل المعادلات الكسرية التي تتضمن دوال

65. للحصول على وظيفة عقلانية$f(x)=\dfrac{x+2}{x^{2}-6 x+8}$،

1. ابحث عن مجال الدالة
2. حل$f(x)=1$
3. ابحث عن النقاط على الرسم البياني عند قيمة الدالة هذه.

إجابة

1. النطاق عبارة عن جميع الأرقام الحقيقية باستثناء$x \neq 2$ و$x \neq 4$
2. $x=1, x=6$
3. $(1,1),(6,1)$

66. للحصول على وظيفة عقلانية$f(x)=\dfrac{2-x}{x^{2}+7 x+10}$،

1. حل$f(x)=2$
2. ابحث عن النقاط على الرسم البياني عند قيمة الدالة هذه.

حل معادلة نسبية لمتغير معين

في التمارين التالية، قم بحل المتغير المشار إليه.

67. $\dfrac{V}{l}=h w$من أجل$l$

إجابة

$l=\dfrac{V}{h w}$

68. $\dfrac{1}{x}-\dfrac{2}{y}=5$من أجل$y$

69. $x=\dfrac{y+5}{z-7}$من أجل$z$

إجابة

$z=\dfrac{y+5+7 x}{x}$

70. $P=\dfrac{k}{V}$من أجل$V$

حل تطبيقات باستخدام المعادلات النسبية

حل النسب

في التمارين التالية، قم بحل.

71. $\dfrac{x}{4}=\dfrac{3}{5}$

إجابة

$x = \dfrac{12}{5}$

72. $\dfrac{3}{y}=\dfrac{9}{5}$

73. $\dfrac{s}{s+20}=\dfrac{3}{7}$

إجابة

$s = 15$

74. $\dfrac{t-3}{5}=\dfrac{t+2}{9}$

حل التطبيقات باستخدام النسب

في التمارين التالية، قم بحل.

75. تناولت راشيل مخفوق الفراولة بسعة 21 أونصة يحتوي على 739 سعرة حرارية. كم عدد السعرات الحرارية الموجودة في مخفوق بحجم 32 أونصة؟

إجابة

1161 سعرة حرارية

76. ذهب ليو إلى المكسيك خلال عطلة عيد الميلاد وقام بتحويل 525 دولارًا إلى بيزو مكسيكي. في ذلك الوقت، كان سعر الصرف 1 دولار أمريكي يساوي 16.25 بيزو مكسيكي. كم عدد البيزو المكسيكي الذي حصل عليه لرحلته؟

حل تطبيقات الأشكال المتشابهة

في التمارين التالية، قم بحل.

77. $\Delta ABC$مشابه لـ$\Delta XYZ$. يوضح الشكل أطوال ضلعي كل مثلث. أوجد أطوال الضلع الثالث.

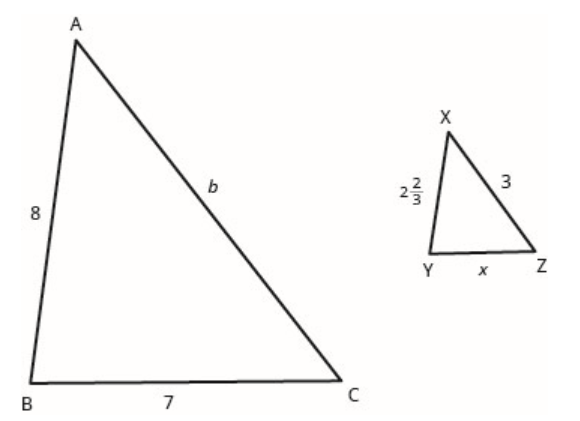
إجابة

$b=9 ; \; x=2 \dfrac{1}{3}$

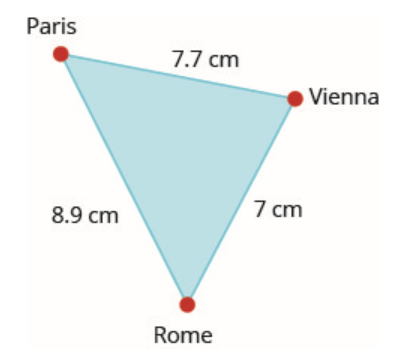
78. على خريطة أوروبا، تشكل باريس وروما وفيينا مثلثًا تظهر أضلاعه في الشكل أدناه. إذا كانت المسافة الفعلية من روما إلى فيينا 700 ميل، فأوجد المسافة من

1. باريس إلى روما
2. باريس إلى فيينا

79. يبلغ طول فرانشيسكا 5.75 قدمًا. في وقت متأخر من بعد ظهر أحد الأيام، كان طولها 8 أقدام. في نفس الوقت، كان ظل شجرة قريبة يبلغ طوله 32 قدمًا. أوجد ارتفاع الشجرة.

إجابة

23 قدمًا

80. يبلغ ارتفاع المنارة في بينساكولا بولاية فلوريدا 150 قدمًا. وبالوقوف بجانب التمثال، ألقت ناتاشا التي يبلغ طولها 5.5 قدمًا بظلالها على 1.1 قدمًا. إلى متى سيظل ظل المنارة؟

حل تطبيقات الحركة الموحدة

في التمارين التالية، قم بحل.

81. عند العودة إلى المنزل لمدة 5 ساعات من زيارة والديها، واجهت لولو طقسًا سيئًا. كانت قادرة على القيادة 176 ميلا في حين كان الطقس جيدا، ولكن بعد ذلك القيادة 10 ميلا في الساعة أبطأ، وذهب 81 ميلا عندما تحولت سيئة. ما مدى سرعتها في القيادة عندما كان الطقس سيئًا؟

إجابة

45 ميلا في الساعة

82. يركب مارك طائرة يمكنها الطيران لمسافة 490 ميلاً مع رياح خلفية تبلغ 20 ميلاً في الساعة في نفس الوقت الذي يمكنها فيه الطيران 350 ميلاً مقابل رياح خلفية تبلغ 20 ميلاً في الساعة. ما سرعة الطائرة؟

83. يمكن لـ Josue ركوب دراجته بسرعة 8 ميل في الساعة أسرع مما يستطيع أرجون ركوب دراجته. يستغرق لوقا 3 ساعات أطول من جوسو لركوب 48 ميلاً. ما مدى السرعة التي يمكن أن يركب بها جون دراجته؟

إجابة

16 ميلا في الساعة

84. كان كورتيس يتدرب على الترياتلون. ركض لمسافة 8 كيلومترات وقاد دراجة لمسافة 32 كيلومترًا في إجمالي 3 ساعات. كانت سرعته في الجري أقل بـ 8 كيلومترات في الساعة من سرعة ركوب الدراجات. ما هي سرعته في الجري؟

حل تطبيقات العمل

في التمارين التالية، قم بحل.

85. يمكن لبراندي تأطير الغرفة في ساعة واحدة، بينما يستغرق جيك 4 ساعات. إلى متى يمكنهم تأطير غرفة تعمل معًا?

إجابة

$\dfrac{4}{5}$ساعة

86. تستغرق بريم 3 ساعات لقص العشب بينما تستغرق ابنة عمها بارب ساعتين. كم من الوقت سيستغرقون العمل معًا؟

87. يمكن لجيفري طلاء منزل في 6 أيام، ولكن إذا حصل على مساعد يمكنه القيام بذلك في 4 أيام. كم من الوقت سيستغرق المساعد لطلاء المنزل بمفرده؟

إجابة

12 يومًا

88. تعمل مارتا وديب معًا في كتابة كتاب يستغرق 90 يومًا. إذا عملت سو بمفردها فسوف يستغرق الأمر 120 يومًا. كم من الوقت ستستغرق ديب لكتابة الكتاب بمفردها?

حل مشاكل التباين المباشر

في التمارين التالية، قم بحل.

89. $y$ويختلف ذلك بشكل مباشر حسب$x$ التوقيت$x=3$،$y=9$ ثم ابحث عن$x$ الوقت$y=21$.

إجابة

$7$

90. $y$يختلف الأمر عكسيًا حسب$x$ الوقت$y=20$$x=2$ والعثور على$y$ الوقت$x=4$.

91. فانيسا تسافر لرؤية خطيبها. المسافة$d$، تختلف بشكل مباشر مع السرعة$v$، فهي تقود. إذا سافرت 258 ميلاً وهي تقود 60 ميلاً في الساعة، إلى أي مدى ستسافر بسرعة 70 ميلاً في الساعة؟

إجابة

301 ميلا في الساعة

92. إذا كانت تكلفة البيتزا تختلف بشكل مباشر مع قطرها، وإذا كانت البيتزا بقطر 8 بوصات تكلف 12 دولارًا، فما تكلفة البيتزا التي يبلغ قطرها 6 بوصات؟

93. تختلف مسافة إيقاف السيارة بشكل مباشر مع مربع سرعتها. يستغرق الأمر 200 قدم لإيقاف سيارة تسير بسرعة 50 ميلاً في الساعة. كم عدد الأقدام التي سيستغرقها إيقاف السيارة عن السير بسرعة 60 ميلاً في الساعة؟

إجابة

288 قدمًا

حل مسائل التباين العكسي

في التمارين التالية، قم بحل.

94. وهي$m$ تختلف عكسياً مع المربع الخاص بـ$n$، ومتى،$m=4$$n=6$ والعثور على$m$ الوقت$n=2$.

95. يختلف عدد تذاكر حملة جمع التبرعات الموسيقية بشكل عكسي مع سعر التذاكر. إذا كان لدى Madelyn ما يكفي من المال لشراء 12 تذكرة مقابل 6 دولارات، فكم عدد التذاكر التي يمكن أن تشتريها Madelyn إذا ارتفع السعر إلى 8 دولارات؟

إجابة

97 تذاكر

96. في الآلة الوترية، يختلف طول الخيط عكسيًا مع تردد اهتزازاته. إذا كان تردد خيط مقاس 11 بوصة على كمان يبلغ 360 دورة في الثانية، فما التردد الذي يحتويه خيط مقاس 12 بوصة؟

حل المتباينات العقلانية

حل المتباينات العقلانية

في التمارين التالية، قم بحل كل تفاوت منطقي واكتب الحل بالتدوين الفاصل الزمني.

97. $\dfrac{x-3}{x+4} \leq 0$

إجابة

$(-4,3]$

98. $\dfrac{5 x}{x-2}>1$

99. $\dfrac{3 x-2}{x-4} \leq 2$

إجابة

$[-6,4)$

100. $\dfrac{1}{x^{2}-4 x-12}<0$

101. $\dfrac{1}{2}-\dfrac{4}{x^{2}} \geq \dfrac{1}{x}$

إجابة

$(-\infty,-2] \cup[4, \infty)$

102. $\dfrac{4}{x-2}<\dfrac{3}{x+1}$

حل عدم المساواة باستخدام الدوال الكسرية

في التمارين التالية، قم بحل كل تفاوت في الدالة الكسرية واكتب الحل في شكل فاصل زمني

103. بمعلومية الدالة$R(x)=\dfrac{x-5}{x-2}$، أوجد القيم$x$ التي تجعل الدالة أكبر من أو تساوي 0.

إجابة

$(-\infty, 2) \cup[5, \infty)$

104. بمعلومية الدالة$R(x)=\dfrac{x+1}{x+3}$، أوجد القيم$x$ التي تجعل الدالة أكبر من أو تساوي 0.

105. $C(x)=150 x+100,000$تمثل الوظيفة تكلفة الإنتاج$x$ وعدد العناصر. ابحث

1. وظيفة متوسط التكلفة،$c(x)$
2. كم عدد العناصر التي يجب إنتاجها بحيث يكون متوسط التكلفة أقل من 160 دولارًا.

إجابة

1. $c(x)=\dfrac{150 x+100000}{x}$
2. يجب إنتاج أكثر من 10000 عنصر للحفاظ على متوسط التكلفة أقل من 160 دولارًا لكل عنصر.

106. بدأ تيلمان مشروعه الخاص من خلال بيع سندويشات التاكو على الشاطئ. $C(x)=2 x+6,000$تمثل الوظيفة تكلفة شاحنة الطعام الخاصة به ومكونات سندويشات التاكو، التكلفة التي يتكبدها تيلمان لإنتاج$x$ سندويشات التاكو. ابحث

1. دالة متوسط التكلفة،$c(x)$ لتاكوس تيلمان
2. كم عدد سندويشات التاكو التي يجب أن ينتجها تيلمان بحيث يكون متوسط التكلفة أقل من 4 دولارات.

اختبار الممارسة

في التمارين التالية، قم بالتبسيط.

1. $\dfrac{4 a^{2} b}{12 a b^{2}}$

إجابة

$\dfrac{a}{3 b}$

2. $\dfrac{6 x-18}{x^{2}-9}$

في التمارين التالية، قم بإجراء العملية المشار إليها وتبسيطها.

3. $\dfrac{4 x}{x+2} \cdot \dfrac{x^{2}+5 x+6}{12 x^{2}}$

إجابة

$\dfrac{x+3}{3 x}$

4. $\dfrac{2 y^{2}}{y^{2}-1} \div \dfrac{y^{3}-y^{2}+y}{y^{3}-1}$

5. $\dfrac{6 x^{2}-x+20}{x^{2}-81}-\dfrac{5 x^{2}+11 x-7}{x^{2}-81}$

إجابة

$\dfrac{x-3}{x+9}$

6. $\dfrac{-3 a}{3 a-3}+\dfrac{5 a}{a^{2}+3 a-4}$

7. $\dfrac{2 n^{2}+8 n-1}{n^{2}-1}-\dfrac{n^{2}-7 n-1}{1-n^{2}}$

إجابة

$\dfrac{3 n-2}{n-1}$

8. $\dfrac{10 x^{2}+16 x-7}{8 x-3}+\dfrac{2 x^{2}+3 x-1}{3-8 x}$

9. $\dfrac{\dfrac{1}{m}-\dfrac{1}{n}}{\dfrac{1}{n}+\dfrac{1}{m}}$

إجابة

$\dfrac{n-m}{m+n}$

في التمارين التالية، قم بحل كل معادلة.

10. $\dfrac{1}{x}+\dfrac{3}{4}=\dfrac{5}{8}$

11. $\dfrac{1}{z-5}+\dfrac{1}{z+5}=\dfrac{1}{z^{2}-25}$

إجابة

$z=\dfrac{1}{2}$

12. $\dfrac{z}{2 z+8}-\dfrac{3}{4 z-8}=\dfrac{3 z^{2}-16 z-16}{8 z^{2}+2 z-64}$

في التمارين التالية، قم بحل كل تفاوت منطقي واكتب الحل بالتدوين الفاصل الزمني.

13. $\dfrac{6 x}{x-6} \leq 2$

إجابة

$[-3,6)$

14. $\dfrac{2 x+3}{x-6}>1$

15. $\dfrac{1}{2}+\dfrac{12}{x^{2}} \geq \dfrac{5}{x}$

إجابة

$(-\infty, 0) \cup(0,4] \cup[6, \infty)$

في التمارين التالية، ابحث عن$R(x)$ المعطى$f(x)=\dfrac{x-4}{x^{2}-3 x-10}$ و$g(x)=\dfrac{x-5}{x^{2}-2 x-8}$.

16. $R(x)=f(x)-g(x)$

17. $R(x)=f(x) \cdot g(x)$

إجابة

$R(x)=\dfrac{1}{(x+2)(x+2)}$

18. $R(x)=f(x) \div g(x)$

19. بمعلومية الدالة$R(x)=\dfrac{2}{2 x^{2}+x-15}$، أوجد القيم$x$ التي تجعل الدالة أقل من أو تساوي 0.

إجابة

$(2,5]$

في التمارين التالية، قم بحل.

20. $y$يختلف بشكل مباشر مع$x=5$ ومتى$x$$y=30$، ابحث عن$x$ الوقت$y=42$.

21. إذا كان$y$ يختلف عكسيًا مع المربع$x$$x=3$ ووقت حدوثه$y=9$، فأوجد$y$ الوقت$x=4$.

إجابة

$y=\dfrac{81}{16}$

22. يستطيع ماثيوس ركوب دراجته لمسافة 30 ميلاً مع الرياح في نفس الفترة الزمنية التي يمكنه خلالها السير 21 ميلاً ضد الرياح. إذا كانت سرعة الرياح ٦ أميال في الساعة، فما سرعة ماثيوس على دراجته؟

23. يمكن لأوليفر تقسيم حمولة شاحنة من جذوع الأشجار في 8 ساعات، ولكن بالعمل مع والده يمكنهم إنجاز ذلك في 3 ساعات. كم من الوقت سيستغرق والد أوليفر في العمل بمفرده لتقسيم السجلات?

إجابة

سيستغرق والد أوليفر$4 \dfrac{4}{5}$ ساعات لتقسيم السجلات بنفسه.

24. يختلف حجم الغاز في الحاوية بشكل عكسي مع الضغط على الغاز. إذا كان حجم حاوية النيتروجين 29.5 لترًا مع 2000 رطل/بوصة مربعة، فما الحجم إذا كان الخزان يحتوي على معدل 14.7 رطل لكل بوصة مربعة؟ قرِّب لأقرب عدد صحيح.

25.

تشكل مدن دايتون وكولومبوس وسينسيناتي مثلثًا في جنوب أوهايو. يوضِّح الشكل مسافات الخريطة بين هذه المدن بالبوصة.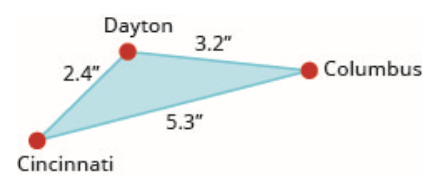

المسافة الفعلية من دايتون إلى سينسيناتي هي 48 اميال. ما هي المسافة الفعلية بين دايتون وكولومبوس؟

إجابة

المسافة بين دايتون وكولومبوس هي 64 ميلا.