2.8: حل تباينات القيمة المطلقة
- Page ID
- 201722
في نهاية هذا القسم، ستكون قادرًا على:
- حل معادلات القيمة المطلقة
- حل تباينات القيمة المطلقة بـ «أقل من»
- حل تباينات القيمة المطلقة بـ «أكبر من»
- حل التطبيقات ذات القيمة المطلقة
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
- تقييم:\(−|7|\).
إذا فاتتك هذه المشكلة، راجع [link]. - املأ\(<,>,<,>,\) أو\(=\) لكل زوج من أزواج الأرقام التالية.
ⓐ\(|−8|\text{___}−|−8|\) ⓑ\(12\text{___}−|−12|\) ⓒ\(|−6|\text{___}−6\) ⓓ\(−(−15)\text{___}−|−15|\)
إذا فاتتك هذه المشكلة، راجع [رابط]. - قم بالتبسيط:\(14−2|8−3(4−1)|\).
إذا فاتتك هذه المشكلة، راجع [link].
حل معادلات القيمة المطلقة
بينما نستعد لحل معادلات القيمة المطلقة، نقوم بمراجعة تعريفنا للقيمة المطلقة.
القيمة المطلقة للرقم هي المسافة من الصفر على خط الأعداد.
تتم كتابة القيمة المطلقة للرقم n\(|n|\) كـ\(|n|\geq 0\) ولجميع الأرقام.
تكون القيم المطلقة دائمًا أكبر من أو تساوي الصفر.
لقد تعلمنا أن كلا من الرقم ونقيضه هما نفس المسافة من الصفر على خط الأعداد. نظرًا لأن لديهم نفس المسافة من الصفر، فإن لديهم نفس القيمة المطلقة. على سبيل المثال:
- \(−5\)تبعد 5 وحدات عن 0، لذا\(|−5|=5\).
- \(5\)تبعد 5 وحدات عن 0، لذا\(|5|=5\).
\(\PageIndex{1}\)يوضح الشكل هذه الفكرة.
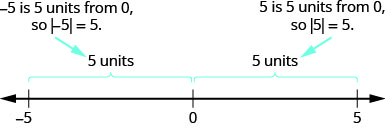
بالنسبة للمعادلة |x|=5، |x|=5، نبحث عن جميع الأرقام التي تجعل هذه العبارة حقيقية. نحن نبحث عن الأرقام التي تبلغ المسافة من الصفر 5. لقد رأينا للتو أن كلا من ٥ و−٥−٥ تمثلان خمس وحدات من الصفر على خط الأعداد. إنها حلول المعادلة.
\(\begin{array} {ll} {\text{If}} &{|x|=5} \\ {\text{then}} &{x=−5\text{ or }x=5} \\ \end{array}\)
يمكن تبسيط الحل إلى عبارة واحدة عن طريق الكتابة\(x=\pm 5\). هذه هي القراءة، «x يساوي الموجب أو السالب 5».
يمكننا تعميم هذا على الخاصية التالية لمعادلات القيمة المطلقة.
بالنسبة لأي تعبير جبري، u، وأي عدد حقيقي موجب، a،
\[\begin{array} {ll} {\text{if}} &{|u|=a} \\ {\text{then}} &{u=−a \text{ or }u=a} \\ \nonumber \end{array}\]
تذكر أن القيمة المطلقة لا يمكن أن تكون رقمًا سالبًا.
حل:
- \(|x|=8\)
- \(|y|=−6\)
- \(|z|=0\)
- الحل أ
-
\(\begin{array} {ll} {} &{|x|=8} \\ {\text{Write the equivalent equations.}} &{x=−8 \text{ or } x=8} \\ {} &{x=\pm 8} \\ \end{array}\)
- الحل ب
-
\(\begin{array} {ll} {} &{|y|=−6} \\ {} &{\text{No solution}} \\ \end{array}\)
نظرًا لأن القيمة المطلقة دائمًا ما تكون موجبة، فلا توجد حلول لهذه المعادلة. - الحل ج
-
\(\begin{array} {ll} {} &{|z|=0} \\ {\text{Write the equivalent equations.}} &{z=−0\text{ or }z=0} \\ {\text{Since }−0=0,} &{z=0} \\ \end{array}\)
تخبرنا كلتا المعادلتين أن z=0z=0 وبالتالي هناك حل واحد فقط.
حل:
- \(|x|=2\)
- \(|y|=−4\)
- \(|z|=0\)
- الإجابة أ
-
\(\pm 2\)
- الإجابة ب
-
لا يوجد حل
- الإجابة ج
-
0
حل:
- \(|x|=11\)
- \(|y|=−5\)
- \(|z|=0\)
- الإجابة أ
-
\(\pm 11\)
- الإجابة ب
-
لا يوجد حل
- الإجابة ج
-
0
لحل معادلة القيمة المطلقة، نقوم أولاً بعزل تعبير القيمة المطلقة باستخدام نفس الإجراءات التي استخدمناها لحل المعادلات الخطية. بمجرد عزل تعبير القيمة المطلقة، نعيد كتابته كمعادلتين متساويتين.
كيفية حل معادلات القيمة المطلقة
حل\(|5x−4|−3=8\).
- الحل
-




حل:\(|3x−5|−1=6\).
- إجابة
-
\(x=4, \space x=−\frac{2}{3}\)
حل:\(|4x−3|−5=2\).
- إجابة
-
\(x=−1,\space x=\frac{5}{2}\)
يتم تلخيص خطوات حل معادلة القيمة المطلقة هنا.
- اعزل تعبير القيمة المطلقة.
- اكتب المعادلات المكافئة.
- حل كل معادلة.
- تحقق من كل حل.
حل\(2|x−7|+5=9\).
- الحل
-
\(2|x−7|+5=9\) اعزل تعبير القيمة المطلقة. \(2|x−7|=4\) \(|x−7|=2\) اكتب المعادلات المكافئة. \(x−7=−2\)أو\(x−7=2\) حل كل معادلة. \(x=5\)أو\(x=9\) تحقق من:
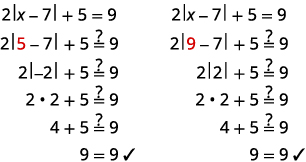
حل:\(3|x−4|−4=8\).
- إجابة
-
\(x=8,\space x=0\)
حل:\(2|x−5|+3=9\).
- إجابة
-
\(x=8,\space x=2\)
تذكر أن القيمة المطلقة دائمًا ما تكون إيجابية!
حل:\(|\frac{2}{3}x−4|+11=3\).
- الحل
-
\(\begin{array} {ll} {} &{|\frac{2}{3}x−4|=−8} \\ {\text{Isolate the absolute value term.}} &{|\frac{2}{3}x−4|=−8} \\ {\text{An absolute value cannot be negative.}} &{\text{No solution}} \\ \end{array}\)
حل:\(|\frac{3}{4}x−5|+9=4\).
- إجابة
-
لا يوجد حل
حل:\(|\frac{5}{6}x+3|+8=6\).
- إجابة
-
لا يوجد حل
يمكن أن تكون بعض معادلات القيمة المطلقة لدينا بالشكل الذي تكون\(|u|=|v|\) فيه u و v تعبيرات جبرية. على سبيل المثال،\(|x−3|=|2x+1|\).
كيف يمكننا حلها؟ إذا كان هناك تعبيران جبريان متساويان في القيمة المطلقة، فإنهما إما مساويان لبعضهما البعض أو سلبيات بعضهما البعض. تقول خاصية معادلات القيمة المطلقة أنه بالنسبة لأي تعبير جبري، u، ورقم حقيقي موجب، a، if\(|u|=a\)، ثم\(u=−a\) أو\(u=a\).
هذا يخبرنا بذلك
\ (\ ابدأ {المصفوفة} {lll}
{\ text {if}} و {u|=|||v|} و {} و {}
\\\\\ text {ثم}} و {|u|=v} و {\\ text {أو}} و {|u|=−v}
\\ {\ نص {وهكذا}} & {u=v\ text {أو} u = −v} و {\ text {أو}} و {u=−v\ text {أو} u = − (−v)}
\\\ النهاية {مصفوفة}\)
هذا يقودنا إلى الخاصية التالية للمعادلات ذات القيمتين المطلقتين.
لأي تعبيرات جبرية، u و v،
\[\begin{array} {ll} {\text{if}} &{|u|=|v|} \\ {\text{then}} &{u=−v\text{ or }u=v} \\ \nonumber \end{array}\]
عندما نأخذ عكس الكمية، يجب أن نكون حذرين مع العلامات وأن نضيف الأقواس عند الحاجة.
حل:\(|5x−1|=|2x+3|\).
- الحل
-
\(\begin{array} {ll} {} &{} &{|5x−1|=|2x+3|} &{} \\ {} &{} &{} &{} \\ {\text{Write the equivalent equations.}} &{5x−1=−(2x+3)} &{\text{or}} &{5x−1=2x+3} \\ {} &{5x−1=−2x−3} &{\text{or}} &{3x−1=3} \\ {\text{Solve each equation.}} &{7x−1=−3} &{} &{3x=4} \\ {} &{7x=−2} &{} &{x=43} \\ {} &{x=−27} &{\text{or}} &{x=43} \\ {\text{Check.}} &{} &{} &{} \\ {\text{We leave the check to you.}} &{} &{} &{} \\ \end{array}\)
حل:\(|7x−3|=|3x+7|\).
- إجابة
-
\(x=−\frac{2}{5}, \space x=\frac{5}{2}\)
حل:\(|6x−5|=|3x+4|\).
- إجابة
-
\(x=3, x=19\)
حل تباينات القيمة المطلقة باستخدام «أقل من»
دعونا ننظر الآن إلى ما يحدث عندما يكون لدينا عدم مساواة في القيمة المطلقة. كل ما تعلمناه عن حل عدم المساواة لا يزال قائمًا، ولكن يجب أن نفكر في كيفية تأثير القيمة المطلقة على عملنا. مرة أخرى سننظر في تعريفنا للقيمة المطلقة. القيمة المطلقة للرقم هي المسافة من الصفر على خط الأعداد. بالنسبة للمعادلة\(|x|=5\)، رأينا أن كلا من 5 و 5\(−5\) وحدات من الصفر على خط الأعداد. إنها حلول المعادلة.
\[\begin{array} {lll} {} &{|x|=5} &{} \\ {x=−5} &{\text{or}} &{x=5} \\ \nonumber \end{array}\]
ماذا عن عدم المساواة\(|x|\leq 5\)؟ أين الأرقام التي تكون مسافتها أقل من أو تساوي 5؟ نحن نعلم\(−5\) و5 كلاهما خمس وحدات من الصفر. جميع الأرقام بين\(−5\) و 5 أقل من خمس وحدات من الصفر (الشكل\(\PageIndex{2}\)).
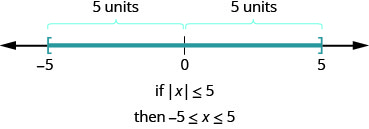
بطريقة أكثر عمومية، يمكننا أن نرى أنه إذا\(|u|\leq a\)، ثم\(−a\leq u\leq a\) (الشكل\(\PageIndex{3}\)).
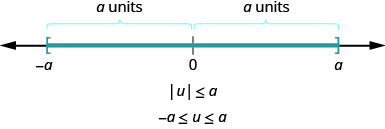
يتم تلخيص هذه النتيجة هنا.
بالنسبة لأي تعبير جبري، u، وأي عدد حقيقي موجب، a،
\[ \text{if} \quad |u|<a, \quad \text{then} \space −a<u<a \\ \text{if} \quad |u|\leq a, \quad \text{then} \space−a\leq u\leq a \nonumber\]
بعد حل عدم المساواة، غالبًا ما يكون من المفيد التحقق من بعض النقاط لمعرفة ما إذا كان الحل منطقيًا. يقسم الرسم البياني للحل خط الأعداد إلى ثلاثة أقسام. اختر قيمة في كل قسم واستبدلها في عدم المساواة الأصلية لمعرفة ما إذا كانت تجعل عدم المساواة صحيحًا أم لا. على الرغم من أن هذا ليس فحصًا كاملاً، إلا أنه غالبًا ما يساعد في التحقق من الحل.
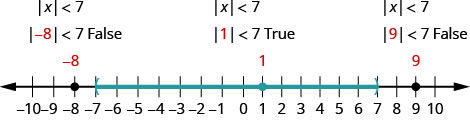
حل\(|x|<7\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.
- الحل
-
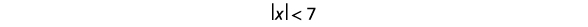
اكتب عدم المساواة المكافئة. 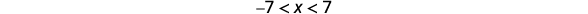
رسم الحل بيانيًا. 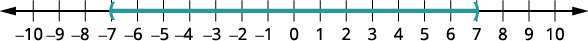
اكتب الحل باستخدام الترميز الفاصل الزمني. 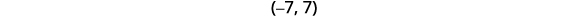
تحقق من:
للتحقق، تحقق من القيمة في كل قسم من سطر الأرقام الذي يعرض الحل. اختر أرقامًا مثل −8 و−8 و1 و9.
قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(|x|<9\).
- إجابة
-
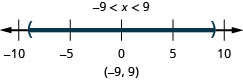
قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(|x|<1\).
- إجابة
-
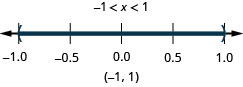
حل\(|5x−6|\leq 4\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.
- الحل
-
الخطوة 1. اعزل تعبير القيمة المطلقة.
إنه معزول.\(|5x−6|\leq 4\) الخطوة 2. اكتب عدم المساواة المركبة المكافئة. \(−4\leq 5x−6\leq 4\) الخطوة 3. حل عدم المساواة المركبة. \(2\leq 5x\leq 10\)
\(\frac{2}{5}\leq x\leq 2\)الخطوة 4. رسم الحل بيانيًا. 
الخطوة 5. اكتب الحل باستخدام الترميز الفاصل الزمني. \([\frac{2}{5}, 2]\) التحقق:
الشيك متروك لك.
حل\(|2x−1|\leq 5\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:
- إجابة
-
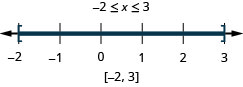
حل\(|4x−5|\leq 3\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:
- إجابة
-
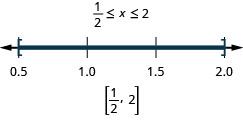
- اعزل تعبير القيمة المطلقة.
- اكتب عدم المساواة المركبة المكافئة.
\[\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{−a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{−a\leq u\leq a} \\ \nonumber \end{array}\]
- حل عدم المساواة المركبة.
- رسم بياني للحل
- اكتب الحل باستخدام الترميز الفاصل الزمني.
حل تباينات القيمة المطلقة باستخدام «أكبر من»
ماذا يحدث لتفاوتات القيمة المطلقة التي «أكبر من»؟ مرة أخرى سننظر في تعريفنا للقيمة المطلقة. القيمة المطلقة للرقم هي المسافة من الصفر على خط الأعداد.
لقد بدأنا بعدم المساواة\(|x|\leq 5\). لقد رأينا أن الأرقام التي تكون مسافتها أقل من أو تساوي خمسة من الصفر على خط الأعداد هي\(−5\) و 5 وجميع الأرقام بين\(−5\) و 5 (الشكل\(\PageIndex{4}\)).
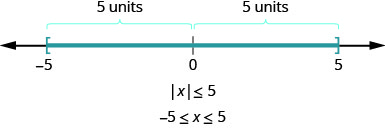
الآن نريد أن ننظر إلى عدم المساواة\(|x|\geq 5\). أين الأعداد التي تكون المسافة من الصفر أكبر من أو تساوي خمسة؟
مرة أخرى\(−5\)، كل من و 5 عبارة عن خمس وحدات من الصفر وبالتالي يتم تضمينها في الحل. الأرقام التي تكون مسافتها من الصفر أكبر من خمس وحدات ستكون أقل من\(−5\) 5 وأكبر من 5 على خط الأعداد (الشكل\(\PageIndex{5}\)).
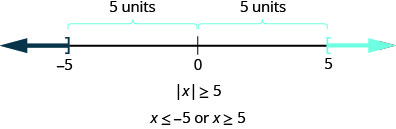
بطريقة أكثر عمومية، يمكننا أن نرى ذلك إذا\(|u|\geq a\)، ثم\(u\leq −a\) أو\(u\leq a\). انظر الشكل.
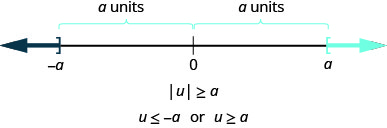
يتم تلخيص هذه النتيجة هنا.
بالنسبة لأي تعبير جبري، u، وأي عدد حقيقي موجب، a،
\[\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\quad \text{then } u<−a \text{ or } u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\quad \text{then } u\leq −a \text{ or } u\geq a} \\ \nonumber \end{array}\]
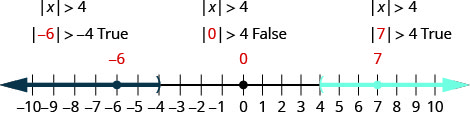
حل\(|x|>4\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.
- الحل
-
\(|x|>4\) اكتب عدم المساواة المكافئة. \(x<−4\)أو\(x>4\) رسم الحل بيانيًا. 
اكتب الحل باستخدام الترميز الفاصل الزمني. \((−\inf ,−4)\cup (4,\inf )\) تحقق من: للتحقق، تحقق من القيمة في كل قسم من سطر الأرقام الذي يعرض الحل. اختر أرقامًا مثل −6 و−6 و0 و7.
حل\(|x|>2\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.
- إجابة
-
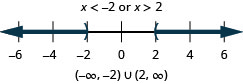
حل\(|x|>1\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.
- إجابة
-
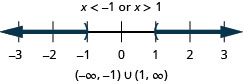
حل\(|2x−3|\geq 5\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.
- الحل
-
\(|2x−3|\geq 5\) الخطوة 1. اعزل تعبير القيمة المطلقة. إنه معزول. الخطوة 2. اكتب عدم المساواة المركبة المكافئة. \(2x−3\leq −5\)أو\(2x−3\geq 5\) الخطوة 3. حل عدم المساواة المركبة. \(2x\leq −2\)أو\(2x\geq 8\)
\(x\leq −1\) أو\(x\geq 4\)الخطوة 4. رسم الحل بيانيًا. 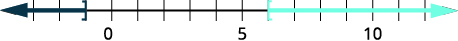
الخطوة 5. اكتب الحل باستخدام الترميز الفاصل الزمني. \((−\inf ,−1]\cup [4,\inf )\) التحقق:
الشيك متروك لك.
حل\(|4x−3|\geq 5\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.
- إجابة
-
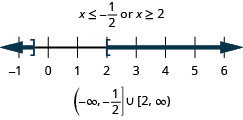
حل\(|3x−4|\geq 2\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.
- إجابة
-
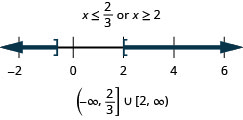
- اعزل تعبير القيمة المطلقة.
- اكتب عدم المساواة المركبة المكافئة.
\ [\ ابدأ {مصفوفة} {lll}
{|u| >a} & {\ رباعي\ نص {يعادل}} و {u<−a\ رباعي\ نص {أو}\ رباعي\ a}
\\\ {|u|\ geq a} و {\ رباعي\ نص {يعادل}} و {u\ leq −a\ quad\ text {أو}\ رباعية\ geq}
\ {|u| >a} & {\ رباعي\ نص {يعادل}} و {u<−a\ رباعي\ نص {أو}\ رباعي\ نص {أو}\ رباعي u>a}
\\\ {|u|\ geq a} و {\ رباعي\ نص {يعادل}} و {u\ leq −a\ quad\ text {أو}\ رباعي\ نص {أو}\ رباعية\ geq a}
\\\ لا يوجد رقم\ نهاية {مصفوفة}\] - حل عدم المساواة المركبة.
- رسم بياني للحل
- اكتب الحل باستخدام الترميز الفاصل الزمني.
حل التطبيقات ذات القيمة المطلقة
غالبًا ما يتم استخدام عدم المساواة في القيمة المطلقة في عملية التصنيع. يجب أن يكون العنصر مصنوعًا بمواصفات شبه مثالية. عادة ما يكون هناك قدر معين من التسامح مع الاختلاف عن المواصفات المسموح بها. إذا تجاوز الاختلاف عن المواصفات الحد المسموح به، يتم رفض العنصر.
\[|\text{actual-ideal}|\leq \text{tolerance} \nonumber\]
القطر المثالي للقضيب المطلوب للآلة هو 60 مم. يمكن أن يختلف القطر الفعلي عن القطر المثالي\(0.075\) بالملليمتر. ما نطاق الأقطار الذي سيكون مقبولاً للعميل دون التسبب في رفض القضيب؟
- الحل
-
\(\begin{array} {ll} {} &{\text{Let }x=\text{ the actual measurement}} \\ {\text{Use an absolute value inequality to express this situation.}} &{|\text{actual-ideal}|\leq \text{tolerance}} \\ {} &{|x−60|\leq 0.075} \\ {\text{Rewrite as a compound inequality.}} &{−0.075\leq x−60\leq 0.075} \\ {\text{Solve the inequality.}} &{59.925\leq x\leq 60.075} \\ {\text{Answer the question.}} &{\text{The diameter of the rod can be between}} \\ {} &{59.925 mm \text{ and } 60.075 mm.} \\ \end{array}\)
القطر المثالي للقضيب المطلوب للآلة هو 80 مم. يمكن أن يختلف القطر الفعلي عن القطر المثالي بمقدار 0.009 مم. ما نطاق الأقطار الذي سيكون مقبولاً للعميل دون التسبب في رفض القضيب؟
- إجابة
-
يمكن أن يتراوح قطر القضيب بين 79.991 و 80.009 ملم.
القطر المثالي للقضيب المطلوب للآلة هو 75 مم. يمكن أن يختلف القطر الفعلي عن القطر المثالي بمقدار 0.05 مم. ما نطاق الأقطار الذي سيكون مقبولاً للعميل دون التسبب في رفض القضيب؟
- إجابة
-
يمكن أن يتراوح قطر القضيب بين 74.95 و 75.05 مم.
يمكنك الوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات إضافية وممارسة حل معادلات القيمة المطلقة الخطية وعدم المساواة.
- حل معادلات ومتباينات القيمة المطلقة الخطية
المفاهيم الرئيسية
- القيمة
المطلقة القيمة المطلقة للرقم هي المسافة من 0 على خط الأعداد.
تتم كتابة القيمة المطلقة للرقم n\(|n|\) كـ\(|n|\geq 0\) ولجميع الأرقام.
تكون القيم المطلقة دائمًا أكبر من أو تساوي الصفر. - معادلات القيمة المطلقة
لأي تعبير جبري، u، وأي رقم حقيقي موجب، a،
\(\begin{array} {ll} {\text{if}} &{\quad |u|=a} \\ {\text{then}} &{\quad u=−a \text{ or } u=a} \\ \end{array}\)
تذكر أن القيمة المطلقة لا يمكن أن تكون رقمًا سالبًا. - كيفية حل معادلات القيمة المطلقة
- اعزل تعبير القيمة المطلقة.
- اكتب المعادلات المكافئة.
- حل كل معادلة.
- تحقق من كل حل.
- معادلات ذات قيمتين مطلقتين
لأي تعبيرات جبرية، u و v،
\(\begin{array} {ll} {\text{if}} &{\quad |u|=|v|} \\ {\text{then}} &{\quad u=−v \text{ or } u=v} \\ \end{array}\) - متباينات القيمة المطلقة مع\(<\) أو\(\leq\)
مع أي تعبير جبري، u، وأي رقم حقيقي موجب، a،
\(\begin{array} {llll} {\text{if}} &{\quad |u|=a} &{\quad \text{then}} &{−a<u<a} \\ {\text{if}} &{\quad |u|\leq a} &{\quad \text{then}} &{−a\leq u\leq a} \\ \end{array}\) - كيفية حل تباينات القيمة المطلقة باستخدام\(<\) أو\(\leq\)
- اعزل تعبير القيمة المطلقة.
- اكتب عدم المساواة المركبة المكافئة.
\(\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{\quad −a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{\quad −a\leq u\leq a} \\ \end{array}\) - حل عدم المساواة المركبة.
- رسم بياني للحل
- اكتب الحل باستخدام الترميز الفاصل الزمني
- متباينات القيمة المطلقة مع\(>\) أو\(\geq\)
مع أي تعبير جبري، u، وأي رقم حقيقي موجب، a،
\(\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\text{then } u<−a\text{ or }u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\text{then } u\leq −a\text{ or }u\geq a} \\ \end{array}\) - كيفية حل تباينات القيمة المطلقة باستخدام\(>\) أو\(\geq\)
- اعزل تعبير القيمة المطلقة.
- اكتب عدم المساواة المركبة المكافئة.
\(\begin{array} {lll} {|u|>a} &{\quad \text{is equivalent to}} &{\quad u<−a\text{ or }u>a} \\ {|u|\geq a} &{\quad \text{is equivalent to}} &{\quad u\leq −a\text{ or }u\geq a} \\ \end{array}\) - حل عدم المساواة المركبة.
- رسم بياني للحل
- اكتب الحل باستخدام الترميز الفاصل الزمني


