Skip to main content
Global

2.7: حل المتباينات المركبة

  1. Last updated
  2. Save as PDF
  • Page ID
    201754

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • حل عدم المساواة المركبة باستخدام «و»
    • حل عدم المساواة المركبة باستخدام «أو»
    • حل التطبيقات ذات المتباينات المركبة

    قبل البدء، قم بإجراء اختبار الاستعداد هذا.

    1. قم بالتبسيط:\(\frac{2}{5}(x+10)\).
      إذا فاتتك هذه المشكلة، راجع [link].
    2. قم بالتبسيط:\(−(x−4)\).
      إذا فاتتك هذه المشكلة، راجع [link].

    حل المتباينات المركبة باستخدام «and»

    الآن بعد أن عرفنا كيفية حل عدم المساواة الخطية، فإن الخطوة التالية هي النظر إلى عدم المساواة المركبة. يتكون عدم المساواة المركب من اثنين من أوجه عدم المساواة المرتبطة بكلمة «و» أو كلمة «أو». على سبيل المثال، فيما يلي تفاوتات مركبة.

    \[\begin{array} {lll} {x+3>−4} &{\text{and}} &{4x−5\leq 3} \\ {2(y+1)<0} &{\text{or}} &{y−5\geq −2} \\ \end{array} \nonumber\]

    عدم المساواة المركبة

    يتكون عدم المساواة المركب من اثنين من أوجه عدم المساواة المرتبطة بكلمة «و» أو كلمة «أو».

    إن حل عدم المساواة المركبة يعني العثور على جميع قيم المتغير التي تجعل من عدم المساواة المركبة بيانًا حقيقيًا. نقوم بحل المتباينات المركبة باستخدام نفس الأساليب التي استخدمناها لحل المتباينات الخطية. نحل كل عدم مساواة بشكل منفصل ثم نفكر في الحلين.

    لحل عدم المساواة المركبة بكلمة «و»، نبحث عن جميع الأرقام التي تجعل كلا المتباينين صحيحين. لحل عدم المساواة المركبة بكلمة «أو»، نبحث عن جميع الأرقام التي تجعل أي من عدم المساواة صحيحًا.

    لنبدأ بأوجه عدم المساواة المركبة بـ «و». سيكون حلنا هو الأرقام التي تمثل حلولًا لكل من أوجه عدم المساواة المعروفة باسم تقاطع المتباينين. ضع في اعتبارك تقاطع شارعين - الجزء الذي تتداخل فيه الشارعان - ينتمي إلى كلا الشارعين.

    هذا الشكل عبارة عن رسم توضيحي لشارعين مع تظليل تقاطعهما.

    للعثور على حل عدم المساواة المركب «و»، ننظر إلى الرسوم البيانية لكل عدم مساواة ثم نجد الأرقام التي تنتمي إلى كلا الرسمين البيانيين - حيث تتداخل الرسوم البيانية.

    بالنسبة للتفاوت المركب\(x>−3\)\(x\leq 2\)، نقوم برسم بياني لكل عدم مساواة. ثم نبحث عن مكان «تداخل» الرسوم البيانية. سيتم تظليل الأرقام المظللة في كلا الرسمين البيانيين على الرسم البياني لحل عدم المساواة المركبة. انظر الشكل\(\PageIndex{1}\).

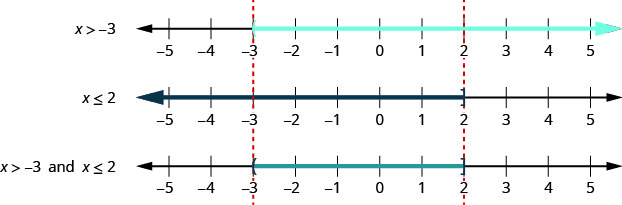
    يوضح الشكل أن الرسم البياني لـ x أكبر من سالب 3 مع وجود قوس يسار عند سالب 3 وتظليل على يمينه، والرسم البياني لـ x أقل من أو يساوي 2 مع وجود قوس عند 2 والتظليل على يساره، والرسم البياني لـ x أكبر من سالب 3 و x أقل من أو يساوي 2 مع الأقواس اليسرى عند السالب 3 والقوس الأيمن عند 2 والتظليل بين السالب 3 و 2. يتم تمييز السالب 3 و 2 بخطوط على كل سطر رقمي.
    الشكل\(\PageIndex{1}\)

    يمكننا أن نرى أن الأرقام الموجودة بين الرسوم البيانية الأولى\(−3\)\(2\) والثانية مظللة على كل من الرسوم البيانية الأولى والثانية. سيتم بعد ذلك تظليلها على الرسم البياني للحل.

    لم\(−3\) يتم تظليل الرقم في الرسم البياني الأول، وبالتالي نظرًا لأنه غير مظلل في كلا الرسمين البيانيين، فلن يتم تضمينه في الرسم البياني للحل.

    الرقم 2 مظلل في كل من الرسوم البيانية الأولى والثانية. لذلك، يتم تظليله على الرسم البياني للحل.

    هذه هي الطريقة التي سنعرض بها حلنا في الأمثلة التالية.

    مثال\(\PageIndex{1}\)

    حل\(6x−3<9\) و\(2x+7\geq 3\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.

    إجابة
      \(6x−3<9\) و \(2x+9\geq 3\)
    الخطوة 1. حل كل
    عدم مساواة.    		 \(6x−3<9\)   \(2x+9\geq 3\)
      \(6x<12\)   \(2x\geq −6\)
      \(x<2\) و \(x\geq −3\)
    الخطوة 2. رسم بياني لكل حل. ثم قم برسم الأرقام التي تجعل كلا المتباينتين صحيحين. سيُظهر الرسم البياني النهائي جميع الأرقام التي تجعل كلا المتباينين صحيحين - الأرقام المظللة على كل من الرسوم البيانية الأولى والثانية. .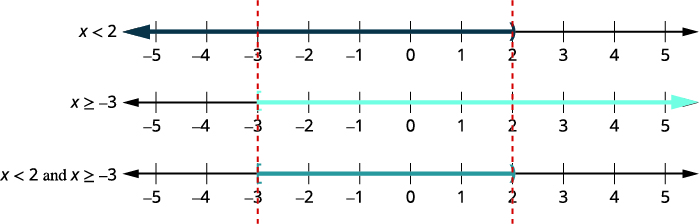
    الخطوة 3. اكتب الحل بالتدوين الفاصل الزمني. \([−3,2)\)
    جميع الأرقام التي تجعل كلا المتباينين صحيحين هي الحل لعدم المساواة المركبة.
    مثال\(\PageIndex{2}\)

    حل عدم المساواة المركبة. قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(4x−7<9\) و\(5x+8\geq 3\).

    إجابة

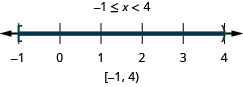
    الحل هو سالب 1 أقل من أو يساوي x وهو أقل من 4. يظهر على خط الأرقام بدائرة مغلقة بسالب 1 ودائرة مفتوحة عند 4 مع تظليل بين الدوائر المغلقة والمفتوحة. رمز الفاصل الزمني الخاص به هو سالب 1 إلى 4 داخل قوس وقوس.

    مثال\(\PageIndex{3}\)

    حل عدم المساواة المركبة. قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(3x−4<5\) و\(4x+9\geq 1\).

    إجابة

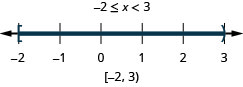
    الحل هو سالب 2 أقل من أو يساوي x وهو أقل من 3. يظهر على خط الأرقام بدائرة مغلقة عند سالب 2 ودائرة مفتوحة عند 3 مع تظليل بين الدوائر المغلقة والمفتوحة. رمز الفاصل الزمني الخاص به هو سالب 2 إلى 3 داخل قوس وقوس.

    حل عدم المساواة المركبة باستخدام «AND».
    1. حل كل عدم مساواة.
    2. رسم بياني لكل حل. ثم قم برسم الأرقام التي تجعل كلا المتباينتين صحيحين.
      يوضح هذا الرسم البياني حل عدم المساواة المركبة.
    3. اكتب الحل بالتدوين الفاصل الزمني.
    مثال\(\PageIndex{4}\)

    حل\(3(2x+5)\leq 18\) و\(2(x−7)<−6\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.

    إجابة
      \(3(2x+5)\leq 18\) و \(2(x−7)<−6\)
    حل كل
    عدم مساواة.    		 \(6x+15\leq 18\)   \(2x−14<−6\)
      \(6x\leq 3\)   \(2x<8\)
      \(x\leq \frac{1}{2}\) و \(x<4\)
    رسم بياني لكل
    حل.    		 .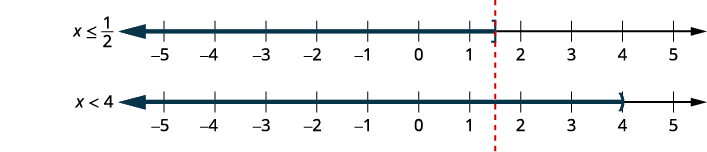
    ارسم بيانيًا الأرقام
    التي تجعل كلا
    المتباينين صحيحين.    		 .
    اكتب الحل
    بالتدوين الفاصل الزمني.    		 \((−\infty, \frac{1}{2}]\)
    مثال\(\PageIndex{5}\)

    حل عدم المساواة المركبة. قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(2(3x+1)\leq 20\) و\(4(x−1)<2\).

    إجابة

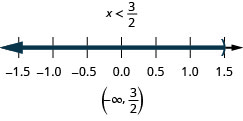
    الحل هو x أقل من ثلاثة أنصاف. يظهر على خط الأعداد بدائرة مفتوحة على ثلاثة أنصاف مع تظليل على يسارها. رمز الفاصل الزمني الخاص به هو سالب اللانهاية إلى ثلاثة أنصاف داخل أقواس.

    مثال\(\PageIndex{6}\)

    حل عدم المساواة المركبة. قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(5(3x−1)\leq 10\) و\(4(x+3)<8\).

    إجابة

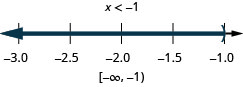
    الحل هو x أقل من السالب 1. يظهر على خط الأرقام بدائرة مفتوحة عند 1 مع تظليل على يسارها. رمز الفاصل الزمني الخاص به هو سالب اللانهاية إلى سالب 1 بين قوسين.

    مثال\(\PageIndex{7}\)

    حل\(\frac{1}{3}x−4\geq −2\) و\(−2(x−3)\geq 4\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.

    إجابة
      \(\frac{1}{3}x−4\geq −2\) و \(−2(x−3)\geq 4\)
    حل كل عدم مساواة. \(\frac{1}{3}x−4\geq −2\)   \(−2x+6\geq 4\)
      \(\frac{1}{3}x\geq 2\)   \(−2x\geq −2\)
      \(x\geq 6\) و \(x\leq 1\)
    رسم بياني لكل حل. ...
    ارسم بيانيًا الأرقام التي
    تجعل كلا المتباينين
    صحيحين.    		 ...
      لا توجد أرقام تجعل كلا عدم المساواة صحيحًا.

    هذا تناقض لذا لا يوجد حل. لا توجد أرقام تجعل كلا عدم المساواة صحيحًا.

    هذا تناقض لذا لا يوجد حل. لا توجد أرقام تجعل كلا عدم المساواة صحيحًا.

    هذا تناقض لذا لا يوجد حل.
    مثال\(\PageIndex{8}\)

    حل عدم المساواة المركبة. قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(\frac{1}{4}x−3\geq −1\) و\(−3(x−2)\geq 2\).

    إجابة

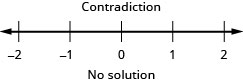
    عدم المساواة هو تناقض. لذلك، لا يوجد حل. ونتيجة لذلك، لا يوجد رسم بياني لخط الأرقام أو الترميز الفاصل الزمني.

    مثال\(\PageIndex{9}\)

    حل عدم المساواة المركبة. قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(\frac{1}{5}x−5\geq −3\) و\(−4(x−1)\geq −2\).

    إجابة

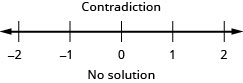
    عدم المساواة هو تناقض. لذلك، لا يوجد حل. ونتيجة لذلك، لا يوجد رسم بياني أو خط الأرقام أو الترميز الفاصل الزمني.

    في بعض الأحيان يكون لدينا عدم مساواة مركبة يمكن كتابتها بشكل أكثر إيجازًا. على سبيل المثال،\(a<x\)\(x<b\) ويمكن كتابتها ببساطة\(a<x<b\) ثم نسميها عدم مساواة مزدوجة. الشكلان متساويان.

    عدم المساواة المزدوجة

    عدم المساواة المزدوجة هي عدم مساواة مركبة مثل\(a<x<b\). إنه يعادل\(a<x\) و\(x<b\).

    \[\text{Other forms:} \quad \begin{array} {lllll} {a<x<b} &{\text{is equivalent to }} &{a<x} &{\text{and}} &{x<b} \\ {a\leq x\leq b} &{\text{is equivalent to }} &{a\leq x} &{\text{and}} &{x\leq b} \\ {a>x>b} &{\text{is equivalent to }} &{a>x} &{\text{and}} &{x>b} \\ {a\geq x\geq b} &{\text{is equivalent to }} &{a\geq x} &{\text{and}} &{x\geq b} \\ \end{array} \nonumber\]

    لحل عدم المساواة المزدوجة، نقوم بإجراء نفس العملية على جميع «الأجزاء» الثلاثة من عدم المساواة المزدوجة بهدف عزل المتغير في المركز.

    مثال\(\PageIndex{10}\)

    حل\(−4\leq 3x−7<8\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.

    إجابة
      \(-4 \leq 3x - 7 < 8\)
    أضف 7 إلى جميع الأجزاء الثلاثة. \( -4 \,{\color{red}{+\, 7}} \leq 3x - 7 \,{\color{red}{+ \,7}} < 8 \,{\color{red}{+ \,7}}\)
    قم بالتبسيط. \( 3 \le 3x < 15 \)
    قسّم كل جزء على ثلاثة. \( \dfrac{3}{\color{red}{3}} \leq \dfrac{3x}{\color{red}{3}} < \dfrac{15}{\color{red}{3}} \)
    قم بالتبسيط. \( 1 \leq x < 5 \)
    رسم الحل بيانيًا. .
    اكتب الحل بالتدوين الفاصل الزمني. \( [1, 5) \)

    عند كتابتها في صورة عدم مساواة مزدوجة\(1\leq x<5\)، يكون من السهل ملاحظة أن الحلول هي الأرقام المحصورة بين واحد وخمسة، بما في ذلك واحد، ولكن ليس خمسة. يمكننا بعد ذلك رسم الحل فورًا كما فعلنا أعلاه.

    هناك طريقة أخرى لرسم الحل\(1\leq x<5\) وهي رسم كل من الحل\(x\geq 1\) والحل\(x<5\). سنجد بعد ذلك الأرقام التي تجعل كلا عدم المساواة صحيحًا كما فعلنا في الأمثلة السابقة.

    مثال\(\PageIndex{11}\)

    حل عدم المساواة المركبة. قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(−5\leq 4x−1<7\).

    إجابة

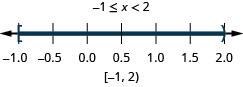
    الحل هو سالب 1 أقل من أو يساوي x وهو أقل من 2. يحتوي الرسم البياني الخاص به على دائرة مغلقة عند سالب 1 ودائرة مفتوحة عند 2 مع تظليل بين الدوائر المغلقة والمفتوحة. رمز الفاصل الزمني الخاص به هو سالب 1 إلى 2 داخل قوس وقوس.

    مثال\(\PageIndex{12}\)

    حل عدم المساواة المركبة. قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(−3<2x−5\leq 1\).

    إجابة

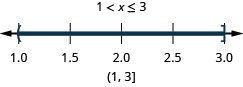
    الحل هو 1 أقل من x وهو أقل من أو يساوي 3. يحتوي الرسم البياني الخاص به على دائرة مفتوحة عند 1 ودائرة مغلقة عند 3 مع تظليل بين الدوائر المغلقة والمفتوحة. رمز الفاصل الزمني الخاص به هو سالب 1 إلى 3 داخل قوس وقوس.

    حل المتباينات المركبة باستخدام «أو»

    لحل عدم المساواة المركبة باستخدام «أو»، نبدأ تمامًا كما فعلنا مع عدم المساواة المركبة بـ «و» - نحل عدم المساواة. ثم نجد جميع الأرقام التي تجعل أي من عدم المساواة صحيحًا.

    تمامًا كما أن الولايات المتحدة هي اتحاد جميع الولايات الخمسين، سيكون الحل هو اتحاد جميع الأرقام التي تجعل أي من عدم المساواة صحيحًا. للعثور على حل عدم المساواة المركبة، ننظر إلى الرسوم البيانية لكل عدم مساواة، ونجد الأرقام التي تنتمي إلى أي رسم بياني ونجمع كل هذه الأرقام معًا.

    لكتابة الحل في الترميز الفاصل الزمني، سنستخدم غالبًا رمز الاتحاد\(\cup\)، لإظهار اتحاد الحلول الموضحة في الرسوم البيانية.

    حل عدم المساواة المركبة باستخدام «OR».
    1. حل كل عدم مساواة.
    2. رسم بياني لكل حل. ثم قم برسم الأرقام التي تجعل أي من عدم المساواة صحيحًا.
    3. اكتب الحل بالتدوين الفاصل الزمني.
    مثال\(\PageIndex{13}\)

    حل\(5−3x\leq −1\) أو\(8+2x\leq 5\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.

    إجابة
      \(5−3x\leq −1\) أو \(8+2x\leq 5\)
    حل كل عدم مساواة. \(5−3x\leq −1\)   \(8+2x\leq 5\)
      \(−3x\leq −6\)   \(2x\leq −3\)
      \(x\geq 2\) أو \(x\leq −\frac{3}{2}\)
    رسم بياني لكل حل. .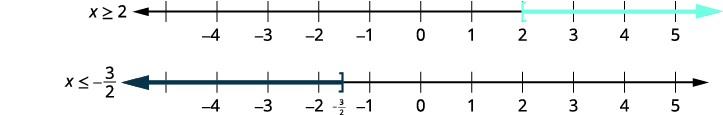
    أرقام الرسم البياني التي
    تجعل أي من عدم المساواة
    صحيحًا.    		 .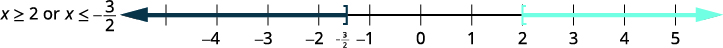
      \((−\infty,−32]\cup[2,\infty)\)
    مثال\(\PageIndex{14}\)

    حل عدم المساواة المركبة. قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(1−2x\leq −3\) أو\(7+3x\leq 4\).

    إجابة

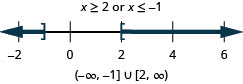
    الحل هو x أكبر من أو يساوي 2 أو x أقل من أو يساوي 1. يحتوي الرسم البياني للحلول على خط الأعداد على دائرة مغلقة عند سالب 1 وتظليل إلى اليسار ودائرة مغلقة عند 2 مع تظليل إلى اليمين. رمز الفاصل الزمني هو اتحاد اللانهاية السالبة إلى سالب 1 داخل قوس وقوس و 2 واللانهاية داخل قوس وقوس.

    مثال\(\PageIndex{15}\)

    حل عدم المساواة المركبة. قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(2−5x\leq −3\) أو\(5+2x\leq 3\).

    إجابة

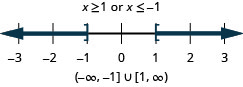
    الحل هو x أكبر من أو يساوي 1 أو x أقل من أو يساوي سالب 1. يحتوي الرسم البياني للحلول على خط الأعداد على دائرة مغلقة عند سالب 1 وتظليل إلى اليسار ودائرة مغلقة عند 1 مع تظليل إلى اليمين. رمز الفاصل الزمني هو اتحاد اللانهاية السالبة إلى سالب 1 داخل الأقواس والقوس و 1 واللانهاية داخل قوس وقوس.

    مثال\(\PageIndex{16}\)

    حل\(\frac{2}{3}x−4\leq 3\) أو\(\frac{1}{4}(x+8)\geq −1\). قم برسم الحل واكتب الحل في تدوين الفاصل الزمني.

    إجابة
      \(\frac{2}{3}x−4\leq 3\) أو \(\frac{1}{4}(x+8)\geq −1\)
    حل كل
    عدم مساواة.    		 \(3(\frac{2}{3}x−4)\leq 3(3)\)   \(4⋅\frac{1}{4}(x+8)\geq 4⋅(−1)\)
      \(2x−12\leq 9\)   \(x+8\geq −4\)
      \(2x\leq 21\)   \(x\geq −12\)
      \(x\leq \frac{21}{2}\)    
      \(x\leq \frac{21}{2}\) أو \(x\geq −12\)
    رسم بياني لكل
    حل.    		 .
    أرقام الرسم البياني
    التي تجعل أي من
    عدم المساواة صحيحًا.    		 .
      يغطي الحل جميع الأرقام الحقيقية.
      \((−\infty ,\infty )\)
    مثال\(\PageIndex{17}\)

    حل عدم المساواة المركبة. قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(\frac{3}{5}x−7\leq −1\) أو\(\frac{1}{3}(x+6)\geq −2\).

    إجابة

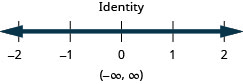
    الحل هو الهوية. يتم تظليل الحل الخاص به على خط الأعداد لجميع القيم. الحل في الترميز الفاصل الزمني هو سالب اللانهاية إلى اللانهاية بين قوسين.

    مثال\(\PageIndex{18}\)

    حل عدم المساواة المركبة. قم برسم الحل واكتب الحل في تدوين الفاصل الزمني:\(\frac{3}{4}x−3\leq 3\) أو\(\frac{2}{5}(x+10)\geq 0\).

    إجابة

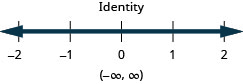
    الحل هو الهوية. يتم تظليل الحل الخاص به على خط الأعداد لجميع القيم. الحل في الترميز الفاصل الزمني هو سالب اللانهاية إلى اللانهاية بين قوسين.

    حل التطبيقات ذات المتباينات المركبة

    الحالات في العالم الحقيقي تنطوي أيضًا على تفاوتات مركبة. سنستخدم نفس استراتيجية حل المشكلات التي استخدمناها لحل المعادلات الخطية وتطبيقات عدم المساواة.

    تذكر أن استراتيجيات حل المشكلات هي قراءة المشكلة أولاً والتأكد من فهم جميع الكلمات. ثم حدد ما نبحث عنه وقم بتعيين متغير لتمثيله. بعد ذلك، كرر المشكلة في جملة واحدة لتسهيل ترجمتها إلى عدم مساواة مركبة. أخيرًا، سنحل عدم المساواة المركبة.

    مثال\(\PageIndex{19}\)

    بسبب الجفاف في كاليفورنيا، فإن العديد من المجتمعات لديها معدلات مياه متدرجة. هناك معدلات مختلفة لاستخدام الحفظ والاستخدام العادي والاستخدام المفرط. يتم قياس الاستخدام بعدد مئات الأقدام المكعبة (hcf) التي يستخدمها مالك العقار.

    خلال فصل الصيف، سيدفع مالك العقار 24.72 دولارًا بالإضافة إلى 1.54 دولارًا لكل hcf للاستخدام العادي. ستكون فاتورة الاستخدام العادي بين أو تساوي 57.06 دولارًا و 171.02 دولارًا. كم عدد hcf الذي يمكن للمالك استخدامه إذا كان يريد أن يظل استخدامه في المعدل الطبيعي؟

    إجابة
    حدد ما نبحث عنه. عدد hcf الذي يمكنه استخدامه والبقاء في نطاق فواتير «الاستخدام العادي».
    اذكر ما نبحث عنه. دع x=x= عدد hcf الذي يمكنه استخدامه.
    ترجم إلى عدم المساواة. تبلغ قيمة الفاتورة 24.72 دولارًا بالإضافة إلى 1.54 دولارًا من عدد hcf الذي يستخدمه\(24.72+1.54x\).
     

    \(\color{Cerulean}{\underbrace{\color{black}{\text{His bill will be between or equal to }$57.06\text{ and }$171.02.}}}\)

    \(57.06 \leq 24.74 + 1.54x \leq 171.02 \)
    حل عدم المساواة.

    \(57.06 \leq 24.74 + 1.54x \leq 171.02\)

    \(57.06 \,{\color{red}{- \,24.72}}\leq 24.74 \,{\color{red}{- \,24.72}} + 1.54x \leq 171.02 \,{\color{red}{- \,24.72}}\)

    \( 32.34 \leq 1.54x \leq 146.3\)

    \( \dfrac{32.34}{\color{red}{1.54}} \leq \dfrac{1.54x}{\color{red}{1.54}} \leq \dfrac{146.3}{\color{red}{1.54}}\)

    \( 21 \leq x \leq 95 \)
    أجب على السؤال. يمكن لمالك العقار استخدام\(21–95\) hcf ولا يزال يقع ضمن نطاق فواتير «الاستخدام العادي».
    مثال\(\PageIndex{20}\)

    بسبب الجفاف في كاليفورنيا، أصبح لدى العديد من المجتمعات الآن معدلات مياه متدرجة. هناك معدلات مختلفة لاستخدام الحفظ والاستخدام العادي والاستخدام المفرط. يتم قياس الاستخدام بعدد مئات الأقدام المكعبة (hcf) التي يستخدمها مالك العقار.

    خلال فصل الصيف، سيدفع مالك العقار 24.72 دولارًا بالإضافة إلى 1.32 دولارًا لكل hcf لاستخدام الحفظ. ستكون فاتورة استخدام الحفظ بين أو تساوي 31.32 دولارًا و 52.12 دولارًا. كم عدد hcf التي يمكن للمالك استخدامها إذا كانت تريد أن يبقى استخدامها في نطاق الحفظ؟

    إجابة

    يمكن لمالك المنزل استخدام\(5–20\) hcf ولا يزال يقع ضمن نطاق فواتير «استخدام الحفظ».

    مثال\(\PageIndex{21}\)

    بسبب الجفاف في كاليفورنيا، فإن العديد من المجتمعات لديها معدلات مياه متدرجة. هناك معدلات مختلفة لاستخدام الحفظ والاستخدام العادي والاستخدام المفرط. يتم قياس الاستخدام بعدد مئات الأقدام المكعبة (hcf) التي يستخدمها مالك العقار.

    خلال فصل الشتاء، سيدفع مالك العقار 24.72 دولارًا بالإضافة إلى 1.54 دولارًا لكل hcf للاستخدام العادي. ستكون فاتورة الاستخدام العادي بين أو تساوي 49.36 دولارًا و 86.32 دولارًا. كم عدد hcf الذي سيُسمح له باستخدامه إذا كان يريد أن يظل استخدامه في المعدل الطبيعي؟

    إجابة

    يمكن لمالك المنزل استخدام\(16–40\) hcf ولا يزال يقع ضمن نطاق فواتير «الاستخدام العادي».

    يمكنك الوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات وممارسة إضافية لحل عدم المساواة المركبة.

    • عدم المساواة المركبة

    المفاهيم الرئيسية

    • كيفية حل عدم المساواة المركبة باستخدام «و»
      1. حل كل عدم مساواة.
      2. رسم بياني لكل حل. ثم قم برسم الأرقام التي تجعل كلا المتباينتين صحيحين. يوضح هذا الرسم البياني حل عدم المساواة المركبة.
      3. اكتب الحل بالتدوين الفاصل الزمني.
    • عدم المساواة المزدوجة
      • عدم المساواة المزدوجة هي عدم مساواة مركبة مثل\(a<x<b\). وهو مكافئ لجميع النماذج\(x<b.\)

        الأخرى:\ [\ begin {align*} a<x<b &\ text {يعادل} & &a<x\؛\ text {و}\\\؛ x<b\\
        a≤x≤b &\ text {يعادل} & &a≤x\؛\ text {و}؛ x≤b\\ text\\(a<x\) \
        a>x> b &\ text {يعادل} & a>x\؛\ text {و}\؛ x>b\\\
        a≥x≥b &\ text {يعادل} & &\ text\؛\ text {و}\؛ x≥b\ end {align*}\
    • كيفية حل عدم المساواة المركبة بـ «أو»
      1. حل كل عدم مساواة.
      2. رسم بياني لكل حل. ثم قم برسم الأرقام التي تجعل أي من عدم المساواة صحيحًا.
      3. اكتب الحل بالتدوين الفاصل الزمني.

    مسرد المصطلحات

    عدم المساواة المركبة
    يتكون عدم المساواة المركب من اثنين من أوجه عدم المساواة المرتبطة بكلمة «و» أو كلمة «أو».