Skip to main content
Global

2.6: حل المتباينات الخطية

  1. Last updated
  2. Save as PDF
  • Page ID
    201729

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • تباينات الرسم البياني على خط الأعداد
    • حل المتباينات الخطية
    • ترجمة الكلمات إلى عدم المساواة وحلها
    • حل التطبيقات ذات المتباينات الخطية

    قبل البدء، قم بإجراء اختبار الاستعداد هذا.

    1. ترجم من الجبر إلى اللغة الإنجليزية:\(15>x\).
      إذا فاتتك هذه المشكلة، راجع [link].
    2. ترجمة إلى تعبير جبري:\(15\) أقل من\(x\).
      إذا فاتتك هذه المشكلة، راجع [link].

    متباينات التمثيل البياني على خط الأعداد

    ما الرقم الذي يجعل عدم المساواة\(x>3\) حقيقة؟ هل تفكر في «\(x\)يمكن أن تكون أربعة»؟ هذا صحيح، ولكن\(x\) يمكن أن يكون 6 أيضًا أو 37 أو حتى 3.001. أي رقم أكبر من ثلاثة هو حل لعدم المساواة\(x>3\). نعرض جميع الحلول لعدم المساواة\(x>3\) على خط الأعداد من خلال تظليل جميع الأرقام الموجودة على يمين ثلاثة، لإظهار أن جميع الأرقام الأكبر من ثلاثة هي حلول. نظرًا لأن الرقم ثلاثة في حد ذاته ليس حلاً، فقد وضعنا قوسًا مفتوحًا عند ثلاثة.

    يمكننا أيضًا تمثيل عدم المساواة باستخدام الترميز الفاصل الزمني. لا يوجد حد أعلى لحل عدم المساواة هذا. في الترميز الفاصل الزمني، نعبر عن\(x>3\) كـ\((3,\infty)\). \(\infty\)تتم قراءة الرمز باسم «اللانهاية». إنه ليس رقمًا فعليًا. \(\PageIndex{1}\)يوضح الشكل كلاً من خط الأرقام وترميز الفاصل الزمني.

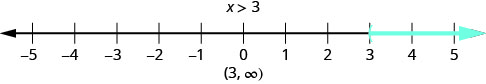
    يوضِّح الشكل عدم الجودة، x أكبر من 3، مُبيَّنًا بيانيًّا على خط الأعداد من سالب ٥ إلى ٥. هناك تظليل يبدأ من 3 ويمتد إلى الأرقام على يمينه. يتم كتابة حل عدم المساواة في تدوين الفاصل الزمني. إنها الفترة من 3 إلى اللانهاية، ولا تشمل 3.
    الشكل\(\PageIndex{1}\): تم رسم عدم المساواة\(x>3\) بيانيًا على خط الأعداد هذا وكتابته بتدوين فاصل زمني.

    نحن نستخدم رمز الأقواس الأيسر، (، لإظهار أن نقطة نهاية عدم المساواة ليست مدرجة. يُظهر رمز القوس الأيسر، [، أن نقطة النهاية مضمنة.

    عدم المساواة\(x\leq 1\) يعني جميع الأرقام التي تقل عن أو تساوي واحدًا. هنا نحتاج إلى إظهار أن المرء هو الحل أيضًا. نقوم بذلك عن طريق وضع قوس عند\(x=1\). ثم نقوم بتظليل جميع الأرقام الموجودة على يسار الرقم، لإظهار أن جميع الأرقام الأقل من واحد هي حلول (الشكل\(\PageIndex{2}\)). لا يوجد حد أدنى لهذه الأرقام. نكتب\(x\leq 1x\leq 1 \) بالتدوين الفاصل الزمني كـ\((−\infty,1]\). \(−\infty\)تتم قراءة الرمز على أنه «اللانهاية السلبية».

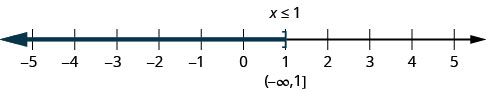
    يوضح الشكل عدم الجودة، x أقل من أو يساوي l، بيانيًا على خط الأعداد من سالب 5 إلى 5. هناك تظليل يبدأ من 1 ويمتد إلى الأرقام على يساره. يتم كتابة حل عدم المساواة في تدوين الفاصل الزمني. إنها الفترة من اللانهاية السالبة إلى واحدة، بما في ذلك 1.
    الشكل\(\PageIndex{2}\): تم رسم عدم المساواة\(x\leq 1\) بيانيًا على خط الأعداد هذا وكتابته بتدوين فاصل زمني.

    \(\PageIndex{3}\)يوضح الشكل كلاً من خط الأرقام والترميز الفاصل الزمني.

    المتباينات وخطوط الأرقام وتدوين الفاصل الزمني

    يوضح الشكل أن حل عدم المساواة x أكبر من a يشار إليه في خط الأرقام مع وجود قوسين يساريين عند a وتظليل إلى اليمين، وأن الحل في الترميز الفاصل الزمني هو الفاصل الزمني من a إلى اللانهاية المحاط بين قوسين. يُظهر حل عدم المساواة x أكبر من أو يساوي a كما هو موضح في خط الأرقام مع وجود قوس يساري عند a وتظليل إلى اليمين، وأن الحل في الترميز الفاصل الزمني هو الفاصل الزمني من a إلى اللانهاية داخل القوس الأيسر والقوس الأيمن. يُظهر أن حل عدم المساواة x أقل من a يشار إليه في خط الأرقام مع وجود قوس أيمن عند a وتظليل إلى اليسار، وأن الحل في الترميز الفاصل الزمني هو الفاصل الزمني اللانهاية السالبة إلى a داخل الأقواس. يُظهر أن حل عدم المساواة x أقل من أو يساوي a يشار إليه على خط الأرقام مع القوس الأيمن عند a والتظليل إلى اليسار، وأن الحل في الترميز الفاصل الزمني هو اللانهاية السالبة إلى a داخل الأقواس اليسرى والقوس الأيمن.

    يستخدم الترميز الخاص بالمتباينات على خط الأرقام وفي الترميز الفاصل نفس الرموز للتعبير عن نقاط نهاية الفواصل.

    مثال\(\PageIndex{1}\)

    ارسم بيانيًا لكل عدم مساواة على خط الأعداد واكتب بتدوين فاصل زمني.

    1. \(x\geq −3\)
    2. \(x<2.5\)
    3. \(x\leq −\frac{3}{5}\)
    إجابة

    ⓐ

      \( x \geq -3 \)
    ظلل على اليمين\(−3\)، ثم ضع قوسًا عليه\(−3\). .
    اكتب بالتدوين الفاصل الزمني. \( [-3, \infty) \)

    ⓑ

      \( x < 2.5 \)
    ظلل على يسار 2.5 ثم ضع قوسًا عند 2.5. .
    اكتب بالتدوين الفاصل الزمني. \( (-\infty, 2.5) \)

    ⓒ

      \( x \leq -\dfrac{3}{5} \)
    ظلل على يسار الصورة\(−\frac{3}{5}\)، ثم ضع قوسًا عليها\(−\frac{3}{5}\). .
    اكتب بالتدوين الفاصل الزمني. \( \bigg( -\infty, \dfrac{3}{5}\bigg] \)
     

    ارسم بيانيًا لكل عدم مساواة على خط الأعداد واكتب بالتدوين الفاصل الزمني:

    1. \(x>2\)
    2. \(x\leq −1.5\)
    3. \(x\geq \frac{3}{4}\).
    إجابة

    ⓐ

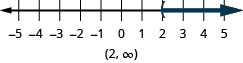
    يُشار إلى الرسم البياني للتفاوت x الذي يزيد عن 2 على خط الأرقام مع وضع الأقواس اليسرى عند 2 والتظليل إلى اليمين. الحل في الترميز الفاصل الزمني هو الفاصل الزمني من 2 إلى اللانهاية المحاط بين قوسين.

    ⓑ

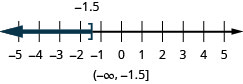
    يشار إلى الرسم البياني للتفاوت x الذي يقل عن أو يساوي سالب 1.5 على خط الأرقام مع القوس الأيمن عند سالب 1.5 والتظليل إلى اليسار. الحل في الترميز الفاصل الزمني هو الفاصل الزمني من اللانهاية السالبة إلى سالب 1.5 المحاطة بالقوس الأيسر والقوس الأيمن.

    ⓒ

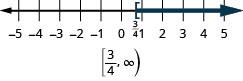
    يشار إلى الرسم البياني للتفاوت x الذي يزيد عن أو يساوي ثلاثة أرباع على خط الأرقام مع القوس الأيسر عند ثلاثة أرباع والتظليل إلى اليمين. الحل في الترميز الفاصل الزمني هو الفاصل الزمني من ثلاثة أرباع إلى ما لا نهاية داخل القوس الأيسر والأقواس اليسرى.

    مثال\(\PageIndex{3}\)

    ارسم بيانيًا لكل عدم مساواة على خط الأعداد واكتب بالتدوين الفاصل الزمني:

    1. \(x\leq −4\)
    2. \(x\geq 0.5\)
    3. \(x<−\frac{2}{3}\).
    إجابة

    ⓐ

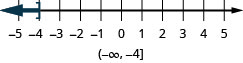
    يشار إلى الرسم البياني للتفاوت x الذي يقل عن أو يساوي سالب 4 على خط الأرقام مع القوس الأيمن عند سالب 4 والتظليل إلى اليسار. الحل في الترميز الفاصل الزمني هو الفاصل الزمني من اللانهاية السالبة إلى سالب 4 المحاطة بالقوس الأيسر والقوس الأيمن.

    ⓑ

    يشار إلى الرسم البياني للتفاوت x الذي يزيد عن أو يساوي 0.5 على خط الأرقام مع القوس الأيسر عند 0.5 والتظليل إلى اليمين. الحل في الترميز الفاصل الزمني هو الفاصل الزمني من 0.5 إلى اللانهاية المحاط بالقوس الأيسر والقوس الأيمن.

    ⓒ

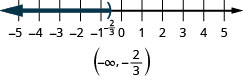
    يشار إلى الرسم البياني للتفاوت x الذي يقل عن سالب الثلثين على خط الأرقام مع وجود قوس أيمن عند سالب الثلثين والتظليل إلى اليسار. الحل في الترميز الفاصل الزمني هو الفاصل الزمني من اللانهاية السالبة إلى السالب الثلثين المحاطين بين قوسين.

    ما الأعداد الأكبر من اثنين ولكن الأقل من خمسة؟ هل تفكر في قول،\(2.5,\space 3,\space 3\frac{2}{3},\space 4,\space 4,\space 99\)؟ يمكننا تمثيل جميع الأرقام بين اثنين وخمسة باستخدام عدم المساواة\(2<x<5\). يمكننا أن نظهر\(2<x<5\) على خط الأعداد بتظليل جميع الأرقام بين اثنين وخمسة. مرة أخرى، نستخدم الأقواس لإظهار أن الرقمين اثنين وخمسة غير مضمنين. انظر الشكل.

    الرسم البياني للتفاوت 2 أقل من x وهو أقل من 5 يُظهر الدوائر المفتوحة a 2 و 5 والتظليل بينهما.
    الشكل\(\PageIndex{3}\)
     

    ارسم بيانيًا لكل عدم مساواة على خط الأعداد واكتب بتدوين فاصل زمني.

    ⓐ\(−3<x<4\) ⓑ\(−6\leq x<−1\) ⓒ\(0\leq x\leq 2.5\)

    إجابة

    ⓐ

        \(-3 < x < 4\)
    ظل بين 2\(−3\) و 4.
    ضع قوسين عند\(−3\) و 4.    		   .
    اكتب بالتدوين الفاصل الزمني.   \( (-3,4) \)

    ⓑ

          \( -6 \leq x < -1 \)
    ظل بين\(−6\) و −1.
    ضع قوسًا عند\(−6\) −1
    وقوسًا عند −1.    		     .
    اكتب بالتدوين الفاصل الزمني.     \( [-6,1) \)

    ⓒ

          \( 0 \leq x \leq 2.5 \)
    ظل بين 0 و 2.5.
    ضع قوسًا عند 0 وعند 2.5.    		     .
    اكتب بالتدوين الفاصل الزمني.     \( [0, 2.5] \)
    مثال\(\PageIndex{5}\)

    ارسم بيانيًا لكل عدم مساواة على خط الأعداد واكتب بالتدوين الفاصل الزمني:

    ⓐ\(−2<x<1\) ⓑ\(−5\leq x<−4\) ⓒ\(1\leq x\leq 4.25\)

    إجابة

    ⓐ

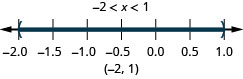
    السالب 2 هو أقل من x وهو أقل من 1. توجد دوائر مفتوحة بسالب 2 و 1 وتظليل بين سالب 2 و 1 على خط الأرقام. ضع الأقواس عند السالب 2 و 1. اكتب بالتدوين الفاصل الزمني.

    ⓑ

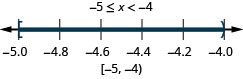
    سالب 5 أقل من أو يساوي x وهو أقل من سالب 4. توجد دائرة مغلقة عند سالب 6 ودائرة مفتوحة عند سالب 4 وتظليل بين سالب 5 وسالب 4 على خط الأعداد. ضع قوسًا عند سالب 5 وقوسًا عند سالب 4. اكتب بالتدوين الفاصل الزمني.

    ⓒ

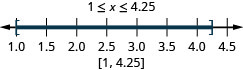
    1 أقل من أو يساوي x وهو أقل من 4.25. توجد دائرة مغلقة عند 1 ودائرة مغلقة عند 4.25 وتظليل بين 1 و 4.25 على خط الأرقام. ضع الأقواس في 1 و 4.25. اكتب بالتدوين الفاصل الزمني.

    مثال\(\PageIndex{6}\)

    ارسم بيانيًا لكل عدم مساواة على خط الأعداد واكتب بالتدوين الفاصل الزمني:

    ⓐ\(−6<x<2\) ⓑ\(−3\leq x< −1\) ⓒ\(2.5\leq x\leq 6\)

    إجابة

    ⓐ

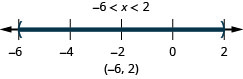
    سالب 6 أقل من x وهو أقل من 2. توجد دائرة مفتوحة عند سالب 6 ودائرة مفتوحة عند 2 وتظليل بين سالب 6 و 2 على خط الأعداد. ضع الأقواس عند سالب 6 و 2. اكتب بالتدوين الفاصل الزمني.

    ⓑ

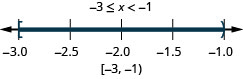
    سالب 3 أقل من أو يساوي x وهو أقل من سالب 1. توجد دائرة مغلقة عند سالب 3 ودائرة مفتوحة عند سالب 1 وتظليل بين سالب 3 وسالب 1 على خط الأعداد. ضع قوسًا عند سالب 3 وقوسًا عند سالب 1. اكتب بالتدوين الفاصل الزمني.

    ⓒ

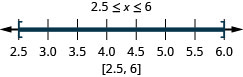
    2.5 أقل من أو يساوي x وهو أقل من أو يساوي 6. توجد دائرة مغلقة عند 2.5 ودائرة مغلقة عند 6 وتظليل بين 2.5 و 6 على خط الأعداد. ضع الأقواس عند 2.5 و 6. اكتب بالتدوين الفاصل الزمني.

    حل المتباينات الخطية

    إن عدم المساواة الخطية يشبه إلى حد كبير المعادلة الخطية - ولكن يتم استبدال علامة المساواة بعلامة عدم المساواة. عدم المساواة الخطية هي عدم مساواة في متغير واحد يمكن كتابته في أحد النماذج، أو\(ax+b<c\)\(ax+b\leq c\)،\(ax+b>c\)، أو\(ax+b\geq c\).

    عدم المساواة الخطية

    عدم المساواة الخطية هي عدم مساواة في متغير واحد يمكن كتابته بأحد الأشكال التالية حيث\(a, \, b,\)\(c\) تكون الأرقام الحقيقية و\(a≠0\):

    \[ \begin{array} {llll} {ax+b<c,} &{ax+b\leq c,} &{ax+b>c,} &{ax+b\geq c.} \\ \nonumber \end{array}\]

    عندما قمنا بحل المعادلات الخطية، تمكنا من استخدام خصائص المساواة لجمع أو طرح أو ضرب أو تقسيم كلا الطرفين مع الحفاظ على المساواة. تنطبق الخصائص المماثلة على عدم المساواة.

    يمكننا إضافة أو طرح نفس الكمية من كلا جانبي عدم المساواة مع الحفاظ على عدم المساواة. على سبيل المثال:

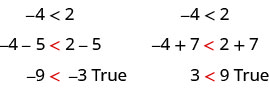
    السالب 4 أقل من 2. سالب 4 ناقص 5 أقل من 2 ناقص 5. سالب 9 أقل من سالب 3، وهذا صحيح. السالب 4 أقل من 2. سالب 4 زائد 7 أقل من 2 زائد 7. 3 أقل من 9، وهذا صحيح.

    لاحظ أن علامة عدم المساواة بقيت كما هي.

    هذا يقودنا إلى خصائص الجمع والطرح لعدم المساواة.

    خاصية الجمع والطرح لعدم المساواة

    للحصول على أي أرقام\(a, \, b,\)\(c,\) وإذا\(a<b\)، ثم

    \[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \nonumber \end{array}\]

    يمكننا إضافة أو طرح نفس الكمية من كلا جانبي عدم المساواة مع الحفاظ على عدم المساواة

    ماذا يحدث لعدم المساواة عندما نقسم أو نضرب كلا الجانبين بثابت؟

    دعونا أولاً نضرب كلا الجانبين ونقسمهما بعدد موجب.

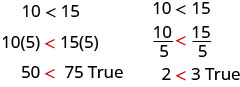
    10 أقل من 15. 10 في 5 أقل من 15 في 5. 50 أقل من 75 صحيح. 10 أقل من 15. 10 أقل من 15. 10 مقسومًا على 5 أقل من 15 مقسومًا على 5. 2 أقل من 3 صحيح.

    بقيت علامات عدم المساواة كما هي.

    هل تظل اللامساواة كما هي عندما نقسم أو نضرب عددًا سالبًا؟

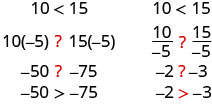
    10 أقل من 15 10 مرات سالب 5 فارغ 15 مرة سالب 5؟ سالب 50 هو فارغ سالب 75. سالب 50 أكبر من سالب 75. 10 أقل من 15. 10 مقسومًا على سالب 5 هو فارغ 15 مقسومًا على سالب 5. السالب 2 هو فارغ سالب 3. السالب 2 هو فارغ سالب 3.

    لاحظ أنه عندما ملأنا علامات عدم المساواة، عكست علامات عدم المساواة اتجاهها.

    عندما نقسم أو نضرب عدم المساواة في رقم موجب، تظل علامة عدم المساواة كما هي. عندما نقسم أو نضرب عدم المساواة برقم سالب، تنعكس علامة عدم المساواة.

    وهذا يعطينا خاصية الضرب والقسمة لعدم المساواة.

    خاصية الضرب والقسمة لعدم المساواة

    لأي أرقام\(a, \, b,\) و\(c,\)

    \[\begin{array} {l} {\text{multiply or divide by a positive}} \\ \\ \space\space\space\space\text{if }a<b\text{ and }c>0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\text{if }a>b\text{ and }c>0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}. \\ \\ \text{ multiply or divide by a negative } \\ \\ \space\space\space\space\text{if }a<b\text{ and }c<0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}.\\ \space\space\space\space\text{if }a>b\text{ and }c<0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}.\\ \nonumber \end{array}\]

    عندما نقسم أو نضرب عدم المساواة من خلال\(a\):

    • الرقم الموجب، يبقى عدم المساواة كما هو.
    • الرقم السالب، ينعكس عدم المساواة.

    في بعض الأحيان عند حل عدم المساواة، كما في المثال التالي، ينتهي المتغير على اليمين. يمكننا إعادة كتابة عدم المساواة في الاتجاه المعاكس للحصول على المتغير إلى اليسار.

    \[x>a \text{ has the same meaning as } a<x \nonumber \]

    فكر في الأمر على أنه «إذا كان زاندر أطول من آندي، فإن آندي أقصر من زاندر».

    مثال\(\PageIndex{7}\)

    حل كل عدم مساواة. قم برسم الحل على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    ⓐ\(x−\frac{3}{8}\leq \frac{3}{4}\) ⓑ\(9y<54\) ⓒ\(−15<\frac{3}{5}z\)

    إجابة

    ⓐ

      .
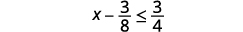
    أضف 3838 إلى كلا جانبي عدم المساواة. .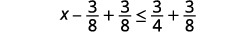
    قم بالتبسيط. .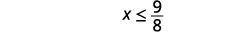
    ارسم حلًا بيانيًا على خط الأعداد. .
    اكتب الحل بالتدوين الفاصل الزمني. .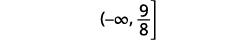

    ⓑ

      .
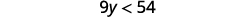
    قسّم كلا جانبي عدم المساواة على 9؛ نظرًا لأن
    9 إيجابية، يبقى عدم المساواة كما هو.    		 .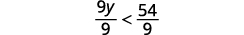
    قم بالتبسيط. .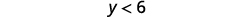
    ارسم حلًا بيانيًا على خط الأعداد. .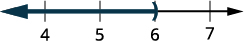
    اكتب الحل بالتدوين الفاصل الزمني. .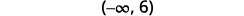

    ⓒ

      .

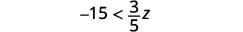
    اضرب كلا جانبي عدم المساواة في\(\frac{5}{3}\).
    نظرًا لأنه\(\frac{5}{3}\) أمر إيجابي، يبقى عدم المساواة على حاله.

    		 .
    قم بالتبسيط. .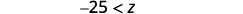
    أعد الكتابة باستخدام المتغير الموجود على اليسار. .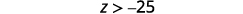
    ارسم حلًا بيانيًا على خط الأعداد. .
    اكتب الحل بالتدوين الفاصل الزمني. .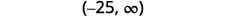
     

    قم بحل كل عدم مساواة، ورسم الحل على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني:

    ⓐ\(p−\frac{3}{4}\geq \frac{1}{6}\) ⓑ\(9c>72\) ⓒ\(24\leq \frac{3}{8}m\)

    إجابة

    ⓐ

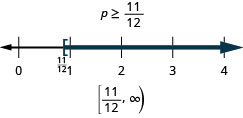
    p هو أقل من أحد عشر إلى اثني عشر. يحتوي الحل الموجود على خط الأعداد على قوس صحيح عند أحد عشر إلى اثني عشر مع تظليل على اليمين. الحل في الترميز الفاصل الزمني هو، من أحد عشر إلى اثني عشر إلى ما لا نهاية داخل قوس وقوس.

    ⓑ

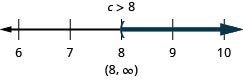
    c أقل من 8. يحتوي الحل الموجود على خط الأرقام على قوس يساري عند 8 مع تظليل إلى اليمين. الحل في الترميز الفاصل الزمني هو 8 إلى ما لا نهاية بين قوسين.

    ⓒ

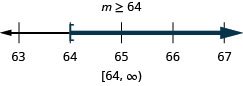
    m أكبر من أو يساوي 8. يحتوي الحل الموجود على خط الأرقام على قوس صحيح عند 64 مع التظليل إلى اليمين. الحل في الترميز الفاصل الزمني هو 64 إلى ما لا نهاية داخل قوس وأقواس.

    مثال\(\PageIndex{9}\)

    قم بحل كل عدم مساواة، ورسم الحل على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني:

    ⓐ\(r−\frac{1}{3}\leq \frac{7}{12}\) ⓑ\(12d\leq 60\) ⓒ\(−24<\frac{4}{3}n\)

    إجابة

    ⓐ

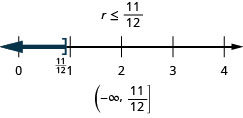
    r أقل من أو يساوي أحد عشر إلى اثني عشر. يحتوي الحل الموجود على خط الأعداد على قوس يساري عند أحد عشر إلى اثني عشر مع تظليل على اليسار. الحل في الترميز الفاصل الزمني هو سالب اللانهاية إلى أحد عشر إلى اثني عشر داخل قوس وقوس.

    ⓑ

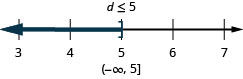
    c أقل من أو يساوي 5. يحتوي الحل الموجود على خط الأرقام على قوس أيمن عند 5 مع تظليل على اليسار. الحل في الترميز الفاصل الزمني هو سالب اللانهاية إلى 5 داخل الأقواس والقوس.

    ⓒ

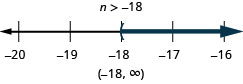
    n أكبر من سالب 18. يحتوي الحل الموجود على خط الأعداد على قوس يسار عند سالب 18 مع التظليل إلى اليمين. الحل في الترميز الفاصل هو سالب 18 إلى اللانهاية بين قوسين.

    كن حذرًا عند الضرب أو القسمة على رقم سالب - تذكر عكس علامة عدم المساواة.

    مثال\(\PageIndex{10}\)

    حل كل تفاوت، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    ⓐ\(−\frac{1}{3}m\geq \frac{6}{5}\) ⓑ\(\frac{n}{−2} \geq 8\)

    إجابة

    ⓐ

      .
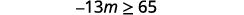
    قسّم جانبي عدم المساواة على\(−\frac{1}{3}\).
    وبما\(−\frac{1}{3}\) أنها سلبية، فإن عدم المساواة ينعكس.    		 .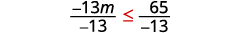
    قم بالتبسيط. .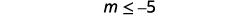
    ارسم حلًا بيانيًا على خط الأعداد. .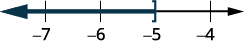
    اكتب الحل بالتدوين الفاصل الزمني. .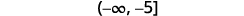

    ⓑ

      .
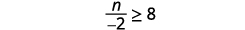
    اضرب كلا جانبي عدم المساواة في\(−2\).
    وبما\(−2\) أنها سلبية، فإن عدم المساواة ينعكس.    		 .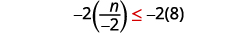
    قم بالتبسيط. .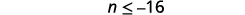
    ارسم حلًا بيانيًا على خط الأعداد. .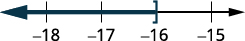
    اكتب الحل بالتدوين الفاصل الزمني. .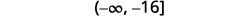
    مثال\(\PageIndex{11}\)

    قم بحل كل عدم مساواة، ورسم الحل على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني:

    ⓐ\(−8q<32\) ⓑ\(\frac{k}{−12} \leq 15\).

    إجابة

    ⓐ

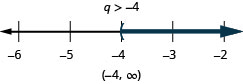
    q أكبر من أو يساوي سالب 4. يحتوي الحل الموجود على خط الأعداد على قوس يسار عند سالب 4 مع التظليل إلى اليمين. الحل في الترميز الفاصل هو سالب 4 إلى اللانهاية بين قوسين.

    ⓑ

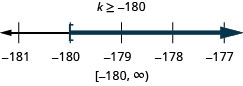
    k أكبر من أو يساوي سالب 180. يحتوي الحل الموجود على خط الأعداد على قوس يساري بسالب 180 مع تظليل إلى اليمين. الحل في الترميز الفاصل هو سالب 180 إلى اللانهاية داخل قوس وقوس.

    مثال\(\PageIndex{12}\)

    قم بحل كل عدم مساواة، ورسم الحل على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني:

    ⓐ\(−7r\leq −70\) ⓑ\(\frac{u}{−4}\geq −16\).

    إجابة

    ⓐ

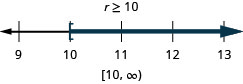
    r أكبر من أو يساوي 10. يحتوي الحل الموجود على خط الأرقام على قوس يساري عند 10 مع تظليل إلى اليمين. الحل في الترميز الفاصل الزمني هو 10 إلى ما لا نهاية داخل القوس والقوس.

    ⓑ

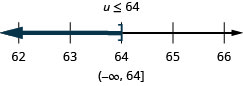
    u أقل من أو يساوي 64. يحتوي الحل الموجود على خط الأرقام على قوس أيمن عند 64 مع تظليل على اليسار. الحل في الترميز الفاصل الزمني هو سالب اللانهاية إلى 64 داخل الأقواس والقوس.

    ستستغرق معظم حالات عدم المساواة أكثر من خطوة لحلها. نتبع نفس الخطوات التي استخدمناها في الإستراتيجية العامة لحل المعادلات الخطية، ولكن تأكد من الانتباه جيدًا عند الضرب أو القسمة لعزل المتغير.

     

    حل عدم المساواة\(6y\leq 11y+17\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    إجابة
      .
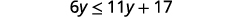
    اطرح 11y11y من كلا الجانبين لجمع المتغيرات
    الموجودة على اليسار.    		 .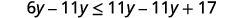
    قم بالتبسيط. .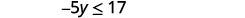
    قسّم كلا جانبي عدم المساواة على −5، −5،
    وقم بعكس عدم المساواة.    		 .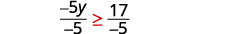
    قم بالتبسيط. .
    ارسم حلًا بيانيًا على خط الأعداد. .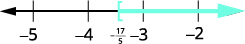
    اكتب الحل بالتدوين الفاصل الزمني. .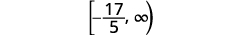
     

    حل عدم المساواة، ورسم الحل على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني:\(3q\geq 7q−23\).

    إجابة

    q أقل من أو يساوي 23 مقسومًا على 4. يحتوي الحل الموجود على خط الأعداد على قوس أيمن عند 23 مقسومًا على 4 مع تظليل على اليسار. الحل في الترميز الفاصل الزمني هو اللانهاية السالبة إلى 23 مقسومًا على 4 داخل قوس وقوس.

    مثال\(\PageIndex{15}\)

    حل عدم المساواة، ورسم الحل على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني:\(6x<10x+19\).

    إجابة

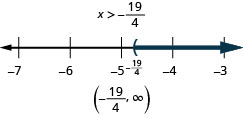
    x أكبر من سالب 19 مقسومًا على 4. يحتوي الحل الموجود على خط الأعداد على قوس يساري عند سالب 19 مقسومًا على 4 مع التظليل إلى اليمين. الحل في الترقيم الفاصل هو سالب 19 مقسومًا على 4 إلى ما لا نهاية بين قوسين.

    عند حل عدم المساواة، يكون من الأسهل عادةً جمع المتغيرات على الجانب الذي يكون فيه معامل المتغير أكبر. هذا يزيل المعاملات السلبية وبالتالي لا يتعين علينا الضرب أو القسمة على سالب - مما يعني أننا لسنا بحاجة إلى تذكر عكس علامة عدم المساواة.

    مثال\(\PageIndex{16}\)

    حل عدم المساواة\(8p+3(p−12)>7p−28\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    إجابة
      \(8p+3(p−12)>7p−28\)
    قم بتبسيط كل جانب قدر الإمكان.  
    توزيع. \(8p+3p−36>7p−28\)
    اجمع بين المصطلحات المتشابهة. \(11p−36>7p−28\)
    اطرح\(7p\) من كلا الجانبين لجمع
    المتغيرات الموجودة على اليسار، منذ ذلك الحين\(11>7\).    		 \(11p−36−7p>7p−28−7p\)
    قم بالتبسيط. \(4p−36>−28\)
    أضف\(36\) إلى كلا الجانبين لجمع
    الثوابت على اليمين.    		 \(4p−36+36>−28+36\)
    قم بالتبسيط. \(4p>8\)
    قسّم جانبي عدم المساواة على النحو التالي
    \(4\)؛ يبقى عدم المساواة على حاله.    		 \(\dfrac{4p}{4}>\dfrac{8}{4}\)
    قم بالتبسيط. \(p>2\)
    ارسم حلًا بيانيًا على خط الأعداد. .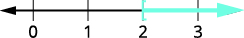
    اكتب الحل بالتدوين الفاصل الزمني. \((2,\infty)\)
    مثال\(\PageIndex{17}\)

    حل عدم المساواة\(9y+2(y+6)>5y−24\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    إجابة

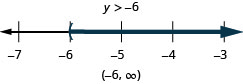
    y أكبر من سالب 6. يحتوي الحل الموجود على خط الأعداد على قوس يساري عند سالب 6 مع التظليل إلى اليمين. الحل في الترميز الفاصل هو سالب 6 إلى اللانهاية بين قوسين.

    مثال\(\PageIndex{18}\)

    حل عدم المساواة\(6u+8(u−1)>10u+32\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    إجابة

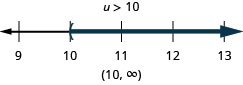
    u أكبر من سالب 10. يحتوي الحل الموجود على خط الأعداد على قوس يسار عند 10 مع تظليل إلى اليمين. الحل في الترميز الفاصل الزمني هو 10 إلى ما لا نهاية بين قوسين.

    تمامًا مثل بعض المعادلات عبارة عن هويات وبعضها تناقضات، قد تكون أوجه عدم المساواة هويات أو تناقضات أيضًا. نحن ندرك هذه الأشكال عندما يتبقى لنا ثوابت فقط أثناء حل عدم المساواة. إذا كانت النتيجة عبارة صحيحة، فلدينا هوية. إذا كانت النتيجة عبارة خاطئة، فلدينا تناقض.

    مثال\(\PageIndex{19}\)

    حل عدم المساواة\(8x−2(5−x)<4(x+9)+6x\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    إجابة
    قم بتبسيط كل جانب قدر الإمكان.   \(8x−2(5−x)<4(x+9)+6x\)
    توزيع.   \(8x−10+2x<4x+36+6x\)
    اجمع بين المصطلحات المتشابهة.   \(10x−10<10x+36\)
    اطرح\({\color{red}{10x}}\) من كلا الجانبين لتجميع المتغيرات الموجودة على اليسار.   \(10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}\)
    قم بالتبسيط.   \(−10<36\)
    لقد ذهبوا، ولدينا
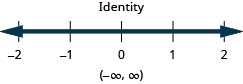
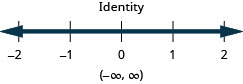
    بيان حقيقي.\(x\)    		   عدم المساواة هي هوية.
    الحل هو جميع الأرقام الحقيقية.
    ارسم حلًا بيانيًا على خط الأعداد.   .
    اكتب الحل بالتدوين الفاصل الزمني.   \((−\infty,\infty)\)
    مثال\(\PageIndex{20}\)

    حل عدم المساواة\(4b−3(3−b)>5(b−6)+2b\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    إجابة

    عدم المساواة هي هوية. يتم تظليل الحل الخاص به على خط الأعداد لجميع القيم. الحل في الترميز الفاصل الزمني هو سالب اللانهاية إلى اللانهاية بين قوسين.

    مثال\(\PageIndex{21}\)

    حل عدم المساواة\(9h−7(2−h)<8(h+11)+8h\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    إجابة

    عدم المساواة هي هوية. يتم تظليل الحل الخاص به على خط الأعداد لجميع القيم. الحل في الترميز الفاصل الزمني هو سالب اللانهاية إلى اللانهاية بين قوسين.

    يمكننا مسح الكسور في المتباينات بقدر ما فعلنا في المعادلات. مرة أخرى، كن حذرًا مع العلامات عند الضرب أو القسمة على السالب.

    مثال\(\PageIndex{22}\)

    حل عدم المساواة\(\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    إجابة
      \(\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}\)
    اضرب كلا الجانبين في شاشة LCD، 24،
    لمسح الكسور.    		 \({\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)\)
    قم بالتبسيط. \( 8a - 3a > 5a + 18 \)
    اجمع بين المصطلحات المتشابهة. \( 5a > 5a + 18\)
    اطرح\(5a\) من كلا الجانبين لتجميع
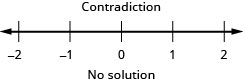
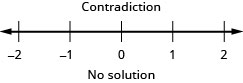
    المتغيرات الموجودة على اليسار.    		 \( 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18\)
    قم بالتبسيط. \(0 > 18 \)
    العبارة خاطئة. عدم المساواة هو تناقض.
    لا يوجد حل.
    ارسم حلًا بيانيًا على خط الأعداد. .
    اكتب الحل بالتدوين الفاصل الزمني. لا يوجد حل.
    مثال\(\PageIndex{23}\)

    حل عدم المساواة\(\frac{1}{4}x−\frac{1}{12}x>\frac{1}{6}x+\frac{7}{8}\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    إجابة

    عدم المساواة هو تناقض. لذلك، لا يوجد حل. ونتيجة لذلك، لا يوجد رسم بياني على خط الأرقام أو الترميز الفاصل الزمني.

    مثال\(\PageIndex{24}\)

    حل عدم المساواة\(\frac{2}{5}z−\frac{1}{3}z<\frac{1}{15}z−\frac{3}{5}\)، ورسم الحل بيانيًا على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    إجابة

    عدم المساواة هو تناقض. لذلك، لا يوجد حل. ونتيجة لذلك، لا يوجد رسم بياني على خط الأرقام أو الترميز الفاصل الزمني.

    ترجم إلى عدم المساواة وحلّها

    لترجمة الجمل الإنجليزية إلى تفاوتات، نحتاج إلى التعرف على العبارات التي تشير إلى عدم المساواة. بعض الكلمات سهلة، مثل «أكثر من» و «أقل من». لكن البعض الآخر ليس واضحًا. يعرض الجدول بعض العبارات الشائعة التي تشير إلى عدم المساواة.

    \(>\) \(\geq\) \(<\) \(\leq\)
    \ (>\) ">\)» data-valign= «middle» class="lt-math-17389">أكبر من أكبر مما



    يتجاوزه

    		 \ (\ geq\)» data-valign= «middle">أكبر من أو



    يساوي على الأقل لا يقل عن

    الحد الأدنى    		 \ <\)» data-valign="middle"> أقل من

    الأصغر من

    الأقل من

    الأقل من    		 \ (\ leq\)» data-valign= «middle">أقل من أو

    يساوي على الأكثر

    وليس أكثر من

    الحد الأقصى
    مثال\(\PageIndex{25}\)

    قم بالترجمة والحل. ثم قم برسم الحل على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    \[\text{Twenty-seven less than }x\text{ is at least }48.\nonumber\]

    إجابة
      .
    ترجم. \(x - 27 \geq 48\)
    الحل - أضف 27 إلى كلا الجانبين. \( x - 27 \, {\color{red}{+\, 27}} \geq 48 \, {\color{red}{+\, 27}}\)
    قم بالتبسيط. \(x \geq 75\)
    رسم بياني على خط الأعداد. .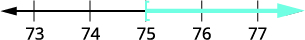
    اكتب بالتدوين الفاصل الزمني. \([75, \infty)\)
     

    قم بالترجمة والحل. ثم قم برسم الحل على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    \[\text{Nineteen less than } p \text{ is no less than }47.\nonumber\]

    إجابة

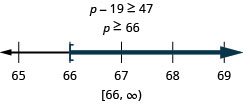
    p ناقص 19 أكبر من أو يساوي 47. حلها هو p أكبر من أو يساوي 66. يحتوي الحل الموجود على خط الأرقام على قوس يساري عند 66 مع تظليل إلى اليمين. الحل في الترميز الفاصل الزمني هو 66 إلى ما لا نهاية داخل قوس وقوس.

    مثال\(\PageIndex{27}\)

    قم بالترجمة والحل. ثم قم برسم الحل على خط الأعداد، واكتب الحل بالتدوين الفاصل الزمني.

    \[\text{Four more than }a\text{ is at most }15.\nonumber\]

    إجابة

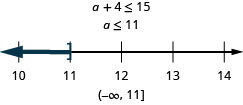
    زائد 4 أقل من أو يساوي 15. الحل الخاص به هو أقل من أو يساوي 11. يحتوي الحل الموجود على خط الأرقام على قوس أيمن عند 11 مع التظليل على اليسار. الحل في الترميز الفاصل الزمني هو سالب اللانهاية إلى 11 داخل الأقواس والقوس.

    حل التطبيقات ذات المتباينات الخطية

    تتطلب العديد من مواقف الحياة الواقعية حل عدم المساواة. الطريقة التي سنستخدمها لحل التطبيقات ذات التفاوتات الخطية تشبه إلى حد كبير الطريقة التي استخدمناها عندما قمنا بحل التطبيقات باستخدام المعادلات.

    سنقرأ المشكلة ونتأكد من فهم جميع الكلمات. بعد ذلك، سنحدد ما نبحث عنه ونخصص متغيرًا لتمثيله. سنعيد ذكر المشكلة في جملة واحدة لتسهيل ترجمتها إلى عدم المساواة. ثم سنحل عدم المساواة.

    في بعض الأحيان يتطلب التطبيق أن يكون الحل رقمًا صحيحًا، لكن الحل الجبري لعدم المساواة ليس رقمًا صحيحًا. في هذه الحالة، يجب علينا تقريب الحل الجبري إلى عدد صحيح. سيحدد سياق التطبيق ما إذا كنا نقوم بالتقريب لأعلى أم لأسفل.

    مثال\(\PageIndex{28}\)

    فازت داون بمنحة صغيرة قدرها 4,000 دولار لشراء أجهزة كمبيوتر لوحية لفصلها الدراسي. تبلغ تكلفة الأجهزة اللوحية التي ترغب في شرائها 254.12 دولارًا لكل منها، بما في ذلك الضرائب والتسليم. ما هو الحد الأقصى لعدد الأجهزة اللوحية التي يمكن لـ Dawn شراؤها؟

    إجابة

    \(\begin{array} {ll} {\textbf{Step 1. Read }\text{ the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the maximum number of tablets Dawn can buy}} \\ {\textbf{Step 3. Name}\text{ what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }n= \text{ the number of tablets.}} \\ {\text{Choose a variable to represent that}} &{} \\{\text{quantity.}} &{} \\ {\textbf{Step 4. Translate.}\text{Write a sentence that gives the}} &{} \\ {\text{information to find it.}} &{$254.12\text{ times the number of tablets is}} \\ {} &{\text{no more than }$4,000.} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space 254.12n\leq 4000} \\ {\text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15.74} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15} \\{\text{But }n\text{ must be a whole number of}} &{} \\ {\text{tablets, so round to }15.} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{Rounding down the price to } $250, 15} &{} \\ {\space\space\space \text{tablets would cost }$3,750,\text{ while } 16} &{} \\ {\space\space\space \text{tablets would be }$4,000.\text{So a}} &{} \\ {\space\space\space \text{maximum of 15 tablets at }$254.12} &{} \\ {\space\space\space \text{seems reasonable.}} &{} \\ {\textbf{Step 7. Answer }\text{the question with a complete sentence.}} &{\text{Dawn can buy a maximum of 15 tablets.}} \\ \end{array}\)

    مثال\(\PageIndex{29}\)

    لدى أنجي 20 دولارًا لإنفاقها على علب العصير لنزهة ابنها في مرحلة ما قبل المدرسة. تبلغ تكلفة كل علبة من علب العصير 2.63 دولارًا. ما هو الحد الأقصى لعدد الباقات التي يمكنها شراؤها؟

    إجابة

    يمكن لـ Angie شراء 7 عبوات من العصير.

    مثال\(\PageIndex{30}\)

    يريد دانيال مفاجأة صديقته بحفلة عيد ميلاد في مطعمها المفضل. تبلغ تكلفة العشاء 42.75 دولارًا للشخص الواحد، بما في ذلك الإكرامية والضرائب. تبلغ ميزانيته للحفلة 500 دولار. ما هو الحد الأقصى لعدد الأشخاص الذين يمكن أن يستضيفهم دانيال في الحفلة؟

    إجابة

    يمكن أن يكون لدى دانيال 11 شخصًا في الحفلة.

    مثال\(\PageIndex{31}\)

    تكلفها خطة هاتف تاليشا 28.80 دولارًا شهريًا بالإضافة إلى 0.20 دولارًا لكل رسالة نصية. كم عدد الرسائل النصية التي يمكنها إرسالها/تلقيها والاحتفاظ بفاتورة هاتفها الشهرية بما لا يزيد عن 50 دولارًا؟

    إجابة

    \(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of text messages Taleisha can make}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }t= \text{the number of text messages.}} \\ {\text{Choose a variable to represent that}} &{} \\ {\text{quantity.}} &{} \\ {\textbf{Step 4. Translate }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$28.80\text{ plus }$0.20\text{ times the number of}} \\ {} &{\text{text messages is less than or equal to }$50.} \\ {} &{28.80+0.20t \leq 50} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 0.2t\leq 21.2} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space t\leq 106\text{ text messages}} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\{\space\space\space \text{Yes, }28.80+0.20(106)=50.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{} \\ {} &{\text{Taleisha can send/receive no more than}} \\ {} &{106\text{ text messages to keep her bill no}} \\ {} &{\text{more than } $50.} \\ \end{array}\)

    مثال\(\PageIndex{32}\)

    لدى سيرجيو وليزيث ميزانية عطلة ضيقة للغاية. إنهم يخططون لاستئجار سيارة من شركة تتقاضى 75 دولارًا في الأسبوع بالإضافة إلى 0.25 دولارًا للميل. كم عدد الأميال التي يمكنهم قطعها خلال الأسبوع مع الاحتفاظ بميزانية 200 دولار؟

    إجابة

    لا يمكن لسيرجيو وليزيث السفر لأكثر من 500 ميل.

    مثال\(\PageIndex{33}\)

    تبلغ فاتورة التدفئة الخاصة بـ Rameen 5.42 دولارًا شهريًا بالإضافة إلى 1.08 دولارًا لكل فصل حراري. كم عدد الترمس الذي يمكن لرامين استخدامه إذا كان يريد أن تكون فاتورة التدفئة بحد أقصى 87.50 دولارًا.

    إجابة

    تبلغ فاتورة التدفئة الخاصة بـ Rameen 5.42 دولارًا شهريًا بالإضافة إلى 1.08 دولارًا لكل فصل حراري. كم عدد الترمس الذي يمكن لرامين استخدامه إذا كان يريد أن تكون فاتورة التدفئة بحد أقصى 87.50 دولارًا.

    الربح هو المال المتبقي عندما يتم خصم التكاليف من الإيرادات. في المثال التالي، سنجد عدد الوظائف التي تحتاج سيدة أعمال صغيرة إلى القيام بها كل شهر من أجل تحقيق قدر معين من الربح.

    مثال\(\PageIndex{34}\)

    فيليسيتي لديها شركة في مجال الخط. تتقاضى 2.50 دولارًا لكل دعوة زفاف. مصروفاتها الشهرية هي 650 دولارًا. كم عدد الدعوات التي يجب أن تكتبها لتحقيق ربح لا يقل عن 2,800 دولار شهريًا؟

    إجابة

    \(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of invitations Felicity needs to write}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{\text{Let }j=\text{ the number of invitations.}} \\ {} &{} \\ {\space\space\space\text{Choose a variable to represent it.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$2.50 \text{ times the number of invitations}} \\ {} &{\text{minus }$650\text{ is at least }$2,800.} \\ {} &{\space\space\space 2.50j−650\geq 2,800} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 2.5j\geq 3,450} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space j\geq 1,380 \text{ invitations}} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{If Felicity wrote }1400\text{ invitations, her}} &{} \\ {\space\space\space \text{profit would be }2.50(1400)−650, \text{or}} &{} \\ {\space\space\space $2,850.\text{ This is more than }$2800.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Felicity must write at least }1,380\text{ invitations.}} \\ \end{array}\)

    مثال\(\PageIndex{35}\)

    لدى كاليب شركة لتربية الحيوانات الأليفة. يتقاضى 32 دولارًا في الساعة. نفقاته الشهرية هي 2272 دولارًا. كم ساعة يجب أن يعمل من أجل تحقيق ربح لا يقل عن 800 دولار شهريًا؟

    إجابة

    يجب أن يعمل كاليب 96 ساعة على الأقل.

    مثال\(\PageIndex{36}\)

    لدى Elliot أعمال صيانة المناظر الطبيعية. نفقاته الشهرية هي 1,100 دولار. إذا كان يتقاضى 60 دولارًا لكل وظيفة، فكم عدد الوظائف التي يجب أن يقوم بها لكسب ربح لا يقل عن 4,000 دولار شهريًا؟

    إجابة

    يجب أن يعمل Elliot على الأقل 85 وظيفة.

    هناك العديد من الحالات التي تساهم فيها عدة كميات في إجمالي النفقات. يجب أن نتأكد من حساب جميع النفقات الفردية عندما نحل مشاكل مثل هذه.

    مثال\(\PageIndex{37}\)

    يخطط مالك لرحلة إجازة صيفية لمدة ستة أيام. لديه 840 دولارًا من المدخرات، ويكسب 45 دولارًا في الساعة مقابل الدروس الخصوصية. ستكلفه الرحلة 525 دولارًا للسفر بالطائرة، و 780 دولارًا للطعام ومشاهدة المعالم السياحية، و 95 دولارًا في الليلة للفندق. كم عدد الساعات التي يجب أن يعلمها للحصول على ما يكفي من المال لدفع ثمن الرحلة؟

    إجابة

    \(\begin{array} {ll} {} &{} \\ {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of hours Malik must tutor}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }h=\text{ the number of hours.}} \\ {\space\space\space\space\space\space\space \text{Choose a variable to represent that}} &{} \\ {\space\space\space\space\space\space\space \text{quantity.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{} \\ {} &{\text{The expenses must be less than or equal to}} \\{} &{\text{the income. The cost of airfare plus the}} \\{} &{\text{cost of food and sightseeing and the hotel}} \\{} &{\text{bill must be less than the savings plus the}} \\{} &{\text{amount earned tutoring.}} \\{} &{} \\ {} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space \text{Translate into an inequality.}} &{525+780+95(6)\leq 840+45h} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,875\leq 840+45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,035\leq 45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 23\leq h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space h\geq 23} \\ {} &{} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {\text{We substitute 23 into the inequality.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45h} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45(23)} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 1875} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Malik must tutor at least }23\text{ hours.}} \\ \end{array}\)

    مثال\(\PageIndex{38}\)

    ستقيم أفضل صديقة لبريندا حفل زفاف في الوجهة وسيستمر الحدث ثلاثة أيام. لدى بريندا 500 دولار من المدخرات ويمكنها كسب 15 دولارًا في الساعة من مجالسة الأطفال. وتتوقع أن تدفع 350 دولارًا أمريكيًا للسفر بالطائرة، و375 دولارًا للطعام والترفيه، و60 دولارًا في الليلة مقابل حصتها من غرفة فندق. كم عدد الساعات التي يجب أن تجالسها للحصول على ما يكفي من المال لدفع ثمن الرحلة؟

    إجابة

    يجب على بريندا رعاية الأطفال لمدة 27 ساعة على الأقل.

    مثال\(\PageIndex{39}\)

    يريد Josue الذهاب في رحلة برية لمدة 10 ليالٍ مع الأصدقاء في الربيع المقبل. سيكلفه 180 دولارًا للغاز، و 450 دولارًا للطعام، و 49 دولارًا في الليلة لمشاركة غرفة في فندق. لديه 520 دولارًا في المدخرات ويمكنه كسب 30 دولارًا لكل ممر يجرف الثلج. كم عدد الممرات التي يجب أن يجارفها للحصول على ما يكفي من المال لدفع ثمن الرحلة؟

    إجابة

    يجب على Josue تجريف 20 ممرًا على الأقل.

    المفاهيم الرئيسية

    • المتباينات وخطوط الأعداد وتدوين الفواصل
      \(x>a \quad x\geq a\quad x<a\quad x\leq a\)
      يوضح الشكل أن حل عدم المساواة x أكبر من a يشار إليه في خط الأرقام مع وجود قوسين يساريين عند a وتظليل إلى اليمين، وأن الحل في الترميز الفاصل الزمني هو الفاصل الزمني من a إلى اللانهاية المحاط بين قوسين. يُظهر حل عدم المساواة x أكبر من أو يساوي a كما هو موضح في خط الأرقام مع وجود قوس يساري عند a وتظليل إلى اليمين، وأن الحل في الترميز الفاصل الزمني هو الفاصل الزمني من a إلى اللانهاية داخل القوس الأيسر والقوس الأيمن. يُظهر أن حل عدم المساواة x أقل من a يشار إليه في خط الأرقام مع وجود قوس أيمن عند a وتظليل إلى اليسار، وأن الحل في الترميز الفاصل الزمني هو الفاصل الزمني اللانهاية السالبة إلى a داخل الأقواس. يُظهر أن حل عدم المساواة x أقل من أو يساوي a يشار إليه على خط الأرقام مع القوس الأيمن عند a والتظليل إلى اليسار، وأن الحل في الترميز الفاصل الزمني هو اللانهاية السالبة إلى a داخل الأقواس اليسرى والقوس الأيمن.
    • عدم المساواة الخطية
      • عدم المساواة الخطية هي عدم مساواة في متغير واحد يمكن كتابته بأحد الأشكال التالية حيث تكون a و b و c أرقامًا حقيقية و\(a\neq 0\):

        \[ax+b<c, \qquad ax+b\leq c, \qquad ax+b>c, \qquad ax+b\geq c.\nonumber\]

    • خاصية الجمع والطرح في عدم المساواة
      • بالنسبة لأي أرقام a و b و c، إذا كانت a <b، ثم <b، ثم

        \[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \end{array} \nonumber\]

      • يمكننا إضافة أو طرح نفس الكمية من كلا جانبي عدم المساواة مع الحفاظ على عدم المساواة.
    • خاصية الضرب والقسمة لعدم المساواة
      • لأي أرقام أ، ب، ج،
        \(\begin{array} {l} \text{multiply or divide by a }\textbf{positive} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c>0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c>0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \text{multiply or divide by a }\textbf{negative} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c<0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c<0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \end{array}\)
    • العبارات التي تشير إلى عدم المساواة
      \(>\) \(\geq\) \(<\) \(\leq\)
      \ (>\) ">أكبر

      من الأكبر

      من

      التجاوز      		 \ (\ geq\)» data-valign= «middle">أكبر من أو



      يساوي على الأقل لا يقل عن

      الحد الأدنى      		 \ <\)» data-valign="middle"> أقل من

      الأصغر من

      الأقل من

      الأقل من      		 \ (\ leq\)» data-valign= «middle">أقل من أو

      يساوي على الأكثر

      وليس أكثر من

      الحد الأقصى