Skip to main content
Global

2.5: حل تطبيقات المزيج والحركة المنتظمة

  1. Last updated
  2. Save as PDF
  • Page ID
    201753

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    أهداف التعلم

    في نهاية هذا القسم، ستكون قادرًا على:

    • حل مشاكل الكلمات النقدية
    • حل مشاكل التذاكر وكلمات الختم
    • حل مشاكل الكلمات المختلطة
    • حل تطبيقات الحركة الموحدة

    قبل البدء، قم بإجراء اختبار الاستعداد هذا.

    1. قم بالتبسيط:\(0.25x+0.10(x+4)\).
      إذا فاتتك هذه المشكلة، راجع [link].
    2. عدد تذاكر البالغين يزيد بثلاثة أضعاف عن ضعف عدد تذاكر الأطفال. دعونا نمثل عدد تذاكر الأطفال. اكتب تعبيرًا عن عدد تذاكر البالغين.
      إذا فاتتك هذه المشكلة، راجع [link].
    3. قم بتحويل 4.2% إلى رقم عشري.
      إذا فاتتك هذه المشكلة، راجع [link].

    حل مشاكل الكلمات النقدية

    قد يبدو استخدام الجبر للعثور على عدد النيكل والبنسات في حصالة على شكل أصبع أمرًا سخيفًا. قد تتساءل لماذا لا نفتح البنك ونعدها. لكن هذا النوع من المشاكل يقدم لنا بعض التقنيات التي ستكون مفيدة ونحن نمضي قدمًا في دراستنا للرياضيات.

    صورة عملات معدنية؛ أكوام منفصلة من النيكل والبنسات والأرباع والدايمات

    إذا كانت لدينا كومة من الدايمات، فكيف سنحدد قيمتها؟ إذا قمنا بحساب عدد الدايمات، فسوف نعرف عدد الدايمات لدينا - عدد الدايمات. لكن هذا لا يخبرنا بقيمة كل الدايمات. لنفترض أننا أحصينا 23 ديمًا، كم تبلغ قيمتها؟ كل عشرة سنتات تساوي 0.10 دولار - وهي قيمة الدايم الواحد. للعثور على القيمة الإجمالية للكومة المكونة من 23 ديمًا، اضرب 23 في 0.10 دولارًا للحصول على 2.30 دولارًا.

    عدد الدايمات مضروبًا في قيمة كل عشرة سنتات يساوي القيمة الإجمالية للدايمات.

    \[\begin{align} \textit{number}·\textit{value} &= \textit{total value} \nonumber\\ 23·$0.10 &= $2.30 \nonumber\\ \end{align} \nonumber\]

    تؤدي هذه الطريقة إلى النموذج التالي.

    القيمة الإجمالية للعملات

    بالنسبة لنفس النوع من العملات، يتم العثور على القيمة الإجمالية لعدد من العملات باستخدام النموذج

    \[\textit{number}·\textit{value}=\textit{total value} \nonumber \]

    • الرقم هو عدد العملات
    • القيمة هي قيمة كل عملة
    • القيمة الإجمالية هي القيمة الإجمالية لجميع العملات

    إذا كان لدينا عدة أنواع من العملات، فيمكننا متابعة هذه العملية لكل نوع من أنواع العملات، ومن ثم سنعرف القيمة الإجمالية لكل نوع من أنواع العملات. للحصول على القيمة الإجمالية لجميع العملات، أضف القيمة الإجمالية لكل نوع من العملات.

    مثال\(\PageIndex{1}\)

    يمتلك جيسي ما قيمته 3.02 دولارًا من البنسات والنيكل في بنكه. يزيد عدد النيكل بثلاثة أضعاف عن ثمانية أضعاف عدد البنسات. كم عدد النيكل وعدد البنسات التي يمتلكها جيسي؟

    إجابة
    الخطوة 1. اقرأ المشكلة.
    حدد أنواع العملات المعنية.
    قم بإنشاء جدول.
    اكتب قيمة كل نوع من العملات.
    تبلغ قيمة

    البنسات والنيكل 0.10 دولارًا.
    تبلغ قيمة النيكل 0.05 دولار.
    الخطوة 2. حدد ما نبحث عنه. عدد البنسات والنيكل
    الخطوة 3. اسم. قم بتمثيل رقم كل نوع من العملات باستخدام المتغيرات.
    يتم تعريف عدد النيكل من حيث
    عدد البنسات، لذا ابدأ بالقروش.
    يزيد عدد النيكل بثلاثة أضعاف عن ثمانية أضعاف
    عدد البنسات.

    دع\(p=\) عدد البنسات.

    \(8p+3=\)عدد النيكل
    في المخطط، اضرب الرقم والقيمة
    للحصول على القيمة الإجمالية لكل نوع من أنواع العملات.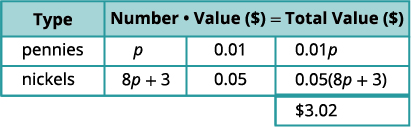
    .
    الخطوة 4. ترجم. اكتب المعادلة بإضافة القيمة الإجمالية لجميع أنواع العملات.
    .
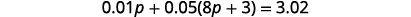
    الخطوة 5. حل المعادلة. .
    كم عدد النيكل؟ .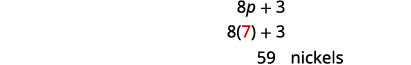

    الخطوة 6. تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
    جيسي لديه 7 بنسات و 59 نيكل.
    هل القيمة الإجمالية\($3.02\)؟

    \(\begin{align} 7(0.01)+59(0.05) &\overset{?}{=} 3.02 \nonumber \\ 3.02 &= 3.02\checkmark \nonumber \\ \end{align}\)
    مثال\(\PageIndex{2}\)

    يمتلك جيسي ما قيمته 6.55 دولارًا من الأرباع والنيكل في جيبه. يزيد عدد النيكل بخمسة أضعاف عدد الأرباع. كم عدد النيكل وعدد الأرباع التي يمتلكها جيسي؟

    إجابة

    يمتلك جيس 41 نيكل و 18 ربعًا.

    مثال\(\PageIndex{3}\)

    تمتلك إيلين 7.00 دولارًا إجماليًا من الدايمات والنيكل في جرة العملات الخاصة بها. يقل عدد الدايمات التي تمتلكها Elane بسبعة عن ثلاثة أضعاف عدد النيكل. كم عدد كل عملة تمتلكها إيلين؟

    إجابة

    تمتلك إيلين 22 نيكلًا و 59 ديمًا.

    يتم تلخيص خطوات حل مشكلة كلمة العملة أدناه.

    حل مشاكل الكلمات النقدية.
    1. اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
      • حدد أنواع العملات المعنية.
      • قم بإنشاء جدول لتنظيم المعلومات.
        • قم بتسمية الأعمدة «النوع» و «الرقم» و «القيمة» و «القيمة الإجمالية».
        • ضع قائمة بأنواع العملات.
        • اكتب قيمة كل نوع من العملات.
        • اكتب القيمة الإجمالية لجميع العملات.
        • يحتوي هذا المخطط على عمودين وأربعة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الأول «النوع» والعمود الثاني «الرقم مضروبًا في القيمة بالدولار يساوي إجمالي القيمة بالدولار». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «الرقم» و «القيمة» و «القيمة الإجمالية». يحتوي عمود القيمة الإجمالية على صف إضافي. المخطط فارغ.
    2. حدد ما تبحث عنه.
    3. قم بتسمية ما تبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.
      • استخدم التعبيرات المتغيرة لتمثيل رقم كل نوع من العملات وكتابتها في الجدول.
      • اضرب الرقم في القيمة للحصول على القيمة الإجمالية لكل نوع من أنواع العملات.
    4. ترجم إلى معادلة.
      • قد يكون من المفيد إعادة ذكر المشكلة في جملة واحدة مع جميع المعلومات المهمة. ثم ترجم الجملة إلى معادلة.
      • اكتب المعادلة عن طريق جمع القيم الإجمالية لجميع أنواع العملات.
    5. حل المعادلة باستخدام تقنيات الجبر الجيدة.
    6. تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
    7. أجب على السؤال بجملة كاملة.

    حل مشاكل التذاكر وختم الكلمات

    المشاكل المتعلقة بالتذاكر أو الطوابع تشبه إلى حد كبير مشاكل العملات. كل نوع من أنواع التذاكر والطوابع له قيمة، تمامًا مثل كل نوع من العملات. لذلك لحل هذه المشاكل، سنتبع نفس الخطوات التي استخدمناها لحل مشاكل العملة.

    مثال\(\PageIndex{4}\)

    دفع داني 15.75 دولارًا مقابل الطوابع. كان عدد الطوابع ذات 49 سنتًا أقل بخمسة من ثلاثة أضعاف عدد الطوابع التي تبلغ 35 سنتًا. كم عدد الطوابع ذات الـ 49 سنتًا وكم عدد الطوابع ذات الـ 35 سنتًا التي اشتراها داني؟

    إجابة
    الخطوة 1. حدد أنواع الطوابع المعنية. طوابع 49 سنتًا وطوابع 35 سنتًا
    الخطوة 2. الهوية التي نبحث عنها. عدد الطوابع ذات 49 سنتًا وعدد الطوابع التي تبلغ 35 سنتًا
    الخطوة 3. اكتب تعبيرات متغيرة لتمثيل رقم كل نوع من أنواع الطوابع. Let x = عدد الطوابع ذات 35 سنتًا.
    «كان عدد الطوابع ذات 49 سنتًا
    أقل بخمسة من ثلاثة أضعاف عدد
    الطوابع البالغ 35 سنتًا.»
    3x−5=3x−5= عدد الطوابع ذات 49 سنتًا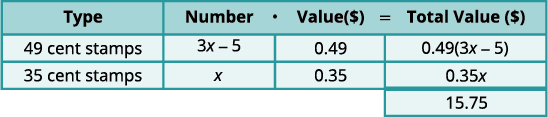
    .
    الخطوة 4. اكتب المعادلة من القيم الإجمالية. .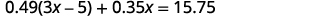
    الخطوة 5. حل المعادلة. .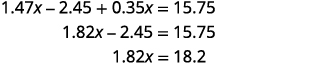
    كم عدد الطوابع ذات الـ 49 سنتًا؟ .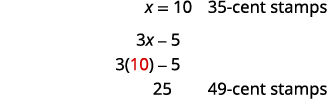
    الخطوة 6. تحقق.
    10 (0.35) +25 (0.49) 3.50+12.2515.75 =؟ =؟ =15.7515.7515.75 ✓ 10 (0.35) +25 (0.49) =؟ 15.753.50+12.25 =؟ 15.7515.75 = 15.75 ✓    		  
    الخطوة 7. أجب على السؤال بجملة كاملة. اشترى داني عشرة طوابع 35 سنتًا وخمسة وعشرين طابعًا 49 سنتًا.
    مثال\(\PageIndex{5}\)

    دفع إريك 19.88 دولارًا مقابل الطوابع. كان عدد الطوابع ذات 49 سنتًا ثمانية أكثر من ضعف عدد الطوابع التي تبلغ 35 سنتًا. كم عدد الطوابع ذات الـ 49 سنتًا وكم عدد الطوابع ذات الـ 35 سنتًا التي اشتراها إريك؟

    إجابة

    اشترى إريك اثنين وثلاثين طابعًا من 49 سنتًا واثني عشر طابعًا بسنتًا.

    مثال\(\PageIndex{6}\)

    دفعت كايلي 14.74 دولارًا مقابل الطوابع. كان عدد الطوابع ذات 49 سنتًا أقل بأربعة من ثلاثة أضعاف عدد الطوابع البالغة 20 سنتًا. كم عدد الطوابع ذات الـ 49 سنتًا وكم عدد الطوابع ذات الـ 20 سنتًا التي اشترتها كايلي؟

    إجابة

    اشترت كايلي ستة وعشرين طابعًا من 49 سنتًا وعشرة طوابع بقيمة 20 سنتًا.

    في معظم الأمثلة حتى الآن، قيل لنا أن كمية واحدة تزيد بأربعة عن ضعف الأخرى، أو شيء مشابه. في المثال التالي، يتعين علينا ربط الكميات بطريقة مختلفة.

    لنفترض أن Aniket باعت ما مجموعه 100 تذكرة. كانت كل تذكرة إما تذكرة للبالغين أو تذكرة طفل. إذا باع 20 تذكرة أطفال، كم عدد تذاكر البالغين التي باعها؟

    هل قلت «80"؟ كيف اكتشفت ذلك؟ هل قمت بطرح 20 من 100؟

    إذا باع 45 تذكرة أطفال، كم عدد تذاكر البالغين التي باعها؟

    هل قلت «55"؟ كيف وجدتها؟ بطرح 45 من 100؟

    الآن، لنفترض أن أنيكي باعت تذاكر للأطفال. إذن كم عدد تذاكر البالغين التي باعها؟ لمعرفة ذلك، سنتبع نفس المنطق الذي استخدمناه أعلاه. في كل حالة، قمنا بطرح عدد تذاكر الأطفال من 100 للحصول على عدد تذاكر البالغين. نحن الآن نفعل نفس الشيء مع x.

    لقد لخصنا هذا في الجدول.

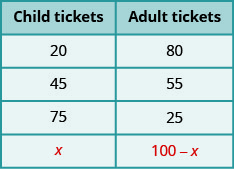
    يحتوي هذا الجدول على عمودين وأربعة صفوف. الصف الأول عبارة عن صف رئيسي ويسمي كل عمود «تذاكر الأطفال» و «تذاكر البالغين». في الصف الثاني، كان عدد تذاكر الأطفال 20 وعدد تذاكر البالغين 80. في الصف الثاني، كان عدد تذاكر الأطفال 45 وعدد تذاكر البالغين 55. في الصف الثالث، كان عدد تذاكر الأطفال x وكان عدد تذاكر البالغين 100 ناقص x.

    سنطبق هذه التقنية في المثال التالي.

    مثال\(\PageIndex{7}\)

    كانت سفينة مراقبة الحيتان تحمل 40 راكبًا يدفعون. بلغ إجمالي الإيرادات المحصلة من التذاكر 1,196 دولارًا. دفع ركاب الأجرة الكاملة 32 دولارًا لكل منهم ودفع الركاب ذوي الأجرة المخفضة 26 دولارًا لكل منهم. كم عدد ركاب الأجرة الكاملة وعدد الركاب ذوي الأجرة المخفضة الذين كانوا على متن السفينة؟

    إجابة
    الخطوة 1. حدد أنواع التذاكر المعنية. تذاكر كاملة السعر وتذاكر مخفضة السعر
    الخطوة 2. حدد ما نبحث عنه. عدد التذاكر ذات السعر الكامل والتذاكر ذات السعر المخفض
    الخطوة 3. اسم. قم بتمثيل رقم كل نوع من التذاكر باستخدام المتغيرات. Let f = عدد التذاكر ذات السعر الكامل.
    40−f=40−f= عدد التذاكر ذات السعر المخفض
    نحن نعلم أن العدد الإجمالي للتذاكر المباعة كان 40. وهذا يعني أن عدد التذاكر ذات السعر المخفض يقل بنسبة 40 عن عدد التذاكر ذات السعر الكامل.
    اضرب الرقم في القيمة للحصول على القيمة الإجمالية لكل نوع من أنواع التذاكر.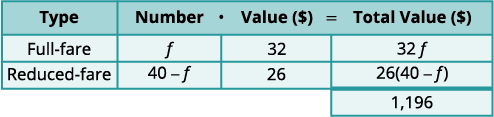    		  
      .
    الخطوة 4. ترجم. اكتب المعادلة بإضافة القيم الإجمالية لكل نوع من أنواع التذاكر. .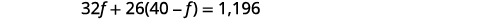
    الخطوة 5. حل المعادلة. .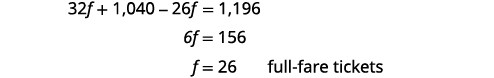
    كم عدد الأجرة المخفضة؟ .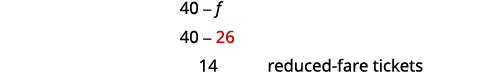
    الخطوة 6. تحقق من الإجابة.
    كانت هناك 26 تذكرة كاملة السعر بسعر 32 دولارًا لكل تذكرة و 14 تذكرة بسعر 26 دولارًا لكل تذكرة. هل القيمة الإجمالية 116 دولارًا؟
    26 · 3214 · 26=832364———1,196 ✓ 26·3214 · 26=364——1,196 ✓    		  
    الخطوة 7. أجب على السؤال. لقد باعوا 26 تذكرة كاملة و 14 تذكرة بسعر مخفض.
    مثال\(\PageIndex{8}\)

    خلال مناوبتها في كشك التذاكر بالمتحف، باعت ليا 115 تذكرة بإجمالي 1163 دولارًا. تبلغ تكلفة تذاكر البالغين 12 دولارًا وتذاكر الطلاب 5 دولارات. كم عدد تذاكر البالغين وكم عدد تذاكر الطلاب التي باعتها ليا؟

    إجابة

    84 تذكرة للبالغين، 31 تذكرة للطلاب

    مثال\(\PageIndex{9}\)

    باع جالينوس 810 تذكرة لكرنفال كنيسته بإيرادات إجمالية قدرها 2,820 دولارًا. تبلغ تكلفة تذاكر الأطفال 3 دولارات لكل منها وتذاكر البالغين 5 دولارات لكل منها. كم عدد تذاكر الأطفال وكم عدد تذاكر البالغين التي باعها؟

    إجابة

    615 تذكرة للأطفال و 195 تذكرة للبالغين

    حل مشاكل الكلمات المختلطة

    الآن سنحل بعض التطبيقات العامة لنموذج الخليط. في مشاكل الخليط، غالبًا ما نقوم بخلط كميتين، مثل الزبيب والمكسرات، لإنشاء خليط، مثل المزيج السريع. في جداولنا سيكون لدينا صف لكل عنصر ليتم خلطه بالإضافة إلى صف للمزيج النهائي.

    مثال\(\PageIndex{10}\)

    يقوم Henning بخلط الزبيب والمكسرات لصنع 25 رطلاً من المزيج السريع. تبلغ تكلفة الزبيب 4.50 دولارًا للرطل والمكسرات 8 دولارات للرطل. إذا أراد هينينغ أن تكون تكلفته لمزيج الدرب 6.60 دولارًا للرطل، فكم رطل من الزبيب وكم رطل من المكسرات يجب أن يستخدمه؟

    إجابة
    الخطوة 1. حدِّد ما يتم خلطه. سيأتي 25 رطلاً من المزيج السريع من خلط الزبيب والمكسرات.
    الخطوة 2. حدد ما نبحث عنه. عدد أرطال الزبيب والمكسرات
    الخطوة 3. قم بتمثيل رقم كل نوع من التذاكر باستخدام المتغيرات.

    كما كان من قبل، نقوم بملء مخطط لتنظيم معلوماتنا.
    نحن ندخل سعر الجنيه لكل عنصر.
    نضرب الرقم في القيمة للحصول على القيمة الإجمالية.    		 دع x=x = عدد أرطال الزبيب.
    25−x=25−x= عدد أرطال المكسرات
    .
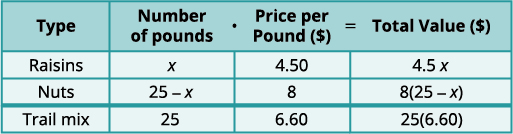
    لاحظ أن العمود الأخير في الجدول يعطي معلومات
    عن الكمية الإجمالية
    للمزيج.
    الخطوة 4. ترجم إلى معادلة. ستكون قيمة الزبيب بالإضافة إلى قيمة المكسرات
    هي قيمة مزيج الدرب.
    الخطوة 5. حل المعادلة. .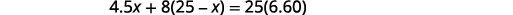
      .
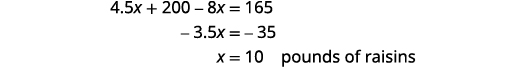
    أوجد عدد أرطال المكسرات. .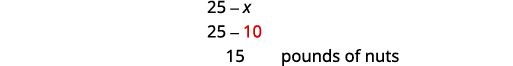
    الخطوة 6. تحقق.
    4.5 (10) +8 (15) 45+120165=? =؟ = 25 (6.60) 165165 ✓ 4.5 (10) +8 (15) =? 25 (6.60) 45+120 =؟ 165165=165 ✓    		  
    الخطوة 7. أجب على السؤال. قام هينينج بخلط عشرة أرطال من الزبيب مع 15 رطلاً من المكسرات.
    مثال\(\PageIndex{11}\)

    تقوم أورلاندو بخلط المكسرات ومربعات الحبوب لعمل مزيج احتفالي. تباع المكسرات مقابل 7 دولارات للرطل وتباع مربعات الحبوب مقابل 4 دولارات للرطل. يريد أورلاندو صنع 30 رطلاً من مزيج الحفلات بتكلفة 6.50 دولارًا للرطل، وكم رطل من المكسرات وكم رطل من مربعات الحبوب التي يجب أن يستخدمها؟

    إجابة

    خلطت أورلاندو خمسة أرطال من مربعات الحبوب و 25 رطلاً من المكسرات.

    مثال\(\PageIndex{12}\)

    تريد Becca خلط عصير الفاكهة والصودا لتحقيق النجاح. يمكنها شراء عصير الفاكهة مقابل 3 دولارات للغالون والصودا مقابل 4 دولارات للغالون. إذا كانت تريد أن تصنع 28 جالونًا من اللكمة بتكلفة 3.25 دولارًا للغالون، فكم جالون من عصير الفاكهة وكم غالون من الصودا يجب أن تشتريه؟

    إجابة

    خلطت بيكا 21 جالونًا من عصير الفاكهة وسبعة جالونات من الصودا.

    حل تطبيقات الحركة الموحدة

    عند القيادة على الطريق السريع باستخدام نظام تثبيت السرعة الخاص بك، تظل سرعة سيارتك كما هي - فهي موحدة. نسمي المشكلة التي تكون فيها سرعة الجسم ثابتة بتطبيق حركة موحدة. سنستخدم صيغة المسافة والمعدل والوقت لمقارنة سيناريوهين\(D=rt\)، مثل سيارتين تسيران بمعدلات مختلفة أو في اتجاهين متعاكسين.

    ستظل استراتيجيات حل المشكلات الخاصة بنا سارية هنا، لكننا سنضيف إلى الخطوة الأولى. ستشمل الخطوة الأولى رسم مخطط يوضح ما يحدث في المثال. يساعدنا رسم المخطط على فهم ما يحدث حتى نكتب معادلة مناسبة. ثم سنقوم بعمل جدول لتنظيم المعلومات، كما فعلنا مع تطبيقات العملات والتذاكر والطوابع.

    يتم سرد الخطوات هنا لسهولة الرجوع إليها:

    حل تطبيق الحركة الموحد.
    1. اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
      • ارسم مخططًا لتوضيح ما يحدث.
      • قم بإنشاء جدول لتنظيم المعلومات.
        • قم بتسمية معدل الأعمدة والوقت والمسافة.
        • ضع قائمة بالسيناريوهين.
        • اكتب المعلومات التي تعرفها.
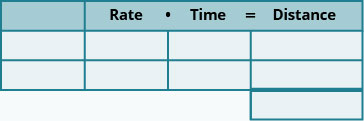
      يحتوي هذا المخطط على عمودين وأربعة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الثاني «معدل الأوقات يساوي المسافة». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «المعدل» و «الوقت» و «المسافة». يحتوي عمود المسافة على صف إضافي. المخطط فارغ.
    2. حدد ما تبحث عنه.
    3. قم بتسمية ما تبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.
      • أكمل المخطط.
      • استخدم التعبيرات المتغيرة لتمثيل تلك الكمية في كل صف.
      • اضرب المعدل في الوقت للحصول على المسافة.
    4. ترجم إلى معادلة.
      • كرر المشكلة في جملة واحدة مع جميع المعلومات المهمة.
      • ثم ترجم الجملة إلى معادلة.
    5. حل المعادلة باستخدام تقنيات الجبر الجيدة.
    6. تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
    7. أجب على السؤال بجملة كاملة.

    يحب واين ودينيس ركوب مسار الدراجات من ريفرسايد بارك إلى الشاطئ. سرعة دنيس أسرع بسبعة أميال في الساعة من سرعة واين، لذلك يستغرق واين ساعتين للركوب إلى الشاطئ بينما يستغرق دينيس 1.5 ساعة للركوب. ابحث عن سرعة كلا السائقين.

    إجابة

    الخطوة 1. اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.

    ارسم مخططًا لتوضيح ما يحدث. يظهر أدناه رسم تخطيطي لما يحدث في المثال.

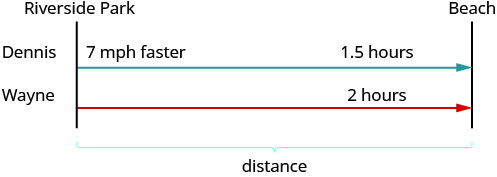    يُظهر الشكل الحركة الموحدة لرحلة دينيس وواين على طول مسار الدراجات من ريفرسايد بارك. يتم تمثيل مسار دينيس بسهم بعنوان «7 أميال في الساعة» و «1.5 ساعة». يتم تمثيل مسار Wayne بسهم ثانٍ بنفس الطول وفي نفس الاتجاه المسمى «ساعتان». يمثل القوس المسافة بين حديقة ريفرسايد والشاطئ.قم بإنشاء جدول لتنظيم المعلومات.

    • قم بتسمية الأعمدة «السعر» و «الوقت» و «المسافة».
    • ضع قائمة بالسيناريوهين.
    • اكتب المعلومات التي تعرفها.
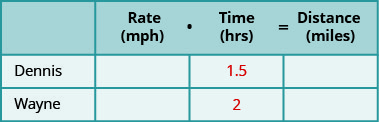
      يحتوي هذا المخطط على عمودين وثلاثة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الثاني «المعدل بالأميال لكل ساعة مضروبًا في الوقت بالساعات يساوي المسافة بالأميال». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «المعدل» و «الوقت» و «المسافة». العمود الأول عبارة عن عنوان ويسمي الصف الثاني «Dennis» والصف الثالث «Wayne». في الصف 2، الوقت هو 1.5 ساعة. في الصف 3، الوقت هو ساعتان.

    الخطوة 2. حدد ما تبحث عنه.

    يُطلب منك معرفة سرعة كلا السائقين.

    لاحظ أن صيغة المسافة تستخدم كلمة «معدل»، ولكن من الشائع استخدام «السرعة»

    عندما نتحدث عن المركبات باللغة الإنجليزية اليومية.

    الخطوة 3. اذكر ما نبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.

    أكمل المخطط استخدم التعبيرات المتغيرة لتمثيل تلك الكمية في كل صف.
    نحن نبحث عن سرعة السائقين. دعونا نمثل سرعة واين. نظرًا لأن سرعة Dennis أسرع بـ 7 ميل في الساعة، فإننا نمثل ذلك من خلال\(r+7\)
    \(\begin{align} r+7 &= \text{Dennis’ speed} \nonumber \\ r &= \text{Wayne’s speed} \nonumber \\ \end{align}\)
    ملء السرعات في المخطط.
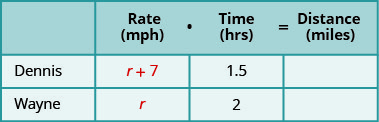
    يحتوي هذا المخطط على عمودين وثلاثة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الثاني «المعدل بالأميال لكل ساعة مضروبًا في الوقت بالساعات يساوي المسافة بالأميال». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «المعدل» و «الوقت» و «المسافة». العمود الأول عبارة عن عنوان ويسمي الصف الثاني «Dennis» والصف الثالث «Wayne». في الصف 2، يكون المعدل هو التعبير r plus 7 والوقت هو 1.5 ساعة. في الصف 3، يكون المعدل r والوقت هو ساعتان.

    اضرب المعدل في الوقت للحصول على المسافة.
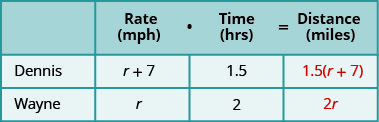
    يحتوي هذا المخطط على عمودين وثلاثة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الثاني «المعدل بالأميال لكل ساعة مضروبًا في الوقت بالساعات يساوي المسافة بالأميال». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «المعدل» و «الوقت» و «المسافة». العمود الأول عبارة عن عنوان ويسمي الصف الثاني «Dennis» والصف الثالث «Wayne». في الصف 2، يكون المعدل هو التعبير r plus 7، والوقت هو 1.5 ساعة، والمسافة هي 1.5 مرة الكمية r زائد 7. في الصف 3، يكون المعدل r، والوقت هو ساعتان، والمسافة هي 2 r.

    الخطوة 4. ترجم إلى معادلة.

    كرر المشكلة في جملة واحدة مع جميع المعلومات المهمة.

    ثم ترجم الجملة إلى معادلة.
    ستأتي معادلة تمثيل هذا الموقف من العلاقة بين المسافات. انظر إلى الرسم التخطيطي الذي رسمناه أعلاه. كيف ترتبط المسافة التي يقطعها دينيس بالمسافة التي قطعها واين؟
    نظرًا لأن كلا سائقي الدراجات يغادرون من ريفرسايد ويسافرون إلى الشاطئ، فإنهم يسافرون بنفس المسافة. لذلك نكتب:

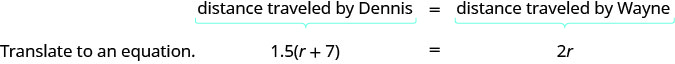
    يوضح الشكل أن المسافة التي قطعها دنيس تساوي المسافة التي قطعها واين، وعند ترجمتها إلى معادلة، تكون النتيجة 1.5 مرة الكمية r زائد 7 تساوي 2 r.

    الخطوة 5. حل المعادلة باستخدام تقنيات الجبر.

    الآن قم بحل هذه المعادلة. .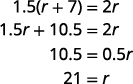
    لذا فإن سرعة واين هي 21 ميلاً في الساعة.
    ابحث عن سرعة دينيس.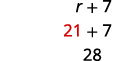

    .
    سرعة دينيس 28 ميل في الساعة.

    الخطوة 6. تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.

    \(\begin{align} \text{} &{28\text{ mph}(1.5\text{ hours}) } &= {42\text{ miles}\checkmark} \nonumber \\ \text{} &{21\text{ mph}(2\text{ hours})} &= {42\text{ miles}\checkmark} \nonumber \\ \end{align} \)

    الخطوة 7. أجب على السؤال بجملة كاملة.

    ركب واين بسرعة 21 ميلاً في الساعة وركب دينيس بسرعة 28 ميلاً في الساعة.

    كرر المشكلة في جملة واحدة مع جميع المعلومات المهمة.

    ثم ترجم الجملة إلى معادلة.
    ستأتي معادلة تمثيل هذا الموقف من العلاقة بين المسافات. انظر إلى الرسم التخطيطي الذي رسمناه أعلاه. كيف ترتبط المسافة التي يقطعها دينيس بالمسافة التي قطعها واين؟
    نظرًا لأن كلا سائقي الدراجات يغادرون من ريفرسايد ويسافرون إلى الشاطئ، فإنهم يسافرون بنفس المسافة. لذلك نكتب:

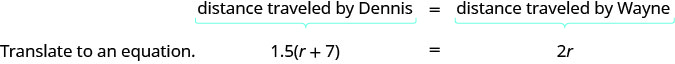
    يوضح الشكل أن المسافة التي قطعها دنيس تساوي المسافة التي قطعها واين، وعند ترجمتها إلى معادلة، تكون النتيجة 1.5 مرة الكمية r زائد 7 تساوي 2 r.

    يغادر قطار سريع وقطار محلي بيتسبرغ للسفر إلى واشنطن العاصمة، ويمكن للقطار السريع القيام بالرحلة في غضون أربع ساعات، ويستغرق القطار المحلي خمس ساعات للرحلة. تبلغ سرعة القطار السريع 12 ميلاً في الساعة أسرع من سرعة القطار المحلي. أوجد سرعة كلا القطارين.

    إجابة

    تبلغ سرعة القطار المحلي 48 ميلاً في الساعة وسرعة القطار السريع 60 ميلاً في الساعة.

    مثال\(\PageIndex{15}\)

    يمكن لجيرومي أن يقود سيارته من منزله في كليفلاند إلى كليته في شيكاغو في 4.5 ساعات. تستغرق والدته ست ساعات للقيام بنفس القيادة. يقود جيرومي 20 ميلاً في الساعة أسرع من والدته. اكتشف سرعة جيرومي وسرعة والدته.

    إجابة

    قاد جيرومي بسرعة 80 ميلاً في الساعة وقادت والدته 60 ميلاً في الساعة.

    على سبيل المثال، كان لدينا سائقان يسافران في نفس المسافة. في المثال التالي، يتجه شخصان نحو بعضهما البعض حتى يلتقيا.

    مثال\(\PageIndex{16}\)

    تقود كارينا السيارة من منزلها في أنهايم إلى بيركلي في نفس اليوم الذي يقود فيه شقيقها السيارة من بيركلي إلى أنهايم، لذلك قرروا الاجتماع لتناول طعام الغداء على طول الطريق في Buttonwillow. المسافة من أنهايم إلى بيركلي هي 395 ميلا. تستغرق كارينا ثلاث ساعات للوصول إلى Buttonwillow، بينما يقود شقيقها أربع ساعات للوصول إلى هناك. يبلغ متوسط سرعة كارينا 15 ميلاً في الساعة أسرع من متوسط سرعة شقيقها. ابحث عن متوسط سرعات كارينا وشقيقها.

    إجابة

    الخطوة 1. اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.

    ارسم مخططًا لتوضيح ما يحدث. يظهر أدناه رسم تخطيطي لما يحدث في المثال.

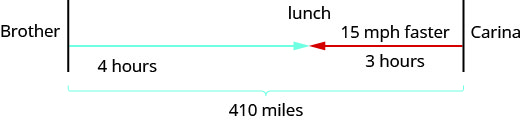
    يوضِّح الشكل الحركة المنتظمة لكارينا وشقيقها باستخدام السهام. يُطلق على سهم كارينا اسم «3 ساعات». يُشار إلى سهم شقيق كارينا في الاتجاه المعاكس ويُسمى «15 ميلاً في الساعة» و «4 ساعات». يُطلق على المكان الذي تلتقي فيه السهام اسم «الغداء». يتم تمثيل مسار كارينا وشقيقها بقوس ويحمل اسم «410 أميال».

    قم بإنشاء جدول لتنظيم المعلومات.

    • قم بتسمية معدل الأعمدة والوقت والمسافة.
    • ضع قائمة بالسيناريوهين.
    • اكتب المعلومات التي تعرفها.
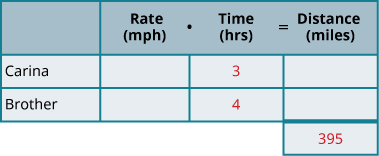
      يحتوي هذا المخطط على عمودين وأربعة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الثاني «المعدل بالأميال لكل ساعة مضروبًا في الوقت بالساعات يساوي المسافة بالأميال». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «المعدل» و «الوقت» و «المسافة». العمود الأول عبارة عن عنوان ويسمي الصف الثاني «كارينا» والصف الثالث «Brother». في الصف 2، الوقت هو 3 ساعات. في الصف 3، الوقت هو 4 ساعات. في الصف 4، المسافة هي 410 أميال.

    الخطوة 2. حدد ما نبحث عنه.

    يُطلب منا العثور على متوسط سرعات كارينا وشقيقها.

    الخطوة 3. اذكر ما نبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.

    أكمل المخطط. استخدم التعبيرات المتغيرة لتمثيل تلك الكمية في كل صف.
    نحن نبحث عن متوسط سرعاتها. دعونا نمثل متوسط سرعة كارينا. نظرًا لأن سرعة الأخ أسرع بـ 15 ميلاً في الساعة، فإننا نمثل ذلك على النحو التالي\(r+15\).
    املأ السرعات في المخطط. اضرب المعدل في الوقت للحصول على المسافة.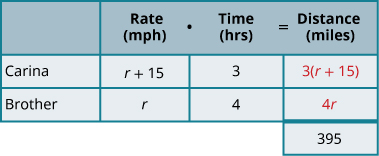

    يحتوي هذا المخطط على عمودين وأربعة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الثاني «المعدل بالأميال لكل ساعة مضروبًا في الوقت بالساعات يساوي المسافة بالأميال». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «المعدل» و «الوقت» و «المسافة». العمود الأول عبارة عن عنوان ويسمي الصف الثاني «كارينا» والصف الثالث «Brother». في الصف 2، يكون المعدل r، والوقت 3 ساعات، والمسافة 3 r، وفي الصف 3، يكون المعدل هو التعبير r زائد 15، والوقت هو 4 ساعات، والمسافة هي 4 أضعاف الكمية r زائد 15. في الصف 4، المسافة هي 410 أميال.

    الخطوة 4. ترجم إلى معادلة.

    كرر المشكلة في جملة واحدة مع جميع المعلومات المهمة. ثم ترجم الجملة إلى معادلة.
    مرة أخرى، نحتاج إلى تحديد العلاقة بين المسافات من أجل كتابة معادلة. انظر إلى الرسم التخطيطي الذي أنشأناه أعلاه ولاحظ العلاقة بين المسافة التي قطعتها كارينا والمسافة التي قطعها شقيقها.
    يجب أن تصل المسافة التي قطعتها كارينا بالإضافة إلى المسافة التي يقطعها شقيقها إلى 410 أميال. لذلك نكتب:

    يوضِّح الشكل أن المسافة التي قطعتها كارينا زائد المسافة التي قطعها شقيقها تساوي 410، وعند ترجمتها إلى معادلة، تكون النتيجة 3 r زائد 4 مضروبة في الكمية r زائد 15 تساوي 410.

    الخطوة 5. حل المعادلة باستخدام تقنيات الجبر.

    الآن قم بحل هذه المعادلة. .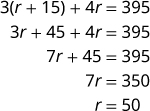
    لذلك كانت سرعة شقيق كارينا 50 ميلاً في الساعة.
    سرعة كارينا هي r+15.r+15. .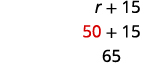
    كانت سرعة شقيقها 65 ميلاً في الساعة.

    الخطوة 6. تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.

    \(\begin{array} {llll} \text{Carina drove} &{65\text{ mph}(3\text{ hours})} &= &{\underline{195 \text{ miles}}} \\ \text{Her brother drove} &{50\text{ mph}(4\text{ hours})} &= &{\underline{200 \text{ miles}}} \\ {} &{} &{} &{395\text{ miles}\checkmark} \\ \end{array} \)

    الخطوة 7. أجب على السؤال بجملة كاملة.

    قادت كارينا 65 ميلاً في الساعة وشقيقها 50 ميلاً في الساعة.

    قدت سيارتي بسرعة 80 ميلاً في الساعة وكانت والدته تقود 60 ميلاً في الساعة.

    مثال\(\PageIndex{17}\)

    يعيش كريستوفر ووالديه على بعد 115 ميلاً. التقيا في مطعم بين منازلهم للاحتفال بعيد ميلاد والدته. قاد كريستوفر سيارة لمدة ساعة ونصف بينما كان والداه يقودان السيارة لمدة ساعة للوصول إلى المطعم. كان متوسط سرعة كريستوفر أسرع بعشرة أميال في الساعة من متوسط سرعة والديه. ما هو متوسط سرعات كريستوفر ووالديه أثناء توجههم إلى المطعم؟

    إجابة

    كانت سرعة كريستوفر 50 ميلاً في الساعة وكانت سرعة والديه 40 ميلاً في الساعة.

    مثال\(\PageIndex{18}\)

    تذهب آشلي إلى الكلية في مينيابوليس، على بعد 234 ميلاً من منزلها في سيوكس فولز. تريد من والديها إحضار المزيد من الملابس الشتوية لها، لذلك قرروا الاجتماع في مطعم على الطريق بين مينيابوليس وسيوكس فولز. سافرت آشلي ووالداها لمدة ساعتين إلى المطعم. كان متوسط سرعة آشلي أسرع بسبعة أميال في الساعة من متوسط سرعة والديها. ابحث عن متوسط سرعة آشلي ووالديها.

    إجابة

    قاد والدا آشلي 55 ميلاً في الساعة وقاد آشلي 62 ميلاً في الساعة.

    عندما تقرأ المثال التالي، فكر في علاقة المسافات المقطوعة. أي من المثالين السابقين أكثر تشابهًا مع هذا الموقف؟

    مثال\(\PageIndex{19}\)

    يغادر اثنان من سائقي الشاحنات منطقة الراحة على الطريق السريع في نفس الوقت. تسافر إحدى الشاحنات شرقًا والأخرى تتجه غربًا. تسير الشاحنة المتجهة غربًا بسرعة 70 ميلاً في الساعة، بينما يبلغ متوسط سرعة الشاحنة المتجهة شرقًا 60 ميلاً في الساعة. إلى متى سيسافرون قبل أن يفصلوا عن بعضهم البعض بـ 325 ميلاً؟

    إجابة

    الخطوة 1. اقرأ المشكلة. اجعل كل الكلمات والأفكار مفهومة.

    ارسم مخططًا لتوضيح ما يحدث.
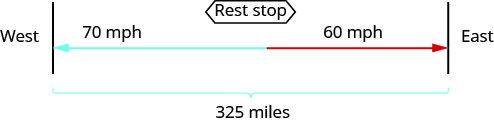
    يوضِّح الشكل الحركة المنتظمة لسائقي شاحنتين يستخدمان السهام. يُطلق على السهم الخاص بسائق الشاحنة المتجه غربًا اسم «70 ميلاً في الساعة». يشير سهم سائق الشاحنة المتجه شرقًا في الاتجاه المعاكس ويحمل علامة «60 ميلًا في الساعة». يُطلق على المكان الذي تلتقي فيه الأسهم اسم «Rest stop». يتم تمثيل مسار سائقي الشاحنات بقوس يسمى «325 ميلًا».

    قم بإنشاء جدول لتنظيم المعلومات.

    • قم بتسمية معدل الأعمدة والوقت والمسافة.
    • ضع قائمة بالسيناريوهين.
    • اكتب المعلومات التي تعرفها.

      يحتوي المخطط على عمودين وأربعة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الثاني «المعدل بالأميال في الساعة مضروبًا في الوقت بالساعات يساوي المسافة بالأميال». العمود الأول عبارة عن عمود العنوان ويطلق على الصف الثاني اسم «الغرب» والصف الثالث «الشرق». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «المعدل» و «الوقت» و «المسافة». يعطي الصف الرابع فقط المسافة الإجمالية التي قطعها سائقو الشاحنات. في الصف 2، يبلغ معدل سائق الشاحنة المتجه غربًا 70 ميلاً في الساعة. في الصف 3، يبلغ معدل سائق الشاحنة المتجه شرقًا 60 ميلاً في الساعة. في الصف 4، يبلغ إجمالي المسافة التي قطعها سائقو الشاحنات 325.

    الخطوة 2. حدد ما نبحث عنه.

    يُطلب منا تحديد مقدار الوقت الذي ستسافر فيه الشاحنات حتى تفصل بينها 325 ميلًا.

    الخطوة 3. اذكر ما نبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.

    أكمل المخطط. استخدم التعبيرات المتغيرة لتمثيل تلك الكمية في كل صف.
    نحن نبحث عن الوقت الذي تم السفر إليه. ستسافر كلتا الشاحنتين بنفس القدر من الوقت.
    دعونا نسمي الوقت t. نظرًا لاختلاف سرعاتها، فإنها ستسافر لمسافات مختلفة.

    اضرب المعدل في الوقت للحصول على المسافة.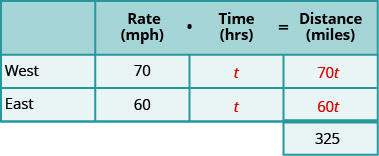

    يحتوي المخطط على عمودين وأربعة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الثاني «المعدل بالأميال في الساعة مضروبًا في الوقت بالساعات يساوي المسافة بالأميال». العمود الأول عبارة عن عمود العنوان ويطلق على الصف الثاني اسم «الغرب» والصف الثالث «الشرق». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «المعدل» و «الوقت» و «المسافة». يعطي الصف الرابع فقط المسافة الإجمالية التي قطعها سائقو الشاحنات. في الصف 2، يبلغ معدل سائق الشاحنة المتجه غربًا 70 ميلًا في الساعة، والوقت في الساعة، والمسافة 70 طنًا. في الصف 3، يبلغ معدل سائق الشاحنة المتجه شرقًا 60 ميلًا في الساعة، والوقت t، ومسافة 60 طنًا، وفي الصف 4، يبلغ إجمالي المسافة التي يقطعها سائقو الشاحنات 325.

    الخطوة 4. ترجم إلى معادلة.

    كرر المشكلة في جملة واحدة مع جميع المعلومات المهمة. ثم ترجم الجملة إلى معادلة.
    نحن بحاجة إلى إيجاد علاقة بين المسافات من أجل كتابة معادلة. بالنظر إلى الرسم التخطيطي، ما العلاقة بين المسافات التي ستقطعها كل شاحنة؟
    يجب أن تصل المسافة التي تقطعها الشاحنة المتجهة غربًا بالإضافة إلى المسافة التي تقطعها الشاحنة المتجهة شرقًا إلى 325 ميلًا. لذلك نكتب:

    يوضِّح الشكل أن المسافة التي تقطعها الشاحنة المتجهة غربًا بالإضافة إلى المسافة التي قطعتها الشاحنة المتجهة شرقًا تساوي 325، وعند ترجمتها إلى معادلة، تكون النتيجة 70 طنًا زائد 60 طنًا تساوي 325.

    الخطوة 5. حل المعادلة باستخدام تقنيات الجبر.

    \( \quad \text{Now solve this equation} \qquad\begin{align} 70t+60t &= 325 \nonumber\\ 130t &= 325 \nonumber\\ t &= 2.5 \nonumber\\ \end{align} \)

    لذلك سوف تستغرق الشاحنات\(2.5\) ساعات لتكون على بعد 325 ميلاً.

    الخطوة 6. تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.

    \(\begin{array} {llll} \text{Truck going West} &{70\text{ mph}(2.5\text{ hours})} &= &{\space175\text{ miles}\space} \\ \text{Truck going East} &{60\text{ mph}(2.5\text{ hours})} &= &{\underline{\space150\text{ miles}\space}} \\ {} &{} &{} &{325\text{ miles}\checkmark} \\ \end{array}\)

    الخطوة 7. أجب على السؤال بجملة كاملة.
    ستستغرق الشاحنات 2.5 ساعة لتكون على بعد 325 ميلاً.

    مثال\(\PageIndex{20}\)

    يغادر بيير ومونيكا منزلهما في بورتلاند في نفس الوقت. يقود بيير شمالًا على الطريق السريع بسرعة 75 ميلاً في الساعة بينما تقود مونيكي جنوبًا بسرعة 68 ميلاً في الساعة. كم من الوقت ستستغرق المسافة بينهما 429 ميلاً؟

    إجابة

    سيتفصل بين بيير ومونك 429 ميلاً في 3 ساعات.

    مثال\(\PageIndex{21}\)

    يغادر Thanh و Nhat مكتبهما في سكرامنتو في نفس الوقت. يقود ثانه شمالًا على I-5 بسرعة 72 ميلاً في الساعة. يقود Nhat جنوبًا على I-5 بسرعة 76 ميل في الساعة. كم من الوقت سيستغرقون ليكونوا على بعد 330 ميلاً؟

    إجابة

    سوف يفصل بين ثانه ونهات 330 ميلاً في غضون 2.2 ساعة.

    من المهم التأكد من تطابق الوحدات عندما نستخدم صيغة معدل المسافة والوقت. على سبيل المثال، إذا كان السعر بالأميال في الساعة، فيجب أن يكون الوقت بالساعات.

    مثال\(\PageIndex{22}\)

    عندما تذهب ناوكو إلى المدرسة، يستغرق الأمر 30 دقيقة. إذا ركبت دراجتها، يستغرق الأمر 15 دقيقة. تكون سرعتها أسرع بثلاثة أميال في الساعة عندما تركب دراجتها مقارنة بالمشي. ما هي سرعة مشيها وسرعتها في ركوب دراجتها؟

    إجابة

    أولاً، نرسم مخططًا يمثل الموقف لمساعدتنا على رؤية ما يحدث.

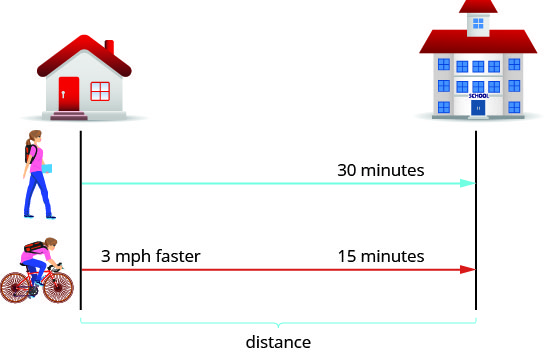
    يُظهر الشكل حركة الزي الرسمي عندما تذهب ناوكو إلى المدرسة وعندما تركب دراجتها إلى المدرسة. يتم تمثيل مشيتها إلى المدرسة بسهم مكتوب عليه «30 دقيقة». يتم تمثيل رحلتها إلى المدرسة بسهم ثانٍ بنفس الطول وفي نفس الاتجاه المسمى «3 أميال في الساعة أسرع» و «15 دقيقة». يمثل القوس المسافة بين منزلها والمدرسة.

    طُلب منا أن نجدها وهي تمشي بسرعة وتركب دراجتها. دعونا نسميها سرعة المشي r. نظرًا لأن سرعة ركوب الدراجات لديها أسرع بثلاثة أميال في الساعة، فسنسمي هذه السرعة\(r+3\). نكتب السرعات في الرسم البياني.

    السرعة بالأميال في الساعة، لذلك نحتاج إلى التعبير عن الأوقات بالساعات أيضًا، حتى تكون الوحدات هي نفسها. تذكر أن ساعة واحدة هي 60 دقيقة. لذلك:

    \[\begin{array} {l} {} \\ \text{30 minutes is } \frac{30}{60} \text{ or }\frac{1}{2}\text{ hour} \\ \text{15 minutes is } \frac{15}{60} \text{ or }\frac{1}{4}\text{ hour} \\ \nonumber \end{array}\]

    نكتب الأوقات في الرسم البياني.

    بعد ذلك، نقوم بضرب معدل مرات الوقت لملء عمود المسافة.

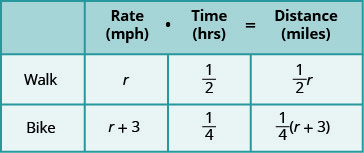
    يحتوي هذا المخطط على عمودين وثلاثة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الثاني «المعدل بالأميال لكل ساعة مضروبًا في الوقت بالساعات يساوي المسافة بالأميال». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «المعدل» و «الوقت» و «المسافة». العمود الأول عبارة عن عنوان ويسمي الصف الثاني «المشي» والصف الثالث «الدراجة». في الصف 2، يكون المعدل r، والوقت هو نصف ساعة، والمسافة نصف r، وفي الصف 3، يكون المعدل هو التعبير r زائد 3، والوقت هو ربع ساعة، والمسافة هي ربع أضعاف الكمية r زائد 3.

    ستأتي المعادلة من حقيقة أن المسافة من منزل ناوكو إلى مدرستها هي نفسها سواء كانت تمشي أو تركب دراجتها.
    لذلك نقول:

      .
    ترجم إلى معادلة. .
    حل هذه المعادلة. .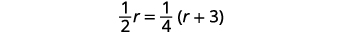
    امسح الكسور بالضرب في شاشة LCD لجميع الكسور في المعادلة. .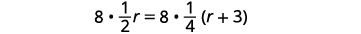
    قم بالتبسيط. .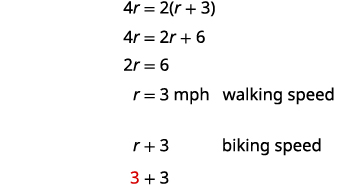
      6

    دعونا نتحقق مما إذا كان هذا يعمل.

    \(\begin{array} {lll} {\text{Walk }3\text{ mph }(0.5\text{ hour})} &= &{1.5\text{ miles}} \\ {\text{Bike }6\text{ mph }(0.25\text{ hour})} &= &{1.5\text{ miles}} \\ \end{array}\)

    نعم، في كلتا الحالتين، تسافر ناوكو 1.5 ميل إلى المدرسة.

    سرعة المشي في Naoko هي 3 ميل في الساعة وسرعتها في ركوب دراجتها هي 6 ميل في الساعة.

    مثال\(\PageIndex{23}\)

    تستغرق سوزي 50 دقيقة للتنزه صعودًا من موقف السيارات إلى برج المراقبة. يستغرق الأمر 30 دقيقة للعودة إلى موقف السيارات. سرعتها في الانحدار أسرع بـ 1.2 ميل في الساعة من سرعتها صعودًا. ابحث عن سرعات Suzy صعودًا وهبوطًا.

    إجابة

    تبلغ سرعة سوزي صعودًا 1.81.8 ميل في الساعة والانحدار ثلاثة أميال في الساعة.

    مثال\(\PageIndex{24}\)

    يستغرق Llewyn 45 دقيقة لقيادة قاربه في اتجاه المنبع من الرصيف إلى مكان الصيد المفضل لديه. يستغرق الأمر 30 دقيقة لقيادة القارب عائدًا إلى المصب إلى الرصيف. سرعة القارب في اتجاه مجرى النهر أسرع بأربعة أميال في الساعة من سرعته في اتجاه المنبع. ابحث عن سرعات القارب في المنبع والمصب.

    إجابة

    تبلغ سرعة القارب في اتجاه المنبع ثمانية أميال في الساعة وفي اتجاه المصب 12 ميلاً في الساعة.

    في صيغة المسافة والمعدل والوقت، يمثل الوقت المقدار الفعلي للوقت المنقضي (بالساعات والدقائق وما إلى ذلك). إذا كانت هناك مشكلة تعطينا أوقات البدء والانتهاء كأوقات الساعة، يجب أن نجد الوقت المنقضي لاستخدام الصيغة.

    مثال\(\PageIndex{25}\)

    يتدرب كروز للتنافس في الترياتلون. غادر منزله في الساعة 6:00 وركض حتى الساعة 7:30. ثم ركب دراجته حتى الساعة 9:45. لقد قطع مسافة إجمالية قدرها 51 ميلاً. كانت سرعته عند ركوب الدراجات 1.6 ضعف سرعته عند الجري. ابحث عن سرعات ركوب الدراجات والجري في Cruz.

    إجابة

    سيساعدنا الرسم التخطيطي في تصميم هذه الرحلة.

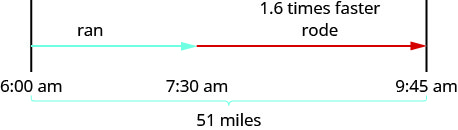
    يوضِّح الشكل الحركة الموحدة لتدريب كروز على الترياتلون. يتم تمثيل مسار كروز بسهم يسمى «الجري» يبدأ من 6 أمتار ويمتد إلى 7:30 مترًا وسهم ثانٍ يحمل اسم «ركب» و «أسرع 1.6 مرة» ويبدأ من الساعة 7:30 مترًا ويمتد إلى 9:45 صباحًا، ويمثل القوس المسافة التي يغطيها كروز ويطلق عليه «51 ميلًا».

    بعد ذلك، نقوم بإنشاء جدول لتنظيم المعلومات. نحن نعلم أن المسافة الإجمالية هي 51 ميلا. نحن نبحث عن معدل السرعة لكل جزء من الرحلة. معدل ركوب الدراجات هو 1.6 مرة من معدل الجري. إذا تركنا r = معدل التشغيل، فإن معدل ركوب الدراجات هو 1.6 r.

    يتم إعطاء الأوقات هنا كأوقات الساعة. بدأ كروز من المنزل في الساعة 6:00 صباحًا وبدأ ركوب الدراجات في الساعة 7:30 صباحًا، لذلك أمضى 1.5 ساعة في الجري. ثم قام بركوب الدراجة من الساعة 7:30 صباحًا حتى الساعة 9:45 صباحًا، لذلك أمضى 2.25 ساعة في ركوب الدراجات.

    الآن، نضرب الأسعار بالأوقات.

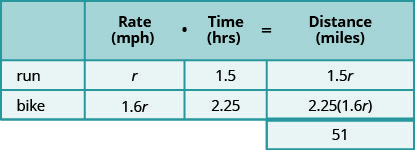
    يحتوي المخطط على عمودين وأربعة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الثاني «المعدل بالأميال في الساعة مضروبًا في الوقت بالساعات يساوي المسافة بالأميال». العمود الأول عبارة عن عمود رئيسي ويطلق على الصف الثاني اسم «الجري» والصف الثالث «الدراجة». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «المعدل» و «الوقت» و «المسافة». يعطي الصف الرابع فقط المسافة الإجمالية المغطاة. في الصف 2، يكون المعدل r، والوقت 1.5 ساعة، والمسافة 1.5 r، وفي الصف 3، يكون المعدل 1.6، والوقت 2.25 ساعة، والمسافة 2.25 مضروبًا في 1.6 r، وفي الصف 4، يبلغ إجمالي المسافة المقطوعة 51 ميلًا.

    من خلال النظر إلى الرسم التخطيطي، يمكننا أن نرى أن مجموع مسافة الجري ومسافة ركوب الدراجات هو 255 ميلاً.

      .
    ترجم إلى معادلة. .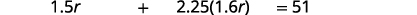
    حل هذه المعادلة. .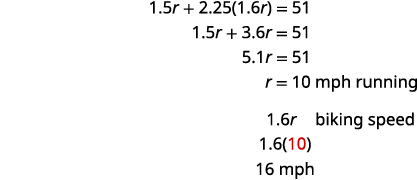

    تحقق.

    \(\begin{array} {lll} {\text{Run }10\text{ mph }(1.5\text{ hour})} &= &{15\text{ mi}} \\ {\text{Bike }16\text{ mph }(2.25\text{ hour})} &= &{\underline{36\text{ mi}}} \\ {} &{} &{} &{51\text{ mi}} \\ \end{array}\)

    		  
    مثال\(\PageIndex{26}\)

    يحب هاملتون السفر إلى لاس فيغاس، على بعد 255 ميلاً من منزله في مقاطعة أورانج. في رحلته الأخيرة، غادر منزله في الساعة 2:00 مساءً، وكان الجزء الأول من رحلته على الطرق السريعة المزدحمة بالمدينة. في الساعة 4:00 مساءً، تم مسح حركة المرور وتمكن من القيادة عبر الصحراء بسرعة 1.75 مرة أسرع مما كان عليه عندما كان يقود سيارته في المنطقة المزدحمة. وصل إلى لاس فيغاس في الساعة 6:30 مساءً. ما مدى سرعة قيادته خلال كل جزء من رحلته؟

    إجابة

    قاد هاملتون 40 ميلاً في الساعة في المدينة و70 ميلاً في الساعة في الصحراء.

    مثال\(\PageIndex{27}\)

    غادر فونج المنزل على دراجته في الساعة 10:00. ركب في الشارع المسطح حتى الساعة 11:15، ثم ركب صعودًا حتى الساعة 11:45. لقد ركب ما مجموعه 31 ميلاً. كانت سرعته صعودًا 0.6 ضعف سرعته في الشارع المسطح. ابحث عن ركوب الدراجات السريعة صعودًا وفي الشارع المسطح.

    إجابة

    ركبت فونج صعودًا بسرعة 12 ميلاً في الساعة وفي الشارع المسطح بسرعة 20 ميلاً في الساعة.

    المفاهيم الرئيسية

    • إجمالي قيمة العملات
      بالنسبة لنفس النوع من العملات      ، يتم العثور على القيمة الإجمالية لعدد من العملات باستخدام رقم الطراز ·
      value=totalvaluenumber·value=totalvalue
      • الرقم هو عدد العملات
      • القيمة هي قيمة كل عملة
      • القيمة الإجمالية هي القيمة الإجمالية لجميع العملات
    • كيفية حل مشاكل الكلمات النقدية.
      1. اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
        حدد أنواع العملات المعنية.
        قم بإنشاء جدول لتنظيم المعلومات.
        قم بتسمية الأعمدة «النوع» و «الرقم» و «القيمة» و «القيمة الإجمالية».
        ضع قائمة بأنواع العملات.
        اكتب قيمة كل نوع من العملات.
        اكتب القيمة الإجمالية لجميع العملات.
        يحتوي هذا المخطط على عمودين وأربعة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الأول «النوع» والعمود الثاني «الرقم مضروبًا في القيمة بالدولار يساوي إجمالي القيمة بالدولار». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «الرقم» و «القيمة» و «القيمة الإجمالية». يحتوي عمود القيمة الإجمالية على صف إضافي. المخطط فارغ.
      2. حدد ما تبحث عنه.
      3. قم بتسمية ما تبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.
        استخدم التعبيرات المتغيرة لتمثيل رقم كل نوع من العملات وكتابتها في الجدول.
        اضرب الرقم في القيمة للحصول على القيمة الإجمالية لكل نوع من أنواع العملات.
      4. ترجم إلى معادلة.
        قد يكون من المفيد إعادة ذكر المشكلة في جملة واحدة مع جميع المعلومات المهمة. ثم ترجم الجملة إلى معادلة.
        اكتب المعادلة عن طريق جمع القيم الإجمالية لجميع أنواع العملات.
      5. حل المعادلة باستخدام تقنيات الجبر الجيدة.
      6. تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
      7. أجب على السؤال بجملة كاملة.
    • كيفية حل تطبيق الحركة الموحدة
      1. اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
        ارسم مخططًا لتوضيح ما يحدث.
        قم بإنشاء جدول لتنظيم المعلومات.
        قم بتسمية معدل الأعمدة والوقت والمسافة.
        ضع قائمة بالسيناريوهين.
        اكتب المعلومات التي تعرفها.
        يحتوي هذا المخطط على عمودين وأربعة صفوف. الصف الأول عبارة عن عنوان ويسمي العمود الثاني «معدل الأوقات يساوي المسافة». ينقسم عمود العنوان الثاني إلى ثلاثة أعمدة لـ «المعدل» و «الوقت» و «المسافة». يحتوي عمود المسافة على صف إضافي. المخطط فارغ.
      2. حدد ما تبحث عنه.
      3. قم بتسمية ما تبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.
        أكمل المخطط.
        استخدم التعبيرات المتغيرة لتمثيل تلك الكمية في كل صف.
        اضرب المعدل في الوقت للحصول على المسافة.
      4. ترجم إلى معادلة.
        كرر المشكلة في جملة واحدة مع جميع المعلومات المهمة.
        ثم ترجم الجملة إلى معادلة.
      5. حل المعادلة باستخدام تقنيات الجبر الجيدة.
      6. تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
      7. أجب على السؤال بجملة كاملة.