2.4: حل صيغة لمتغير معين
- Page ID
- 201706
في نهاية هذا القسم، ستكون قادرًا على:
- حل صيغة لمتغير معين
- استخدم الصيغ لحل تطبيقات الهندسة
قبل البدء، قم بإجراء اختبار الاستعداد هذا.
حل صيغة لمتغير معين
ربما عملنا جميعًا مع بعض الصيغ الهندسية في دراستنا للرياضيات. يتم استخدام الصيغ في العديد من المجالات، ومن المهم التعرف على الصيغ والقدرة على التعامل معها بسهولة.
غالبًا ما يكون من المفيد حل صيغة لمتغير معين. إذا كنت بحاجة إلى وضع صيغة في جدول بيانات، فليس من غير المعتاد حلها لمتغير معين أولاً. نعزل هذا المتغير على أحد جانبي علامة التساوي بمعامل واحد وجميع المتغيرات والثوابت الأخرى على الجانب الآخر من علامة التساوي.
غالبًا ما تحتاج الصيغ الهندسية إلى حل لمتغير آخر أيضًا. \(V=\frac{1}{3}πr^2h\)تُستخدم الصيغة لإيجاد حجم المخروط الدائري الأيمن عند إعطاء نصف قطر القاعدة والارتفاع. في المثال التالي، سنحل هذه الصيغة للارتفاع.
حل\(V=\frac{1}{3}πr^2h\) صيغة h.
- إجابة
-
اكتب الصيغة. 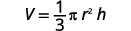
أزل الكسر الموجود على اليمين. 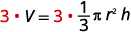
قم بالتبسيط. 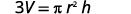
قسّم كلا الجانبين على\(πr^2\). 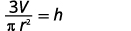
يمكننا الآن استخدام هذه الصيغة لإيجاد ارتفاع مخروط دائري قائم عندما نعرف حجم ونصف قطر القاعدة، باستخدام الصيغة\(h=\frac{3V}{πr^2}\).
استخدم الصيغة\(A=\frac{1}{2}bh\) لحل b.
- إجابة
-
\(b=\frac{2A}{h}\)
استخدم الصيغة\(A=\frac{1}{2}bh\) لحل h.
- إجابة
-
\(h=\frac{2A}{b}\)
في العلوم، نحتاج غالبًا إلى تغيير درجة الحرارة من فهرنهايت إلى درجة مئوية أو العكس. إذا كنت تسافر في بلد أجنبي، فقد ترغب في تغيير درجة الحرارة المئوية إلى درجة حرارة فهرنهايت الأكثر شيوعًا.
حل\(C=\frac{5}{9}(F−32)\) صيغة F.
- إجابة
-
اكتب الصيغة. 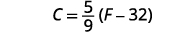
أزل الكسر الموجود على اليمين. 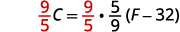
قم بالتبسيط. 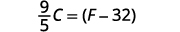
أضف 32 إلى كلا الجانبين. 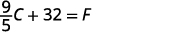
يمكننا الآن استخدام الصيغة\(F=\frac{9}{5}C+32\) للعثور على درجة حرارة فهرنهايت عندما نعرف درجة الحرارة المئوية.
حل\(F=\frac{9}{5}C+32\) صيغة C.
- إجابة
-
\(C=\frac{5}{9}(F−32)\)
حل\(A=\frac{1}{2}h(b+B)\) صيغة b.
- إجابة
-
\(b=\frac{2A−Bh}{h}\)
يستخدم المثال التالي صيغة مساحة سطح الأسطوانة اليمنى.
حل الصيغة\(S=2πr^2+2πrh\) لـ\(h\).
- إجابة
-
اكتب الصيغة. 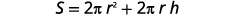
اعزل\(h\) المصطلح بالطرح\(2πr^2\) من كل جانب. 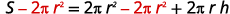
قم بالتبسيط. 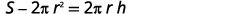
حل المشكلة\(h\) بتقسيم كلا الجانبين على\(2πr.\) 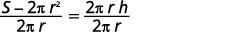
قم بالتبسيط. 
حل الصيغة\(A=P+Prt\) لـ\(t\).
- إجابة
-
\(t=\frac{A−P}{Pr}\)
حل الصيغة\(A=P+Prt\) لـ\(r\).
- إجابة
-
\(r=\frac{A−P}{Pt}\)
في بعض الأحيان قد نحصل على معادلة تم حلها\(y\) ونحتاج إلى حلها\(x\) أو العكس. في المثال التالي، نحصل على معادلة بكلا الجانبين\(x\)\(y\) وعلى نفس الجانب وسنقوم بحلها\(y\).
حل الصيغة\(8x+7y=15\) لـ\(y\).
- إجابة
-
سوف نعزل\(y\) على جانب واحد من المعادلة. 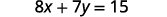
اطرح\(6x\) من كلا الجانبين لعزل المصطلح بـ\(y\). 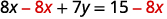
قم بالتبسيط. 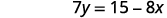
قسّم كلا الجانبين\(7\) لجعل معامل\(y\) واحد. 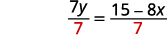
قم بالتبسيط. 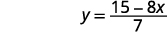
حل الصيغة\(4x+7y=9\) لـ\(y\).
- إجابة
-
\(y=\frac{9−4x}{7}\)
حل الصيغة\(5x+8y=1\) لـ\(y\).
- إجابة
-
\(y=\frac{1−5x}{8}\)
استخدم الصيغ لحل تطبيقات الهندسة
في هذا الهدف، سنستخدم بعض الصيغ الهندسية الشائعة. سنقوم بتكييف إستراتيجية حل المشكلات الخاصة بنا حتى نتمكن من حل التطبيقات الهندسية. ستقوم الصيغة الهندسية بتسمية المتغيرات وتعطينا المعادلة التي يجب حلها.
بالإضافة إلى ذلك، نظرًا لأن جميع هذه التطبيقات ستشمل أشكالًا من نوع ما، يجد معظم الأشخاص أنه من المفيد رسم الشكل وتسميته بالمعلومات المحددة. سنقوم بتضمين هذا في الخطوة الأولى من استراتيجية حل المشكلات لتطبيقات الهندسة.
- اقرأ المشكلة وتأكد من فهم جميع الكلمات والأفكار.
- حدد ما تبحث عنه.
- قم بتسمية ما نبحث عنه باختيار متغير لتمثيله. ارسم الشكل وقم بتسميته بالمعلومات المعطاة.
- ترجم إلى معادلة بكتابة الصيغة أو النموذج المناسب للموقف. استبدل المعلومات المعطاة.
- حل المعادلة باستخدام تقنيات الجبر الجيدة.
- تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
- أجب على السؤال بجملة كاملة.
عندما نحل تطبيقات الهندسة، غالبًا ما يتعين علينا استخدام بعض خصائص الأشكال. سنراجع هذه الخصائص حسب الحاجة.
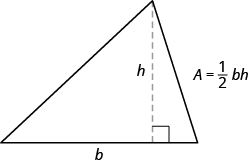
يتضمن المثال التالي مساحة المثلث. مساحة المثلث تساوي نصف القاعدة في الارتفاع. يمكننا كتابة هذا كـ\(A=\frac{1}{2}bh\)، حيث\(b\) = طول القاعدة و\(h\) = الارتفاع.
تبلغ مساحة اللوحة الثلاثية بوصة\(126\) مربعة. القاعدة هي\(18\) بوصات. ما هو الارتفاع؟
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما تبحث عنه. ارتفاع المثلث الخطوة 3. اسم. اختر متغيرًا لتمثيله. \(h=\)دع الارتفاع. ارسم الشكل وقم بتسميته بالمعلومات المعطاة. المساحة = 126 متر مربع. 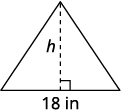
الخطوة 4. ترجم. اكتب الصيغة المناسبة. \(A=\frac{1}{2}bh\) استبدل المعلومات المعطاة. \(126=\frac{1}{2}·18·h\) الخطوة 5. حل المعادلة. \(126=9h\) قسّم كلا الجانبين على 9. \(14=h\) الخطوة 6. تحقق. \(\begin{align*} A &= \frac{1}{2}bh \\126 & \stackrel{?}{=} 12·18·14 \\ 126 &=126✓ \end{align*}\)
الخطوة 7. أجب على السؤال. ارتفاع المثلث هو\(14\) بوصة.
تبلغ مساحة نافذة الكنيسة الثلاثية مترًا\(90\) مربعًا. قاعدة النافذة هي\(15\) الأمتار. ما هو ارتفاع النافذة؟
- إجابة
-
ارتفاع النافذة هو\(12\) أمتار.
\(15\)تبلغ مساحة باب الخيمة الثلاثي قدم مربع. الارتفاع هو خمسة أقدام. ما طول القاعدة؟
- إجابة
-
طول القاعدة هو\(6\) القدمين.
في المثال التالي، سنعمل مع مثلث قائم. لحل قياس كل زاوية، نحتاج إلى استخدام خاصيتي المثلث. في أي مثلث، يكون مجموع قياسات الزوايا هو\(180°\). يمكننا كتابة هذا كصيغة:\(m∠A+m∠B+m∠C=180\). أيضًا، نظرًا لأن المثلث هو مثلث قائم، فإننا نتذكر أن المثلث الأيمن له\(90°\) زاوية واحدة.
هنا، سيتعين علينا تحديد زاوية واحدة بدلالة أخرى. سننتظر رسم الشكل حتى نكتب تعبيرات لجميع الزوايا التي نبحث عنها.
قياس زاوية واحدة للمثلث الأيمن يزيد بمقدار 40 درجة عن قياس أصغر زاوية. أوجد قياسات الزوايا الثلاث.
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما تبحث عنه. مقاييس الزوايا الثلاث الخطوة 3. اسم. اختر متغيرًا لتمثيله. \(\begin{align*} \text{Let }a \; & = \; \mathrm{1^{st} \; angle.} \\ a+40 &= \mathrm{2^{nd} \; angle} \\90 &= \mathrm{3^{rd} \; angle \; (the \; right \; angle)} \end{align*}\) ارسم الشكل وقم بتسميته بالمعلومات المعطاة. 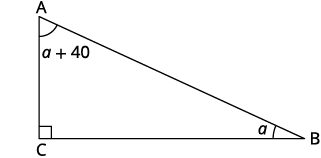
الخطوة 4. ترجم. اكتب الصيغة المناسبة. 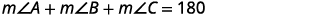
استبدل الصيغة. 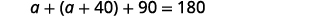.jpg)
الخطوة 5. حل المعادلة. 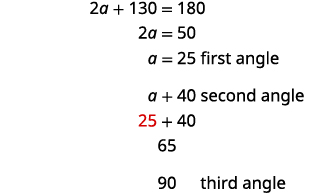
الخطوة 6. تحقق. \( \begin{align*} 25+65+90 & \stackrel{?}{=} 180\\ 180 &= 180✓ \end{align*}\) الخطوة 7. أجب على السؤال. تقيس الزوايا الثلاث\(25°,\;65°\)، و\(90°\).
يزيد قياس إحدى زوايا المثلث القائم على الزاوية بمقدار 50 عن قياس أصغر زاوية. أوجد قياسات الزوايا الثلاث.
- إجابة
-
مقاييس الزوايا هي\(20°, \;70°\)، و\(90°\).
قياس زاوية واحدة للمثلث الأيمن هو\(30\) أكثر من قياس أصغر زاوية. أوجد قياسات الزوايا الثلاث.
- إجابة
-
مقاييس الزوايا هي\(30°,\; 60°\)، و\(90°\).
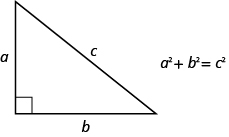
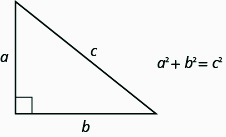
يستخدم المثال التالي صيغة هندسية مهمة أخرى. توضح نظرية فيثاغورس كيفية ارتباط أطوال الأضلاع الثلاثة للمثلث القائم الزاوية ببعضها البعض. قد تساعدك كتابة الصيغة في كل تمرين وقولها بصوت عالٍ أثناء كتابتها على حفظ نظرية فيثاغورس.
في أي مثلث قائم الزاوية، حيث a و b هما أطوال الأرجل، و c هو طول الوتر، يساوي مجموع مربعات أطوال الساقين مربع طول الوتر.
سنستخدم نظرية فيثاغورس في المثال التالي.
استخدم نظرية فيثاغورس لإيجاد طول الساق الأخرى في
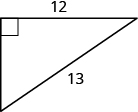
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما تبحث عنه. طول ساق المثلث الخطوة 3. اسم. اختر متغيرًا لتمثيله. Let\(a\) = ساق المثلث. جانب التسمية أ. 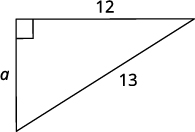
الخطوة 4. ترجم. اكتب الصيغة المناسبة. بديل. \(\begin{align*}a^2+b^2 &=c ^2 \\ a^2+12^2 &=13^2 \end{align*}\) الخطوة 5. حل المعادلة. اعزل مصطلح المتغير. استخدم تعريف الجذر التربيعي. قم بالتبسيط. \(\begin{align*} a^2+144 &= 169 \\ a^2 &= 25 \\ a &= \sqrt{25} \\ a&=5 \end{align*}\) الخطوة 6. تحقق. 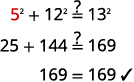
الخطوة 7. أجب على السؤال. طول الساق هو\(5\).
استخدم نظرية فيثاغورس لإيجاد طول الساق في الشكل.
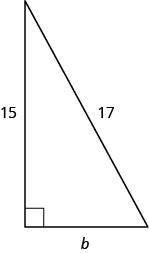
- إجابة
-
طول الساق هو\(8\).
استخدم نظرية فيثاغورس لإيجاد طول الساق في الشكل.
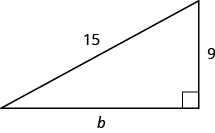
- إجابة
-
طول الساق هو\(12\).
المثال التالي هو حول محيط المستطيل. بما أن المحيط هو مجرد المسافة حول المستطيل، نجد مجموع أطوال أضلاعه الأربعة، أي مجموع طولين وعرضين. يمكننا الكتابة\(P=2L+2W\) حيث\(L\) يكون الطول والعرض\(W\). لحل المثال، سنحتاج إلى تحديد الطول من حيث العرض.
يزيد طول المستطيل بمقدار ستة سنتيمترات عن ضعف العرض. المحيط هو\(96\) السنتيمترات. ابحث عن الطول والعرض.
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما نبحث عنه. الطول والعرض الخطوة 3. اسم. اختر متغيرًا لتمثيل العرض. الطول يزيد بمقدار ستة عن ضعف العرض. \(w=\)عرض الساق. \(2w+6=\)الطول
\(P=96\)سم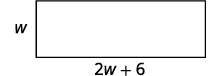
الخطوة 4. ترجم. اكتب الصيغة المناسبة. 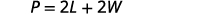
استبدل المعلومات المعطاة. 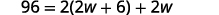
الخطوة 5. حل المعادلة. 
الخطوة 6. تحقق.
\(\begin{align*} P &=2L+2W \\ 96 & \stackrel{?}{=}2·34+2·14 \\ 96 &=96✓ \end{align*}\)
الخطوة 7. أجب على السؤال. الطول هو\(34\) سم والعرض هو\(14\) سم
يزيد طول المستطيل بسبعة عن ضعف العرض. المحيط هو\(110\) بوصة. ابحث عن الطول والعرض.
- إجابة
-
الطول هو\(16\) بوصة والعرض هو\(39\) بوصة.
يقل عرض المستطيل بثمانية ياردات عن ضعف الطول. المحيط هو\(86\) ياردات. ابحث عن الطول والعرض.
- إجابة
-
الطول\(17\) ياردات والعرض\(26\) ياردات.
المثال التالي هو حول محيط المثلث. بما أن المحيط هو مجرد المسافة حول المثلث، نجد مجموع أطوال أضلاعه الثلاثة. يمكننا كتابة هذا\(P=a+b+c\) على النحو\(b\) التالي: أطوال الأضلاع وأين\(a\).\(c\)
يزيد أحد ضلعي المثلث بمقدار ثلاث بوصات عن الضلع الأول. الجانب الثالث يزيد بمقدار بوصتين عن ضعف الأول. المحيط هو\(29\) بوصة. أوجد طول أضلاع المثلث الثلاثة.
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما نبحث عنه. أطوال أضلاع المثلث الثلاثة الخطوة 3. اسم. اختر متغيرًا لتمثيل طول الضلع الأول. \( \begin{align*} \mathrm{Let \;}x \;& \mathrm{= \; length \; of \;1^{st} \;side.} \\ x+3 \; &= \; \mathrm{length \; of \; 2^{nd} \; side} \\ 2x+2 \; &= \; \mathrm{length \; of \;3^{rd} \; side} \end{align*}\)
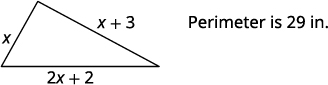
الخطوة 4. ترجم. اكتب الصيغة المناسبة. استبدل المعلومات المعطاة. 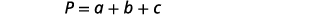
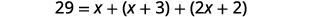
الخطوة 5. حل المعادلة. 
الخطوة 6. تحقق.
\(\begin{align*} 29 & \stackrel{?}{=}6+9+14 \\ 29 &= 29✓ \end{align*}\)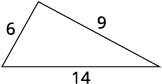
الخطوة 7. أجب على السؤال. أطوال أضلاع المثلث هي\(6\),\(9\),\(14\) وبوصة.
يزيد أحد ضلعي المثلث بمقدار سبع بوصات عن الضلع الأول. الجانب الثالث أقل بأربع بوصات من ثلاثة أضعاف الأول. المحيط هو\(28\) بوصة. أوجد طول أضلاع المثلث الثلاثة.
- إجابة
-
أطوال أضلاع المثلث هي\(5\) 4\(11\)\(12\) بوصات.
يقل أحد أضلاع المثلث بمقدار ثلاثة أقدام عن الضلع الأول. أما الجانب الثالث فهو أقل بخمسة أقدام من ضعف الأول. المحيط هو\(20\) أقدام. أوجد طول أضلاع المثلث الثلاثة.
- إجابة
-
أطوال أضلاع المثلث هي\(4\)،\(7\)\(9\) والأقدام.
محيط ملعب كرة قدم مستطيل هو\(360\) أقدام. الطول أكبر\(40\) بالأقدام من العرض. ابحث عن الطول والعرض.
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما نبحث عنه. طول وعرض ملعب كرة القدم الخطوة 3. اسم. اختر متغيرًا لتمثيله. الطول يزيد بمقدار 40 قدمًا عن العرض. ارسم الشكل وقم بتسميته بالمعلومات المعطاة. دعونا = العرض. \(w+40=\)الطول 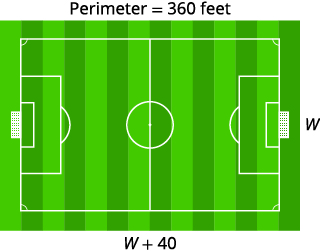
الخطوة 4. ترجم. اكتب الصيغة المناسبة واستبدلها. 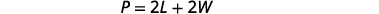
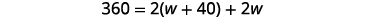
الخطوة 5. حل المعادلة. الخطوة 6. تحقق. \( \begin{align*} P &=2L+2W \\ 360 & \stackrel{?}{=} 2(110)+2(70) \\360 &=360✓ \end{align*}\) 
الخطوة 7. أجب على السؤال. طول ملعب كرة القدم هو\(110\) القدمين والعرض هو\(70\) القدمين.
محيط حوض السباحة المستطيل هو\(200\) أقدام. الطول أكبر\(40\) بالأقدام من العرض. ابحث عن الطول والعرض.
- إجابة
-
طول حمام السباحة هو\(70\) قدم وعرضه\(30\) قدم.
يبلغ طول الحديقة المستطيلة\(30\) ياردة أكثر من العرض. المحيط هو\(300\) ياردات. ابحث عن الطول والعرض.
- إجابة
-
يبلغ طول الحديقة\(90\) ياردات وعرضها\(60\) ياردات.
يمكن العثور على تطبيقات هذه الخصائص الهندسية في العديد من المواقف اليومية كما هو موضح في المثال التالي.
يقوم Kelvin ببناء شرفة ويريد دعم كل زاوية بوضع قطعة من الخشب مقاس 10 بوصات قطريًا كما هو موضح.
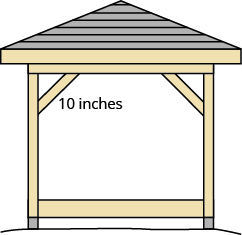
إلى أي مدى يجب أن يربط الخشب من الزاوية إذا أراد أن تكون المسافات من الزاوية متساوية؟ تقريبًا لأقرب عُشر بوصة.
- إجابة
-
الخطوة 1. اقرأ المشكلة. الخطوة 2. حدد ما نبحث عنه. المسافة من الزاوية التي يجب ربط القوس بها الخطوة 3. اسم. اختر متغيرًا لتمثيله. ارسم الشكل وقم بتسميته بالمعلومات المعطاة. دع\(x=\) المسافة من الزاوية. 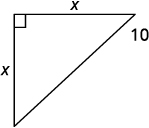
الخطوة 4. ترجم. اكتب الصيغة المناسبة واستبدلها. \(a^2+b^2=c^2\)\(x^2+x^2=10^2\) الخطوة 5. حل المعادلة. اعزل المتغير.
استخدم تعريف الجذر التربيعي.قم بالتبسيط. تقريبًا لأقرب جزء من عشرة.
\( \begin{align*} 2x^2 &= 100 \\ \\ x^2 &=50 \\ \\ x &= \sqrt{50} \\ \\ x &≈7.1 \end{align*}\)
الخطوة 6. تحقق. \( \begin{align*} a^2+b^2 &= c^2 \\ (7.1)^2+(7.1)^2 &≈10^2 \; \;\;\;\; \text{Yes.} \end{align*}\)
الخطوة 7. أجب على السؤال. يجب أن يربط كلفن كل قطعة من الخشب بحوالي 7.1 بوصة من الزاوية.
يضع جون قاعدة سلم\(13\) بطول 5 أقدام من جدار منزله كما هو موضح في الشكل. إلى أي مدى يصل السلم إلى الجدار؟

- إجابة
-
يصل السلم إلى\(12\) القدمين.
يريد راندي ربط سلسلة من الأضواء\(17\) بطول قدم بأعلى سارية\(15\) القدم في مركبه الشراعي, كما هو موضح في الشكل. إلى أي مدى يجب أن يربط نهاية خيط الضوء من قاعدة الصاري؟
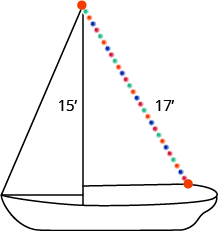
- إجابة
-
يجب أن يربط\(8\) أقدام الأضواء من قاعدة الصاري.
قم بالوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات إضافية وممارسة حل متغير في المعادلات الحرفية.
- حل المعادلات الحرفية
المفاهيم الرئيسية
- كيفية حل تطبيقات الهندسة
- اقرأ المشكلة وتأكد من فهم جميع الكلمات والأفكار.
- حدد ما تبحث عنه.
- قم بتسمية ما تبحث عنه عن طريق اختيار متغير لتمثيله. ارسم الشكل وقم بتسميته بالمعلومات المعطاة.
- ترجم إلى معادلة بكتابة الصيغة أو النموذج المناسب للموقف. استبدل المعلومات المعطاة.
- حل المعادلة باستخدام تقنيات الجبر الجيدة.
- تحقق من الإجابة في المشكلة وتأكد من أنها منطقية.
- أجب على السؤال بجملة كاملة.
- نظرية فيثاغورس
- في أي مثلث قائم الزاوية، حيث a و b هما أطوال الأرجل، و c هو طول الوتر، يساوي مجموع مربعات أطوال الساقين مربع طول الوتر.