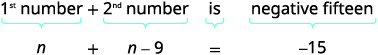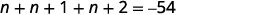2.3: استخدم استراتيجية حل المشكلات

أهداف التعلم

في نهاية هذا القسم، ستكون قادرًا على:

• استخدم استراتيجية حل المشكلات لمشاكل الكلمات
• حل مشاكل عدد الكلمات
• حل تطبيقات النسبة المئوية
• حل تطبيقات الاهتمامات البسيطة

قبل البدء، قم بإجراء اختبار الاستعداد هذا.

1. ترجم عبارة «ستة أقل من مرتين\(x\)» إلى تعبير جبري.
   إذا فاتتك هذه المشكلة، راجع [link].
2. قم بتحويل 4.5% إلى رقم عشري.
   إذا فاتتك هذه المشكلة، راجع [link].
3. قم بتحويل 0.6 إلى نسبة مئوية.
   إذا فاتتك هذه المشكلة، راجع [link].

هل سبق لك أن واجهت أي تجارب سلبية في الماضي مع مشاكل الكلمات؟ عندما نشعر بأننا لا نملك السيطرة، ونستمر في تكرار الأفكار السلبية، نضع حواجز أمام النجاح. اعلم أن تجاربك السلبية مع مشاكل الكلمات هي في الماضي. للمضي قدمًا، تحتاج إلى تهدئة مخاوفك وتغيير مشاعرك السلبية.

ابدأ بقائمة جديدة وابدأ في التفكير بأفكار إيجابية. قد يكون تكرار بعض العبارات التالية مفيدًا لتحويل أفكارك إلى إيجابية. التفكير في الأفكار الإيجابية هو الخطوة الأولى نحو النجاح.

• أعتقد أنني أستطيع! أعتقد أنني أستطيع!
• بينما كانت مشاكل الكلمات صعبة في الماضي، أعتقد أنه يمكنني تجربتها الآن.
• أنا مستعد بشكل أفضل الآن - أعتقد أنني سأبدأ في فهم مشاكل الكلمات.
• أنا قادر على حل المعادلات لأنني مارست العديد من المشكلات وحصلت على المساعدة عندما كنت بحاجة إليها - يمكنني تجربة ذلك مع مشاكل الكلمات.
• قد يستغرق الأمر بعض الوقت، ولكن يمكنني البدء في حل مشاكل الكلمات.
• أنت الآن مستعد جيدًا وأنت مستعد للنجاح. إذا كنت تتحكم وتعتقد أنك يمكن أن تكون ناجحًا، فستتمكن من إتقان مشاكل الكلمات.

استخدم إستراتيجية حل المشكلات لمشاكل الكلمات

الآن بعد أن تمكنا من حل المعادلات، نحن على استعداد لتطبيق مهاراتنا الجديدة على المسائل الكلامية. سنطور استراتيجية يمكننا استخدامها لحل أي مشكلة كلامية بنجاح.

مثال\(\PageIndex{1}\)

يبلغ تساقط الثلوج السنوي العادي في منتجع التزلج المحلي 12 بوصة أكثر من ضعف الكمية التي تلقاها الموسم الماضي. تساقط الثلوج السنوي العادي هو 62 بوصة. ماذا كان تساقط الثلوج في الموسم الماضي في منتجع التزلج؟

الحل:

الخطوة 1. اقرأ المشكلة.
الخطوة 2. حدد ما تبحث عنه.	ماذا كان تساقط الثلوج في الموسم الماضي؟
الخطوة 3. قم بتسمية ما نبحث عنه واختر متغيرًا لتمثيله.	دع تساقط الثلوج\(s=\) في الموسم الماضي.
الخطوة 4. ترجم. كرر المشكلة في جملة واحدة مع جميع المعلومات المهمة.
ترجم إلى معادلة.
الخطوة 5. حل المعادلة.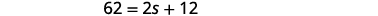
اطرح 12 من كل جانب.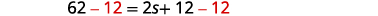
قم بالتبسيط.
قسّم كل جانب على اثنين.
قم بالتبسيط.
الخطوة 6. تحقق: أولاً، هل إجابتنا معقولة؟ نعم، يبدو وجود 25 بوصة من الثلج أمرًا جيدًا. تقول المشكلة أن تساقط الثلوج العادي يزيد بمقدار 12 بوصة عن ضعف عدد الموسم الماضي. ضعف 25 هو 50 و 12 أكثر من ذلك هو 62.
الخطوة 7. أجب على السؤال.	كان تساقط الثلوج في الموسم الماضي 25 بوصة.

جرب ذلك! \(\PageIndex{1}\)

اشترى غييرمو الكتب المدرسية والدفاتر من متجر الكتب. كان عدد الكتب المدرسية ثلاثة أكثر من ضعف عدد دفاتر الملاحظات. اشترى سبعة كتب مدرسية. كم عدد أجهزة الكمبيوتر المحمولة التي اشتراها؟

إجابة

اشترى اثنين من أجهزة الكمبيوتر المحمولة

جرب ذلك! \(\PageIndex{2}\)

عمل جيري على ألغاز سودوكو وألغاز الكلمات المتقاطعة هذا الأسبوع. عدد ألغاز سودوكو التي أكملها هو ثمانية أكثر من ضعف عدد الألغاز المتقاطعة. أكمل 22 لغز سودوكو. كم عدد الألغاز المتقاطعة التي قام بها?

إجابة

لقد قام بسبع ألغاز متقاطعة

نحن نلخص استراتيجية فعالة لحل المشكلات.

إستراتيجية حل المشكلات لمشاكل الكلمات

1. اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
2. حدد ما تبحث عنه.
3. قم بتسمية ما تبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.
4. ترجم إلى معادلة. قد يكون من المفيد إعادة ذكر المشكلة في جملة واحدة مع جميع المعلومات المهمة. ثم ترجم الجملة الإنجليزية إلى معادلة الجبر.
5. حل المعادلة باستخدام تقنيات الجبر المناسبة.
6. تحقق من الإجابة في المشكلة للتأكد من أنها منطقية.
7. أجب على السؤال بجملة كاملة.

حل مشاكل الكلمات العددية

سنقوم الآن بتطبيق استراتيجية حل المشكلات على «مشاكل الكلمات العددية». تعطي مشاكل الكلمات العددية بعض الأدلة حول رقم واحد أو أكثر ونستخدم هذه القرائن لكتابة معادلة. توفر مشاكل الكلمات العددية ممارسة جيدة لاستخدام إستراتيجية حل المشكلات.

مثال\(\PageIndex{2}\)

مجموع سبعة ضرب العدد وثمانية يساوي ستة وثلاثين. ابحث عن الرقم.

الحل:

الخطوة 1. اقرأ المشكلة.
الخطوة 2. حدد ما تبحث عنه.	الرقم
الخطوة 3. قم بتسمية ما تبحث عنه و اختر متغيرًا لتمثيله.	دع\(n=\) الرقم.
الخطوة 4. ترجمة: كرر المشكلة كجملة واحدة. ترجم إلى معادلة.
الخطوة 5. حل المعادلة. اطرح ثمانية من كل جانب وقم بتبسيطه. قسّم كل جانب على سبعة وقم بالتبسيط.
الخطوة 6. تحقق. هل مجموع سبعة في أربعة زائد ثمانية يساوي 36؟ \[\begin{align*} 7·4+8 & \stackrel{?}{=}36 \\ 28+8 & \stackrel{?}{=}36 \\ 36 & =36✓ \end{align*}\]
الخطوة 7. أجب على السؤال.	الرقم هو 4.

هل لاحظت أننا تركنا بعض الخطوات عند حل هذه المعادلة؟ إذا لم تكن مستعدًا بعد لترك هذه الخطوات، فاكتب العدد الذي تريده.

جرب ذلك! \(\PageIndex{3}\)

مجموع أربعة أضعاف العدد واثنين هو أربعة عشر. ابحث عن الرقم.

إجابة

\(3\)

جرب ذلك! \(\PageIndex{4}\)

مجموع ثلاثة في العدد وسبعة يساوي خمسة وعشرين. ابحث عن الرقم.

إجابة

\(6\)

تطلب منا بعض مشاكل الكلمات الرقمية العثور على رقمين أو أكثر. قد يكون من المغري تسميتها جميعًا بمتغيرات مختلفة، ولكن حتى الآن، قمنا بحل المعادلات بمتغير واحد فقط. من أجل تجنب استخدام أكثر من متغير واحد، سنحدد الأرقام من حيث نفس المتغير. تأكد من قراءة المشكلة بعناية لاكتشاف كيفية ارتباط جميع الأرقام ببعضها البعض.

مثال\(\PageIndex{3}\)

مجموع الرقمين هو سالب خمسة عشر. رقم واحد أقل بتسعة من الآخر. ابحث عن الأرقام.

الحل:

الخطوة 1. اقرأ المشكلة.
الخطوة 2. حدد ما تبحث عنه.	رقمين
الخطوة 3. قم بتسمية ما تبحث عنه باختيار متغير لتمثيل الرقم الأول. «رقم واحد أقل بتسعة من الآخر.»	\(n=1^{\text{st}}\)رقم السماح. \(n−9=2^{\text{nd}}\)رقم
الخطوة 4. ترجم. اكتب كجملة واحدة. ترجم إلى معادلة.	مجموع الرقمين هو سالب خمسة عشر.
الخطوة 5. حل المعادلة. اجمع بين المصطلحات المتشابهة. أضف تسعة إلى كل جانب وقم بالتبسيط. قم بالتبسيط.	\(n+n-9=-15\) \(2 n=-6\)
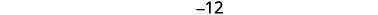الخطوة 6. تحقق. هل\(−12\) تسعة أقل من\(−3\)؟ \[\begin{align*}−3−9 & \stackrel{?}{=}−12 \\ −12 & =−12✓ \end{align*}\]هو مجموعهم\(−15?\)\[\begin{align*} −3+(−12) & \stackrel{?}{=}−15 \\ −15 & =−15✓ \end{align*}\]
الخطوة 7. أجب على السؤال.	الأرقام هي\(−3\) و\(−12\).

جرب ذلك! \(\PageIndex{5}\)

مجموع رقمين هو سالب ثلاثة وعشرين. رقم واحد أقل بسبعة من الآخر. ابحث عن الأرقام.

إجابة

\(−15,−8\)

جرب ذلك! \(\PageIndex{6}\)

مجموع عددين هو سالب ثمانية عشر. رقم واحد يزيد بأربعين عن الآخر. ابحث عن الأرقام.

إجابة

\(−29,11\)

تتضمن بعض مشكلات الأرقام أعدادًا صحيحة متتالية. الأعداد الصحيحة المتتالية هي أعداد صحيحة تتبع بعضها البعض على الفور. أمثلة على الأعداد الصحيحة المتتالية هي:

\[\begin{array}{rrrr} 1, & 2, & 3, & 4 \\ −10, & −9, & −8, & −7\\ 150, & 151, & 152, & 153 \end{array}\nonumber\]

لاحظ أن كل رقم يزيد بمقدار واحد عن الرقم الذي يسبقه. لذلك، إذا حددنا العدد الصحيح الأول باعتباره العدد\(n,\) الصحيح التالي على التوالي\(n+1\). الواحد بعد ذلك يزيد\(n+1\) بمقدار واحد عن\(n+1+1\)، وهو كذلك\(n+2\).

\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]

سنستخدم هذا الترميز لتمثيل الأعداد الصحيحة المتتالية في المثال التالي.

مثال\(\PageIndex{4}\)

ابحث عن ثلاثة أعداد صحيحة متتالية مجموعها\(−54\).

الحل:

الخطوة 1. اقرأ المشكلة.
الخطوة 2. حدد ما تبحث عنه.	ثلاثة أعداد صحيحة متتالية
الخطوة 3. قم بتسمية كل رقم من الأرقام الثلاثة	دعونا\(n=1^{\text{st}} \text{integer}\). \(n+1=2^{\text{nd}} \text{consecutive integer}\)\(n+2=3^{\text{rd}} \text{consecutive integer}\)
الخطوة 4. ترجم. كرر كجملة واحدة. ترجم إلى معادلة.	مجموع الأعداد الصحيحة الثلاثة هو\(−54\).
الخطوة 5. حل المعادلة. اجمع بين المصطلحات المتشابهة. اطرح ثلاثة من كل جانب. قسّم كل جانب على ثلاثة.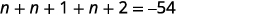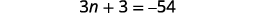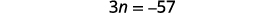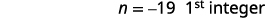
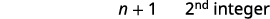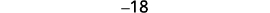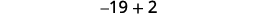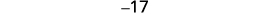الخطوة 6. تحقق. \(\begin{align*} −19+(−18)+(−17) & =−54 \\ −54 & =−54✓ \end{align*}\)
الخطوة 7. أجب على السؤال.	الأعداد الصحيحة الثلاثة المتتالية هي −17 و−18 و−19.

جرب ذلك! \(\PageIndex{7}\)

ابحث عن ثلاثة أعداد صحيحة متتالية مجموعها\(−96\).

إجابة

\(−33,−32,−31\)

جرب ذلك! \(\PageIndex{8}\)

ابحث عن ثلاثة أعداد صحيحة متتالية مجموعها\(−36\).

إجابة

\(−13,−12,−11\)

الآن وقد عملنا مع الأعداد الصحيحة المتتالية، سنقوم بتوسيع عملنا ليشمل الأعداد الصحيحة المتتالية والأعداد الفردية المتتالية. الأعداد الصحيحة المتتالية هي حتى الأعداد الصحيحة التي تتبع بعضها البعض على الفور. أمثلة على الأعداد الصحيحة الزوجية المتتالية هي:

\[24, 26, 28\nonumber\]

\[−12,−10,−8\nonumber\]

لاحظ أن كل عدد صحيح يزيد بمقدار اثنين عن الرقم الذي يسبقه. إذا اتصلنا بالأول،\(n,\) فسيكون التالي هو\(n+2\). الشخص الذي يليه سيكون\(n+2+2\) أو\(n+4\).

\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]

الأعداد الصحيحة الفردية المتتالية هي أعداد صحيحة فردية تتبع بعضها البعض على الفور. ضع في اعتبارك الأعداد الصحيحة الفردية المتتالية 63 و 65 و 67.

\[63, 65, 67\nonumber\]

\[n,n+2,n+4\nonumber\]

\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]

هل يبدو من الغريب إضافة اثنين (رقم زوجي) للحصول على الرقم الفردي التالي؟ هل نحصل على رقم فردي أو رقم زوجي عندما نضيف 2 إلى 3؟ إلى 11؟ إلى 47؟

سواء كانت المشكلة تتطلب أرقامًا زوجية متتالية أو أرقامًا فردية، فليس عليك القيام بأي شيء مختلف. لا يزال النمط هو نفسه - للوصول إلى العدد الفردي التالي أو العدد الصحيح التالي، أضف اثنين.

مثال\(\PageIndex{5}\)

ابحث عن ثلاثة أعداد صحيحة زوجية متتالية مجموعها\(120\).

الحل:

الخطوة 1. اقرأ المشكلة.
الخطوة 2. حدد ما تبحث عنه.	ثلاثة أعداد صحيحة من سبعة أرقام متتالية
الخطوة 3. قم بتسمية كل رقم من الأرقام الثلاثة	دعونا\(n = 1^{\text{st}} \text{consecutive even integer}\). \(n + 2 = 2^{\text{nd}} \text{consecutive even integer}\). \(n + 4 = 3^{\text{rd}} \text{consecutive even integer}\).
الخطوة 4. ترجم. كرر كجملة واحدة. ترجم إلى معادلة.	مجموع الأعداد الصحيحة الثلاثة الزوجية هو 120 \(n + n + 2 + n + 4 = 120\)
الخطوة 5. حل المعادلة. اجمع بين المصطلحات المتشابهة. اطرح ثلاثة من كل جانب. قسّم كل جانب على ثلاثة.	\(n + n + 2 + n + 4 = 120\) \(\begin{aligned} &{3n+6=120} \\ &{3n=114} \\ &{n=38} &{1^\text{st} \text{integer}}\end{aligned}\) \(\begin{aligned} &{n+2} & &{2^\text{nd} \text{integer}}\\ &{38+2} \\ &{40} \end{aligned}\) \(\begin{aligned} &{n+2} & &{3^\text{rd} \text{integer}}\\ &{38+4} \\ &{42} \end{aligned}\)
الخطوة 6. تحقق. \(\begin{align*} 38 + 40 + 42 &\overset{?}{=} &120 \nonumber\\ 120 &=& 120 &✓ \nonumber\end{align*}\)
الخطوة 7. أجب على السؤال.	الأعداد الصحيحة الثلاثة المتتالية هي 38 و40 و42.

جرب ذلك! \(\PageIndex{9}\)

ابحث عن ثلاثة أعداد صحيحة زوجية متتالية مجموعها 102.

إجابة

\(32, 34, 36\)

جرب ذلك! \(\PageIndex{10}\)

ابحث عن ثلاثة أعداد صحيحة زوجية متتالية مجموعها\(−24\).

إجابة

\(−10,−8,−6\)

عندما تكون مشكلة الأرقام في سياق الحياة الحقيقية، فإننا لا نزال نستخدم نفس الاستراتيجيات التي استخدمناها في الأمثلة السابقة.

مثال\(\PageIndex{6}\)

يكسب الزوجان معًا 110,000 دولار سنويًا. تكسب الزوجة 16 ألف دولار أقل من ضعف ما يكسبه زوجها. ماذا يكسب الزوج؟

الحل:

الخطوة 1. اقرأ المشكلة.
الخطوة 2. حدد ما تبحث عنه.	كم يكسب الزوج؟
الخطوة 3. قم بتسمية كل رقم من الأرقام الثلاثة	دعونا\(h=\text{the amount the husband earns}\).
الخطوة 4. ترجم. كرر المشكلة في جملة واحدة مع جميع المعلومات المهمة. ترجم إلى معادلة.	\(2h−16,000=\text{the amount the wife earns}.\)يكسب الزوج والزوجة معًا 110,000 دولار. \(h+2h−16,000=110,000\)
الخطوة 5. حل المعادلة. اجمع بين المصطلحات المتشابهة. أضف 16000 إلى كلا الجانبين وقم بالتبسيط. قسّم كل جانب على ثلاثة.	\(h+2h−16,000=110,000\) \(\begin{aligned} &{3h−16,000=110,000} \\ &{3h=126,000} \\ &{h=42,000} &{\text{amount husband earns}} \end{aligned}\) \(\begin{aligned} &{2h−16,000} &{\text{ amount wife earns}} \\ &{2(42,000)−16,000} \\ &{84,000−16,000} \\ &{68,000} \end{aligned}\)
الخطوة 6. تحقق. إذا كانت الزوجة تكسب 68,000 دولار والزوج 42 ألف دولار، فهل هذا هو 110,000 دولار؟ نعم!
الخطوة 7. أجب على السؤال.	يكسب الزوج 42,000 دولار في السنة.

 

وفقًا للرابطة الوطنية لتجار السيارات، بلغ متوسط تكلفة السيارة في عام 2014 28400 دولار. كان هذا أقل بـ 1,600 دولار من ستة أضعاف التكلفة في عام 1975. ما هو متوسط تكلفة السيارة في عام 1975؟

إجابة

كان متوسط التكلفة 5,000 دولار.

جرب ذلك! \(\PageIndex{11}\)

تظهر بيانات تعداد الولايات المتحدة أن متوسط سعر المنزل الجديد في الولايات المتحدة في نوفمبر 2014 كان 280,900 دولار. كان هذا 10700 دولار أكثر من 14 ضعف السعر في نوفمبر 1964. ما هو متوسط سعر المنزل الجديد في نوفمبر 1964؟

إجابة

كان متوسط السعر 19,300 دولار.

حل تطبيقات النسبة المئوية

هناك عدة طرق لحل معادلات النسبة المئوية. في الجبر، يكون الأمر أسهل إذا قمنا بترجمة الجمل الإنجليزية إلى معادلات جبرية ثم حل المعادلات. تأكد من تغيير النسبة المئوية المعطاة إلى عدد عشري قبل استخدامها في المعادلة.

مثال\(\PageIndex{7}\)

ترجمة وحل:

1. ما العدد 45% من 84؟
2. 8.5% من أي مبلغ هو 4.76 دولار؟
3. 168 هي ما النسبة المئوية من 112؟

الحل:

أ.

ترجم إلى الجبر. دعونا n = الرقم.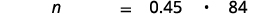
اضرب.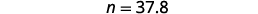
	37.8 هو 45% من 84.

ب.

ترجم. دع\(n =\) المبلغ.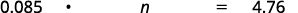
اضرب.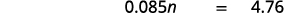
قسّم كلا الجانبين بمقدار 0.085 وقم بالتبسيط.
	8.5٪ من 56 دولارًا هو 4.76 دولارًا

ج.

يُطلب منا العثور على النسبة المئوية، لذلك يجب أن نحصل على النتيجة في شكل النسبة المئوية.
ترجم إلى الجبر. دع\(p = \) النسبة المئوية.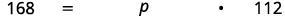
اضرب.
قسّم كلا الجانبين على 112 وقم بالتبسيط.
تحويل إلى النسبة المئوية.
	168 هو 150% من 112.

جرب ذلك! \(\PageIndex{12}\)

ترجمة وحل:

1. ما العدد 45% من 80؟
2. 7.5% من أي مبلغ هو 1.95 دولار؟
3. ما مقدار ١١٠ في المئة من ٨٨؟

إجابة

أ. 36 ب. 26 دولارًا ج.\(125 \% \)

جرب ذلك! \(\PageIndex{13}\)

ترجمة وحل:

1. ما هو الرقم 55% من 60؟
2. 8.5٪ من أي مبلغ هو 3.06 دولار؟
3. 126 هي ما النسبة المئوية من 72؟

إجابة

أ. 33 ب. 36 دولارًا ج.\(175 \% \)

الآن لدينا إستراتيجية حل المشكلات للإشارة إليها، وتدربنا على حل معادلات النسبة المئوية الأساسية، نحن على استعداد لحل تطبيقات النسبة المئوية. تأكد من أن تسأل نفسك ما إذا كانت إجابتك النهائية منطقية - نظرًا لأن العديد من التطبيقات التي سنحلها تتضمن مواقف يومية، يمكنك الاعتماد على تجربتك الخاصة.

مثال\(\PageIndex{8}\)

جاء في الملصق الموجود على زبادي أودري أن الحصة الواحدة توفر 12 جرامًا من البروتين، وهو 24٪ من الكمية اليومية الموصى بها. ما إجمالي الكمية اليومية الموصى بها من البروتين؟

الحل:

ما الذي يُطلب منك العثور عليه؟	ما إجمالي كمية البروتين الموصى بها؟
اختر متغيرًا لتمثيله.	دع الكمية\(a=\) الإجمالية من البروتين.
اكتب جملة تعطي المعلومات للعثور عليها.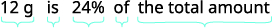
ترجم إلى معادلة.
حل.
تحقق: هل هذا منطقي؟ نعم، يمثل 24٪ تقريبًا\(\frac{1}{4}\) من الإجمالي و 12 يمثل حوالي\(\frac{1}{4}\) 50.
اكتب جملة كاملة للإجابة على السؤال.	كمية البروتين الموصى بها هي 50 جرامًا.

جرب ذلك! \(\PageIndex{14}\)

تحتوي حصة واحدة من حبوب القمح المربعة على 7 غرامات من الألياف، أي 28٪ من الكمية اليومية الموصى بها. ما إجمالي الكمية اليومية الموصى بها من الألياف؟

إجابة

25 غرامًا

جرب ذلك! \(\PageIndex{15}\)

تحتوي حصة واحدة من حبوب الأرز على 190 ملغ من الصوديوم، وهو 8٪ من الكمية اليومية الموصى بها. ما إجمالي الكمية اليومية الموصى بها من الصوديوم؟

إجابة

2,375 ملغم

تذكر أن تضع الإجابة في النموذج المطلوب. في المثال التالي نبحث عن النسبة المئوية.

مثال\(\PageIndex{9}\)

تخطط فيرونيكا لصنع الكعك من المزيج. تقول الحزمة أن كل فطيرة ستكون 240 سعرة حرارية و 60 سعرة حرارية ستكون من الدهون. ما النسبة المئوية من إجمالي السعرات الحرارية من الدهون؟

الحل:

ما الذي يُطلب منك العثور عليه؟	ما النسبة المئوية للدهون من إجمالي السعرات الحرارية؟
اختر متغيرًا لتمثيله.	دع\(p=\) نسبة الدهون.
اكتب جملة تعطي المعلومات للعثور عليها.
ترجم الجملة إلى معادلة.
اضرب.
قسّم كلا الجانبين على 240.
ضع في شكل النسبة المئوية.
تحقق: هل هذا منطقي؟ نعم،\(25 \% \) هو الربع؛ 60 هو ربع 240. لذلك، من\(25 \%\) المنطقي.
اكتب جملة كاملة للإجابة على السؤال.	الدهون هي من إجمالي السعرات الحرارية في كل فطيرة.\(25 \%\)

جرب ذلك! \(\PageIndex{16}\)

تلقت ميتزي بعض البراونيز الذواقة كهدية. قال الغلاف إن كل كعكة براوني بنسبة 28% تحتوي على 480 سعرة حرارية وتحتوي على 240 سعرة حرارية من الدهون. ما النسبة المئوية من إجمالي السعرات الحرارية في كل كعكة براوني التي تأتي من الدهون؟ قرِّب الإجابة لأقرب نسبة مئوية صحيحة.

إجابة

50%

جرب ذلك! \(\PageIndex{17}\)

يقول المزيج الذي يخطط ريكاردو لاستخدامه في صنع البراونيز أن كل براوني سيكون 190 سعرًا حراريًا، و 76 سعرًا حراريًا من الدهون. ما النسبة المئوية من إجمالي السعرات الحرارية من الدهون؟ قرِّب الإجابة لأقرب نسبة مئوية صحيحة.

إجابة

40%

غالبًا ما يكون من المهم في العديد من المجالات - الأعمال والعلوم والثقافة الشعبية - التحدث عن مقدار زيادة المبلغ أو انخفاضه خلال فترة زمنية معينة. يتم التعبير عن هذه الزيادة أو النقصان عمومًا كنسبة مئوية وتسمى النسبة المئوية للتغير.

للعثور على النسبة المئوية للتغيير، نجد أولاً مقدار التغيير، من خلال إيجاد الفرق بين المبلغ الجديد والمبلغ الأصلي. ثم نجد النسبة المئوية لمقدار التغيير من المبلغ الأصلي.

ابحث عن النسبة المئوية للتغيير

1. ابحث عن مقدار التغيير.

   \[\text{change}= \text{new amount}−\text{original amount}\]

2. ابحث عن النسبة المئوية لمقدار التغيير من المبلغ الأصلي.

   التغيير هو ما النسبة المئوية من المبلغ الأصلي؟

مثال\(\PageIndex{10}\)

في الآونة الأخيرة، اقترح حاكم كاليفورنيا رفع رسوم الكليات المجتمعية من 36 دولارًا للوحدة إلى 46 دولارًا للوحدة. ابحث عن النسبة المئوية للتغير. (قرِّب إلى أقرب عُشر بالمائة.)

الحل:

ابحث عن مقدار التغيير.	\(46−36=10\)
ابحث عن النسبة المئوية.	التغيير هو ما النسبة المئوية من المبلغ الأصلي؟
دع\(p=\) النسبة المئوية.
ترجم إلى معادلة.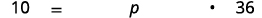
قم بالتبسيط.	\(10=36 p\)
قسّم كلا الجانبين بمقدار 36.	\(0.278 \approx p\)
التغيير إلى شكل النسبة المئوية؛ تقريبه إلى أقرب جزء من عشرة	\(27.8 \% \approx p\)
اكتب جملة كاملة للإجابة على السؤال.	الرسوم الجديدة هي\(27.8 \% \) زيادة تقريبًا عن الرسوم القديمة.
تذكر تقريب القسمة إلى أقرب جزء من ألف لتقريب النسبة المئوية لأقرب جزء من عشرة.

جرب ذلك! \(\PageIndex{18}\)

ابحث عن النسبة المئوية للتغير. (قرِّب إلى أقرب عُشر بالمائة.) في عام 2011، زادت مصلحة الضرائب الأمريكية تكلفة الأميال القابلة للخصم إلى 55.5 سنتًا من 51 سنتًا.

إجابة

\(8.8 \% \)

جرب ذلك! \(\PageIndex{19}\)

ابحث عن النسبة المئوية للتغير. (قرِّب إلى أقرب عُشر بالمائة.) في عام 1995، كانت أجرة الحافلة القياسية في شيكاغو 1.50 دولار. في عام 2008، كانت أجرة الحافلة القياسية 2.25.

إجابة

\(50%\)

تطبيقات الخصم وهامش الربح شائعة جدًا في إعدادات البيع بالتجزئة.

عند شراء سلعة معروضة للبيع، تم خصم السعر الأصلي بمبلغ معين بالدولار. يتم استخدام معدل الخصم، الذي يتم تقديمه عادةً كنسبة مئوية، لتحديد مبلغ الخصم. لتحديد مقدار الخصم، نقوم بضرب معدل الخصم بالسعر الأصلي.

يُطلق على السعر الذي يدفعه بائع التجزئة مقابل عنصر ما التكلفة الأصلية. يقوم بائع التجزئة بعد ذلك بإضافة هامش إلى التكلفة الأصلية للحصول على قائمة الأسعار، وهو السعر الذي يبيع به السلعة. عادةً ما يتم حساب الهامش كنسبة مئوية من التكلفة الأصلية. لتحديد مقدار الزيادة، اضرب معدل الزيادة بالتكلفة الأصلية.

خصم

\[ \begin{align*} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align*}\]

يجب أن يكون سعر البيع دائمًا أقل من السعر الأصلي.

وضع العلامات

\[\begin{align*} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align*}\]

يجب أن تكون قائمة الأسعار دائمًا أكثر من التكلفة الأصلية.

مثال\(\PageIndex{11}\)

اشترى معرض ليام للفنون لوحة بتكلفة أصلية قدرها 750 دولارًا. قام ليام برفع السعر بنسبة 40٪. ابحث

1. مقدار الترميز و
2. قائمة أسعار اللوحة.

الحل:

أ.

حدد ما يُطلب منك البحث عنه، واختر متغيرًا لتمثيله.	ما مقدار الهامش؟ \(m=\)دع مقدار الترميز.
اكتب جملة تعطي المعلومات للعثور عليها.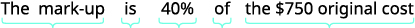
ترجم إلى معادلة.
حل المعادلة.
اكتب جملة كاملة.	كان الهامش على اللوحة 300 دولار.

ب.

حدد ما يُطلب منك البحث عنه، واختر متغيرًا لتمثيله.	ما هي قائمة الأسعار؟ \(p=\)دع قائمة الأسعار.
اكتب جملة تعطي المعلومات للعثور عليها.
ترجم إلى معادلة.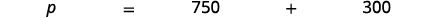
حل المعادلة.
تحقق.	هل سعر القائمة أكثر من التكلفة الأصلية؟ هل يزيد مبلغ 1,050 دولارًا عن 750 دولارًا؟ نعم.
اكتب جملة كاملة.	كانت قائمة أسعار اللوحة 1050 دولارًا.

جرب ذلك! \(\PageIndex{20}\)

ابحث عن أ. مبلغ الترميز و ب. قائمة الأسعار: اشترى متجر موسيقى Jim غيتارًا بالتكلفة الأصلية 1,200 دولار. قام جيم برفع السعر بنسبة 50٪.

إجابة

(أ) 600 دولار (800 1 دولار)

جرب ذلك! \(\PageIndex{21}\)

ابحث عن أ. مبلغ الزيادة و ب. قائمة الأسعار: اشترى متجر إعادة بيع السيارات سيارة Pablo Toyota مقابل 8,500 دولار. لقد رفعوا السعر بنسبة 35٪.

إجابة

(أ) 975 2 دولاراً (ب) 475 11 دولاراً

حل تطبيقات الاهتمامات البسيطة

الاهتمام هو جزء من حياتنا اليومية. من الفائدة المكتسبة على مدخراتنا إلى الفائدة التي ندفعها على قرض السيارة أو ديون بطاقات الائتمان، لدينا جميعًا بعض الخبرة في الاهتمام بحياتنا.

يُطلق على المبلغ المالي الذي تودعه مبدئيًا في أحد البنوك اسم رأس المال،\(P,\) ويدفع لك البنك الفائدة،\(I.\) وعندما تحصل على قرض، تدفع فائدة على المبلغ الذي تقترضه، والذي يُطلق عليه أيضًا رأس المال.

في كلتا الحالتين، يتم احتساب الفائدة كنسبة مئوية معينة من رأس المال، تسمى سعر الفائدة،\(r.\) وعادة ما يتم التعبير عن سعر الفائدة كنسبة مئوية في السنة، ويتم حسابه باستخدام المكافئ العشري للنسبة المئوية. يمثل المتغير\(t,\) (للوقت) عدد السنوات التي يتم فيها حفظ الأموال أو اقتراضها.

يتم احتساب الفائدة على أنها فائدة بسيطة أو فائدة مركبة. هنا سوف نستخدم الاهتمام البسيط.

اهتمام بسيط

إذا تم استثمار مبلغ من المال،\(P,\) يسمى رأس المال، أو اقتراضه لمدة\(t\) سنوات بمعدل فائدة سنوي،\(r,\) فإن مبلغ الفائدة،\(I,\) المكتسبة أو المدفوعة، هو

\[ \begin{array}{ll} I=Prt \; \; \; \; \; \; \; \; \; \; \; \; \text{where} & { \begin{align*} I &= \text{interest} \\ P &= \text{principal} \\ r &= \text{rate} \\ t &= \text{time} \end{align*}} \end{array}\]

تسمى الفائدة المكتسبة أو المدفوعة وفقًا لهذه الصيغة الفائدة البسيطة.

الصيغة التي نستخدمها لحساب الفائدة هي\(I=Prt\). لاستخدام الصيغة، نستبدل القيم بالمتغيرات المعطاة، ثم نحلها للمتغير المجهول. قد يكون من المفيد تنظيم المعلومات في مخطط.

مثال\(\PageIndex{12}\)

استثمرت أريلي مبلغًا أساسيًا قدره 950 دولارًا في حسابها المصرفي الذي حصل على فائدة بسيطة بسعر فائدة قدره 3٪. ما مقدار الفائدة التي كسبتها في خمس سنوات؟

الحل:

\( \begin{aligned} I & = \; ? \\ P & = \; \$ 950 \\ r & = \; 3 \% \\ t & = \; 5 \text{ years} \end{aligned}\)

\(\begin{array}{ll} \text{Identify what you are asked to find, and choose a} & \text{What is the simple interest?} \\ \text{variable to represent it.} & \text{Let } I= \text{interest.} \\ \text{Write the formula.} & I=Prt \\ \text{Substitute in the given information.} & I=(950)(0.03)(5) \\ \text{Simplify.} & I=142.5 \\ \text{Check.} \\ \text{Is } \$142.50 \text{ a reasonable amount of interest on } \$ \text{ 950?} \; \;\;\;\;\; \;\;\;\;\;\; \\ \text{Yes.} \\ \text{Write a complete sentence.} & \text{The interest is } \$ \text{142.50.} \end{array}\)

جرب ذلك! \(\PageIndex{22}\)

أودعت ناتالي 12,500 دولار في حسابها المصرفي حيث ستكسب فائدة بسيطة بنسبة 4٪. ما مقدار الفائدة التي ستكسبها ناتالي في خمس سنوات؟

إجابة

سوف يكسب 2,500 دولار.

جرب ذلك! \(\PageIndex{23}\)

استثمرت سوزانا رأس مال قدره 36,000 دولار في حسابها المصرفي الذي حصل على فائدة بسيطة بسعر فائدة 6.5%. ما مقدار الفائدة التي كسبتها في ثلاث سنوات؟

إجابة

حصلت على 7,020 دولارًا.

قد تكون هناك أوقات نعرف فيها مقدار الفائدة المكتسبة على أصل معين خلال فترة زمنية معينة، لكننا لا نعرف السعر.

مثال\(\PageIndex{13}\)

اقترضت هانغ 7,500 دولار من والديها لدفع الرسوم الدراسية. في غضون خمس سنوات، دفعت لهم فائدة قدرها 1500 دولار بالإضافة إلى 7500 دولار اقترضتها. ما هو معدل الفائدة البسيطة؟

الحل:

\( \begin{aligned} I & = \; \$ 1500 \\ P & = \; \$ 7500 \\ r & = \; ? \\ t & = \; 5 \text{ years} \end{aligned}\)

\ (\ text {حدد ما يُطلب منك البحث عنه،}\ qquad\ quad\ text {ما هو معدل الفائدة البسيطة؟} \\
\ ابدأ {align*}
&\ text {واختر متغيرًا لتمثيله.} &\ text {Let} r\; &=\;\ النص {معدل الفائدة}\\
&\ النص {اكتب الصيغة.} & I\; &=\; Prt\\
&\ text {استبدل المعلومات المعطاة.} & 1,500\; &=\; (7,500) r (5)\\
&\ نص {اضرب.} & 1,500\; &=\; 37,500r\\\
\\ نص {تقسيم.} & 0.04\; &=\; r\\\
&\ text {التغيير إلى شكل النسبة المئوية} & r\; &=\; 4\%
\ النهاية {align*}\)

تحقق.

\ (\ ابدأ {align*} I\; &=\; الجزء\\
1,500\; &\ stackrel {?} {=}\; (7,500) (0.04) (5)\\
1,500\; &=\; 1,500 ✓\\ النهاية {align*}\)

اكتب جملة كاملة. كان معدل الفائدة\(4\%.\)

جرب ذلك! \(\PageIndex{24}\)

أقرض جيم أخته 5000 دولار لمساعدتها في شراء منزل. في غضون ثلاث سنوات، دفعت له 5000 دولار، بالإضافة إلى فائدة 900 دولار. ما هو معدل الفائدة البسيطة؟

إجابة

كان معدل الفائدة البسيطة 6٪.

جرب ذلك! \(\PageIndex{25}\)

أقرض لورين شقيقه 3000 دولار لمساعدته في شراء سيارة. في غضون أربع سنوات، سدد له شقيقه 3,000 دولار بالإضافة إلى 660 دولارًا في الفائدة. ما هو معدل الفائدة البسيطة؟

إجابة

كان معدل الفائدة البسيطة 5.5٪.

في المثال التالي، يُطلب منا العثور على رأس المال - المبلغ المقترض.

مثال\(\PageIndex{14}\)

قال بيان قرض السيارة الجديد لشون إنه سيدفع 4,866,25 دولارًا كفائدة من سعر فائدة بسيط يبلغ 8.5٪ على مدى خمس سنوات. كم اقترض لشراء سيارته الجديدة؟

الحل:

\( \begin{aligned} I & = \; 4,866.25 \\ P & = \; ? \\ r & = \; 8.5 \% \\ t & = \; 5 \text{ years} \end{aligned}\)

\ (\ text {حدد ما يُطلب منك البحث عنه،}\ qquad\ quad\ text {ما هو المبلغ المقترض (رأس المال)؟} \\
\ ابدأ {align*}
&\ text {واختر متغيرًا لتمثيله.} &\ text {Let} P\; &=\;\ النص {المستعار الرئيسي}\\
&\ النص {اكتب الصيغة.} & I\; &=\; Prt\\
&\ text {استبدل المعلومات المعطاة.} & 4,866.25\; &=\; P (0.085) (5)\\
&\ النص {اضرب.} & 4,866.25\; &=\; 0.425 بكسل\\
&\ نص {تقسيم.} & 11,450\; &=\; P
\ end {align*}\)

تحقق.

\ (\ ابدأ {align*}\\; I\; &=\; الجزء\\
4,866.25\; &\ ستاكريل {?} {=}\; (11,450) (0.085) (5)\\
4,866.25\; &=\; 4,866.25 ✓\ النهاية {align*}\)

اكتب جملة كاملة. كان المدير\($11,450.\)

جرب ذلك! \(\PageIndex{26}\)

لاحظ إدواردو أن أوراق قرض السيارة الجديدة الخاصة به تنص على أنه بسعر فائدة بسيط قدره 7.5٪، سيدفع 6,596.25 دولارًا كفائدة على مدى خمس سنوات. كم اقترض لدفع ثمن سيارته؟

إجابة

دفع 17,590 دولارًا.

جرب ذلك! \(\PageIndex{27}\)

في غضون خمس سنوات، حصل حساب Gloria المصرفي على فائدة قدرها 2,400 دولار بفائدة بسيطة بنسبة 5٪. ما المبلغ الذي أودعته في الحساب؟

إجابة

قامت بإيداع 9,600 دولار.

يمكنك الوصول إلى هذا المورد عبر الإنترنت للحصول على تعليمات وممارسة إضافية باستخدام استراتيجية حل المشكلات.

• بدء المسائل الحسابية

المفاهيم الرئيسية

• كيفية استخدام إستراتيجية حل المشكلات لمشاكل الكلمات
  1. اقرأ المشكلة. تأكد من فهم جميع الكلمات والأفكار.
  2. حدد ما تبحث عنه.
  3. قم بتسمية ما تبحث عنه. اختر متغيرًا لتمثيل تلك الكمية.
  4. ترجم إلى معادلة. قد يكون من المفيد إعادة ذكر المشكلة في جملة واحدة مع جميع المعلومات المهمة. ثم ترجم الجملة الإنجليزية إلى معادلة الجبر.
  5. حل المعادلة باستخدام تقنيات الجبر المناسبة.
  6. تحقق من الإجابة في المشكلة للتأكد من أنها منطقية.
  7. أجب على السؤال بجملة كاملة.
• كيفية العثور على النسبة المئوية للتغيير
  1. ابحث عن مقدار التغيير

     \(\text{change}=\text{new amount}−\text{original amount}\)

  2. ابحث عن النسبة المئوية لمقدار التغيير من المبلغ الأصلي.

     \(\text{change is what percent of the original amount?}\)

• \( \begin{align*} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align*}\)
• \(\begin{align*} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align*}\)
• إذا تم استثمار مبلغ من المال،\(P,\) يسمى رأس المال، أو اقتراضه لمدة سنوات بمعدل فائدة سنوي،\(r,\) فإن مبلغ الفائدة،\(I,\) المكتسبة أو المدفوعة، هو:\[\begin{aligned} &{} &{} &{I=interest} \nonumber\\ &{I=Prt} &{\text{where} \space} &{P=principal} \nonumber\\ &{} &{\space} &{r=rate} \nonumber\\ &{} &{\space} &{t=time} \nonumber \end{aligned}\]