10.2: תורת פיזור נוספת - גלים חלקיים

גלי מטוס וגלים חלקיים

אנו שוקלים את הפתרון למשוואת שרדינגר לפיזור גל מישור נכנס בכיוון z על ידי פוטנציאל הממוקם באזור ליד המקור, כך שלפונקציית הגל הכוללת מעבר לטווח הפוטנציאל יש את הצורה \[ \psi(r,\theta,\varphi)= e^{ikr\cos\theta}+f(\theta,\varphi)\frac{e^{ikr}}{r}. \label{10.2.1}\]

הנורמליזציה הכוללת אינה מעוררת דאגה, אנו מעוניינים רק בשבריר הגל הנכנס המפוזר. ברור שהזרם היוצא שנוצר על ידי פיזור לזווית מוצקה \(d\Omega\) בזווית \(\theta, \varphi\) \(|f(\theta,\varphi)|^2d\Omega\) מוכפל בגורם מהירות המופיע גם בגל הנכנס.

פוטנציאלים רבים בטבע הם סימטריים כדורית, או כמעט כך, ומבחינת תיאורטיקן יהיה נחמד אם הניסויים יוכלו לנצל את הסימטריה הזו על ידי סידור לשלוח גלים כדוריים המתאימים למומנטה זוויתית שונה במקום לשבור את הסימטריה על ידי בחירת כיוון מסוים. למרבה הצער, קשה לסדר את זה, ועלינו להסתפק בסימטריה האזימוטלית הנותרת של סיבובים לגבי כיוון הקורה הבולטת.

אולם למעשה, ניתוח מלא של הגלים המפוזרים היוצאים מגל מישור נכנס מניב את אותו מידע כמו פיזור הגלים הכדוריים. הסיבה לכך היא שגל מישורי יכול למעשה להיכתב כסכום על גלים כדוריים: \[ e^{i\vec{k}\cdot\vec{r}}=e^{ikr\cos\theta}=\sum_l i^l(2l+1)j_l(kr)P_l(\cos\theta) \label{10.2.2}\]

בהדמיה של גל מישור זה הזורם על פני המקור, ברור שבמונחים כדוריים גל המישור מכיל גלים כדוריים נכנסים ויוצאים כאחד. כפי שנדון ביתר פירוט בעמודים הבאים, הפונקציה האמיתית \(j_l(kr)\) היא גל עומד, המורכב מגלים נכנסים ויוצאים בעלי משרעת שווה.

אנו, כמובן, מעוניינים רק בגלים הכדוריים היוצאים שמקורם בפיזור מהפוטנציאל, ולכן עלינו להיזהר שלא לבלבל בין מרכיבי הגל היוצא הקיימים של גל המישור לבין הגלים היוצאים החדשים הנוצרים מהפוטנציאל.

הפונקציות הרדיאליות \(j_l(kr)\) המופיעות בהתרחבות לעיל של גל מישור במרכיביו הכדוריים הן פונקציות הבסל הכדוריות, הנדונות להלן. הסימטריה הסיבובית האזימוטלית של גל מישור+פוטנציאל כדורי סביב כיוון הגל הנכנס מבטיחה שהתלות הזוויתית של פונקציית הגל היא פשוט, לא. \(P_l(\cos\theta)\) \(Y_{lm}(\theta,\varphi)\) המקדם \(i^l(2l+1)\) נגזר בלנדאו ובליפשיץ, \(\S\) 34, \((kr\cos\theta)^n\) על ידי השוואת המקדם של משני צידי המשוואה: כפי שנראה בהמשך, \((kr)^n\) אינו מופיע \(j_l(kr)\) עבור \(l\) גדול מ-\(n\), \((\cos\theta)^n\) ואינו מופיע \(l\) בפחות מ- \(P_l(\cos\theta)\)\(n\), ולכן השילוב מתרחש \((kr\cos\theta)^n\) רק פעם אחת - \(n^{th}\) במונח, וניתן להתאים את המקדמים משני צידי המשוואה. (כדי לקבל את המקדם נכון, עלינו כמובן לציין את הנורמליזציות לפונקציית בסל - ראה להלן - ואת הפולינום של Legendre.)

מרווח מתמטי: פונקציות בסל ונוימן הכדוריות

גל המישור \(e^{i\vec{k}\cdot\vec{r}}\) הוא פתרון טריוויאלי של משוואת שרדינגר עם פוטנציאל אפס, ולכן, מכיוון \(P_l(\cos\theta)\) שהצורה קבוצה עצמאית ליניארית, כל מונח \(j_l(kr)P_l(\cos\theta)\) בסדרת גלי המישור חייב להיות בעצמו פתרון למשוואת אפס הפוטנציאל של שרדינגר. מכאן נובע כי \(j_l(kr)\) עונה על משוואת שרדינגר הרדיאלית של אפס פוטנציאל: \[ \frac{d^2}{dr^2}R_l(r)+\frac{2}{r}\frac{d}{dr}R_l(r)+\left( k^2-\frac{l(l+1)}{r^2}\right) R_l(r)=0. \label{10.2.3}\]

התחליף הסטנדרטי \(R_l(r)=u_l(r)/r\) מניב \[ \frac{d^2u_l(r)}{dr^2}+\left( k^2-\frac{l(l+1)}{r^2}\right)u(r)=0 \label{10.2.4}\]

במקרה \(l=0\) הפשוט שני הפתרונות הם \(u_0(r)=\sin kr,  \cos kr.\) הפונקציות הרדיאליות המתאימות \(R_0(r)\) הן (מלבד הקבועים הכוללים) פונקציות בסל ונוימן מסדר אפס בהתאמה.

הנורמליזציה הסטנדרטית לפונקציית בסל מסדר אפס היא \[ j_0(kr)=\frac{\sin kr}{kr}, \label{10.2.5}\]

ופונקציית נוימן מסדר אפס \[ n_0(kr)=-\frac{\cos kr}{kr}. \label{10.2.6}\]

שים לב שפונקציית בסל היא זו שמתנהגת היטב במקור: היא יכולה להיווצר על ידי שילוב מהמקור עם תנאי גבול ראשוניים של ערך אחד, שיפוע אפס.

הנה עלילה של \(j_0(kr)\) \(n_0(kr)\) וממנה\(kr=0.1\; to\; 20\):

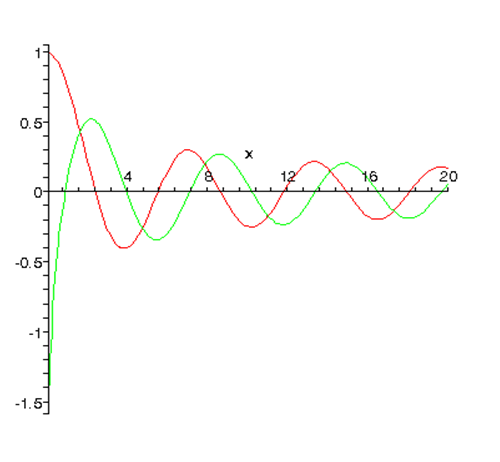
עבור nonzero\(l\), ליד המקור \(R_l(r)\sim r^l\) או\(\sim r^{-(l+1)}\). \(\sim r^l\)הפיתרון המתנהג היטב הוא פונקציית בסל, הפונקציה היחידה פונקציית נוימן. הנורמליזציות הסטנדרטיות של פונקציות אלה ניתנות להלן.

הנה \(j_5(kr)\) ו\(j_{50}(kr)\):

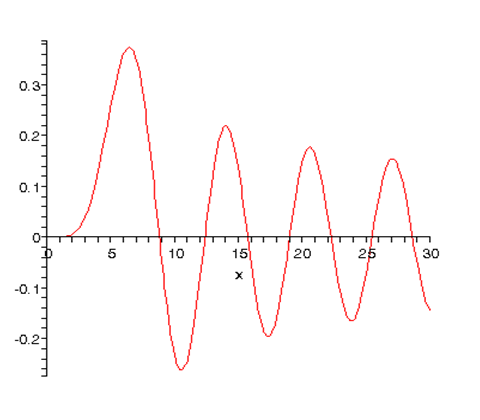
גזירה מפורטת של פונקציות בסל ונוימן

סעיף קטן זה הוא רק כאן לשלמות. אנו משתמשים במשתנה חסר הממדים. \(\rho=kr\)

כדי למצוא את \(l\) הפתרונות הגבוהים יותר, אנו עוקבים אחר טריק חכם שניתן בלנדאו ובליפשיץ (33). \(\S\)

קבע את \(\rho^l\) ההתנהגות ליד המקור על ידי כתיבה \[ R_l=(\rho)^l\chi_l(\rho). \label{10.2.7}\]

הפונקציה \(\chi_l(\rho)\) מספקת \[ \frac{d^2}{d\rho^2}\chi_l(\rho)+\frac{2(l+1)}{\rho}\frac{d}{d\rho}\chi_l(\rho)+\chi_l(\rho)=0. \label{10.2.8}\]

החוכמה היא להבדיל משוואה זו ביחס ל\(\rho\): \[ \frac{d^3}{d\rho^3}\chi_l(\rho)+\frac{2(l+1)}{\rho}\frac{d^2}{d\rho^2}\chi_l(\rho)+\left( 1-\frac{2(l+1)}{\rho^2}\right)\frac{d}{d\rho}\chi_l(\rho)=0. \label{10.2.9}\]

כתיבה רשמית בלבד\(\frac{d}{d\rho}\chi_l(\rho)=\rho\chi_{l+1}(\rho)\), המשוואה הופכת \[ \frac{d^2}{d\rho^2}\chi_{l+1}(\rho)+\frac{2(l+2)}{\rho}\frac{d}{d\rho}\chi_{l+1}(\rho)+\chi_{l+1}(\rho)=0. \label{10.2.10}\]

אבל זו המשוואה \(\chi_{l+1}(\rho)\) שחייבת לציית! אז יש לנו נוסחת רקורסיה ליצירת כל \(j_l(\rho)\) מהאפס: \(\chi_{l+1}(\rho)=\frac{1}{\rho}\frac{d}{d\rho}\chi_l(\rho)\)\(j_l(\rho)=(\rho)^l\chi_l(\rho)\), ועד קבוע נורמליזציה שנקבע על ידי מוסכמה.

למעשה, הנורמליזציה הסטנדרטית היא \[ j_l(\rho)=(-\rho)^l\left(\frac{1}{\rho}\frac{d}{d\rho}\right)^l\left(\frac{\sin\rho}{\rho}\right). \label{10.2.11}\]

עכשיו \[ (\sin\rho)/\rho=\sum_0^{\infty} (-1)^n\rho^{2n}/(2n+1)! \label{10.2.12}\]

זהו סכום של כוחות אפילו בלבד של\(\rho\). ניתן לבדוק בקלות שהפעלה בסדרה זו לעולם לא \(\left(\frac{1}{\rho}\frac{d}{d\rho}\right)^l\) יכולה לייצר כוחות שליליים של\(\rho\). מכאן נובע\(j_l(\rho)\), שנכתב כסדרת כוח ב-\(\rho\), יש מונח מוביל ביחס ל\(\rho^l\). ניתן למצוא את המקדם של מונח מוביל זה על ידי החלת המפעיל הדיפרנציאלי על הסדרה עבור\((\sin\rho)/\rho\), \[ j_l(\rho)\sim \frac{\rho^l}{(2l+1)!!} \; as \; \rho\to0. \label{10.2.13}\]

\(r^l\)התנהגות זו בסמוך למקור היא הפיתרון הרגיל המתנהג היטב למשוואת שרדינגר באזור בו שולט המונח הצנטריפוגלי.

שים לב \(\rho\) שההתנהגות הקטנה אינה ניכרת מיד מההצגה הרגילה של ה- \(j_l(\rho)\)'s, שנכתבה כתערובת של כוחות ופונקציות טריגונומטריות, למשל \[ j_1(\rho)=\frac{\sin\rho}{\rho^2}-\frac{\cos\rho}{\rho},\;\; j_2(\rho)=\left( \frac{3}{\rho^3}-\frac{1}{\rho}\right)\sin\rho-\frac{3\cos\rho}{\rho^2}, \; etc. \label{10.2.14}\]

פונה כעת להתנהגות \(j_l(\rho)\) של בגדול\(\rho\), מ \[ j_l(\rho)=(-\rho)^l\left(\frac{1}{\rho}\frac{d}{d\rho}\right)^l\left(\frac{\sin\rho}{\rho}\right) \label{10.2.15}\]

ניכר כי המונח הדומיננטי \(\rho\) במשטר הגדול (זה של הסדר\(1/\rho\)) נוצר על ידי הבחנה רק של הפונקציה הטריגונומטרית בכל שלב. ניתן לראות כי כל בידול כזה שווה ערך להכפלה ב- (-1) וחיסור \(\pi /2\) מהטיעון, כך \[ j_l(\rho)\to \frac{1}{\rho}\sin\left(\rho-\frac{l\pi}{2}\right) \; as\; \rho\to\infty . \label{10.2.16}\]

אלה\(j_l(\rho)\), אם כן, הם הפתרונות הפיזיים של גל חלקי למשוואת שרדינגר עם אפס פוטנציאל. כאשר פוטנציאל מופעל, פונקציית הגל ליד המקור עדיין \(\sim \rho^l\) (בהנחה, כפי שאנו עושים תמיד, שהפוטנציאל זניח בהשוואה \(l(l+1)/\rho^2\) למונח קרוב מספיק למקור). ניתן למצוא את פונקציית הגל מעבר לטווח הפוטנציאל באופן מספרי באופן עקרוני על ידי השתלבות מהמקור, ולמעשה תהיה כמו \(j_l(\rho)\) לעיל אלא שיהיה גורם פאזה נוסף, הנקרא "שינוי פאזה" ומסומן על ידי\(\delta\)) בסינוס. המשמעות של זה היא שבאזור הרחוק, פונקציית הגל היא שילוב ליניארי של פונקציית בסל ופונקציית נוימן (הפתרון למשוואת שרדינגר אפס פוטנציאל יחיד במקור). לכן יש לבחון גם את פונקציות נוימן.

כאמור לעיל, פונקציית \(l=0\) נוימן היא \[ n_0(\rho)=-\frac{\cos\rho}{\rho}, \label{10.2.17}\]

סימן המינוס הוא האמנה הסטנדרטית.

טיעון מקביל לזה שלמעלה עבור פונקציות בסל קובע כי פונקציות נוימן מסדר גבוה יותר ניתנות על ידי: \[ n_l(\rho)=(-\rho)^l\left(\frac{1}{\rho}\frac{d}{d\rho}\right)^l\left(-\frac{\cos\rho}{\rho}\right). \label{10.2.18}\]

ליד המקור \[ n_l(\rho)\sim \frac{(2l-1)!!}{\rho^{l+1}} \; as\; \rho\to0 \label{10.2.19}\]

ולגדול \(\rho\) \[ n_l(\rho)\to -\frac{1}{\rho}\cos\left(\rho-\frac{l\pi}{2}\right)\; as\; \rho\to\infty , \label{10.2.20}\]

כך שניתן לכתוב פונקציה של הצורה באופן \(\frac{1}{\rho}\sin\left(\rho-\frac{l\pi}{2}+\delta\right)\) אסימפטוטי כשילוב ליניארי של פונקציות בסל ונוימן באזור זה.

לבסוף, פונקציות הנקל הכדוריות הן רק השילובים של פונקציות בסל ונוימן שנראות כמו גלי מישור יוצאים או נכנסים באזור האסימפטוטי: \[ h_l(\rho)=j_l(\rho)+in_l(\rho),\;\; h_l^*(\rho)=j_l(\rho)-in_l(\rho), \label{10.2.21}\]

אז עבור גדול\(\rho\), \[ h_l(\rho)\to \frac{e^{i(\rho-l\pi /2)}}{i\rho},\;\; h_l^*(\rho)\to -\frac{e^{-i(\rho-l\pi /2)}}{i\rho}. \label{10.2.22}\]

מטריצת פיזור הגל החלקי

הבה נדמיין לרגע שנוכל פשוט לשלוח גל כדורי (בלתי תלוי בזמן), עם וריאציה\ תטא הניתנת על ידי. \(P_l(\cos\theta)\) עבור גל \(l^{th}\) חלקי זה (הורדת קבועי הנורמליזציה הכוללים כרגיל) הפונקציה הרדיאלית רחוקה מהמקור לאפס פוטנציאל היא \[ j_l(kr)\to \frac{1}{kr}\sin\left(kr-\frac{l\pi}{2}\right)=\frac{i}{2k}\left(\frac{e^{-i(kr-l\pi /2)}}{r}-\frac{e^{+i(kr-l\pi /2)}}{r}\right). \label{10.2.23}\]

אם כעת מופעל הפוטנציאל (הסימטרי הכדורי), השינוי האפשרי היחיד לפתרון גל עומד זה באזור הרחוק (שבו הפוטנציאל הוא אפס) הוא שינוי פאזה: \(\delta\) \[ \sin\left(kr-\frac{l\pi}{2}\right)\to \sin\left(kr-\frac{l\pi}{2}+\delta_l(k)\right). \label{10.2.24}\]

זה מה שהיינו מוצאים על שילוב משוואת שרדינגר מתוך התנהגות לא יחידה במקור.

אך בפועל, גל ההטלה ניתן, ולא ניתן להשפיע על השלב שלו על ידי הפעלת הפוטנציאל. עם זאת, עדיין עלינו לקבל את הפתרון לאותה משוואת שרדינגר, כך שכדי להתאים לתוצאה שלמעלה נכפיל את כל פונקציית הגל החלקי בגורם הפאזה. \(e^{i\delta_l(k)}\) התוצאה היא לשים פעמיים את שינוי הפאזה על הגל היוצא, כך שכאשר הפוטנציאל מופעל השינוי בפונקציית הגל האסימפטוטי חייב להיות \[ \frac{i}{2k}\left(\frac{e^{-i(kr-l\pi /2)}}{r}-\frac{e^{+i(kr-l\pi /2)}}{r}\right)\to \frac{i}{2k}\left(\frac{e^{-i(kr-l\pi /2)}}{r}-\frac{S_l(k)e^{+i(kr-l\pi /2)}}{r}\right). \label{10.2.25}\]

משוואה זו מציגה את מטריצת הפיזור \[ S_l(k)=e^{2i\delta_l(k)}, \label{10.2.26}\]

אשר חייב לשכב על מעגל היחידה \(|S|=1\) כדי לשמור על הסתברות - הזרם היוצא חייב להיות שווה לזרם הנכנס. אם אין פיזור, כלומר שינוי פאזה אפס, מטריצת הפיזור היא אחדות.

יש לציין שכאשר משוואת שרדינגר הרדיאלית נפתרת לפוטנציאל שאינו אפס על ידי השתלבות מהמקור, עם \(\psi=0\) \(\psi′=1\) ובתחילה, הפונקציה האמיתית שנוצרת כך שונה מפונקציית הגל שניתנה לעיל על ידי גורם פאזה כולל. \(e^{i\delta_l(k)}\)

פיזור גל מטוס

כעת אנו מוכנים לקחת את גל המישור הנכנס, לפרק אותו לרכיבי הגל החלקי שלו המתאימים למומנטה זוויתית שונה, להעביר את הגלים החלקיים בנפרד על ידי \(l\) שלבים תלויים, ולהוסיף את הכל בחזרה יחד כדי לקבל את גל המישור המקורי בתוספת הגל המפוזר.

אנו מעוניינים כאן רק בפונקציית הגל הרחק מהפוטנציאל. באזור זה, גל המישור המקורי הוא \[ \begin{matrix} e^{i\vec{k}\cdot\vec{r}}=e^{ikr\cos\theta}=\sum_l i^l(2l+1)j_l(kr)P_l(\cos\theta) \\ =\sum_l i^l(2l+1)\frac{i}{2k}(\frac{e^{-i(kr-l\pi /2)}}{r}-\frac{e^{+i(kr-l\pi /2)}}{r})P_l(\cos\theta). \end{matrix}\label{10.2.27}\]

הפעלת השלב הפוטנציאלי משנה את הגל היוצא: \[ \frac{e^{+i(kr-l\pi /2)}}{r}\to \frac{S_l(k)e^{+i(kr-l\pi /2)}}{r} \label{10.2.28}\]

הפיזור בפועל לפי הפוטנציאל הוא ההבדל בין שני המונחים הללו. פונקציית הגל השלמה באזור הרחוק (כולל גל המישור הנכנס) היא אפוא: \[ \psi(r,\theta,\varphi)=e^{ikr\cos\theta}+\left(\sum_l(2l+1)\frac{(S_l(k)-1)}{2ik}P_l(\cos\theta)\right)\frac{e^{ikr}}{r}. \label{10.2.29}\]

\(i^l\)הגורם ביטל את\(e^{-il\pi /2}\). ה--1 פנימה \((S_l(k)-1)\) נמצא שם כי אפס פיזור פירושו\(S=1\). לחלופין, ניתן לראות בכך הפחתת הגלים היוצאים שכבר קיימים בגל המישור, כפי שנדון לעיל. אין תלות מכיוון שהפוטנציאל הוא \(\varphi\) כדור-סימטרי כל הבעיה היא אזימוטרית-סימטרית לגבי כיוון הגל הנכנס.

אולי ראוי להזכיר כי לפיזור בגל חלקי אחד בלבד, הזרם היוצא שווה לזרם הנכנס, בין אם יש שינוי פאזה ובין אם לאו. לכן, אם הפעלת הפוטנציאל אינה משפיעה על הזרם הכולל המפוזר בכל גל חלקי, כיצד הוא יכול לגרום לפיזור כלשהו? הנקודה היא שעבור גל מישור מתגלגל עם פוטנציאל אפס, לרכיבים הנכנסים והיוצאים יש את השלב היחסי הנכון להוסיף לרכיב של גל מישורי - אולי טאוטולוגיה. אבל אם שלב נוסף יוכנס לגל היוצא בלבד, ה- ingoing + היוצא כבר לא ייתן גל מישורי - יהיה חלק יוצא נוסף ביחס ל. \((S_l(k)-1)\)

נזכיר כי משרעת הפיזור \(f(\theta,\varphi)\) הוגדרה במונחים של הפתרון למשוואת שרדינגר בעלת גל מישור מטיל על ידי \[ \psi(r,\theta,\varphi)=e^{ikr\cos\theta}+f(\theta,\varphi)\frac{e^{ikr}}{r}. \label{10.2.30}\]

כעת אנו מוכנים לבטא את משרעת הפיזור במונחים של משמרות שלב הגל החלקי (לפוטנציאל סימטרי כדורית, כמובן): \[ f(\theta,\varphi)=f(\theta)=\sum_l(2l+1)\frac{(S_l(k)-1)}{2ik} P_l(\cos\theta)=\sum_l(2l+1)f_l(k)P_l(\cos\theta) \label{10.2.31}\]

איפה \[ f_l(k)=\frac{1}{k}e^{i\delta_l(k)}\sin\delta_l(k) \label{10.2.32}\]

נקרא משרעת פיזור הגל החלקי, או רק משרעת הגל החלקית.

אז משרעת הפיזור הכוללת היא סכום אמפליטודות הגל החלקיות הללו: \[ f(\theta)=\frac{1}{k}\sum_l(2l+1)e^{i\delta_l(k)}\sin\delta_l(k)P_l(\cos\theta). \label{10.2.33}\]

חתך הפיזור הכולל \[ \begin{matrix} \sigma =\int |f(\theta)|^2d\Omega \\ =2\pi \int_0^{\pi} |f(\theta)|^2\sin\theta d\theta \\ =2\pi \int_0^{\pi}  |\frac{1}{k}\sum_l(2l+1)e^{i\delta_l(k)}\sin\delta_l(k)P_l(\cos\theta)|^2​\sin\theta d\theta \end{matrix} \label{10.2.34}\]

נותן \[ \sigma =4\pi \sum_{l=0}^{\infty} (2l+1)|f_l(k)|^2=\frac{4\pi}{k^2}\sum_{l=0}^{\infty} (2l+1)\sin^2\delta_l.\label{10.2.35}\]

אז החתך הכולל הוא סכום החתכים עבור כל \(l\) ערך. עם זאת, אין זה אומר שחתך ההפרש לפיזור לזווית מוצקה נתונה הוא סכום על \(l\) ערכים נפרדים - המרכיבים השונים מפריעים. רק כאשר כל הזוויות משולבות, האורתוגונליות של הפולינומים של Legendre מבטיחה שהמונחים הצולבים ייעלמו.

שימו לב שחתך הפיזור המרבי האפשרי לחלקיקים במצב מומנטום זוויתי \(l\) הוא\((4\pi /k^2)(2l+1)\), שהוא פי ארבעה מהחתך הקלאסי עבור אותו גל חלקי הפוגע, למשל, בכדור קשה! (דמיין חלקיקים למחצה באזור טבעתי: תנע זוויתי\(L=rp\), נניח, אבל וכך. \(L=\hbar l\) \(p=\hbar k\) \(l=rk\) לכן האזור הטבעתי המתאים למומנטום הזוויתי "בין" \(l\) ויש \(l+1\) לו רדיוסים פנימיים \(l/k\) \((l+1)/k\) וחיצוניים ולכן שטח) התוצאה הקוונטית היא בעצם אפקט דיפרקטיבי, נדון בה בהמשך\(\pi (2l+1)/k^2\).

קל להוכיח את המשפט האופטי לפוטנציאל כדור-סימטרי: פשוט קח את החלק הדמיוני של כל צד של המשוואה \[ f(\theta)=\frac{1}{k}\sum_l(2l+1)e^{i\delta_l(k)}\sin\delta_l(k)P_l(\cos\theta) \label{10.2.36}\]

ב\(\theta=0\), באמצעות\(P_l(1)=1\), \[ Im\, f(\theta=0)=\frac{1}{k}\sum_l(2l+1)\sin^2\delta_l(k) \label{10.2.37}\]

שממנו \(Im\, f(0)=k\sigma /4\pi\) יוצא המשפט האופטי באופן מיידי.

ראוי גם לציין מה המשמעות של היחידות של מטריצת פיזור הגל \(l^{th}\) החלקי עבור \(S_l^{\dagger}S_l=1\) משרעת הגל החלקית. \(f_l(k)=\frac{1}{k}e^{i\delta_l(k)}\sin\delta_l(k)\) מאז\(S_l(k)=e^{2i\delta_l(k)}\), מכאן נובע \[ S_l(k)=1+2ikf_l(k). \label{10.2.38}\]

מכאן, \(S_l^{\dagger}S_l=1\) נותן: \[ Im\, f_l(k)=k|f_l(k)|^2. \label{10.2.39}\]

זה יכול להיות פשוט יותר: \[Im\, \frac{1}{f_l(k)}=-k. \label{10.2.40}\]

למעשה, \[ f_l(k)=\frac{1}{k(\cot\delta_l(k)-i)}. \label{10.2.41}\]

משמרות שלב ופוטנציאלים: כמה דוגמאות

אנו מניחים בסעיף זה שניתן לקחת את הפוטנציאל לאפס מעבר לרדיוס גבול כלשהו\(b\). זהו קירוב הולם לכל הפוטנציאלים המצויים בפועל למעט פוטנציאל קולומב, שיידון בנפרד בהמשך.

באופן אסימפטוטי, אם כן, \[ \begin{matrix} \psi_l(r)=\frac{i}{2k}\left(\frac{e^{-i(kr-l\pi /2)}}{r}-\frac{e^{2i\delta_l(k)}e^{+i(kr-l\pi /2)}}{r}\right) \\ =\frac{e^{i\delta_l(k)}}{kr}\sin(kr+\delta_l(k)-l\pi /2) \\ =\frac{e^{i\delta_l(k)}}{kr}(\sin(kr-l\pi /2)\cos\delta_l(k)+\cos(kr-l\pi /2)\sin\delta_l(k)). \end{matrix} \label{10.2.42}\]

ביטוי זה מדויק רק בגבול\(r\to \infty\), אך מכיוון שניתן לקחת את הפוטנציאל אפס מעבר\(r=b\), פונקציית הגל חייבת להיות בעלת הצורה \[ \psi_l(r)=e^{i\delta_l(k)}(\cos\delta_l(k)j_l(kr)-\sin\delta_l(k)n_l(kr)) \label{10.2.43}\]

עבור\(r>b\).

(הסימן - מגיע מהמוסכמה הסטנדרטית לפונקציות בסל ונוימן - ראה קודם לכן.)

הכדור הקשה

הדוגמה הפשוטה ביותר לפוטנציאל פיזור: \[ \begin{matrix} V(r)=\infty \; for\; r<R, \\ V(r)=0\; for\; r\ge R. \end{matrix}\label{10.2.44}\]

פונקציית הגל חייבת להיות שווה לאפס ב\(r=R\), כך מהצורה הנ"ל של\(\psi_l(r)\), \[ \tan\delta_l(k)=\frac{j_l(kR)}{n_l(kR)} .\label{10.2.45}\]

עבור\(l=0\), \[ \tan\delta_0(k)=-\frac{(\sin kR)/kR}{(\cos kR)/kR}=-\tan kR, \label{10.2.46}\]

כך\(\delta_0(k)=-kR\). זה מסתכם בפונקציית הגל המועברת ביעילות כדי להתחיל \(R\) במקום במקור: \[ \frac{\sin kr}{kr}\to \frac{\sin k(r+\delta)}{kr}=\frac{\sin k(r-R)}{kr} \label{10.2.47}\]

עבור\(r>R\), כמובן \(\psi=0\) עבור\(r<R\).

למצבי תנע זוויתי גבוהים יותר באנרגיות נמוכות\(( kR\ll 1 )\), \[ \tan\delta_l(k)=\frac{j_l(kR)}{n_l(kR)}\approx \frac{-(kR)^l/(2l+1)!!}{(2l-1)!!/(kR)^{l+1}}=-\frac{(kR)^{2l+1}}{(2l+1)((2l-1)!!)^2}. \label{10.2.48}\]

לכן באנרגיה נמוכה מספיק, רק \(l=0\) פיזור חשוב - כפי שמובן מאליו, מכיוון שחלקיק נכנס עם תנע \(p=\hbar k\) ותנע זוויתי \(l\hbar\) נמצא ככל הנראה במרחק \(l/k\) ממרכז הפוטנציאל בגישה הקרובה ביותר, כך שאם זה גדול בהרבה מ\(R\), הסטת הפאזה תהיה קטנה.

הקירוב שנולד לגלים חלקיים

מתוך ההגדרה של \(f(\theta,\varphi)\) \[ \psi_{\vec{k}}(\vec{r})=e^{i \vec{k}\cdot\vec{r}}+f(\theta,\varphi)\frac{e^{ikr}}{r} \label{10.2.49}\]

ו \[ \psi_{\vec{k}}(\vec{r})=e^{i \vec{k}\cdot\vec{r}}-\frac{m}{2\pi \hbar^2}\frac{e^{ikr}}{r}\int d^3 r'e^{-i \vec{k}_f\cdot\vec{r}'}V(\vec{r}') \psi_{\vec{k}}(\vec{r}') \label{10.2.50}\]

זכור את קירוב Born מסתכם בהחלפת פונקציית הגל \(\psi_{\vec{k}}(\vec{r}')\) באינטגרל מימין בגל המישור הנכנס, ולכן מתעלם משינוי מחדש.

כדי לתרגם זאת לקירוב גל חלקי, אנו לוקחים תחילה את הנכנס \(\vec{k}\) להיות בכיוון z, כך שבאינטגרנד אנו מחליפים ב \(\psi_{\vec{k}}(\vec{r}')\) \[ e^{ikr'\cos\theta}=\sum_l i^l(2l+1)j_l(kr')P_l(\cos\theta'). \label{10.2.51}\]

תיוג הזווית בין \(\vec{k}_f\) לבין \(\vec{r}'\)\(\gamma\), \[ e^{-i \vec{k}_f\cdot\vec{r}'}=\sum_l(-i)^l(2l+1)j_l(kr')P_l(\cos\gamma). \label{10.2.52}\]

עכשיו \(\vec{k}_f\)הוא \(\vec{r}'\) בכיוון \((\theta,\varphi)\) ובכיוון\((\theta',\varphi')\), \(\gamma\) והוא הזווית ביניהם. למצב זה, יש משפט תוספת להרמוניות כדוריות: \[ P_l(\cos\gamma)=\frac{4\pi}{2l+1}\sum_{m=-l}^{l} Y^∗_{lm}(\theta',\varphi')Y_{lm}(\theta,\varphi). \label{10.2.53}\]

על הכנסת ביטוי זה ושילוב יתר\(\theta',\varphi'\), \(m\) המונחים הלא-אפסיים נותנים אפס, למעשה המונח היחיד שאינו אפס הוא \(l\) שזהה למונח \(\psi_{\vec{k}}(\vec{r}')\) בהרחבה, נותן \[ f(\theta)=\frac{-2m}{\hbar^2}\sum_{l=0}^{\infty} (2l+1)P_l(\cos\theta)\int_0^{\infty} r^2drV(r)(j_l(kr))^2 \label{10.2.54}\]

ולזכור \[ f(\theta)=\frac{1}{k}\sum_l(2l+1)e^{i\delta_l(k)}\sin\delta_l(k)P_l(\cos\theta) \label{10.2.55}\]

מכאן נובע כי עבור משמרות פאזה קטנות (המקום היחיד שהוא תקף) נקרא קירוב Born של גל חלקי \[ \delta_l(k)\approx -\frac{2mk}{\hbar^2}\int_0^{\infty} r^2drV(r)(j_l(kr))^2. \label{10.2.56}\]

פיזור אנרגיה נמוכה: אורך הפיזור

מ

\[ f_l(k)=\frac{1}{k(\cot\delta_l(k)-i)}, \label{10.2.41B}\]

\(l=0\)חתך הרוחב הוא

\[ \sigma_{l=0}=\frac{4\pi}{k^2|\cot\delta_0(k)-i|^2}. \label{10.2.57}\]

באנרגיה \(E\to0\) הופכת משוואת שרדינגר הרדיאלית \(u=r\psi\) הרחק מהפוטנציאל\(d^2u/dr^2=0\), עם פתרון קו ישר. \(u(r)=C(r-a)\) זה חייב להיות \(k\to 0\) הגבול של\(u(r)=C′\sin(kr+\delta_0(k))\), שיכול להיות נכון רק אם \(\delta_0\) הוא עצמו ליניארי \(k\) עבור קטן מספיק\(k\), ואז זה חייב להיות\(\delta_0(k)=-ka\), ישות הנקודה שבה פונקציית הגל החיצונית המוחצנת מצטלבת את הציר (אולי בשלילה!) \(r\) אז, כפי \(k\) שמגיע לאפס, מונח העריסה שולט במכנה ו \[ \sigma_{l=0}(k\to 0)=4\pi a^2.\label{10.2.58}\]

הכמות a נקראת אורך הפיזור.

שילוב משוואת שרדינגר הרדיאלית של אפס אנרגיה מתוך \(u(r)=0\) המקור לפוטנציאל באר מרובע חלש (כדורי), קל לבדוק ש- a חיובי לפוטנציאל \(a\) דוחה, שלילי לפוטנציאל אטרקטיבי.

פוטנציאל דוחה, פונקציית גל אפס אנרגיה (כך שזה קו ישר מחוץ לבאר!) :

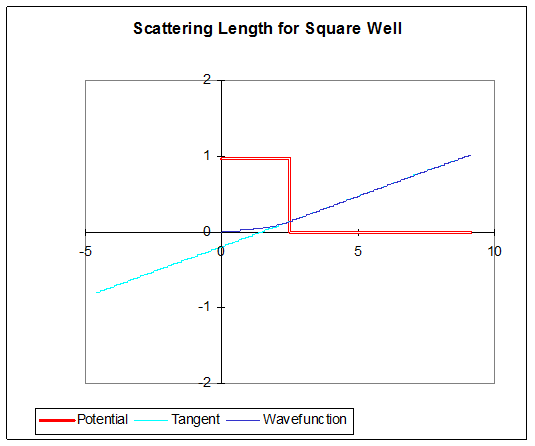
פוטנציאל אטרקטיבי:

על הגדלת חוזק הפוטנציאל הדוחה, שעדיין פותר את פונקציית גל האנרגיה האפסית, \(a\) נוטה לקיר הפוטנציאלי - הנה פונקציית הגל של אפס אנרגיה למחסום גובה 6:

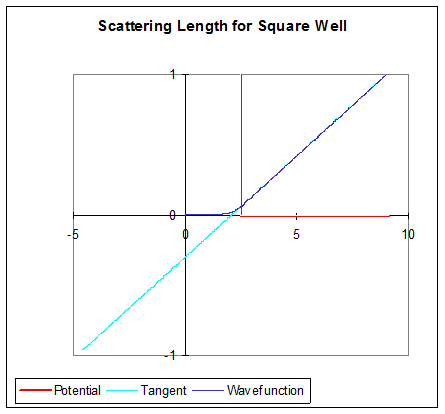
עבור מחסום גבוה לאין שיעור, פונקציית הגל נדחפת החוצה מהמחסום לחלוטין, ותוצאת הכדור הקשה מתאוששת: אורך פיזור\(a\), חתך רוחב\(4\pi a^2\).

על הגדלת כוחו של באר אטרקטיבי, אם יש שינוי פאזה גדול יותר \(\pi /2\) בתוך הבאר, \(a\) יהפוך חיובי. למעשה, ממש ב\(\pi /2\), \(a\) הוא אינסופי!

וקצת יותר עומק לבאר נותן אורך פיזור חיובי:

למעשה, לבאר עמוקה מספיק כדי לקבל אורך פיזור חיובי תהיה גם מצב כבול. זה מתברר כאשר לוקחים בחשבון שניתן לחשוב על העומק שבו אורך הפיזור הופך לאינסופי כבעל מצב קשור לאנרגיה אפסית, בכך שלמרות שפונקציית הגל בחוץ אינה ניתנת לנורמליזציה, היא שקולה לפונקציה מתפוררת אקספוננציאלית עם אורך ריקבון אינסופי. אם כעת מעמיקים מעט את הבאר, פונקציית גל האנרגיה האפסית בתוך הבאר מתעקלת מעט יותר מהר, כך ששיפוע פונקציית הגל בקצה הבאר הופך לשלילי, כמו בתמונה למעלה. עם באר מעט עמוקה יותר זו, כעת אנו יכולים להוריד מעט את האנרגיה לערכים שליליים. לכך תהיה השפעה מועטה על פונקציית הגל בתוך הבאר, אך תאפשר התאמה בקצה הבאר לריקבון מעריכי בחוץ - מצב כבול אמיתי, עם פונקציית גל \(\sim e^{-\kappa r}\) מחוץ לבאר.

אם אנרגיית הקישור של המצב ממש נמוכה, פונקציית גל פיזור האנרגיה האפסית בתוך הבאר כמעט זהה לזו של מצב זה הקשור באנרגיה נמוכה מאוד, ובפרט הנגזרת הלוגריתמית בקיר תהיה קרובה מאוד\(\kappa \cong 1/a\), אז לוקח \(a\) להיות גדול בהרבה מרדיוס הבאר.

זה מחבר את אורך הפיזור הגדול לאנרגיה של המצב הכבול חלש, \[ B. E. =\hbar^2k^2/2m=\hbar^2/2ma^2. \label{10.2.59}\]

וויגנר היה הראשון שהשתמש בזה כדי להעריך את אנרגיית הקישור של הדויטרון מהחתך הנצפה לפיזור נויטרון-פרוטון באנרגיה נמוכה.