10.1: תורת הפיזור

כמעט כל מה שאנחנו יודעים על גרעינים וחלקיקים אלמנטריים התגלה בניסויי פיזור, מההפתעה של רתרפורד לגלות כי לאטומים המסה והמטען החיובי שלהם מרוכזים בגרעינים כמעט דמויי נקודה, ועד לתגליות האחרונות, בקנה מידה אורך קטן בהרבה, שפרוטונים ונויטרונים מורכבים בעצמם מקווארקים דמויי נקודה לכאורה.

המודל הפשוט ביותר של ניסוי פיזור ניתן על ידי פתרון משוואת שרדינגר לגל מישורי הפוגע בפוטנציאל מקומי. פוטנציאל \(V(r)\) עשוי לייצג את מה שאלקטרון מהיר נתקל בפגיעה באטום, או בחלקיק אלפא בגרעין. ברור שייצוג כל מערכת כזו על ידי פוטנציאל הוא רק התחלה, אך בטווחי אנרגיה מסוימים זה די סביר, ועלינו להתחיל איפשהו!

התרחיש הבסיסי הוא לירות בזרם של חלקיקים, כולם באותה אנרגיה, ולגלות כמה מוסטים לסוללת גלאים המודדים זוויות סטיה. אנו מניחים שכל החלקיקים הנכנסים מיוצגים על ידי מנות גל בעלות צורה וגודל זהים, ולכן עלינו לפתור את המשוואה התלויה בזמן של שרדינגר עבור חבילת גל כזו ולמצוא את אמפליטודות ההסתברות לגלים יוצאים בכיוונים שונים בזמן מאוחר יותר לאחר שהפיזור התרחש. אך אנו נוקטים גישה פשוטה יותר: אנו מניחים שלחבילת הגל יש אנרגיה מוגדרת היטב (ומכאן מומנטום), ולכן אורכה אורכי גל רבים. המשמעות היא שבתהליך הפיזור הוא נראה הרבה כמו גל מישורי, ולמשך פרק זמן הפיזור אינו תלוי בזמן. אנו מניחים, אם כן, שהבעיה מקורבת היטב על ידי פתרון משוואת שרדינגר הבלתי תלויה בזמן עם גל מישור מטיל. זה הרבה יותר קל!

כל מה שאנחנו יכולים לזהות הם גלים יוצאים הרחק מחוץ לאזור הפיזור. עבור גל מישור נכנס\(e^{i\vec{k}\cdot\vec{r}}\), פונקציית הגל הרחוקה מאזור הפיזור חייבת להיות בעלת הצורה \[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}+f(\theta,\varphi)\frac{e^{i k r}}{r} \label{10.1.1}\]

היכן \(\theta,\varphi\) נמדדים ביחס לכיוון הכניסה.

שים לב כי משרעת פיזור \(f(\theta,\varphi)\) יש את הממדים של אורך.

אנחנו לא דואגים לנורמליזציה הכוללת, כי מה שרלוונטי הוא החלק של הקורה הנכנסת המפוזרת בכיוון מסוים, או ליתר דיוק, לזווית \(d\Omega\) מוצקה קטנה בכיוון\(\theta,\varphi\). זרם החלקיקים הנכנס (עם הנורמליזציה לעיל) הוא \(\hbar k/m=v\) דרך שטח היחידה בניצב לקרן הכניסה, הזרם היוצא לזווית הקטנה הוא. \(d\Omega\) \((\hbar k/m)|f(\theta,\varphi)|^2d\Omega\) ניכר כי זרם יוצא זה תואם את זרם הכניסה המקורי הזורם דרך שטח ניצב בגודל\(d\sigma(\theta,\varphi)=|f(\theta,\varphi)|^2d\Omega\), ו \[ \frac{d\sigma}{d\Omega}=|f(\theta,\varphi)|^2 \label{10.1.2}\]

נקרא חתך הדיפרנציאלי לפיזור בכיוון\( \theta,\varphi\).

התיאור הבלתי תלוי בזמן

נסקור את הניסוח הבלתי תלוי בזמן של תורת הפיזור, תחילה כפי שהוא מוצג ב- Baym, במונחים של פונקציות הגל הסטנדרטיות של משוואת שרדינגר, ואז נעשה את אותו הדבר a la Sakurai, בשפה הפורמלית יותר, אך כמובן המקבילה, של חזיות ו- kets. גישת פונקציית הגל של שרדינגר היא מבוא קל יותר, אך השפה הפורמלית נוחה יותר לניתוח המבנה של מונחים מסדר גבוה יותר.

למעשה, הטיפול של Baym אינו תלוי בזמן, בכך שהוא משתמש במנת גל מטביעה, אך הוא באורך רב, בקירוב היטב על ידי גל מישורי. Sakurai הולך ישר לגל המטוס, וגם אנחנו עושים. מקרה זה מזכיר מאוד פיזור חד ממדי, בו גל מישורי משמאל מייצר גלים יוצאים לשני הכיוונים, וניתן לחשב את המשרעת ממשוואת שרדינגר למצב עצמי אנרגטי יחיד. ההבדל היחיד הוא שבתלת מימד יהיו גלים יוצאים לכל הכיוונים.

בעקבות Baym, המשוואה של שרדינגר היא:

\[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right)\psi_{\vec{k}}(\vec{r})=V(\vec{r})\psi_{\vec{k}}(\vec{r}),\;\; where\;\; E_k=\frac{\hbar^2k^2}{2m}. \label{10.1.3}\]

\(\psi_{\vec{k}}\)אנחנו לוקחים את זה כדי שיהיה לנו רכיב גל מטוס נכנס\(e^{i\vec{k}\cdot\vec{r}}\). הנורמליזציה הכוללת אינה רלוונטית, שכן חתך הדיפרנציאלי תלוי רק ביחס בין משרעת הגל המפוזר לזו של הגל הנכנס.

הגישה הסטנדרטית למשוואה כמו זו שלמעלה היא להפוך אותה למשוואה אינטגרלית באמצעות הפונקציות של גרין. אם \(V(\vec{r})\) הוא קטן (עד כמה הוא צריך להיות קטן יתברר בהמשך) ניתן לפתור את המשוואה האינטגרלית על ידי איטרציה.

הפונקציה של הירוק \(G(\vec{r},\vec{k})\) היא בעצם ההופכי של האופרטור הדיפרנציאלי, \[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right)G(\vec{r},\vec{k})=\delta(\vec{r}). \label{10.1.4}\]

זו אינה הגדרה ייחודית מבחינה מתמטית: ברור, אנו יכולים להוסיף \(G(\vec{r},\vec{k})\) לכל פתרון של המשוואה ההומוגנית \[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right)\varphi (\vec{r},\vec{k})=0, \label{10.1.5}\]

לדוגמה, גל המטוס הנכנס.

אם נכתוב את המשוואה האינטגרלית

\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}+\int d^3r' G(\vec{r}-\vec{r}' )V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ) \label{10.1.6}\]

\(\psi_{\vec{k}}(\vec{r})\)זה בהחלט פיתרון למשוואת שרדינגר המקורית, כפי שנבדק בקלות על ידי יישום המפעיל \[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right) \label{10.1.7}\]

לשני צידי המשוואה.

ניתן לפתור את המשוואה האינטגרלית באופן רשמי על ידי איטרציה, ועבור "קטן" \(V\) הפתרון יתכנס. אבל זה לא באמת יעשה - זכרו, אין לנו ייחודי! \(G(\vec{r},\vec{k})\) עלינו לתקן \(G(\vec{r},\vec{k})\) על ידי חיבור טוב יותר לבעיית הפיזור שאנו מנסים לפתור.

אנו יודעים שלפתרון שלנו יש גל מישור יחיד, וגלים יוצאים לכל הכיוונים האחרים, הנוצרים על ידי האינטראקציה של גל המישור עם הפוטנציאל. אבל משוואת שרדינגר יכולה לתאר באותה מידה גלים מטילים בכיוונים האחרים. בהגדרת הפונקציה של הירוק וכתיבת המשוואה האינטגרלית, לא ציינו בשום מקום את הצורה הרחוקה של פונקציית הגל, כלומר, לא דרשנו שהפונקציה של הירוק בצד ימין של המשוואה האינטגרלית תיצור רק גלים יוצאים. כדי לראות כיצד לעשות זאת, עלינו לכתוב את הפונקציה של הירוק עצמו כסכום על פני גלים, במילים אחרות טרנספורמציה פורייה, ולראות כיצד לחסל את הגלים הנכנסים הלא פיזיים (לבעיה הנוכחית) בסכום זה.

הצורה המפורשת של תפקידו של הירוק היא \[ G(r,k)=\int \frac{d^3k'}{(2\pi)^3}\frac{e^{i\vec{k}' \cdot\vec{r}}}{E_k-\frac{\hbar^2k'^2}{2m}}=-\frac{m}{2\pi^2ir\hbar^2}\int_{-\infty}^{\infty}\frac{k' dk' e^{ik'r}}{k'^2-k^2}. \label{10.1.8}\]

שים לב שתלוי \(G(r,k)\) רק \(\vec{k}\) דרך\(E_k\), ורק \(\vec{r}\) דרך\(r\), מכיוון שהאינטגרציה הסתיימה \(\vec{k}'\)היא על כל הכיוונים. קל לוודא שתפקודו של גרין זה עונה על המשוואה הדיפרנציאלית, על ידי החלת האופרטור הדיפרנציאלי על האינטגרל הראשון שלמעלה: התוצאה היא לבטל את המכנה באינטגרל, ולהשאיר רק\(\int \frac{d^3k'}{(2\pi)^3}e^{i\vec{k}' \cdot\vec{r}}\), שהוא הפונקציה \(\delta\) - ב. \(\vec{r}\)

כדי לקבל את הצורה השנייה של \(G(r,k)\) במשוואה לעיל, אנו מבצעים תחילה את האינטגרציה הזוויתית \(d(\cos\theta)\) כדי לקבל\((e^{ik'r}-e^{-ik'r})/ik' r\), ואז מסדרים מחדש את האינטגרל על פני \(-e^{-ik'r}\) המונח על ידי החלפת הסימן של\(k' \), כך שהוא הופך \(-\infty\) לאינטגרל מ- 0 במקום 0 ל\(\infty\). לאחר מכן אנו מוסיפים את שני המונחים (ה \(e^{ik'r}\) וה\(-e^{-ik'r}\)) יחד כדי לתת אינטגרל מ- \(-\infty\) to\(\infty\). אינטגרל זה מ- \(-\infty\) \(\infty\) to נעשה לאחר מכן על ידי שילוב קווי מתאר - לפחות, לאחר שהבנו מה לעשות בקשר לסינגולריות ב. \(k' =\pm k\)

כדי להגדיר את האינטגרל, יש לעוות מעט את קווי המתאר כך שהוא עוקף את הקטבים הללו.

בנקודה זו אנו ניזונים מהידע הפיזי שלנו על המצב: שבתהליך הפיזור, המונח השני ב \[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}+\int d^3r' G(\vec{r}-\vec{r}' )V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ), \label{10.1.9}\]

כלומר, מונח הפונקציה של הירוק, צריך להיות סכום על פני גלים יוצאים בלבד. בנוסף, אנו יכולים להבטיח זאת על ידי עיוות קווי המתאר של האינטגרציה בכיוון הנכון, כדלקמן.

יש להעריך את אינטגרל המתאר על ידי סגירת קווי המתאר. מכיוון \(r\) שהוא חיובי \(e^{ik'r}\) הולך לאפס בחצי \(k'\) המישור העליון, אך מתפצל במחצית התחתונה, ולכן עלינו לסגור את קווי המתאר בחצי המישור העליון כדי להבטיח שום תרומה מחצי המעגל באינסוף. לכן, כדי לקבל את הגלים היוצאים הרצויים, \(e^{ikr}\) אך לא\(e^{-ikr}\), קווי המתאר שלנו סגורים בחצי המישור העליון חייבים להקיף את הקוטב ב- \(k' =+k\) אך לא את זה ב\(k' =-k\). (\(e^{ikr}\)אכן מייצג גלים יוצאים: תלות הזמן המודחקת היא\(e^{-iEt/\hbar} =e^{-i\omega t}\), נתינה\(e^{i(kr-\omega t)}\).) במילים אחרות, התצורה היחסית של החלק הציר האמיתי של קווי המתאר ושני הקטבים צריכה להיות:

x (מוט)

____________________________________________________________________________________________________________________________

x (מוט ב\(k' =-k-i\varepsilon\)) (מוט ב\(k' =+k+i\varepsilon\))

במקום להזיז את קווי המתאר מעט מהציר האמיתי כדי להימנע מהקטבים, הזזנו מעט את הקטבים במקום. תנועות אלה הן אינסופיות, כך שזז לא משנה את ערך האינטגרל. נוח יותר להזיז את הקטבים, כפי שמוצג, מכיוון שניתן לכלול מהלך זה ביעילות באינטגרל רק על ידי הוספת חלק דמיוני אינסופי למכנה: \[ G_+(r,k)=\int \frac{d^3k'}{(2\pi)^3}\frac{e^{i\vec{k}' \cdot\vec{r}}}{E_k-\frac{\hbar^2k'^2}{2m}+i\varepsilon}=-\frac{m}{2\pi^2ir\hbar^2}\int_{-\infty}^{\infty}\frac{k' dk' e^{ik'r}}{k'^2-k2-i\varepsilon}. \label{10.1.10}\]

שימו לב שכתבנו \(G_+\) במקום\(G\), כי \(G\) יכול לציין כל פתרון של \[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right)G(\vec{r},\vec{k})=\delta(\vec{r}) \label{10.1.11}\]

ואנחנו מציינים את הפתרון המסוים שיש רק גלים יוצאים. בניגוד\(G\), \(G_+\) מוגדר היטב וייחודי. (יש עוד פתרון תקף לחלוטין שיש בו רק גלים מטילים, אך הוא אינו רלוונטי לבעיית הפיזור. ההבדל בין הפתרונות הנכנסים והיוצאים עונה על המשוואה ההומוגנית שיש לה אפס בצד ימין.)

ברגע שאנו מזיזים מעט את הקטבים כמתואר לעיל, הקוטב ב \(k' =+k+i\varepsilon\) הוא למעשה הייחודיות היחידה של האינטגרנד השוכן בתוך קווי המתאר של האינטגרציה (סגור בחצי המישור העליון), כך שערך האינטגרל הוא רק התרומה מהקוטב הזה, כלומר, \[ G_+(r,k)=-\frac{m}{2\pi^2ir\hbar^2}(2\pi i)\frac{ke^{ikr}}{2k}=-\frac{m}{2\pi\hbar^2}\frac{e^{ikr}}{r} \label{10.1.12}\]

.

לכן \(i\varepsilon\) המרשם (כפי שהוא מכונה לפעמים) \(G_+\) אכן נותן לנו את מה שאנחנו רוצים: פתרון שיש בו רק גלים יוצאים, והמשוואה האינטגרלית הופכת ל: \[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}-\frac{m}{2\pi\hbar^2}\int d^3r' \frac{e^{ik |  \vec{r}-\vec{r}' |}}{|\vec{r}-\vec{r}' |}V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ). \label{10.1.13}\]

ניתן לכתוב זאת בפשטות רבה יותר אם אנו מניחים את הפוטנציאל להיות מקומי, כך שנוכל לקחת\(|\vec{r}|\gg |\vec{r}' |\). במקרה זה, זהו קירוב טוב לקחת את \(|\vec{r}-\vec{r}' |=r\) המכנה. עם זאת, לא ניתן לבצע קירוב זה באקספוננציאלי, מכיוון שלסדר מוביל (ראה תרשים) ולמרות שהמונח השני קטן בהרבה מהראשון, זהו שלב שעשוי להיות באחדות סדר. כמובן שיש לכלול גורם כזה כך שהתרומות לאינטגרל מאזורים שונים של הפוטנציאל יתווספו עם השלבים היחסיים הנכונים.

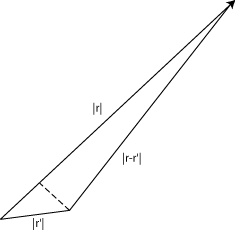
\[ k|\vec{r}-\vec{r}' |=kr-k\hat{\vec{r}}\cdot\vec{r}' =kr-\vec{k}_f\cdot\vec{r}' \label{10.1.14}\]

לכן, בהנחה \(r\) שמרחק הגלאי גדול בהרבה מטווח הפוטנציאל, נוכל לכתוב \[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}-\frac{m}{2\pi\hbar^2}\frac{e^{i kr}}{r}\int d^3r' e^{-i \vec{k}_f\cdot\vec{r}'} V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ). \label{10.1.15}\]

הקירוב שנולד

מהמשוואה לעיל, קירוב הסדר הראשון לפיזור ניתן על ידי החלפת \(\psi\) האינטגרל מימין במונח מסדר אפס, \(e^{i\vec{k}\cdot\vec{r}}\) \[ \psi_{\vec{k}(Born)}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}-\frac{m}{2\pi\hbar^2}\frac{e^{i kr}}{r}\int d^3r' e^{i\vec{k}\cdot\vec{r}' -\vec{k}_f\cdot\vec{r}'} V(\vec{r}' ) . \label{10.1.16}\]

זהו קירוב בורן. מבחינת משרעת הפיזור\(f(\theta,\varphi)\), שהגדרנו במונחים של פונקציית הגל האסימפטוטי:

\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}+f(\theta,\varphi)\frac{e^{ikr}}{r} \label{10.1.17}\]

קירוב נולד הוא:

\[ f_{Born}(\theta,\varphi)=-\frac{m}{2\pi\hbar^2}\int d^3r' e^{i \vec{k}\cdot\vec{r}' -\vec{k}_f\cdot\vec{r}'} V(\vec{r}' ) =-\frac{m}{2\pi\hbar^2}\int d^3r' e^{-i \vec{q}\cdot\vec{r}'} V(\vec{r}' ) \label{10.1.18}\]

\(\hbar \vec{q}\)איפה העברת המומנטום,\(\hbar \vec{q}=\hbar (\vec{k}_f-\vec{k})\). (מכיוון שלמומנטה הנכנסת והיוצאת יש גודל שווה, קל לבדוק זאת\(q=2k\sin\theta/2\).)

הפיזיקה המהותית כאן היא שחלקיק המפוזר בשינוי \(\hbar \vec{q}\) מומנטום מפוזר על ידי הרכיב \(\vec{q}\) -פורייה של הפוטנציאל - אפשר לדמיין את הפוטנציאל הבנוי מרכיבי פורייה שכל אחד מהם פועל כמו סורג עקיפה. תיקונים מסדר גבוה יותר לקירוב Born תואמים לפיזור רצוף מהסורגים הללו - הזמנות גבוהות יותר אלה נוצרות על ידי איטרציה של \[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}-\frac{m}{2\pi\hbar^2}\int d^3r' \frac{e^{ik |  \vec{r}-\vec{r}' |}}{|\vec{r}-\vec{r}'|}V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ). \label{10.1.19}\]

חשוב לקבוע מתי קירוב בורן הוא טוב: לפעמים זה לא. למעשה, אנחנו רק עושים את תורת ההפרעות בתחפושת, אז אנחנו צריכים שההפרעה תהיה קטנה, כלומר החלפה באינטגרל מימין \(e^{i\vec{k}\cdot\vec{r}'}\) במשוואה לעיל צריכה רק לעשות הבדל קטן לערך הנתון על \(\psi_{\vec{k}}(\vec{r}' )\) ידי ביצוע האינטגרל. \(\psi_{\vec{k}}(\vec{r})\) זהו כמובן תרגיל מסובך למדי בעקביות עצמית.

הבה ננסה להעריך איזה הבדל מחליפה \(\psi_{\vec{k}}(\vec{r}' )\) על ידי \(e^{i\vec{k}\cdot\vec{r}'}\) באינטגרנד במקרה הנפוץ של פוטנציאל סימטרי כדורית המתאפיין בעומק \(V(r)\) ובטווח. \(V_0\) \(r_0\) האינטגרל הוא למעשה רק על פני אזור בגודל \(r_0\) סביב המקור.

ראשית שקול פיזור אנרגיה נמוכה, \(kr_0<1\) נניח, כך שלמטרות הערכה נוכל להחליף את המונח האקספוננציאלי ב -1 באזור האינטגרציה. אנו גם מניחים כי היכן \(\psi\) שמופיע באינטגרל בצד ימין של המשוואה \(|\psi_{\vec{k}}(\vec{r}' )|\) הוא גם די קרוב ל -1 (זכרו שהאינטגרל הוא רק על נפח בתוך המקור \(r_0\) בערך) ולכן אנו פשוט מחליפים אותו ב -1. במילים אחרות, אנו מניחים שגל המישור הנכנס, ה-\(e^{i\vec{k}\cdot\vec{r}'}\), אינו מעוות באופן דרמטי בתוך אותו נפח בו הפוטנציאל משמעותי.

כעת, הנחנו שפונקציית הגל ליד המקור קרובה ל -1, כך שעדיף לשים את הערך הזה באינטגרנד מימין לתת ערך עבור \(\psi_{\vec{k}}(\vec{r})\) בצד שמאל של המשוואה שהוא די קרוב ל -1. הקירובים נותנים: \[ \psi_k(0)\approx 1-\frac{m}{2\pi\hbar^2}\int d^3r' \frac{V(r' )}{r'} ,\label{10.1.20}\]

כך שקירוב Born יהיה סביר באנרגיות נמוכות (\(kr_0<1\)) אם המונח השני בצד ימין הוא הרבה פחות מאחדות.

מתי זה נכון לגבי פוטנציאל אמיתי? אם ניקח \(V(r)\) עומק \(V_0\) וטווח\(r_0\), קירוב Born טוב אם: \[ \frac{m}{2\pi\hbar^2}\int_0^{r_0}4\pi r^2\frac{V_0}{r}dr\ll 1,\;\; or\;\; V_0\ll \frac{\hbar^2}{mr^2_0}. \label{10.1.21}\]

שימו לב שהצד הימני של אי השוויון הזה הוא בסדר האנרגיה הקינטית של חלקיק המוגבל לנפח השווה לטווח הפוטנציאל, כך שקירוב Born תקף באנרגיות נמוכות בתנאי שהפוטנציאל נמצא הרבה מתחת לחוזק הדרוש למצב כבול.

למעשה, קירוב בורן עובד טוב יותר באנרגיות גבוהות יותר, מכיוון שמונח הפאזה המתנדנד \(-\frac{m}{2\pi\hbar^2}\int d^3r' e^{-i \vec{q}\cdot\vec{r}'} V(\vec{r}' )\) מצמצם את ערך האינטגרל בגורם בסדר גודל. \(1/(kr_0)\) המשמעות היא שהמצב הופך להיות\(V_0\ll kr_0\frac{\hbar^2}{mr^2_0}\), תמיד מרוצה באנרגיות גבוהות מספיק.

משוואת ליפמן-שווינגר

זה מוכיח מאיר, במיוחד בהבנת הפיזור מעבר לקירוב Born, לעצב מחדש את נגזרת הפונקציה של הירוק של משרעת הפיזור בשפה הפורמלית יותר של חזיות, חזיות ומפעילים. הפונקציה של הירוק הוצגה בסעיף הקודם כהיפוך (הלא ייחודי) של המפעיל \[ E_k-H_0=\left(\frac{\hbar^2}{2m}\nabla^2+E_k\right) .\label{10.1.22}\]

(הערה סוגריים: בחישוב מספרי, פונקציית הגל עשויה להיות מוגדרת בנקודות על סריג בחלל, ומפעיל דיפרנציאלי כזה יוצג כמפעיל הבדל, כלומר כמטריצה גדולה אך סופית הפועלת על וקטור גדול שהאלמנטים שלו היו ערכי פונקציית הגל בנקודות על הסריג. הפונקציה של הירוק תהיה אז המטריצה ההפוכה עם תנאי גבול מתאימים שצוינו כדי להבטיח ייחודיות.)

באופן רשמי בלבד (ובעקבות Sakurai)\(H=H_0+V\), כותב, עם מפעיל האנרגיה \(H_0\) הקינטית\(\vec{p}^2/2m\), מצב גל המישור הנכנס הוא פתרון של \[ H_0|\vec{k}\rangle  =E_k|\vec{k}\rangle . \label{10.1.23}\]

אנחנו רוצים לפתור \[ (H_0+V)|\psi\rangle  =E_k|\psi\rangle . \label{10.1.24}\]

הטרנספורמציה ממשוואה דיפרנציאלית למשוואה אינטגרלית בשפה זו היא: \[ |\psi\rangle  = |\vec{k}\rangle +\frac{1}{E_k-H_0}V|\psi\rangle . \label{10.1.25}\]

זה נותן את הגל הנכנס הבלתי מופרע עבור\(V=0\), ועל ידי פעולה משני צידי המשוואה עם\(E-H_0\), אנו מוצאים \(|\psi\rangle\) שאכן מספק את משוואת שרדינגר המלאה. אך כמובן שלטרנספורמציה זו ממשוואה דיפרנציאלית למשוואה אינטגרלית יש את אותו פגם כמו הטיפול הקודם: \(H_0\) יש רצף של ערכים עצמיים במגבלת הנפח האינסופית, כך שמשוואת האופרטור הופכת לא מוגדרת עבור אותם מצבים עצמיים עם אנרגיה קרובה באופן שרירותי ל אנרגיה נכנסת, ואלה בדיוק מצבי הרלוונטיות הפיזית.

כדי להבהיר שזו אכן הבעיה שכבר פתרנו, הבה נתרגם אותה לשפה הקודמת. ראשית קח את המוצר הפנימי עם החזייה\(\langle \vec{r}|\): \[ \langle \vec{r}|\psi\rangle  = \langle \vec{r}|\vec{k}\rangle +\langle \vec{r}|\frac{1}{E_k-H_0}V|\psi\rangle . \label{10.1.26}\]

לאחר מכן, הכנס ייצוג של אחדות כסכום על מצבים עצמיים של מומנטום (ולכן של\(H_0\)) למונח האחרון:

\[ \begin{matrix} \langle \vec{r}|\psi\rangle  = \langle \vec{r}|\vec{k}\rangle +\int \frac{dk' }{(2\pi)^3}\langle \vec{r}|\vec{k}' \rangle \langle \vec{k}' |\frac{1}{E_k-H_0}V|\psi\rangle \\ = \langle \vec{r}|\vec{k}\rangle +\int \frac{dk' }{(2\pi)^3}\langle \vec{r}|\vec{k}' \rangle \frac{1}{E_k-E_k'} \langle \vec{k}' |V|\psi\rangle . \end{matrix} \label{10.1.27}\]

לבסוף, הכנס ייצוג נוסף של אחדות כסכום על מצבי עמדה עצמיים בקדנציה האחרונה: \[ \langle \vec{r}|\psi\rangle  = \langle \vec{r}|\vec{k}\rangle +\int d^3r' \int \frac{dk' }{(2\pi)^3}\langle \vec{r}|\vec{k}' \rangle \frac{1}{E_k-E_k'}\langle \vec{k}' |\vec{r}' \rangle \langle \vec{r}' |V|\psi\rangle . \label{10.1.28}\]

בהשוואת ביטוי זה למשוואה האינטגרלית בדיון הקודם, ניכר כי הם אכן שווים, ולכן מרשם ה- i\ varepsilon הנכון לתת את פונקציית הגל המפוזר, \[ |\psi\rangle  =  |\vec{k}\rangle +\frac{1}{E_k-H_0+i\varepsilon}V|\psi\rangle  =  |\vec{k}\rangle+G_+ V|\psi\rangle \label{10.1.29}\]

איפה \[ G_+=\frac{1}{E_k-H_0+i\varepsilon}=\int \frac{d^3k'}{(2\pi)^3}\frac{|\vec{k}' \rangle \langle \vec{k}' |}{E_k-E_k' +i\varepsilon} \label{1.1.30}\]

באיזו צורה ניכר \(\langle \vec{r}|G_+|\vec{r}' \rangle\) כי זהה \(G_+(\vec{r}-\vec{r}' )\) לעבודה הקודמת.

משוואה זו לגל המפוזר \(|\psi\rangle\) נקראת משוואת ליפמן-שווינגר.

הערה: סאקוראי מגדיר את תפקידו של הירוק כ

\[ G_+(Sakurai)=\frac{\hbar^2}{2m}\frac{1}{E-H_0+i\varepsilon}\cdot\label{10.1.31}\]

כעת, לאחר שיש לנו מפעיל פונקציות מוגדר היטב של גרין\(G_+\), ניתן לפתור באופן רשמי את משוואת ליפמן-שווינגר: \[ |\psi\rangle  =  |\vec{k}\rangle +G_+ V|\psi\rangle , \;\; so \;\; |\psi\rangle  = \frac{1}{1-G_+ V}|\vec{k}\rangle , \label{10.1.32}\]

עם פתרון סדרה \[ |\psi\rangle  =  |\vec{k}\rangle +G_+ V|\vec{k}\rangle +G_+ VG_+ V|\vec{k}\rangle +G_+ VG_+ VG_+ V|\vec{k}\rangle +\dots \label{10.1.33}\]

רק גרסה רשמית של הפתרון שמצאנו קודם לכן.

מטריצת המעבר

פועל משני צידי המשוואה לעיל עם\(V\), \[ V|\psi\rangle  =  V|\vec{k}\rangle +VG_+ V|\vec{k}\rangle +VG_+ VG_+ V|\vec{k}\rangle +\dots=T|\vec{k}\rangle \label{10.1.34}\]

הגדרת "מטריצת המעבר" \(T\) על ידי \[ T=V+VG_+V+VG_+VG_+V+\dots=V+V\frac{1}{E-H_0+i\varepsilon}V+\dots \label{10.1.35}\]

במונחים של מפעיל מטריצת מעבר זה, ניתן לכתוב את הגל המפוזר \[ |\psi\rangle = |\vec{k}\rangle  +G_+ T|\vec{k}\rangle . \label{10.1.36}\]

להשוות את זה עם \[ |\psi\rangle  =  |\vec{k}\rangle +G_+ V|\psi\rangle , \label{10.1.37}\]

ונזכר כי קירוב Born ניתן על ידי \[ |\psi\rangle_{Born}= |\vec{k}\rangle +G_+ V|\vec{k}\rangle , \label{10.1.38}\]

אנו רואים \(T\) שזה סוג של פוטנציאל כללי, כולל כל מונחי הסדר הגבוה יותר, כך שכמו שהקירוב Born נתן את משרעת הפיזור במונחים של, \(V\) \[ f^{Born}(\theta,\varphi)=-\frac{m}{2\pi\hbar^2}\int d^3r' e^{i \vec{k}\cdot\vec{r}' -\vec{k}_f\cdot\vec{r}'} V(\vec{r}' )  \label{10.1.39}\]

התוצאה המדויקת הכוללת את כל תנאי ההזמנה הגבוהים חייבת להיות בעלת מבנה זהה \(T\) להחלפה\(V\). כמובן, שלא כמו\(V(\vec{r})\), \(T\) אינה מטריצה אלכסונית במרחב: היא תלויה בשני משתני חלל, והתמרת הפורייה שלה היא אפוא פונקציה של שתי מומנטות, כלומר הנכנסות \(\vec{k}\) והמפוזרות. \(r\) \(\vec{k}'\) כך אנו מוצאים: \[ f(\theta,\varphi)=-\frac{m}{2\pi\hbar^2}\int d^3r\int d^3r' e^{i \vec{k}\cdot\vec{r}-\vec{k}' \cdot\vec{r}'} T(\vec{r}' ,\vec{r})=-\frac{m}{2\pi\hbar^2}\langle \vec{k}' |T|\vec{k}\rangle . \label{10.1.40}\]

החלפנו את הביטוי \(\vec{k}_f\) ב- Born ב-\(\vec{k}'\). לסקוראי יש תוספת \((2\pi)^3\) במונח מימין, כי הוא משתמש,\(\langle \vec{k}|\vec{k}' \rangle =\delta(\vec{k}-\vec{k'})\), אנו משתמשים \(\langle \vec{r}|\vec{k}\rangle =\frac{e^{i\vec{k}\cdot\vec{r}}}{(2\pi)^{3/2}}\)\(\langle \vec{k}|\vec{k}' \rangle =(2\pi)^3\delta(\vec{k}-\vec{k'})\),. \(\langle \vec{r}|\vec{k}\rangle =e^{i\vec{k}\cdot\vec{r}}\)

המשפט האופטי

המשפט האופטי מתייחס לחלק הדמיוני של משרעת הפיזור קדימה לחתך הכולל, \[ Im\, f(\theta=0)=\frac{k\sigma_{tot}}{4\pi}. \label{10.1.41}\]

התוכן הפיזי של משפט מסתורי זה בתחילה יתבהר הרבה יותר לאחר שנדון בגלים חלקיים ובכמה השפעות גיאומטריות. זה כן אומר לנו שזה \(f\) לא יכול להיות אמיתי לכל הכיוונים, וכי בפרט \(f\) יש חלק דמיוני חיובי בכיוון קדימה. כללנו את ההוכחה כאן לפרוטוקול, אבל אתה יכול לדלג עליה לעת עתה. אך שימו לב כי הוכחה זו כללית יותר מהפשוטה שניתנה (בהמשך) בסעיף על גלים חלקיים, בכך שאיננו מניחים כאן את הפוטנציאל לסימטריה כדורית.

מן הביטוי \(f(\theta,\varphi)\) לעיל, אנו רואים כי עלינו למצוא את החלק הדמיוני של\(\langle \vec{k}|T|\vec{k}\rangle\).

נזכיר כי \[ V|\psi\rangle =  T|\vec{k}\rangle , \label{10.1.42}\]

אז אנחנו צריכים למצוא \[ Im\,\langle \vec{k}|V|\psi\rangle =Im\left[\left(\langle \psi|-\langle \psi|V\frac{1}{E-H_0-i\varepsilon}\right) V|\psi\rangle \right]. \label{10.1.43}\]

מכיוון \(V\) שהוא הרמיטי, החלק הדמיוני היחיד של אלמנט המטריצה לעיל מגיע מה-\(i\varepsilon\), ונזכר בכך \[ \frac{1}{E-H_0-i\varepsilon}=\frac{P}{E-H_0}+i\pi\delta(E-H_0). \label{10.1.44}\]

לכן, \[ Im\,\langle \vec{k}|V|\psi\rangle =-\pi\langle \psi|V\delta(E-H_0)V|\psi\rangle . \label{10.1.45}\]

שוב באמצעות \[ V|\psi\rangle =  T|\vec{k}\rangle \label{10.1.42}\]

אנחנו יכולים לשכתב את המשוואה \[ Im\,\langle \vec{k}|T|\vec{k}\rangle =Im\,\langle \vec{k}|V|\psi\rangle =-\pi\langle \psi|V\delta(E-H_0)V|\psi\rangle =-\pi\langle \vec{k}|T^{\dagger}\delta(E-H_0)T|\vec{k}\rangle . \label{10.1.46}\]

הכנסת קבוצה שלמה של מצבי גל מישוריים באלמנט המטריצה הסופי לעיל נותנת \[ \begin{matrix} Im\,\langle \vec{k}|T|\vec{k}\rangle =-\pi\langle \vec{k}|T^{\dagger}\delta(E-H_0)T|\vec{k}\rangle \\ =-\pi\int \frac{d^3k'}{(2\pi)^3}\langle \vec{k}|T^{\dagger}|\vec{k}' \rangle \langle \vec{k}' |T|\vec{k}\rangle \delta(E-\frac{\hbar^2k'^2}{2m}) \\ =-\pi\int \frac{d\Omega' }{(2\pi)^3}\frac{mk}{\hbar^2}|\langle \vec{k}' |T|\vec{k}\rangle |^2. \end{matrix} \label{10.1.47}\]

(זוהי אותה נוסחה כמו זו של סאקוראי בשנת 7.3: התוספת שלנו \((2\pi)^3\) במכנה ניכרת רק מכיוון שמצבי גל המישור שלנו שונים משלו על ידי גורם.) \((2\pi)^{3/2}\)

ניסוח תלוי זמן של תורת הפיזור

בניסוח הבלתי תלוי בזמן שהוצג לעיל, פתרנו את משוואת ליפמן-שווינגר כדי למצוא \[ |\psi\rangle  =  |\vec{k}\rangle +G_+ V|\vec{k}\rangle +G_+ VG_+ V|\vec{k}\rangle +G_+ VG_+ VG_+ V|\vec{k}\rangle +\dots \label{10.1.48}\]

איפה \[ G_+(E)=\frac{1}{E-H_0+i\varepsilon}=\int \frac{d^3k'}{(2\pi)^3}\frac{|\vec{k'}\rangle\langle\vec{k'}|}{E-E_{k'} +i\varepsilon} \label{10.1.49}\]

ו\(E=E_k\).

(תזכורת על אמנת הנורמליזציה של פונקציית הגל שלנו: תמיד יש לנו מכנה \(2\pi\) לאינטגרל. \(dk\) המשמעות היא שמפעיל הזהות כסכום על פני מפעילי הקרנת גלי מישור הוא\(I=\int \frac{d^3k}{(2\pi)^3}|\vec{k}\rangle \langle \vec{k}| \). הנורמליזציה היא\(\langle \vec{k}|\vec{k}' \rangle =(2\pi)^3\delta(\vec{k}-\vec{k'})\), ו\(\langle \vec{r}|\vec{k}\rangle =e^{i\vec{k}\cdot\vec{r}}\). סקוראי משתמש\(\langle \vec{k}|\vec{k}' \rangle =\delta(\vec{k}-\vec{k'})\), \(\langle \vec{r}|\vec{k}\rangle =\frac{e^{i\vec{k}\cdot\vec{r}}}{(2\pi)^{3/2}}\) \(I=\int d^3k|\vec{k}\rangle \langle \vec{k}|\) וכמו שנקר בפרק 1, למימד אחד, עמוד 67, אך מאוחר יותר, פרק 21 עמוד 585, שנקר עבר לסימון שלנו - אז היזהרו! האמנה שלנו משמשת גם את Baym ועל ידי Peskin.)

למעשה, פונקציה זו \(G_+\) היא טרנספורמציית פורייה של המפיץ עליו דנו בסמסטר שעבר. כדי לראות כיצד זה מתרחש, קח את אלמנט המטריצה בין שני מצבים עצמיים של מיקום והתמרת פורייה מאנרגיה לזמן: \[ \begin{matrix} G_+(\vec{r},\vec{r'},t)=\frac{1}{2\pi}\int e^{-iEt/\hbar} dE\langle \vec{r}|G_+|\vec{r'}\rangle \\ =\frac{1}{2\pi}\int e^{-iEt/\hbar} dE\int \frac{d^3k'}{(2\pi)^3}\frac{\langle \vec{r}|k' \rangle \langle k' |\vec{r}' \rangle}{E-E_{k'} +i\varepsilon} \\ =\frac{1}{2\pi}\int e^{-iEt/\hbar} dE\int \frac{d^3k'}{(2\pi)^3}\frac{e^{i\vec{k'}\cdot(\vec{r}-\vec{r'})}}{E-E_{k'} +i\varepsilon}. \end{matrix} \label{10.1.50}\]

האינטגרל מעל \(E\) הוא לאורך הציר האמיתי, והמתאר סגור בחצי המישור שבו האינטגרנד הולך לאפס עבור בכיוון הדמיוני, כלומר בחצי המישור התחתון עבור \(t>0\) ובחצי המישור העליון עבור\(t<0\). אך עם \(i\varepsilon\) המונח המוצג, כל הייחודיות של האינטגרנד נמצאות בחצי המישור התחתון. לפיכך \(G_+\) הוא אפס זהה עבור. \(t<0\)

שכן\(t>0\), \(G_+\) הוא רק מפיץ החלקיקים החופשי בין שתי הנקודות (מלבד גורם הפאזה\(-i\)): \[ G_+(\vec{r},\vec{r'},t)=-i\int \frac{d^3k'}{(2\pi)^3}e^{i\vec{k'}\cdot(\vec{r}-\vec{r'})-iE_{k'}t/\hbar} . \label{10.1.51}\]

לסיכום: ניתן לפרש מונחים בפתרון הסדרה של משוואת ליפמן-שווינגר כפיזור עוקב אחר מרכיבי פורייה של פוטנציאל, כאשר התפשטות גל מישור בין לבין, כאשר סימן \(i\varepsilon\) המונח מבטיח שיש רק גלים יוצאים מכל פיזור. בגרסה שעברה טרנספורמציה של פורייה לעיל, הסכום מתפזר יתר על המידה בכל הנקודות האפשריות שבהן הפוטנציאל אינו אפס, עם \(G_+\) התפשטות בין לבין, \(i\varepsilon\) מה שמבטיח שנתיב הפיזור רק יתקדם בזמן.

בסמסטר שעבר הגדרנו את מפיץ החלקיקים החופשיים כמפעיל. \(U(t)=e^{-iH_0t/\hbar}\) המפיץ מתאר התפתחות של פונקציית גל החלקיקים החופשיים בזמן, באופן טבעי \(U(t)=0\) כל כך עבור. \(t<0\) לאחר מכן פורייה הופך את המפיץ \(t\) מ-אל\(E\), ומכניס גורם מתפורר אקספוננציאלי אינסופי להגדרת האינטגרל באינסוף, אנו מוצאים \[ U(E)=\int_{0}^{\infty} e^{iEt/\hbar} e^{-iH_0t/\hbar}e^{-\varepsilon t/\hbar} dt=\frac{i\hbar}{E-H_0+i\varepsilon}. \label{10.1.52}\]

שים לב שהמפיצים \(U\) \(G_+\) ונבדלים זה מזה לפי גורם של\(i\hbar\), במיוחד \[ G_+(t)=\frac{-i}{\hbar} \theta(t)e^{-iH_0t/\hbar}. \label{10.1.53}\]

אנו עוקבים אחר הסימון של סאקוראי (סעיף 7.11), זוהי הפונקציה הנורמלית של גרין למשוואת שרדינגר החלקיק החופשי התלויה בזמן: זהו הפתרון של \[ \left( i\hbar \frac{\partial}{\partial t}-H_0\right) G_+(t)=\delta(t) \label{10.1.54}\]

אשר מתפשט קדימה בזמן. הסיבה שהמפיצים \(U\) \(G_+\) ונבדלים זה מזה בגורם \(i\hbar\) היא שניתן ליצור את משוואת ליפמן-שווינגר כרצף זמן תוך שימוש בייצוג האינטראקציה של תיאוריית ההפרעות מסדר גבוה שתואר קודם לכן במהלך, ובעצם מתרחבת \(e^{-i(H_0+V)t/\hbar}\) כהרחבת סדרה מסודרת בזמן ב, ולכל גורם \(V\) יש מלווה \(V\)\(1/(i\hbar )\), גורמים אלה מטופלים על ידי שימוש במקום. \(G_+\) \(U\)

תרגיל: באותה הרצאה קודמת, נתנו את המונח מסדר שני כ: \[ c^{(2)}_n(t)=\left(\frac{1}{i\hbar}\right)^2\sum_n\int_0^t\int_0^{t'} dt' dt' ' e^{-i\omega_f(t-t' )}\langle f|V_S(t' )|n\rangle e^{-i\omega_n(t' -t' ' )}\langle n|V_S(t' ' )|i\rangle e^{-i\omega it' '} \label{10.1.55}\]

נניח \(V\) שהפוטנציאל קבוע בזמן. פורייה הופך את הביטוי הזה מ- \(t\) ל\(E\),\(E=\hbar \omega\), וקובע שיש לו את המבנה\(G_+(E)VG_+(E)VG_+(E)\).

חתך הנולד מתיאוריה תלויה בזמן

קבענו בהרצאה על תורת ההפרעה התלויה בזמן כי לסדר המוביל בהפרעה, שיעור המעבר ממצב התחלתי \(i\) למצב סופי ניתן על ידי \(f\) כלל הזהב של פרמי: \[ R_{i\to f}=\frac{2\pi}{\hbar} |\langle f|V|i\rangle |^2\delta(E_f-E_i). \label{10.1.56}\]

אנו יכולים להשתמש בתוצאה זו כדי למצוא - בסדר מוביל - את קצב הפיזור מגל מישור נכנס לכל מצב גל מישורי יוצא בעל אותה אנרגיה, ומכאן על ידי הוספת הקצב על פני כיווני גל המישור המצביעים בתוך זווית מוצקה קטנה נתונה\(d\Omega\), נגזר מחדש את קירוב Born.

מבחינה רעיונית, עם זאת, זה קצת מסובך. מהפתרון לעיל של משוואת שרדינגר, אנו יודעים שהגל היוצא הוא כדור, ולכן בכיוון מסוים המשרעת יורדת. אבל זה לא קורה עם גל מטוס! הדרך הברורה ביותר להתמודד עם זה היא להכניס את המערכת לקופסה גדולה, קוביית צד\(L\), עם תנאי גבול תקופתיים. זה מקל על ספירת מצבים ונורמליזציה של גלי המישור כראוי - כמובן, בגבול של קופסה גדולה, גלי המישור יוצרים סט שלם, כך שכל גל כדורי יכול לבוא לידי ביטוי כסכום מעל גלי המישור הללו.

בחלק זה, אם כן, אנו משתמשים בגלי מישור מנורמלים בתיבה: \[ |\vec{k}\rangle =\frac{1}{L^{3/2}}e^{i\vec{k}\cdot\vec{r}},\;\; \langle \vec{k'}|\vec{k}\rangle =\delta_{\vec{k}\vec{k'}} . \label{10.1.57}\]

אז \[ \langle f|V|i\rangle =\frac{1}{L^3}\int d^3re^{-i\vec{k}_f\cdot\vec{r}}V(\vec{r}) e^{i\vec{k}_i\cdot\vec{r}}=\frac{1}{L^3}\int d^3re^{-i\vec{q}\cdot\vec{r}}V(\vec{r}) \label{10.1.58}\]

שבו המומנטום מועבר לחלקיק\(\hbar \vec{q}=\hbar (\vec{k}_f-\vec{k}_i)\).

חשוב לציין כי אנו לוקחים את הגל הנכנס להיות רק אחד ממצבי גל המישור המנורמלים המספקים את תנאי הגבול התקופתיים של התיבה, כך שכעת הזרם הנכנס, שהוא רק מאחד מגלי המישור הללו, הוא \[ j_{in}=|\psi|^2v=\frac{1}{L^3}\frac{p}{m}. \label{10.1.59}\]

חוק הזהב הופך \[ R_{i\to(f\; in\; d\Omega)}=\frac{2\pi}{\hbar} |\langle f|V|i\rangle |^2\delta(E_f-E_i)d\Omega \label{10.1.60}\]

\(f\)המציין גל מישור היוצא החוצה בתוך הזווית המוצקה. \(d\Omega\)

כעת, הפונקציה \(\delta\) - פשוט סופרת את מספר המצבים הזמינים באנרגיה הנכונה (ההתחלתית), בזווית הכיוון המוצקה הסופית שצוינה. צפיפות המצבים במרחב המומנטום (לנפח \(L^3\) המרחב האמיתי) היא מצב אחד בכל נפח מרחב מומנטום\((2\pi\hbar)^3/L^3\), ולכן באמצעות\(dE/dp=p/m\), צפיפות המצבים באנרגיה לזווית מוצקה יוצאת היא. \(d\Omega\) \(L^3mpd\Omega/(2\pi\hbar)^3\)

לשים את כל זה ביחד \[ R_{i\to(f\; in\; d\Omega)}=\frac{2\pi}{\hbar} |\frac{1}{L^3}\int d^3xe^{-i\vec{q}\cdot\vec{x}}V(\vec{x})|^2L^3mpd\Omega/(2\pi\hbar)^3. \label{10.1.61}\]

קצב המעבר, קצב הפיזור לתוכו\(d\Omega\), הוא רק זרם האירוע כפול חתך הפיזור האינסופי \(d\sigma(\theta,\varphi)\) (זו הייתה ההגדרה שלנו ל), \(d\sigma\)

\[ j_{in}(\frac{d\sigma(\theta,\varphi)}{d\Omega})d\Omega=R_{i\to(f\; in\; d\Omega)} \label{10.1.62}\]

מכיוון שההגדרה שלנו \(R_{i\to(f\; in\; d\Omega)}\) כללה את גל הכניסה המנורמל כראוי.

אז סוף סוף \[ \frac{d\sigma(\theta,\varphi)}{d\Omega}=\frac{R_{i\to(f\; in\; d\Omega)}}{j_{in}d\Omega}=\frac{m}{p}\frac{2\pi}{\hbar} |\int d^3re^{-i\vec{q}\cdot\vec{r}}V(\vec{r})|^2mp/(2\pi\hbar)^3=|\frac{m}{2\pi\hbar^2}\int d^3re^{-i\vec{q}\cdot\vec{r}}V(\vec{r})|^2. \label{10.1.63}\]

הערת שוליים: גרסת הרצף.

\[ R_{i\to(f\; in\; d\Omega)}=\frac{2\pi}{\hbar} |\langle f|V|i\rangle |^2\delta(E_f-E_i)d\Omega. \label{10.1.60}\]

בגרסת הרצף,\(\langle \vec{r}|\vec{k}\rangle =e^{i\vec{k}\cdot\vec{r}}\), כך שמונח אלמנט המטריצה הוא צודק\(|\int d^3re^{-i\vec{q}\cdot\vec{r}}V(\vec{r})|^2\). פונקציית האנרגיה \(\delta\) היא בעלת משמעות רק בתוך אינטגרל, במקרה זה על פני הנפח הקטן של מצבי פיזור יוצאים בזווית המוצקה \(d\Omega\) ובאנרגיה השווה לאנרגיית הכניסה. אבל המרחב האינטגרלי הזה חייב לכלול את \(1/(2\pi)^3\) הגורם, על פי הכלל שלנו, נותן מונח מרחב פאזה יוצא \(k'\) \[ \int \frac{d^3k'}{(2\pi)^3}\delta(E_{k'}-E_k)=d\Omega\int \frac{k'^2dk' }{(2\pi)^3} \delta\left(\frac{\hbar^2k'^2}{2m}-\frac{\hbar^2k^2}{2m}\right)=d\Omega\frac{k^2}{(2\pi)^3}\frac{m}{\hbar^2k}=d\Omega\frac{mp}{(2\pi\hbar)^3}. \label{10.1.64}\]

זה קובע כי מוסכמות הנורמליזציה של הרצף שלנו נותנות את אותה תוצאה כמו זו המתקבלת מנורמליזציה של התיבה.

אלקטרונים מתפזרים מאטומים

אותה גישה, תוך שימוש בכלל הזהב להפקת קצב פיזור הסדר המוביל, שימושית היא ניתוח פיזור האלקטרונים המהירים על ידי אטומים. הבעיה באלקטרונים איטיים היא שתפקוד הגל צריך להיות אנטי-סימטרי ביחס לכל האלקטרונים הקיימים. אנו מניחים שלאלקטרונים מהירים יש חפיפה מועטה עם פונקציות גל האלקטרונים האטומיים במרחב המומנטום, כך שאיננו צריכים לדאוג לסימטריה.

עם קירוב זה, בעקבות Sakurai (עמוד 431) אלמנט מטריצת משרעת הפיזור הוא \[ \int d^3re^{i\vec{q}\cdot\vec{r}}\langle n|\left( -\frac{Ze^2}{r}+\sum_i\frac{e^2}{|\vec{r}-\vec{r}_i|}\right) |0\rangle \label{10.1.65}\]

כאשר המונח הפוטנציאלי \(V(\vec{x})\) הוא זה מהגרעין, בתוספת הדחייה מהאלקטרונים האחרים במיקומים\(\vec{x}_i\). לקיחת המצב האטומי הסופי \(n\) מאפשרת אפשרות לפיזור לא אלסטי.

מכיוון שלמרחק \(r\) האלקטרון המפוזר מהגרעין אין שום קשר למצב האטומי, \(n=0\) לתרומה הגרעינית, שהיא אז רק פיזור קולומב, ו \[ \int d^3r\frac{e^{i\vec{q}\cdot\vec{r}}}{r}=\frac{4\pi}{q^2}. \label{10.1.66}\]

(כדי לעשות אינטגרל זה, הכנס גורם התכנסות \(e^{-\varepsilon r}\) ואז תן\(\varepsilon\to 0\).)

המונח המערב את האלקטרונים האטומיים הוא עניין אחר: עבור \(i^{th}\) האלקטרון, שילוב על הקואורדינטה של האלקטרון המפוזר נותן גורם\((4\pi/q^2)e^{i\vec{q}\cdot\vec{r}_i}\), אך החלק הקשה הוא מציאת הערך של יסוד המטריצה של מפעיל זה בין המצבים האטומיים. שימו לב שזו רק התמרת פורייה של הפוטנציאל האלקטרוסטטי מצפיפות המטען של \(i^{th}\) האלקטרון,

\( \nabla^2V_i(\vec{r}i)=4\pi\rho_i(\vec{r}_i)\)הופך ל \(V_i(\vec{q})=(4\pi/q^2)\rho_i(\vec{q})\) \(\rho_i(\vec{r})=e\delta(\vec{r}-\vec{r}_i)\) ופורייה הופך ל\(e(e^{i\vec{q}\cdot\vec{r}_i})\).

גורם הצורה

לפיזור אלסטי, אם כן, התרומה של האלקטרונים האטומיים מתפרשת בפשטות: צפיפות המטען שלהם מולידה פוטנציאל על ידי המשוואה האלקטרוסטטית הרגילה, והאלקטרון (המהיר) מפוזר על ידי פוטנציאל זה. לפיזור לא-אלסטי, טרנספורמציית פורייה של צפיפות האלקטרונים מוערכת בין מצבים אטומיים שונים. בשני המקרים, אלמנט המטריצה נקרא גורם הצורה \(F_n(\vec{q})\) לפיזור, למעשה\(ZF_n(\vec{q})=\langle n|\sum_i e^{i\vec{q}\cdot\vec{r}_i}|0\rangle \). הגורם המנרמל \(Z\) מוצג כך לפיזור אלסטי, \(F_n(\vec{q})\to 1\) כמו\(q\to0\).

אז גורם הצורה הוא מפה של צפיפות המטען בחלל. \(q\) על ידי מדידת קצב הפיזור בזוויות שונות וניתוח פורייה, ניתן לתחום את התפלגות המטען במרחב הרגיל. אותה טכניקה פועלת עבור גרעינים, ולמעשה עבור חלקיקים - הנייטרון, למשל, למרות שהוא ניטרלי חשמלי, יש חלוקת מטען חשמלי לא טריוויאלי בנפחו, המתגלה על ידי פיזור אלקטרונים מהירים מאוד.

גורמי צורה כלליים יותר מתארים את התפלגות הספין, וגם תלות בזמן של התפלגויות מטען או ספין במערכות נרגשות. ניתן למדוד את כל אלה באמצעות ניסויי פיזור מעוצבים כראוי.