9.7: שורשים גבוהים יותר

מטרות למידה

בסוף פרק זה, תוכל:

• פשט ביטויים עם שורשים גבוהים יותר
• השתמש במאפיין המוצר כדי לפשט ביטויים עם שורשים גבוהים יותר
• השתמש במאפיין Quotient כדי לפשט ביטויים עם שורשים גבוהים יותר
• הוסף וחסר שורשים גבוהים יותר

הערה

1. פשט:$y^{5}y^{4}$.
   אם פספסת בעיה זו, עיין בדוגמה 6.2.7.
2. פשט:$(n^2)^6$.
   אם פספסת בעיה זו, עיין בדוגמה 6.2.19.
3. פשט:$\frac{x^8}{x^3}$.
   אם פספסת בעיה זו, עיין בדוגמה 6.5.1.

פשט ביטויים עם שורשים גבוהים יותר

עד כה, בפרק זה עבדנו עם ריבועים ושורשים מרובעים. כעת נרחיב את עבודתנו כך שתכלול כוחות עליונים ושורשים גבוהים יותר.

בואו נסקור תחילה כמה אוצר מילים.

$$\begin{array}{cc} {}&{}\\ {\textbf{We write:}}&{\textbf{We say:}}\\ {n^2}&{\text{n squared}}\\ {n^3}&{\text{n cubed}}\\ {n^4}&{\text{n to the fourth}}\\ {n^5}&{\text{n to the fifth}}\\ \nonumber \end{array}$$

המונחים 'בריבוע' ו'קוביות 'מגיעים מהנוסחאות לשטח ריבוע ונפח של קובייה.

זה יהיה מועיל לקבל טבלה של כוחות המספרים השלמים מ -5to5. ראה איור$\PageIdnex{1}$.

איור$\PageIndex{1}$: כוחות ראשונים עד חמישיים של מספרים שלמים מ -5 עד 5.

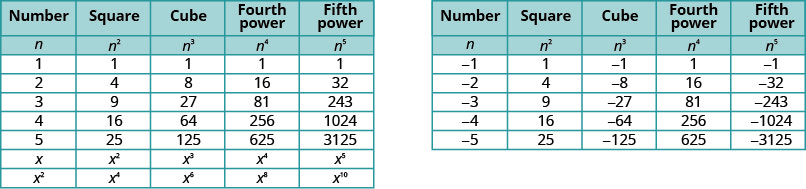
שימו לב לסימנים באיור$\PageIndex{1}$. כל הכוחות של מספרים חיוביים הם חיוביים, כמובן. אבל כשיש לנו מספר שלילי, הכוחות הזוגיים הם חיוביים והכוחות המוזרים הם שליליים. נעתיק את השורה עם הכוחות של -2 למטה כדי לעזור לך לראות זאת.

מוקדם יותר בפרק זה הגדרנו את השורש הריבועי של מספר.

אם$n^2=m$, אז n הוא שורש ריבועי של m.

והשתמשנו בסימון $\sqrt{m}$ כדי לציין את השורש הריבועי העיקרי. אז $\sqrt{m} \ge 0$ תמיד.

כעת נרחיב את ההגדרה לשורשים גבוהים יותר.

הגדרה: שורש N של מספר

אם$b^n=a$, אז b הוא שורש n של מספר a.

שורש ה - n העיקרי של a כתוב $\sqrt[n]{a}=b$

n נקרא מדד הרדיקל.

אנחנו לא כותבים את האינדקס לשורש ריבועי. בדיוק כמו שאנחנו משתמשים במילה 'קוביות' עבור$b^3$, אנו משתמשים במונח 'שורש קוביות' עבור. $\sqrt[3]{a}$

אנו מתייחסים לאיור $\PageIndex{1}$ כדי לעזור לנו למצוא שורשים גבוהים יותר.

$$\begin{array}{cc} {4^3=64}&{\sqrt[3]{64}=4}\\ {3^4=81}&{\sqrt[4]{81}=3}\\ {(−2)^5=−32}&{\sqrt[5]{−32}=−2}\\ \nonumber \end{array}$$

האם יכול להיות שיש לנו שורש שווה של מספר שלילי? לא. אנו יודעים שהשורש הריבועי של מספר שלילי אינו מספר ממשי. הדבר נכון גם לגבי כל שורש אחיד. אפילו שורשים של מספרים שליליים אינם מספרים ממשיים. שורשים מוזרים של מספרים שליליים הם מספרים ממשיים.

הגדרה: מאפיינים של $\sqrt[n]{a}$

כאשר n הוא מספר זוגי ו

• $a\ge 0$, אז $\sqrt[n]{a}$ הוא מספר אמיתי
• $a < 0$, אז $\sqrt[n]{a}$ הוא לא מספר אמיתי

כאשר n הוא מספר אי זוגי, $\sqrt[n]{a}$ הוא מספר ממשי לכל הערכים של a.

דוגמא $\PageIndex{1}$

פשט:

1. $\sqrt[3]{8}$
2. $\sqrt[4]{81}$
3. $\sqrt[5]{32}$.

תשובה

1.	$\sqrt[3]{8}$
מאז$(2)^3=8$.	2
2.	$\sqrt[4]{81}$
מאז$(3)^4=81$.	3
3.	$\sqrt[5]{32}$
מאז$(2)^5=32$.	2

דוגמא $\PageIndex{2}$

פשט:

1. $\sqrt[3]{27}$
2. $\sqrt[4]{256}$
3. $\sqrt[5]{243}$.

תשובה

1. 3
2. 4
3. 3

דוגמא $\PageIndex{3}$

פשט:

1. $\sqrt[3]{1000}$
2. $\sqrt[4]{16}$
3. $\sqrt[5]{32}$.

תשובה

1. 10
2. 2
3. 2

דוגמא $\PageIndex{4}$

פשט:

1. $\sqrt[3]{−64}$
2. $\sqrt[4]{−16}$
3. $\sqrt[5]{−243}$.

תשובה

1.	$\sqrt[3]{−64}$
מאז$(−4)^3=−64$.	-4
2.	$\sqrt[4]{−16}$
תחשוב, $(?)^4=−16$ אף מספר ממשי שהועלה לכוח הרביעי אינו חיובי.	לא מספר אמיתי.
3.	$\sqrt[5]{−243}$
מאז$(−3)^5=−243$.	-3

דוגמא $\PageIndex{5}$

פשט:

1. $\sqrt[3]{−125}$
2. $\sqrt[4]{−16}$
3. $\sqrt[5]{−32}$.

תשובה

1. -5
2. לא אמיתי
3. -2

דוגמא $\PageIndex{6}$

פשט:

1. $\sqrt[3]{−216}$
2. $\sqrt[4]{−81}$
3. $\sqrt[5]{−1024}$.

תשובה

1. −6
2. לא אמיתי
3. -4

כשעבדנו עם שורשים מרובעים שהיו להם משתנים ברדיקנד, הגבלנו את המשתנים לערכים לא שליליים. כעת נסיר את ההגבלה הזו.

השורש המוזר של מספר יכול להיות חיובי או שלילי. ראינו את זה$\sqrt[3]{−64}=−4$.

אבל השורש השווה של מספר לא שלילי הוא תמיד לא שלילי, כי אנחנו לוקחים את השורש n העיקרי.

נניח שנתחיל עם a=−5.

$$\begin{array}{cc} {(−5)^4=625}&{\sqrt[4]{625}=5}\\ \nonumber \end{array}$$

כיצד נוכל לוודא שהשורש הרביעי של -5 שהועלה לכוח הרביעי, $(−5)^4$ הוא 5? נראה בנכס הבא.

הגדרה: פישוט שורשים מוזרים ואחידים

עבור כל מספר שלם$n \ge 2$,

$$\begin{array}{cc} {\text{when n is odd}}&{\sqrt[n]{a^n}=a}\\ {\text{when n is even}}&{\sqrt[n]{a^n}=|a|}\\ \nonumber \end{array}$$

עלינו להשתמש בסימני הערך המוחלטים כאשר אנו לוקחים שורש אחיד של ביטוי עם משתנה ברדיקל.

דוגמא $\PageIndex{7}$

פשט:

1. $\sqrt{x^2}$
2. $\sqrt[3]{n^3}$
3. $\sqrt[4]{p^4}$
4. $\sqrt[5]{y^5}$.

תשובה

אנו משתמשים בערך המוחלט כדי להיות בטוחים לקבל את השורש החיובי.

1.	$\sqrt{x^2}$
מאז $(x)^2=x^2$ ואנחנו רוצים את השורש החיובי.	|איקס|
2.	$\sqrt[3]{n^3}$
מאז$(n)^3=n^3$. זהו שורש מוזר ולכן אין צורך בסימן ערך מוחלט.	n
3.	$\sqrt[4]{p^4}$
מאז $(p)^4=p^4$ ואנחנו רוצים את השורש החיובי.	|p |
4.	$\sqrt[5]{y^5}$
מאז$(y)^5=y^5$. זהו שורש מוזר ולכן אין צורך בסימן ערך מוחלט.	y

דוגמא $\PageIndex{8}$

פשט:

1. $\sqrt{b^2}$
2. $\sqrt[3]{w^3}$
3. $\sqrt[4]{m^4}$
4. $\sqrt[5]{q^5}$.

תשובה

1. |b|
2. w
3. |m |
4. q

דוגמא $\PageIndex{9}$

פשט:

1. $\sqrt{y^2}$
2. $\sqrt[3]{p^3}$
3. $\sqrt[4]{z^4}$
4. $\sqrt[5]{q^5}$

תשובה

1. |y|
2. p
3. | z |
4. q

דוגמא $\PageIndex{10}$

פשט:

1. $\sqrt[3]{y^{18}}$
2. $\sqrt[4]{z^8}$.

תשובה

1.	$\sqrt[3]{y^{18}}$
מאז$(y^6)^3=y^18$.	$\sqrt[3]{(y^6)^3}$
	$y^6$
2.	$\sqrt[4]{z^8}$
מאז$(z^2)^4=z^8$.	$\sqrt[4]{(z^2)^4}$
מכיוון $z^2$ שהוא חיובי, איננו זקוקים לסימן ערך מוחלט.	$z^2$

דוגמא $\PageIndex{11}$

פשט:

1. $\sqrt[4]{u^{12}}$
2. $\sqrt[3]{v^{15}}$.

תשובה

1. $u^3$
2. $v^5$

דוגמא $\PageIndex{12}$

פשט:

1. $\sqrt[5]{c^{20}}$
2. $\sqrt[6]{d^{24}}$.

תשובה

1. $c^4$
2. $d^4$

דוגמא $\PageIndex{13}$

פשט:

1. $\sqrt[3]{64p^6}$
2. $\sqrt[4]{16q^{12}}$.

תשובה

1.	$\sqrt[3]{64p^6}$
לשכתב $64p^6$ כמו$(4p^2)^3$.	$\sqrt[3]{(4p^2)^3}$
קח את שורש הקוביה.	$4p^2$
2.	$\sqrt[4]{16q^{12}}$
לשכתב את הרדיקנד ככוח רביעי.	$\sqrt[4]{(2q^3)^4}$
קח את השורש הרביעי.	$2|q^3|$

דוגמא $\PageIndex{14}$

פשט:

1. $\sqrt[3]{27x^{27}}$
2. $\sqrt[4]{81q^{28}}$.

תשובה

1. $3x^9$
2. $3∣q^7∣$

דוגמא $\PageIndex{15}$

פשט:

1. $\sqrt[3]{125p^9}$
2. $\sqrt[5]{243q^{25}}$

תשובה

1. $5p^3$
2. $3q^5$

השתמש במאפיין המוצר כדי לפשט ביטויים עם שורשים גבוהים יותר

אנו נפשט ביטויים עם שורשים גבוהים יותר באותה צורה שבה פשטנו ביטויים עם שורשים מרובעים. שורש n נחשב לפשוט יותר אם אין לו גורמים של$m^n$.

הגדרה: שורש N TH פשוט

$\sqrt[n]{a}$נחשב פשוט אם אין גורמים של$m^n$.

אנו נכליל את מאפיין המוצר של שורשים מרובעים כך שיכלול כל שורש שלם $n \ge 2$.

הגדרה: נכס מוצר של שורשים N

$\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}$ו $\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}$

מתי $\sqrt[n]{a}$ $\sqrt[n]{b}$ והם מספרים ממשיים ולכל מספר שלם $n \ge 2$

דוגמא $\PageIndex{16}$

פשט:

1. $\sqrt[3]{x^4}$
2. $\sqrt[4]{x^7}$.

תשובה

1.	$\sqrt[3]{x^4}$
כתוב מחדש את הרדיקנד כמוצר באמצעות גורם הקוביה המושלם הגדול ביותר.	$\sqrt[3]{x^3·x}$
לשכתב את הרדיקל כתוצר של שני רדיקלים.	$\sqrt[3]{x^3}·\sqrt[3]{x}$
לפשט.	$x\sqrt[3]{x}$
2.	$\sqrt[4]{x^7}$
כתוב מחדש את הרדיקנד כמוצר באמצעות גורם הכוח הרביעי המושלם הגדול ביותר.	$\sqrt[4]{x^4·x^3}$
לשכתב את הרדיקל כתוצר של שני רדיקלים.	$\sqrt[4]{x^4}·\sqrt[4]{x^3}$
לפשט.	$|x|\sqrt[4]{x^3}$

דוגמא $\PageIndex{17}$

פשט:

1. $\sqrt[4]{y^6}$
2. $\sqrt[3]{z^5}$.

תשובה

1. $|y∣\sqrt[4]{y^2}$
2. $z\sqrt[3]{z^2}$

דוגמא $\PageIndex{18}$

פשט:

1. $\sqrt[5]{p^8}$
2. $\sqrt[6]{q^{13}}$.

תשובה

1. $p\sqrt[5]{p^3}$
2. $q^2\sqrt[6]{q}$

דוגמא $\PageIndex{19}$

פשט:

1. $\sqrt[3]{16}$
2. $\sqrt[4]{243}$.

תשובה

1.	$\sqrt[3]{16}$
	$\sqrt[3]{2^4}$
כתוב מחדש את הרדיקנד כמוצר באמצעות גורם הקוביה המושלם הגדול ביותר.	$\sqrt[3]{2^3·2}$
לשכתב את הרדיקל כתוצר של שני רדיקלים.	$\sqrt[3]{2^3}·\sqrt[3]{2}$
לפשט.	$2\sqrt[3]{2}$
2.	$\sqrt[4]{243}$
	$\sqrt[4]{3^5}$
כתוב מחדש את הרדיקנד כמוצר באמצעות גורם הכוח הרביעי המושלם הגדול ביותר.	$\sqrt[4]{3^4·3}$
לשכתב את הרדיקל כתוצר של שני רדיקלים.	$\sqrt[4]{3^4}·\sqrt[4]{3}$
לפשט.	$3\sqrt[4]{3}$

דוגמא $\PageIndex{20}$

פשט:

1. $\sqrt[3]{81}$
2. $\sqrt[4]{64}$.

תשובה

1. $3\sqrt[3]{3}$
2. $2\sqrt[4]{4}$

דוגמא $\PageIndex{21}$

פשט:

1. $\sqrt[3]{625}$
2. $\sqrt[4]{729}$.

תשובה

1. $5\sqrt[3]{5}$
2. $3\sqrt[4]{9}$

אל תשכח להשתמש בסימני הערך המוחלטים כשאתה לוקח שורש אחיד של ביטוי עם משתנה ברדיקל.

דוגמא $\PageIndex{22}$

פשט:

1. $\sqrt[3]{24x^7}$
2. $\sqrt[4]{80y^{14}}$.

תשובה

1.	$\sqrt[3]{24x^7}$
כתוב מחדש את הרדיקנד כמוצר באמצעות גורמי קובייה מושלמים.	$\sqrt[3]{2^{3}x^{6}·3x}$
לשכתב את הרדיקל כתוצר של שני רדיקלים.	$\sqrt[3]{2^{3}x^{6}}·\sqrt[3]{3x}$
לשכתב את הרדיקנד הראשון כ $(2x^2)^3$	$\sqrt[3]{(2x^{2})^3}·\sqrt[3]{3x}$
לפשט.	$2x^2\sqrt[3]{3x}$
2.	$\sqrt[4]{80y^{14}}$
כתוב מחדש את הרדיקנד כמוצר באמצעות גורמי כוח רביעיים מושלמים.	$\sqrt[4]{2^{4}y^{12}·5y^2}$
לשכתב את הרדיקל כתוצר של שני רדיקלים.	$\sqrt[4]{2^{4}y^{12}}·\sqrt[4]{5y^2}$
לשכתב את הרדיקנד הראשון כ $(2y^3)^4$	$\sqrt[4]{(2y^3)^4}·\sqrt[4]{5y^2}$
לפשט.	$2|y^3|\sqrt[4]{5y^2}$

דוגמא $\PageIndex{23}$

פשט:

1. $\sqrt[3]{54p^[10}]$
2. $\sqrt[4]{64q^{10}}$.

תשובה

1. $3p^3\sqrt[3]{2p}$
2. $2q^2\sqrt[4]{4q^2}$

דוגמא $\PageIndex{24}$

פשט:

1. $\sqrt[3]{128m^{11}}$
2. $\sqrt[4]{162n^7}$.

תשובה

1. $4m^3\sqrt[3]{2m^2}$
2. $3|n|\sqrt[4]{2n^3}$

דוגמא $\PageIndex{25}$

פשט:

1. $\sqrt[3]{−27}$
2. $\sqrt[4]{−16}$.

תשובה

1.	$\sqrt[3]{−27}$
כתוב מחדש את הרדיקנד כמוצר באמצעות גורמי קובייה מושלמים.	$\sqrt[3]{(−3)^3}$
קח את שורש הקוביה.	-3
2.	$\sqrt[4]{−16}$
אין מספר אמיתי n איפה$n^4=−16$.	לא מספר אמיתי.

דוגמא $\PageIndex{26}$

פשט:

1. $\sqrt[3]{−108}$
2. $\sqrt[4]{−48}$.

תשובה

1. $−3\sqrt[3]{4}$
2. לא אמיתי

דוגמא $\PageIndex{27}$

פשט:

1. $\sqrt[3]{−625}$
2. $\sqrt[4]{−324}$.

תשובה

1. $−5\sqrt[3]{5}$
2. לא אמיתי

השתמש במאפיין המנה כדי לפשט ביטויים עם שורשים גבוהים יותר

אנו יכולים לפשט שורשים גבוהים יותר עם מנות באותו אופן שבו פשטנו שורשים מרובעים. ראשית אנו מפשטים את כל השברים בתוך הרדיקל.

דוגמא $\PageIndex{28}$

פשט:

1. $\sqrt[3]{\frac{a^8}{a^5}}$
2. $\sqrt[4]{\frac{a^{10}}{a^2}}$.

תשובה

1.	$\sqrt[3]{\frac{a^8}{a^5}}$
פשט תחילה את השבר מתחת לרדיקל.	$\sqrt[3]{a^3}$
לפשט.	א
2.	$\sqrt[4]{\frac{a^{10}}{a^2}}$
פשט תחילה את השבר מתחת לרדיקל.	$\sqrt[4]{a^8}$
לשכתב את הרדיקנד באמצעות גורמי כוח רביעיים מושלמים.	$\sqrt[4]{(a^2)^4}$
לפשט.	$a^2$

דוגמא $\PageIndex{29}$

פשט:

1. $\sqrt[4]{\frac{x^7}{x^3}}$
2. $\sqrt[4]{\frac{y^{17}}{y^5}}$.

תשובה

1. |איקס|
2. $y^3$

דוגמא $\PageIndex{30}$

פשט:

1. $\sqrt[3]{\frac{m^{13}}{m^7}}$
2. $\sqrt[5]{\frac{n^{12}}{n^2}}$.

תשובה

1. $m^2$
2. $n^2$

בעבר השתמשנו במאפיין Quotient 'הפוך' כדי לפשט שורשים מרובעים. כעת נכליל את הנוסחה כך שתכלול שורשים גבוהים יותר.

הגדרה: מאפיין מנה של שורשים N

$\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$ו $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$

מתי $\sqrt[n]{a}$ and $\sqrt[n]{b}$ are real numbers, $b \ne 0$, and for any integer $n \ge 2$

תרגיל $\PageIndex{31}$

פשט:

1. $\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}$
2. $\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}$

תשובה

1.	$\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}$
אף רדיקנד אינו קוביה מושלמת, לכן השתמש במאפיין Quotient כדי לכתוב כרדיקל אחד.	$\sqrt[3]{\frac{−108}{2}}$
פשט את השבר מתחת לרדיקל.	$\sqrt[3]{−54}$
כתוב מחדש את הרדיקנד כמוצר באמצעות גורמי קובייה מושלמים.	$\sqrt[3]{(−3)^3·2}$
לשכתב את הרדיקל כתוצר של שני רדיקלים.	$\sqrt[3]{(−3)^3}·\sqrt[3]{2}$
לפשט.	$−3\sqrt[3]{2}$
2.	$\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}$
אף רדיקנד אינו כוח רביעי מושלם, לכן השתמש במאפיין Quotient כדי לכתוב כרדיקל אחד	$\sqrt[4]{\frac{96x^7}{3x^2}}$
פשט את השבר מתחת לרדיקל.	$\sqrt[4]{32x^5}$
כתוב מחדש את הרדיקנד כמוצר באמצעות גורמי כוח רביעיים מושלמים.	$\sqrt[4]{2^{4}x^4·2x}$
לשכתב את הרדיקל כתוצר של שני רדיקלים.	$\sqrt[4]{(2x)^4}·\sqrt[4]{2x}$
לפשט.	$2|x|\sqrt[4]{2x}$

דוגמא $\PageIndex{32}$

פשט:

1. $\frac{\sqrt[3]{−532}}{\sqrt[3]{2}}$
2. $\frac{\sqrt[4]{486m^{11}}}{\sqrt[4]{3m^5}}$

תשובה

1. לא אמיתי
2. $3|m|\sqrt[4]{2m^2}$

דוגמא $\PageIndex{33}$

פשט:

1. $\frac{\sqrt[3]{−192}}{\sqrt[3]{3}}$
2. $\frac{\sqrt[4]{324n^7}}{\sqrt[4]{2n^3}}$.

תשובה

1. -4
2. $3|n|\sqrt[4]{2}$

אם לא ניתן לפשט את השבר בתוך הרדיקל, אנו משתמשים בצורה הראשונה של המאפיין Quotient כדי לשכתב את הביטוי כמנה של שני רדיקלים.

דוגמא $\PageIndex{34}$

פשט:

1. $\sqrt[3]{\frac{24x^7}{y^3}}$
2. $\sqrt[4]{\frac{48x^{10}}{y^8}}$.

תשובה

1.	$\sqrt[3]{\frac{24x^7}{y^3}}$
לא ניתן לפשט את השבר ברדיקנד. השתמש במאפיין Quotient כדי לכתוב כשני רדיקלים.	$\frac{\sqrt[3]{24x^7}}{\sqrt[3]{y^3}}$
כתוב מחדש כל רדיקנד כמוצר באמצעות גורמי קובייה מושלמים.	$\frac{\sqrt[3]{8x^6·3x}}{\sqrt[3]{y^3}}$
לשכתב את המונה כתוצר של שני רדיקלים.	$\frac{\sqrt[3]{(2x^2)^3}·\sqrt[3]{3x}}{\sqrt[3]{y^3}}$
לפשט.	$\frac{2x^2\sqrt[3]{3x}}{y}$
2.	$\sqrt[4]{\frac{48x^{10}}{y^8}}$
לא ניתן לפשט את השבר ברדיקנד. השתמש במאפיין Quotient כדי לכתוב כשני רדיקלים.	$\frac{\sqrt[4]{48x^{10}}}{\sqrt[4]{y^8}}$
כתוב מחדש כל רדיקנד כמוצר באמצעות גורמי קובייה מושלמים.	$\frac{\sqrt[4]{16x^8·3x^2}}{\sqrt[4]{y^8}}$
לשכתב את המונה כתוצר של שני רדיקלים.	$\frac{\sqrt[4]{(2x^2)^4}·\sqrt[4]{3x^2}}{\sqrt[4]{(y^2)^4}}$
לפשט.	$\frac{2x^2\sqrt[4]{3x^2}}{y^2}$

דוגמא $\PageIndex{35}$

פשט:

1. $\sqrt[3]{\frac{108c^{10}}{d^6}}$
2. $\sqrt[4]{\frac{80x^{10}}{y^5}}$.

תשובה

1. $\frac{3c^3\sqrt[3]{4c}}{d^2}$
2. $\frac{x^2}{∣y∣}\sqrt[4]{\frac{80x^2}{y}}$

דוגמא $\PageIndex{36}$

פשט:

1. $\sqrt[3]{\frac{40r^3}{s}}$
2. $\sqrt[4]{\frac{162m^{14}}{n^{12}}}$

תשובה

1. $r\sqrt[3]{\frac{40}{s}}$
2. $\frac{3m^3\sqrt[4]{2m^2}}{∣n^3∣}$

הוסף וחסר שורשים גבוהים יותר

אנו יכולים להוסיף ולחסר שורשים גבוהים יותר כמו שהוספנו וחיסרנו שורשים מרובעים. ראשית אנו מספקים הגדרה רשמית של רדיקלים דומים.

הגדרה: כמו רדיקלים

רדיקלים עם אותו אינדקס ואותו רדיקנד נקראים כמו רדיקלים.

כמו לרדיקלים יש אותו אינדקס ואותו רדיקנד.

• $9\sqrt[4]{42x}$$−2\sqrt[4]{42x}$והם כמו רדיקלים.
• $5\sqrt[3]{125x}$$6\sqrt[3]{125y}$והם לא כמו רדיקלים. הרדיקנדים שונים.
• $2\sqrt[5]{1000q}$$−4\sqrt[4]{1000q}$והם לא כמו רדיקלים. המדדים שונים.

אנו מוסיפים ומחסירים כמו רדיקלים באותו אופן שאנו מוסיפים ומחסירים מונחים דומים. אנחנו יכולים להוסיף $9\sqrt[4]{42x}+(−2\sqrt[4]{42x})$ והתוצאה היא$7\sqrt[4]{42x}$.

דוגמא $\PageIndex{37}$

פשט:

1. $\sqrt[3]{4x}+\sqrt[3]{4x}$
2. $4\sqrt[4]{8}−2\sqrt[4]{8}$

תשובה

1.	$\sqrt[3]{4x}+\sqrt[3]{4x}$
הרדיקלים הם כמו, אז אנחנו מוסיפים את המקדמים	$2\sqrt[3]{4x}$
2.	$4\sqrt[4]{8}−2\sqrt[4]{8}$
הרדיקלים הם כמו, אז אנחנו מפחיתים את המקדמים.	$2\sqrt[4]{8}$

דוגמא $\PageIndex{38}$

פשט:

1. $\sqrt[5]{3x}+\sqrt[5]{3x}$
2. $3\sqrt[3]{9}−\sqrt[3]{9}$

תשובה

1. $2\sqrt[5]{3x}$
2. $2\sqrt[3]{9}$

דוגמא $\PageIndex{39}$

פשט:

1. $\sqrt[4]{10y}+\sqrt[4]{10y}$
2. $5\sqrt[6]{32}−3\sqrt[6]{32}$.

תשובה

1. $2\sqrt[4]{10y}$
2. $2\sqrt[6]{32}$

כאשר נראה כי לביטוי אין רדיקלים דומים, נפשט תחילה כל רדיקל. לפעמים זה מוביל לביטוי עם רדיקלים דומים.

דוגמא $\PageIndex{40}$

פשט:

1. $\sqrt[3]{54}−\sqrt[3]{16}$
2. $\sqrt[4]{48}+\sqrt[4]{243}$.

תשובה

1.	$\sqrt[3]{54}−\sqrt[3]{16}$
לשכתב כל רדיקנד באמצעות גורמי קובייה מושלמים.	$\sqrt[3]{27}·\sqrt[3]{2}−\sqrt[3]{8}·\sqrt[3]{2}$
לשכתב את הקוביות המושלמות.	$\sqrt[3]{(3)^3}·\sqrt[3]{2}−\sqrt[3]{(2)^3}·\sqrt[3]{2}$
פשט את הרדיקלים במידת האפשר.	$3\sqrt[3]{2}−2\sqrt[3]{2}$
לשלב כמו רדיקלים.	$\sqrt[3]{2}$
2.	$\sqrt[4]{48}+\sqrt[4]{243}$
לשכתב באמצעות גורמי כוח רביעיים מושלמים.	$\sqrt[4]{16}·\sqrt[4]{3}+\sqrt[4]{81}·\sqrt[4]{3}$
כתוב מחדש כל רדיקנד כמוצר באמצעות גורמי קובייה מושלמים.	$\sqrt[4]{(2)^4}·\sqrt[4]{3}+\sqrt[4]{(3)^4}·\sqrt[4]{3}$
לשכתב את המונה כתוצר של שני רדיקלים.	$2\sqrt[4]{3}+3\sqrt[4]{3}$
לפשט.	$5\sqrt[4]{3}$

דוגמא $\PageIndex{41}$

פשט:

1. $\sqrt[3]{192}−\sqrt[3]{81}$
2. $\sqrt[4]{32}+\sqrt[4]{512}$.

תשובה

1. $\sqrt[3]{3}$
2. $6\sqrt[4]{2}$

דוגמא $\PageIndex{42}$

פשט:

1. $\sqrt[3]{108}−\sqrt[3]{250}$
2. $\sqrt[5]{64}+\sqrt[5]{486}$.

תשובה

1. $−\sqrt[3]{2}$
2. $5\sqrt[5]{2}$

דוגמא $\PageIndex{43}$

פשט:

1. $\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}$
2. $\sqrt[4]{162y^9}+\sqrt[4]{512y^5}$.

תשובה

1.	$\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}$
לשכתב כל רדיקנד באמצעות גורמי קובייה מושלמים.	$\sqrt[3]{8x^3}·\sqrt[3]{3x}−\sqrt[3]{−27x^6}·\sqrt[3]{3x}$
לשכתב את הקוביות המושלמות.	$\sqrt[3]{(2x)^3}·\sqrt[3]{3x}−\sqrt[3]{(−3x^2)^3}·\sqrt[3]{3x}$
פשט את הרדיקלים במידת האפשר.	$2x\sqrt[3]{3x}−(−3x^2\sqrt[3]{3x})$
2.	$\sqrt[4]{162y^9}+\sqrt[4]{516y^5}$
לשכתב באמצעות גורמי כוח רביעיים מושלמים.	$\sqrt[4]{81y^8}·\sqrt[4]{2y}+\sqrt[4]{256y^4}·\sqrt[4]{2y}$
כתוב מחדש כל רדיקנד כמוצר באמצעות גורמי קובייה מושלמים.	$\sqrt[4]{(3y^2)^4}·\sqrt[4]{2y}+\sqrt[4]{(4y)^4}·\sqrt[4]{2y}$
לשכתב את המונה כתוצר של שני רדיקלים.	$3y^2\sqrt[4]{2y}+4|y|\sqrt[4]{2y}$

דוגמא $\PageIndex{44}$

פשט:

1. $\sqrt[3]{32y^5}−\sqrt[3]{−108y^8}$
2. $\sqrt[4]{243r^{11}}+\sqrt[4]{768r^{10}}$.

תשובה

1. $2y\sqrt[3]{4y^2}+3y^2\sqrt[3]{4y^2}$
2. $3r^2\sqrt[4]{3r^3}+4r^2\sqrt[4]{3r^2}$

דוגמא $\PageIndex{45}$

פשט:

1. $\sqrt[3]{40z^7}−\sqrt[3]{−135z^4}$
2. $\sqrt[4]{80s^{13}}+\sqrt[4]{1280s^6}$.

תשובה

1. $2z^2\sqrt[3]{5z}+3z^5\sqrt[3]{5z}$
2. $2∣s^3∣\sqrt[4]{5s}+4|s|\sqrt[4]{5s}$

גש למשאבים מקוונים אלה להדרכה ותרגול נוספים עם פישוט שורשים גבוהים יותר.

• פישוט שורשים גבוהים יותר
• הוספה/הפחת שורשים עם מדדים גבוהים יותר

מושגי מפתח

• מאפיינים של
• $\sqrt[n]{a}$כאשר n הוא מספר זוגי ו
  • $a \ge 0$, אז $\sqrt[n]{a}$ הוא מספר אמיתי
  • $a < 0$, אז $\sqrt[n]{a}$ הוא לא מספר אמיתי
  • כאשר n הוא מספר אי זוגי, $\sqrt[n]{a}$ הוא מספר ממשי לכל הערכים של a.
  • עבור כל מספר שלם$n \ge 2$, כאשר n הוא מוזר $\sqrt[n]{a^n}=a$
  • עבור כל מספר שלם$n \ge 2$, כאשר n הוא אפילו $\sqrt[n]{a^n}=|a|$
• $\sqrt[n]{a}$נחשב פשוט אם אין גורמים של$m^n$.
• $\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}$ו $\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}$
• $\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$ו $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$
• כדי לשלב כמו רדיקלים, פשוט הוסף או הפחת את המקדמים תוך שמירה על הרדיקל זהה.

רשימת מילים

שורש n של מספר

אם$b^n=a$, אז b הוא שורש n של a.

שורש n עיקרי

שורש ה - n העיקרי של a כתוב$\sqrt[n]{a}$.

מדד

$\sqrt[n]{a}$n נקרא מדד הרדיקל.

כמו רדיקלים

רדיקלים עם אותו אינדקס ואותו רדיקנד נקראים כמו רדיקלים.