9.4E: תרגילים
- Page ID
- 205519
תרגול הופך מושלם
הכפל שורשים מרובעים
בתרגילים הבאים, לפשט.
- \(\sqrt{2}·\sqrt{8}\)
- \((3\sqrt{3})(2\sqrt{18})\)
- תשובה
-
- \(44\)
- \(18\sqrt{6}\)
- \(\sqrt{6}·\sqrt{6}\)
- \((3\sqrt{2})(2\sqrt{32})\)
- \(\sqrt{7}·\sqrt{14}\)
- \((4\sqrt{8})(5\sqrt{8})\)
- תשובה
-
- \(7\sqrt{2}\)
- 160
- \(\sqrt{6}·\sqrt{12}\)
- \((2\sqrt{5})(2\sqrt{10})\)
\((5\sqrt{2})(3\sqrt{6})\)
- תשובה
-
\(30\sqrt{3}\)
\((2\sqrt{3})(4\sqrt{6})\)
\((−2\sqrt{3})(3\sqrt{18})\)
- תשובה
-
\(−18\sqrt{6}\)
\((−4\sqrt{5})(5\sqrt{10})\)
\((5\sqrt{6})(−\sqrt{12})\)
- תשובה
-
\(−30\sqrt{2}\)
\((6\sqrt{2})(−\sqrt{10})\)
\((−2\sqrt{7})(−2\sqrt{14})\)
- תשובה
-
\(28\sqrt{2}\)
\((−2\sqrt{11})(−4\sqrt{22})\)
- \((\sqrt{15y})(\sqrt{5y^3})\)
- \((\sqrt{2n^2})(\sqrt{18n^3})\)
- תשובה
-
- \(5y^2\sqrt{3}\)
- \(6n^2\sqrt{n}\)
- \((\sqrt{14x^3})(\sqrt{7x^3})\)
- \((\sqrt{3q^2})(\sqrt{48q^3})\)
- \((\sqrt{16y^2})(\sqrt{8y^4})\)
- \((\sqrt{11s^6})(\sqrt{11s})\)
- תשובה
-
- \(8y^3\sqrt{2}\)
- \(11s^3\sqrt{s}\)
ⓐ \((\sqrt{8x^3})(\sqrt{3x})\)
ⓑ \((\sqrt{7r})(\sqrt{7r^8})\)
\((2\sqrt{5b^3})(4\sqrt{15b})\)
- תשובה
-
\(40b^2\sqrt{3}\)
\((\sqrt{38c^5})(\sqrt{26c^3})\)
\((6\sqrt{3d^3})(4\sqrt{12d^5})\)
- תשובה
-
\(144d^4\)
\((2\sqrt{5b^3})(4\sqrt{15b})\)
\((2\sqrt{5d^6})(3\sqrt{20d^2})\)
- תשובה
-
\(60d^4\)
\((−2\sqrt{7z^3})(3\sqrt{14z^8})\)
\((4\sqrt{2k^5})(−3\sqrt{32k^6})\)
- תשובה
-
\(−96k^5\sqrt{k}\)
- \((\sqrt{7})^2\)
- \((−\sqrt{15})^2\)
- \((\sqrt{11})^2\)
- \((−\sqrt{21})^2\)
- תשובה
-
- 11
- 21
- \((\sqrt{19})^2\)
- \((−\sqrt{5})^2\)
- \((\sqrt{23})^2\)
- \((−\sqrt{3})^2\)
- תשובה
-
- 23
- 3
- \((4\sqrt{11})(−3\sqrt{11})\)
- \((5\sqrt{3})^2\)
- \((2\sqrt{13})(−9\sqrt{13})\)
- \((6\sqrt{5})^2\)
- תשובה
-
- -234
- 180
- \((−3\sqrt{12})(−2\sqrt{6})\)
- \( (−4\sqrt{10})^2\)
- \((−7\sqrt{5})(−3\sqrt{10})\)
- \( (−2\sqrt{14})^2\)
- תשובה
-
- \(105\sqrt{2}\)
- 56
השתמש בכפל פולינומי כדי להכפיל שורשים מרובעים
בתרגילים הבאים, לפשט.
- \(3(4−\sqrt{3})\)
- \(\sqrt{2}(4−\sqrt{6})\)
- \(4(6−\sqrt{11})\)
- \(\sqrt{2}(5−\sqrt{12})\)
- תשובה
-
- \(24−4\sqrt{11}\)
- \(5\sqrt{2}−2\sqrt{6}\)
- \(5(3−\sqrt{7})\)
- \(\sqrt{3}(4−\sqrt{15})\)
- \(7(−2−\sqrt{11})\)
- \(\sqrt{7}(6−\sqrt{14})\)
- תשובה
-
- \(−14−7\sqrt{11}\)
- \(6\sqrt{7}−7\sqrt{2}\)
- \(\sqrt{7}(5+2\sqrt{7})\)
- \(\sqrt{5}(\sqrt{10}+\sqrt{18})\)
- \(\sqrt{11}(8+4\sqrt{11})\)
- \(\sqrt{3}(\sqrt{12}+\sqrt{27})\)
- תשובה
-
- \(44+8\sqrt{11}\)
- 15
- \(\sqrt{11}(−3+4\sqrt{1})\)
- \(\sqrt{3}(\sqrt{15}−\sqrt{18})\)
- \(\sqrt{2}(−5+9\sqrt{2})\)
- \(\sqrt{7}(\sqrt{3}−\sqrt{21})\)
- תשובה
-
- \(18−5\sqrt{2}\)
- \(\sqrt{21}−7\sqrt{3}\)
\((8+\sqrt{3})(2−\sqrt{3})\)
\((7+\sqrt{3})(9−\sqrt{3})\)
- תשובה
-
\(60+2\sqrt{3}\)
\((8−\sqrt{2})(3+\sqrt{2})\)
\((9−\sqrt{2})(6+\sqrt{2})\)
- תשובה
-
\(52+3\sqrt{2}\)
\((3−\sqrt{7})(5−\sqrt{7})\)
\((5−\sqrt{7})(4−\sqrt{7})\)
- תשובה
-
\(27−9\sqrt{7}\)
\((1+3\sqrt{10})(5−2\sqrt{10})\)
\((7−2\sqrt{5})(4+9\sqrt{5})\)
- תשובה
-
\(−62+55\sqrt{5}\)
\((\sqrt{3}+\sqrt{10})(\sqrt{3}+2\sqrt{10})\)
\((\sqrt{11}+\sqrt{5})(\sqrt{11}+6\sqrt{5})\)
- תשובה
-
\(41+7\sqrt{55}\)
\((2\sqrt{7}−5\sqrt{11})(4\sqrt{7}+9\sqrt{11})\)
\((4\sqrt{6}+7\sqrt{13})(8\sqrt{6}−3\sqrt{13})\)
- תשובה
-
\(−81+44\sqrt{78}\)
\((5−\sqrt{u})(3+\sqrt{u})\)
\((9−\sqrt{w})(2+\sqrt{w})\)
- תשובה
-
\(18+7\sqrt{w}\)
\((7+2\sqrt{m})(4+9\sqrt{m})\)
\((6+5\sqrt{n})(11+3\sqrt{n})\)
- תשובה
-
\(66+73\sqrt{n}+15n\)
- \((3+\sqrt{5})^2\)
- \((2−5\sqrt{3})^2\)
- \((4+\sqrt{11})^2\)
- \((3−2\sqrt{5})^2\)
- תשובה
-
- \(27+8\sqrt{11}\)
- \(29−12\sqrt{5}\)
- \((9−\sqrt{6})^2\)
- \((10+3\sqrt{7})^2\)
- \((5−\sqrt{10})^2\)
- \((8+3\sqrt{2})^2\)
- תשובה
-
- \(35−10\sqrt{10}\)
- \(82+48\sqrt{2}\)
\((3−\sqrt{5})(3+\sqrt{5})\)
\((10−\sqrt{3})(10+\sqrt{3})\)
- תשובה
-
97
\((4+\sqrt{2})(4−\sqrt{2})\)
\((7+\sqrt{10})(7−\sqrt{10})\)
- תשובה
-
39
\((4+9\sqrt{3})(4−9\sqrt{3})\)
\((1+8\sqrt{2})(1−8\sqrt{2})\)
- תשובה
-
-127
\((12−5\sqrt{5})(12+5\sqrt{5})\)
\((9−4\sqrt{3})(9+4\sqrt{3})\)
- תשובה
-
33
תרגול מעורב
בתרגילים הבאים, לפשט.
\(\sqrt{3}·\sqrt{21}\)
\((4\sqrt{6})(−\sqrt{18})\)
- תשובה
-
\(−24\sqrt{3}\)
\((−5+\sqrt{7})(6+\sqrt{21})\)
\((−5\sqrt{7})(6\sqrt{21})\)
- תשובה
-
\(−210\sqrt{3}\)
\((−4\sqrt{2})(2\sqrt{18})\)
\((\sqrt{35y^3})(\sqrt{7y^3})\)
- תשובה
-
\(7y^3\sqrt{5}\)
\((4\sqrt{12x^5})(2\sqrt{6x^3})\)
\((\sqrt{29})^2\)
- תשובה
-
29
\((−4\sqrt{17})(−3\sqrt{17})\)
\((−4+\sqrt{17})(−3+\sqrt{17})\)
- תשובה
-
\(29−7\sqrt{17}\)
מתמטיקה יומיומית
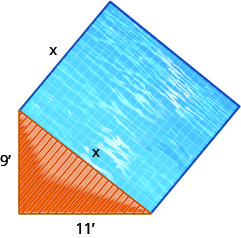
מעצב נוף רוצה לשים בריכה מחזירה מרובעת ליד סיפון משולש, כפי שמוצג להלן. הסיפון המשולש הוא משולש ימני, עם רגליים באורך 9 רגל ו-11 רגל, והבריכה תהיה צמודה להיפוטנוזה.
- השתמש במשפט פיתגורס כדי למצוא את אורך הצד של הבריכה. עגול את תשובתך לעשירית הרגל הקרובה ביותר.
- מצא את האזור המדויק של הבריכה.
אמן רוצה ליצור אנדרטה קטנה בצורת בסיס מרובע שבראשו משולש ימני, כמוצג להלן. הבסיס המרובע יהיה צמוד לרגל אחת של המשולש. הרגל השנייה של המשולש תמדוד 2 רגל והיפוטנוזה תהיה מטר וחצי.
- השתמש במשפט פיתגורס כדי למצוא את אורך הצד של הבסיס המרובע. עגול את תשובתך לעשירית הרגל הקרובה ביותר.
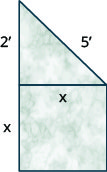
- מצא את השטח המדויק של הפנים של הבסיס המרובע.
- תשובה
-
- 4.6 רגל
- 21 מ"ר. רגל
גן מרובע ייעשה עם גבול אבן בקצה אחד. אם רק \(3+\sqrt{10}\) מטרים של אבן זמינים, פשט \((3+\sqrt{10})^2\) כדי לקבוע את השטח של הגן הגדול ביותר כזה.
גינה תיווצר כך שתכיל שני חלקים מרובעים, קטע אחד עם \(\sqrt{5}+\sqrt{6}\) חצרות באורך צד וקטע אחד עם \(\sqrt{2}+\sqrt{3}\) חצרות באורך צד. פשט \((\sqrt{5}+\sqrt{6})(\sqrt{2}+\sqrt{3})\) כדי לקבוע את השטח הכולל של הגן.
נניח שקטע שלישי יתווסף לגינה בתרגיל הקודם. החלק השלישי הוא שיש רוחב של \(\sqrt{432}\) רגליים. כתוב ביטוי שנותן את השטח הכולל של הגן.
תרגילי כתיבה
- הסבר מדוע \((−\sqrt{n})^2\) הוא תמיד חיובי, שכן\(n \ge 0\).
- הסבר מדוע \(−(\sqrt{n})^2\) הוא תמיד שלילי, שכן\(n \ge 0\).
- תשובה
-
- כאשר בריבוע שלילי, זה הופך לחיובי
- מכיוון שהשלילי אינו נכלל בסוגריים, הוא אינו בריבוע ונשאר שלילי
השתמש בתבנית הריבועית הבינומית כדי לפשט. \((3+\sqrt{2})^2\) הסבר את כל הצעדים שלך.
בדיקה עצמית
ⓐ לאחר השלמת התרגילים, השתמש ברשימת בדיקה זו כדי להעריך את שליטתך ביעדי סעיף זה.
ⓑ בסולם של 1-10, כיצד היית מדרג את השליטה שלך בסעיף זה לאור תגובותיך ברשימת הבדיקה? איך אתה יכול לשפר את זה?


