9.4: הכפל שורשים מרובעים
- Page ID
- 205514
בסוף פרק זה תוכל:
- הכפל שורשים מרובעים
- השתמש בכפל פולינומי כדי להכפיל שורשים מרובעים
לפני שתתחיל, קח את חידון המוכנות הזה.
- לפשט: (3u) (8v).
אם פספסת בעיה זו, עיין בדוגמה 6.2.31. - פשט: 6 (12-7n).
אם פספסת בעיה זו, עיין בדוגמה 6.3.1. - פשט: (2+א) (4−a).
אם פספסת בעיה זו, עיין בדוגמה 6.3.34.
הכפל שורשים מרובעים
השתמשנו במאפיין המוצר של שורשים מרובעים כדי לפשט שורשים מרובעים על ידי הסרת הגורמים המרובעים המושלמים. נכס המוצר של שורשים מרובעים אומר
\[\sqrt{ab}=\sqrt{a}·\sqrt{b} \nonumber\]
אנו יכולים להשתמש במאפיין המוצר של שורשים מרובעים 'הפוך' כדי להכפיל שורשים מרובעים.
\[\sqrt{a}·\sqrt{b}=\sqrt{ab} \nonumber\]
זכור, אנו מניחים שכל המשתנים גדולים או שווים לאפס.
אנו נכתוב מחדש את מאפיין המוצר של שורשים מרובעים כך שנראה את שני הדרכים יחד.
אם a, b הם מספרים ממשיים לא שליליים, אז
\(\sqrt{ab}=\sqrt{a}·\sqrt{b}\)ו\(\sqrt{a}·\sqrt{b}=\sqrt{ab}\).
אז אנחנו יכולים להכפיל \(\sqrt{3}·\sqrt{5}\) in this way:
\[\begin{array}{l} {\sqrt{3}·\sqrt{5}}\\ {\sqrt{3·5}}\\ {\sqrt{15}}\\ \nonumber \end{array}\]
לפעמים המוצר נותן לנו ריבוע מושלם:
\[\begin{array}{l} {\sqrt{2}·\sqrt{8}}\\ {\sqrt{2·8}}\\ {\sqrt{16}}\\ {4}\\ \nonumber \end{array}\]
גם כאשר המוצר אינו ריבוע מושלם, עלינו לחפש גורמים מרובעים מושלמים ולפשט את הרדיקל בכל הזדמנות אפשרית.
הכפלת רדיקלים עם מקדמים דומה מאוד להכפלת משתנים עם מקדמים. כדי להכפיל 4x·3y אנו מכפילים את המקדמים יחד ואז את המשתנים. התוצאה היא 12xy. זכור זאת כשאתה עושה את הדוגמאות האלה.
פשט:
- \(\sqrt{2}·\sqrt{6}\)
- \((4\sqrt{3})(2\sqrt{12})\).
- תשובה
-
1. \(\sqrt{2}·\sqrt{6}\) הכפל באמצעות מאפיין המוצר. \(\sqrt{12}\) לפשט את הרדיקלי. \(\sqrt{4}·\sqrt{3}\) לפשט. \(2\sqrt{3}\) 2. \((4\sqrt{3})(2\sqrt{12})\) הכפל באמצעות מאפיין המוצר. \(8\sqrt{36}\) לפשט את הרדיקלי. \(8·6\) לפשט. \(48\)
פשט:
- \(\sqrt{3}·\sqrt{6}\)
- \((2\sqrt{6})(3\sqrt{12})\).
- תשובה
-
- \(3\sqrt{2}\)
- \(36\sqrt{2}\)
פשט:
- \(\sqrt{5}·\sqrt{10}\)
- \((6\sqrt{3})(5\sqrt{6})\)
- תשובה
-
- \(5\sqrt{2}\)
- \(90\sqrt{2}\)
פשט: \((6\sqrt{2})(3\sqrt{10})\)
- תשובה
-
\((6\sqrt{2})(3\sqrt{10})\) הכפל באמצעות מאפיין המוצר. \(18\sqrt{20}\) לפשט את הרדיקלי. \(18\sqrt{4}·\sqrt{5}\) לפשט. \(18·2·\sqrt{5}\) \(36\sqrt{5}\)
פשט: \((3\sqrt{2})(2\sqrt{30})\)
- תשובה
-
\(12\sqrt{15}\)
פשט:\((3\sqrt{3})(3\sqrt{6})\).
- תשובה
-
\(27\sqrt{2}\)
כאשר עלינו להכפיל שורשים מרובעים, אנו מוצאים תחילה את המוצר ואז מסירים את כל הגורמים המרובעים המושלמים.
פשט:
- \((\sqrt{8x^3})(\sqrt{3x})\)
- \((\sqrt{20y^2})(\sqrt{5y^3})\)
- תשובה
-
1. \((\sqrt{8x^3})(\sqrt{3x})\) הכפל באמצעות מאפיין המוצר. \(\sqrt{24x^4}\) לפשט את הרדיקלי. \(\sqrt{4x^4}·\sqrt{6}\) לפשט. \(2x^2\sqrt{6}\) 2. \((\sqrt{20y^2})(\sqrt{5y^3})\) הכפל באמצעות מאפיין המוצר. \(\sqrt{100y^5}\) לפשט את הרדיקלי. \(10y^2\sqrt{y}\)
פשט:
- \((\sqrt{6x^3})(\sqrt{3x})\)
- \((\sqrt{2y^3})(\sqrt{50y^2})\).
- תשובה
-
- \(3x^2\sqrt{2}\)
- \(10y^2\sqrt{y}\)
פשט:
- \((\sqrt{6x^5})(\sqrt{2x})\)
- \((\sqrt{12y^2})(\sqrt{3y^5})\)
- תשובה
-
- \(2x^3\sqrt{3}\)
- \(6y^2\sqrt{y}\)
פשט: \((10\sqrt{6p^3})(3\sqrt{18p})\)
- תשובה
-
\((10\sqrt{6p^3})(3\sqrt{18p})\) להכפיל. \(30\sqrt{108p^4}\) לפשט את הרדיקלי. \(30\sqrt{36p^4}·\sqrt{3}\) \(30·6p^2·\sqrt{3}\) \(180p^2\sqrt{3}\)
פשט: \((\sqrt{62x^2})(8\sqrt{45x^4})\)
- תשובה
-
\(144x^3\sqrt{10}\)
פשט:\((2\sqrt{6y^4})(12\sqrt{30y})\).
- תשובה
-
\(144y^2\sqrt{5y}\)
פשט:
- \((\sqrt{2})^2\)
- \((−\sqrt{11})^2\).
- תשובה
-
1. \((\sqrt{2})^2\) לשכתב כמוצר. \((\sqrt{2})(\sqrt{2})\) להכפיל. \(\sqrt{4}\) לפשט. 2 2. \((−\sqrt{11})^2\) לשכתב כמוצר. \((−\sqrt{11})(−\sqrt{11})\) להכפיל. \(\sqrt{121}\) לפשט. 11
פשט:
- \((\sqrt{12})^2\)
- \((−\sqrt{15})^2\).
- תשובה
-
- 12
- 15
פשט:
- \((\sqrt{16})^2\)
- \((−\sqrt{20})^2\).
- תשובה
-
- 16
- 20
תוצאות הדוגמה הקודמת מובילות אותנו לנכס זה.
אם a הוא מספר ממשי לא שלילי, אז
\((\sqrt{a})^2=a\)
על ידי הבנה כי ריבוע ולקיחת שורש ריבועי הם פעולות 'הפוכות', אנו יכולים לפשט \((\sqrt{2})^2\) ולקבל 2 מיד. כאשר אנו מכפילים את השניים כמו שורשים מרובעים בחלק (א) מהדוגמה הבאה, זהה לריבוע.
פשט:
- \((2\sqrt{3})(8\sqrt{3})\)
- \((3\sqrt{6})^2\).
- תשובה
-
1. \((2\sqrt{3})(8\sqrt{3})\) להכפיל. זכור, \((\sqrt{3}^2)\) 16·3 לפשט. 48 2. \((3\sqrt{6})^2\) להכפיל. 9·6 לפשט. 54
פשט:
- \((6\sqrt{11})(5\sqrt{11})\)
- \((5\sqrt{8})^2\).
- תשובה
-
- 330
- 200
פשט:
- \((3\sqrt{7})(10\sqrt{7})\)
- \((−4\sqrt{6})^2\).
- תשובה
-
- 210
- 96
השתמש בכפל פולינומי כדי להכפיל שורשים מרובעים
בדוגמאות הבאות נשתמש במאפיין החלוקה כדי להכפיל ביטויים עם שורשים מרובעים.
תחילה נפיץ ואז נפשט את השורשים המרובעים במידת האפשר.
פשט:
- \(3(5−\sqrt{2})\)
- \(\sqrt{2}(4−\sqrt{10})\).
- תשובה
-
1. \(3(5−\sqrt{2})\) להפיץ. \(15−3\sqrt{2})\) 2. \(\sqrt{2}(4−\sqrt{10})\) להפיץ. \(4\sqrt{2}−\sqrt{20}\) לפשט. \(4\sqrt{2}−2\sqrt{5}\)
פשט:
- \(2(3−\sqrt{5})\)
- \(\sqrt{3}(2−\sqrt{18})\).
- תשובה
-
- \(6−2\sqrt{5}\)
- \(2\sqrt{3}−3\sqrt{6}\)
פשט:
- \(6(2+\sqrt{6})\)
- \(\sqrt{7}(1+\sqrt{14})\).
- תשובה
-
- \(12+\sqrt{6}\)
- \(\sqrt{7}+7\sqrt{2}\)
פשט:
- \(\sqrt{5}(7+2\sqrt{5})\)
- \(\sqrt{6}(\sqrt{2}+\sqrt{18})\).
- תשובה
-
1. \(\sqrt{5}(7+2\sqrt{5})\) להפיץ. \(7\sqrt{5}+2·5\) לפשט. \(7\sqrt{5}+10\) \(10+7\sqrt{5}\) 2. \(\sqrt{6}(\sqrt{2}+\sqrt{18})\) להכפיל. \(\sqrt{12}+\sqrt{108}\) לפשט. \((\sqrt{4}·\sqrt{3}+\sqrt{36}·\sqrt{3})\) \(2\sqrt{3}+6\sqrt{3}\) לשלב כמו רדיקלים. \(8\sqrt{3}\)
פשט:
- \(\sqrt{6}(1+3\sqrt{6})\)
- \(\sqrt{12}(\sqrt{3}+\sqrt{24})\)
- תשובה
-
- \(18+\sqrt{6}\)
- \(6+12\sqrt{2}\)
פשט:
- \(\sqrt{8}(2−5\sqrt{8})\)
- \(\sqrt{14}(\sqrt{2}+\sqrt{42})\)
- תשובה
-
- \(−40+4\sqrt{2}\)
- \(2\sqrt{7}+14\sqrt{3}\)
כשעבדנו עם פולינומים, הכפלנו בינומים בבינומים. זכור, זה נתן לנו ארבעה מוצרים לפני ששילבנו מונחים דומים. כדי להיות בטוח להשיג את כל ארבעת המוצרים, ארגנו את העבודה שלנו - בדרך כלל בשיטת FOIL.
פשט: \((2+\sqrt{3})(4−\sqrt{3})\)
- תשובה
-
\((2+\sqrt{3})(4−\sqrt{3})\) להכפיל. \(8−2\sqrt{3}+4\sqrt{3}−3\) לשלב מונחים כמו. \(5+2\sqrt{3}\)
פשט:\((1+\sqrt{6})(3−\sqrt{6})\).
- תשובה
-
\(−3+2\sqrt{6}\)
פשט:\((4−\sqrt{10})(2+\sqrt{10})\).
- תשובה
-
\(−2+2\sqrt{10}\)
פשט:\((3−2\sqrt{7})(4−2\sqrt{7})\).
- תשובה
-
\((3−2\sqrt{7})(4−2\sqrt{7})\) להכפיל. \(12−6\sqrt{7}−8\sqrt{7}+4·7\) לפשט. \(12−6\sqrt{7}−8\sqrt{7}+28\) לשלב מונחים כמו. \(40−14\sqrt{7}\)
פשט:\((6−3\sqrt{7})(3+4\sqrt{7})\).
- תשובה
-
\(−66+15\sqrt{7}\)
פשט: \((2−3\sqrt{11})(4−\sqrt{11})\)
- תשובה
-
\(41+14\sqrt{11}\)
פשט:\((3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\).
- תשובה
-
\(3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\) להכפיל. \(3·2+12\sqrt{10}−\sqrt{10}−4·5\) לפשט. \(6+12\sqrt{10}−\sqrt{10}−20\) לשלב מונחים כמו. \(−14+11\sqrt{10}\)
פשט: \((5\sqrt{3}−\sqrt{7})(\sqrt{3}+2\sqrt{7})\)
- תשובה
-
\(1+9\sqrt{21}\)
פשט: \((\sqrt{6}−3\sqrt{8})(2\sqrt{6}+\sqrt{8})\)
- תשובה
-
\(−12−20\sqrt{3}\)
פשט:\((4−2\sqrt{x})(1+3\sqrt{x})\).
- תשובה
-
\((4−2\sqrt{x})(1+3\sqrt{x})\). להכפיל. \(4+12\sqrt{x}−2\sqrt{x}−6x\) לשלב מונחים כמו. \(4+10\sqrt{x}−6x\)
פשט:\((6−5\sqrt{m})(2+3\sqrt{m})\).
- תשובה
-
\(12+8\sqrt{m}−15m\)
פשט: \((10+3\sqrt{n})(1−5\sqrt{n})\)
- תשובה
-
\(10−47\sqrt{n}−15n\)
שים לב שכמה מוצרים מיוחדים הקלו על העבודה שלנו כאשר הכפלנו בינומים קודם לכן. זה נכון גם כשאנחנו מכפילים שורשים מרובעים. נוסחאות המוצר המיוחדות בהן השתמשנו מוצגות להלן.
\[\begin{array}{ll} {\textbf{Binomial Squares}}&{\textbf{Product of Conjugates}}\\ {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2}&{}\\ \nonumber \end{array}\]
נשתמש בנוסחאות המוצר המיוחדות בדוגמאות הבאות. נתחיל בנוסחת הריבועים הבינומיים.
פשט:
- \((2+\sqrt{3})^2\)
- \((4−2\sqrt{5})^2\).
- תשובה
-
הקפד לכלול את המונח 2ab בעת ריבוע בינומי.
1.
2.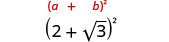
הכפל באמצעות התבנית הריבועית הבינומית. 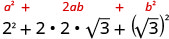
לפשט. 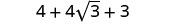
לשלב מונחים כמו. 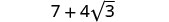
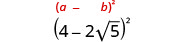
הכפל באמצעות התבנית הריבועית הבינומית. 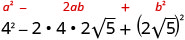
לפשט. 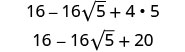
לשלב מונחים כמו. 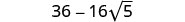
פשט:
- \((10+\sqrt{2})^2\)
- \((1+3\sqrt{6})^2\).
- תשובה
-
- \(102+20\sqrt{2}\)
- \(55+6\sqrt{6}\)
פשט:
- \((6-\sqrt{5})^2\)
- \((9-2\sqrt{10})^2\).
- תשובה
-
- \(41-12\sqrt{5}\)
- \(121-36\sqrt{10}\)
פשט:\((1+3\sqrt{x})^2\).
- תשובה
-
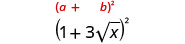
הכפל באמצעות התבנית הריבועית הבינומית. 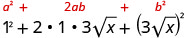
לפשט. 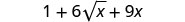
פשט:\((2+5\sqrt{m})^2\).
- תשובה
-
\(4+20\sqrt{m}+25m\)
פשט:\((3−4\sqrt{n})^2\).
- תשובה
-
\(9−24\sqrt{n}+16n\)
בשתי הדוגמאות הבאות, נמצא תוצר של מצמידים.
פשט:\((4−\sqrt{2})(4+\sqrt{2})\).
- תשובה
-
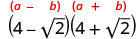
הכפל באמצעות התבנית הריבועית הבינומית. 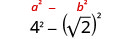
לפשט. 
פשט: \((2−\sqrt{3})(2+\sqrt{3})\)
- תשובה
-
1
פשט: \((1+\sqrt{5})(1−\sqrt{5})\)
- תשובה
-
-4
פשט: \((5−2\sqrt{3})(5+2\sqrt{3})\)
- תשובה
-
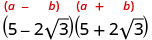
הכפל באמצעות התבנית הריבועית הבינומית. 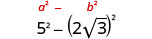
לפשט. 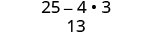
פשט:\((3−2\sqrt{5})(3+2\sqrt{5})\).
- תשובה
-
−11
פשט:\((4+5\sqrt{7})(4−5\sqrt{7})\).
- תשובה
-
-159
גש למשאבים מקוונים אלה להדרכה ותרגול נוספים עם הכפלת שורשים מרובעים.
- נכס מוצר
- הכפל בינומים עם שורשים מרובעים
מושגי מפתח
- מאפיין המוצר של שורשים מרובעים אם a, b הם מספרים ממשיים לא שליליים, אז
\(\sqrt{ab}=\sqrt{a·b}\)ו \(\sqrt{a}·\sqrt{b}=\sqrt{ab}\)
- נוסחאות מיוחדות להכפלת בינומים ומצמידים:
\[\begin{array}{ll} {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2 }&{}\\ \nonumber \end{array}\]
- ניתן להשתמש בשיטת FOIL להכפלת בינומים המכילים רדיקלים.


