9.5: מחלקים שורשים מרובעים
- Page ID
- 205509
בסוף פרק זה תוכל:
- מחלקים שורשים מרובעים
- רציונליזציה של מכנה חד-פעמי
- רציונליזציה של מכנה דו-מונח
לפני שתתחיל, קח את חידון המוכנות הזה.
- מצא שבר שווה ערך \(\frac{5}{8}\) למכנה 48.
אם פספסת בעיה זו, עיין בתרגיל 1.6.1. - פשט:\((\sqrt{5})^2\).
אם פספסת בעיה זו, עיין בדוגמה 9.4.13. - הכפל: (7+3x) (7-3x).
אם פספסת בעיה זו, עיין בתרגיל 6.4.22.
מחלקים שורשים מרובעים
אנו יודעים שאנו מפשטים שברים על ידי הסרת גורמים המשותפים למונה ולמכנה. כאשר יש לנו שבר עם שורש ריבועי במונה, ראשית אנו מפשטים את השורש הריבועי. אז נוכל לחפש גורמים משותפים.
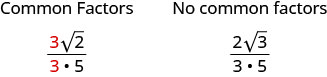
פשט: \(\frac{\sqrt{54}}{6}\)
- תשובה
-
\(\frac{\sqrt{54}}{6}\) לפשט את הרדיקלי. \(\frac{\sqrt{9}·\sqrt{6}}{6}\) לפשט. \(\frac{3\sqrt{6}}{6}\) הסר את הגורמים הנפוצים. \(\frac{3\sqrt{6}}{3·2}\) לפשט. \(\frac{\sqrt{6}}{2}\)
פשט:\(\frac{\sqrt{32}}{8}\).
- תשובה
-
\(\frac{\sqrt{2}}{2}\)
פשט:\(\frac{\sqrt{75}}{15}\).
- תשובה
-
\(\frac{\sqrt{3}}{3}\)
פשט:\(\frac{6−\sqrt{24}}{12}\).
- תשובה
-
\(\frac{6−\sqrt{24}}{12}\) לפשט את הרדיקלי. \(\frac{6−\sqrt{4}·\sqrt{6}}{12}\) לפשט. \(\frac{6−2\sqrt{6}}{12}\) פקטור הגורם המשותף מן המונה. \(\frac{2(3−\sqrt{6})}{12}\) הסר את הגורמים הנפוצים. \(\frac{2(3−\sqrt{6})}{2·6}\) לפשט. \(\frac{3−\sqrt{6}}{6}\)
פשט:\(\frac{8−\sqrt{40}}{10}\).
- תשובה
-
\(\frac{4−\sqrt{10}}{5}\)
פשט:\(\frac{10−\sqrt{75}}{20}\).
- תשובה
-
\(\frac{5−\sqrt{3}}{4}\)
השתמשנו במאפיין המנה של שורשים מרובעים כדי לפשט שורשים מרובעים של שברים. המאפיין הממנה של שורשים מרובעים אומר
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\),\(b \ne 0\).
לפעמים נצטרך להשתמש במאפיין המנה של שורשים מרובעים 'הפוך' כדי לפשט שבר עם שורשים מרובעים.
\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\),\(b \ne 0\).
נכתוב מחדש את המאפיין המנה של שורשים מרובעים כך שנראה את שני הדרכים יחד. זכור: אנו מניחים שכל המשתנים גדולים או שווים לאפס כך שהשורשים הריבועיים שלהם הם מספרים ממשיים.
אם a, b הם מספרים ממשיים לא שליליים\(b \ne 0\), ואז
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)ו \(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)
נשתמש במאפיין המנה של שורשים מרובעים 'הפוך' כאשר השבר שאנו מתחילים איתו הוא המנה של שני שורשים מרובעים, ואף רדיקנד אינו ריבוע מושלם. כאשר אנו כותבים את השבר בשורש ריבועי יחיד, אנו עשויים למצוא גורמים משותפים במונה ובמכנה.
פשט: \(\frac{\sqrt{27}}{\sqrt{75}}\)
- תשובה
-
\(\frac{\sqrt{27}}{\sqrt{75}}\) אף רדיקנד אינו ריבוע מושלם, לכן שכתוב מחדש באמצעות המאפיין המנה של השורש הריבועי. \(\sqrt{\frac{27}{75}}\) הסר גורמים נפוצים במונה ובמכנה. \(\sqrt{\frac{9}{25}}\) לפשט. \(\frac{3}{5}\)
פשט: \(\frac{\sqrt{48}}{\sqrt{108}}\)
- תשובה
-
\(\frac{2}{3}\)
פשט: \(\frac{\sqrt{96}}{\sqrt{54}}\)
- תשובה
-
\(\frac{4}{3}\)
אנו נשתמש במאפיין Quotient עבור אקספוננטים\(\frac{a^m}{a^n}=a^{m−n}\), כאשר יש לנו משתנים עם אקספוננטים ברדיקנדס.
פשט: \(\frac{\sqrt{6y^5}}{\sqrt{2y}}\)
- תשובה
-
\(\frac{\sqrt{6y^5}}{\sqrt{2y}}\) אף רדיקנד אינו ריבוע מושלם, לכן שכתוב מחדש באמצעות המאפיין המנה של השורש הריבועי. \(\sqrt{\frac{6y^5}{2y}}\) הסר גורמים נפוצים במונה ובמכנה. \(\sqrt{3y^4}\) לפשט. \(y^2\sqrt{3}\)
פשט:\(\frac{\sqrt{12r^3}}{\sqrt{6r}}\).
- תשובה
-
\(r\sqrt{2}\)
פשט: \(\frac{\sqrt{14p^9}}{\sqrt{2p^5}}\)
- תשובה
-
\(p^2\sqrt{7}\)
פשט: \(\frac{\sqrt{72x^3}}{\sqrt{162x}}\)
- תשובה
-
\(\frac{\sqrt{72x^3}}{\sqrt{162x}}\) כתוב מחדש באמצעות המאפיין המנה של שורשים מרובעים. \(\sqrt{\frac{72x^3}{162x}}\) הסר גורמים נפוצים. \(\sqrt{\frac{18·4·x^2·x}{18·9·x}}\) לפשט. \(\sqrt{\frac{4x^2}{9}}\) לפשט את הרדיקלי. \(\frac{2x}{3}\)
פשט:\(\frac{\sqrt{50s^3}}{\sqrt{128s}}\).
- תשובה
-
\(\frac{5s}{8}\)
פשט:\(\frac{\sqrt{75q^5}}{\sqrt{108q}}\).
- תשובה
-
\(\frac{5q^2}{6}\)
פשט:\(\frac{\sqrt{147ab^8}}{\sqrt{3a^3b^4}}\).
- תשובה
-
\(\frac{\sqrt{147ab^8}}{\sqrt{3a^{3}b^{4}}}\) כתוב מחדש באמצעות המאפיין המנה של שורשים מרובעים. \(\sqrt{\frac{147ab^8}{3a^{3}b^{4}}}\) הסר גורמים נפוצים. \ (\ sqrt {\ frac {49b ^4} {a^2}}\ לפשט את הרדיקלי. \(\frac{7b^2}{a}\)
פשט:\(\frac{\sqrt{162x^{10}y^{2}}}{\sqrt{2x^6y^6}}\).
- תשובה
-
\(\frac{9x^2}{y^2}\)
פשט:\(\frac{\sqrt{300m^{3}n^{7}}}{\sqrt{3m^{5}n}}\).
- תשובה
-
\(\frac{10n^3}{m}\)
רציונליזציה של מכנה מונח אחד
לפני שהמחשבון הפך לכלי בחיי היומיום, נעשה שימוש בטבלאות של שורשים מרובעים למציאת ערכים משוערים של שורשים מרובעים. איור מציג חלק מטבלה של ריבועים ושורשים מרובעים. שורשים מרובעים משוערים לחמישה מקומות עשרוניים בטבלה זו.
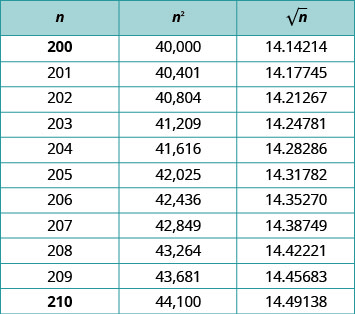
אם מישהו היה צריך להעריך שבר עם שורש ריבועי במכנה, זה אומר לעשות חלוקה ארוכה עם מחלק של חמישה מקומות עשרוניים. זה היה תהליך מסורבל מאוד.
מסיבה זו פותח תהליך שנקרא רציונליזציה של המכנה. שבר עם רדיקל במכנה מומר לשבר שווה ערך שהמכנה שלו הוא מספר שלם. תהליך זה משמש עד היום והוא שימושי גם בתחומים אחרים של המתמטיקה.
תהליך המרת שבר עם רדיקל במכנה לשבר שווה ערך שהמכנה שלו הוא מספר שלם נקרא רציונליזציה של המכנה.
שורשים מרובעים של מספרים שאינם ריבועים מושלמים הם מספרים לא הגיוניים. כאשר אנו מנמקים את המכנה, אנו כותבים שבר שווה ערך עם מספר רציונלי במכנה.
בואו נסתכל על דוגמה מספרית.
\[\begin{array}{ll} {\text{Suppose we need an approximate value for the fraction.}}&{\frac{1}{\sqrt{2}}}\\ {\text{A five decimal place approximation to} \sqrt{2} \text{is} 1.41421}&{\frac{1}{1.41421}}\\ {\text{Without a calculator, would you want to do this division?}}&{1.41421) \overline{1.0}}\\ \nonumber \end{array}\]
אבל אנחנו יכולים למצוא שבר שווה ערך על \(\frac{1}{\sqrt{2}}\) ידי הכפלת המונה והמכנה על ידי. \(\sqrt{2}\)
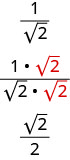
עכשיו אם אנחנו צריכים ערך משוער, אנחנו מחלקים\(2) \overline{1.41421}\). זה הרבה יותר קל.
למרות שיש לנו מחשבונים זמינים כמעט בכל מקום, עדיין יש לתרץ חלק עם רדיקל במכנה. זה לא נחשב לפשוט אם המכנה מכיל שורש ריבועי.
באופן דומה, שורש ריבועי אינו נחשב לפשוט אם הרדיקנד מכיל שבריר.
שורש ריבועי נחשב לפשוט יותר אם יש
- אין גורמים מרובעים מושלמים ברדיקנד
- אין שברים ברדיקנד
- אין שורשים מרובעים במכנה של שבר
כדי לתרץ מכנה, אנו משתמשים בנכס ש \((\sqrt{a})^2=a\). If we square an irrational square root, we get a rational number.
נשתמש במאפיין זה כדי לתרץ את המכנה בדוגמה הבאה.
פשט:\(\frac{4}{\sqrt{3}}\).
- תשובה
-
כדי להסיר את השורש הריבועי מהמכנה, אנו מכפילים אותו מעצמו. כדי לשמור על השברים שווים, אנו מכפילים גם את המונה וגם את המכנה באותו גורם.
\(\frac{4}{\sqrt{3}}\)
הכפל הן את המונה והן את המכנה על ידי \(\sqrt{3}\)\(\frac{4·\sqrt{3}}{\sqrt{3}·\sqrt{3}}\) לפשט. \(\frac{4\sqrt{3}}{3}\)
פשט:\(\frac{5}{\sqrt{3}}\).
- תשובה
-
\(\frac{5\sqrt{3}}{3}\)
פשט:\(\frac{6}{\sqrt{5}}\).
- תשובה
-
\(\frac{6\sqrt{5}}{5}\)
פשט: \(−\frac{8}{3\sqrt{6}}\)
- תשובה
-
כדי להסיר את השורש הריבועי מהמכנה, אנו מכפילים אותו מעצמו. כדי לשמור על השברים שווים, אנו מכפילים גם את המונה וגם את המכנה ב. \(\sqrt{6}\)
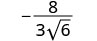
הכפל הן את המונה והן את המכנה על ידי. \(\sqrt{6}\) 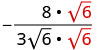
לפשט. 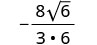
הסר גורמים נפוצים. 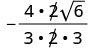
לפשט. 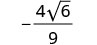
פשט:\(\frac{5}{2\sqrt{5}}\).
- תשובה
-
\(\frac{\sqrt{5}}{2}\)
פשט:\(−\frac{9}{4\sqrt{3}}\).
- תשובה
-
\(−\frac{3\sqrt{3}}{4}\)
תמיד פשט תחילה את הרדיקל במכנה, לפני שאתה מתרץ אותו. בדרך זו המספרים נשארים קטנים יותר וקל יותר לעבוד איתם.
פשט:\(\sqrt{\frac{5}{12}}\).
- תשובה
-
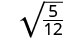
השבר אינו ריבוע מושלם, לכן כתוב מחדש באמצעות המאפיין
Quotient.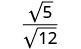
פשט את המכנה. 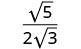
רציונליזציה של המכנה. 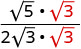
לפשט. 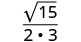
לפשט. 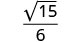
פשט:\(\sqrt{\frac{7}{18}}\).
- תשובה
-
\(\frac{\sqrt{14}}{6}\)
פשט:\(\sqrt{\frac{3}{32}}\).
- תשובה
-
\(\frac{\sqrt{6}}{8}\)
פשט: \(\sqrt{\frac{11}{28}}\)
- תשובה
-
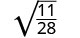
כתוב מחדש באמצעות המאפיין Quotient. 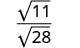
פשט את המכנה. 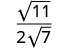
רציונליזציה של המכנה. 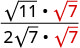
לפשט. 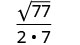
לפשט. 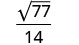
פשט:\(\sqrt{\frac{3}{27}}\).
- תשובה
-
\(\frac{1}{3}\)
פשט: \(\sqrt{\frac{10}{50}}\)
- תשובה
-
\(\frac{\sqrt{5}}{5}\)
רציונליזציה של מכנה דו-מונח
כאשר המכנה של שבר הוא סכום או הבדל עם שורשים מרובעים, אנו משתמשים בתבנית המוצר של מצומדים כדי לתרץ את המכנה.
\[\begin{array}{ll} {(a−b)(a+b)}&{(2−\sqrt{5})(2+\sqrt{5})}\\ {a^2−b^2}&{2^2−(\sqrt{5})^2}\\ {}&{4−5}\\ {}&{−1}\\ \nonumber \end{array}\]
כאשר אנו מכפילים בינומיום הכולל שורש ריבועי על ידי הצמידה שלו, למוצר אין שורשים מרובעים.
פשט:\(\frac{4}{4+\sqrt{2}}\).
- תשובה
-
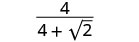
הכפל את המונה והמכנה על ידי הצמידה של המכנה. 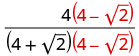
הכפל את המצמידים במכנה. 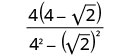
פשט את המכנה. 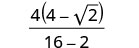
פשט את המכנה. 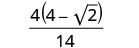
הסר גורמים משותפים מהמונה והמכנה. 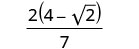
אנו משאירים את המונה בצורה מחושבת כדי להקל על חיפוש גורמים משותפים לאחר שפשטנו את המכנה.
פשט:\(\frac{2}{2+\sqrt{3}}\).
- תשובה
-
\(\frac{2(2−\sqrt{3})}{1}\)
פשט:\(\frac{5}{5+\sqrt{3}}\).
- תשובה
-
\(\frac{5(5−\sqrt{3})}{22}\)
פשט:\(\frac{5}{2−\sqrt{3}}\).
- תשובה
-
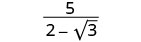
הכפל את המונה והמכנה על ידי הצמידה של המכנה. 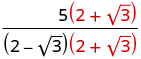
הכפל את המצמידים במכנה. 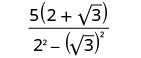
פשט את המכנה. 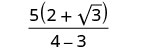
פשט את המכנה. 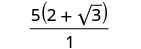
לפשט. 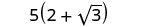
פשט:\(\frac{3}{1−\sqrt{5}}\).
- תשובה
-
\(−\frac{3(1+\sqrt{5})}{4}\)
פשט:\(\frac{2}{4−\sqrt{6}}\).
- תשובה
-
\(\frac{4+\sqrt{6}}{5}\)
פשט:\(\frac{\sqrt{3}}{\sqrt{u}−\sqrt{6}}\).
- תשובה
-
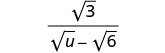
הכפל את המונה והמכנה על ידי הצמידה של המכנה. 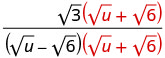
הכפל את המצמידים במכנה. 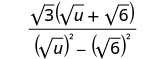
פשט את המכנה. 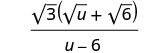
פשט:\(\frac{\sqrt{5}}{\sqrt{x}+\sqrt{2}}\).
- תשובה
-
\(\frac{\sqrt{5}(\sqrt{x}−\sqrt{2})}{x−2}\)
פשט:\(\frac{\sqrt{10}}{\sqrt{y}−\sqrt{3}}\).
- תשובה
-
\(\frac{\sqrt{10}(\sqrt{y}+\sqrt{3})}{y−3}\)
פשט:\(\frac{\sqrt{x}+\sqrt{7}}{\sqrt{x}−\sqrt{7}}\).
- תשובה
-
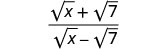
הכפל את המונה והמכנה על ידי הצמידה של המכנה. 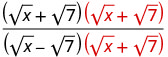
הכפל את המצמידים במכנה. 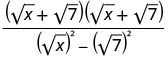
פשט את המכנה. 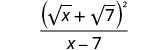
אנחנו לא מרובעים את המונה. בצורה מחושבת, אנו יכולים לראות שאין גורמים משותפים להסרה מהמונה והמכנה.
פשט: \(\frac{\sqrt{p}+\sqrt{2}}{\sqrt{p}−\sqrt{2}}\).
- תשובה
-
\(\frac{(\sqrt{p}+\sqrt{2})^2}{p−2}\)
פשט:\(\frac{\sqrt{q}−\sqrt{10}}{\sqrt{q}+\sqrt{10}}\).
- תשובה
-
\(\frac{(\sqrt{q}−\sqrt{10})^2}{q−10}\)
גש למשאב מקוון זה לקבלת הדרכה ותרגול נוספים עם חלוקה ורציונליזציה.
- חלוקה ורציונליזציה
מושגי מפתח
- נכס מנה של שורשים מרובעים
- אם a, b הם מספרים ממשיים לא שליליים\(b \ne 0\), ואז
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)ו \(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)
- אם a, b הם מספרים ממשיים לא שליליים\(b \ne 0\), ואז
- שורשים
מרובעים פשוטים שורש ריבועי נחשב לפשוט יותר אם יש- אין גורמים מרובעים מושלמים ברדיקנד
- אין שברים ברדיקנד
- אין שורשים מרובעים במכנה של שבר
רשימת מילים
- רציונליזציה של המכנה
- תהליך המרת שבר עם רדיקל במכנה לשבר שווה ערך שהמכנה שלו הוא מספר שלם נקרא רציונליזציה של המכנה.


