7.6: משוואות ריבועיות
- Page ID
- 205468
בסוף פרק זה תוכל:
- לפתור משוואות ריבועיות באמצעות מאפיין מוצר אפס
- לפתור משוואות ריבועיות פקטורינג
- לפתור יישומים לפי מודל משוואות ריבועיות
לפני שתתחיל, קח את חידון המוכנות הזה.
- לפתור:\(5y−3=0\).
אם פספסת בעיה זו, עיין בתרגיל 2.3.1. - לפתור:\(10a=0\).
אם פספסת בעיה זו, עיין בתרגיל 2.2.1. - שלב מונחים דומים:\(12 x^{2}-6 x+4 x\).
אם פספסת בעיה זו, סקור את תרגיל 1.3.37. - פקטור \(n^{3}-9 n^{2}-22 n\) לחלוטין.
אם פספסת בעיה זו, עיין בתרגיל 7.3.10.
כבר פתרנו משוואות לינאריות, משוואות של הצורה\(a x+b y=c\). במשוואות לינאריות, למשתנים אין אקספוננטים. משוואות ריבועיות הן משוואות בהן המשתנה בריבוע. להלן כמה דוגמאות למשוואות ריבועיות:
\[x^{2}+5 x+6=0 \quad 3 y^{2}+4 y=10 \quad 64 u^{2}-81=0 \quad n(n+1)=42\]
נראה כי המשוואה האחרונה לא כוללת את המשתנה בריבוע, אך כאשר אנו מפשטים את הביטוי משמאל נקבל\(n^{2}+n\).
הצורה הכללית של משוואה ריבועית היא\(a x^{2}+b x+c=0\), עם\(a \neq 0\).
משוואה של הצורה \(a x^{2}+b x+c=0\) נקראת משוואה ריבועית.
\[a, b, \text { and } c \text { are real numbers and } a \neq 0\]
כדי לפתור משוואות ריבועיות אנו זקוקים לשיטות שונות מאלה בהן השתמשנו בפתרון משוואות לינאריות. נבחן כאן שיטה אחת ואז על כמה אחרות בפרק מאוחר יותר.
לפתור משוואות ריבועיות באמצעות מאפיין המוצר האפס
תחילה נפתור כמה משוואות ריבועיות באמצעות מאפיין מוצר אפס. מאפיין אפס המוצר אומר שאם התוצר של שתי כמויות הוא אפס, חייב להיות שלפחות אחת מהכמויות היא אפס. הדרך היחידה להשיג מוצר שווה לאפס היא להכפיל באפס עצמו.
\(\text { If } a \cdot b=0, \text { then either } a=0 \text { or } b=0 \text { or both. }\)
כעת נשתמש במאפיין אפס המוצר, כדי לפתור משוואה ריבועית.
לפתור: \((x+1)(x-4)=0\)
- תשובה
-



לפתור: \((x-3)(x+5)=0\)
- תשובה
-
\(x=3, x=-5\)
לפתור: \((y-6)(y+9)=0\)
- תשובה
-
\(y=6, y=-9\)
בדרך כלל נעשה קצת יותר עבודה ממה שעשינו בדוגמה האחרונה הזו כדי לפתור את המשוואות הליניאריות הנובעות משימוש במאפיין אפס המוצר.
לפתור: \((5 n-2)(6 n-1)=0\)
- תשובה
-
\((5 n-2)(6 n-1)=0\) השתמש במאפיין אפס מוצר כדי להגדיר
כל גורם ל- 0.\(5 n-2=0 \)
\(6 n-1=0\) לפתור את המשוואות. \(n=\frac{2}{5}\) \(n = \frac{1}{6}\) בדוק את התשובות שלך. 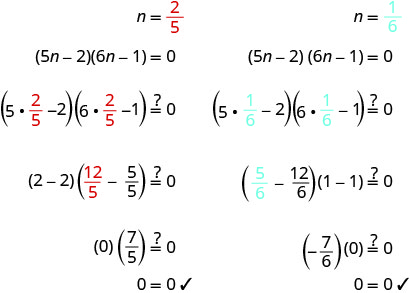
לפתור: \((3 m-2)(2 m+1)=0\)
- תשובה
-
\(m=\frac{2}{3}, m=-\frac{1}{2}\)
לפתור: \((4 p+3)(4 p-3)=0\)
- תשובה
-
\(p=-\frac{3}{4}, p=\frac{3}{4}\)
שימו לב כשבדקנו את הפתרונות שכל אחד מהם עשה רק גורם אחד שווה לאפס. אבל המוצר היה אפס עבור שני הפתרונות.
לפתור: \(3 p(10 p+7)=0\)
- תשובה
-
\(3p(10p+7)=0\) השתמש במאפיין אפס מוצר כדי להגדיר
כל גורם ל- 0.3p = 0 10p+7=0 לפתור את המשוואות. p=0 10p = −7 \(p=-\frac{7}{10}\) בדוק את התשובות שלך. 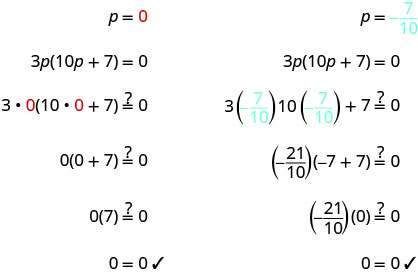
לפתור: \(2 u(5 u-1)=0\)
- תשובה
-
\(u=0, u=\frac{1}{5}\)
לפתור: \(w(2 w+3)=0\)
- תשובה
-
\(w=0, w=-\frac{3}{2}\)
נראה כי יש רק גורם אחד בדוגמה הבאה. זכור, עם זאת, זה \((y-8)^{2}\) אומר\((y-8)(y-8)\).
לפתור: \((y-8)^{2}=0\)
- תשובה
-
\((y−8)^{2}=0\) כתוב מחדש את הצד השמאלי כמוצר. (י−8) (י−8) =0 השתמש במאפיין אפס מוצר
והגדר כל גורם ל-0.y−8=0 y−8=0 לפתור את המשוואות. y=8 y=8 כאשר פתרון חוזר, אנו קוראים לזה
שורש כפול.בדוק את תשובתך. 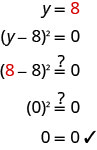
לפתור: \((x+1)^{2}=0\)
- תשובה
-
\(x=1\)
לפתור: \((v-2)^{2}=0\)
- תשובה
-
\(v=2\)
לפתור משוואות ריבועיות על ידי פקטורינג
לכל אחת מהמשוואות שפתרנו בסעיף זה עד כה היה צד אחד בצורה מחושבת. על מנת להשתמש במאפיין אפס המוצר, יש לקחת בחשבון את המשוואה הריבועית, עם אפס בצד אחד. אז אנחנו מקפידים להתחיל עם המשוואה הריבועית בצורה סטנדרטית,\(a x^{2}+b x+c=0\). לאחר מכן אנו מביאים בחשבון את הביטוי משמאל.
לפתור: \(x^{2}+2 x-8=0\)
- תשובה
-

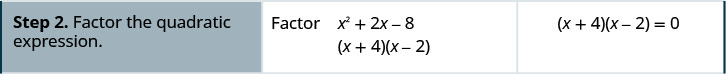



לפתור: \(x^{2}-x-12=0\)
- תשובה
-
\(x=4, x=-3\)
לפתור: \(b^{2}+9 b+14=0\)
- תשובה
-
\(b=-2, b=-7\)
- כתוב את המשוואה הריבועית בצורה סטנדרטית,\(a x^{2}+b x+c=0\).
- גורם לביטוי הריבועי.
- השתמש במאפיין מוצר אפס.
- לפתור את המשוואות הליניאריות.
- בדוק.
לפני שנביא בחשבון, עלינו לוודא שהמשוואה הריבועית היא בצורה סטנדרטית.
לפתור: \(2 y^{2}=13 y+45\)
- תשובה
-
\(2 y^{2}=13 y+45\) כתוב את המשוואה הריבועית בצורה סטנדרטית. \(2 y^{2}-13 y-45=0\) גורם לביטוי הריבועי. \((2 y+5)(y-9)=0\) השתמש במאפיין אפס מוצר
כדי להגדיר כל גורם ל- 0.\(2 y+5=0\) \(y-9=0\) לפתור כל משוואה. \(y=-\frac{5}{2}\) \(y=9\) בדוק את התשובות שלך. 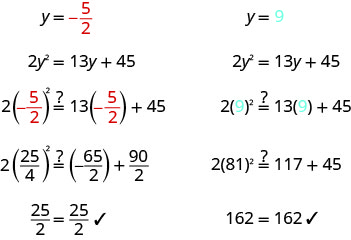
לפתור: \(3 c^{2}=10 c-8\)
- תשובה
-
\(c=0, c=\frac{4}{3}\)
לפתור: \(2 d^{2}-5 d=3\)
- תשובה
-
\(d=3, d=-\frac{1}{2}\)
לפתור: \(5 x^{2}-13 x=7 x\)
- תשובה
-
\(5 x^{2}-13 x=7 x\) כתוב את המשוואה הריבועית בצורה סטנדרטית. \(5 x^{2}-20 x=0\) פקטור בצד שמאל של המשוואה. \(5 x(x-4)=0\) השתמש במאפיין אפס מוצר
כדי להגדיר כל גורם ל- 0.\(5x=0\) \(x−4=0\) לפתור כל משוואה. \(x=0\) \(x=4\) בדוק את התשובות שלך. 
לפתור: \(6 a^{2}+9 a=3 a\)
- תשובה
-
\(a=0, a=-1\)
לפתור: \(45 b^{2}-2 b=-17 b\)
- תשובה
-
\(b=0, b=-\frac{1}{3}\)
פתרון משוואות ריבועיות על ידי פקטורינג יעשה שימוש בכל טכניקות הפקטורינג שלמדת בפרק זה! האם אתה מזהה את דפוס המוצר המיוחד בדוגמה הבאה?
לפתור: \(144 q^{2}=25\)
- תשובה
-
\(\begin{array}{lrllrl} & 144 q^{2}&=&25 \\ \text { Write the quadratic equation in standard form. }& 144 q^{2}-25&=& 0 \\ \text { Factor. It is a difference of squares. } & (12 q-5)(12 q+5) & = & 0 \\ \text { Use the Zero Product Property to set each factor to } 0 . & 12 q-5&=&0 & 12 q+5&=&0 \\\text { Solve each equation. } & 12 q & = & 5 & 12 q&=&-5 \\ & q&=&\frac{5}{12} & q & =&-\frac{5}{12} \\ \text { Check your answers. }\end{array}\)
לפתור: \(25 p^{2}=49\)
- תשובה
-
\(p=\frac{7}{5}, p=-\frac{7}{5}\)
לפתור: \(36 x^{2}=121\)
- תשובה
-
\(x=\frac{11}{6}, x=-\frac{11}{6}\)
הצד השמאלי בדוגמה הבאה נלקח בחשבון, אך הצד הימני אינו אפס. על מנת להשתמש במאפיין אפס המוצר, צד אחד של המשוואה חייב להיות אפס. נכפיל את הגורמים ואז נכתוב את המשוואה בצורה סטנדרטית.
לפתור: \((3 x-8)(x-1)=3 x\)
- תשובה
-
\(\begin{array}{ll} & (3 x-8)(x-1)=3 x \\ \text { Multiply the binomials. }& 3 x^{2}-11 x+8=3 x \\ \text { Write the quadratic equation in standard form. }& 3 x^{2}-14 x+8=0\\ \text { Factor the trinomial. }& (3 x-2)(x-4)=0\\\text { Use the Zero Product Property to set each factor to } 0 . & 3 x-2=0 \quad x-4=0 \\ \text { Solve each equation. } & 3 x=2 \quad x=4 \\ & x=\frac{2}{3} \\ \text { Check your answers. } & \text {The check is left to you! } \end{array}\)
לפתור: \((2 m+1)(m+3)=12 m\)
- תשובה
-
\(m=1, m=\frac{3}{2}\)
לפתור: \((k+1)(k-1)=8\)
- תשובה
-
\(k=3, k=-3\)
נכס מוצר אפס חל גם על תוצר של שלושה גורמים או יותר. אם המוצר הוא אפס, לפחות אחד הגורמים חייב להיות אפס. אנחנו יכולים לפתור כמה משוואות של מעלה יותר משניים על ידי שימוש במאפיין אפס המוצר, בדיוק כמו שפתרנו משוואות ריבועיות.
לפתור: \(9 m^{3}+100 m=60 m^{2}\)
- תשובה
-
\(\begin{array}{lrllrl} & 9 m^{3}+100 m&=&60 m^{2}\\ \text { Bring all the terms to one side so that the other side is zero. } & 9 m^{3}-60 m^{2}+100 m&=&0 \\ \text { Factor the greatest common factor first. } & m\left(9 m^{2}-60 m+100\right)&=&0 \\ \text { Factor the trinomial. } & m(3 m-10)(3 m-10)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & m&=&0 & 3 m-10&=&0 & 3 m-10&=&0 \\ \text { Solve each equation. } & m&=&0 & m&=&\frac{10}{3}& m&=&\frac{10}{3} \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
לפתור: \(8 x^{3}=24 x^{2}-18 x\)
- תשובה
-
\(x=0, x=\frac{3}{2}\)
לפתור: \(16 y^{2}=32 y^{3}+2 y\)
- תשובה
-
\(y=0, y=\frac{1}{4}\)
כאשר נביא בחשבון את המשוואה הריבועית בדוגמה הבאה נקבל שלושה גורמים. עם זאת הגורם הראשון הוא קבוע. אנו יודעים שגורם זה אינו יכול להיות שווה ל- 0.
לפתור: \(4 x^{2}=16 x+84\)
- תשובה
-
\(\begin{array}{lrllrl} & 4 x^{2}&=&16 x+84\\ \text { Write the quadratic equation in standard form. }& 4 x^{2}-16 x-84&=&0 \\ \text { Factor the greatest common factor first. }& 4\left(x^{2}-4 x-21\right)&=&0 \\ \text { Factor the trinomial. } & 4(x-7)(x+3)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & 4&\neq&0 & x-7&=&0 & x +3&=&0 \\ \text { Solve each equation. } & 4&\neq&0 & x&=&7& x&=&-3 \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
לפתור: \(18 a^{2}-30=-33 a\)
- תשובה
-
\(a=-\frac{5}{2}, a=\frac{2}{3}\)
לפתור: \(123 b=-6-60 b^{2}\)
- תשובה
-
\(b=2, b=\frac{1}{20}\)
לפתור יישומים לפי מודל משוואות ריבועיות
אסטרטגיית פתרון הבעיות בה השתמשנו קודם לכן עבור יישומים המתורגמים למשוואות לינאריות תעבוד באותה מידה עבור יישומים המתורגמים למשוואות ריבועיות. נעתיק כאן את האסטרטגיה לפתרון בעיות כדי שנוכל להשתמש בה לעיון.
- קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.
- זהה את מה שאנחנו מחפשים.
- תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.
- תרגם למשוואה. זה עשוי להיות מועיל לשחזר את הבעיה במשפט אחד עם כל המידע החשוב. לאחר מכן, תרגם את המשפט האנגלי למשוואת אלגברה.
- לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
- בדוק את התשובה בבעיה וודא שהיא הגיונית.
- ענה על השאלה במשפט שלם.
נתחיל בבעיית מספר כדי להתאמן בתרגום מילים למשוואה ריבועית.
המכפלה של שני מספרים שלמים רצופים היא \(132 .\) מצא את המספרים השלמים.
- תשובה
-
\(\begin{array}{ll} \textbf { Step 1. Read} \text { the problem. } \\ \textbf { Step 2. Identify} \text { what we are looking for. } & \text { We are looking for two consecutive integers. } \\ \textbf { Step 3. Name} \text{ what we are looking for. } & \begin{array}{l}{\text { Let } n=\text { the first integer }} \\ {\space n+1=\text { the next consecutive integer }}\end{array} \\\textbf { Step 4. Translate} \text { into an equation. Restate the } & \text { The product of the two consecutive integers is } 132 . \\ \text { problem in a sentence. } \\ \text { Translate to an equation. } & \begin{array}{c}{\text { The first integer times the next integer is } 132 .} \\ {n(n+1)=132}\end{array} \\ \textbf { Step 5. Solve}\text { the equation. } & n^{2}+n=132 \\ \text { Bring all the terms to one side. } & n^{2}+n-132=0 \\ \text { Factor the trinomial. } & (n-11)(n+12)=0 \\ \text { Use the zero product property. } & n-11=0 \quad n+12=0 \\ \text { Solve the equations. } & n=11 \quad n=-12 \end{array}\)
המכפלה של שני מספרים שלמים רצופים היא \(240 .\) מצא את המספרים השלמים.
- תשובה
-
\(-15,-16\)ו \(15,16\)
המכפלה של שני מספרים שלמים רצופים היא \(420 .\) מצא את המספרים השלמים.
- תשובה
-
\(-21,-20\)ו \(20,21\)
הופתעת מצמד המספרים השלמים השליליים שהוא אחד הפתרונות לדוגמא הקודמת? התוצר של שני המספרים השלמים החיוביים והתוצר של שני המספרים השלמים השליליים נותנים שניהם 132.
ביישומים מסוימים, פתרונות שליליים ייגרמו מהאלגברה, אך לא יהיו מציאותיים למצב.
גינה מלבנית בשטח של 15 רגל מרובע. אורך הגן הוא שני מטרים יותר מהרוחב. מצא את אורך ורוחב הגן.
- תשובה
-
שלב 1. קרא את הבעיה. בבעיות הכרוכות בדמויות גיאומטריות, סקיצה יכולה לעזור לך לדמיין את המצב. 
שלב 2. זהה את מה שאתה מחפש. אנו מחפשים את האורך והרוחב. שלב 3. תן שם למה שאתה מחפש.
האורך הוא שני מטרים יותר מרוחב.תן W = רוחב הגן.
W+ 2 = אורך הגןשלב 4. תרגם למשוואה.
שחזר את המידע החשוב במשפט.
שטח הגן המלבני הוא 15 רגל מרובע.השתמש בנוסחה לאזור המלבן. \(A=L \cdot W\) תחליף במשתנים. \(15=(W+2) W\) שלב 5. לפתור את המשוואה. להפיץ תחילה. \(15=W^{2}+2 W\) קבל אפס בצד אחד. \(0=W^{2}+2 W-15\) פקטור הטרינום. \(0=(W+5)(W-3)\) השתמש במאפיין מוצר אפס. \(0=W+5\) \(0=W−3\) לפתור כל משוואה. \(−5=W\) \(3=W\) מכיוון ש- W הוא רוחב הגן,
לא הגיוני שהוא יהיה
שלילי. אנו מבטלים את הערך הזה עבור W.\(W=−5\) cannot be the width, since it's negative.
\(W=3\)\(3=W\)
הרוחב הוא 3 רגל.מצא את הערך של האורך. \(\text{length}=W+2\) \(\text{length}=3+2\) \(\text{length}=5\) אורך הוא 5 רגל. שלב 6. בדוק את התשובה.
האם התשובה הגיונית?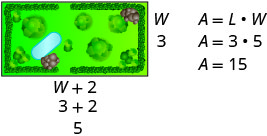
כן, זה הגיוני. שלב 7. תענה על השאלה. רוחב הגינה הוא 3 רגל
והאורך הוא 5 רגל.
שלט מלבני בשטח של 30 רגל מרובע. אורך השלט הוא רגל אחת יותר מהרוחב. מצא את אורך ורוחב השלט.
- תשובה
-
55 רגל ו -66 רגל
פטיו מלבני יש שטח של 180 מטרים רבועים. רוחב הפטיו הוא שלושה מטרים פחות מהאורך. מצא את אורך ורוחב הפטיו.
- תשובה
-
12 רגל ו -15 רגל
בפרק קודם השתמשנו במשפט פיתגורס. \(\left(a^{2}+b^{2}=c^{2}\right)\) זה נתן את היחס בין הרגליים להיפוטנוזה של משולש ימני.
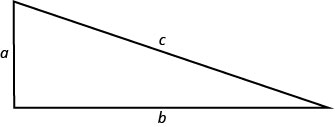
נשתמש בנוסחה זו בדוגמה הבאה.
ג'סטין רוצה לשים סיפון בפינת החצר האחורית שלה בצורת משולש ימני, כפי שמוצג להלן. אורך ההיפוטנוזה יהיה 17 מטר. אורכו של צד אחד יהיה 7 רגל פחות מאורך הצד השני. מצא את אורכי צידי הסיפון.
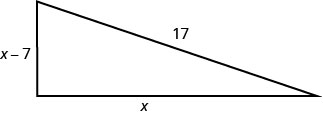
- תשובה
-
שלב 1. קרא את הבעיה. שלב 2. זהה את מה שאתה מחפש. אנחנו מחפשים את אורכי הצדדים
של הסיפון.שלב 3. תן שם למה שאתה מחפש.
צד אחד הוא 7 פחות מהשני.תן x = אורך הצד של הסיפון
x − 7 = אורך הצד השנישלב 4. תרגם למשוואה.
מכיוון שמדובר במשולש ימני נוכל להשתמש
במשפט פיתגורס.\(a^{2}+b^{2}=c^{2}\) תחליף במשתנים. \(x^{2}+(x-7)^{2}=17^{2}\) שלב 5. לפתור את המשוואה. \(x^{2}+x^{2}-14 x+49=289\) לפשט. \(2 x^{2}-14 x+49=289\) זו משוואה ריבועית, אז קבל אפס בצד אחד. \(2 x^{2}-14 x-240=0\) גורם הגורם המשותף הגדול ביותר. \(2\left(x^{2}-7 x-120\right)=0\) פקטור הטרינום. \(2(x-15)(x+8)=0\) השתמש במאפיין מוצר אפס. \(2\neq 0\) \(x−15=0\) \(x+8=0\) לפתור. \(2\neq 0\) \(x=15\) \(x=-8\) מאז \(x\) הוא צד של המשולש, \(x=−8\) לא
הגיוני.\(2\neq 0\) \(x=15\) \(\cancel{x=−8}\) מצא את אורך הצד השני. אם אורך צד אחד הוא \(x=15\) אז אורך הצד השני הוא \(x-7\) \(15 - 7 = 8\) 8 הוא אורך הצד השני. שלב 6. בדוק את התשובה.
האם המספרים האלה הגיוניים?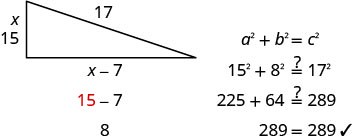
שלב 7. תענה על השאלה. צידי הסיפון הם 8, 15 ו-17 רגל.
מפרש של סירה הוא משולש ימני. אורכו של צד אחד של המפרש הוא 7 רגל יותר מהצד השני. ההיפוטנוזה היא 13. מצא את אורכי שני צידי המפרש.
- תשובה
-
5 רגל ו -12 רגל
גן מדיטציה הוא בצורת משולש ימני, עם רגל אחת 7 רגל. אורך ההיפוטנוזה הוא אחד יותר מאורך אחת הרגליים האחרות. מצא את אורכי ההיפוטנוזה ואת הרגל השנייה.
- תשובה
-
24 רגל ו -25 רגל
מושגי מפתח
- אפס נכס מוצר אם\(a \cdot b=0\), אז או a = 0 או b = 0 או שניהם. ראה דוגמה.
- לפתור משוואה ריבועית על ידי פקטורינג כדי לפתור משוואה ריבועית על ידי פקטורינג: ראה דוגמה.
- כתוב את המשוואה הריבועית בצורה סטנדרטית,\(a x^{2}+b x+c=0\).
- גורם לביטוי הריבועי.
- השתמש במאפיין מוצר אפס.
- לפתור את המשוואות הליניאריות.
- בדוק.
- השתמש באסטרטגיה לפתרון בעיות כדי לפתור בעיות מילים ראה דוגמה.
- קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.
- זהה את מה שאנחנו מחפשים.
- תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.
- תרגם למשוואה. זה עשוי להיות מועיל לשחזר את הבעיה במשפט אחד עם כל המידע החשוב. לאחר מכן, תרגם את המשפט האנגלי למשוואת אלגברה.
- לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
- בדוק את התשובה בבעיה וודא שהיא הגיונית.
- ענה על השאלה במשפט שלם.
רשימת מילים
- משוואות ריבועיות
- הן משוואות שבהן המשתנה בריבוע.
- נכס מוצר אפס
- מאפיין מוצר אפס קובע שאם המכפלה של שתי כמויות היא אפס, לפחות אחת מהכמויות היא אפס.


