7.5: אסטרטגיה כללית לפקטורינג פולינומים

מטרות למידה

בסוף פרק זה, תוכל:

• הכירו את השיטה המתאימה והשתמשו בה כדי לגבש פולינום לחלוטין

הערה

לפני שתתחיל, קח את חידון המוכנות הזה.

1. פקטור\(y^{2}-2 y-24\).
   אם פספסת בעיה זו, עיין בתרגיל 7.2.19.
2. פקטור\(3 t^{2}+17 t+10\).
   אם פספסת בעיה זו, עיין בתרגיל 7.3.28.
3. פקטור\(36 p^{2}-60 p+25\).
   אם פספסת בעיה זו, עיין בתרגיל 7.4.1.
4. פקטור\(5 x^{2}-80\).
   אם פספסת בעיה זו, עיין בתרגיל 7.4.31.

הכירו את השיטה המתאימה והשתמשו בה כדי ליצור פולינום לחלוטין

כעת הכרת את כל שיטות הפקטורינג שתזדקק להן בקורס זה. (בקורס האלגברה הבא שלך יתווספו שיטות נוספות לרפרטואר שלך.) האיור שלהלן מסכם את כל שיטות הפקטורינג שכיסינו. איור \(\PageIndex{1}\) מתאר אסטרטגיה שעליך להשתמש בה בעת פקטורינג פולינומים.

איור \(\PageIndex{1}\)

פולינומים של פקטור.

1. האם יש גורם משותף גדול ביותר?
   • פקטור את זה.
2. האם הפולינום הוא בינומי, טרינומי, או שיש יותר משלושה מונחים?
   • אם זה בינומי:
     האם זה סכום?
     • של ריבועים? סכומי הריבועים אינם גורמים.
     • של קוביות? השתמש בסכום של תבנית קוביות.
     האם זה הבדל?
     • של ריבועים? גורם כתוצר של מצמידים.
     • של קוביות? השתמש בהבדל של תבנית קוביות.
   • אם זה טרינום:
     האם זה מהצורה? \(x^{2}+b x+c ?\) בטל את נייר הכסף.
     האם זה מהצורה\(a x^{2}+b x+c\)?
     • אם aa ו- cc הם ריבועים, בדוק אם הוא מתאים לתבנית הריבועית הטרינומית.
     • השתמש בשיטת ניסוי וטעייה או בשיטת "ac".
   • אם יש לו יותר משלושה מונחים:
     השתמש בשיטת הקיבוץ.
3. בדוק.
   • האם זה נלקח בחשבון לחלוטין?
   • האם הגורמים מתרבים בחזרה לפולינום המקורי?

זכור, פולינום נלקח בחשבון לחלוטין אם, מלבד מונומיאלים, הגורמים שלו הם ראשוניים!

תרגיל \(\PageIndex{1}\)

גורם לחלוטין: \(4 x^{5}+12 x^{4}\)

תשובה

\ (\ התחל {מערך} {lll}\ טקסט {האם יש GCF? } &\ text {כן,} 4 x^ {4} & 4 x^ {5} +12 x^ {4}\\ טקסט {גורם החוצה את ה- GCF.} & & & & 4 x ^ {4} (x+3)\\ טקסט {בסוגריים, האם זה בינומי, a} & &\\ טקסט {טרינומי, או שיש יותר משלושה מונחים? } &\ text {בינומיאלי.} &\\\ quad\ text {האם זה סכום? } & &\ text {כן.}\\\ מרובע\ טקסט {של ריבועים? של קוביות? } & &\ text {No.}\\\ text {בדוק.}
\\\\ quad\ text {האם הביטוי נלקח בחשבון במלואו? } &\ טקסט {כן.}\\\ מרובע\ טקסט {הכפל.}\\\ התחל {מערך} {l} {4 x ^ {4} (x+3)}\\ {4 x ^ {4}\ cdot x+4 x ^ {4}\ cdot 3}\ {4 x ^ {5} +12 x ^ {4}\ {4}\ סימן ביקורת\ סוף {מערך}\ סוף {{4 x ^ {5} +12 x ^ {4}\ {4} x ^ {4}\ {4} x ^ {4}\ {4} x ^ {4}\ {4} x ^ {4}\ {4} x ^ {4}\ {4} x ^ {4}\ {4} x ^ {4}\\ סימן ביקורת\ סוף {מערך}\ סוף {{4 x ^ מערך}\)

תרגיל \(\PageIndex{2}\)

גורם לחלוטין: \(3 a^{4}+18 a^{3}\)

תשובה

3 \(a^{3}(a+6)\)

תרגיל \(\PageIndex{3}\)

גורם לחלוטין: \(45 b^{6}+27 b^{5}\)

תשובה

9 \(b^{5}(5 b+3)\)

תרגיל \(\PageIndex{4}\)

גורם לחלוטין: \(12 x^{2}-11 x+2\)

תשובה

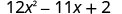
האם יש GCF?	לא.
האם זה בינומי, טרינומי, או שיש יותר משלושה מונחים?	טרינום.
האם a ו - c ריבועים מושלמים?	לא, א = 12, לא ריבוע מושלם.
השתמש בניסוי וטעייה או בשיטת "ac". אנו נשתמש כאן בניסוי וטעייה.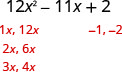

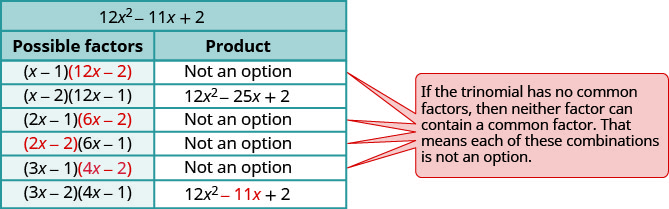
בדוק. \(\begin{array}{l}{(3 x-2)(4 x-1)} \\ {12 x^{2}-3 x-8 x+2} \\ {12 x^{2}-11 x+2 }\checkmark \end{array}\)

תרגיל \(\PageIndex{5}\)

גורם לחלוטין: \(10 a^{2}-17 a+6\)

תשובה

\((5 a-6)(2 a-1)\)

תרגיל \(\PageIndex{6}\)

גורם לחלוטין: \(8 x^{2}-18 x+9\)

תשובה

\((2 x-3)(4 x-3)\)

תרגיל \(\PageIndex{7}\)

גורם לחלוטין: \(g^{3}+25 g\)

תשובה

\(\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, g.} &g^{3}+25 g \\\text { Factor out the GCF. } & &g\left(g^{2}+25\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } &\text { Binomial. } & \\ \quad \text { Is it a sum? Of squares? } & \text { Yes. } & \text { Sums of squares are prime. } \\\text { Check. } \\ \\ \quad \text { Is the expression factored completely? } &\text { Yes. } \\ \quad \text { Multiply. } \\ \qquad \begin{array}{l}{g\left(g^{2}+25\right)} \\ {g^{3}+25 g }\checkmark \end{array} \end{array}\)

תרגיל \(\PageIndex{8}\)

גורם לחלוטין: \(x^{3}+36 x\)

תשובה

\(x\left(x^{2}+36\right)\)

תרגיל \(\PageIndex{9}\)

גורם לחלוטין: \(27 y^{2}+48\)

תשובה

3 \(\left(9 y^{2}+16\right)\)

תרגיל \(\PageIndex{10}\)

גורם לחלוטין: \(12 y^{2}-75\)

תשובה

\(\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, 3.} &12 y^{2}-75 \\\text { Factor out the GCF. } & &3\left(4 y^{2}-25\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } &\text { Binomial. } & \\ \text { Is it a sum?} & \text { No. } & \\ \text { Is it a difference? Of squares or cubes? } &\text { Yes, squares. } & 3\left((2 y)^{2}-(5)^{2}\right) \\ \text { Write as a product of conjugates. } & &3(2 y-5)(2 y+5)\\\text { Check. } \\ \\ \text { Is the expression factored completely? } & \text{ Yes.}& \\ \text { Neither binomial is a difference of } \\ \text { squares. } \\ \text{ Multiply.} \\ \quad \begin{array}{l}{3(2 y-5)(2 y+5)} \\ {3\left(4 y^{2}-25\right)} \\ {12 y^{2}-75}\checkmark \end{array} \end{array}\)

תרגיל \(\PageIndex{11}\)

גורם לחלוטין: \(16 x^{3}-36 x\)

תשובה

4 \(x(2 x-3)(2 x+3)\)

תרגיל \(\PageIndex{12}\)

גורם לחלוטין: \(27 y^{2}-48\)

תשובה

3 \((3 y-4)(3 y+4)\)

תרגיל \(\PageIndex{13}\)

גורם לחלוטין: \(4 a^{2}-12 a b+9 b^{2}\)

תשובה

האם יש GCF?	לא.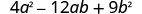
האם זה בינומי, טרינומי, או שיש מונחים נוספים?
טרינום עם. \(a\neq 1\) אבל המונח הראשון הוא ריבוע מושלם.
האם המונח האחרון הוא ריבוע מושלם?	כן.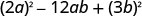
האם זה מתאים לתבנית,\(a^{2}-2 a b+b^{2}\)?	כן.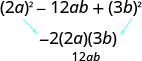
כתוב את זה כריבוע.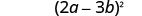
בדוק את תשובתך.
האם הביטוי נלקח בחשבון לחלוטין?
כן.
הבינום אינו הבדל של ריבועים.
להכפיל.
\((2 a-3 b)^{2}\)
\((2 a)^{2}-2 \cdot 2 a \cdot 3 b+(3 b)^{2}\)
\(4 a^{2}-12 a b+9 b^{2} \checkmark\)

תרגיל \(\PageIndex{14}\)

גורם לחלוטין: \(4 x^{2}+20 x y+25 y^{2}\)

תשובה

\((2 x+5 y)^{2}\)

תרגיל \(\PageIndex{15}\)

גורם לחלוטין: \(9 m^{2}+42 m n+49 n^{2}\)

תשובה

\((3 m+7 n)^{2}\)

תרגיל \(\PageIndex{16}\)

גורם לחלוטין: \(6 y^{2}-18 y-60\)

תשובה

\(\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, 6.} &6 y^{2}-18 y-60 \\\text { Factor out the GCF. } & \text { Trinomial with leading coefficient } 1&6\left(y^{2}-3 y-10\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more terms? } & & \\ \text { "Undo' FOIL. } & 6(y\qquad )(y\qquad ) &6(y+2)(y-5) \\ \text { Check your answer. } \\ \text { Is the expression factored completely? } & & \text{ Yes.} \\ \text { Neither binomial is a difference of squares. } \\ \text { Multiply. } \\ \\\qquad \begin{array}{l}{6(y+2)(y-5)} \\ {6\left(y^{2}-5 y+2 y-10\right)} \\ {6\left(y^{2}-3 y-10\right)} \\ {6 y^{2}-18 y-60} \checkmark \end{array} \end{array}\)

תרגיל \(\PageIndex{17}\)

גורם לחלוטין: \(8 y^{2}+16 y-24\)

תשובה

8 \((y-1)(y+3)\)

תרגיל \(\PageIndex{18}\)

גורם לחלוטין: \(5 u^{2}-15 u-270\)

תשובה

5 \((u-9)(u+6)\)

תרגיל \(\PageIndex{19}\)

גורם לחלוטין: \(24 x^{3}+81\)

תשובה

האם יש GCF?	כן, 3.	\(24 x^{3}+81\)
פקטור את זה.		3 \(\left(8 x^{3}+27\right)\)
בסוגריים, האם זה בינומי, טרינומי, או שיש יותר משלושה מונחים?	בינומי.
האם זה סכום או הבדל?	סכום.
של ריבועים או קוביות?	סכום הקוביות.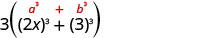
כתוב את זה באמצעות סכום של תבנית קוביות.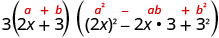
האם הביטוי נלקח בחשבון לחלוטין?	כן.	3 \((2 x+3)\left(4 x^{2}-6 x+9\right)\)
בדוק על ידי הכפלת.		אנו משאירים לך את הצ'ק.

תרגיל \(\PageIndex{20}\)

גורם לחלוטין: \(250 m^{3}+432\)

תשובה

2 \((5 m+6)\left(25 m^{2}-30 m+36\right)\)

תרגיל \(\PageIndex{21}\)

גורם לחלוטין: \(81 q^{3}+192\)

תשובה

\(3(3q+4)\left(9q^{2}-12 q+16\right)\)

תרגיל \(\PageIndex{22}\)

גורם לחלוטין: \(2 x^{4}-32\)

תשובה

\(\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 2.} &2 x^{4}-32 \\\text { Factor out the GCF. } & &2\left(x^{4}-16\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } & \text { Binomial. }& \\ \text { Is it a sum or difference? } &\text { Yes. }& \\\text { Of squares or cubes? } & \text { Difference of squares. } & 2\left(\left(x^{2}\right)^{2}-(4)^{2}\right) \\ \text { Write it as a product of conjugates. } & & 2\left(x^{2}-4\right)\left(x^{2}+4\right) \\ \text { The first binomial is again a difference of squares. } & & 2\left((x)^{2}-(2)^{2}\right)\left(x^{2}+4\right) \\ \text { Write it as a product of conjugates. } & & 2(x-2)(x+2)\left(x^{2}+4\right) \\ \text { Is the expression factored completely? } &\text { Yes. } & \\ \\ \text { None of these binomials is a difference of squares. } \\ \text { Check your answer. } \\ \text{ Multiply. }\\ \\ \qquad \qquad \begin{array}{l}{2(x-2)(x+2)\left(x^{2}+4\right)} \\ {2(x-2)(x+2)\left(x^{2}+4\right)} \\ {2(x-10)} \\ {2 x^{4}-32} \checkmark \end{array} \end{array}\)

תרגיל \(\PageIndex{23}\)

גורם לחלוטין: \(4 a^{4}-64\)

תשובה

4 \(\left(a^{2}+4\right)(a-2)(a+2)\)

תרגיל \(\PageIndex{24}\)

גורם לחלוטין: \(7 y^{4}-7\)

תשובה

7 \(\left(y^{2}+1\right)(y-1)(y+1)\)

תרגיל \(\PageIndex{25}\)

גורם לחלוטין: \(3 x^{2}+6 b x-3 a x-6 a b\)

תשובה

\(\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 3.} &3 x^{2}+6 b x-3 a x-6 a b\\\text { Factor out the GCF. } & &3\left(x^{2}+2 b x-a x-2 a b\right)\\ \text { In the parentheses, is it a binomial, trinomial, } &\text { More than } 3 & \\ \text { or are there more terms? } &\text { terms. } & \\ \text { Use grouping. } & & \begin{array}{c}{3[x(x+2 b)-a(x+2 b)]} \\ {3(x+2 b)(x-a)}\end{array} \\ \text { Check your answer. } \\ \\ \text { Is the expression factored completely? Yes. } \\ \text { Multiply. } \\\qquad \qquad \begin{array}{l}{3(x+2 b)(x-a)} \\ {3\left(x^{2}-a x+2 b x-2 a b\right)} \\ {3 x^{2}-3 a x+6 b x-6 a b} \checkmark \end{array}\end{array}\)

תרגיל \(\PageIndex{26}\)

גורם לחלוטין: \(6 x^{2}-12 x c+6 b x-12 b c\)

תשובה

6 \((x+b)(x-2 c)\)

תרגיל \(\PageIndex{27}\)

גורם לחלוטין: \(16 x^{2}+24 x y-4 x-6 y\)

תשובה

2 \((4 x-1)(x+3 y)\)

תרגיל \(\PageIndex{28}\)

גורם לחלוטין: \(10 x^{2}-34 x-24\)

תשובה

\(\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 2.} &10 x^{2}-34 x-24\\\text { Factor out the GCF. } & &2\left(5 x^{2}-17 x-12\right)\\ \text { In the parentheses, is it a binomial, trinomial, } &\text { Trinomial with } & \\ \text { or are there more than three terms? } &\space a \neq 1 & \\ \text { Use trial and error or the "ac" method. } & & 2\left(5 x^{2}-17 x-12\right) \\ & & 2(5 x+3)(x-4) \\ \text { Check your answer. Is the expression factored } \\\text { completely? Yes. }\\ \\ \text { Multiply. } \\ \qquad \begin{array}{l}{2(5 x+3)(x-4)} \\ {2\left(5 x^{2}-20 x+3 x-12\right)} \\ {2\left(5 x^{2}-17 x-12\right)} \\ {10 x^{2}-34 x-24}\checkmark \end{array}\end{array}\)

תרגיל \(\PageIndex{29}\)

גורם לחלוטין: \(4 p^{2}-16 p+12\)

תשובה

4 \((p-1)(p-3)\)

תרגיל \(\PageIndex{30}\)

גורם לחלוטין: \(6 q^{2}-9 q-6\)

תשובה

3 \((q-2)(2 q+1)\)

מושגי מפתח

• אסטרטגיה כללית לפקטורינג פולינומים ראה איור. \(\PageIndex{1}\)
• כיצד לבצע פולינומים
  1. האם יש גורם משותף גדול ביותר? פקטור את זה.
  2. האם הפולינום הוא בינומי, טרינומי, או שיש יותר משלושה מונחים?
     • אם זה בינומי:
       האם זה סכום?
       • של ריבועים? סכומי הריבועים אינם גורמים.
       • של קוביות? השתמש בסכום של תבנית קוביות.
       האם זה הבדל?
       • של ריבועים? גורם כתוצר של מצמידים.
       • של קוביות? השתמש בהבדל של תבנית קוביות.
     • אם זה טרינום:
       האם זה מהצורה? \(x^{2}+b x+c\) בטל את נייר הכסף.
       האם זה מהצורה\(a x^{2}+b x+c\)?
       • אם 'a' ו- 'c' הם ריבועים, בדוק אם הוא מתאים לתבנית הריבועית הטרינומית.
       • השתמש בשיטת ניסוי וטעייה או בשיטת 'ac'.
     • אם יש לו יותר משלושה מונחים:
       השתמש בשיטת הקיבוץ.
  3. בדוק. האם זה נלקח בחשבון לחלוטין? האם הגורמים מתרבים בחזרה לפולינום המקורי?