4.3: גרף עם יירוט
- Page ID
- 205740
בסוף פרק זה תוכל:
- זהה את יירוט ה- x ו- y בגרף
- מצא את יירוט ה- x ו- y ממשוואה של קו
- גרף קו באמצעות היירוט
לפני שתתחיל, קח את חידון המוכנות הזה.
- לפתור:\(3\cdot 0+4y=−2\).
אם פספסת בעיה זו, עיין בתרגיל 2.2.13.
זהה את יירוטי x - ו- y - בגרף
כל משוואה לינארית יכולה להיות מיוצגת על ידי קו ייחודי המציג את כל הפתרונות של המשוואה. ראינו שכאשר גרפים קו על ידי התוויית נקודות, אתה יכול להשתמש בכל שלושה פתרונות לתרשים. המשמעות היא ששני אנשים המתרפים את הקו עשויים להשתמש בקבוצות שונות של שלוש נקודות.
במבט ראשון, שתי השורות שלהם עשויות שלא להיראות זהות, מכיוון שיהיו להן נקודות שונות המסומנות. אבל אם כל העבודה נעשתה כראוי, הקווים צריכים להיות בדיוק אותו הדבר. אחת הדרכים להכיר בכך שהם אכן אותו קו היא להסתכל היכן הקו חוצה את ציר ה - x ואת ציר ה - y. נקודות אלה נקראות יירוט הקו.
הנקודות בהן קו חוצה את ציר ה- x וציר y נקראות יירוט של קו.
בואו נסתכל על הגרפים של השורות באיור\(\PageIndex{1}\).
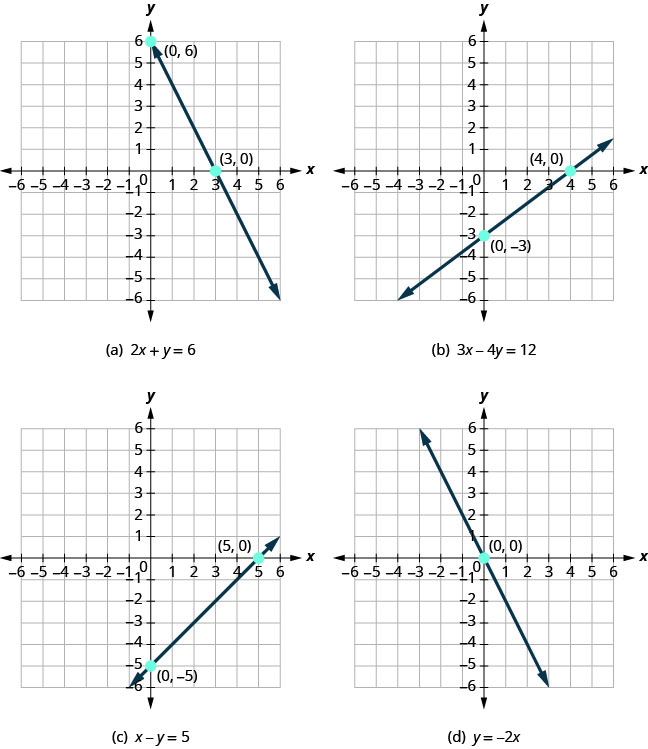
ראשית, שימו לב היכן כל אחד מהקווים הללו חוצה את הציר השלילי x. ראה איור\(\PageIndex{1}\).
| איור | הקו חוצה את ציר ה- x ב: | זוג מסודר של נקודה זו |
|---|---|---|
| איור (א) | 3 | (3.0) |
| איור (ב) | 4 | (4.0) |
| איור (ג) | 5 | (5.0) |
| איור (ד) | 0 | (0,0) |
האם אתה רואה דפוס?
עבור כל שורה, קואורדינטת ה- y של הנקודה בה הקו חוצה את ציר ה - x היא אפס. הנקודה בה הקו חוצה את ציר ה - x היא בעלת הצורה (a,0) והיא נקראת x - יירוט של קו. ה - x - יירוט מתרחש כאשר y הוא אפס. כעת, בואו נסתכל על הנקודות בהן קווים אלה חוצים את ציר ה- y. ראה טבלה\(\PageIndex{2}\).
| איור | הקו חוצה את ציר ה- x ב: | זוג מסודר של נקודה זו |
|---|---|---|
| איור (א) | 6 | (0,6) |
| איור (ב) | -3 | (0, -3) |
| איור (ג) | -5 | (0.5) |
| איור (ד) | 0 | (0,0) |
מה הדפוס כאן?
בכל שורה, קואורדינטת ה - x של הנקודה בה הקו חוצה את ציר y היא אפס. הנקודה בה הקו חוצה את ציר y היא בעלת הצורה (0, b) והיא נקראת יירוט y של הקו. יירוט y מתרחש כאשר x הוא אפס.
ה - x - יירוט הוא הנקודה (a,0) בה הקו חוצה את ציר ה - x.
יירוט y הוא הנקודה (0, b) בה הקו חוצה את ציר y.

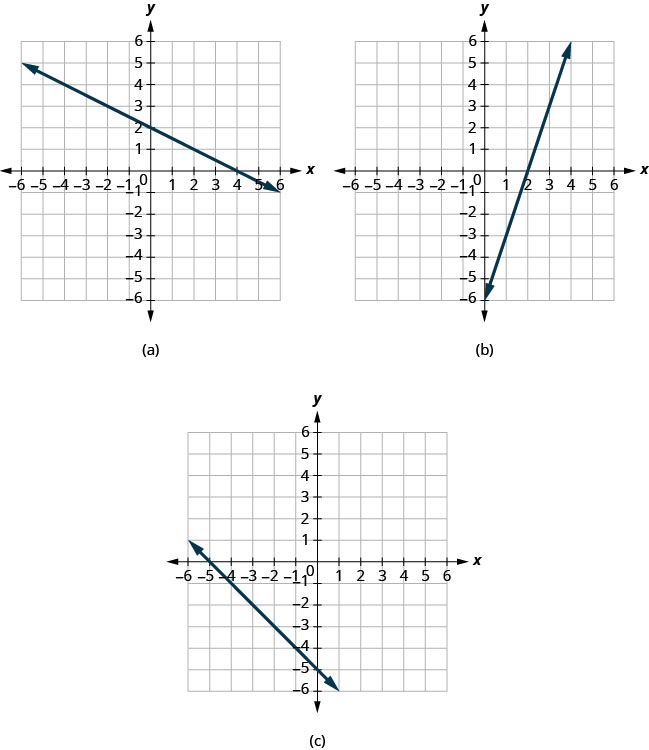
מצא את יירוט x - ו - y - בכל גרף.
- תשובה
-
(א) הגרף חוצה את ציר ה- x בנקודה (4,0). x - יירוט הוא (4,0).
הגרף חוצה את ציר y בנקודה (0,2). ה - y - יירוט הוא (0,2).
(ב) הגרף חוצה את ציר ה- x בנקודה (2,0). ה - x - יירוט הוא (2,0)
הגרף חוצה את ציר y בנקודה (0, −6). ה y - יירוט הוא (0, -6).
(ג) הגרף חוצה את ציר ה - x בנקודה (-5,0). ה איקס - יירוט הוא (-5,0).
הגרף חוצה את ציר y בנקודה (0, -5). ה y - יירוט הוא (0, -5).
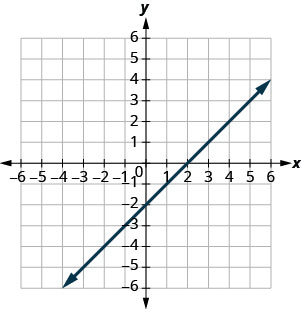
מצא את x - ו - y - יירוט על הגרף.
- תשובה
-
x - יירוט: (2,0); y - יירוט: (0, -2)
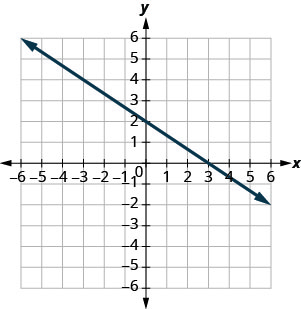
מצא את x - ו - y - יירוט על הגרף.
- תשובה
-
x - יירוט: (3,0), y - יירוט: (0,2)
מצא את יירוט x - ו- y - ממשוואת קו
ההכרה בכך שיירוט ה - x מתרחש כאשר y הוא אפס וכי יירוט ה- y מתרחש כאשר x הוא אפס, נותן לנו שיטה למצוא את היירוט של קו מהמשוואה שלו. כדי למצוא את x - ליירט, תן y = 0 ולפתור עבור x. כדי למצוא את y - ליירט, תן x = 0 ולפתור עבור y.
השתמש במשוואת הקו. כדי למצוא:
- x - יירוט של הקו, תן y = 0 ולפתור עבור x.
- y - יירוט של הקו, תן איקס=0 ולפתור עבור y.
מצא את היירוט של 2x+y = 6.
- תשובה
-
אנו נותנים ל- y=0 למצוא את ה - x - ליירט, ולתת ל- x = 0 למצוא את y - יירוט. נמלא את השולחן, שמזכיר לנו את מה שאנחנו צריכים למצוא.

-
כדי למצוא את x - יירוט, תן y = 0.
טבלה \(\PageIndex{3}\) 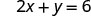
תן y = 0. 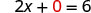
לפשט. 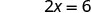
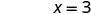
יירוט ה- x הוא (3, 0) כדי למצוא את יירוט y, תן ל - x = 0. 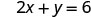
תן x = 0. 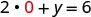
לפשט. 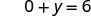
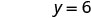
יירוט y הוא (0, 6) - היירוטים הם הנקודות (3,0) ו- (0,6) כפי שמוצג בטבלה. \(\PageIndex{4}\)
טבלה \(\PageIndex{4}\) 2איקס+y = 6 x y 3 0 0 6
מצא את היירוט של 3x+y = 12.
- תשובה
-
x - יירוט: (4,0), y - יירוט: (0,12)
מצא את היירוט של x+4y = 8.
- תשובה
-
x - יירוט: (8,0), y - יירוט: (0,2)
מצא את היירוט של 4x—3y = 12.
- תשובה
-
כדי למצוא את ה - x -יירוט, תן y = 0. 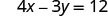
תן y = 0. 
לפשט. 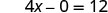
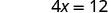
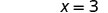
יירוט ה- x הוא (3, 0) כדי למצוא את יירוט y, תן ל - x = 0. 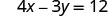
תן x = 0. 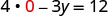
לפשט. 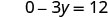
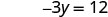
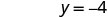
יירוט y הוא (0, -4) - טבלה \(\PageIndex{5}\)
-
היירוטים הם הנקודות (3, 0) ו- (0, -4) כפי שמוצג בטבלה הבאה.
טבלה \(\PageIndex{6}\) 4איקס-3 י=12 x y 3 0 0 -4
מצא את היירוט של 3x—4y = 12.
- תשובה
-
x - יירוט: (4,0), y - יירוט: (0, -3)
מצא את היירוט של 2x—4y = 8.
- תשובה
-
x - יירוט: (4,0), y - יירוט: (0, -2)
גרף קו באמצעות היירוט
כדי לתאר משוואה ליניארית על ידי התוויית נקודות, עליך למצוא שלוש נקודות שהקואורדינטות שלהן הן פתרונות למשוואה. אתה יכול להשתמש ביירוט x - ו - y - כשתיים משלוש הנקודות שלך. מצא את היירוט, ולאחר מכן למצוא נקודה שלישית כדי להבטיח דיוק. ודא שהנקודות מתיישרות - ואז צייר את הקו. שיטה זו היא לרוב הדרך המהירה ביותר לתרשים קו.
גרף -איקס+2y = 6 באמצעות היירוטים.
- תשובה
-


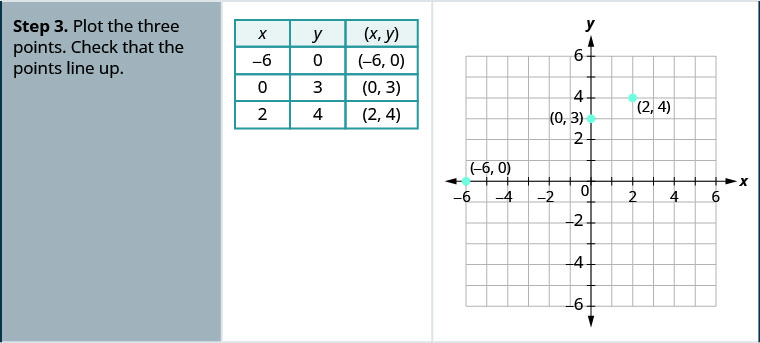
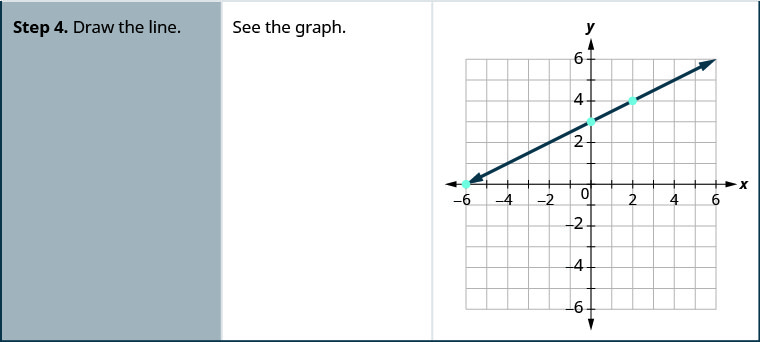
גרף x—2y = 4 באמצעות היירוטים.
- תשובה
-
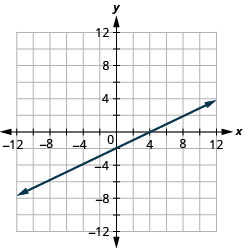
גרף -איקס+3y = 6 באמצעות היירוטים.
- תשובה
-
השלבים לתרשים משוואה לינארית באמצעות היירוטים מסוכמים להלן.
- מצא את x - ו - y - יירוט של הקו.
- תן y = 0 ולפתור עבור x
- תן x = 0 ולפתור עבור y.
- מצא פתרון שלישי למשוואה.
- התווה את שלוש הנקודות ובדוק שהן מסתדרות.
- צייר את הקו.
גרף 4x—3y = 12 באמצעות היירוטים.
- תשובה
-
מצא את היירוט ונקודה שלישית.
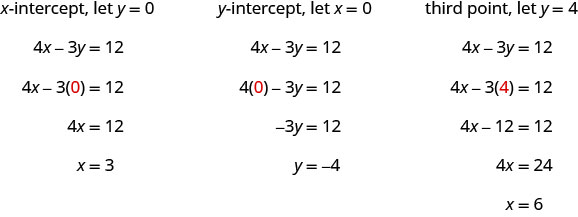
אנו מפרטים את הנקודות בטבלה \(\PageIndex{7}\) ומציגים את הגרף שלהלן.
4איקס-3 י=12 x y (איקס, y) 3 0 (3.0) 0 -4 (0, -4) 6 4 (6.4) - טבלה \(\PageIndex{7}\)
-
גרף 5x—2y = 10 באמצעות היירוטים.
- תשובה
-
גרף 3x—4y = 12 באמצעות היירוטים.
- תשובה
-
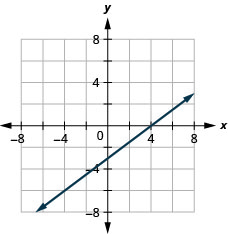
גרף y = 5x באמצעות היירוטים.
- תשובה
-

לקו הזה יש רק יירוט אחד. זו הנקודה (0,0).
כדי להבטיח דיוק אנחנו צריכים לתכנן שלוש נקודות. מכיוון שהיירוט x - ו - y - הוא אותה נקודה, אנו זקוקים לשתי נקודות נוספות כדי לתאר את הקו.
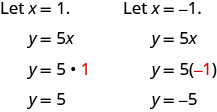
ראה טבלה\(\PageIndex{8}\).
y = 5 איקס x y (איקס, y) (0,0) (1,5) -1 -5 (-1, -5) - טבלה \(\PageIndex{8}\)
-
התווה את שלוש הנקודות, בדוק שהן מתיישרות ושרטט את הקו.
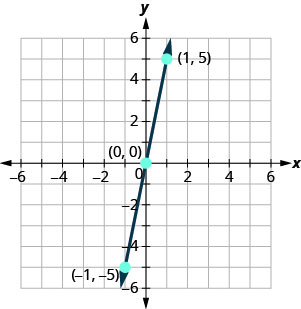
גרף y = 4x באמצעות היירוט.
- תשובה
-
גרף y=−x היירוטים.
- תשובה
-
מושגי מפתח
- מצא את יירוט x - ו- y - ממשוואת קו
- השתמש במשוואת הקו כדי למצוא את x - יירוט של הקו, תן y = 0 ולפתור עבור x.
- השתמש במשוואת הקו כדי למצוא את y - יירוט של הקו, תן x = 0 ולפתור עבור y.
- גרף משוואה לינארית באמצעות היירוטים
- מצא את x - ו - y - יירוט של הקו.
תן y = 0 ולפתור עבור x.
תן x = 0 ולפתור עבור y. - מצא פתרון שלישי למשוואה.
- התווה את שלוש הנקודות ואז בדוק שהן מסתדרות.
- צייר את הקו.
- מצא את x - ו - y - יירוט של הקו.
- אסטרטגיה לבחירת השיטה הנוחה ביותר לתרשים קו:
- שקול את צורת המשוואה.
- אם יש לו רק משתנה אחד, זהו קו אנכי או אופקי.
x = a הוא קו אנכי העובר דרך ציר x ב-
y = b הוא קו אופקי העובר דרך ציר y ב- b. - אם y מבודד בצד אחד של המשוואה, גרף על ידי התוויית נקודות.
- בחר כל שלושה ערכים עבור x ולאחר מכן לפתור את ערכי y המתאימים.
- אם המשוואה היא מהצורה ax+by=c, מצא את היירוטים. מצא את x - ו - y - יירוט ולאחר מכן נקודה שלישית.
רשימת מילים
- יירוט של קו
- הנקודות בהן קו חוצה את ציר ה- x וציר y נקראות יירוט הקו.
- x - יירוט
- הנקודה (a,0) בה הקו חוצה את ציר ה - x; ה- x - יירוט מתרחש כאשר y הוא אפס.
- y -יירוט
- הנקודה (0, b) בה הקו חוצה את ציר y; ה- y - יירוט מתרחש כאשר x הוא אפס.


