4.2: גרף משוואות לינאריות בשני משתנים
- Page ID
- 205720
בסוף פרק זה, תוכל:
- הכירו את הקשר בין פתרונות המשוואה לגרף שלה.
- גרף משוואה לינארית על ידי התוויית נקודות.
- תרשים קווים אנכיים ואופקיים.
לפני שתתחיל, קח את חידון המוכנות הזה.
- להעריך \(3x+2\) מתי\(x=−1\).
אם פספסת בעיה זו, סקור את תרגיל 1.5.34. - לפתור \(3x+2y=12\) עבור y באופן כללי.
אם פספסת בעיה זו, עיין בתרגיל 2.6.16.
הכירו את הקשר בין פתרונות המשוואה לגרף שלה
בחלק הקודם מצאנו מספר פתרונות למשוואה\(3x+2y=6\). הם מפורטים בטבלה\(\PageIndex{1}\). אז, הזוגות המסודרים (0,3), (2,0), \((1,\frac{3}{2})\) והם כמה פתרונות למשוואה. \(3x+2y=6\) אנו יכולים לשרטט פתרונות אלה במערכת הקואורדינטות המלבנית כפי שמוצג באיור\(\PageIndex{1}\).
| 3x+2y=6 | ||
| x | y | (איקס, y) |
| 0 | 3 | (0.3) |
| 2 | 0 | (2.0) |
| 1 | \(\frac{3}{2}\) | \((1, \frac{3}{2})\) |
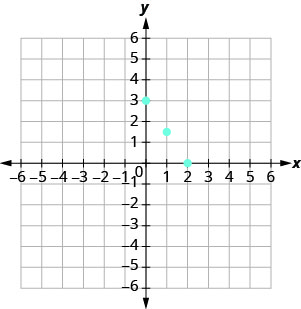
שימו לב איך הנקודות מסתדרות בצורה מושלמת? אנו מחברים את הנקודות עם קו כדי לקבל את הגרף של המשוואה 3x+2y = 6. ראה איור\(\PageIndex{2}\). שימו לב לחצים על הקצוות של כל צד של הקו. חיצים אלה מציינים שהקו ממשיך.
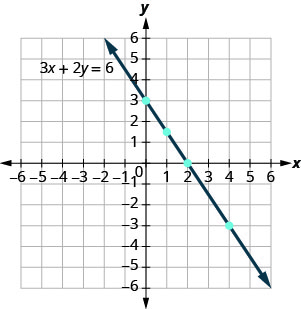
כל נקודה על הקו היא פתרון של המשוואה. כמו כן, כל פתרון של משוואה זו הוא נקודה בקו זה. נקודות שאינן על הקו אינן פתרונות.
שימו לב שהנקודה שהקואורדינטות שלה (-2,6) נמצאת על הקו המוצג באיור. \(\PageIndex{3}\) אם אתה מחליף x = −2 ו- y = 6 במשוואה, אתה מגלה שזה פיתרון למשוואה.
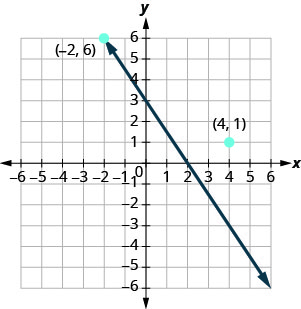
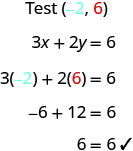
אז הנקודה (-2,6) היא פיתרון למשוואה. \(3x+2y=6\) (הביטוי "הנקודה שהקואורדינטות שלה הן (-2,6)" מתקצר לעתים קרובות ל"נקודה (-2,6).
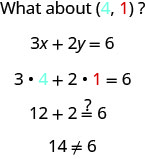
הגרף של משוואה ליניארית Ax+By=C הוא קו.
- כל נקודה על הקו היא פתרון של המשוואה.
- כל פתרון של משוואה זו הוא נקודה בקו זה.
הגרף של y = 2x−3 מוצג.
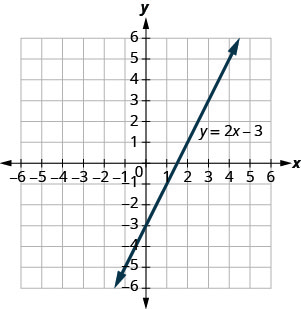
עבור כל זוג שהוזמן, החליטו:
- האם הזוג המסודר הוא פתרון למשוואה?
- האם הנקודה על הקו?
א (0, -3) ב (3,3) ג (2, -3) ד (-1, -5)
- תשובה
-
החלף את ערכי x - ו - y - במשוואה כדי לבדוק אם הזוג המסודר הוא פיתרון למשוואה.
- 1.
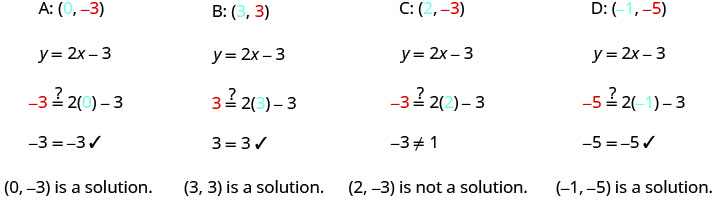
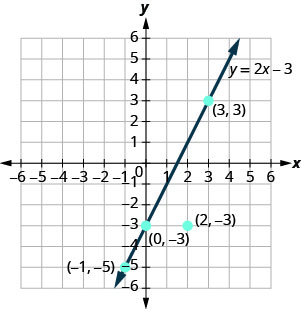
- 2. התווה את הנקודות A (0,3), B (3,3), C (2, -3) ו- D (-1, −5).
-
הנקודות שהן פתרונות ל- y= 2x−3 נמצאות על הקו, אך הנקודה שאינה פתרון אינה על הקו.
הנקודות (0,3), (3,3) ו- (−1, −5) נמצאות על הקו y = 2x−3, והנקודה (2, −3) אינה על הקו.
השתמש בגרף של y = 3x−1 כדי להחליט אם כל זוג מסודר הוא:
- פתרון למשוואה.
- על הקו.
- (0, -1)
- (2.5)
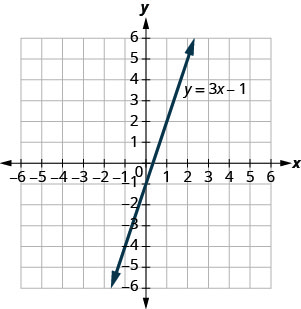
- תשובה
-
- כן, כן
- כן, כן
השתמש בגרף של y = 3x−1 כדי להחליט אם כל זוג מסודר הוא:
- פתרון למשוואה
- על הקו
- (3, -1)
- (-1, -4)
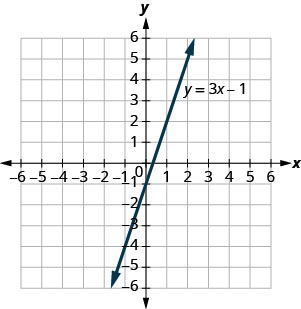
- תשובה
-
- לא, לא
- כן, כן
גרף משוואה לינארית על ידי התוויית נקודות
ישנן מספר שיטות בהן ניתן להשתמש כדי לתאר משוואה לינארית. השיטה בה השתמשנו לתרשים 3x+2y=6 נקראת נקודות התוויית, או שיטת נקודה-התוויית.
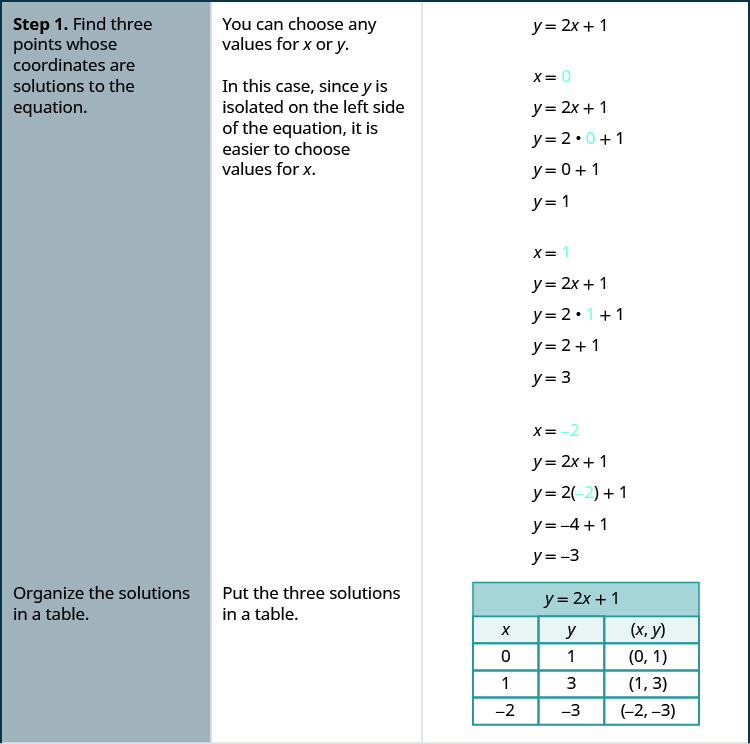
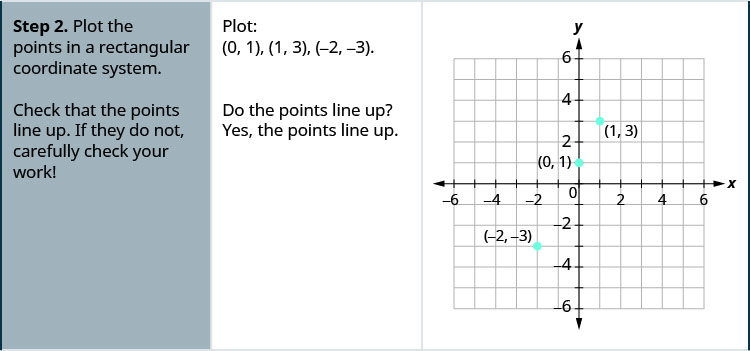
גרף את המשוואה y = 2x+1 על ידי התוויית נקודות.
- תשובה
-
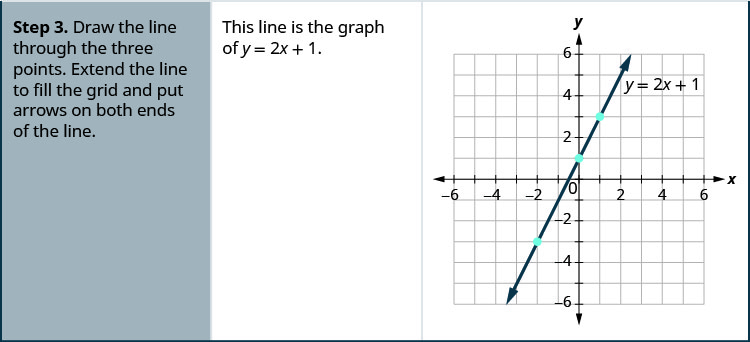
גרף את המשוואה על ידי שרטוט נקודות: y = 2x−3.
- תשובה
-
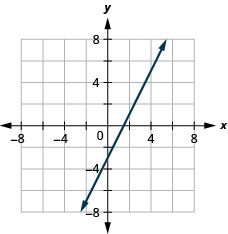
גרף את המשוואה על ידי התוויית נקודות: y = −2x+4.
- תשובה
-
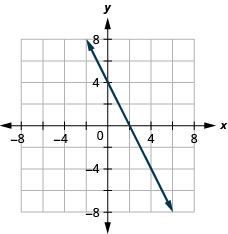
השלבים שיש לנקוט בעת גרף משוואה לינארית על ידי התוויית נקודות מסוכמים להלן.
- מצא שלוש נקודות שהקואורדינטות שלהן הן פתרונות למשוואה. ארגן אותם בטבלה.
- התווה את הנקודות במערכת קואורדינטות מלבנית. בדוק שהנקודות מסתדרות. אם הם לא עושים זאת, בדוק היטב את עבודתך.
- צייר את הקו דרך שלוש הנקודות. הרחב את הקו כדי למלא את הרשת ולשים חצים על שני הקצוות של הקו.
נכון שצריך רק שתי נקודות כדי לקבוע קו, אבל זה הרגל טוב להשתמש בשלוש נקודות. אם אתה מתווה רק שתי נקודות ואחת מהן שגויה, אתה עדיין יכול לשרטט קו אך הוא לא ייצג את הפתרונות למשוואה. זה יהיה הקו הלא נכון.
אם אתה משתמש בשלוש נקודות, ואחת שגויה, הנקודות לא יסתדרו בשורה. זה אומר לך שמשהו לא בסדר ואתה צריך לבדוק את העבודה שלך. התבונן בהבדל בין חלק (א) לחלק (ב) באיור\(\PageIndex{4}\).

בואו נעשה דוגמה נוספת. הפעם, נציג את שני השלבים האחרונים כולם ברשת אחת.
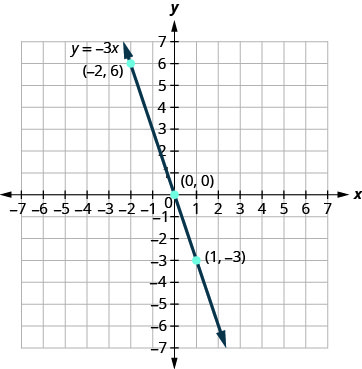
גרף את המשוואה y = −3x.
- תשובה
-
מצא שלוש נקודות שהן פתרונות למשוואה. כאן, שוב, קל יותר לבחור ערכים עבור x האם אתה מבין מדוע?
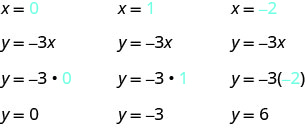
-
אנו מפרטים את הנקודות בטבלה\(\PageIndex{2}\).
טבלה \(\PageIndex{2}\) y = −3איקס x y (איקס, y) 0 0 (0,0) 1 -3 (1, -3) -2 6 (-2,6) התווה את הנקודות, בדוק שהן מתיישרות ושרטט את הקו.
גרף את המשוואה על ידי התוויית נקודות: y = −4x.
- תשובה
-
גרף את המשוואה על ידי התוויית נקודות: y = x.
- תשובה
-

כאשר משוואה כוללת שבר כמקדם של x, אנחנו עדיין יכולים להחליף כל מספרים ב-x. אבל המתמטיקה קלה יותר אם נעשה בחירות 'טובות' לערכים של x. בדרך זו נמנע מתשובות שברים, שקשה לתאר אותן במדויק.
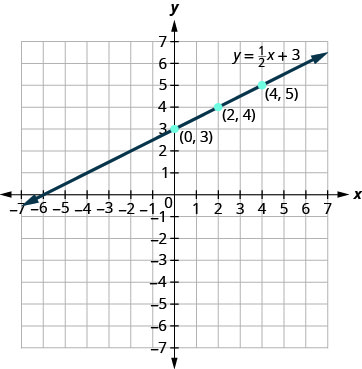
גרף את המשוואה\(y = \frac{1}{2}x + 3\).
- תשובה
-
מצא שלוש נקודות שהן פתרונות למשוואה. מכיוון שלמשוואה זו יש את השבר \(\frac{1}{2}\) כמקדם של x, אנו נבחר ערכים של x בזהירות. נשתמש באפס כבחירה אחת וכפולות של 2 לבחירות האחרות. מדוע מכפילים של 2 הם בחירה טובה לערכים של x?
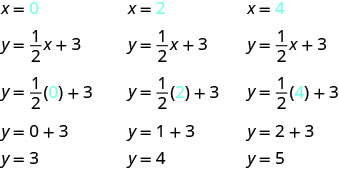
-
הנקודות מוצגות בטבלה\(\PageIndex{3}\).
טבלה \(\PageIndex{3}\) y = 12 איקס+3 x y (איקס, y) 0 3 (0.3) 2 4 (2.4) 4 5 (4.5) -
התווה את הנקודות, בדוק שהן מתיישרות ושרטט את הקו.
גרף את המשוואה\(y = \frac{1}{3}x - 1\).
- תשובה
-
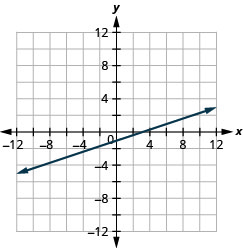
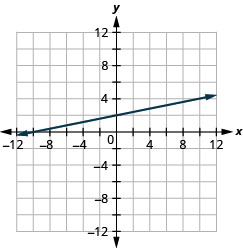
גרף את המשוואה\(y = \frac{1}{4}x + 2\).
- תשובה
-
עד כה, כל המשוואות שציירנו נתנו y במונחים של x, כעת נגרף משוואה עם x ו- y באותו צד. בואו נראה מה קורה במשוואה 2x+y = 3. אם y=0 מהו הערך של x?
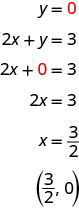
לנקודה זו יש שבר עבור קואורדינטת x, ולמרות שנוכל לתאר את הנקודה הזו, קשה לדייק שברים גרפים. זכור בדוגמה y = 12x+3, בחרנו בקפידה ערכים עבור x כדי לא לשרטט שברים כלל. אם נפתור את המשוואה 2x+y = 3 עבור y, יהיה קל יותר למצוא שלושה פתרונות למשוואה.
\[\begin{aligned} 2 x+y &=3 \\ y &=-2 x+3 \end{aligned}\]
הפתרונות עבור איקס=0, איקס=1, ו איקס=−1 מוצגים בטבלה. \(\PageIndex{4}\) הגרף מוצג באיור\(\PageIndex{5}\).
| 2איקס+y = 3 | ||
| x | y | (איקס, y) |
| 0 | 3 | (0.3) |
| 1 | 1 | (1,1) |
| −1−1 | 5 | (-1,5) |
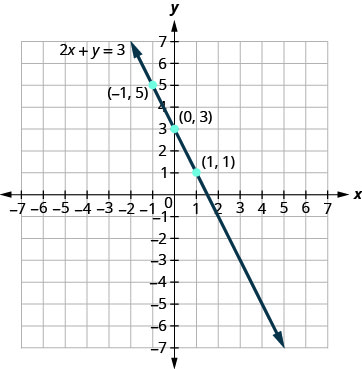
האם אתה יכול לאתר את הנקודה \((\frac{3}{2}, 0)\) שמצאנו על ידי מתן y = 0, על הקו?
גרף את המשוואה 3x+y = −1.
- תשובה
-
\(\begin{array}{lrll} { \text { Find three points that are solutions to the equation. } } & {3 x+y} &{=} &{-1} \\ {\text { First solve the equation for } y.} &{y} &{=} &{-3 x-1} \end{array}\)
אנו נותנים ל- x להיות 0, 1 ו- -1 כדי למצוא 3 נקודות. הזוגות המסודרים מוצגים בטבלה\(\PageIndex{5}\). התווה את הנקודות, בדוק שהן מתיישרות ושרטט את הקו. ראה איור\(\PageIndex{6}\).
טבלה \(\PageIndex{5}\) 3איקס+y = −1 x y (איקס, y) 0 -1 (0, -1) 1 -4 (1, -4) -1 2 (-1,2) -
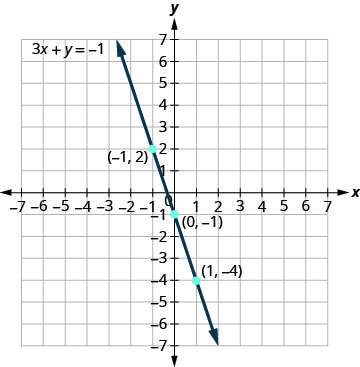
איור \(\PageIndex{6}\)
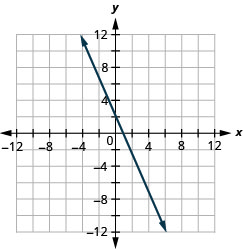
גרף את המשוואה 2x+y = 2.
- תשובה
-
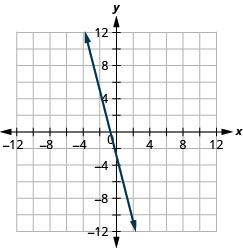
גרף את המשוואה 4x+y = −3.
- תשובה
-
אם אתה יכול לבחור שלוש נקודות כלשהן לתרשים קו, איך תדע אם הגרף שלך תואם לזה שמוצג בתשובות בספר? אם הנקודות בהן הגרפים חוצים את ציר ה - x ו- y זהים, הגרפים תואמים!
המשוואה בתרגיל \(\PageIndex{13}\) נכתבה בצורה סטנדרטית, כאשר גם x וגם y באותו צד. פתרנו את המשוואה הזו עבור y בצעד אחד בלבד. אבל עבור משוואות אחרות בצורה סטנדרטית זה לא כל כך קל לפתור עבור y, אז נשאיר אותם בצורה סטנדרטית. אנחנו עדיין יכולים למצוא נקודה ראשונה להתוות על ידי מתן איקס=0 ופתרון עבור y. אנו יכולים לשרטט נקודה שנייה על ידי מתן y = 0 ולאחר מכן לפתור עבור x. לאחר מכן נתווה נקודה שלישית על ידי שימוש בערך אחר עבור x או y.
גרף את המשוואה\(2x−3y=6\).
- תשובה
-
\(\begin{array}{lrll} \text { Find three points that are solutions to the } & 2 x-3 y &= &6 \\ \text { equation. } & 2 x-3 y&=&6 \\ \text { First let } x=0 . & 2(0)-3 y&=&6 \\ \text { Solve for } y . &-3 y&=&6 \\ & y&=&-2 \\\\ \text { Now let } y=0 . & 2 x-3(0)&=&6 \\ \text { Solve for } x . & 2 x&=&6 \\ & x&=& 3 \\ \\ \text{ We need a third point. Remember, we can}&2(6)-3 y &=&6 \\ \text{ choose any value for x or y. We’ll let x = 6.}&12-3 y &=&6 \\ \text{ Solve fory.}&-3 y &=&-6 \\ &y &=&2\end{array}\)
אנו מפרטים את הזוגות המסודרים בטבלה\(\PageIndex{6}\). התווה את הנקודות, בדוק שהן מתיישרות ושרטט את הקו. ראה איור\(\PageIndex{7}\).
טבלה \(\PageIndex{6}\) 2איקס-3 י=6 x Yt (איקס, y) 0 -2 (0, -2) 3 0 (3.0) 6 2 (6.2) 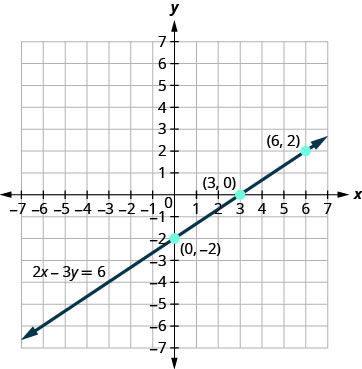
איור \(\PageIndex{7}\)
גרף את המשוואה\(4x+2y=8\).
- תשובה
-
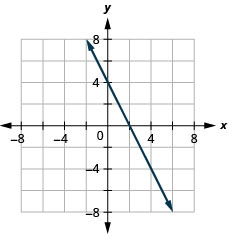
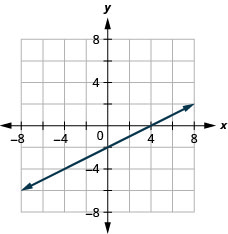
גרף את המשוואה\(2x−4y=8\).
- תשובה
-
תרשים קווים אנכיים ואופקיים
האם נוכל לשרטט משוואה עם משתנה אחד בלבד? רק x ולא y, או סתם y בלי x? כיצד נכין טבלת ערכים כדי לקבל את הנקודות לעלילה?
הבה נבחן את המשוואה איקס=−3. למשוואה זו יש רק משתנה אחד, x. המשוואה אומרת ש- x תמיד שווה ל- -3, ולכן הערך שלה אינו תלוי ב- y. לא משנה מה y הוא, הערך של x הוא תמיד −3.
אז כדי ליצור טבלת ערכים, כתוב -3 עבור כל ערכי x. לאחר מכן בחר ערכים כלשהם עבור y מכיוון ש- x אינו תלוי ב- y, אתה יכול לבחור את כל המספרים שאתה אוהב. אך כדי להתאים לנקודות בגרף הקואורדינטות שלנו, נשתמש ב -1, 2 ו -3 עבור קואורדינטות y. ראה טבלה \(\PageIndex{7}\)
| איקס=−3 | ||
|---|---|---|
| x | y | (איקס, y) |
| -3 | 1 | (-3,1) |
| -3 | 2 | (-3,2) |
| -3 | 3 | (-3,3) |
התווה את הנקודות מהטבלה \(\PageIndex{7}\) וחבר אותן בקו ישר. שימו לב באיור \(\PageIndex{8}\) שיש לנו תרשים קו אנכי.
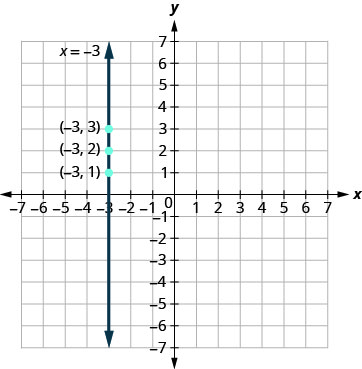
קו אנכי הוא הגרף של משוואה של הצורה x = a.
הקו עובר דרך ציר x ב (a,0).
תרשים המשוואה x = 2.
- תשובה
-
למשוואה יש רק משתנה אחד, x ו- x תמיד שווה ל- 2. אנו יוצרים טבלה \(\PageIndex{8}\) שבה x הוא תמיד 2 ואז מכניסים ערכים כלשהם ל- y הגרף הוא קו אנכי העובר דרך ציר x ב -2. ראה איור\(\PageIndex{9}\).
טבלה \(\PageIndex{8}\) איקס=2 x y (איקס, y) 2 1 (2.1) 2 2 (2.2) 2 3 (2.3) -
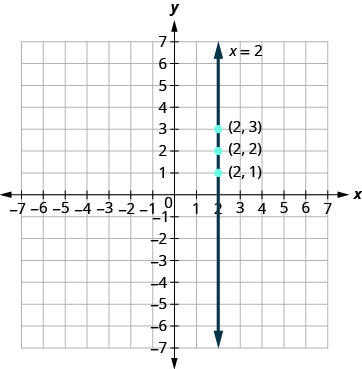
איור \(\PageIndex{9}\)
תרשים המשוואה x = 5.
- תשובה
-
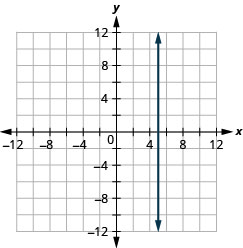
גרף את המשוואה איקס=−2.
- תשובה
-
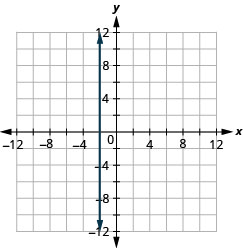
מה אם למשוואה יש y אך אין x? בואו נגרף את המשוואה y = 4. הפעם ערך ה - y הוא קבוע, ולכן במשוואה זו y אינו תלוי ב- xx. מלא 4 עבור כל ה- y בטבלה \(\PageIndex{9}\) ולאחר מכן בחר ערכים עבור x. נשתמש 0, 2, ו 4 עבור x -קואורדינטות.
| y=4 | ||
| x | y | (איקס, y) |
| 0 | 4 | (0,4) |
| 2 | 4 | (2.4) |
| 4 | 4 | (4,4) |
הגרף הוא קו אופקי העובר דרך ציר y ב -4. ראה איור\(\PageIndex{10}\).
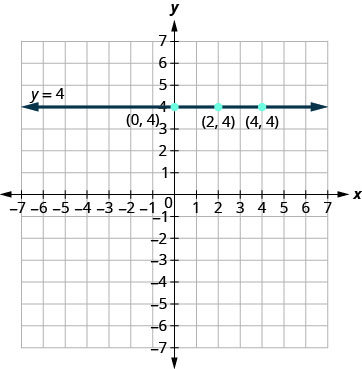
קו אופקי הוא הגרף של משוואה של הצורה y = b.
הקו עובר דרך ציר y ב- (0, b).
גרף את המשוואה y = −1.
- תשובה
-
למשוואה y=−1y=−1 יש רק משתנה אחד, y הערך של y הוא קבוע. לכל הזוגות המסודרים בטבלה \(\PageIndex{10}\) יש את אותה קואורדינטת y. הגרף הוא קו אופקי העובר דרך ציר y ב -1 -1, כפי שמוצג באיור. \(\PageIndex{11}\)
טבלה \(\PageIndex{10}\) y=−1 x y (איקס, y) טה-1 (0, -1) -1 (3, -1) -3 -1 (-3, -1) 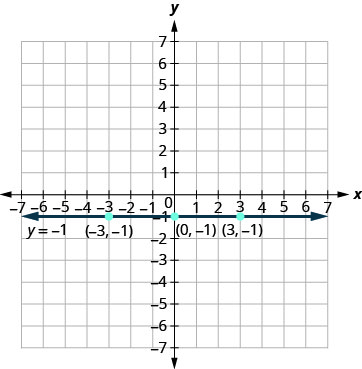
- איור \(\PageIndex{11}\)
גרף את המשוואה y = −4.
- תשובה
-
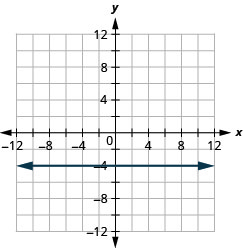
גרף את המשוואה y = 3.
- תשובה
-
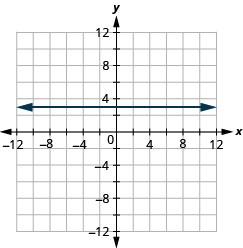
המשוואות לקווים אנכיים ואופקיים נראות דומות מאוד למשוואות כמו y = 4x. מה ההבדל בין המשוואות y = 4x ו- y = 4?
למשוואה y = 4x יש גם x וגם y. הערך של y תלוי בערך של x. קואורדינטת y משתנה לפי הערך של x. למשוואה y=4 יש משתנה אחד בלבד. הערך של y הוא קבוע. קואורדינטת y היא תמיד 4. זה לא תלוי בערך של x ראה טבלה\(\PageIndex{11}\).
| y = 4x | y=4 | |||||
| x | y | (איקס, y) | x | y | (איקס, y) | |
| 0 | 0 | (0,0) | 0 | 4 | (0,4) | |
| 1 | 4 | (1,4) | 1 | 4 | (1,4) | |
| 2 | 8 | (2.8) | 2 | 4 | (2.4) | |
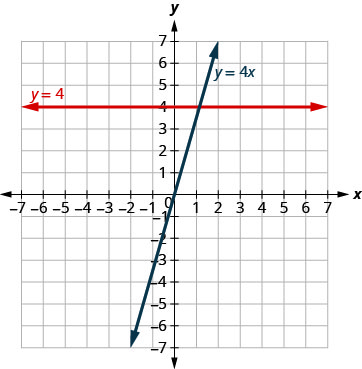
שימו לב, באיור\(\PageIndex{12}\), המשוואה y = 4x נותנת קו משופע, ואילו y = 4 נותן קו אופקי.
תרשים y = −3x ו- y = −3 באותה מערכת קואורדינטות מלבנית.
- תשובה
-
שימו לב שלמשוואה הראשונה יש את המשתנה x, ואילו השנייה לא. ראה טבלה\(\PageIndex{12}\). שני הגרפים מוצגים באיור\(\PageIndex{13}\).
טבלה \(\PageIndex{12}\) y = −3איקס y=−3 x y (איקס, y) x y (איקס, y) (0,0) -3 (0, -3) -3 (1, -3) -3 (1, -3) −6 (2, -6) -3 (2, -3) 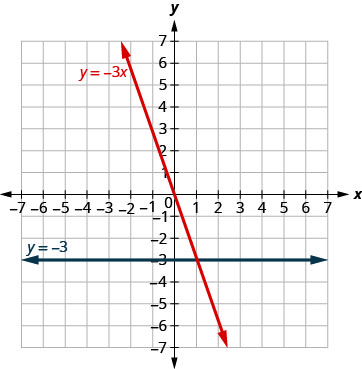
- איור \(\PageIndex{13}\)
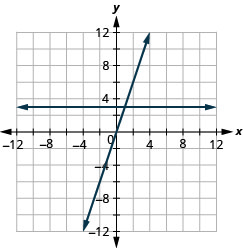
תרשים y = −4x ו- y = −4 באותה מערכת קואורדינטות מלבנית.
- תשובה
-
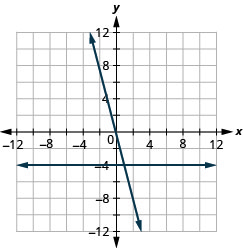
תרשים y = 3 ו- y = 3x באותה מערכת קואורדינטות מלבנית.
- תשובה
-
מושגי מפתח
- גרף משוואה לינארית על ידי התוויית נקודות
- מצא שלוש נקודות שהקואורדינטות שלהן הן פתרונות למשוואה. ארגן אותם בטבלה.
- התווה את הנקודות במערכת קואורדינטות מלבנית. בדוק שהנקודות מסתדרות. אם הם לא, לבדוק היטב את העבודה שלך!
- צייר את הקו דרך שלוש הנקודות. הרחב את הקו כדי למלא את הרשת ולשים חצים על שני הקצוות של הקו.
רשימת מילים
- גרף של משוואה ליניארית
- הגרף של משוואה ליניארית Ax+By=C הוא קו ישר. כל נקודה על הקו היא פתרון של המשוואה. כל פתרון של משוואה זו הוא נקודה בקו זה.
- קו אופקי
- קו אופקי הוא הגרף של משוואה של הצורה y = b הקו עובר דרך ציר y ב- (0, b).
- קו אנכי
- קו אנכי הוא הגרף של משוואה של הצורה איקס=א הקו עובר דרך ציר x ב- (a,0).


