4.1: השתמש במערכת הקואורדינטות המלבנית
- Page ID
- 205721
בסוף פרק זה תוכל:
- נקודות עלילה במערכת קואורדינטות מלבנית
- אמת פתרונות למשוואה בשני משתנים
- השלם טבלת פתרונות למשוואה לינארית
- מצא פתרונות למשוואה לינארית בשני משתנים
לפני שתתחיל, קח את חידון המוכנות הזה.
- להעריך \(x+3\) מתי\(x=−1\).
אם פספסת בעיה זו, סקור את תרגיל 1.5.25. - הערך \(2x−5y\) מתי \(x=3\) ו- y = −2.
אם פספסת בעיה זו, עיין בתרגיל 1.5.28. - פתור עבור y: \(40−4y=20\)
אם פספסת בעיה זו, עיין בתרגיל 2.3.1.
נקודות עלילה במערכת קואורדינטות מלבנית
בדיוק כמו שמפות משתמשות במערכת רשת לזיהוי מיקומים, מערכת רשת משמשת באלגברה כדי להראות קשר בין שני משתנים במערכת קואורדינטות מלבנית. מערכת הקואורדינטות המלבנית נקראת גם מישור xy או 'מישור הקואורדינטות '.
קו המספרים האופקי נקרא ציר ה- x. קו המספרים האנכי נקרא ציר y. ציר x וציר y יחד יוצרים את מערכת הקואורדינטות המלבנית. צירים אלה מחלקים מישור לארבעה אזורים, הנקראים רביעים. הרביעים מזוהים על ידי ספרות רומיות, המתחילות בצד ימין למעלה ומתקדמות נגד כיוון השעון. ראה איור\(\PageIndex{1}\).
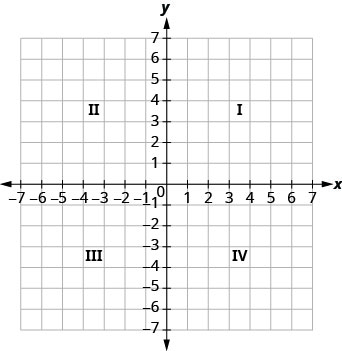
במערכת הקואורדינטות המלבנית, כל נקודה מיוצגת על ידי זוג מסודר. המספר הראשון בצמד המסודר הוא קואורדינטת x של הנקודה, והמספר השני הוא ה- y -קואורדינטה של הנקודה.
זוג מסודר, (x, y) (x, y), נותן את הקואורדינטות של נקודה במערכת קואורדינטות מלבנית.
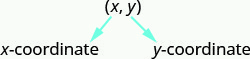
המספר הראשון הוא קואורדינטת x.
המספר השני הוא ה- y -קואורדינטה.
הביטוי 'זוג מסודר' פירושו שהסדר חשוב. מהו הצמד המסודר של הנקודה בה הצירים חוצים? בשלב זה שתי הקואורדינטות הן אפס, כך שהזוג המסודר שלה הוא\((0,0)\). לנקודה \((0,0)\) יש שם מיוחד. זה נקרא המקור.
הנקודה \((0,0)\) נקראת המקור. זו הנקודה בה מצטלבים ציר x וציר y.
אנו משתמשים בקואורדינטות כדי לאתר נקודה במישור xy. בואו נתווה את הנקודה \((1,3)\) כדוגמה. ראשית, אתר 1 על ציר x ושרטט קלות קו אנכי דרך x = 1x=1. לאחר מכן, אתר 3 על ציר y ושרטט קו אופקי דרך y = 3y = 3. כעת, מצא את הנקודה בה שתי השורות הללו נפגשות - זו הנקודה עם קואורדינטות. \((1,3)\)
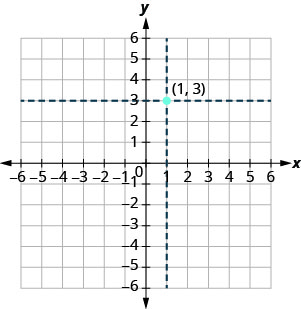
שימו לב שהקו האנכי דרכו \(x=1\) והקו האופקי דרכו \(y=3\) אינם חלק מהגרף. רק השתמשנו בהם כדי לעזור לנו לאתר את הנקודה\((1,3)\).
התווה כל נקודה במערכת הקואורדינטות המלבנית וזהה את הרבע בו נמצאת הנקודה:
- (-5,4)
- (-3, -4)
- (2, -3)
- (-2,3)
- \((3, \frac{5}{2})\)
- תשובה
-
המספר הראשון של צמד הקואורדינטות הוא קואורדינטת x, והמספר השני הוא ה- y -קואורדינטה.
- מאז איקס=−5, הנקודה היא משמאל לציר y. כמו כן, מאז y = 4, הנקודה היא מעל ציר x. הנקודה (-5,4) נמצאת ברביע II.
- מאז איקס=−3, הנקודה היא משמאל לציר y. כמו כן, מאז y = −4, הנקודה נמצאת מתחת לציר x. הנקודה (-3, -4) נמצאת ברבע השלישי.
- מכיוון ש- x = 2, הנקודה היא מימין לציר y. מאז y = −3, הנקודה נמצאת מתחת לציר x. הנקודה (2, -3) נמצאת ברבע lV.
- מאז איקס=−2, הנקודה היא משמאל לציר y. מאז y = 3, הנקודה היא מעל ציר x. הנקודה (-2,3) נמצאת ברביע II.
- מכיוון ש- x = 3, הנקודה היא מימין לציר y. מכיוון \(y = \frac{5}{2}\) שהנקודה היא מעל ציר ה - x. (זה עשוי להיות מועיל לכתוב \(\frac{5}{2}\) כמספר מעורב או עשרוני.) הנקודה \((3, \frac{5}{2})\) היא ברביע I.
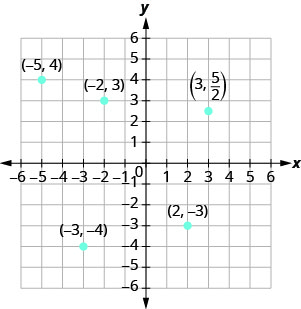
איור \(\PageIndex{4}\)
התווה כל נקודה במערכת קואורדינטות מלבנית וזהה את הרבע בו נמצאת הנקודה:
- (-2,1)
- (-3, -1)
- (4, -4)
- (-4,4)
- \((-4, \frac{3}{2})\)
- תשובה
-
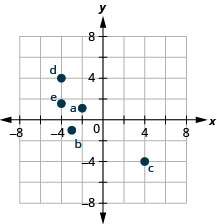
התווה כל נקודה במערכת קואורדינטות מלבנית וזהה את הרבע בו נמצאת הנקודה:
- (-4,1)
- (-2,3)
- (2, -5)
- (-2,5)
- \((-3, \frac{5}{2})\)
- תשובה
-
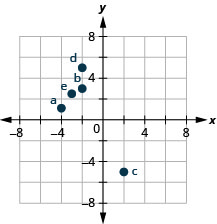
כיצד משפיעים השלטים על מיקום הנקודות? יתכן ששמת לב לדפוסים מסוימים בזמן שרשמת את הנקודות בדוגמה הקודמת.
לגבי הנקודה \(\PageIndex{4}\) באיור ברבע הרביעי, מה אתה מבחין בסימני הקואורדינטות? מה לגבי הסימנים של הקואורדינטות של נקודות ברבע השלישי? הרביע השני? הרביע הראשון?
האם אתה יכול לדעת רק על ידי התבוננות בקואורדינטות באיזה רביע הנקודה (-2,5) נמצאת? באיזה רביע נמצא (2, -5)?
אנו יכולים לסכם דפוסי סימנים של הרביעים בדרך זו.
\[\begin{array}{ccc}{\text { Quadrant I }} & {\text { Quadrant II }} & {\text { Quadrant III }} & {\text { Quadrant IV }} \\ {(x, y)} & {(x, y)} & {(x, y)} & {(x, y)} \\ {(+,+)} & {(-,+)} & {(-,-)} & {(+,-)}\end{array}\]
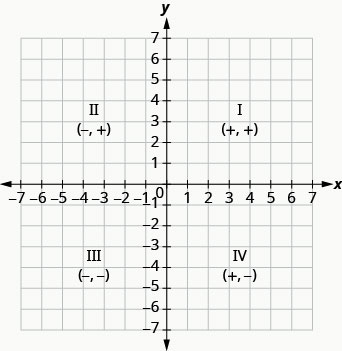
מה אם קואורדינטה אחת היא אפס כפי שמוצג באיור\(\PageIndex{6}\)? היכן נמצאת הנקודה (0,4)? היכן ממוקמת הנקודה (-2,0)?
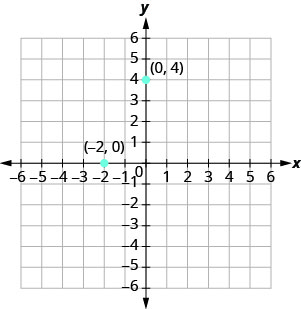
הנקודה (0,4) נמצאת על ציר y והנקודה (-2,0) נמצאת על ציר x.
נקודות עם קואורדינטת y שווה ל- 0 נמצאות על ציר x, ויש להן קואורדינטות (a,0).
נקודות עם קואורדינטת x שווה ל- 0 נמצאות על ציר y, ויש להן קואורדינטות (0, b).
התווה כל נקודה:
- (0.5)
- (4.0)
- (−3,0)
- (0,0)
- (0, -1)
- תשובה
-
- מכיוון ש- x = 0, הנקודה שהקואורדינטות שלה הן (0,5) נמצאת על ציר y.
- מאז y = 0, הנקודה שהקואורדינטות שלה (4,0) נמצאת על ציר x.
- מאז y = 0, הנקודה שהקואורדינטות שלה (−3,0) נמצאת על ציר x.
- מכיוון ש- x = 0 ו- y = 0, הנקודה שהקואורדינטות שלה הן (0,0) היא המקור.
- מאז איקס=0, הנקודה שהקואורדינטות שלה הן (0, −1) נמצאת על ציר y.
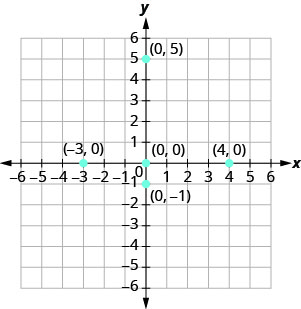
איור \(\PageIndex{7}\)
התווה כל נקודה:
- (4.0)
- (−2,0)
- (0,0)
- (0,2)
- (0, -3).
- תשובה
-
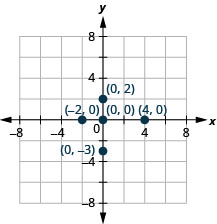
התווה כל נקודה:
- (−5,0)
- (3.0)
- (0,0)
- (0, -1)
- (0,4).
- תשובה
-
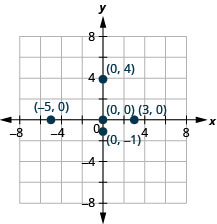
באלגברה, היכולת לזהות את הקואורדינטות של נקודה המוצגת בגרף חשובה לא פחות מהיכולת לשרטט נקודות. כדי לזהות את קואורדינטת ה- x של נקודה בגרף, קרא את המספר על ציר ה - x ישירות מעל או מתחת לנקודה. כדי לזהות את ה- y -קואורדינטה של נקודה, קרא את המספר על ציר y ישירות משמאל או מימין לנקודה. זכור, כשאתה כותב את הזוג שהוזמן השתמש בסדר הנכון, (x, y).
תן שם לזוג המסודר של כל נקודה המוצגת במערכת הקואורדינטות המלבנית.
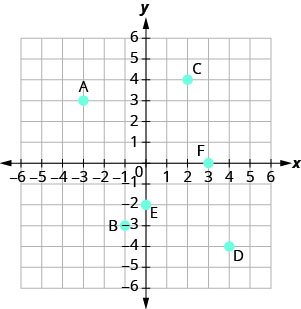
- תשובה
-
נקודה A היא מעל -3 על ציר x, כך שקואורדינטת x של הנקודה היא -3.
הנקודה היא משמאל ל -3 על ציר y, כך שקואורדינטת y של הנקודה היא 3. - הקואורדינטות של הנקודה הן (-3,3).
-
נקודה B נמצאת מתחת ל -1 על ציר x, כך שקואורדינטת x של הנקודה היא -1.
הנקודה היא משמאל ל -3 על ציר y, כך שקואורדינטת y של הנקודה היא -3. - הקואורדינטות של הנקודה הן (-1, -3).
נקודה C היא מעל 2 בציר x, כך שקואורדינטת ה - x של הנקודה היא 2.
הנקודה היא מימין ל -4 על ציר y, כך שקואורדינטת y של הנקודה היא 4. - הקואורדינטות של הנקודה הן (2,4).
- נקודה D נמצאת מתחת ל -4 בציר x, כך שקואורדינטת ה - x של הנקודה היא 4.
- הנקודה היא מימין ל -4 על ציר y, כך שקואורדינטת y של הנקודה היא -4.
- הקואורדינטות של הנקודה הן (4, -4).
-
נקודה E נמצאת על ציר y ב- y = −2. הקואורדינטות של נקודה E הן (0, -2).
נקודה F נמצאת על ציר x ב- x = 3. הקואורדינטות של נקודה F הן (3,0).
תן שם לזוג המסודר של כל נקודה המוצגת במערכת הקואורדינטות המלבנית.
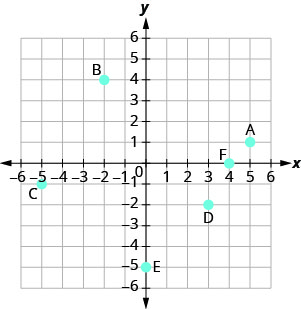
- תשובה
-
א: (5,1) ב: (-2,4) ג: (-5, -1) ד: (3, -2) ה: (0, -5) ו: (4,0)
תן שם לזוג המסודר של כל נקודה המוצגת במערכת הקואורדינטות המלבנית.
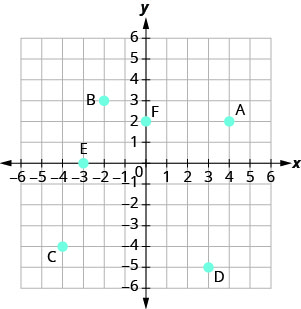
- תשובה
-
א: (4,2) ב: (-2,3) ג: (-4, -4) ד: (3, -5) ה: (−3,0) ו: (0,2)
אמת פתרונות למשוואה בשני משתנים
עד כה, כל המשוואות שפתרת היו משוואות עם משתנה אחד בלבד. כמעט בכל מקרה, כשפתרת את המשוואה קיבלת פתרון אחד בדיוק. תהליך פתרון המשוואה הסתיים בהצהרה כמו x = 4. (לאחר מכן, בדקת את הפתרון על ידי החלפה חזרה למשוואה.)
הנה דוגמה למשוואה במשתנה אחד, והפתרון האחד שלה.
\[\begin{aligned} 3 x+5 &=17 \\ 3 x &=12 \\ x &=4 \end{aligned}\]
אבל למשוואות יכולות להיות יותר ממשתנה אחד. משוואות עם שני משתנים עשויות להיות בצורה Ax+By=C משוואות של צורה זו נקראות משוואות לינאריות בשני משתנים.
משוואה של הצורה Ax+By=C, כאשר A ו- B אינם שניהם אפס, נקראת משוואה לינארית בשני משתנים.
שימו לב לשורת המילה ליניארית. להלן דוגמה למשוואה לינארית בשני משתנים, x ו- y.
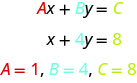
המשוואה y = −3x+5 היא גם משוואה לינארית. אבל זה לא נראה בצורה Ax+By=C. אנו יכולים להשתמש במאפיין התוספת של שוויון ולשכתב אותו בצורה Ax+By=C.
\(\begin{array}{llll} {} &{y} &{=} &{-3x + 5} \\ {\text{Add to both sides.}} &{y + 3x } &{=} &{-3x + 5 + 3x} \\{\text{Simplify.}} &{y + 3x} &{=} &{5} \\{\text{Use the Commutative Property to put it in}} &{3x + y} &{=} &{5} \\{Ax+By = C\text{ form.}} &{} &{} &{} \end{array}\)
על ידי שכתוב y = −3x+5 כ- 3x+y = 5, אנו יכולים לראות בקלות שמדובר במשוואה לינארית בשני משתנים מכיוון שהיא מהצורה Ax+By=C כאשר משוואה היא בצורה Ax+By=C, אנו אומרים שהיא בצורה סטנדרטית.
משוואה לינארית היא בצורה סטנדרטית כאשר היא כתובה Ax+By=C.
רוב האנשים מעדיפים ש- A, B ו- C יהיו מספרים שלמים \(A\geq 0\) וכאשר כותבים משוואה לינארית בצורה סטנדרטית, אם כי זה לא הכרחי בהחלט.
למשוואות לינאריות יש אינסוף פתרונות רבים. לכל מספר שמוחלף ב- x יש ערך y מתאים. צמד ערכים זה הוא פיתרון למשוואה הליניארית ומיוצג על ידי הזוג המסודר (x, y). כאשר אנו מחליפים ערכים אלה של x ו- y במשוואה, התוצאה היא אמירה אמיתית, מכיוון שהערך בצד שמאל שווה לערך בצד ימין.
זוג מסודר (x, y) הוא פתרון של המשוואה הליניארית Ax+By=C, אם המשוואה היא אמירה אמיתית כאשר ערכי x - ו- y של הזוג המסודר מוחלפים במשוואה.
קבע אילו זוגות מסודרים הם פתרונות למשוואה איקס+4y = 8.
(א) (0,2)
(ב) (2, -4)
(ג) (-4,3)
- תשובה
-
החלף את ערכי x - ו- y מכל זוג מסודר למשוואה וקבע אם התוצאה היא אמירה אמיתית.
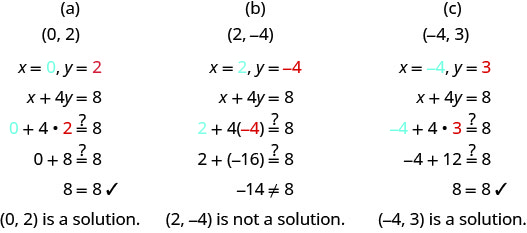
אילו מהזוגות המסודרים הבאים הם פתרונות ל- 2x+3y = 6?
- (3.0)
- (2.0)
- (6, -2)
- תשובה
-
1, 3
אילו מהזוגות המסודרים הבאים הם פתרונות למשוואה 4x−y = 8?
- (0.8)
- (2.0)
- (1, -4)
- תשובה
-
2, 3
אילו מהזוגות המסודרים הבאים הם פתרונות למשוואה y = 5איקס−1?
(א) (0, -1)
(ב) (1,4)
(ג) (-2, −7)
- תשובה
-
החלף את ערכי x - ו- y מכל זוג מסודר למשוואה וקבע אם התוצאה היא אמירה אמיתית.
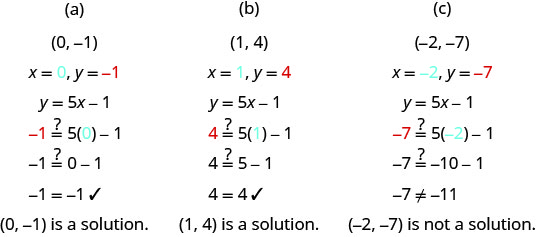
אילו מהזוגות המסודרים הבאים הם פתרונות למשוואה y = 4x−3?
- (0,3)
- (1,1)
- (-1, -1)
- תשובה
-
2
אילו מהזוגות המסודרים הבאים הם פתרונות למשוואה y = −2x+6?
- (0,6)
- (1,4)
- (-2, -2)
- תשובה
-
1, 2
השלם טבלת פתרונות למשוואה לינארית בשני משתנים
בדוגמאות לעיל החלפנו את ערכי x - ו- y של זוג מסודר נתון כדי לקבוע אם זה פיתרון למשוואה לינארית או לא. אבל איך מוצאים את הזוגות שהוזמנו אם הם לא ניתנים? זה קל יותר ממה שאתה חושב - אתה יכול פשוט לבחור ערך עבור xx ואז לפתור את המשוואה עבור yy. לחלופין, בחר ערך עבור yy ואז פתר עבור xx.
נתחיל בבחינת הפתרונות למשוואה y = 5x−1 שמצאנו בתרגיל. \(\PageIndex{13}\) אנו יכולים לסכם מידע זה בטבלת פתרונות, כפי שמוצג בטבלה\(\PageIndex{1}\).
| y=5איקס−1 | ||
| x | y | (איקס, y) |
| 0 | -1 | (0, -1) |
| 1 | 4 | (1,4) |
כדי למצוא פיתרון שלישי, אנו נותנים ל- x = 2 ונפתור עבור y.
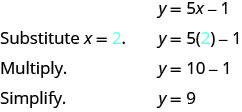
הזוג המסודר (2,9) הוא פתרון ל- y = 5x−1. נוסיף אותו לטבלה\(\PageIndex{2}\).
| y=5איקס−1 | ||
| x | y | (איקס, y) |
| 0 | -1 | (0, -1) |
| 1 | 4 | (1,4) |
| 2 | 9 | (2.9) |
אנו יכולים למצוא פתרונות נוספים למשוואה על ידי החלפת ערך כלשהו של x או כל ערך של y ופתרון המשוואה המתקבלת כדי לקבל זוג מסודר אחר שהוא פיתרון. יש אינסוף פתרונות למשוואה זו.
השלם את הטבלה כדי למצוא שלושה פתרונות למשוואה y = 4x−2.
| y = 4איקס-2 | ||
| x | y | (איקס, y) |
| 0 | ||
| -1 | ||
| 2 | ||
- תשובה
-
תחליף איקס=0, איקס=−1, ו איקס=2 לתוך y = 4איקס−2.
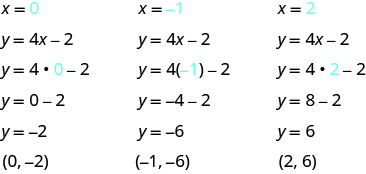
-
התוצאות מסוכמות בטבלה\(\PageIndex{4}\).
y = 4איקס-2 x y (איקס, y) 0 -2 (0, -2) -1 −6 (-1, -6) 2 6 (2.6) טבלה \(\PageIndex{4}\)
השלם את הטבלה כדי למצוא שלושה פתרונות למשוואה זו: y = 3x−1.
| y=3איקס−1 | ||
| x | y | (איקס, y) |
| 0 | ||
| -1 | ||
| 2 | ||
- תשובה
-
y=3איקס−1 x y (איקס, y) 0 -1 (0, -1) -1 -4 (-1, -4) 2 5 (2, 5) טבלה \(\PageIndex{6}\)
השלם את הטבלה כדי למצוא שלושה פתרונות למשוואה זו: y = 6x+1.
| y = 6x+1 | ||
| x | y | (איקס, y) |
| -2 | ||
- תשובה
-
y = 6x+1 x y (איקס, y) 0 1 (0.1) 1 7 (1,7) -2 −11 (-2, -11) טבלה \(\PageIndex{8}\)
השלם \(\PageIndex{9}\) את הטבלה כדי למצוא שלושה פתרונות למשוואה 5x−4y = 20.
| 5איקס−4y = 20 | ||
| x | y | (איקס, y) |
| 0 | ||
| 5 | ||
- תשובה
-
החלף את הערך הנתון במשוואה 5x−4y = 20 ופתור עבור המשתנה האחר. לאחר מכן, מלא את הערכים בטבלה.
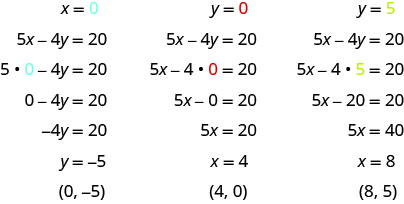
-
התוצאות מסוכמות בטבלה\(\PageIndex{10}\).
5איקס−4y = 20 x y (איקס, y) 0 -5 (0, -5) 4 0 (4.0) 8 5 (8.5) טבלה \(\PageIndex{10}\)
השלם את הטבלה כדי למצוא שלושה פתרונות למשוואה זו: 2x−5y = 20.
| 2איקס−5 י=20 | ||
| x | y | (איקס, y) |
| -5 | ||
- תשובה
-
2איקס−5 י=20 x y (איקס, y) 0 -4 (0, -4) 10 0 (10.0) -5 −6 (-5, -6) טבלה \(\PageIndex{12}\)
השלם את הטבלה כדי למצוא שלושה פתרונות למשוואה זו: 3x−4y = 12.
| 3איקס−4y = 12 | ||
| x | y | (איקס, y) |
| -4 | ||
- תשובה
-
3איקס−4y = 12 x y (איקס, y) 0 -3 (0, -3) 4 0 (4.0) -4 −6 (-4, -6) טבלה \(\PageIndex{14}\)
מצא פתרונות למשוואה לינארית
כדי למצוא פתרון למשוואה ליניארית, אתה באמת יכול לבחור כל מספר שאתה רוצה להחליף במשוואה עבור x או y. אבל מכיוון שתצטרך להשתמש במספר הזה כדי לפתור עבור המשתנה השני, זה רעיון טוב לבחור מספר שקל לעבוד איתו.
כאשר המשוואה היא בצורת y, כאשר ה- y בפני עצמו בצד אחד של המשוואה, בדרך כלל קל יותר לבחור ערכים של x ואז לפתור עבור y.
מצא שלושה פתרונות למשוואה y = −3x+2.
- תשובה
-
אנחנו יכולים להחליף כל ערך שאנחנו רוצים עבור x או כל ערך עבור y. מכיוון שהמשוואה היא בצורת y, זה יהיה קל יותר להחליף בערכים של x. בואו לבחור איקס=0, איקס=1, ו איקס=−1.



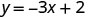
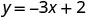
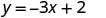
החלף את הערך במשוואה. 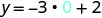
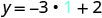
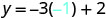
לפשט. 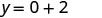
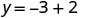
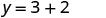
לפשט. 
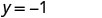

כתוב את הזוג שהוזמן. (0, 2) (1, -1) (-1, 5) בדוק. y = −3איקס+2 y = −3איקס+2 y = −3איקס+2 \(2 \stackrel{?}{=} -3 \cdot 0 + 2\) \(-1 \stackrel{?}{=} -3 \cdot 1 + 2\) \(5 \stackrel{?}{=} -3 (-1) + 2\) \(2 \stackrel{?}{=} 0 + 2\) \(-1 \stackrel{?}{=} -3 + 2\) \(5 \stackrel{?}{=} -3 + 2\) \(2 = 2\checkmark\) \(-1 = -1\checkmark\) \(5 = 5\checkmark\) - טבלה \(\PageIndex{15}\)
-
אז, (0,2), (1, -1) ו- (-1,5) הם כולם פתרונות ל- y=−3x+2. אנו מראים אותם בטבלה\(\PageIndex{16}\).
y = -3איקס+2 x y (איקס, y) 0 2 (0,2) 1 -1 (1, -1) -1 5 (-1,5) טבלה \(\PageIndex{16}\)
מצא שלושה פתרונות למשוואה זו: y = −2x+3.
- תשובה
-
התשובות ישתנו.
מצא שלושה פתרונות למשוואה זו: y = −4x+1.
- תשובה
-
התשובות ישתנו.
ראינו כיצד השימוש באפס כערך אחד של x הופך את מציאת הערך של y לקלה. כאשר משוואה היא בצורה סטנדרטית, כאשר גם x וגם y באותו צד של המשוואה, בדרך כלל קל יותר למצוא פתרון אחד כאשר איקס=0 למצוא פתרון שני כאשר y=0, ואז למצוא פתרון שלישי.
מצא שלושה פתרונות למשוואה 3x+2y = 6.
- תשובה
-
אנחנו יכולים להחליף כל ערך שאנחנו רוצים עבור x או כל ערך עבור y. מכיוון שהמשוואה היא בצורה סטנדרטית, בואו לבחור תחילה x=0, ואז y=0, ולאחר מכן למצוא נקודה שלישית.

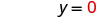

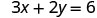
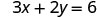
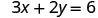
החלף את הערך במשוואה. 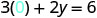
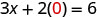
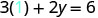
לפשט. 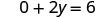
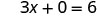
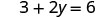
לפתור. 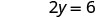
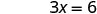
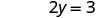
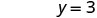

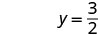
כתוב את הזוג שהוזמן. (0, 3) (2, 0) \((1,\frac{3}{2})\) בדוק. 3x+2y=6 3x+2y=6 3x+2y=6 \(3\cdot 0 + 2\cdot 3 \stackrel{?}{=} 6\) \(3\cdot 2 + 2\cdot 0 \stackrel{?}{=} 6\) \(3\cdot 1 + 2\cdot \frac{3}{2} \stackrel{?}{=} 6\) \(0 + 6 \stackrel{?}{=} 6\) \(6 + 0 \stackrel{?}{=} 6\) \(3 + 3 \stackrel{?}{=} 6\) \(6 = 6\checkmark\) \(6 = 6\checkmark\) \(6 = 6\checkmark\) טבלה \(\PageIndex{17}\) אז (0,3), (2,0), וכולם פתרונות למשוואה \((1,\frac{3}{2})\) 3x+2y = 6. אנו יכולים לרשום את שלושת הפתרונות הללו בטבלה\(\PageIndex{18}\).
3x+2y = 63 איקס+2y = 6 x y (איקס, y) 0 3 (0,3) 2 0 (2.0) 1 \(\frac{3}{2}\) \((1, \frac{3}{2})\) טבלה \(\PageIndex{18}\)
מצא שלושה פתרונות למשוואה 2x+3y = 6.
- תשובה
-
התשובות ישתנו.
מצא שלושה פתרונות למשוואה 4x+2y = 8.
- תשובה
-
התשובות ישתנו.
מושגי מפתח
- דפוסי סימנים של הרביעים
\(\begin{array}{ll}{\text { Quadrant I }} & {\text { Quadrant II }} & {\text { Quadrant III }} & {\text { Quadrant IV }} \\ {(x, y)} & {(x, y)} & {(x, y)} & {(x, y)} \\ {(+,+)} & {(-,+)} & {(-,-)} & {(+,-)}\end{array}\) - נקודות על הצירים
- על ציר x, y = 0. נקודות עם קואורדינטת y שווה ל- 0 נמצאות על ציר x, ויש להן קואורדינטות (a,0).
- על ציר y, איקס=0. נקודות עם קואורדינטת x שווה ל- 0 נמצאות על ציר y, ויש להן קואורדינטות (0, b).
- פתרון משוואה לינארית
- זוג מסודר (x, y) הוא פתרון של המשוואה הליניארית Ax+By=C, אם המשוואה היא אמירה אמיתית כאשר ערכי x - ו- y - של הזוג המסודר מוחלפים במשוואה.
רשימת מילים
- משוואה לינארית
- משוואה לינארית היא מהצורה Ax+By=C, כאשר A ו- B אינם שניהם אפס, נקראת משוואה לינארית בשני משתנים.
- זוג שהוזמן
- זוג מסודר (x, y) נותן את הקואורדינטות של נקודה במערכת קואורדינטות מלבנית.
- מוצא
- הנקודה (0,0) (0,0) נקראת המקור. זו הנקודה בה מצטלבים ציר x וציר y.
- רביע
- ציר ה- x וציר y מחלקים מישור לארבעה אזורים, הנקראים רביעים.
- מערכת קואורדינטות מלבנית
- מערכת רשת משמשת באלגברה כדי להראות קשר בין שני משתנים; נקרא גם ה- xy -plane או 'מישור הקואורדינטות '.
- x -קואורדינטה
- המספר הראשון בזוג מסודר (x, y).
- y -קואורדינטה
- המספר השני בזוג מסודר (x, y).


