פרק 4 תרגילי סקירה
- Page ID
- 205759
פרק 4 תרגילי סקירה
מערכת קואורדינטות מלבנית
נקודות עלילה במערכת קואורדינטות מלבנית
בתרגילים הבאים, התווה כל נקודה במערכת קואורדינטות מלבנית.
- (-1, -5)
- (-3,4)
- (2, -3)
- \(\left(1, \frac{5}{2}\right)\)
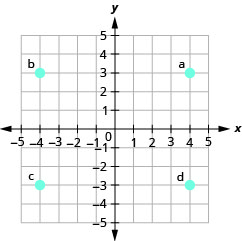
- (4.3)
- (-4,3)
- (-4, -3)
- (4, -3)
- תשובה
-
- (−2,0)
- (0, -4)
- (0.5)
- (3.0)
- \(\left(2, \frac{3}{2}\right)\)
- \(\left(3, \frac{4}{3}\right)\)
- \(\left(\frac{1}{3},-4\right)\)
- \(\left(\frac{1}{2},-5\right)\)
- תשובה
-
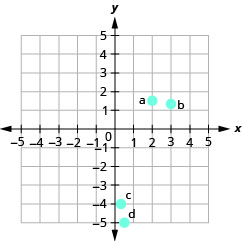
זיהוי נקודות בגרף
בתרגילים הבאים, ציין את הצמד המסודר של כל נקודה המוצגת במערכת הקואורדינטות המלבנית.
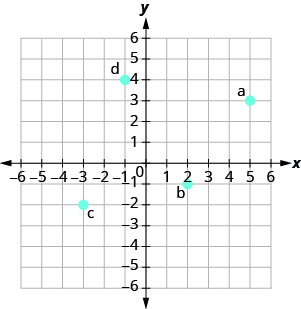
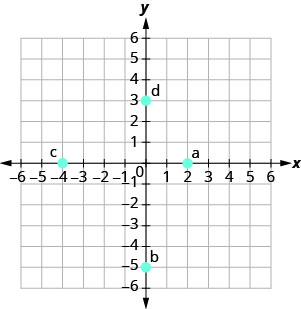
- תשובה
-
א. (2,0)
ב (0, -5)
ג (-4.0)
ד (0,3)
אמת פתרונות למשוואה בשני משתנים
בתרגילים הבאים, אילו זוגות מסודרים הם פתרונות למשוואות הנתונות?
\(5x+y=10\)
- (5.1)
- (2.0)
- (4, -10)
\(y=6x−2\)
- (1,4)
- \(\left(\frac{1}{3}, 0\right)\)
- (6, -2)
- תשובה
-
1, 2
השלם טבלת פתרונות למשוואה לינארית בשני משתנים
בתרגילים הבאים, השלם את הטבלה כדי למצוא פתרונות לכל משוואה לינארית.
\(y=4 x-1\)
| x | y | (איקס, y) |
| 0 | ||
| 1 | ||
| -2 |
\(y=-\frac{1}{2} x+3\)
| x | y | (איקס, y) |
| 0 | ||
| 4 | ||
| -2 |
- תשובה
-
x y (איקס, y) 0 3 (0,3) 4 1 (4, 1) -2 4 (-2,4)
\(x+2 y=5\)
| x | y | (איקס, y) |
| 0 | ||
| 1 | ||
| -1 |
\(3x+2y=6\)
| x | y | (איקס, y) |
| 0 | ||
| 0 | ||
| -2 |
- תשובה
-
x y (איקס, y) 0 -3 (0, -3) 2 0 (2.0) -2 −6 (-2, -6)
מצא פתרונות למשוואה לינארית בשני משתנים
בתרגילים הבאים, מצא שלושה פתרונות לכל משוואה לינארית.
\(x+y=3\)
\(x+y=-4\)
- תשובה
-
התשובות ישתנו.
\(y=3 x+1\)
\(y=-x-1\)
- תשובה
-
התשובות ישתנו.
גרף משוואות לינאריות
הכירו את הקשר בין הפתרונות של משוואה לגרף שלה
בתרגילים הבאים, עבור כל זוג שהוזמן, החליטו:
- האם הזוג המסודר הוא פתרון למשוואה?
- האם הנקודה על הקו?
\(y=−x+4\)
(0,4) (−1,3)
(2,2) (-2,6)
\(y=\frac{2}{3} x-1\)
\((0,-1) (3,1)\)
\((-3,-3) (6,4)\)
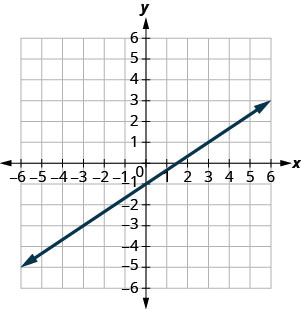
- תשובה
-
- כן; כן
- כן; לא
גרף משוואה לינארית על ידי התוויית נקודות
בתרגילים הבאים, גרף על ידי התוויית נקודות.
\(y=4x-3\)
\(y=-3x\)
- תשובה
-
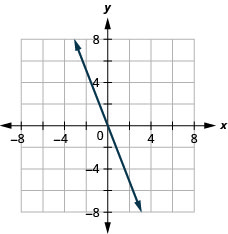
\(y=\frac{1}{2} x+3\)
\(x-y=6\)
- תשובה
-
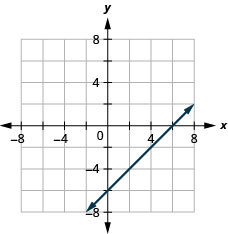
\(2x+y=7\)
\(3x-2y=6\)
- תשובה
-
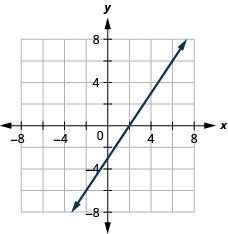
תרשים קווים אנכיים ואופקיים
בתרגילים הבאים, גרף כל משוואה.
\(y=-2\)
\(x=3\)
- תשובה
-
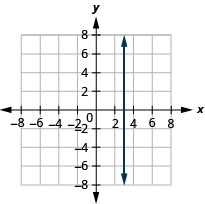
בתרגילים הבאים, גרף כל זוג משוואות באותה מערכת קואורדינטות מלבנית.
\(y=-2 x\)ו \(y=-2\)
\(y=\frac{4}{3} x\)ו \(y=\frac{4}{3}\)
- תשובה
-
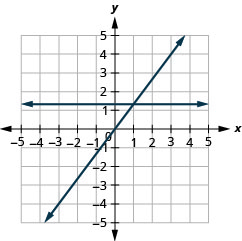
גרפים עם יירוטים
זהה את \(x\) - ו \(y\) -יירוט על גרף
בתרגילים הבאים, מצא את \(x\) - ו- \(y\) -מיירט.
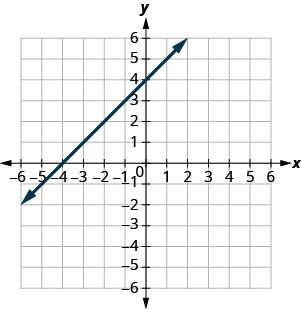
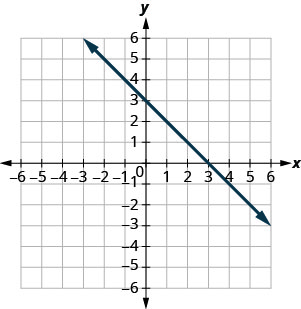
- תשובה
-
\((3,0)\)ו \((0,3)\)
מצא את \(x\) - ו \(y\) -יירוט ממשוואה של קו
בתרגילים הבאים, מצא את היירוט של כל משוואה.
\(x+y=5\)
\(x-y=-1\)
- תשובה
-
\((-1,0),(0,1)\)
\(x+2y=6\)
\(2x+3y=12\)
- תשובה
-
\((6,0),(0,4)\)
\(y=\frac{3}{4} x-12\)
\(y=3x\)
- תשובה
-
\((0,0)\)
גרף קו באמצעות היירוטים
בתרגילים הבאים, גרף באמצעות היירוט.
\(-x+3y=3\)
\(x+y=-2\)
- תשובה
-
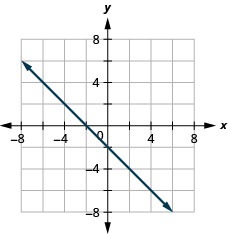
\(x-y=4\)
\(2x-y=5\)
- תשובה
-
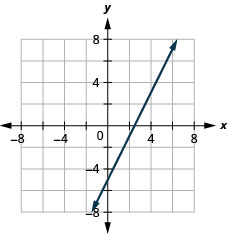
\(2x-4y=8\)
\(y=2x\)
- תשובה
-
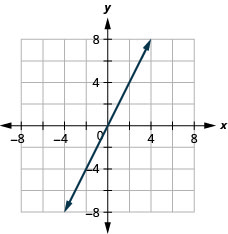
שיפוע של קו
השתמש בגיאובורדים כדי לדגמן שיפוע
בתרגילים הבאים, מצא את המדרון המעוצב על כל לוח גיאוגרפי.
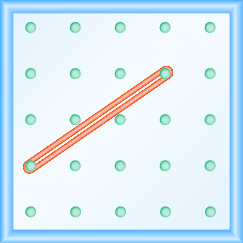
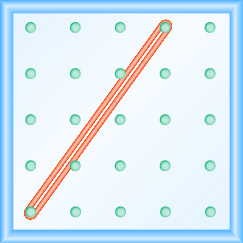
- תשובה
-
\(\frac{4}{3}\)
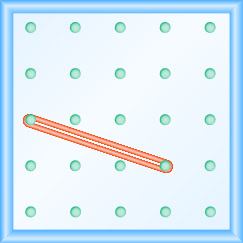
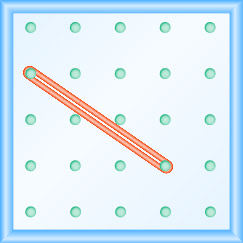
- תשובה
-
\(-\frac{2}{3}\)
\(\frac{1}{3}\)
\(\frac{3}{2}\)
- תשובה
-
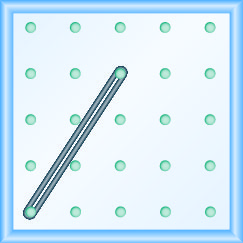
\(-\frac{2}{3}\)
\(-\frac{1}{2}\)
- תשובה
-
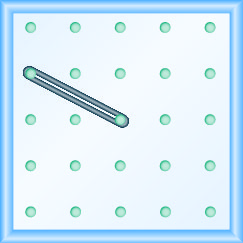
השתמש \(m=\frac{\text { rise }}{\text { run }}\) כדי למצוא את שיפוע הקו מהגרף שלו
בתרגילים הבאים, מצא את השיפוע של כל שורה המוצגת.
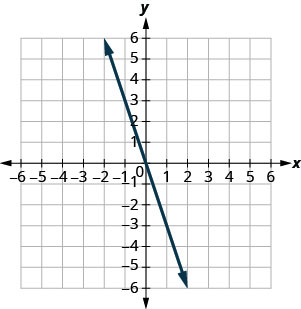
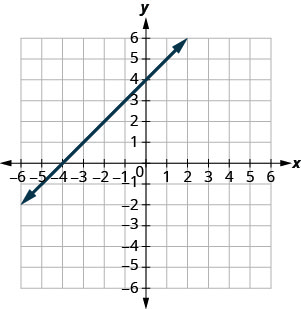
- תשובה
-
1
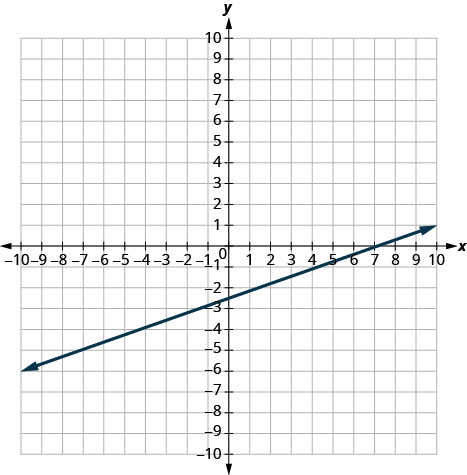
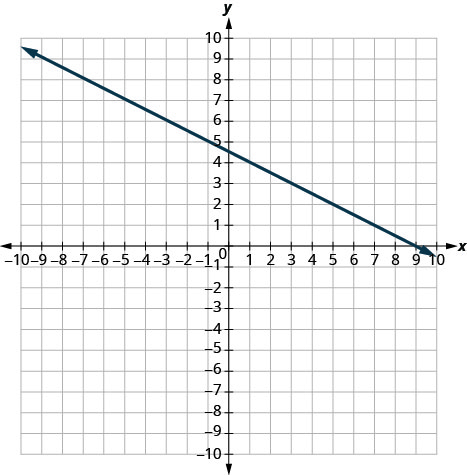
- תשובה
-
\(-\frac{1}{2}\)
מצא את שיפוע הקווים האופקיים והאנכיים
בתרגילים הבאים, מצא את השיפוע של כל שורה.
\(y=2\)
\(x=5\)
- תשובה
-
לא מוגדר
\(x=-3\)
\(y=-1\)
- תשובה
-
0
השתמש בנוסחת השיפוע כדי למצוא את שיפוע הקו בין שתי נקודות
בתרגילים הבאים, השתמש בנוסחת השיפוע כדי למצוא את שיפוע הקו בין כל זוג נקודות.
\((-1,-1),(0,5)\)
\((3,5),(4,-1)\)
- תשובה
-
−6
\((-5,-2),(3,2)\)
\((2,1),(4,6)\)
- תשובה
-
\(\frac{5}{2}\)
גרף קו בהינתן נקודה והשיפוע
בתרגילים הבאים, גרף כל שורה עם הנקודה והשיפוע הנתונים.
\((2,-2) ; \quad m=\frac{5}{2}\)
\((-3,4) ; \quad m=-\frac{1}{3}\)
- תשובה
-
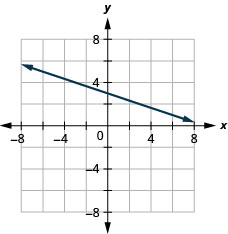
\(x\)-ליירט \(-4 ; \quad m=3\)
\(y\)-ליירט \(1 ; \quad m=-\frac{3}{4}\)
- תשובה
-
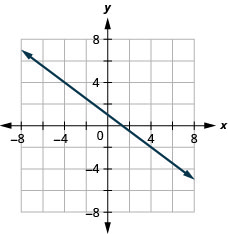
לפתור יישומי שיפוע
בתרגילים הבאים, פתור יישומי שיפוע אלה.
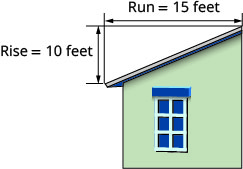
לגג בתמונה למטה יש עלייה של \(10\) רגליים וריצה של \(15\) רגליים. מהו המדרון שלה?
דרך הררית מתנשאת \(50\) רגליים \(500\) לריצה של רגל. מהו המדרון שלה?
- תשובה
-
\(\frac{1}{10}\)
צורת יירוט של משוואת קו
הכירו את הקשר בין הגרף לצורת השיפוע — יירוט של משוואת קו
בתרגילים הבאים, השתמש בתרשים כדי למצוא את השיפוע ו- y -יירוט של כל שורה. השווה את הערכים למשוואה\(y=mx+b\).
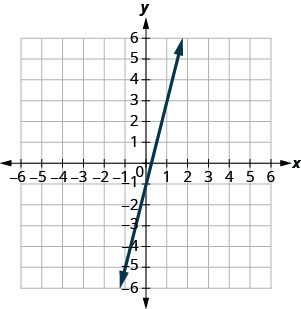
\(y=4x−1\)
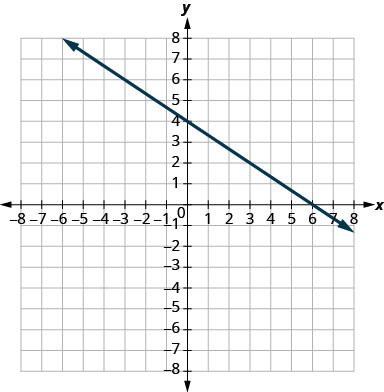
\(y=-\frac{2}{3} x+4\)
- תשובה
-
שיפוע \(m=-\frac{2}{3}\) ו \(y\) -יירוט \((0,4)\)
זהה את השיפוע ואת יירוט ה- Y ממשוואת קו
בתרגילים הבאים, לזהות את המדרון ו \(y\) -יירוט של כל שורה.
\(y=-4 x+9\)
\(y=\frac{5}{3} x-6\)
- תשובה
-
\(\frac{5}{3} ;(0,-6)\)
\(5x+y=10\)
\(4x-5y=8\)
- תשובה
-
\(\frac{4}{5} ;\quad \left(0,-\frac{8}{5}\right)\)
גרף קו באמצעות השיפוע והיירוט שלו
בתרגילים הבאים, גרף את הקו של כל משוואה באמצעות השיפוע \(y\) והיירוט שלה.
\(y=2x+3\)
\(y=-x-1\)
- תשובה
-
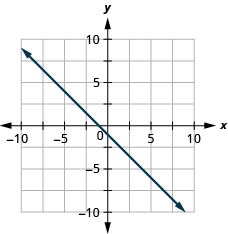
\(y=-\frac{2}{5} x+3\)
\(4x-3y=12\)
- תשובה
-
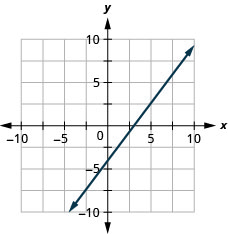
בתרגילים הבאים, קבע את השיטה הנוחה ביותר לתרשים כל שורה.
\(x=5\)
\(y=-3\)
- תשובה
-
קו אופקי
\(2x+y=5\)
\(x-y=2\)
- תשובה
-
מיירט
\(y=x+2\)
\(y=\frac{3}{4} x-1\)
- תשובה
-
מזימה נקודות
גרף ופרש יישומים של שיפוע — יירוט
קתרין היא שפית פרטית. המשוואה \(C=6.5m+42\) מדגמנת את הקשר בין העלות השבועית שלה\(C\), בדולרים ומספר הארוחות שהיא מגישה. \(m\)
- מצא את העלות של קתרין לשבוע כשהיא לא מגישה ארוחות.
- מצא את העלות במשך שבוע כאשר היא מגישה \(14\) ארוחות.
- פרש את השיפוע \(C\) והיירוט של המשוואה.
- גרף את המשוואה.
מרג'ורי מלמדת פסנתר. המשוואה \(P=35h−250\) מדגמנת את הקשר בין הרווח השבועי שלה\(P\), בדולרים ומספר שיעורי התלמידים\(s\),, שהיא מלמדת.
- מצא את הרווח של מרג'ורי לשבוע כשהיא לא מלמדת שיעורי סטודנטים.
- מצא את הרווח במשך שבוע כאשר היא מלמדת שיעורי \(20\) סטודנטים.
- פרש את השיפוע \(P\) והיירוט של המשוואה.
- גרף את המשוואה.
- תשובה
-
- \(−$250\)
- \($450\)
- המדרון,\(35\), פירושו שהרווח השבועי של מרג'ורי\(P\), גדל בכל שיעור תלמיד נוסף שהיא מלמדת. \($35\) משמעות \(P\) היירוט היא שכאשר מספר השיעורים הוא\(0\), מרג'ורי מפסידה. \($250\)
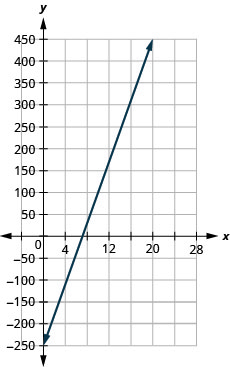
השתמש במדרונות כדי לזהות קווים מקבילים
בתרגילים הבאים, השתמש במדרונות ו \(y\) -יירוט כדי לקבוע אם הקווים מקבילים.
\(4x-3y=-1 ; \quad y=\frac{4}{3} x-3\)
\(2 x-y=8 ; \quad x-2 y=4\)
- תשובה
-
לא מקביל
השתמש במדרונות כדי לזהות קווים בניצב
בתרגילים הבאים, השתמש במדרונות וביירוט y כדי לקבוע אם הקווים בניצב.
\(y=5x-1 ; \quad 10x+2y=0\)
\(3x-2y=5 ; \quad 2x+3y=6\)
- תשובה
-
ניצב
מצא את המשוואה של קו
מצא משוואה של הקו בהתחשב בשיפוע ו- y -יירוט
בתרגילים הבאים, מצא את המשוואה של קו עם שיפוע נתון ו \(y\) -יירוט. כתוב את המשוואה בצורת שיפוע — יירוט.
שיפוע \(\frac{1}{3}\) ו \(y\) -יירוט \((0,-6)\)
שיפוע \(-5\) ו \(y\) -יירוט \((0,-3)\)
- תשובה
-
\(y=-5x-3\)
שיפוע \(0\) ו \(y\) -יירוט \((0,4)\)
שיפוע \(-2\) ו \(y\) -יירוט \((0,0)\)
- תשובה
-
\(y=-2x\)
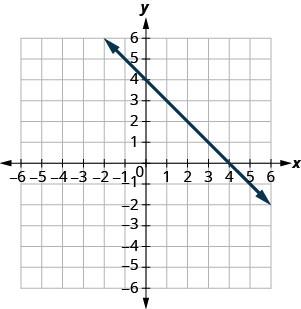
בתרגילים הבאים, מצא את משוואת הקו המוצג בכל גרף. כתוב את המשוואה בצורת שיפוע — יירוט.
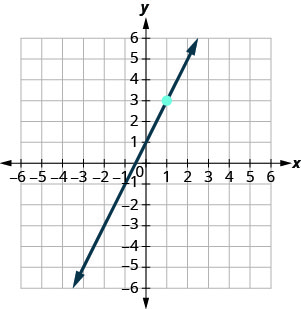
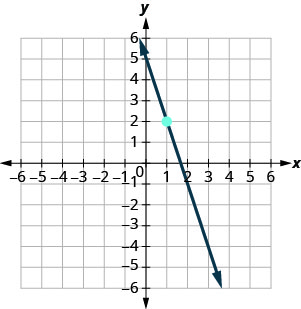
- תשובה
-
\(y=-3x+5\)
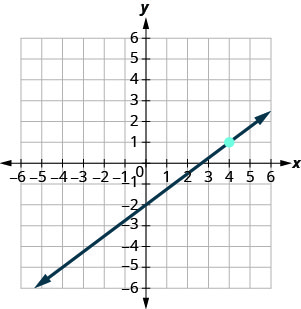
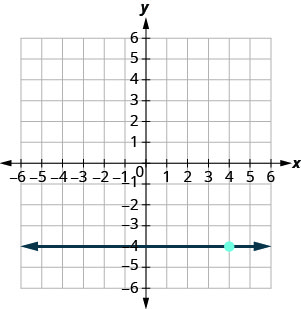
- תשובה
-
\(y=-4\)
מצא משוואה של הקו בהינתן המדרון ונקודה
בתרגילים הבאים, מצא את המשוואה של קו עם שיפוע נתון ומכיל את הנקודה הנתונה. כתוב את המשוואה בצורת שיפוע — יירוט.
\(m=-\frac{1}{4},\)נקודה \((-8,3)\)
\(m=\frac{3}{5},\)נקודה \((10,6)\)
- תשובה
-
\(y=\frac{3}{5} x\)
קו אופקי המכיל \((-2,7)\)
\(m=-2,\)נקודה \((-1,-3)\)
- תשובה
-
\(y=-2x-5\)
מצא משוואה של הקו בהינתן שתי נקודות
בתרגילים הבאים, מצא את המשוואה של קו המכיל את הנקודות הנתונות. כתוב את המשוואה בצורת שיפוע — יירוט.
\((2,10)\)ו \((-2,-2)\)
\((7,1)\)ו \((5,0)\)
- תשובה
-
\(y=\frac{1}{2} x-\frac{5}{2}\)
\((3,8)\)ו \((3,-4)\)
\((5,2)\)ו \((-1,2)\)
- תשובה
-
\(y=2\)
מצא משוואה של קו מקביל לקו נתון
בתרגילים הבאים, מצא משוואה של קו מקביל לקו הנתון ומכיל את הנקודה הנתונה. כתוב את המשוואה בצורת שיפוע — יירוט.
\(y=-3x+6,\)נקודת קו \((1,-5)\)
\(2x+5y=-10,\)נקודת קו \((10,4)\)
- תשובה
-
\(y=-\frac{2}{5} x+8\)
\(x=4,\)נקודת קו \((-2,-1)\)
\(y=-5,\)נקודת קו \((-4,3)\)
- תשובה
-
\(y=3\)
מצא משוואה של קו בניצב לקו נתון
בתרגילים הבאים, מצא משוואה של קו בניצב לקו הנתון ומכיל את הנקודה הנתונה. כתוב את המשוואה בצורת שיפוע — יירוט.
\(y=-\frac{4}{5} x+2,\)נקודת קו \((8,9)\)
\(2x-3y=9,\)נקודת קו \((-4,0)\)
- תשובה
-
\(y=-\frac{3}{2} x-6\)
\(y=3,\)נקודת קו \((-1,-3)\)
\(x=-5\)נקודת קו \((2,1)\)
- תשובה
-
\(y=1\)
גרף אי שוויון לינארי
אמת פתרונות לאי שוויון בשני משתנים
בתרגילים הבאים, קבע אם כל זוג מסודר הוא פיתרון לאי השוויון הנתון.
קבע אם כל זוג שהוזמן הוא פיתרון לאי השוויון\(y<x−3\):
- \((0,1)\)
- \((−2,−4)\)
- \((5,2)\)
- \((3,−1)\)
- \((−1,−5)\)
קבע אם כל זוג שהוזמן הוא פיתרון לאי השוויון\(x+y>4\):
- \((6,1)\)
- \((−3,6)\)
- \((3,2)\)
- \((−5,10)\)
- \((0,0)\)
- תשובה
-
- כן
- לא
- כן
- כן
- לא
הכירו את הקשר בין פתרונות אי השוויון לבין הגרף שלו
בתרגילים הבאים, כתוב את אי השוויון שמוצג על ידי האזור המוצל.
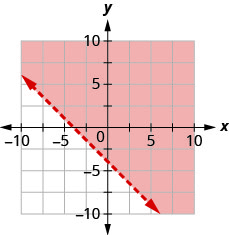
כתוב את אי השוויון שמוצג על ידי הגרף עם קו הגבול\(y=−x+2\).
כתוב את אי השוויון שמוצג על ידי הגרף עם קו הגבול \(y=\frac{2}{3} x-3\)
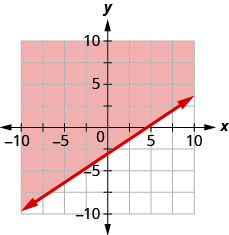
- תשובה
-
\(y>\frac{2}{3} x-3\)
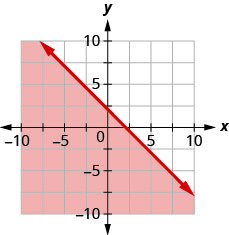
כתוב את אי השוויון שמוצג על ידי האזור המוצל בגרף עם קו הגבול\(x+y=−4\).
כתוב את אי השוויון שמוצג על ידי האזור המוצל בגרף עם קו הגבול\(x−2y=6\).
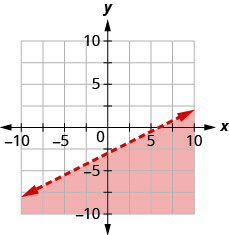
- תשובה
-
\(x-2 y \geq 6\)
גרף אי שוויון לינארי
בתרגילים הבאים, גרף כל אי שוויון ליניארי.
גרף את אי השוויון הליניארי \(y>\frac{2}{5} x-4\)
גרף את אי השוויון הליניארי \(y \leq-\frac{1}{4} x+3\)
- תשובה
-
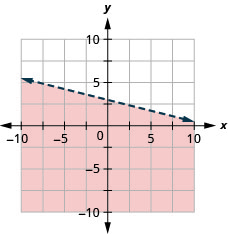
גרף את אי השוויון הליניארי \(x-y \leq 5\)
גרף את אי השוויון הליניארי \(3 x+2 y>10\)
- תשובה
-
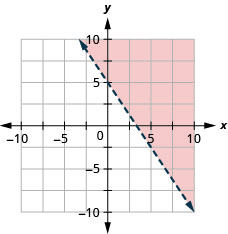
גרף את אי השוויון הליניארי \(y \leq-3 x\)
גרף את אי השוויון הליניארי \(y<6\)
- תשובה
-
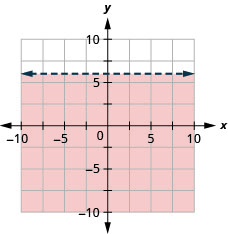
מבחן תרגול
התווה כל נקודה במערכת קואורדינטות מלבנית.
- \((2,5)\)
- \((−1,−3)\)
- \((0,2)\)
- \(\left(-4, \frac{3}{2}\right)\)
- \((5,0)\)
אילו מהזוגות המסודרים הנתונים הם פתרונות למשוואה\(3x−y=6\)?
- \((3,3)\)
- \((2,0)\)
- \((4,−6)\)
- תשובה
-
- כן
- כן
- לא
מצא שלושה פתרונות למשוואה הליניארית \(y=-2x-4\)
מצא את \(x\) - ו \(y\) - -יירוט של המשוואה \(4x-3y=12\)
- תשובה
-
\((3,0),(0,-4)\)
מצא את השיפוע של כל שורה המוצגת.
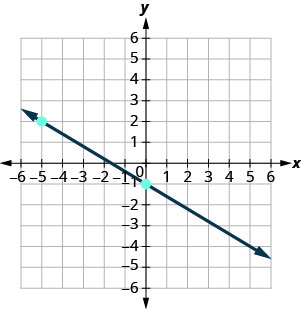
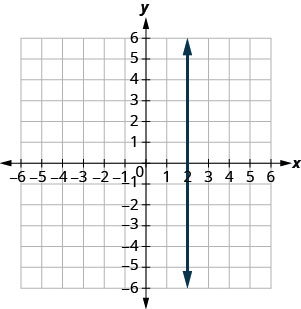
- תשובה
-
לא מוגדר
מצא את שיפוע הקו בין הנקודות \((5,2)\) ו \((-1,-4)\)
- תשובה
-
1
גרף את הקו עם שיפוע \(\frac{1}{2}\) המכיל את הנקודה \((-3,-4)\)
גרף את הקו עבור כל אחת מהמשוואות הבאות.
\(y=\frac{5}{3} x-1\)
- תשובה
-
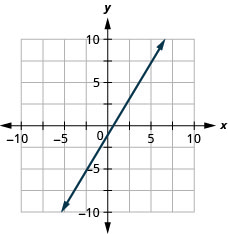
\(y=-x\)
\(x-y=2\)
- תשובה
-
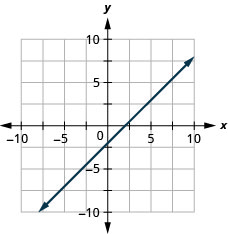
\(4x+2y=-8\)
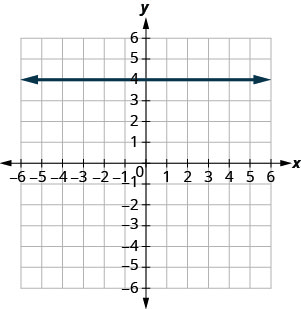
\(y=2\)
- תשובה
-
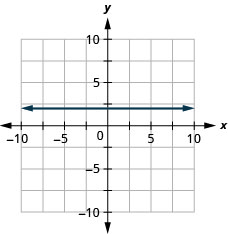
\(x=-3\)
מצא את המשוואה של כל שורה. כתוב את המשוואה בצורת שיפוע — יירוט.
שיפוע \(-\frac{3}{4}\) ו \(y\) -יירוט \((0,-2)\)
- תשובה
-
\(y=-\frac{3}{4} x-2\)
\(m=2,\)נקודה \((-3,-1)\)
המכיל \((10,1)\) ו \((6,-1)\)
- תשובה
-
\(y=\frac{1}{2} x-4\)
במקביל לקו \(y=-\frac{2}{3} x-1,\) המכיל את הנקודה \((-3,8)\)
בניצב לקו \(y=\frac{5}{4} x+2,\) המכיל את הנקודה \((-10,3)\)
- תשובה
-
\(y=-\frac{4}{5} x-5\)
כתוב את אי השוויון שמוצג על ידי הגרף עם קו הגבול\(y=−x−3\).
גרף כל אי שוויון ליניארי.
\(y>\frac{3}{2} x+5\)
- תשובה
-
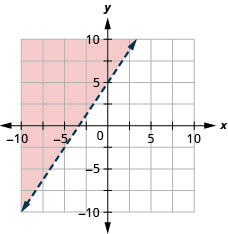
\(x-y \geq-4\)
\(y \leq-5 x\)
- תשובה
-
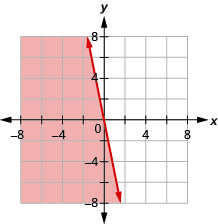
\(y<3\)