3.2: לפתור יישומי אחוזים

מטרות למידה

בסוף פרק זה, תוכל:

• תרגם ופתור משוואות אחוזים בסיסיות
• לפתור אחוז יישומים
• מצא עלייה באחוזים ואחוז ירידה
• לפתור יישומי עניין פשוטים
• לפתור יישומים עם הנחה או סימון

להיות מוכן

לפני שתתחיל, קח את חידון המוכנות הזה.

1. המר 4.5% לעשרוני.
   אם פספסת בעיה זו, סקור את [קישור].
2. המר 0.6 לאחוז.
   אם פספסת בעיה זו, סקור את [קישור].
3. סיבוב 0.875 למאה הקרובה ביותר.
   אם פספסת בעיה זו, סקור את [קישור].
4. הכפל (4.5) (2.38).
   אם פספסת בעיה זו, סקור את [קישור].
5. לפתור 3.5 = 0.7 נ.
   אם פספסת בעיה זו, סקור את [קישור].
6. חיסור 50-37.45.
   אם פספסת בעיה זו, סקור את [קישור].

תרגם ופתור משוואות אחוזים בסיסיות

נפתור משוואות אחוזים בשיטות בהן השתמשנו כדי לפתור משוואות עם שברים או עשרוניים. ללא הכלים של אלגברה, השיטה הטובה ביותר לפתור בעיות באחוזים הייתה על ידי הגדרתן כפרופורציות. עכשיו כתלמיד אלגברה, אתה יכול פשוט לתרגם משפטים באנגלית למשוואות אלגבריות ואז לפתור את המשוואות.

אנו יכולים להשתמש בכל אות שתרצה כמשתנה, אך כדאי לבחור אות שתזכיר לנו את מה שאתה מחפש. עלינו להיות בטוחים לשנות את האחוז הנתון לעשרוני כאשר אנו מכניסים אותו למשוואה.

תרגיל $\PageIndex{1}$

תרגם ופתור: איזה מספר הוא 35% מתוך 90?

תשובה

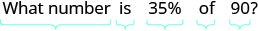
תרגם לאלגברה. תן n = המספר.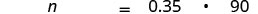
זכור "של" פירושו להכפיל, "הוא" פירושו שווה.
להכפיל.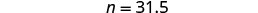
	31.5 זה 35% מתוך 90

תרגיל $\PageIndex{2}$

תרגם ופתור:

מהו המספר של 45% מתוך 80?

תשובה

36

תרגיל $\PageIndex{3}$

תרגם ופתור:

איזה מספר הוא 55% מתוך 60?

תשובה

33

עלינו להיות זהירים מאוד כאשר אנו מתרגמים את המילים בדוגמה הבאה. הכמות הלא ידועה לא תתבודד בהתחלה, כמו שהייתה בדוגמה. נשתמש שוב בתרגום ישיר כדי לכתוב את המשוואה.

תרגיל $\PageIndex{4}$

תרגם ופתור: 6.5% מהמספר הוא 1.17$?

תשובה

תרגם. תן n = המספר.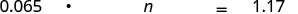
להכפיל.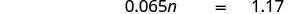
מחלקים את שני הצדדים ב -0.065 ופשטו.
	6.5% מתוך 18 דולר הם 1.17 דולר

תרגיל $\PageIndex{5}$

תרגם ופתור:

7.5% מהמספר הוא 1.95 דולר?

תשובה

$26

תרגיל $\PageIndex{6}$

תרגם ופתור:

8.5% מהמספר הוא 3.06 דולר?

תשובה

$36

בדוגמה הבאה, אנחנו מחפשים את האחוזים.

תרגיל $\PageIndex{7}$

תרגם ופתור: 144 הוא איזה אחוז של 96?

תשובה

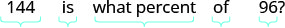
תרגם לאלגברה. תנו ל- p = האחוז.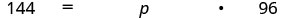
להכפיל.
מחלקים ב 96 ופשטו.
המר לאחוזים.
	144 הוא 150% מתוך 96

שים לב שאנחנו מתבקשים למצוא אחוזים, ולכן עלינו לקבל את התוצאה הסופית שלנו בצורה באחוזים.

תרגיל $\PageIndex{8}$

תרגם ופתור:

110 זה איזה אחוז מתוך 88?

תשובה

125%

תרגיל $\PageIndex{9}$

תרגם ופתור:

126 זה איזה אחוז מתוך 72?

תשובה

175%

לפתור יישומים של אחוזים

יישומים רבים באחוזים - כגון טיפים, מס מכירה, הנחות וריבית - מתרחשים בחיי היומיום שלנו. כדי לפתור יישומים אלה נתרגם למשוואת אחוזים בסיסית, בדיוק כמו אלה שפתרנו בדוגמאות קודמות. ברגע שאנחנו מתרגמים את המשפט למשוואת אחוזים, אנחנו יודעים איך לפתור את זה.

אנו נשחזר את אסטרטגיית פתרון הבעיות בה השתמשנו קודם לכן לצורך התייחסות קלה.

השתמש באסטרטגיה לפתרון בעיות כדי לפתור יישום.

1. קרא את הבעיה. ודא שכל המילים והרעיונות מובנים.
2. זהה את מה שאנחנו מחפשים.
3. תן שם למה שאנחנו מחפשים. בחר משתנה שייצג את הכמות הזו.
4. תרגם למשוואה. זה עשוי להיות מועיל לשחזר את הבעיה במשפט אחד עם כל המידע החשוב. לאחר מכן, תרגם את המשפט האנגלי למשוואה אלגברית.
5. לפתור את המשוואה באמצעות טכניקות אלגברה טובות.
6. בדוק את התשובה בבעיה וודא שהיא הגיונית.
7. ענה על השאלה במשפט שלם.

כעת, לאחר שיש לנו את האסטרטגיה להתייחס אליה, והתאמנו בפתרון משוואות אחוזים בסיסיות, אנו מוכנים לפתור יישומי אחוזים. הקפד לשאול את עצמך אם התשובה הסופית שלך היא הגיונית - מכיוון שרבים מהיישומים יהיו כרוכים במצבים יומיומיים, אתה יכול לסמוך על הניסיון שלך.

תרגיל $\PageIndex{10}$

דזון וחברתו נהנו מארוחת ערב נחמדה במסעדה והחשבון שלו היה 68.50 דולר. הוא רוצה להשאיר טיפ של 18%. אם הטיפ יהיה 18% מסך החשבון, כמה טיפ עליו להשאיר?

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.	את כמות הטיפ צריך Dezohn לעזוב
שלב 3. תן שם למה שאנחנו מחפשים.
בחר משתנה שייצג אותו.	תן t = כמות הטיפ.
שלב 4. תרגם למשוואה.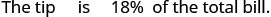
כתוב משפט שנותן את המידע כדי למצוא אותו.
תרגם את המשפט למשוואה.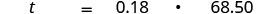
שלב 5. לפתור את המשוואה. להכפיל.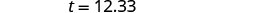
שלב 6. בדוק. האם זה הגיוני?
כן, 20% מ -70 דולר זה 14 דולר.
שלב 7. ענה על השאלה במשפט שלם.	דזון צריך להשאיר טיפ של 12.33 דולר.

שימו לב שהשתמשנו ב-t כדי לייצג את הטיפ הלא ידוע.

תרגיל $\PageIndex{11}$

סיירה ואחותה נהנו מארוחת ערב במסעדה והחשבון היה 81.50 דולר. אם היא רוצה להשאיר 18% מכלל החשבון כטיפ שלה, כמה עליה להשאיר?

תשובה

14.67 דולר

תרגיל $\PageIndex{12}$

קימנגוק אכלה ארוחת צהריים במסעדה האהובה עליה. היא רוצה להשאיר 15% מסך החשבון כטיפ שלה. אם החשבון שלה היה 14.40 דולר, כמה היא תשאיר לטיפ?

תשובה

2.16 דולר

תרגיל $\PageIndex{13}$

התווית על דגני הבוקר של מסאו אמרה כי מנה אחת של דגני בוקר מספקת 85 מיליגרם (מ"ג) אשלגן, שהם 2% מהכמות היומית המומלצת. מהי הכמות היומית המומלצת הכוללת של אשלגן?

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.	כמות האשלגן הכוללת המומלצת
שלב 3. תן שם למה שאנחנו מחפשים.
בחר משתנה שייצג אותו.	תן a= כמות אשלגן כוללת.
שלב 4. תרגם. כתוב משפט שנותן את המידע כדי למצוא אותו.
תרגם למשוואה.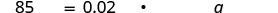
שלב 5. לפתור את המשוואה.
שלב 6. בדוק. האם זה הגיוני?
כן, 2% הם אחוז קטן ו -85 הם חלק קטן מ -4,250.
שלב 7. ענה על השאלה במשפט שלם.	כמות האשלגן המומלצת היא 4,250 מ"ג.

תרגיל $\PageIndex{14}$

מנה אחת של דגני בוקר מרובעים מחיטה מכילה שבעה גרם סיבים, שהם 28% מהכמות היומית המומלצת. מהי כמות הסיבים היומית המומלצת הכוללת?

תשובה

25 גרם

תרגיל $\PageIndex{15}$

מנה אחת של דגני אורז מכילה 190 מ"ג נתרן, שהם 8% מהכמות היומית המומלצת. מהי הכמות היומית המומלצת הכוללת של נתרן?

תשובה

2,375 מ"ג

תרגיל $\PageIndex{16}$

מיצי קיבל כמה בראוניז גורמה במתנה. העטיפה אמרה שכל בראוניז היה 480 קלוריות, ויש בו 240 קלוריות שומן. איזה אחוז מסך הקלוריות בכל בראוניז מגיע משומן?

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.	אחוז מכלל הקלוריות משומן
שלב 3. תן שם למה שאנחנו מחפשים.
בחר משתנה שייצג אותו.	תן p = אחוז שומן.
שלב 4. תרגם. כתוב משפט שנותן את המידע כדי למצוא אותו.
תרגם למשוואה.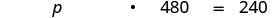
שלב 5. לפתור את המשוואה.
מחלקים על ידי 480.
שים טופס אחוז.
שלב 6. בדוק. האם זה הגיוני?
כן, 240 זה חצי מ -480, אז 50% הגיוניים.
שלב 7. ענה על השאלה במשפט שלם.	מכלל הקלוריות בכל בראוניז, 50% הם שומן.

תרגיל $\PageIndex{17}$

לפתור. עגול לאחוז השלם הקרוב ביותר.

ורוניקה מתכננת להכין מאפינס מתערובת. החבילה אומרת שכל מאפין יהיה 230 קלוריות ו -60 קלוריות יהיו משומן. איזה אחוז מסך הקלוריות הוא משומן?

תשובה

26%

תרגיל $\PageIndex{18}$

לפתור. עגול לאחוז השלם הקרוב ביותר.

התמהיל שריקרדו מתכנן להשתמש בו להכנת בראוניז אומר שכל בראוניז יהיה 190 קלוריות, ו -76 קלוריות משומן. איזה אחוז מסך הקלוריות הם משומן?

תשובה

40%

מצא עלייה באחוזים וירידה באחוזים

אנשים בתקשורת מדברים לעתים קרובות על כמה כמות גדלה או פחתה בפרק זמן מסוים. בדרך כלל הם מבטאים עלייה או ירידה זו כאחוז.

כדי למצוא את העלייה באחוזים, ראשית אנו מוצאים את כמות הגידול, את ההפרש של הסכום החדש ואת הסכום המקורי. ואז אנו מוצאים איזה אחוז כמות הגידול היא מהסכום המקורי.

מצא את העלייה באחוזים.

1. מצא את כמות הגידול.
   
   $\text{new amount }−\text{ original amount }=\text{ increase}$
2. מצא את העלייה באחוזים.
   
   הגידול הוא איזה אחוז מהסכום המקורי?

תרגיל $\PageIndex{19}$

בשנת 2011 הציע מושל קליפורניה להעלות את דמי המכללה הקהילתית מ -26 דולר ליחידה ל -36 דולר ליחידה. מצא את העלייה באחוזים. (סיבוב לעשירית האחוז הקרובה ביותר.)

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.	האחוזים עולים
שלב 3. תן שם למה שאנחנו מחפשים.
בחר משתנה שייצג אותו.	תן p = p = האחוז.
שלב 4. תרגם. כתוב משפט שנותן את המידע כדי למצוא אותו.
ראשית מצא את כמות הגידול.	כמות חדשה - כמות מקורית = עלייה
	36-26=10
מצא את האחוזים.	עלייה היא איזה אחוז מהסכום המקורי?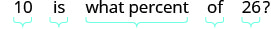
תרגם למשוואה.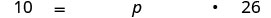
שלב 5. לפתור את המשוואה.
מחלקים על ידי 26.
שינוי לצורת אחוז; עגול לעשירית הקרובה ביותר.
שלב 6. בדוק. האם זה הגיוני?
כן, 38.4% קרוב ל$\frac{1}{3}$, ו -10 קרוב ל 26$\frac{1}{3}$.
שלב 7. ענה על השאלה במשפט שלם.	העמלות החדשות מייצגות עלייה של 38.4% לעומת העמלות הישנות.

תרגיל $\PageIndex{20}$

מצא את העלייה באחוזים. (סיבוב לעשירית האחוז הקרובה ביותר.)

בשנת 2011 העלה מס הכנסה את עלות הקילומטראז 'לניכוי ל -55.5 סנט מ -51 סנט.

תשובה

8.8%

תרגיל $\PageIndex{21}$

מצא את העלייה באחוזים.

בשנת 1995, מחיר האוטובוס הסטנדרטי בשיקגו היה 1.50 דולר. בשנת 2008, מחיר האוטובוס הסטנדרטי היה 2.25 דולר.

תשובה

50%

מציאת הירידה באחוזים דומה מאוד למציאת העלייה באחוזים, אך כעת כמות הירידה היא ההפרש של הסכום המקורי והסכום החדש. ואז אנו מוצאים איזה אחוז כמות הירידה היא מהסכום המקורי.

מצא את הירידה באחוזים.

1. מצא את כמות הירידה.
   
   $\text{original amount }−\text{ new amount }=\text{ decrease}$
2. מצא את הירידה באחוזים.
   
   הירידה היא איזה אחוז מהסכום המקורי?

תרגיל $\PageIndex{22}$

המחיר הממוצע של גלון גז בעיר אחת ביוני 2014 היה 3.71 דולר. המחיר הממוצע בעיר ביולי היה 3.64 דולר. מצא את הירידה באחוזים.

תשובה

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.	האחוזים יורדים
שלב 3. תן שם למה שאנחנו מחפשים.
בחר משתנה שייצג את הכמות הזו.	תנו ל- p = האחוז לרדת.
שלב 4. תרגם. כתוב משפט שנותן את המידע כדי למצוא אותו.
ראשית מצא את כמות הירידה.	3.71—3.64 =0.07
מצא את האחוזים.	ירידה היא כמה אחוזים של amaount המקורי?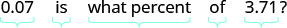
תרגם למשוואה.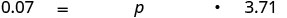
שלב 5. לפתור את המשוואה.
מחלקים ב -3.71.
שינוי לצורת אחוז; עגול לעשירית הקרובה ביותר.
שלב 6. בדוק. האם זה הגיוני?
כן, אם המחיר המקורי היה 4 דולר, ירידה של 2% תהיה 8 סנט.
שלב 7. ענה על השאלה במשפט שלם.	מחיר הגז ירד ב -1.9%.

תרגיל $\PageIndex{23}$

מצא את הירידה באחוזים. (סיבוב לעשירית האחוז הקרובה ביותר.)

אוכלוסיית צפון דקוטה מנתה כ -672,000 בשנת 2010. האוכלוסייה צפויה להיות כ -630,000 בשנת 2020.

תשובה

6.3%

תרגיל $\PageIndex{24}$

מצא את הירידה באחוזים.

בשנה שעברה שכרה של שילה היה 42 אלף דולר. בגלל ימי חופשה, השנה, משכורתה הייתה 37,800 דולר.

תשובה

10%

לפתור יישומי עניין פשוטים

האם אתה יודע שהבנקים משלמים לך כדי לשמור על הכסף שלך? הכסף שלקוח מכניס לבנק נקרא הקרן, P, והכסף שהבנק משלם ללקוח נקרא הריבית. הריבית מחושבת כאחוז מסוים מהקרן; נקרא שיעור הריבית, r. בדרך כלל אנו מבטאים את שיעור הריבית כאחוז לשנה, ואנחנו מחשבים אותו על ידי שימוש במקבילה העשרונית של האחוזים. המשתנה t, (לזמן) מייצג את מספר השנים שהכסף נמצא בחשבון.

כדי למצוא את העניין אנו משתמשים בנוסחת העניין הפשוטה, I = Prt.

עניין פשוט

אם סכום כסף, P, הנקרא הקרן, מושקע לתקופה של t שנים בריבית שנתית r, סכום הריבית, אני, הרוויח הוא

$$\begin{array}{lllll} {} &{} &{I} &{=} &{\text { interest }}\\ {I = Prt} &{\text{where}} &{P} &{=} &{\text { principle }}\\ {} &{} &{r} &{=} &{\text { rate }}\\ {} &{} &{t} &{=} &{\text { time }} \end{array}$$

ריבית שנצברה על פי נוסחה זו נקראת ריבית פשוטה.

ניתן לחשב ריבית גם בדרך אחרת, הנקראת ריבית דריבית. סוג זה של עניין יכוסה בשיעורי מתמטיקה מאוחרים יותר.

הנוסחה בה אנו משתמשים לחישוב ריבית פשוטה היא I = Prt. כדי להשתמש בנוסחה, אנו מחליפים בערכים שהבעיה נותנת לנו עבור המשתנים ואז פותרים עבור המשתנה הלא ידוע. זה עשוי להיות מועיל לארגן את המידע בתרשים.

תרגיל $\PageIndex{25}$

נתלי הפקידה 12,500 דולר בחשבון הבנק שלה שם היא תרוויח 4% ריבית. כמה ריבית תרוויח נתלי בעוד 5 שנים?

$$\begin{aligned} I &=? \\ P &=\$ 12,500 \\ r &=4 \% \\ t &=5 \text { years } \end{aligned}$$

תשובה

$\begin{array} {ll} {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount of interest earned}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for.}} &{\text{Let I = the amount of interest.}} \\ {\text{Choose a variable to represent that quantity}} &{\text{}} \\\\ {\textbf{Step 4.} \text{ Translate into an equation.}} &{} \\ {\qquad\text{Write the formula.}} &{I = Prt} \\ {\qquad\text{Substitute in the given information.}} &{I = (12500)(.04)(5)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{I = 2500} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\\\ {\qquad \text{Is } $2,500 \text{ is a reasonable interest} } &{} \\ {\qquad \text{on }$12,500? \text{ Yes.}} \\ {\textbf{Step 7. Answer} \text{ the question with a}} &{\text{The interest is }$2500} \\ {\text{complete sentence.}} &{} \ \end{array}$

תרגיל $\PageIndex{26}$

ארלי השקיעה קרן של 950 דולר בחשבון הבנק שלה עם ריבית של 3%. כמה ריבית היא הרוויחה בחמש שנים?

תשובה

142.50 דולר

תרגיל $\PageIndex{27}$

סוזנה השקיעה קרן של 36,000 דולר בחשבון הבנק שלה עם ריבית של 6.5%. כמה ריבית היא הרוויחה בשלוש שנים?

תשובה

7020 דולר

ייתכנו מקרים בהם אנו יודעים את סכום הריבית שנצברה על קרן נתונה לאורך זמן מסוים, אך איננו יודעים את התעריף. כדי למצוא את התעריף, אנו משתמשים בנוסחת הריבית הפשוטה, מחליפים בערכים הנתונים את הקרן והזמן ואז פותרים את התעריף.

תרגיל $\PageIndex{28}$

לורן הלווה לאחיו 3,000 דולר כדי לעזור לו לקנות מכונית. תוך 4 שנים אחיו החזיר לו את 3,000 הדולר בתוספת 660 דולר בריבית. מה היה שיעור הריבית?

$$\begin{array}{lll} {I} &{=} &{\$ 660} \\ {P} &{=} &{\$ 3000} \\ {r} &{=} &{?} \\ {t} &{=} &{4 \text { years } }\end{array}$$

תשובה

$\begin{array} {ll} {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the rate of interest}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. Choose}} &{\text{Let r = the rate of interest.}} \\ {\text{ a variable to represent that quantity}} &{\text{}} \\\\ {\textbf{Step 4.} \text{ Translate into an equation.}} &{} \\ {\qquad\text{Write the formula.}} &{I = Prt} \\ {\qquad\text{Substitute in the given information.}} &{660 = (3000)r(4)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{} \\ {} &{660 = (12000)r} \\ {\text{Divide.}} &{0.055 = r} \\ {\text{Change to percent form.}} &{5.5\% = r} \\\\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\\\ {I = Prt} &{} \\ {660 \stackrel{?}{=} (3000)(0.055)(4)} &{} \\ {660 = 660\checkmark} &{} \\ {\textbf{Step 7. Answer} \text{ the question with a}} &{\text{The rate of interest was }5.5%} \\ {\text{complete sentence.}} &{} \end{array}$

שימו לב שבדוגמה זו אחיו של לורן שילם ריבית ללורן, ממש כמו שבנק היה משלם ריבית אם לורן השקיע שם את כספו.

תרגיל $\PageIndex{29}$

ג'ים הלווה לאחותו 5,000 דולר כדי לעזור לה לקנות בית. בתוך 3 שנים, היא שילמה לו 5,000$, בתוספת 900$ ריבית. מה היה שיעור הריבית?

תשובה

6%

תרגיל $\PageIndex{30}$

האנג לוותה 7,500 דולר מהוריה כדי לשלם את שכר הלימוד שלה. תוך 5 שנים היא שילמה להם ריבית של 1,500 דולר בנוסף ל -7,500 דולר שלוותה. מה היה שיעור הריבית?

תשובה

4%

תרגיל $\PageIndex{31}$

אדוארדו הבחין כי במסמכי הלוואת הרכב החדשים שלו נאמר כי בריבית של 7.5% הוא ישלם ריבית של 6,596.25 דולר במשך 5 שנים. כמה הוא לווה כדי לשלם עבור המכונית שלו?

תשובה

$\begin{array} {ll} {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount borrowed (the principal)}} \\ {\text{a variable to represent that quantity.}} &{} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. }} &{\text{Let P = principal borrowed.}} \\ {\text{Choose a variable to represent that quantity}} &{\text{}} \\\\ {\textbf{Step 4. Translate} \text{ into an equation.}} &{} \\ {\qquad\text{Write the formula.}} &{I = Prt} \\ {\qquad\text{Substitute in the given information.}} &{6596.25 = P(0.075)(5)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{} \\ {} &{6596.25 = 0.375P} \\ {\text{Divide.}} &{17590 = P} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\ {I = Prt} &{} \\ {6596.25 \stackrel{?}{=} (17590)(0.075)(5)} &{} \\ {6596.25 = 6596.25\checkmark} &{} \\\\ {\textbf{Step 7. Answer} \text{ the question with a}} &{\text{The principal is }$17590} \\ {\text{complete sentence.}} &{} \ \end{array}$

תרגיל $\PageIndex{32}$

הצהרת הלוואת הרכב החדשה של שון אמרה שהוא ישלם 4,866.25 דולר בריבית מריבית של 8.5% במשך 5 שנים. כמה הוא לווה כדי לקנות את המכונית החדשה שלו?

תשובה

11,450 דולר

תרגיל $\PageIndex{33}$

תוך 5 שנים, חשבון הבנק של גלוריה הרוויח 2,400 דולר ריבית בשיעור של 5%. כמה היא הפקידה בחשבון?

תשובה

$9,600

לפתור יישומים עם הנחה או סימון

יישומי הנחה נפוצים מאוד בהגדרות הקמעונאיות. כאשר אתה קונה פריט במבצע, המחיר המקורי הוזל בסכום דולר כלשהו. שיעור ההיוון, הניתן בדרך כלל כאחוז, משמש לקביעת סכום ההנחה. כדי לקבוע את סכום ההנחה, אנו מכפילים את שיעור ההיוון במחיר המקורי.

אנו מסכמים את מודל ההנחה בתיבה למטה.

דיסקונט

$$\begin{array}{l}{\text { amount of discount }=\text { discount rate } \times \text { original price }} \\ {\text { sale price }=\text { original price - amount of discount }}\end{array}$$

זכור כי מחיר המכירה צריך תמיד להיות פחות מהמחיר המקורי.

תרגיל $\PageIndex{34}$

אליס קנתה שמלה שהוזלה ב -35% מהמחיר המקורי של 140 דולר. מה היה ⓐ סכום ההנחה ו ⓑ מחיר המכירה של השמלה?

תשובה

1. $\begin{array} {lll} {\text{Original price}} &{=} &{$140} \\ {\text{Discount rate}} &{=} &{35\%} \\ {\text{Discount?}} &{=} &{?} \end{array}$
$\begin{array} {ll} \\ {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount of discount}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. }} &{\text{}} \\ {\text{Choose a variable to represent that quantity.}} &{\text{Let d = the amount of discount.}} \\\\ {\textbf{Step 4. Translate} \text{ into an equation. Write a}} &{} \\ {\text{sentence that gives the information to find it.}} &{} \\ {\text{Translate into an equation}} &{d = 0.35(140)} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{d = 49} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\ \\ {\text{Is a }$49\text{ discount reasonable for a}} &{} \\ {$140\text{ dress? Yes.}} &{} \\\\ {\textbf{Step 7. Write} \text{ a complete sentence to answer}} &{\text{The amount of discount was }$49} \\ {\text{the question.}} &{} \ \end{array}$

2.
קרא שוב את הבעיה.

שלב 1. זהה את מה שאנחנו מחפשים.	מחיר המכירה של השמלה
שלב 2. תן שם למה שאנחנו מחפשים.
בחר משתנה שייצג את הכמות הזו.	תן s= מחיר המכירה.
שלב 3. תרגם למשוואה.
כתוב משפט שנותן את המידע כדי למצוא אותו.
תרגם למשוואה.
שלב 4. לפתור את המשוואה.
שלב 5. בדוק. האם זה הגיוני?
האם מחיר המכירה נמוך מהמחיר המקורי?
כן, 91 דולר זה פחות מ -140 דולר.
שלב 6. ענה על השאלה במשפט שלם.	מחיר המכירה של השמלה היה 91 דולר.

תרגיל $\PageIndex{35}$

מצא ⓐ את סכום ההנחה ו ⓑ את מחיר המכירה:

סרחיו קנה חגורה שהוזלה ב -40% ממחיר מקורי של 29 דולר.

תשובה

ⓐ $11.60 ⓑ $17.40

תרגיל $\PageIndex{36}$

מצא ⓐ את סכום ההנחה ו ⓑ את מחיר המכירה:

אוסקר קנה ברביקיו שהוזל 65% ממחיר מקורי של 395 דולר.

תשובה

ⓐ 256.75 דולר ⓑ 138.25 דולר

יתכנו מקרים בהם אנו יודעים מה המחיר המקורי ומחיר המכירה, ואנחנו רוצים לדעת את שיעור ההיוון. כדי למצוא את שיעור ההיוון, ראשית נמצא את סכום ההנחה ואז נשתמש בו לחישוב התעריף כאחוז מהמחיר המקורי. תרגיל $\PageIndex{37}$ יראה את המקרה הזה.

תרגיל $\PageIndex{37}$

ג'נט קנתה בגד ים במחיר מכירה של 13.95 דולר. המחיר המקורי של בגד הים היה 31$. מצא את סכום ההנחה ⓐ ושיעור ההנחה ⓑ.

תשובה

ⓐ $\begin{array} {lll} {\text{Original price}} &{=} &{$31} \\ {\text{Discount}} &{=} &{?} \\ {\text{Sale Price}} &{=} &{$ 13.95} \end{array}$
$\begin{array} {ll} \\ {\textbf{Step 1. Read} \text{ the problem.}} &{} \\ \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} &{\text{the amount of discount}} \\\\ {\textbf{Step 3. Name} \text{ what we are looking for. }} &{\text{}} \\ {\text{Choose a variable to represent that quantity.}} &{\text{Let d = the amount of discount.}} \\\\ {\textbf{Step 4. Translate} \text{ into an equation. Write a}} &{} \\ {\text{sentence that gives the information to find it.}} &{\text{The discount is the difference between the original}} \\ {} &{\text{price and the sale price.}} \\{\text{Translate into an equation}} &{d = 31 - 13.95} \\ \\ {\textbf{Step 5. Solve} \text{ the equation.}} &{d = 17.05} \\ \\ {\textbf{Step 6. Check} \text{: Does this make sense?}} &{} \\ \\ {\text{Is }17.05\text{ less than 31? Yes.}} &{} \\\\ {\textbf{Step 7. Answer} \text{ the question with a complete sentence.}} &{\text{The amount of discount was }$17.05} \end{array}$

ⓑ
קרא את הבעיה שוב.

1. כאשר אנו מתרגמים זאת למשוואה, נקבל 17.05 שווה r כפול 31. נאמר לנו לפתור את המשוואה 17.05 שווה 31r. אנו מחלקים ב -31 כדי להשיג 0.55 שווה r שמנו את זה בצורה באחוזים כדי להשיג r שווה 55%. נאמר לנו לבדוק: האם זה הגיוני? האם 7.05 שווה ל 55% של >1? מתחת לזה, יש לנו 17.05 שווים עם סימן שאלה מעליו 0.55 פעמים 31. מתחת לזה, יש לנו 17.05 שווה 17.05 עם סימן ביקורת לידו. ואז נאמר לנו לענות על השאלה במשפט שלם: שיעור ההנחה היה 55%". >

שלב 1. זהה את מה שאנחנו מחפשים.	שיעור ההיוון
שלב 2. תן שם למה שאנחנו מחפשים.
בחר משתנה שייצג אותו.	תן r=r = שיעור ההיוון.
שלב 3. תרגם למשוואה.
כתוב משפט שנותן את המידע כדי למצוא אותו.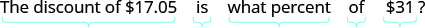
תרגם למשוואה.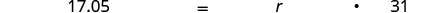
שלב 4. לפתור את המשוואה.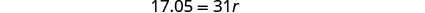
מחלקים את שני הצדדים ב -31.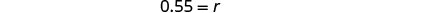
שינוי לטופס אחוזים.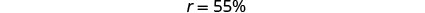
שלב 5. בדוק. האם זה הגיוני?
האם 17.05$ שווה ל 55% מתוך 31$?
$17.05\stackrel{?}{=}0.55(31)$
$17.05=17.05\checkmark$
שלב 6. ענה על השאלה במשפט שלם.	שיעור ההנחה היה 55%.

תרגיל $\PageIndex{38}$

למצוא

1. סכום ההנחה ו
2. שיעור ההיוון.

לנה קנתה שולחן מטבח במחיר המכירה של 375.20 דולר. המחיר המקורי של השולחן היה 560 דולר.

תשובה

1. 184.80 דולר
2. 33%

תרגיל $\PageIndex{39}$

למצוא

1. סכום ההנחה ו
2. שיעור ההיוון.

ניק קנה מזגן רב חדרים במחיר מכירה של 340 דולר. המחיר המקורי של המזגן היה 400 דולר.

תשובה

1. $60
2. 15%

יישומי סימון נפוצים מאוד בהגדרות קמעונאיות. המחיר שקמעונאי משלם עבור פריט נקרא העלות המקורית. לאחר מכן הקמעונאי מוסיף סימון לעלות המקורית כדי לקבל את מחיר המחירון, את המחיר עבורו הוא מוכר את הפריט. הסימון מחושב בדרך כלל כאחוז מהעלות המקורית. כדי לקבוע את כמות הסימון, הכפל את שיעור הסימון בעלות המקורית.

אנו מסכמים את מודל הסימון בתיבה למטה.

סימון

$$\begin{array}{l}{\text { amount of mark-up }=\text { mark-up rate } \times \text { original cost }} \\ {\text { list price }=\text { original cost }+\text { amount of mark up }}\end{array}$$

זכור כי מחיר המחירון צריך תמיד להיות יותר מהעלות המקורית.

תרגיל $\PageIndex{40}$

גלריית האמנות של אדם קנתה תמונה בעלות מקורית 250 דולר. אדם סימן את המחיר בעלייה של 40%. מצא את

1. כמות הסימון ו
2. מחיר המחירון של התמונה.

תשובה

1.

שלב 1. קרא את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.	כמות הסימון
שלב 3. תן שם למה שאנחנו מחפשים.
בחר משתנה שייצג אותו.	תן ל- m = כמות הסימון.
שלב 4. תרגם למשוואה.
כתוב משפט שנותן את המידע כדי למצוא אותו.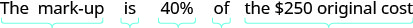
תרגם למשוואה.
שלב 5. לפתור את המשוואה.
שלב 6. בדוק. האם זה הגיוני?
כן, 40% הם פחות ממחצית ו 100 הם פחות ממחצית 250.
שלב 7. ענה על השאלה במשפט שלם.	הסימון בתצלום היה 100 דולר.

2.

שלב 1. קרא שוב את הבעיה.
שלב 2. זהה את מה שאנחנו מחפשים.	מחיר המחירון
שלב 3. תן שם למה שאנחנו מחפשים.
בחר משתנה שייצג אותו.	תן p = מחיר המחירון.
שלב 4. תרגם למשוואה.
כתוב משפט שנותן את המידע כדי למצוא אותו.
תרגם למשוואה.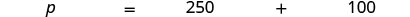
שלב 5. לפתור את המשוואה.
שלב 6. בדוק. האם זה הגיוני?
האם מחיר המחירון גבוה מהמחיר הנקי? האם 350 דולר יותר מ -250 דולר? כן.
שלב 7. ענה על השאלה במשפט שלם.	מחיר המחירון של התצלום היה 350 דולר.

תרגיל $\PageIndex{41}$

למצוא

1. כמות הסימון ו
2. מחיר המחירון.

חנות המוזיקה של ג'ים קנתה גיטרה בעלות מקורית של 1,200 דולר. ג'ים סימן את המחיר ב -50%.

תשובה

1. 600 דולר
2. 1,800 דולר

תרגיל $\PageIndex{42}$

למצוא

1. כמות הסימון ו
2. מחיר המחירון.

חנות המכירה האוטומטית קנתה את טויוטה של פבלו תמורת 8,500 דולר. הם סימנו את המחיר בעלייה של 35%.

תשובה

1. 2,975 דולר
2. 11,475 דולר

מושגי מפתח

• עלייה באחוזים כדי למצוא את העלייה באחוזים:
  1. מצא את כמות הגידול. הגדלה = כמות חדשה—סכום מקוריותהגדלה=כמות חדשה—סכום מקורי
  2. מצא את העלייה באחוזים. עלייה היא איזה אחוז מהסכום המקורי?
• ירידה באחוזים כדי למצוא את הירידה באחוזים:
  1. מצא את כמות הירידה. ירידה = כמות מקורית - כמות חדשהירידה = סכום מקורי - סכום חדש
  2. מצא את הירידה באחוזים. ירידה היא איזה אחוז מהסכום המקורי?
• ריבית פשוטה אם סכום כסף, P, הנקרא הקרן, מושקע לתקופה של t שנים בריבית שנתית r, סכום הריבית, I, הרוויח הוא

  $$\begin{aligned} I &=P r t \\ \text { where } I &=\text { interest } \\ P &=\text { principal } \\ r &=\text { rate } \\ t &=\text { time } \end{aligned}$$

• הנחה
  • סכום ההנחה הוא שיעור ההיוון ·· מחיר מקורי
  • מחיר המכירה הוא מחיר מקורי - הנחה
• סימון
  • סכום הסימון הוא שיעור סימון · · עלות מקורית
  • מחיר המחירון הוא עלות מקורית+סימון

רשימת מילים

סכום ההנחה

סכום ההנחה הוא הסכום הנובע כאשר שיעור ההיוון מוכפל במחיר המקורי של פריט.

שיעור היוון

שיעור ההיוון הוא האחוז המשמש לקביעת סכום ההנחה, הנפוץ במסגרות קמעונאיות.

ריבית

ריבית היא הכסף שבנק משלם ללקוחותיו על שמירת כספם בבנק.

מחירון

מחיר המחירון הוא המחיר עבורו מוכר קמעונאי פריט.

סימון

סימון הוא אחוז מהעלות המקורית המשמשת להעלאת מחיר הפריט.

עלות מקורית

העלות המקורית בסביבה קמעונאית, היא המחיר שקמעונאי משלם עבור פריט.

המנהלת

הקרן היא הסכום המקורי של הכסף שהושקע או לווה לתקופה של זמן בריבית מסוימת.

שיעור הריבית

שיעור הריבית הוא אחוז מהקרן, מבוטא בדרך כלל כאחוז בשנה.

עניין פשוט

ריבית פשוטה היא הריבית שנצברה על פי הנוסחה I=Prt.