1.10: מאפיינים של מספרים ממשיים
- Page ID
- 205656
בסוף פרק זה תוכל:
- השתמש בתכונות הקומוטטיביות והאסוציאטיביות
- השתמש בזהות ובמאפיינים ההפוכים של חיבור וכפל
- השתמש במאפיינים של אפס
- פשט ביטויים באמצעות המאפיין החלוקתי
מבוא יסודי יותר לנושאים המכוסים בחלק זה ניתן למצוא בפרק Prealgebra, המאפיינים של מספרים אמיתיים.
השתמש בתכונות הקומוטטיביות והאסוציאטיביות
תחשוב על הוספת שני מספרים, נניח 5 ו -3. הסדר שאנו מוסיפים להם אינו משפיע על התוצאה, נכון?
\[\begin{array} { cc } { 5 + 3 } & { 3 + 5 } \\ { 8 } & { 8 } \\ { 5 + 3 = } & { 3 + 5 } \end{array}\]
התוצאות זהות.
כפי שאנו רואים, הסדר בו אנו מוסיפים לא משנה!
מה לגבי הכפלת 5 ו -3?
\[\begin{array} { c c } { 5 \cdot 3 } & { 3 \cdot 5 } \\ { 15 } & { 15 } \\ { 5 \cdot 3=} &{3 \cdot 5 } \end{array}\]
שוב, התוצאות זהות!
הסדר שבו אנו מתרבים לא משנה!
דוגמאות אלה ממחישות את המאפיין הקומוטטיבי. בעת הוספה או הכפלה, שינוי הסדר נותן את אותה תוצאה.
\[\begin{array} { l l } { \textbf { of Addition } } & { \text { If } a , b \text { are real numbers, then } \quad a + b = b + a } \\ { \textbf { of Multiplication } } & { \text { If } a , b \text { are real numbers, then } \quad a \cdot b = b \cdot a } \end{array}\]
בעת הוספה או הכפלה, שינוי הסדר נותן את אותה תוצאה.
הרכוש הקומוטטיבי קשור לסדר. אם תשנה את סדר המספרים בעת הוספה או הכפלה, התוצאה זהה.
מה לגבי חיסור? האם סדר משנה כאשר אנו מחסירים מספרים? האם 7—3 נותן את אותה תוצאה כמו 3—7?
\[\begin{array} { c c } { 7 - 3 } & { 3 - 7 } \\ { 4 } & { - 4 } \end{array}\]
\[\begin{aligned} 4 & \neq - 4 \\ 7 - 3 & \neq 3 - 7 \end{aligned}\]
התוצאות אינן זהות.
מכיוון ששינוי סדר החיסור לא נתן את אותה תוצאה, אנו יודעים שחיסור אינו קומוטטיבי.
בואו נראה מה קורה כשאנחנו מחלקים שני מספרים. האם חלוקה קומוטטיבית?
\[\begin{array} { cc} { 12 \div 4 } & { 4 \div 12 } \\ { \frac { 12 } { 4 } } & { \frac { 4 } { 12 } } \\ { 3 } & { \frac { 1 } { 3 } } \end{array}\]
\[\begin{aligned} 3 \neq & \frac { 1 } { 3 } \\ 12 \div 4 & \neq 4 \div 12 \end{aligned}\]
התוצאות אינן זהות.
מאחר ששינוי סדר החלוקה לא נתן את אותה תוצאה, החלוקה אינה קומוטטיבית. המאפיינים הקומוטטיביים חלים רק על תוספת וכפל!
- תוספת וכפל הם קומוטטיביים.
- חיסור וחלוקה אינם קומוטטיביים.
אם היית מתבקש לפשט את הביטוי הזה, איך היית עושה את זה ומה תהיה התשובה שלך?
\[7 + 8 + 2\]
יש אנשים שיחשבו \(7+8\) שהוא 15 ואז \(15+2\) הוא 17. אחרים עשויים להתחיל עם \(8+2\) עושה 10 ואז \(7+10\) עושה 17.
כך או כך נותן את אותה התוצאה. זכור, אנו משתמשים בסוגריים כסמלי קיבוץ כדי לציין איזו פעולה יש לבצע תחילה.
\[\begin{array} { ll } { \text{ Add } 7 + 8 . } & { ( 7 + 8 ) + 2 } \\ { \text { Add. } } & { 15 + 2 } \\ { \text { Add. } } & { 17 } \\ \\ { } & { 7 + ( 8 + 2 ) } \\ { \text { Add } 8 + 2 . } & { 7 + 10 } \\ { \text { Add. } } & { 77 } \\\\ { ( 7 + 8 ) + 2 = 7 + ( 8 + 2 ) } \end{array}\]
בעת הוספת שלושה מספרים, שינוי קיבוץ המספרים נותן את אותה תוצאה.
זה נכון גם לגבי הכפל.
\[\begin{array} { ll } { } & { (5\cdot \frac{1}{3})\cdot 3 } \\ { \text { Multiply. } 5\cdot \frac{1}{3} } & { \frac{5}{3}\cdot 3 } \\ { \text { Multiply. } } & { 5 } \\ \\ { } & { 5\cdot (\frac{1}{3}\cdot 3) } \\ { \text { Multiply. } \frac{1}{3}\cdot 3 } & { 5\cdot 1 } \\ { \text { Multiply. } } & { 5 } \\ \\ { (5\cdot \frac{1}{3})\cdot 3 = 5\cdot (\frac{1}{3}\cdot 3) } \end{array}\]
כאשר מכפילים שלושה מספרים, שינוי קיבוץ המספרים נותן את אותה תוצאה.
אתה בטח יודע את זה, אבל המינוח עשוי להיות חדש לך. דוגמאות אלה ממחישות את המאפיין האסוציאטיבי.
\[\begin{array} { l l } { \textbf { of Addition } } & { \text { If } a , b , c \text { are real numbers, then } ( a + b ) + c = a + ( b + c ) } \\ { \textbf { of Multiplication } } & { \text { If } a , b , c \text { are real numbers, then } ( a \cdot b ) \cdot c = a \cdot ( b \cdot c ) } \end{array}\]
בעת הוספה או הכפלה, שינוי הקיבוץ נותן את אותה תוצאה.
בואו נחשוב שוב על הכפלה\(5\cdot \frac{1}{3}\cdot 3\). קיבלנו את אותה התוצאה בשני הכיוונים, אבל איזו דרך הייתה קלה יותר? הכפלה \(\frac{1}{3}\) ו -3 תחילה, כפי שמוצג לעיל בצד ימין, מבטלת את השבר בשלב הראשון. שימוש במאפיין האסוציאטיבי יכול להקל על המתמטיקה!
המאפיין האסוציאטיבי קשור לקיבוץ. אם נשנה את אופן קיבוץ המספרים, התוצאה תהיה זהה. שימו לב שמדובר באותם שלושה מספרים באותו סדר - ההבדל היחיד הוא הקיבוץ.
ראינו שהחיסור והחלוקה אינם קומוטטיביים. הם גם לא אסוציאטיביים.
כשמפשטים ביטוי, תמיד כדאי לתכנן מה יהיו הצעדים. על מנת לשלב מונחים דומים בדוגמה הבאה, נשתמש במאפיין הקומוטטיבי של תוספת כדי לכתוב את המונחים הדומים יחד.
פשט:\(18p+6q+15p+5q\).
- תשובה
-
\[\begin{array} { l l} {} &{18p+6q+15p+5q}\\ \\{ \text { Use the commutative property of addition } } &{} \\ { \text {to re-order so that like terms are together.} } &{18p+15p+ 6q+5q} \\ \\ {\text{Add like terms.}} &{33p + 11q} \end{array}\]
פשט:\(23r+14s+9r+15s\).
- תשובה
-
\(32r+29s\)
פשט:\(37m+21n+4m−15n\).
- תשובה
-
\(41m+6n\)
כאשר עלינו לפשט ביטוי אלגברי s, לעתים קרובות אנו יכולים להקל על העבודה על ידי יישום המאפיין הקומוטטיבי או האסוציאטיבי תחילה, במקום לבצע באופן אוטומטי את סדר הפעולות. בעת הוספה או חיסור של שברים, שלב תחילה את אלה עם מכנה משותף.
פשט: \((\frac{5}{13} + \frac{3}{4}) + \frac{1}{4}\)
- תשובה
-
\[\begin{array} { l l } {} &{(\frac{5}{13} + \frac{3}{4}) + \frac{1}{4}} \\{ \text { Notice that the last } 2 \text { terms have a } } \\ { \text { common denominator, so change the } } &{\frac { 5 } { 13 } + \left( \frac { 3 } { 4 } + \frac { 1 } { 4 } \right)}\\ { \text { grouping. } } &{}\\ \\ {\text{Add in parentheses first.}} &{\frac{5}{13} + (\frac{4}{4})} \\ \\ {\text{Simplify the fraction.}} &{\frac{5}{13} + 1} \\ \\ {\text{Add.}} &{1\frac{5}{13}} \\ \\ {\text{Convert to an improper fraction.}} &{\frac{18}{13}} \end{array}\]
פשט: \((\frac{7}{15} + \frac{5}{8}) + \frac{3}{8}\)
- תשובה
-
\(1\frac{7}{15}\)
פשט: \((\frac{2}{9} + \frac{7}{12}) + \frac{5}{12}\)
- תשובה
-
\(1\frac{2}{9}\)
השתמש במאפיין האסוציאטיבי כדי לפשט\(6(3x)\).
- תשובה
-
השתמש במאפיין האסוציאטיבי של הכפל,\((a\cdot b)\cdot c=a\cdot (b\cdot c)\), כדי לשנות את הקיבוץ.
\[\begin{array} { ll } {} &{ 6 ( 3 x ) } \\ { \text { Change the grouping. } } &{(6\cdot 3)x} \\ { \text { Multiply in the parentheses. } } &{18} \end{array}\]
שימו לב שאנחנו יכולים להכפיל \(6\cdot 3\) אבל לא יכולנו להכפיל \(3x\) בלי שיהיה לנו ערך עבור\(x\).
השתמש במאפיין האסוציאטיבי כדי לפשט\(8(4x)\).
- תשובה
-
\(32x\)
השתמש במאפיין האסוציאטיבי כדי לפשט\(-9(7y)\).
- תשובה
-
\(-63y\)
השתמש בזהות ובמאפיינים ההפוכים של תוספת וכפל
מה קורה כשאנחנו מוסיפים 0 למספר כלשהו? הוספת 0 לא משנה את הערך. מסיבה זו אנו מכנים 0 זהות התוסף.
לדוגמה,
\[\begin{array} { c c c } { 13 + 0 } & { - 14 + 0 } & { 0 + ( - 8 ) } \\ { 13 } & { - 14 } & { - 8 } \end{array}\]
דוגמאות אלה ממחישות את נכס הזהות של התוספת הקובע כי עבור כל מספר ממשי\(a\), \(a+0=a\) ו\(0+a=a\).
מה קורה כשאנחנו מכפילים מספר כלשהו באחד? הכפלת 1 לא משנה את הערך. אז אנחנו קוראים 1 הזהות הכפולה.
לדוגמה, \[\begin{array} { r r r } { 43 \cdot 1 } & { - 27 \cdot 1 } & { 1 \cdot \frac { 3 } { 5 } } \\ { 43 } & { - 27 } & { \frac { 3 } { 5 } } \end{array}\]
דוגמאות אלה ממחישות את תכונת הזהות של הכפל הקובעת כי עבור כל מספר ממשי\(a\), \(a\cdot 1=a\) ו\(1\cdot a=a\).
אנו מסכמים את מאפייני הזהות להלן.
\[\begin{array} { l l} { \textbf {of addition}\text{ For any real number } a : } &{ a + 0 = a \quad 0 + a = a } \\ { \textbf{0} \text { is the}\textbf{ additive identity } } \\ {\textbf {of multiplication}\text{ For any real number } a : } &{ a \cdot 1 = a \quad 1 \cdot a = a } \\ { \textbf{1}\text{ is the}\textbf{ multiplicative identity } } \end{array}\]

שימו לב שבכל מקרה, המספר החסר היה ההפך מהמספר!
אנחנו קוראים\(−a\). התוסף ההפוך של א. ההפך ממספר הוא ההפוך התוסף שלו. מספר וההיפך שלו מוסיפים לאפס, שהוא הזהות התוסף. זה מוביל לתכונה ההפוכה של תוספת הקובעת עבור כל מספר \(a, a+(−a)=0\) ממשי. זכור, מספר וההיפך שלו מוסיפים לאפס.
איזה מספר מוכפל \(\frac{2}{3}\) נותן את הזהות הכפולה, 1? במילים אחרות, \(\frac{2}{3}\) פעמים מה התוצאה ב -1?

איזה מספר כפול 2 נותן את הזהות הכפולה, 1? במילים אחרות 2 פעמים מה התוצאה 1?

שימו לב שבכל מקרה, המספר החסר היה ההדדי של המספר!
אנו מכנים \(\frac{1}{a}\) את ההיפוך הכפול של א. ההדדי של מספר aa הוא ההופכי הכפל שלו. מספר וההדדיות שלו מתרבים לאחד, שהוא הזהות הכפולה. זה מוביל לתכונה ההפוכה של הכפל הקובעת כי עבור כל מספר \(a, a\neq 0, a\cdot \frac{1}{a}=1\) ממשי.
נציין רשמית את המאפיינים ההפוכים כאן:
\[\begin{array} { l l l } { \textbf { of addition } } &{ \text { For any real number } a,} &{a + (-a) = 0}\\{} &{-a \text{. is the}\textbf{ additive inverse} \text{ of }a} &{}\\ {} &{ \text { A number and its opposite add to zero. } }&{}\\ \\{ \textbf { of multiplication } } &{ \text { For any real number } a, a\neq 0} &{a\cdot \frac{1}{a} = 1}\\{} &{\frac{1}{a} \text{. is the}\textbf{ multiplicative inverse} \text{ of }a} &{}\\ {} &{ \text { A number and its reciprocal multiply to zero. } }&{} \end{array}\]
מצא את התוסף ההפוך של
- \(\frac{5}{8}\)
- \(0.6\)
- \(-8\)
- \(-\frac{4}{3}\)
- תשובה
-
כדי למצוא את התוסף ההפוך, אנו מוצאים את ההפך.
- ההיפוך התוסף של \(\frac{5}{8}\) הוא ההפך מ. \(\frac{5}{8}\) ההיפוך התוסף של הוא \(\frac{5}{8}\) \(-\frac{5}{8}\)
- ההיפוך התוסף של \(0.6\) הוא ההפך מ. \(0.6\) ההיפוך התוסף של \(0.6\) הוא\(-0.6\).
- ההיפוך התוסף של \(-8\) הוא ההפך מ. \(-8\) אנו כותבים את ההפך מ- \(-8\) AS \(-(-8)\) ואז מפשטים אותו ל\(8\). לכן, ההפוך התוסף של \(-8\) הוא\(8\).
- ההיפוך התוסף של \(-\frac{4}{3}\) הוא ההפך מ. \(-\frac{4}{3}\) אנחנו כותבים את זה כמו\(-(-\frac{4}{3})\), ולאחר מכן לפשט\(\frac{4}{3}\). לפיכך, ההיפוך התוסף של \(-\frac{4}{3}\) הוא\(\frac{4}{3}\).
מצא את התוסף ההפוך של
- \(\frac{7}{9}\)
- \(1.2\)
- \(-14\)
- \(-\frac{9}{4}\)
- תשובה
-
- \(-\frac{7}{9}\)
- \(-1.2\)
- \(14\)
- \(\frac{9}{4}\)
מצא את התוסף ההפוך של
- \(\frac{7}{13}\)
- \(8.4\)
- \(-46\)
- \(-\frac{5}{2}\)
- תשובה
-
- \(-\frac{7}{13}\)
- \(-8.4\)
- \(46\)
- \(\frac{5}{2}\)
מצא את ההופכי הכפל של
- \(9\)
- \(-\frac{1}{9}\)
- \(0.9\)
- תשובה
-
כדי למצוא את ההופכי הכפול, אנו מוצאים את ההדדי.
- ההיפוך הכפול של \(9\) הוא ההדדי של\(9\), שהוא. \(\frac{1}{9}\) לכן, ההיפוך הכפול של \(9\) הוא. \(\frac{1}{9}\)
- ההיפוך הכפול של \(-\frac{1}{9}\) הוא ההדדי של\(-\frac{1}{9}\), שהוא. \(−9\) לפיכך, ההיפוך הכפול של \(-\frac{1}{9}\) הוא. \(-9\)
- כדי למצוא את ההיפוך הכפול של\(0.9\), אנו ממירים תחילה \(0.9\) לשבר,. \(\frac{9}{10}\) ואז אנו מוצאים את ההדדיות של השבר. ההדדי של \(\frac{9}{10}\) הוא\(\frac{10}{9}\). אז ההיפוך הכפול של \(0.9\) הוא. \(\frac{10}{9}\)
מצא את ההופכי הכפל של
- \(4\)
- \(-\frac{1}{7}\)
- \(0.3\)
- תשובה
-
- \(\frac{1}{4}\)
- \(-7\)
- \(\frac{10}{3}\)
מצא את ההופכי הכפל של
- \(18\)
- \(-\frac{4}{5}\)
- \(0.6\)
- תשובה
-
- \(\frac{1}{18}\)
- \(-\frac{5}{4}\)
- \(\frac{5}{3}\)
השתמש במאפיינים של אפס
מאפיין הזהות של התוספת אומר שכאשר אנו מוסיפים 0 למספר כלשהו, התוצאה היא אותו מספר. מה קורה כשאנחנו מכפילים מספר ב- 0? הכפלת 0 הופכת את המוצר לשווה לאפס.
עבור כל מספר אמיתי א.
\[a \cdot 0 = 0 \quad 0 \cdot a = 0\]
התוצר של כל מספר ממשי ו- 0 הוא 0.
מה לגבי חלוקה הכוללת אפס? מה זה\(0\div 3\)? חשבו על דוגמה אמיתית: אם אין עוגיות בצנצנת העוגיות ושלושה אנשים אמורים לשתף אותן, כמה עוגיות כל אדם מקבל? אין עוגיות לשיתוף, כך שכל אדם מקבל 0 עוגיות. אז,
\[0\div 3 = 0\]
אנו יכולים לבדוק חלוקה עם עובדת הכפל הקשורה.
\[12 \div 6 = 2 \text { because } 2 \cdot 6 = 12\]
אז אנחנו יודעים \(0\div 3=0\) כי\(0\cdot 3=0\).
עבור כל מספר אמיתי a, למעט \(0, \frac{0}{a}=0\) ו\(0\div a=0\).
אפס חלקי כל מספר ממשי מלבד אפס הוא אפס.
עכשיו תחשוב על חלוקה באפס. מה התוצאה של חלוקת 4 על 0? חשבו על עובדת הכפל הקשורה: \(4\div 0=?\) פירושו\(?\cdot 0=4\). האם יש מספר כפול 0 נותן 4? מכיוון שכל מספר אמיתי כפול 0 נותן 0, אין מספר אמיתי שניתן להכפיל ב- 0 כדי להשיג 4.
אנו מסיקים כי אין תשובה \(4\div 0\) ולכן אנו אומרים כי חלוקה ב- 0 אינה מוגדרת.
עבור כל מספר ממשי a, למעט \(0, \frac{a}{0}\) \(a\div 0\) ואינם מוגדרים.
חלוקה באפס אינה מוגדרת.
אנו מסכמים את המאפיינים של אפס להלן.
כפל באפס: לכל מספר ממשי א,
\[a \cdot 0 = 0 \quad 0 \cdot a = 0 \quad \text { The product of any number and } 0 \text { is } 0\]
חלוקת אפס, חלוקה באפס: לכל מספר ממשי \(a, a\neq 0\)
\[\begin{array} { l l } { \frac { 0 } { a } = 0 } & { \text { Zero divided by any real number, except itself is zero. } } \\ { \frac { a } { 0 } \text { is undefined } } & { \text { Division by zero is undefined. } } \end{array}\]
פשט:
- \(-8\cdot 0\)
- \(\frac{0}{-2}\)
- \(\frac{-32}{0}\)
- תשובה
-
- \[\begin{array} { cc } { } &{-8\cdot 0}\\{\text{The product of any real number and 0 is 0}} &{0}\end{array}\]
- \[\begin{array} { ll } { } &{\frac{0}{-2}}\\{\text{Zero divided by any real number, except}} &{} \\ {\text{itself, is 0}} &{0}\end{array}\]
- \[\begin{array} { ll } { } &{\frac{-32}{0}}\\ {\text{Division by 0 is undefined.}} &{\text{undefined}} \end{array}\]
פשט:
- \(-14\cdot 0\)
- \(\frac{0}{-6}\)
- \(\frac{-2}{0}\)
- תשובה
-
- \(0\)
- \(0\)
- לא מוגדר
פשט:
- \(0(-17)\)
- \(\frac{0}{-10}\)
- \(\frac{-5}{0}\)
- תשובה
-
- \(0\)
- \(0\)
- לא מוגדר
כעת נתרגל שימוש בתכונות של זהויות, היפוכים ואפס כדי לפשט ביטויים.
פשט:
- \(\frac{0}{n + 5}\), איפה \(n\neq −5\)
- \(\frac{10 - 3p}{0}\)איפה \(10 - 3p \neq 0\)
- תשובה
-
- \[\begin{array} { ll } { } &{\frac{0}{n + 5}}\\ {\text { Zero divided by any real number except }} &{0} \\ { \text { itself is } 0.} &{} \end{array}\]
- \[\begin{array} { ll } { } &{\frac{10 - 3p}{0}}\\ {\text { Division by 0 is undefined }} &{\text{undefined}} \end{array}\]
פשט:\(−84n+(−73n)+84n\).
- תשובה
-
\[\begin{array} { l l } { } &{−84n+(−73n)+84n} \\ { \text { Notice that the first and third terms are } } &{}\\ { \text { opposites; use the commutative property of } } &{- 84 n + 84 n + ( - 73 n ) } \\ { \text { addition to re-order the terms. } } &{} \\ \\ { \text { Add left to right. } } &{0 + (-73)}\\ \\{ \text { Add. } } &{-73n} \end{array}\]
פשט:\(−27a+(−48a)+27a\).
- תשובה
-
\(−48a\)
פשט:\(39x+(−92x)+(−39x)\).
- תשובה
-
\(−92x\)
כעת נראה כיצד זיהוי הדדיות מועיל. לפני הכפלה משמאל לימין, חפש הדדיות - המוצר שלהם הוא 1.
פשט: \(\frac{7}{15}\cdot\frac{8}{23}\cdot\frac{15}{7}\)
- תשובה
-
\[\begin{array} { l l } { } &{\frac{7}{15}\cdot\frac{8}{23}\cdot\frac{15}{7}} \\ { \text { Notice that the first and third terms are } } &{}\\ { \text { reciprocals, so use the commutative } } &{\frac{7}{15}\cdot\frac{15}{7}\cdot\frac{8}{23}} \\ { \text { property of multiplication to re-order the } } &{} \\ { \text { factors. } } &{}\\ \\{ \text { Multiply left to right. } } &{1\cdot\frac{8}{23}} \\\\{\text{Multiply.}} &{\frac{8}{23}}\end{array}\]
פשט: \(\frac{9}{16}\cdot\frac{5}{49}\cdot\frac{16}{9}\)
- תשובה
-
\(\frac{5}{49}\)
פשט: \(\frac{6}{17}\cdot\frac{11}{25}\cdot\frac{17}{6}\)
- תשובה
-
\(\frac{11}{25}\)
פשט:
- \(\frac{0}{m + 7}\), איפה \(m \neq -7\)
- \(\frac{18 - 6c}{0}\), איפה \(18 - 6c \neq 0\)
- תשובה
-
- 0
- לא מוגדר
פשט:
- \(\frac{0}{d - 4}\), איפה \(d \neq 4\)
- \(\frac{15 - 4q}{0}\), איפה \(15 - 4q \neq 0\)
- תשובה
-
- 0
- לא מוגדר
פשט: \(\frac{3}{4}\cdot\frac{4}{3}(6x + 12)\)
- תשובה
-
\[\begin{array} { l l } { } &{\frac{3}{4}\cdot\frac{4}{3}(6x + 12)} \\ { \text { There is nothing to do in the parentheses, } } &{}\\ { \text { so multiply the two fractions first—notice, } } &{1(6x + 12)} \\ { \text { they are reciprocals. } } &{} \\ \\{ \text { Simplify by recognizing the multiplicative } } &{} \\{\text{ identity.}} &{6x + 12} \end{array}\]
פשט: \(\frac{2}{5}\cdot\frac{5}{2}(20y + 50)\)
- תשובה
-
\(20y + 50\)
פשט: \(\frac{3}{8}\cdot\frac{8}{3}(12z + 16)\)
- תשובה
-
\(12z + 16\)
פשט ביטויים באמצעות המאפיין החלוקתי
נניח ששלושה חברים הולכים לקולנוע. כל אחד מהם צריך 9.25 דולר - זה 9 דולר ורבע אחד - כדי לשלם עבור הכרטיסים שלהם. כמה כסף הם צריכים כולם ביחד?
אתה יכול לחשוב על דולרים בנפרד מן הרבעונים. הם צריכים 3 פעמים $9 אז $27, ו 3 פעמים 1 ברבעון, אז 75 סנט. בסך הכל הם זקוקים ל -27.75 דולר. אם אתה חושב לעשות את המתמטיקה בדרך זו, אתה משתמש במאפיין החלוקה.
\[\begin{array} { rr } {\text { If } a , b , c \text { are real numbers, then }} &{a ( b + c ) = a b + a c} \\ \\{ \text { Also,} } &{( b + c ) a = b a + c a} \\ {} &{a ( b - c ) = a b - a c } &{} \\{} &{( b - c ) a = b a - c a } \end{array}\]
בחזרה לחברים שלנו בסרטים, נוכל למצוא את הסכום הכולל של הכסף שהם צריכים ככה:
\[\begin{array} { c } { 3 ( 9.25 ) } \\ { 3 ( 9 + 0.25 ) } \\ { 3 ( 9 ) + 3 ( 0.25 ) } \\ { 27 + 0.75 } \\ \\ { 27.75 } \end{array}\]
באלגברה, אנו משתמשים במאפיין החלוקה כדי להסיר סוגריים כאשר אנו מפשטים ביטויים.
לדוגמה, אם אנו מתבקשים לפשט את הביטוי\(3(x+4)\), סדר הפעולות אומר לעבוד בסוגריים תחילה. אך איננו יכולים להוסיף x ו- 4, מכיוון שהם אינם דומים למונחים. אז אנו משתמשים במאפיין החלוקה, כפי שמוצג בתרגיל\(\PageIndex{31}\).
פשט:\(3(x+4)\).
- תשובה
-
\[\begin{array} { l l } { } & { 3 ( x + 4 ) } \\ { \text { Distribute. } } & { 3 \cdot x + 3 \cdot 4 } \\ { \text { Multiply. } } & { 3 x + 12 } \end{array}\]
פשט:\(4(x+2)\).
- תשובה
-
\(4x + 8\)
פשט:\(6(x+7)\).
- תשובה
-
\(6x + 42\)
חלק מהתלמידים מוצאים שזה מועיל לצייר חצים כדי להזכיר להם כיצד להשתמש במאפיין החלוקה. ואז השלב הראשון בתרגיל \(\PageIndex{31}\) ייראה כך:
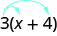
פשט:\(8(\frac{3}{8}x+\frac{1}{4})\).
- תשובה
-
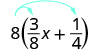
להפיץ. 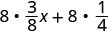
להכפיל. 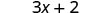
פשט:\(6(\frac{5}{6}y+\frac{1}{2})\).
- תשובה
-
\(5y + 3\)
פשט:\(12(\frac{1}{3}n+\frac{3}{4})\).
- תשובה
-
\(4n + 9\)
השימוש בנכס החלוקתי כפי שמוצג בתרגיל \(\PageIndex{37}\) יהיה שימושי מאוד כאשר אנו פותרים יישומי כסף בפרקים מאוחרים יותר.
פשט:\(100(0.3+0.25q)\).
- תשובה
-
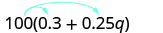
להפיץ. 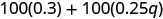
להכפיל. 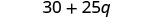
פשט:\(100(0.7+0.15p)\).
- תשובה
-
\(70 + 15p\)
פשט:\(100(0.04+0.35d)\).
- תשובה
-
\(4 + 35d\)
כאשר אנו מפיצים מספר שלילי, עלינו להקפיד במיוחד על מנת לתקן את השלטים!
פשט:\(−2(4y+1)\).
- תשובה
-
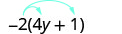
להפיץ. 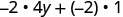
להכפיל. 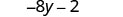
פשט:\(−3(6m+5)\).
- תשובה
-
\(−18m-15)\)
פשט:\(−6(8n+11)\).
- תשובה
-
\(−48n- 66)\)
פשט:\(−11(4-3a)\).
- תשובה
-
להפיץ. 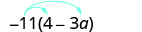
להכפיל. 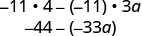
לפשט. 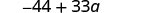
שים לב שאתה יכול גם לכתוב את התוצאה כ\(33a−44\). אתה יודע למה?
פשט:\(−5(2-3a)\).
- תשובה
-
\(10+ 15a\)
פשט:\(−7(8-15y)\).
- תשובה
-
\(-56 + 105y\)
תרגיל \(\PageIndex{46}\) יראה כיצד להשתמש במאפיין החלוקה כדי למצוא את ההפך מביטוי.
פשט:\(−(y+5)\).
- תשובה
-
\[\begin{array} { ll } {} &{-(y + 5)} \\ \\{ \text {Multiplying by -1 results in the opposite.} } &{-1( y + 5 )} \\ \\ {\text{Distribute.}} &{-1\cdot y + (-1)\cdot 5}\\ \\{\text{Simplify.}} &{-y + (-5)} \\ \\ {} &{-y - 5} \end{array}\]
פשט:\(−(z-11)\).
- תשובה
-
\(-z + 11\)
פשט:\(−(x -4)\).
- תשובה
-
\(-x + 4\)
יהיו מקרים בהם נצטרך להשתמש בנכס החלוקה כחלק מסדר הפעולות. התחל בהסתכלות על הסוגריים. אם לא ניתן לפשט את הביטוי שבתוך הסוגריים, השלב הבא יהיה הכפל באמצעות המאפיין החלוקתי, המסיר את הסוגריים. שתי הדוגמאות הבאות ימחישו זאת.
פשט:\(8−2(x + 3)\).
הקפד לבצע את סדר הפעולות. הכפל מגיע לפני החיסור, לכן נחלק את ה -2 תחילה ואז נחסר.
- תשובה
-
\[\begin{array} { ll } {} &{8−2(x + 3)} \\ \\{ \text {Distribute.} } &{8−2\cdot x -2\cdot 3} \\ \\ {\text{Multiply.}} &{8 - 2x - 6}\\ \\{\text{Combine like terms.}} &{-2x + 2} \end{array}\]
פשט:\(9−3(x + 2)\).
- תשובה
-
\(3 - 3x\)
פשט:\(7x−5(x + 4)\).
- תשובה
-
\(2x - 20\)
פשט:\(4(x - 8)−(x + 3)\).
- תשובה
-
\[\begin{array} { ll } {} &{4(x - 8)−(x + 3)} \\ \\{ \text {Distribute.} } &{4x - 32 - x - 3} \\ \\{\text{Combine like terms.}} &{3x - 35} \end{array}\]
פשט:\(6(x - 9)−(x + 12)\).
- תשובה
-
\(5x - 66\)
פשט:\(8(x - 1)-(x + 5)\).
- תשובה
-
\(7x - 13\)
כל המאפיינים של מספרים ממשיים בהם השתמשנו בפרק זה מסוכמים בטבלה\(\PageIndex{1}\).
| רכוש קומוטטיבי | |
| של תוספת אם a, b הם מספרים ממשיים, אז של כפל אם a, b הם מספרים ממשיים, אז |
\(a+b=b+a\) \(a\cdot b=b\cdot a\) |
| רכוש אסוציאטיבי | |
| אם a, b, c הם מספרים ממשיים, אז של כפל אם a, b, c הם מספרים ממשיים, אז |
\((a+b)+c=a+(b+c)\) \((a\cdot b)\cdot c=a\cdot (b\cdot c)\) |
| רכוש חלוקתי | |
| אם a, b, c הם מספרים ממשיים, | \(a(b+c)=ab+ac\) |
| נכס זהות | |
|
של תוספת עבור כל מספר ממשי a: של כפל עבור כל מספר ממשי a: |
\(a+0=a\) \(0+a=a\) \(1·a=a\) |
| נכס הפוך | |
| של תוספת עבור כל מספר ממשי a, \(−a\) הוא ההיפוך התוסף של a של כפל שכן כל מספר ממשי \(a,a\neq 0\) \(\frac{1}{a}\) הוא ההיפוך הכפול של a |
\(a+(−a)=0\) \(a\cdot\frac{1}{a}=1\) |
| מאפיינים של אפס | |
|
עבור כל מספר אמיתי א, עבור כל מספר אמיתי \(a,a\neq 0\) |
\(a\cdot 0=0\) \(0\cdot a=0\) \(\frac{0}{a} = 0\) |
מושגי מפתח
- רכוש קומוטטיבי של
- תוספת: אם a, b הם מספרים ממשיים, אז\(a+b=b+a\).
- כפל: אם a, b הם מספרים ממשיים, אז\(a\cdot b=b\cdot a\). בעת הוספה או הכפלה, שינוי הסדר נותן את אותה תוצאה.
- רכוש אסוציאטיבי של
- תוספת: אם a, b, c הם מספרים ממשיים, אז\((a+b)+c=a+(b+c)\).
- כפל: אם a, b, c הם מספרים ממשיים, אז\((a\cdot b)\cdot c=a\cdot (b\cdot c)\).
בעת הוספה או הכפלה, שינוי הקיבוץ נותן את אותה תוצאה.
- נכס חלוקתי: אם a, b, c הם מספרים ממשיים, אז
- \(a(b+c)=ab+ac\)
- \((b+c)a=ba+ca\)
- \(a(b-c)=ab-ac\)
- \((b+c)a=ba+ca\)
- נכס זהות
- של תוספת: עבור כל מספר ממשי a: \(a+0=a\)
0 הוא הזהות הנוספת - של כפל: עבור כל מספר ממשי a: \(a\cdot 1=a \quad 1·a=a\)
1 1 הוא הזהות הכפולה
- של תוספת: עבור כל מספר ממשי a: \(a+0=a\)
- נכס הפוך
- תוספת: לכל מספר אמיתי\(a, a+(−a)=0\). מספר וההיפך שלו מוסיפים לאפס. \(−a\)הוא ההופכי התוסף של א.
- של כפל: לכל מספר אמיתי\(a,(a\neq 0)a\cdot\frac{1}{a}=1\). מספר וההדדיות שלו מתרבים לאחד. \(\frac{1}{a}\)הוא ההופכי הכפול של א.
- מאפיינים של אפס
- עבור כל מספר ממשי a,
\(a\cdot 0=0 \quad 0·a=0\) — התוצר של כל מספר ממשי ו-0 הוא 0. - \(\frac{0}{a}=0\)עבור \(a\neq 0\) - אפס חלקי כל מספר ממשי למעט אפס הוא אפס.
- \(\frac{a}{0}\)אינו מוגדר - חלוקה באפס אינה מוגדרת.
- עבור כל מספר ממשי a,


