Skip to main content
Global

1.9: המספרים האמיתיים

  1. Last updated
  2. Save as PDF
  • Page ID
    205668

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    מטרות למידה

    בסוף פרק זה תוכל:

    • פשט ביטויים עם שורשים מרובעים
    • זהה מספרים שלמים, מספרים רציונליים, מספרים לא רציונליים ומספרים ממשיים
    • אתר שברים בשורת המספרים
    • אתר עשרונים בשורת המספרים
    הערה

    מבוא יסודי יותר לנושאים המכוסים בחלק זה ניתן למצוא בפרקי הפרה-אלגברה, עשרוניות ומאפיינים של מספרים אמיתיים.

    פשט ביטויים עם שורשים מרובעים

    זכרו שכאשר מספר \(n\) מוכפל בעצמו, אנו כותבים \(n^{2}\) וקוראים אותו "\(n\)בריבוע". התוצאה נקראת הריבוע של\(n\). לדוגמה,

    \[\begin{array} { l l } { 8 ^ { 2 } } & { \text { read '8 squared' } } \\ { 64 } & { 64 \text { is called the square of } 8 \text { . } } \end{array}\]

    באופן דומה, 121 הוא הריבוע של 11, כי \(11^{2}\) הוא 121.

    ריבוע של מספר

    אם\(n^{2}=m\), אז \(m\) הוא הריבוע של\(n\).

    הערה

    ביצוע פעילות המתמטיקה המניפולטיבית "מספרים מרובעים" יעזור לך לפתח הבנה טובה יותר של מספרים מרובעים מושלמים.

    השלם את הטבלה הבאה כדי להציג את הריבועים של מספרי הספירה 1 עד 15.

    יש טבלה עם שתי שורות ו -17 עמודות. השורה הראשונה קוראת משמאל לימין מספר, n, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 ו- 15. השורה השנייה קוראת משמאל לימין ריבוע, n בריבוע, ריק, ריק, ריק, ריק, ריק, ריק, ריק, 64, ריק, ריק, 121, ריק, ריק, ריק, ריק.
    איור \(\PageIndex{1}\)

    המספרים בשורה השנייה נקראים מספרים מרובעים מושלמים. זה יהיה מועיל ללמוד לזהות את המספרים המרובעים המושלמים.

    הריבועים של מספרי הספירה הם מספרים חיוביים. מה לגבי הריבועים של מספרים שליליים? אנו יודעים שכאשר הסימנים של שני מספרים זהים, המוצר שלהם חיובי. אז הריבוע של כל מספר שלילי הוא גם חיובי.

    \[( - 3 ) ^ { 2 } = 9 \quad ( - 8 ) ^ { 2 } = 64 \quad ( - 11 ) ^ { 2 } = 121 \quad ( - 15 ) ^ { 2 } = 225\]

    שמתם לב שהריבועים האלה זהים לריבועים של המספרים החיוביים?

    לפעמים נצטרך להסתכל על הקשר בין מספרים לריבועים שלהם הפוך. כי\(10^{2}=100\), אנחנו אומרים 100 הוא ריבוע של 10. אנו גם אומרים כי 10 הוא שורש ריבועי של 100. מספר שהריבוע שלו הוא מ"מ נקרא שורש ריבועי של\(m\).

    שורש ריבועי של מספר

    אם\(n^{2}=m\), אז \(n\) הוא שורש ריבועי של\(m\).

    שימו לב \((−10)^{2}=100\) גם, \(−10\) כך גם שורש ריבועי של\(100\). לכן, שניהם \(10\) \(−10\) והם שורשים מרובעים של\(100\).

    לכן, לכל מספר חיובי יש שני שורשים מרובעים - אחד חיובי ואחד שלילי. מה אם היינו רוצים רק את השורש הריבועי החיובי של מספר חיובי? הסימן הרדיקלי,\(\sqrt{m}\), מציין את השורש הריבועי החיובי. השורש הריבועי החיובי נקרא השורש הריבועי העיקרי. כאשר אנו משתמשים בסימן הרדיקלי זה תמיד אומר שאנחנו רוצים את השורש הריבועי העיקרי.

    אנו משתמשים גם בסימן הרדיקלי לשורש הריבועי של אפס. בגלל\(0^{2}=0, \sqrt{0}=0\). שימו לב שלאפס יש רק שורש ריבועי אחד.

    סימון שורש ריבועי

    \(\sqrt{m}\)נקרא "השורש הריבועי של\(m\)"

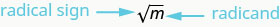
    ניתן שורש ריבועי, עם חץ לסימן הרדיקלי (הוא נראה כמו סימן ביקורת עם קו אופקי המשתרע מקצהו הארוך) מסומן סימן רדיקלי וחץ למספר שמתחת לסימן הרדיקלי, המסומן רדיקנד.

    אם\(m = n^{2}\), אז\(\sqrt{m} = n\), עבור\(n\geq 0\).

    השורש הריבועי של\(m\),\(\sqrt{m}\), הוא המספר החיובי שהריבוע שלו הוא\(m\).

    מכיוון ש- 10 הוא השורש הריבועי העיקרי של 100, אנו כותבים\(\sqrt{100}=10\). ייתכן שתרצה להשלים את הטבלה הבאה כדי לעזור לך לזהות שורשים מרובעים.

    יש טבלה עם שתי שורות ו -15 עמודות. השורה הראשונה קוראת משמאל לימין שורש ריבועי של 1, שורש ריבועי של 4, שורש ריבועי של 9, שורש ריבועי של 16, שורש ריבועי של 25, שורש ריבועי של 36, שורש ריבועי של 49, שורש ריבועי של 64, שורש ריבועי של 81, שורש ריבועי של 100, שורש ריבועי של 121, שורש ריבועי של 144, שורש ריבועי של 169, שורש ריבועי של 196 ושורש ריבועי של 225. השורה השנייה מורכבת מכל החסר למעט התא העשירי מתחת לשורש הריבועי של 100, שקורא 10.
    איור \(\PageIndex{2}\)
    תרגיל \(\PageIndex{1}\)

    פשט:

    1. \(\sqrt{25}\)
    2. \(\sqrt{121}\)
    תשובה
    1. \[\begin{array} {ll} {} &{\sqrt{25}} \\ {\text {Since }5^{2} = 25} &{5} \end{array}\]
    2. \[\begin{array} {ll} {} &{\sqrt{121}} \\ {\text {Since }11^{2} = 121} &{11} \end{array}\]
    תרגיל \(\PageIndex{2}\)

    פשט:

    1. \(\sqrt{36}\)
    2. \(\sqrt{169}\)
    תשובה
    1. 6
    2. 13
    תרגיל \(\PageIndex{3}\)

    פשט:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    תשובה
    1. 4
    2. 14

    אנו יודעים שלכל מספר חיובי יש שני שורשים מרובעים והסימן הרדיקלי מציין את החיובי. אנחנו כותבים\(\sqrt{100)=10\). אם אנו רוצים למצוא את השורש הריבועי השלילי של מספר, אנו מציבים שלילי מול הסימן הרדיקלי. לדוגמה,\(-\sqrt{100)=-10\). אנו קוראים \(-\sqrt{100)\) כ"ההפך מהשורש הריבועי של 10".

    תרגיל \(\PageIndex{4}\)

    פשט:

    1. \(-\sqrt{9}\)
    2. \(-\sqrt{144}\)
    תשובה
    1. \[\begin{array} {ll} {} &{-\sqrt{9}} \\ {\text {The negative is in front of the radical sign.}} &{-3} \end{array}\]
    2. \[\begin{array} {ll} {} &{-\sqrt{144}} \\ {\text {The negative is in front of the radical sign.}} &{-12} \end{array}\]
    תרגיל \(\PageIndex{5}\)

    פשט:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    תשובה
    1. -2
    2. -15
    תרגיל \(\PageIndex{6}\)

    פשט:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    תשובה
    1. −9
    2. −10

    זיהוי מספרים שלמים, מספרים רציונליים, מספרים לא רציונליים ומספרים ממשיים

    כבר תיארנו מספרים כספירת מספר s, מספר שלם s ומספרים שלמים. מה ההבדל בין סוגים אלה של מספרים?

    \[\begin{array} { l l } { \text { Counting numbers } } & { 1,2,3,4 , \ldots } \\ { \text { Whole numbers } } & { 0,1,2,3,4 , \ldots } \\ { \text { Integers } } & { \dots - 3 , - 2 , - 1,0,1,2,3 , \ldots } \end{array}\]

    איזה סוג מספרים היינו מקבלים אם היינו מתחילים עם כל המספרים השלמים ואז נכלול את כל השברים? המספרים שהיו לנו מהווים את קבוצת המספרים הרציונליים. מספר רציונלי הוא מספר שניתן לכתוב כיחס של שני מספרים שלמים.

    מספר רציונלי

    מספר רציונלי הוא מספר מהצורה\(\dfrac{p}{q}\), כאשר p ו- q הם מספרים שלמים ו \(q \neq 0\)

    ניתן לכתוב מספר רציונלי כיחס בין שני מספרים שלמים.

    כל השברים החתומים, כגון\(\dfrac{4}{5}\),\(-\dfrac{7}{8}\),\(\dfrac{13}{4}\), \(-\dfrac{20}{3}\) הם מספרים רציונליים. כל מונה וכל מכנה הוא מספר שלם.

    האם מספרים שלמים הם מספרים רציונליים? כדי להחליט אם מספר שלם הוא מספר רציונלי, אנו מנסים לכתוב אותו כיחס של שני מספרים שלמים. ניתן לכתוב כל מספר שלם כיחס של מספרים שלמים במובנים רבים. לדוגמה, 3 שווה ערך ל \(\dfrac{3}{1}\)\(-\dfrac{6}{2}\),\(\dfrac{9}{3}\),\(\dfrac{12}{4}\), \(-\dfrac{15}{5} \ldots\)

    דרך קלה לכתוב מספר שלם כיחס של מספרים שלמים היא לכתוב אותו כשבר עם מכנה אחד.

    \[3 = \frac { 3 } { 1 } \quad - 8 = - \frac { 8 } { 1 } \quad 0 = \frac { 0 } { 1 }\]

    מכיוון שניתן לכתוב כל מספר שלם כיחס בין שני מספרים שלמים, כל המספרים השלמים הם מספרים רציונליים! זכרו שמספרי הספירה והמספרים השלמים הם גם מספרים שלמים, וכך גם הם רציונליים.

    מה לגבי מספרים עשרוניים? האם הם רציונליים? בואו נסתכל על כמה כדי לראות אם נוכל לכתוב כל אחד מהם כיחס של שני מספרים שלמים.

    כבר ראינו שמספרים שלמים הם מספרים רציונליים. המספר השלם \(−8\) יכול להיכתב כעשרוני\(−8.0\). אז, ברור, כמה עשרונים הם רציונליים.

    תחשוב על הנקודה העשרונית\(7.3\). האם נוכל לכתוב את זה כיחס של שני מספרים שלמים? כי \(7.3\) אומר\(7\dfrac{3}{10}\), אנחנו יכולים לכתוב את זה כשבר לא תקין,\(\dfrac{73}{10}\). כך \(7.3\) גם היחס בין המספרים השלמים \(73\) ו\(10\). זהו מספר רציונלי.

    באופן כללי, כל עשרוני שמסתיים לאחר מספר ספרות (כגון \(7.3\) או\(−1.2684\)) הוא מספר רציונלי. אנו יכולים להשתמש בערך המקום של הספרה האחרונה כמכנה בעת כתיבת העשרוני כשבר.

    תרגיל \(\PageIndex{7}\)

    כתוב כיחס בין שני מספרים שלמים:

    1. −27
    2. 7.31
    תשובה
    1. \[\begin{array} {ll} {} &{-27} \\ {\text {Write it as a fraction with denominator 1.}} &{\dfrac{-27}{1}} \end{array}\]
    2. \[\begin{array} {ll} {} &{7.31} \\ {\text {Write is as a mixed number. Remember.}} &{} \\ {\text {7 is the whole number and the decimal}} &{7\dfrac{31}{100}} \\ {\text {part, 0.31, indicates hundredths.}} &{} \\ {\text{Convert to an improper fraction.}} &{\dfrac{731}{100}} \end{array}\]

    אז אנו רואים ש -27 ו- 7.31 שניהם מספרים רציונליים, מכיוון שניתן לכתוב אותם כיחס של שני מספרים שלמים.

    תרגיל \(\PageIndex{8}\)

    כתוב כיחס בין שני מספרים שלמים:

    1. −24
    2. 3.57
    תשובה
    1. \(\dfrac{-24}{1}\)
    2. \(\dfrac{357}{100}\)
    תרגיל \(\PageIndex{9}\)

    כתוב כיחס בין שני מספרים שלמים:

    1. −19
    2. 8.41
    תשובה
    1. \(\dfrac{-19}{1}\)
    2. \(\dfrac{841}{100}\)
    בואו נסתכל על הצורה העשרונית של המספרים שאנו יודעים שהם רציונליים.

    ראינו שכל מספר שלם הוא מספר רציונלי, שכן \(a = \dfrac{a}{1}\) עבור כל מספר שלם,. \(a\) אנו יכולים גם לשנות כל מספר שלם לעשרוני על ידי הוספת נקודה עשרונית ואפס.

    \[\begin{array} { l l l l l l l } { \text { Integer } } & { - 2 } & { - 1 } & { 0 } & { 1 } & { 2 } & { 3 } \\ { \text { Decimal form } } & { - 2.0 } & { - 1.0 } & { 0.0 } & { 1.0 } & { 2.0 } & { 3.0 } \\ { } & { \text { These decimal numbers stop. } } \end{array}\]

    ראינו גם שכל שבר הוא מספר רציונלי. התבונן בצורה העשרונית של השברים ששקלנו לעיל.

    \[\begin{array} { l l l l } { \text { Ratio of integers } } & { \frac { 4 } { 5 } } & { - \frac { 7 } { 8 } } & { \frac { 13 } { 4 } } & { - \frac { 20 } { 3 } } \\ { \text { The decimal form } } & { 0.8 } & { - 0.875 } & { 3.25 } & { - 6.666 \dots } \\ { } & { } & { } & { - 6.\overline{6} } \\ { } & { \text { These decimal either stop or repeat. } } \end{array}\]

    מה הדוגמאות הללו מספרות לנו?

    ניתן לכתוב כל מספר רציונלי הן כיחס של מספרים שלמים, (\(\dfrac{p}{q}\), כאשר p ו- q הם מספרים שלמים ו\(q\neq 0\)), והן כעשרוני שעוצר או חוזר על עצמו.

    להלן המספרים שהסתכלנו לעיל המתבטאים כיחס של מספרים שלמים וכעשרוני:

    שברים מספרים שלמים
    מספר \(\frac{4}{5}\) \(\frac{7}{8}\) \(\frac{13}{4}\) \(-\frac{20}{3}\) -2 -1 0 1 2 3
    יחס מספרים שלמים \(\frac{4}{5}\) \(\frac{7}{8}\) \(\frac{13}{4}\) \(-\frac{20}{3}\) \(-\frac{2}{1}\) \(-\frac{1}{1}\) \(\frac{0}{1}\) \(\frac{1}{1}\) \(\frac{2}{1}\) \(\frac{3}{1}\)
    צורה עשרונית 0.8 -0.875 3.25 \(−6.\overline{6}\) −2.0 -1.0 0.0 1.0 2.0 3.0
    טבלה \(\PageIndex{1}\)
    מספר רציונלי

    מספר רציונלי הוא מספר מהצורה\(\frac{p}{q}\), כאשר p ו- q הם מספרים שלמים ו \(q\neq 0\)

    צורתו העשרונית נעצרת או חוזרת.

    האם יש עשרונים שלא מפסיקים או חוזרים? כן!

    למספר \(\pi\) (האות היוונית pi, מבוטא "פאי"), החשוב מאוד בתיאור מעגלים, יש צורה עשרונית שאינה נעצרת או חוזרת.

    \[\pi =3.141592654\ldots\]

    אנו יכולים אפילו ליצור תבנית עשרונית שאינה נעצרת או חוזרת, כגון

    \[2.01001000100001\ldots\]

    לא ניתן לכתוב מספרים שצורתם העשרונית אינה נעצרת או חוזרת כשבריר של מספרים שלמים. אנחנו קוראים למספרים האלה לא הגיוניים.

    מספר לא רציונלי

    מספר לא רציונלי הוא מספר שלא ניתן לכתוב כיחס בין שני מספרים שלמים.

    צורתו העשרונית אינה נעצרת ואינה חוזרת.

    בואו נסכם שיטה בה אנו יכולים להשתמש כדי לקבוע אם מספר הוא רציונלי או לא רציונלי.

    רציונלי או לא רציונלי?

    אם הצורה העשרונית של מספר

    • חוזר או מפסיק, המספר הוא רציונלי.
    • לא חוזר ולא מפסיק, המספר הוא לא רציונלי.
    תרגיל \(\PageIndex{10}\)

    בהתחשב \(0.58\overline{3}, 0.47, 3.605551275\ldots\) ברשימת המספרים

    1. מספרים רציונליים
    2. מספרים לא רציונליים.
    תשובה
    1. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{\text{The 3 repeats in }0.58\overline{3}.} \\ {} &{\text {The decimal 0.47 stops after the 7.}}\\ {} &{\text {So } 0.58\overline{3} \text{ and } 0.47 \text{are rational}} \end{array}\]
    2. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{3.605551275\ldots\text{has no repeating block of}} \\ {} &{\text {digits and it does not stop.}}\\ {} &{\text {So } 3.605551275\ldots \text{ is irrational.}} \end{array}\]
    תרגיל \(\PageIndex{11}\)

    עבור המספרים הנתונים רשימת

    1. מספרים רציונליים
    2. מספרים לא רציונליים: \(0.29, 0.81\overline{6}, 2.515115111….\)
    תשובה
    1. \(0.29, 0.81\overline{6}\)
    2. \(2.515115111….\)
    תרגיל \(\PageIndex{12}\)

    עבור המספרים הנתונים רשימת

    1. מספרים רציונליים
    2. מספרים לא רציונליים: \(2.6\overline{3}, 0.125, 0.418302…\)
    תשובה
    1. \(2.6\overline{3}, 0.125\)
    2. \(0.418302…\)
    תרגיל \(\PageIndex{13}\)

    עבור כל מספר שניתן, זהה אם הוא רציונלי או לא הגיוני:

    1. \(\sqrt{36}\)
    2. \(\sqrt{44}\)
    תשובה
    1. הכירו בכך ש 36 הוא ריבוע מושלם, מאז\(6^{2} = 36\). לכן\(\sqrt{36} = 6\), לכן \(\sqrt{36}\) הוא רציונלי.
    2. זכור \(7^{2} = 49\) זאת \(6^{2} = 36\) וכך \(44\) גם לא ריבוע מושלם. לכן הצורה העשרונית של לעולם לא \(\sqrt{44}\) תחזור ולעולם לא תפסיק, כך \(\sqrt{44}\) שהיא לא הגיונית.
    תרגיל \(\PageIndex{14}\)

    עבור כל מספר שניתן, זהה אם הוא רציונלי או לא הגיוני:

    1. \(\sqrt{81}\)
    2. \(\sqrt{17}\)
    תשובה
    1. הגיוני
    2. לא הגיוני
    תרגיל \(\PageIndex{15}\)

    עבור כל מספר שניתן, זהה אם הוא רציונלי או לא הגיוני:

    1. \(\sqrt{116}\)
    2. \(\sqrt{121}\)
    תשובה
    1. לא הגיוני
    2. הגיוני

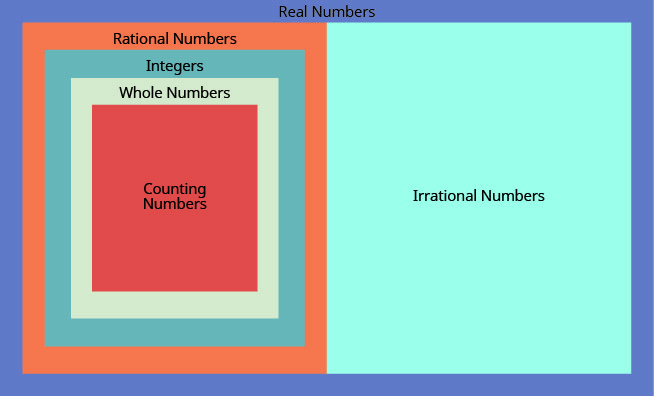
    ראינו שכל מספרי הספירה הם מספרים שלמים, כל המספרים השלמים הם מספרים שלמים וכל המספרים השלמים הם מספרים רציונליים. המספרים הלא רציונליים הם מספרים שצורתם העשרונית אינה נעצרת ואינה חוזרת. כאשר אנו מרכיבים את המספרים הרציונליים ואת המספרים הלא רציונליים, אנו מקבלים את קבוצת המספרים האמיתיים s.

    מספר אמיתי

    מספר ממשי הוא מספר שהוא רציונלי או לא רציונלי.

    כל המספרים שאנו משתמשים באלגברה היסודית הם מספרים ממשיים. איור \(\PageIndex{3}\) ממחיש כיצד קבוצות המספרים עליהן דנו בסעיף זה משתלבות זו בזו.

    נתון זה מורכב מתרשים של ון. כדי להתחיל יש מלבן גדול המסומן מספרים אמיתיים. החצי הימני של המלבן מורכב ממספרים לא הגיוניים. החצי השמאלי מורכב ממספרים רציונליים. בתוך מלבן המספרים הרציונליים, ישנם מספרים שלמים..., שלילי 2, שלילי 1, 0, 1, 2,... בתוך מלבן המספרים השלמים, ישנם מספרים שלמים 0, 1, 2, 3,... בתוך מלבן המספרים השלמים, ישנם מספרים מספרים 1, 2, 3,...
    איור\(\PageIndex{3}\): תרשים זה מציג את ערכות המספרים המרכיבות את קבוצת המספרים הממשיים. האם המונח "מספרים אמיתיים" נראה לך מוזר? האם יש מספרים שאינם "אמיתיים", ואם כן, מה הם יכולים להיות?

    האם נוכל לפשט\(\sqrt{-25}\)? האם יש מספר שהריבוע שלו\(−25\)?

    \[(\quad)^{2}=−25?\]

    לאף אחד מהמספרים שעסקנו בהם עד כה אין ריבוע כלומר\(−25\). למה? כל מספר חיובי בריבוע הוא חיובי. כל מספר שלילי בריבוע הוא חיובי. אז אנחנו אומרים שאין מספר אמיתי שווה ל\(\sqrt{-25}\).

    השורש הריבועי של מספר שלילי אינו מספר ממשי.

    תרגיל \(\PageIndex{16}\)

    עבור כל מספר שניתן, זהה אם מדובר במספר ממשי או לא במספר ממשי:

    1. \(\sqrt{-169}\)
    2. \(-\sqrt{64}\)
    תשובה
    1. אין מספר אמיתי שהריבוע שלו הוא\(−169\). לכן, \(\sqrt{-169}\) הוא לא מספר אמיתי.
    2. מכיוון שהשלילי נמצא מול הרדיקלי, \(-\sqrt{64}\) הוא\(−8\), מאז \(−8\) הוא מספר ממשי, \(-\sqrt{64}\) הוא מספר ממשי.
    תרגיל \(\PageIndex{17}\)

    עבור כל מספר שניתן, זהה אם מדובר במספר ממשי או לא במספר ממשי:

    1. \(\sqrt{-196}\)
    2. \(-\sqrt{81}\)
    תשובה
    1. לא מספר אמיתי
    2. מספר אמיתי
    תרגיל \(\PageIndex{18}\)

    עבור כל מספר שניתן, זהה אם מדובר במספר ממשי או לא במספר ממשי:

    1. \(-\sqrt{49}\)
    2. \(\sqrt{-121}\)
    תשובה
    1. מספר אמיתי
    2. לא מספר אמיתי
    תרגיל \(\PageIndex{19}\)

    בהתחשב במספרים\(−7, \frac{14}{5}, 8, \sqrt{5}, 5.9, \sqrt{64}\), רשום את

    1. מספרים שלמים
    2. מספרים שלמים
    3. מספרים רציונליים
    4. מספרים לא רציונליים
    5. מספרים ממשיים
    תשובה
    1. זכור, המספרים השלמים הם 0, 1, 2, 3,... ו 8 הוא המספר השלם היחיד שניתן.
    2. המספרים השלמים הם המספרים השלמים, הניגודים שלהם ו- 0. אז המספר השלם 8 הוא מספר שלם, ו -7 הוא ההפך ממספר שלם ולכן הוא גם מספר שלם. כמו כן, שימו לב ש 64 הוא הריבוע של 8 כך\(-\sqrt{64} = -8\). אז המספרים השלמים הם\(−7, 8, \sqrt{64}\).
    3. מכיוון שכל המספרים השלמים הם רציונליים, אז \(-7, 8, -\sqrt{64}\) הם רציונליים. מספרים רציונליים כוללים גם שברים ועשרונים שחוזרים או מפסיקים, כך \(\frac{14}{5}\) \(5.9\) והם רציונליים. אז רשימת המספרים הרציונליים היא \(−7, \frac{14}{5}, 8, 5.9, \sqrt{64}\)
    4. זכור כי 5 הוא לא ריבוע מושלם, כך \(\sqrt{5}\) הוא לא רציונלי.
    5. כל המספרים הרשומים הם מספרים אמיתיים.
    תרגיל \(\PageIndex{20}\)

    עבור המספרים הנתונים, רשום את

    1. מספרים שלמים
    2. מספרים שלמים
    3. מספרים רציונליים
    4. מספרים לא רציונליים
    5. מספרים ממשיים: \(−3, -\sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    תשובה
    1. \(4, \sqrt{49}\).
    2. \(−3, 4, \sqrt{49}\)
    3. \(−3, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    4. \( -\sqrt{2}\)
    5. \(−3, \sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    תרגיל \(\PageIndex{21}\)

    עבור המספרים הנתונים, רשום את

    1. מספרים שלמים
    2. מספרים שלמים
    3. מספרים רציונליים
    4. מספרים לא רציונליים
    5. מספרים ממשיים: \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)
    תשובה
    1. \(6, \sqrt{121}\).
    2. \(−\sqrt{25}, −1, 6, \sqrt{121}\)
    3. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}\)
    4. \(2.041975…\)
    5. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)

    אתר שברים בשורת המספרים

    בפעם האחרונה שהסתכלנו על שורת המספרים, היו עליה רק מספרים שלמים חיוביים ושליליים. כעת אנו רוצים לכלול עליו שברים ועשרוניים.

    הערה

    ביצוע פעילות המתמטיקה המניפולטיבית "מספר שורה חלק 3" יעזור לך לפתח הבנה טובה יותר של מיקום השברים בשורת המספרים.

    נתחיל בשברים ונאתר \(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) \(\frac{8}{3}\) ובשורת המספרים.

    נתחיל עם המספרים השלמים 3 ו -5. כי הם הקלים ביותר לשרטט. ראה איור\(\PageIndex{4}\).

    השברים המתאימים המפורטים הם\(\frac{1}{5}\text{ and } -\frac{4}{5}\). אנו יודעים שלשבר הנכון \(\frac{1}{5}\) יש ערך פחות מאחד ולכן יהיה ממוקם בין 0 ל -1. המכנה הוא 5, ולכן אנו מחלקים את היחידה מ -0 ל -1 ל -5 חלקים שווים. \(\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}\) אנחנו מתכננים\(\frac{1}{5}\). ראה איור\(\PageIndex{4}\).

    באופן דומה, \(-\frac{4}{5}\) הוא בין 0 ל -1. לאחר חלוקת היחידה ל -5 חלקים שווים אנו מתווים\(-\frac{4}{5}\). ראה איור\(\PageIndex{4}\).

    לבסוף, התבונן בשברים הלא תקינים\(\frac{7}{4}, -\frac{9}{2}, \frac{8}{3}\). אלה שברים שבהם המונה גדול מהמכנה. איתור נקודות אלה עשוי להיות קל יותר אם תשנה כל אחת מהן למספר מעורב. ראה איור\(\PageIndex{4}\).

    \[\frac { 7 } { 4 } = 1 \frac { 3 } { 4 } \quad - \frac { 9 } { 2 } = - 4 \frac { 1 } { 2 } \quad \frac { 8 } { 3 } = 2 \frac { 2 } { 3 }\]

    איור \(\PageIndex{4}\) מציג את שורת המספרים עם כל הנקודות המתוות.

    מוצגת שורת מספרים שעוברת בין 6 שלילי לחיובי 6. משמאל לימין המספרים המסומנים הם שליליים 5, שלילי 9/2, שלילי 4/5, 1/5, 4/5, 8/3 ו- 3. המספר השלילי 9/2 הוא באמצע הדרך בין שלילי 5 לשלילי 4. המספר השלילי 4/5 נמצא מעט מימין לשלילי 1. המספר 1/5 נמצא מעט מימין ל- 0. המספר 4/5 נמצא מעט משמאל ל -1. המספר 8/3 הוא בין 2 ל -3, אבל קצת יותר קרוב ל -3.
    איור \(\PageIndex{4}\)
    תרגיל \(\PageIndex{22}\)

    אתר ותייג את הדברים הבאים בשורת מספרים: \(4, \frac{3}{4}, -\frac{1}{4}, -3, \frac{6}{5}, -\frac{5}{2}\) ו\(\frac{7}{3}\).

    תשובה

    אתר ושרטט את המספרים השלמים, 4, -3.

    אתר \(\frac{3}{4}\) תחילה את השבר המתאים. השבר \(\frac{3}{4}\) הוא בין 0 ל -1. מחלקים את המרחק בין 0 ל -1 לארבעה חלקים שווים ואז אנו מתווים\(\frac{3}{4}\). עלילה דומה\(-\frac{1}{4}\).

    כעת אתר את השברים הלא תקינים\(\frac{6}{5}\),\(-\frac{5}{2}\),\(\frac{7}{3}\). קל יותר לשרטט אותם אם נמיר אותם למספרים מעורבים ואז נתווה אותם כמתואר לעיל:\(\frac{6}{5} = 1\frac{1}{5}\),\(-\frac{5}{2} = -2\frac{1}{2}\),\(\frac{7}{3} = 2\frac{1}{3}\).

    מוצגת שורת מספרים שעוברת בין 6 שלילי לחיובי 6. משמאל לימין המספרים המסומנים הם שליליים 3, שלילי 5/2, שלילי 1/4, 3/4, 6/5, 7/3 ו -4. המספר השלילי 5/2 נמצא באמצע הדרך בין שלילי 3 לשלילי 2. המספר השלילי 1/4 נמצא מעט משמאל ל- 0. המספר 3/4 נמצא מעט משמאל ל -1. המספר 6/5 נמצא מעט מימין ל -1. המספר 7/3 הוא בין 2 ל -3, אך קצת יותר קרוב ל -2.

    תרגיל \(\PageIndex{23}\)

    אתר ותייג את הדברים הבאים בשורת מספרים: \(-1, \frac{1}{3}, \frac{6}{5}, -\frac{7}{4}, \frac{9}{2}, 5\) ו\(-\frac{8}{3}\).

    תשובה

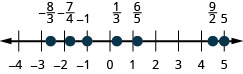
    מוצגת שורת מספרים שעוברת משלילי 4 לחיובי 5. משמאל לימין המספרים המסומנים הם שליליים 8/3, שלילי 7/4, שלילי 1, 1/3, 6/5, 9/2 ו- 5. המספר השלילי 8/3 הוא בין שלילי 3 לשלילי 2 אך מעט קרוב יותר לשלילי 3. המספר השלילי 7/4 הוא מעט מימין לשלילי 2. המספר 1/3 נמצא מעט מימין ל- 0. המספר 6/5 נמצא מעט מימין ל -1. המספר 9/2 הוא באמצע הדרך בין 4 ל -5.

    תרגיל \(\PageIndex{24}\)

    אתר ותייג את הדברים הבאים בשורת מספרים: \(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) ו\(\frac{8}{3}\).

    תשובה

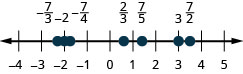
    מוצגת שורת מספרים שעוברת משלילי 4 לחיובי 5. משמאל לימין המספרים המסומנים הם שליליים 7/3, שלילי 2, שלילי 7/4, 2/3, 7/5, 3 ו- 7/2. המספר השלילי 7/3 הוא בין שלילי 3 לשלילי 2 אך מעט קרוב יותר לשלילי 2. המספר השלילי 7/4 הוא מעט מימין לשלילי 2. המספר 2/3 נמצא מעט משמאל ל -1. המספר 7/5 הוא בין 1 ל -2, אך קרוב יותר ל -1. המספר 7/2 הוא באמצע הדרך בין 3 ל -4.

    בתרגיל \(\PageIndex{25}\) נשתמש בסמלי אי השוויון כדי להזמין שברים. בפרקים הקודמים השתמשנו בשורת המספרים להזמנת מספרים.

    • \(a < b\)"a הוא פחות מ - b" כאשר a נמצא משמאל ל - b בשורת המספרים
    • \(a > b\)"a גדול מ - b" כאשר a נמצא מימין ל - b בשורת המספרים

    כאשר אנו עוברים משמאל לימין בשורת מספרים, הערכים גדלים.

    תרגיל \(\PageIndex{25}\)

    סדר כל אחד מזוגות המספרים הבאים, באמצעות \(<\) או\(>\). זה עשוי להיות מועיל להפנות איור\(\PageIndex{5}\).

    1. \(−\frac{2}{3}\text{___}-1\)
    2. \(−3\frac{1}{2}\text{___}-3\)
    3. \(−\frac{3}{4}\text{___}-\frac{1}{4}\)
    4. \(−2\text{___}-\frac{8}{3}\)
    מוצגת שורת מספרים שעוברת משלילי 4 לחיובי 4. משמאל לימין המספרים המסומנים הם שליליים 3 ו- 1/2, שלילי 3, שלילי 8/3, שלילי 2, שלילי 1, שלילי 3/4, שלילי 2/3 ושלילי 1/4. המספר השלילי 3 ו- 1/2 הוא בין שלילי 4 לשלילי 3 המספר שלילי 8/3 הוא בין שלילי 3 לשלילי 2, אך קרוב יותר לשלילי 3. המספרים שליליים 3/4, שלילי 2/3 ושלילי 1/4 הם כולם בין שלילי 1 ל -0.
    איור \(\PageIndex{5}\)
    תשובה

    היזהר בעת הזמנת מספרים שליליים.

    1. \(\begin{array} { r r } { } & { - \frac { 2 } { 3 } \text{ ___ } -1 } \\ { - \frac { 2 } { 3 } \text { is to the right of } - 1 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
    2. \(\begin{array} { r r } { } & { - 3\frac { 1 } { 2 } \text{ ___ } -3 } \\ { - 3\frac { 1 } { 2 } \text { is to the right of } - 3 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
    3. \(\begin{array} { r r } { } & { - \frac { 3 } { 4 } \text{ ___ } -\frac{1}{4} } \\ { - \frac { 3 } { 4 } \text { is to the right of } - \frac{1}{4} \text { on the number line. } } & { - \frac{3}{4} < - \frac{1}{4} } \end{array}\)
    4. \(\begin{array} { r r } { } & { - \-2 \text{ ___ } -\frac{8}{3} } \\ { -2 \text { is to the right of } - \frac{8}{3} \text { on the number line. } } & { -2 > -\frac{8}{3} } \end{array}\)
    תרגיל \(\PageIndex{26}\)

    סדר כל אחד מזוגות המספרים הבאים, באמצעות \(<\) או\(>\).

    1. \(−\frac{1}{3}\text{___}-1\)
    2. \(−1\frac{1}{2}\text{___}-2\)
    3. \(−\frac{2}{3}\text{___}-\frac{1}{3}\)
    4. \(−3\text{___}-\frac{7}{3}\)
    תשובה
    1. \(>\)
    2. \(>\)
    3. \(<\)
    4. \(<\)
    תרגיל \(\PageIndex{27}\)

    סדר כל אחד מזוגות המספרים הבאים, באמצעות \(<\) או\(>\).

    1. \(−1\text{___}-\frac{2}{3}\)
    2. \(−2\frac{1}{4}\text{___}-2\)
    3. \(−\frac{3}{5}\text{___}-\frac{4}{5}\)
    4. \(−4\text{___}-\frac{10}{3}\)
    תשובה
    1. \(<\)
    2. \(<\)
    3. \(>\)
    4. \(<\)

    אתר ספרות עשרוניות בשורת המספרים

    מכיוון שעשרונים הם צורות של שברים, איתור עשרונים בשורת המספרים דומה לאיתור שברים בשורת המספרים.

    תרגיל \(\PageIndex{28}\)

    אתר 0.4 בשורת המספרים.

    תשובה

    לשבר תקין יש ערך פחות מאחד. המספר העשרוני \(0.4\) שווה \(\frac{4}{10}\) לשבר תקין, כך \(0.4\) שהוא ממוקם בין 0 ל -1. בשורת מספרים, חלקו את המרווח בין 0 ל -1 לעשרה חלקים שווים. עכשיו תייג את החלקים\(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0\). אנו כותבים 0 כ- 0.0 ו- 1 ו- 1.0, כך שהמספרים יהיו בעקביות בעשיריות. לבסוף, סמן \(0.4\) בשורת המספרים. ראה איור\(\PageIndex{6}\).

    מוצגת שורת מספרים שעוברת בין 0.0 ל -1. הנקודה היחידה שניתנה היא 0.4, שהיא בין 0.3 ל 0.5.
    איור \(\PageIndex{6}\)
    תרגיל \(\PageIndex{29}\)

    אתר בשורת המספרים: 0.6.

    תשובה

    מוצגת שורת מספרים שעוברת בין 0.0 ל -1. הנקודה היחידה שניתנה היא 0.6, שהיא בין 0.5 ל 0.7.

    תרגיל \(\PageIndex{30}\)

    אתר בשורת המספרים: 0.9.

    תשובה

    מוצגת שורת מספרים שעוברת בין 0.0 ל -1. הנקודה היחידה שניתנה היא 0.9, שהיא בין 0.8 ל -1.

    תרגיל \(\PageIndex{31}\)

    אתר \(−0.74\) בשורת המספרים.

    תשובה

    העשרוני (-0.74\) שווה ערך ל-\(-\frac{74}{100}\), ולכן הוא ממוקם בין 0 ל -1. בשורת מספרים, סמן ותייג את המאות במרווח שבין 0 ל -1. ראה איור\(\PageIndex{7}\).

    מוצגת שורת מספרים שעוברת בין 1.00 ל- 0.00 שלילי. הנקודה היחידה שניתנה היא 0.74 שלילית, שהיא בין 0.8 שלילי לשלילי 0.7.
    איור \(\PageIndex{7}\)
    תרגיל \(\PageIndex{32}\)

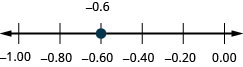
    אתר בשורת המספרים: -0.6.

    תשובה

    מוצגת שורת מספרים שעוברת בין 1.00 ל- 0.00 שלילי. הנקודה היחידה שניתנה היא 0.6 שלילי, שהוא בין 0.8 שלילי לשלילי 0.4.

    תרגיל \(\PageIndex{33}\)

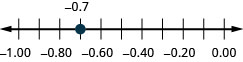
    אתר בשורת המספרים: -0.7.

    תשובה

    מוצגת שורת מספרים שעוברת בין 1.00 ל- 0.00 שלילי. הנקודה היחידה שניתנה היא 0.7 שלילית, שהיא בין 0.8 שלילי לשלילי 0.6.

    מה גדול יותר, 0.04 או 0.40? אם אתה חושב על זה כעל כסף, אתה יודע ש- 0.40$ (ארבעים סנט) גדולים מ- 0.04$ (ארבעה סנט). אז, \(0.40 > 0.04\)

    שוב, אנו יכולים להשתמש בשורת המספרים להזמנת מספרים.

    • \(a < b\)"a הוא פחות מ - b" כאשר a נמצא משמאל ל - b בשורת המספרים
    • \(a > b\)"a גדול מ - b" כאשר a נמצא מימין ל - b בשורת המספרים

    היכן נמצאים 0.04 ו- 0.40 בשורת המספרים? ראה איור\(\PageIndex{8}\).

    מוצגת שורת מספרים שעוברת מ- 0.0 שלילי ל- 1.0. משמאל לימין יש נקודות 0.04 ו -0.4 מסומנות. הנקודה 0.04 היא בין 0.0 ל 0.1. הנקודה 0.4 היא בין 0.3 ל 0.5.
    איור \(\PageIndex{8}\)

    אנו רואים ש- 0.40 נמצא מימין ל- 0.04 בשורת המספרים. זוהי דרך נוספת להוכיח זאת\(0.40 > 0.04\).

    איך 0.31 משתווה ל 0.308? זה לא מתורגם לכסף כדי להקל על ההשוואה. אבל אם נמיר 0.31 ו- 0.308 לשברים, נוכל לדעת מה גדול יותר.

      0.31 0.308
    המר לשברים. \(\frac{31}{100}\) \(\frac{308}{1000}\)
    אנחנו צריכים מכנה משותף כדי להשוות ביניהם. . .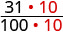
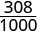      \(\frac{310}{1000}\) \(\frac{308}{1000}\)
    טבלה \(\PageIndex{2}\)

    כי \(310 > 308\) אנחנו יודעים את זה\(\frac{310}{1000} > \frac{308}{1000}\). לכן,\(0.31 > 0.308\).

    שימו לב מה עשינו בהמרה \(0.31\) לשבר - התחלנו עם השבר \(\frac{31}{100}\) וסיימנו בשבר המקביל\(\frac{310}{1000}\). המרה \(\frac{310}{1000}\) חזרה לעשרונית נותנת 0.310. אז 0.31 שווה ל 0.310. כתיבת אפסים בסוף עשרוני אינה משנה את ערכה!

    \[\frac { 31 } { 100 } = \frac { 310 } { 1000 } \quad \text { and } \quad 0.31 = 0.310\]

    אנו אומרים 0.31 ו- 0.310 הם עשרוניים שווים.

    ספרות עשרוניות שוות ערך

    שני עשרונים שווים אם הם ממירים לשברים שווים.

    אנו משתמשים בעשרונים שווים כאשר אנו מזמינים עשרונים.

    הצעדים שאנו נוקטים להזמנת עשרונים מסוכמים כאן.

    סדר עשרונים.
    1. כתוב את המספרים אחד מתחת לשני, מסדר את הנקודות העשרוניות.
    2. בדוק אם לשני המספרים יש מספר זהה של ספרות. אם לא, כתוב אפסים בסוף זה עם פחות ספרות כדי להתאים אותם.
    3. השווה את המספרים כאילו היו מספרים שלמים.
    4. הזמינו את המספרים באמצעות סימן אי השוויון המתאים.
    תרגיל \(\PageIndex{34}\)

    הזמינו \(0.64 \text{ ___ } 0.6\) באמצעות \(<\) או\(>\).

    תשובה

    \(\begin{array} { ll } { \text {Write the numbers one under the other, } } &{0.64} \\ { \text {lining up the decimal points. } } &{0.6} \\ \\ { \text {Add a zero to 0.6 to make it a decimal } } &{0.64} \\ {\text{with 2 decimal places.}} &{0.60} \\ {\text{Now they are both hundredths.}} &{} \\ \\ {\text{64 is greater than 60.}} &{64 > 60} \\ \\ {\text{64 hundredths is greater than 60 hundredths.}} &{0.64 > 0.60} \\ \\ {} &{0.64 > 0.6}\end{array}\)

    תרגיל \(\PageIndex{35}\)

    הזמינו כל אחד מזוגות המספרים הבאים, באמצעות \(<\) או\(>\):\(0.42 \text{ ___ } 0.4\).

    תשובה

    \(>\)

    תרגיל \(\PageIndex{36}\)

    הזמינו כל אחד מזוגות המספרים הבאים, באמצעות \(<\) או\(>\):\(0.18 \text{ ___ } 0.1\).

    תשובה

    \(>\)

    תרגיל \(\PageIndex{37}\)

    הזמינו \(0.83 \text{ ___ } 0.803\) באמצעות \(<\) או\(>\).

    תשובה

    \(\begin{array} { ll } {} &{0.83\text{ ___ }0.803} \\ \\{ \text {Write the numbers one under the other, } } &{0.83} \\ { \text {lining up the decimal points. } } &{0.803} \\ \\ { \text {They do not have the same number of} } &{0.830} \\ {\text{digits.}} &{0.803} \\ {\text{Write one zero at the end of 0.83.}} &{} \\ \\ {\text{Since 830 > 803, 830 hundredths is}} &{0.830 > 0.803} \\ {\text{greater than 803 thousandths.}} &{}\\ \\ {} &{0.83 > 0.803}\end{array}\)

    תרגיל \(\PageIndex{38}\)

    הזמינו כל אחד מזוגות המספרים הבאים, באמצעות \(<\) או\(>\):\(0.76 \text{ ___ } 0.706\).

    תשובה

    \(>\)

    תרגיל \(\PageIndex{39}\)

    הזמינו כל אחד מזוגות המספרים הבאים, באמצעות \(<\) או\(>\):\(0.305 \text{ ___ } 0.35\).

    תשובה

    \(<\)

    כאשר אנו מזמינים עשרונים שליליים, חשוב לזכור כיצד להזמין מספרים שלמים שליליים. נזכיר כי מספרים גדולים יותר נמצאים מימין בשורת המספרים. לדוגמה, מכיוון ש -2 נמצא מימין ל -3 בשורת המספרים, אנו יודעים זאת\(−2>−3\). באופן דומה, מספרים קטנים יותר שוכבים משמאל בשורת המספרים. לדוגמה, מכיוון ש -9 נמצא משמאל ל -6 בשורת המספרים, אנו יודעים זאת. \(−9<−6\) ראה איור\(\PageIndex{9}\).

    מוצגת שורת מספרים שעוברת מ- 10 ל- 0 שלילי. לא ניתנות נקודות וסימני ה- hashmarks קיימים בכל מספר שלם בין 10 ל- 0 שלילי.
    איור \(\PageIndex{9}\)

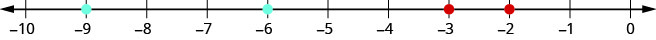
    אם היינו מתקרבים למרווח שבין 0 ל -1, כפי שמוצג בתרגיל\(\PageIndex{40}\), היינו רואים באותו אופן ש \(−0.2>−0.3\) ו. \(−0.9<−0.6\)

    תרגיל \(\PageIndex{40}\)

    השתמש \(<\) או \(>\) להזמין\(−0.1\text{ ___ }−0.8\).

    תשובה

    \(\begin{array} { ll } {} &{-0.1 \text{ ___ } -0.8} \\ \\ { \text { Write the numbers one under the other, lining up the } } &{-0.1} \\ { \text { decimal points. } } &{-0.8} \\ { \text { They have the same number of digits. } } &{} \\ \\ { \text { since } - 1 > - 8 , - 1 \text { tenth is greater than } - 8 \text { tenths. } } &{-0.1 > -0.8} \end{array}\)

    תרגיל \(\PageIndex{41}\)

    הזמינו את צמד המספרים הבא, באמצעות \(<\) או\(>\):\(−0.3\text{ ___ }−0.5\).

    תשובה

    \(>\)

    תרגיל \(\PageIndex{42}\)

    הזמינו את צמד המספרים הבא, באמצעות \(<\) או\(>\):\(−0.6\text{ ___ }−0.7\).

    תשובה

    \(>\)

    מושגי מפתח

    • סימון שורש ריבועי
      \(\sqrt{m}\) נקרא 'השורש הריבועי של'\(m\). אם\(m = n^{2}\), אז\(\sqrt{m} = n\), עבור\(n \geq 0\).
    • סדר עשרונים
      1. כתוב את המספרים אחד מתחת לשני, מסדר את הנקודות העשרוניות.
      2. בדוק אם לשני המספרים יש מספר זהה של ספרות. אם לא, כתוב אפסים בסוף זה עם פחות ספרות כדי להתאים אותם.
      3. השווה את המספרים כאילו היו מספרים שלמים.
      4. הזמינו את המספרים באמצעות סימן אי השוויון המתאים.

    תרגול הופך מושלם

    פשט ביטויים עם שורשים מרובעים

    בתרגילים הבאים, לפשט.