1.5: הכפל וחלק מספרים שלמים
- Page ID
- 205713
בסוף פרק זה תוכל:
- הכפל מספרים שלמים
- מחלקים מספרים שלמים
- פשט ביטויים עם מספרים שלמים
- הערך ביטויים משתנים עם מספרים שלמים
- תרגם ביטויים באנגלית לביטויים אלגבריים
- השתמש במספרים שלמים ביישומים
מבוא יסודי יותר לנושאים המכוסים בחלק זה ניתן למצוא בפרק Prealgebra, מספרים שלמים.
הכפל מספרים שלמים
מכיוון שכפל הוא קיצור מתמטי להוספה חוזרת, ניתן ליישם את המודל שלנו בקלות כדי להראות כפל של מספרים שלמים. בואו נסתכל על המודל הקונקרטי הזה כדי לראות באילו דפוסים אנו מבחינים. נשתמש באותן דוגמאות בהן השתמשנו לחיבור וחיסור. כאן נשתמש במודל רק כדי לעזור לנו לגלות את התבנית.
אנו זוכרים שזה \(a\cdot b\) אומר להוסיף \(a,\, b\) זמנים. כאן, אנו משתמשים במודל רק כדי לעזור לנו לגלות את התבנית.
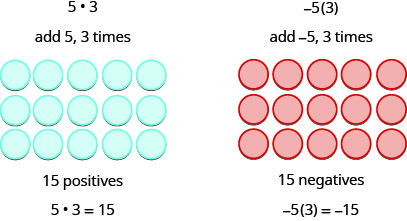
שתי הדוגמאות הבאות מעניינות יותר.
מה זה אומר \(5\) להכפיל\(−3\)? זה אומר להפחית \(5, 3\) פעמים. כשמסתכלים על חיסור כ"לקחת משם ", זה אומר לקחת \(5, 3\) זמנים. אבל אין מה לקחת, אז אנחנו מתחילים על ידי הוספת זוגות ניטרליים על סביבת העבודה. ואז אנחנו לוקחים \(5\) שלוש פעמים.
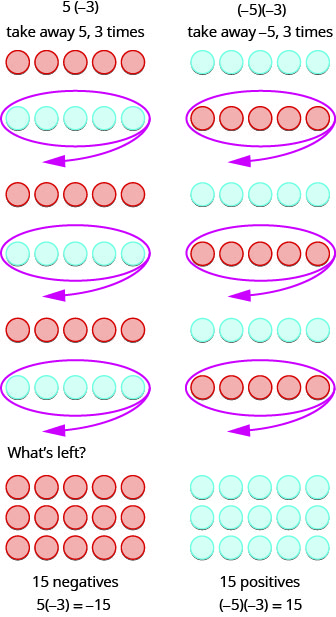
לסיכום:
\[\begin{array} {ll} {5 \cdot 3 = 15} &{-5(3) = -15} \\ {5(-3) = -15} &{(-5)(-3) = 15} \end{array}\]
שים לב כי עבור כפל של שני מספרים חתומים, כאשר:
- סימנים זהים, המוצר הוא חיובי.
- סימנים שונים, המוצר הוא שלילי.
נרכיב את כל זה בתרשים שלהלן.
להכפלה של שני מספרים חתומים:
| אותם סימנים | מוצר | דוגמא |
|---|---|---|
| שתי תוצאות חיוביות | חיובי | \(7\cdot 4 = 28\) |
| שני תשלילים | חיובי | \(-8(-6) = 48\) |
| סימנים שונים | מוצר | דוגמא |
|---|---|---|
| חיובי שלילי \(\cdot\) | שלילי | \(7(-9) = -63\) |
| \(\cdot\)תוצאות חיוביות שליליות | שלילי | \(-5\cdot 10= -50\) |
הכפל:
- \(-9\cdot 3\)
- \(-2(-5)\)
- \(4(-8)\)
- \(7\cdot 6\)
- תשובה
-
- \[\begin{array} {ll} {} &{-9\cdot 3} \\ {\text{Multiply, noting that the signs are different, so the product is negative.}} &{-27} \end{array}\]
- \[\begin{array} {ll} {} &{-2(-5)} \\ {\text{Multiply, noting that the signs are same, so the product is positive.}} &{10} \end{array}\]
- \[\begin{array} {ll} {} &{4(-8)} \\ {\text{Multiply, with different signs.}} &{-32} \end{array}\]
- \[\begin{array} {ll} {} &{7\cdot 6} \\ {\text{Multiply, with different signs.}} &{42} \end{array}\]
הכפל:
- \(-6\cdot 8\)
- \(-4(-7)\)
- \(9(-7)\)
- \(5\cdot 12\)
- תשובה
-
- \(-48\)
- \(28\)
- \(-63\)
- \(60\)
הכפל:
- \(-8\cdot 7\)
- \(-6(-9)\)
- \(7(-4)\)
- \(3\cdot 13\)
- תשובה
-
- \(-56\)
- \(54\)
- \(-28\)
- \(39\)
כאשר אנו מכפילים מספר ב-\(1\), התוצאה היא אותו מספר. מה קורה כשאנחנו מכפילים מספר\(−1\)? בואו נכפיל מספר חיובי ואז מספר שלילי על ידי \(−1\) כדי לראות מה אנחנו מקבלים.
\[\begin{array} {lll} {} &{-1\cdot 4} &{-1(-3)}\\ {\text{Multiply.}} &{-4} &{3} \\ {} &{-4\text{ is the opposite of 4.}} &{3\text{ is the opposite of } -3} \end{array}\]
בכל פעם שאנחנו מכפילים מספר ב\(−1\), אנחנו מקבלים את ההפך!
כפל ב -1
\[−1a=−a\]
הכפלת מספר על ידי \(−1\) נותן את ההפך.
הכפל:
- \(-1 \cdot 7\)
- \(-1(-11)\)
- תשובה
-
- \[\begin{array} {ll} {} &{-1\cdot 7} \\ {\text{Multiply, noting that the signs are different}} &{-7} \\ {\text{so the product is negative.}} &{-7\text{ is the opposite of 7.}} \end{array}\]
- \[\begin{array} {ll} {} &{-1(-11)} \\ {\text{Multiply, noting that the signs are different}} &{11} \\ {\text{so the product is positive.}} &{11\text{ is the opposite of -11.}} \end{array}\]
הכפל:
- \(-1\cdot 9\)
- \(-1\cdot(-17)\)
- תשובה
-
- \(-9\)
- \(17\)
הכפל:
- \(-1\cdot 8\)
- \(-1\cdot(-16)\)
- תשובה
-
- \(-8\)
- \(16\)
מחלקים מספרים שלמים
מה לגבי הדיוויזיה? חלוקה היא הפעולה ההפוכה של הכפל. אז, \(15\div 3=5\) בגלל\(5 \cdot 3 = 15\). במילים, ביטוי זה אומר \(15\) שניתן לחלק לשלוש קבוצות של חמש כל אחת מכיוון שהוספת חמש שלוש פעמים נותנת\(15\). תסתכל על כמה דוגמאות של הכפלת מספרים שלמים, כדי להבין את הכללים לחלוקת מספרים שלמים.
\[\begin{array} {ll} {5\cdot 3 = 15\text{ so }15\div 3 = 5} &{-5(3) = -15\text{ so }-15\div 3 = -5} \\ {(-5)(-3) = 15\text{ so }15\div (-3) = -5} &{5(-3) = -15\text{ so }-15\div (-3) = 5} \end{array}\]
החלוקה עוקבת אחר אותם כללים כמו כפל!
לחלוקה של שני מספרים חתומים, כאשר:
- הסימנים זהים, המנה חיובית.
- הסימנים שונים, המנה שלילית.
וזכרו שתמיד נוכל לבדוק את התשובה לבעיית חלוקה על ידי הכפלה.
לכפל וחלוקה של שני מספרים חתומים:
- אם הסימנים זהים, התוצאה חיובית.
- אם הסימנים שונים, התוצאה שלילית.
| אותם סימנים | תוצאה |
|---|---|
| שתי תוצאות חיוביות | חיובי |
| שני תשלילים | חיובי |
| אם הסימנים זהים, התוצאה חיובית. | |
| סימנים שונים | תוצאה |
|---|---|
| חיובי ושלילי | שלילי |
| שלילי וחיובי | שלילי |
| אם הסימנים שונים, התוצאה שלילית. | |
- \(-27\div 3\)
- \(-100\div (-4)\)
- תשובה
-
- \[\begin{array} {ll} {} &{-27 \div 3} \\ {\text{Divide, with different signs, the quotient is}} &{-9} \\ {\text{negative.}} &{} \end{array}\]
- \[\begin{array} {ll} {} &{-100 \div (-4)} \\ {\text{Divide, with signs that are the same the}} &{25} \\ {\text{ quotient is negative.}} &{} \end{array}\]
לחלק:
- \(-42\div 6\)
- \(-117\div (-3)\)
- תשובה
-
- \(-7\)
- \(39\)
לחלק:
- \(-63\div 7\)
- \(-115\div (-5)\)
- תשובה
-
- \(-9\)
- \(23\)
פשט ביטויים עם מספרים שלמים
מה קורה כשיש יותר משני מספרים בביטוי? סדר הפעולות עדיין חל כאשר כלולים שליליות. זוכר את דודתי היקרה סאלי?
בואו ננסה כמה דוגמאות. אנו נפשט ביטויים המשתמשים בכל ארבע הפעולות עם מספרים שלמים - חיבור, חיסור, כפל וחילוק. זכור לעקוב אחר סדר הפעולות.
פשט:
\(7(-2)+4(-7)-6\)
- תשובה
-
\[\begin{array} {ll} {} &{7(-2)+4(-7)-6} \\ {\text{Multiply first.}} &{-14+(-28)-6} \\ {\text{Add.}} &{-42-6} \\{\text{Subtract}} &{-48} \end{array}\]
פשט:
\(8(-3)+5(-7)-4\)
- תשובה
-
\(-63\)
פשט:
\(9(-3)+7(-8)-1\)
- תשובה
-
\(-84\)
פשט:
- \((-2)^{4}\)
- \(-2^{4}\)
- תשובה
-
- \[\begin{array} {ll} {} &{(-2)^{4}} \\ {\text{Write in expanded form.}} &{(-2)(-2)(-2)(-2)} \\ {\text{Multiply}} &{4(-2)(-2)} \\{\text{Multiply}} &{-8(-2)} \\{\text{Multiply}} &{16} \end{array}\]
- \[\begin{array} {ll} {} &{-2^{4}} \\ {\text{Write in expanded form. We are asked to find the opposite of }2^{4}.} &{-(2\cdot 2\cdot 2 \cdot 2)} \\ {\text{Multiply}} &{-(4\cdot 2\cdot 2)} \\{\text{Multiply}} &{-(8\cdot 2)} \\{\text{Multiply}} &{-16} \end{array}\]
שימו לב להבדל בחלקים (1) ו- (2). בחלק (1), המעריך פירושו להעלות את מה שיש בסוגריים, \((−2)\) את \(4^{th}\) הכוח. בחלק (2), המעריך פירושו להעלות רק \(2\) את \(4^{th}\) הכוח ואז לקחת את ההפך.
פשט:
- \((-3)^{4}\)
- \(-3^{4}\)
- תשובה
-
- \(81\)
- \(-81\)
פשט:
- \((-7)^{2}\)
- \(-7^{2}\)
- תשובה
-
- \(49\)
- \(-49\)
הדוגמה הבאה מזכירה לנו לפשט תחילה את הסוגריים הפנימיים.
פשט:
\(12-3(9 - 12)\)
- תשובה
-
\[\begin{array} {llll} {} &{12-3(9 - 12)} \\ {\text{Subtract parentheses first}} &{12-3(-3)} \\ {\text{Multiply.}} &{12-(-9)} \\{\text{Multiply}} &{-(8\cdot 2)} \\{\text{Subtract}} &{21} \end{array}\]
פשט:
\(17 - 4(8 - 11)\)
- תשובה
-
\(29\)
פשט:
\(16 - 6(7 - 13)\)
- תשובה
-
\(52\)
פשט:
\(8(-9)\div (-2)^{3}\)
- תשובה
-
\[\begin{array} {ll} {} &{8(-9)\div(-2)^{3}} \\ {\text{Exponents first}} &{8(-9)\div(-8)} \\ {\text{Multiply.}} &{-72\div (-8)} \\{\text{Divide}} &{9} \end{array}\]
פשט:
\(12(-9)\div (-3)^{3}\)
- תשובה
-
\(4\)
פשט:
\(18(-4)\div (-2)^{3}\)
- תשובה
-
\(9\)
פשט:
\(-30\div 2 + (-3)(-7)\)
- תשובה
-
\[\begin{array} {ll} {} &{-30\div 2 + (-3)(-7)} \\ {\text{Multiply and divide left to right, so divide first.}} &{-15+(-3)(-7)} \\ {\text{Multiply.}} &{-15+ 21} \\{\text{Add}} &{6} \end{array}\]
פשט:
\(-27\div 3 + (-5)(-6)\)
- תשובה
-
\(21\)
פשט:
\(-32\div 4 + (-2)(-7)\)
- תשובה
-
\(6\)
הערכת ביטויים משתנים עם מספרים שלמים
זכור כי הערכת ביטוי פירושה להחליף מספר במשתנה בביטוי. כעת אנו יכולים להשתמש במספרים שליליים כמו גם במספרים חיוביים.
מתי\(n=−5\), הערך:
- \(n+1\)
- \(−n+1\).
- תשובה
-
- \[\begin{array} {ll} {} &{n+ 1} \\ {\text{Substitute}-5\text{ for } n} &{-5+1} \\ {\text{Simplify.}} &{-4} \end{array}\]
- \[\begin{array} {ll} {} &{-n+ 1} \\ {\text{Substitute}-5\text{ for } n} &{-(-5)+1} \\ {\text{Simplify.}} &{-4} \\{\text{Add.}} &{6} \end{array}\]
מתי\(n=−8\), הערך:
- \(n+2\)
- \(−n+2\).
- תשובה
-
- \(-6\)
- \(10\)
מתי\(y=−9\), הערך:
- \(y+8\)
- \(−y+8\).
- תשובה
-
- \(-1\)
- \(17\)
להעריך \((x+y)^{2}\) מתי \(x = -18\) ו\(y = 24\).
- תשובה
-
\[\begin{array} {ll} {} &{(x+y)^{2}} \\ {\text{Substitute }-18\text{ for }x \text{ and } 24 \text{ for } y} &{(-18 + 24)^{2}} \\ {\text{Add inside parentheses}} &{(6)^{2}} \\{\text{Simplify.}} &{36} \end{array}\]
להעריך \((x+y)^{2}\) מתי \(x = -15\) ו\(y = 29\).
- תשובה
-
\(196\)
להעריך \((x+y)^{3}\) מתי \(x = -8\) ו\(y = 10\).
- תשובה
-
\(8\)
להעריך \(20 -z \) מתי
- \(z = 12\)
- \(z = -12\)
- תשובה
-
- \[\begin{array} {ll} {} &{20 - z} \\ {\text{Substitute }12\text{ for }z.} &{20 - 12} \\ {\text{Subtract}} &{8} \end{array}\]
- \[\begin{array} {ll} {} &{20 - z} \\ {\text{Substitute }-12\text{ for }z.} &{20 - (-12)} \\ {\text{Subtract}} &{32} \end{array}\]
להעריך \(17 - k\) מתי
- \(k = 19\)
- \(k = -19\)
- תשובה
-
- \(-2\)
- \(36\)
להעריך \(-5 - b\) מתי
- \(b = 14\)
- \(b = -14\)
- תשובה
-
- \(-19\)
- \(9\)
להעריך:
\(2x^{2} + 3x + 8\)מתי\(x = 4\).
- תשובה
-
תחליף \(4\) ל\(x\). השתמש בסוגריים כדי להציג כפל.
\[\begin{array} {ll} {} &{2x^{2} + 3x + 8} \\ {\text{Substitute }} &{2(4)^{2} + 3(4) + 8} \\ {\text{Evaluate exponents.}} &{2(16) + 3(4) + 8} \\ {\text{Multiply.}} &{32 + 12 + 8} \\{\text{Add.}} &{52} \end{array}\]
להעריך:
\(3x^{2} - 2x + 6\)מתי\(x =-3\).
- תשובה
-
\(39\)
להעריך:
\(4x^{2} - x - 5\)מתי\(x = -2\).
- תשובה
-
\(13\)
תרגם ביטויים לביטויים עם מספרים שלמים
העבודה הקודמת שלנו בתרגום אנגלית לאלגברה חלה גם על ביטויים הכוללים מספרים חיוביים ושליליים כאחד.
תרגם ופשט: סכום \(8\) ו\(−12\), גדל ב\(3\).
- תשובה
-
\[\begin{array} {ll} {} &{\text{the } \textbf{sum} \text{of 8 and -12, increased by 3}} \\ {\text{Translate.}} &{[8 + (-12)] + 3} \\ {\text{Simplify. Be careful not to confuse the}} &{(-4) + 3} \\{\text{brackets with an absolute value sign.}} \\{\text{Add.}} &{-1} \end{array}\]
תרגם ופשט: סכום \(9\) ו\(−16\), גדל ב\(4\).
- תשובה
-
\((9 + (-16)) + 4 - 3\)
תרגם ופשט: סכום \(-8\) ו\(−12\), גדל ב\(7\).
- תשובה
-
\((-8 + (-12)) + 7 - 13\)
כאשר הצגנו לראשונה את סמלי הפעולה, ראינו שניתן לקרוא את הביטוי בכמה אופנים. הם מפורטים בתרשים שלהלן.
| \(a−b\) |
|---|
| \ (a−b\)" ערך נתונים="top"> \(a\) מינוס ההפרש של פחות מ \(b\) \(a\) \(b\) \(b\) \(a\) \(b\) \(a\) |
היזהר לקבל a ו - b בסדר הנכון!
תרגם ואז פשט
- ההבדל של \(13\) ו \(−21\)
- לחסר \(24\) מ\(−19\).
- תשובה
-
- \[\begin{array} {ll} {} &{\text{the } \textbf{difference } \text{of 13 and -21}} \\ {\text{Translate.}} &{13 - (-21)} \\ {\text{Simplify.}} &{34} \end{array}\]
- \[\begin{array} {ll} {} &\textbf{subtract }24 \textbf{ from }-19 \\ {\text{Translate.}} &{-19 - 24} \\ {\text{Remember, subtract b from a means }a - b} &{} \\{\text{Simplify.}} &{-43} \end{array}\]
תרגם ופשט
- ההבדל של \(14\) ו \(−23\)
- לחסר \(21\) מ\(−17\).
- תשובה
-
- \(14 - (-23); 37\)
- \(-17 - 21; -38\)
תרגם ופשט
- ההבדל של \(11\) ו \(−19\)
- לחסר \(18\) מ\(−11\).
- תשובה
-
- \(11 - (-19); 30\)
- \(-11 - 18; -29\)
שוב, העבודה הקודמת שלנו בתרגום אנגלית לאלגברה עוברת לביטויים הכוללים גם הכפלה וגם חלוקה של מספרים שלמים. זכור כי מילת המפתח לכפל היא "מוצר" ולחלוקה היא "מנה".
תרגם לביטוי אלגברי ופשט במידת האפשר: תוצר של \(−2\) ו. \(14\)
- תשובה
-
\[\begin{array} {ll} {} &{\text{the product of }-2 \text{ and } 14} \\ {\text{Translate.}} &{(-2)(14)} \\{\text{Simplify.}} &{-28} \end{array}\]
תרגם לביטוי אלגברי ופשט במידת האפשר: תוצר של \(−5\) ו. \(12\)
- תשובה
-
\(-5(12); -60\)
תרגם לביטוי אלגברי ופשט במידת האפשר: תוצר של \(8\) ו. \(-13\)
- תשובה
-
\(-8(13); -104\)
תרגם לביטוי אלגברי ופשט במידת האפשר: המנה של ו. \(−56\) \(−7\)
- תשובה
-
\[\begin{array} {ll} {} &{\text{the quotient of }-56 \text{ and } -7} \\ {\text{Translate.}} &{-56\div(-7)} \\{\text{Simplify.}} &{8} \end{array}\]
תרגם לביטוי אלגברי ופשט במידת האפשר: המנה של ו. \(−63\) \(−9\)
- תשובה
-
\(-63\div (-9); 7\)
תרגם לביטוי אלגברי ופשט במידת האפשר: המנה של ו. \(−72\) \(−9\)
- תשובה
-
\(-72\div (-9); 8\)
השתמש במספרים שלמים ביישומים
נתאר תוכנית לפתרון יישומים. קשה למצוא משהו אם אנחנו לא יודעים מה אנחנו מחפשים או איך לקרוא לזה! לכן כאשר אנו פותרים יישום, ראשית עלינו לקבוע מה הבעיה מבקשת מאיתנו למצוא. לאחר מכן נכתוב ביטוי שנותן את המידע כדי למצוא אותו. נתרגם את הביטוי לביטוי ואז נפשט את הביטוי כדי לקבל את התשובה. לבסוף, אנו מסכמים את התשובה במשפט כדי לוודא שהיא הגיונית.
כיצד ליישם אסטרטגיה לפתרון יישומים עם מספרים שלמים
הטמפרטורה באורבנה, אילינוי בוקר אחד הייתה \(11\) מעלות. באמצע אחר הצהריים הטמפרטורה ירדה \(−9\) למעלות. מה היה ההבדל בטמפרטורות הבוקר והצהריים?
- תשובה
-
שלב 1. קרא את הבעיה. ודא שכל המילים והרעיונות מובנים. שלב 2. זהה את מה שאנו מתבקשים למצוא. ההבדל בטמפרטורות הבוקר והצהריים שלב 3. כתוב ביטוי שנותן את המידע כדי למצוא אותו. ההבדל של \(11\) ו \(-9\) שלב 4. תרגם את הביטוי לביטוי. \(11 - (-9)\) שלב 5. פשט את הביטוי. \(20\) שלב 6. כתוב משפט שלם שעונה על השאלה. ההבדל בטמפרטורות היה 20 מעלות.
הטמפרטורה באנקורג ', אלסקה בוקר אחד הייתה \(15\) מעלות. באמצע אחר הצהריים הטמפרטורה ירדה \(30\) למעלות מתחת לאפס. מה היה ההבדל בטמפרטורות הבוקר והצהריים?
- תשובה
-
ההבדל בטמפרטורות היה \(45\) מעלות.
הטמפרטורה בדנבר הייתה \(−6\) מעלות בצהריים. עם השקיעה הטמפרטורה ירדה \(−15\) למעלות. מה היה ההבדל בטמפרטורות הצהריים והשקיעה?
- תשובה
-
ההבדל בטמפרטורות היה \(9\) מעלות.
- קרא את הבעיה. ודא שכל המילים והרעיונות מובנים
- זהה את מה שאנו מתבקשים למצוא.
- כתוב ביטוי שנותן את המידע כדי למצוא אותו.
- תרגם את הביטוי לביטוי.
- פשט את הביטוי.
- ענה על השאלה במשפט שלם.
קבוצת הכדורגל של מוסטנג קיבלה שלושה פנדלים ברבע השלישי. כל עונש נתן להם הפסד של חמישה עשר יארד. מה מספר המטרים שאבדו?
- תשובה
-
שלב 1. קרא את הבעיה. ודא שכל המילים והרעיונות מובנים. שלב 2. זהה את מה שאנו מתבקשים למצוא. מספר המטרים שאבדו שלב 3. כתוב ביטוי שנותן את המידע כדי למצוא אותו. שלוש פעמים עונש \(15\) יארד שלב 4. תרגם את הביטוי לביטוי. \(3(-15)\) שלב 5. פשט את הביטוי. \(-45\) שלב 6. כתוב משפט שלם שעונה על השאלה. הקבוצה הפסידה \(45\) יארדים.
הדובים שיחקו גרוע והיו להם שבעה פנדלים במשחק. כל עונש הביא לאובדן \(15\) יארדים. מה מספר המטרים שאבדו בגלל עונשים?
- תשובה
-
הדובים איבדו \(105\) חצרות.
ביל משתמש בכספומט בקמפוס כי זה נוח. עם זאת, בכל פעם שהוא משתמש בו הוא מחויב בתשלום של 2 דולר. בחודש שעבר הוא השתמש בכספומט שמונה פעמים. כמה היה התשלום הכולל שלו עבור השימוש בכספומט?
- תשובה
-
תשלום של 16 דולר נוכה מחשבון העו "ש שלו.
מושגי מפתח
- כפל וחילוק של שני מספרים חתומים
- אותם סימנים — המוצר חיובי
- סימנים שונים - המוצר שלילי
- אסטרטגיה ליישומים
- זהה את מה שאתה מתבקש למצוא.
- כתוב ביטוי שנותן את המידע כדי למצוא אותו.
- תרגם את הביטוי לביטוי.
- פשט את הביטוי.
- ענה על השאלה במשפט שלם.


