1.4: הוסף וחסר מספרים שלמים
- Page ID
- 205628
- השתמש בתשלילים וניגודים
- פשט: ביטויים בעלי ערך מוחלט
- הוסף מספרים שלמים
- הפחת מספרים שלמים
מבוא יסודי יותר לנושאים המכוסים בחלק זה ניתן למצוא בפרק Prealgebra, מספרים שלמים.
השתמש בשלילים וניגודים
עבודתנו עד כה כללה רק את מספרי הספירה ואת המספרים השלמים. אבל אם אי פעם חווית טמפרטורה מתחת לאפס או משיכת יתר בטעות את חשבון הבדיקה שלך, אתה כבר מכיר מספרים שליליים. מספרים שליליים הם מספרים פחות\(0\). המספרים השליליים נמצאים משמאל לאפס בשורת המספרים. ראה איור\(\PageIndex{1}\).
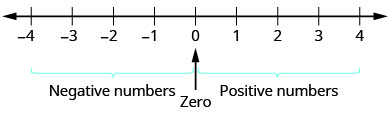
החצים בקצות שורת המספרים מצביעים על כך שהמספרים ממשיכים לנצח. אין מספר חיובי גדול ביותר, ואין מספר שלילי קטן ביותר.
האם אפס הוא מספר חיובי או שלילי? מספרים גדולים מאפס הם חיוביים, ומספרים קטנים מאפס הם שליליים. אפס אינו חיובי ואינו שלילי.
שקול כיצד מספרים מסודרים בשורת המספרים. משמאל לימין, המספרים עולים בערכם. מימין לשמאל, המספרים יורדים בערך. ראה איור\(\PageIndex{2}\).
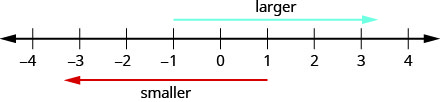
ביצוע פעילות המתמטיקה המניפולטיבית "קו מספר חלק 2" יעזור לך לפתח הבנה טובה יותר של מספרים שלמים.
זכור כי אנו משתמשים בסימון:
\(a \lt b\)(לקרוא "\(a\)הוא פחות מ\(b\)") כאשר \(a\) הוא בצד שמאל של \(b\) על שורת המספרים.
\(a \gt b\)(קרא "\(a\)גדול מ-\(b\)") כאשר \(a\) הוא מימין לשורת המספרים. \(b\)
כעת עלינו להרחיב את שורת המספרים שהראתה את המספרים השלמים כך שתכלול גם מספרים שליליים. המספרים המסומנים בנקודות באיור\(\PageIndex{3}\). נקראים מספרים שלמים. המספרים השלמים הם המספרים \(...−3, −2, −1, 0, 1, 2, 3…\)

סדר כל אחד מזוגות המספרים הבאים, באמצעות \(<\) או\(>\):
- \(14 \; \_\_\_\; 6\)
- \(-1\; \_\_\_ \;9\)
- \(-1\; \_\_\_ -4\)
- \(\;\; 2 \;\_\_\_ -20\)
פתרון:
זה עשוי להיות מועיל להתייחס לשורת המספרים המוצגת.

איור \(\PageIndex{4}\)
\ (\ התחל {יישור*} 1. \ מרובע & 14\;\ _\ _\\\; 6\\ [4pt]
& 14 > 6 &&\ טקסט {\(14\)נמצא מימין לשורת המספרים.}\\ [8pt] 2. \(6\)
\ מרובע & -1\;\ _\ _\\\; 9\\ [4pt]
& -1 < 9 &&\ טקסט {\(-1\)הוא משמאל \(9\) על שורת המספרים.}\\ [8pt] 3.
\ מרובע & -1\;\ _\ _\ _-4\\ [4pt]
& -1 > -4 &&\ טקסט {\(-1\)נמצא מימין לשורת המספרים.}\\ [8pt] 4. \(-4\)
\ מרובע & 2\;\ _\ _\ _-20\\ [4pt]
& 2 > -20 &&\ טקסט {\(2\)הוא בצד ימין של \(-20\) בשורת המספרים.} \
\ סוף {יישור*}\)
סדר כל אחד מזוגות המספרים הבאים, באמצעות \(<\) or \(>\):
- \(15 \; \_\_\_\; 7\)
- \(-2 \; \_\_\_\; 5\)
- \(-3 \; \_\_\_\; -7\)
- \(5 \; \_\_\_\; -17\)
- Answer
-
- \(<\)
- \(>\)
- \(<\)
- \(>\)
סדר כל אחד מזוגות המספרים הבאים, באמצעות \(<\) או\(>\):
- \(8 \; \_\_\_\; 13\)
- \(3 \; \_\_\_\; -4\)
- \(-5 \; \_\_\_\; -2\)
- \(9 \; \_\_\_\; -21\)
- תשובה
-
- \(<\)
- \(>\)
- \(<\)
- \(>\)
אולי שמתם לב שבשורת המספרים המספרים השליליים הם תמונת מראה של המספרים החיוביים, עם אפס באמצע. מכיוון שהמספרים \(2\) \(−2\) נמצאים באותו מרחק מאפס, הם נקראים מנוגדים s. ההפך \(2\) הוא\(−2\), וההיפך \(−2\) הוא\(2\).
ההפך ממספר הוא המספר שנמצא באותו מרחק מאפס בשורת המספרים אך בצד הנגדי של אפס.
איור \(\PageIndex{5}\) ממחיש את ההגדרה.

לפעמים באלגברה לאותו סמל יש משמעויות שונות. בדיוק כמו כמה מילים באנגלית, המשמעות הספציפית מתבהרת על ידי התבוננות כיצד משתמשים בה. ראית את הסמל "\(−\)" בשימוש בשלוש דרכים שונות.
\ [\ התחל {align*} &10 − 4\ quad\ text {בין שני מספרים, זה מציין את הפעולה של}\ textit {חיסור}.\\ &\ qquad\ qquad\ text {אנו קוראים} 10 - 4\,\ text {מינוס}\, 4. \ text {"}\\ [5pt]
&-8\ quad\ text {מול מספר, הוא מציין}\ textit {שלילי}\ text {number.}\\\ qquad\ qquad\ text {אנו קוראים} -8\ טקסט {כמו "שמונה שלילי."}\ [5pt]
&-x\ quad\ text {מול משתנה, הוא מציין את}\ text\ text tit {ממול.}\\ &\ qquad\ text {אנחנו קוראים} -x\ טקסט {כמו "ההפך מ} x\ text {"}\\ [5pt]
&- (-2)\ quad\ text {כאן יש שני סימנים "−".} \\
&\ qquad\ qquad\ text {זה שבסוגריים אומר לנו שהמספר שלילי} 2. \\
&\ qquad\ qquad\ text {זה שמחוץ לסוגריים אומר לנו לקחת את}\ textit {ממול}\ text {of} −2. \\
&\ qquad\ qquad\ text {אנו קוראים} - (-2)\ טקסט {כמו "ההפך משני שלילי."} \ סוף {יישור*}\]
\(−a\)פירושו ההפך מהמספר\(a\).
הסימון \(−a\) נקרא "ההפך מ"\(a\).
למצוא:
- ההפך מ \(7\)
- ההפך מ \(−10\)
- ההפך מ \(−(−6)\)
פתרון:
1. \( \quad −7\)הוא אותו מרחק מ \(0\) כמו\(7\), אבל בצד הנגדי של\(0\). ההפך \(7\) הוא\(-7\).

2. \( \quad 10\)הוא אותו מרחק מ \(0\) כמו\(−10\), אבל בצד הנגדי של\(0\). ההפך \(-10\) הוא\(10\).

3. \(\quad\)ההפך מ \(-(-6)\) הוא\(-6\).

למצוא:
- ההפך מ \(4\)
- the opposite of \(−3\)
- \(−(−1)\)
- Answer
-
- \(-4\)
- \(3\)
- \(1\)
למצוא:
- ההפך מ \(8\)
- ההפך מ \(−5\)
- \(−(−5)\)
- תשובה
-
- \(-8\)
- \(5\)
- \(5\)
העבודה שלנו עם ניגודים נותנת לנו דרך להגדיר את המספרים השלמים. המספרים השלמים והניגודים שלהם נקראים מספרים שלמים. המספרים השלמים הם המספרים \(…−3,−2,−1,0,1,2,3…\)
המספרים השלמים והניגודים שלהם נקראים מספרים שלמים.
המספרים השלמים הם המספרים
\[…−3,−2,−1,0,1,2,3… \nonumber \]
כאשר אנו מעריכים את ההפך ממשתנה, עלינו להיות זהירים מאוד. מבלי לדעת אם המשתנה מייצג מספר חיובי או שלילי, איננו יודעים אם −איקס−איקס חיובי או שלילי. אנו יכולים לראות זאת בדוגמה\(\PageIndex{1}\).
להעריך
- \(-x\), כאשר \(x = 8\)
- \(-x\), כאשר \(x = -8\)
פתרון:
-

-x 
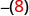
כתוב את ההפך מ 8. -8 -

-x 
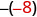
כתוב את ההפך מ -8. 8
להעריך \(-n\), when
- \(n = 4\)
- \(n = -4\)
- Answer
-
- \(-4\)
- \(4\)
להעריך\(-m\), מתי
- \(m = 11\)
- \(m = -11\)
- תשובה
-
- \(-11\)
- \(11\)
פשט: ביטויים בעלי ערך מוחלט
ראינו שמספרים כמו \(2\) \(−2\) והינם הפכים מכיוון שהם נמצאים \(0\) באותו מרחק מקו המספרים. שניהם שתי יחידות מ\(0\). המרחק \(0\) בין מספר למספר כלשהו בשורת המספרים נקרא הערך המוחלט של אותו מספר.
הערך המוחלט של מספר הוא המרחק שלו \(0\) משורת המספרים.
הערך המוחלט של מספר \(n\) כתוב כ\(|n|\).
לדוגמה,
- \(−5\)הוא במרחק \(5\) יחידות\(0\), אז\(|−5|=5\).
- \(5\)הוא במרחק \(5\) יחידות\(0\), אז\(|5|=5\).
איור \(\PageIndex{6}\) ממחיש רעיון זה.
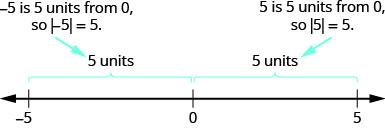
הערך המוחלט של מספר לעולם אינו שלילי (מכיוון שהמרחק אינו יכול להיות שלילי). המספר היחיד עם הערך המוחלט השווה לאפס הוא המספר אפס עצמו, מכיוון שהמרחק מ- \(0\) אל \(0\) בשורת המספרים הוא אפס יחידות.
\(|n| \geq 0\)לכל המספרים
ערכים מוחלטים תמיד גדולים או שווים לאפס!
מתמטיקאים אומרים זאת ביתר דיוק, "ערכים מוחלטים הם תמיד לא שליליים." לא שלילי פירושו גדול או שווה לאפס.
פשט:
- \(|3|\)
- \(|-44|\)
- \(|0|\)
פתרון:
הערך המוחלט של מספר הוא המרחק בין המספר לאפס. המרחק לעולם אינו שלילי, ולכן הערך המוחלט לעולם אינו שלילי.
- \( |3| = 3\)
- \(|-44| = 44\)
- \( |0| = 0\)
פשט:
- \(|4|\)
- \(|-28|\)
- \(|0|\)
- Answer
-
- \(4\)
- \(28\)
- \(0\)
פשט:
- \(|-13|\)
- \(|47|\)
- תשובה
-
- \(13\)
- \(47\)
בדוגמה הבאה, נזמין ביטויים עם ערכים מוחלטים. זכרו, מספרים חיוביים תמיד גדולים יותר ממספרים שליליים!
מלא \(<, >, \text{or} =\) עבור כל אחד מזוגות המספרים הבאים:
- \(|−5| \; {\underline{\hspace {2 em}}} \;−|−5|\)
- \(8 \;{\underline{\hspace {2 em}}} \;−|−8|\)
- \(-9 \;{\underline{\hspace {2 em}}} \;−|−9|\)
- \(-(-16) \;{\underline{\hspace {2 em}}}\; −|−16|\)
פתרון:
\(\begin{array} {llll} {\text{Simplification}} &{|-5|} & {\underline{\hspace {2 em}}} &{-|-5|} \\ {\text{Order.}} &{5} &{\underline{\hspace {2 em}}} &{-5} \\ {} &{5} &{>} &{-5} \\ {} &{|-5|} &{>} &{-|-5|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{8} & {\underline{\hspace {2 em}}} &{-|-8|} \\ {\text{Order.}} &{8} &{\underline{\hspace {2 em}}} &{-8} \\ {} &{8} &{>} &{-8} \\ \text{so }\\ {} & {|8|} &{>} &{-|-8|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{-9} & {\underline{\hspace {2 em}}} &{-|-9|} \\ {\text{Order.}} &{-9} &{\underline{\hspace {2 em}}} &{-9} \\ {} &{-9} &{=} &{-9} \\ \text{so } \\ {} & {-9} &{=} &{-|-9|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{-(-16)} & {\underline{\hspace {2 em}}} &{-|16|} \\ {\text{Order.}} &{16} &{\underline{\hspace {2 em}}} &{-16} \\ {} &{16} &{>} &{-16} \\ \text{so } \\ {} & {-(-16)} &{>} &{-|-16|} \\ \end{array}\)
מלא \(<, >, \text{or} =\) for each of the following pairs of numbers:
- \(|−9| \;{\underline{\hspace {2 em}}} \; −|−9|\)
- \(2 \;{\underline{\hspace {2 em}}} \; −|−2|\)
- \(-8 \;{\underline{\hspace {2 em}}} \; −|−8|\)
- \(-(-9) \;{\underline{\hspace {2 em}}} \; −|−9|\)
- Answer
-
- \(>\)
- \(>\)
- \(<\)
- \(>\)
מלא \(<, >, \text{or} =\) עבור כל אחד מזוגות המספרים הבאים:
- \(7 \;{\underline{\hspace {2 em}}} \; −|−7|\)
- \(-(-10) \;{\underline{\hspace {2 em}}} \; −|−10|\)
- \(|-4| \;{\underline{\hspace {2 em}}} \; −|−4|\)
- \(-1 \;{\underline{\hspace {2 em}}} \; |−1|\)
- תשובה
-
- \(>\)
- \(>\)
- \(>\)
- \(<\)
כעת אנו מוסיפים סרגלי ערך מוחלטים לרשימת סמלי הקיבוץ שלנו. כאשר אנו משתמשים בסדר הפעולות, ראשית אנו מפשטים בתוך סרגלי הערך המוחלטים ככל האפשר, ואז אנו לוקחים את הערך המוחלט של המספר המתקבל.
\[\begin{array} {llll} {\text{Parentheses}} &{()} & {\text{Braces}} & {\{\}} \\ {\text{Brackets}} &{[\space]} &{\text{Absolute}} &{|\space|} \\ \end{array} \nonumber\]
בדוגמה הבאה, אנו מפשטים תחילה את הביטויים בתוך פסי ערך מוחלטים, בדיוק כמו שאנחנו עושים בסוגריים.
פשט: \(24 - |19 - 3(6 - 2)|\)
פתרון:
\[\begin{array} {ll} {} &{24 - |19 - 3(6 - 2)|} \\ {\text{Work inside parentheses first: subtract } 2\space \text{from } 6} &{24 - |19 - 3(4)|} \\ {\text{Multiply }3(4)} &{24 - |19 - 12|} \\ {\text{Subtract inside the absolute value bars. }} &{24 - |7|} \\ {\text{Take the absolute value.}} &{24 - 7} \\ {\text{Subtract.}} &{17} \end{array}\nonumber\]
פשט: \(19 - |11 - 4(3 - 1)|\)
- Answer
-
\(16\)
פשט: \(9 - |8 - 4(7 - 5)|\)
- תשובה
-
\(9\)
להעריך:
- \(|x|\)מתי \(x = -35\)
- \(|y|\)מתי \(y = -20\)
- \(-|u|\)מתי \(u = 12\)
- \(-|p|\)מתי \(p = -14\)
פתרון:
1. \(|x|\)מתי \(x = -35\)
\(\begin{array} {ll} {} &{|x|} \\ {\text{Substitute } -35 \space \text{for }x} &{|-35|} \\ {\text{Take the absolute value.}} &{35} \end{array}\)
2. \(|y|\)מתי \(y = -20\)
\(\begin{array} {ll} {} &{|-y|} \\ {\text{Substitute } -20 \space \text{for }y} &{|-(-20)|} \\ {\text{Simplify}} &{|20|} \\ {\text{Take the absolute value.}} &{20} \end{array}\)
3. \(-|u|\)מתי \(u = 12\)
\(\begin{array} {ll} {} &{-|u|} \\ {\text{Substitute } 12 \space \text{for }u} &{|-12|} \\ {\text{Take the absolute value.}} &{-12} \end{array}\)
4. \(-|p|\)מתי \(p = -14\)
\(\begin{array} {ll} {} &{-|p|} \\ {\text{Substitute } -14 \space \text{for }p} &{-|-14|} \\ {\text{Take the absolute value.}} &{-14} \end{array}\)
להעריך:
- \(|x|\) when \(x = -17\)
- \(|y|\) when \(y = -39\)
- \(-|m|\) when \(m = 22\)
- \(-|p|\) when \(p = -11\)
- Answer
-
- \(17\)
- \(39\)
- \(-22\)
- \(-11\)
להעריך:
- \(|y|\)מתי \(y = -23\)
- \(|-y|\)מתי \(y = -21\)
- \(-|n|\)מתי \(n = 37\)
- \(-|q|\)מתי \(q = -49\)
- תשובה
-
- \(23\)
- \(21\)
- \(-37\)
- \(-49\)
הוסף מספרים שלמים
לרוב התלמידים נוח עם עובדות החיבור והחיסור למספרים חיוביים. אבל ביצוע חיבור או חיסור עם מספרים חיוביים ושליליים עשוי להיות מאתגר יותר.
ביצוע פעילות המתמטיקה המניפולטיבית "הוספת מספרים חתומים" יעזור לך לפתח הבנה טובה יותר של הוספת מספרים שלמים.
אנו נשתמש בשני מוני צבע כדי לדגמן חיבור וחיסור של שליליות, כך שתוכל לדמיין את הנהלים במקום לשנן את הכללים.
אנו נותנים לצבע אחד (כחול) לייצג חיובי. הצבע השני (אדום) ייצג את השליליות. אם יש לנו מונה חיובי אחד ומונה שלילי אחד, ערך הצמד הוא אפס. הם יוצרים זוג ניטרלי. הערך של זוג ניטרלי זה הוא אפס.
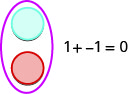
אנו נשתמש בדלפקים כדי להראות כיצד להוסיף את ארבע עובדות התוספת באמצעות המספרים \(5, −5\) ו\(3,−3\).
\[\begin{array} {llll} {5 + 3} &{-5 + (-3)} &{-5 + 3} &{5 + (-3)} \end{array} \nonumber \]
כדי להוסיף\(5+3\), אנו מבינים שזה \(5+3\) אומר סכום \(5\) ו\(3\).
| אנחנו מתחילים עם \(5\) חיובי. |  |
| ואז נוסיף \(3\) תוצאות חיוביות. |  |
| עכשיו יש לנו \(8\) תוצאות חיוביות. הסכום של \(5\) \(3\) והוא\(8\). |  |
עכשיו נוסיף\(−5 + (−3)\). שימו לב לדמיון לדוגמא האחרונה\(5 + 3 = 8\).
כדי להוסיף\(−5 + (−3)\), אנו מבינים שזה אומר סכום \(−5\) ו\(−3\).
| אנחנו מתחילים עם \(5\) שליליות. |  |
| ואז נוסיף \(3\) שליליות. |  |
| עכשיו יש לנו \(8\) שלילי. הסכום של \(-5\) \(-3\) והוא\(-8\). |  |
באילו דרכים היו שתי הדוגמאות הראשונות דומות?
- הדוגמה הראשונה מוסיפה \(5\) חיוביות וחיוביות - שניהם \(3\) חיוביים.
- הדוגמה השנייה מוסיפה \(5\) שליליות ושליליות - שניהם \(3\) שליליים.
בכל מקרה קיבלנו \(8\) - \(8\) חיובי או \(8\) שלילי.
כאשר השלטים היו זהים, הדלפקים היו כולם באותו צבע, ולכן הוספנו אותם.

הוסף:
- \(1 + 4\)
- \(-1 + (-4)\)
פתרון:
1. 
\(1\)חיובי פלוס \(4\) חיובי הוא \(5\) חיובי.
2. 
\(1\)שלילי פלוס \(4\) שלילי הוא \(5\) שלילי.
הוסף:
- \(2 + 4\)
- \(-2 + (-4)\)
- Answer
-
- \(6\)
- \(-6\)
הוסף:
- \(2 + 5\)
- \(-2 + (-5)\)
- תשובה
-
- \(7\)
- \(-7\)
אז מה קורה כאשר הסימנים שונים? בואו נוסיף\(−5+3\). אנו מבינים שזה אומר סכום \(−5\) ו\(3\). כאשר הדלפקים היו באותו צבע, שמנו אותם בשורה. כאשר הדלפקים בצבע שונה, אנו מסדרים אותם אחד מתחת לשני.
| \(-5 + 3\)פירושו סכום \(-5\) ו\(3\). | |
| אנחנו מתחילים עם \(5\) שליליות. |  |
| ואז נוסיף \(3\) תוצאות חיוביות. | 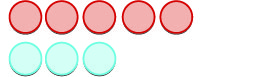 |
| אנו מסירים כל זוגות ניטרליים. | 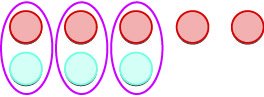 |
| נשארו לנו \(2\) תשלילים. |  |
| הסכום של \(-5\) \(3\) והוא\(-2\). | \(-5 + 3 = 2\) |
שימו לב שהיו יותר שליליות מאשר חיוביות, כך שהתוצאה הייתה שלילית.
בואו עכשיו להוסיף את השילוב האחרון,\(5+(−3)\).
| \(5 + (-3)\)פירושו סכום \(-5\) ו\(-3\). | |
| אנחנו מתחילים עם \(5\) חיובי. |  |
| ואז נוסיף \(3\) שליליות. | 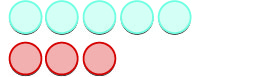 |
| אנו מסירים כל זוגות ניטרליים. | 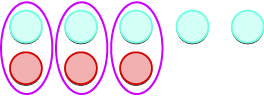 |
| נשארו לנו \(2\) דברים חיוביים. |  |
| הסכום של \(5\) \(-3\) והוא\(2\). | \(5 + (-3) = 2\) |
כאשר אנו משתמשים במונים כדי לדגמן תוספת של מספרים שלמים חיוביים ושליליים, קל לראות אם יש מונים חיוביים יותר או שליליים יותר. אז אנחנו יודעים אם הסכום יהיה חיובי או שלילי.
הוסף:
- \(-1 + 5\)
- \(1 + (-5)\)
פתרון:
1. \(-1 + 5\)

יש יותר תוצאות חיוביות, כך שהסכום חיובי.
אז,\(-1 + 5 = 4\).
2. \(1 + (-5)\)

יש יותר שליליות, כך שהסכום שלילי.
אז, \(1 + (-5) = -4\)
הוסף:
- \(-2 + 4\)
- \(2 + (-4)\)
- Answer
-
- \(2\)
- \(-2\)
הוסף:
- \(-2 + 5\)
- \(2 + (-5)\)
- תשובה
-
- \(3\)
- \(-3\)
כעת, לאחר שהוספנו מספרים שלמים חיוביים ושליליים קטנים עם מודל, אנו יכולים לדמיין את המודל במוחנו כדי לפשט בעיות במספרים כלשהם.
כאשר אתה צריך להוסיף מספרים כגון\(37+(−53)\), אתה באמת לא רוצה לספור מונים \(37\) כחולים ודלפקים \(53\) אדומים. עם המודל בראש שלך, אתה יכול לדמיין מה היית עושה כדי לפתור את הבעיה?
דלפקי תמונה \(37\) כחולים עם דלפקים \(53\) אדומים בשורה מתחת. מכיוון שיהיו יותר מונים אדומים (שליליים) מאשר מונים כחולים (חיוביים), הסכום יהיה שלילי. כמה דלפקים אדומים נוספים יהיו? כי\(53−37=16\), יש דלפקים אדומים \(16\) יותר.
לכן, הסכום של \(37+(−53)\) הוא\(−16\).
\[37+(−53)=−16\nonumber\]
בוא ננסה עוד אחד. נוסיף\(−74+(−27)\). שוב, דמיין דלפקים \(74\) אדומים \(27\) ועוד דלפקים אדומים, כך שיהיו לנו דלפקים \(101\) אדומים. זה אומר שהסכום הוא\(−101\).
\[−74+(−27)=−101\nonumber\]
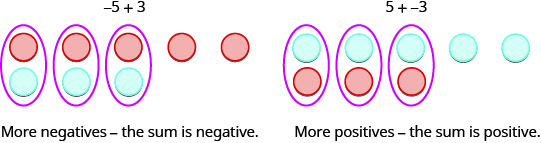
בואו נסתכל שוב על התוצאות של הוספת שילובים שונים של \(5,−5\) ו\(3, -3\).
\[\begin{array} {ll} {5 + 3=8} &{-5 + (-3)=-8} \\{\text{both positive, sum positive}} &{\text{both negative, sum negative}} \end{array}\nonumber\]
כאשר השלטים זהים, הדלפקים יהיו באותו צבע, אז הוסף אותם.
\[\begin{array} {ll} {-5 + 3=-2} &{5 + (-3)=2} \\{\text{different signs, more negatives, sum negative}} &{\text{different signs, more positives, sum positive}} \end{array}\nonumber\]
כאשר השלטים שונים, חלק מהדלפקים היו יוצרים זוגות ניטרליים, אז גרעו כדי לראות כמה נותרו.
דמיינו את המודל כשאתם מפשטים את הביטויים בדוגמאות הבאות.
פשט:
- \(19 + (-47)\)
- \(-14 + (-36)\)
פתרון:
1. מכיוון שהסימנים שונים, אנו מחסרים \(19\) מ\(47\). התשובה תהיה שלילית מכיוון שיש יותר שליליות מאשר חיוביות.
\(\text{Add.} \qquad 19 + (-47) = -28\)
2. מכיוון שהסימנים זהים, אנו מוסיפים. התשובה תהיה שלילית מכיוון שיש יותר שליליות מאשר חיוביות.
\(\text{Add.} \qquad-14 + (-36) = -50\)
פשט:
- \(-31 + (-19)\)
- \(15 + (-32)\)
- Answer
-
- \(-50\)
- \(-17\)
פשט:
- \(-42 + (-28)\)
- \(25 + (-61)\)
- תשובה
-
- \(-70\)
- \(-36\)
הטכניקות בהן נעשה שימוש עד כה מתרחבות לבעיות מסובכות יותר, כמו אלה שראינו בעבר. זכור לבצע את סדר הפעולות!
פשט:
\(-5 + 3(-2 + 7)\)
פתרון:
\[\begin{array} {ll} {} &{-5 + 3(-2 + 7)} \\ {\text{Simplify inside the parenthesis}} &{-5 + 3(5)} \\{\text{Multiply}} &{-5 + 15} \\{\text{add left to right}} &{10} \end{array}\nonumber\]
פשט:
\(-2 + 5(-4 + 7)\)
- Answer
-
\(13\)
פשט:
\(-4 + 2(-3 + 5)\)
- תשובה
-
\(0\)
הפחת מספרים שלמים
ביצוע פעילות המתמטיקה המניפולטיבית "חיסור מספרים חתומים" יעזור לך לפתח הבנה טובה יותר של חיסור מספרים שלמים.
אנו נמשיך להשתמש במונים כדי לדגמן את החיסור. זכור, המונים הכחולים מייצגים מספרים חיוביים והמונים האדומים מייצגים מספרים שליליים.
אולי כשהיית צעיר יותר, קראת "\(5−3\)" \(5\) כ"קח משם"\(3\). כשאתה משתמש במונים אתה יכול לחשוב על חיסור באותה צורה!
נדגמן את ארבע עובדות החיסור באמצעות המספרים \(5\) ו\(3\).
\[\begin{array} {llll} {5 - 3} &{-5 - (-3))} &{-5 -3} &{5 - (-3)} \end{array}\nonumber\]
כדי לחסר\(5−3\), אנו משחזרים את הבעיה \(5\) כ"קח משם"\(3\).
| אנחנו מתחילים עם \(5\) חיובי. |  |
| אנחנו "לוקחים" דברים חיוביים. \(3\) |  |
| נשארו לנו \(2\) דברים חיוביים. | |
| ההבדל בין \(5\) לבין \(3\) הוא\(2\). | \(2\) |
עכשיו נחסר\(−5−(−3)\). שימו לב לדמיון לדוגמא האחרונה\(5−3=2\).
כדי לחסר\(−5−(−3)\), אנו משחזרים זאת מחדש \(–5\) כ"קח משם\(–3\)"
| אנחנו מתחילים עם \(5\) שליליות. |  |
|
אנחנו "לוקחים" שליליות. \(3\) |
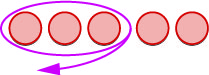 |
| נשארו לנו \(2\) תשלילים. | |
| ההבדל בין \(-5\) לבין \(-3\) הוא\(-2\). |
\(-2\) |
שימו לב ששתי הדוגמאות הללו דומות מאוד: הדוגמה הראשונה, אנו מפחיתים 3 תוצאות חיוביות מ -5 תוצאות חיוביות ובסופו של דבר עם 2 תוצאות חיוביות.
בדוגמה השנייה, אנו מפחיתים 3 שליליות מ -5 שליליות ובסופו של דבר עם 2 שליליות.
כל דוגמה השתמשה במונים בצבע אחד בלבד, ומודל החיסור "לקחת משם" היה קל ליישום.
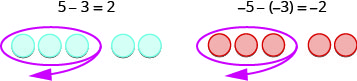
חיסור:
- \(7 - 5\)
- \(-7 - (-5)\)
פתרון:
- \[\begin{array} {ll} {7 - 5} \\ {2}&{\text{Take }5\space \text{positives from }7 \space \text{positives and get }2\space \text{positives}} & \end{array}\nonumber\]
- \[\begin{array} {ll} {-7 - (-5)} \\ {-2} &{\text{Take }5\space \text{negatives from }7 \space \text{negatives and get }2\space \text{negatives}} \end{array}\nonumber\]
חיסור:
- \(6 - 4\)
- \(-6 - (-4)\)
- Answer
-
- \(2\)
- \(-2\)
חיסור:
- \(7 - 4\)
- \(-7 - (-4)\)
- תשובה
-
- \(3\)
- \(-3\)
מה קורה כשאנחנו צריכים לחסר מספר חיובי ואחד שלילי? נצטרך להשתמש במונים לבנים ואדומים, כמו גם בכמה זוגות ניטרליים. הוספת זוג ניטרלי אינה משנה את הערך. זה כמו להחליף רבעים לניקלים - הערך זהה, אבל זה נראה אחרת.
- כדי לחסר\(−5−3\), אנו משחזרים את זה כמו \(−5\) לקחת משם. \(3\)
אנחנו מתחילים עם \(5\) שליליות. אנחנו צריכים לקחת \(3\) דברים חיוביים, אבל אין לנו שום דבר חיובי לקחת.
זכור, לזוג ניטרלי יש ערך אפס. אם נוסיף \(0\) \(5\) לערכו הוא עדיין\(5\). אנו מוסיפים זוגות ניטרליים \(5\) לתשלילים עד שנקבל \(3\) תוצאות חיוביות לקחת.
| \(-5 -3\)פירושו \(-5\) לקחת \(3\) | |
| אנחנו מתחילים עם \(5\) שליליות. |  |
| כעת אנו מוסיפים את הנייטרלים הדרושים כדי לקבל \(3\) תוצאות חיוביות. |  |
| אנו מסירים את \(3\) החיוביות. | 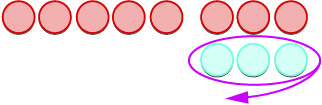 |
| נשארנו עם \(8\) שליליות. |  |
| ההבדל בין \(-5\) לבין \(3\) הוא\(-8\). | \(-5 - 3 = -8\) |
ועכשיו, המקרה הרביעי,\(5−(−3)\). אנחנו מתחילים עם \(5\) חיובי. אנחנו צריכים לקחת \(3\) שליליות, אבל אין שליליות לקחת. אז אנו מוסיפים זוגות ניטרליים עד שיש לנו \(3\) שליליות לקחת.
| \(5 -(-3)\)פירושו \(5\) לקחת \(-3\) | |
| אנחנו מתחילים עם \(5\) חיובי. |  |
| כעת אנו מוסיפים את הזוגות הנייטרלים הדרושים. |  |
| אנו מסירים את \(3\) התשלילים. | 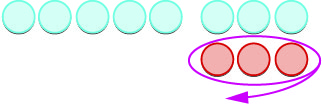 |
| נשארנו עם \(8\) תוצאות חיוביות. |  |
| ההבדל בין \(5\) לבין \(-3\) הוא\(8\). | \(5 - (-3) = 8\) |
חיסור:
- \(-3 -1\)
- \(3 - (-1)\)
פתרון:
1.
|
קח 1 חיובי מהזוג הנייטרלי שנוסף. |
  |
\(\begin{array} {l} {-3 -1} \\ {-4} \end{array}\) |
|
קח 1 שלילי מהזוג הנייטרלי שנוסף. |
  |
\(\begin{array} {l} {3 - (-1)} \\ {4} \end{array}\) |
חיסור:
- \(-6 -4\)
- \(6 - (-4)\)
- Answer
-
- \(-10\)
- \(10\)
חיסור:
- \(-7-4\)
- \(7 - (-4)\)
- תשובה
-
- \(-11\)
- \(11\)
שמתם לב שניתן לבצע חיסור של מספרים חתומים על ידי הוספת ההפך? בתרגיל\(\PageIndex{33}\), \(−3−1\) זהה לזה \(−3+(−1)\) \(3−(−1)\) וזהה לזה\(3+1\). לעתים קרובות תראה רעיון זה, מאפיין החיסור, שנכתב באופן הבא:
\[a−b=a+(−b) \nonumber\]
חיסור מספר זהה להוספת ההפך.
תסתכל על שתי הדוגמאות האלה.
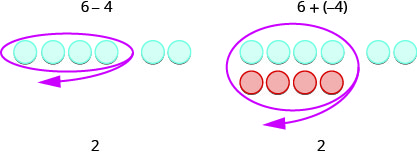
כמובן, כאשר יש לך בעיית חיסור שיש לה רק מספרים חיוביים, כמו\(6−4\), אתה פשוט עושה את החיסור. כבר ידעת איך לחסר \(6−4\) מזמן. אבל הידיעה הזו \(6−4\) נותנת את אותה התשובה \(6+(−4)\) שעוזרת כשאתה מחסר מספרים שליליים. ודא שאתה מבין איך \(6−4\) \(6+(−4)\) ולתת את אותן תוצאות!
פשט:
- \(13 - 8 \space \text{and } 13 + (-8)\)
- \(-17 - 9 \space \text{and } -17 + (-9)\)
פתרון:
- \(\begin{array} {llll} {\text{Subtract.}} &{13 - 8} &{\text{and}} &{13 + (-8)} \\ {} &{5} &{} &{5} \end{array}\)
- \(\begin{array} {llll} {\text{Subtract.}} &{-17 - 9} &{\text{and}} &{-17 + (-9)} \\ {} &{-26} &{} &{-26} \end{array}\)
פשט:
- \(21 - 13 \space \text{and } 21 + (-13)\)
- \(-11 - 7 \space \text{and } -11 + (-7)\)
- Answer
-
- \(8\)
- \(-18\)
פשט:
- \(15 - 7 \space \text{and } 15 + (-7)\)
- \(-14 - 8 \space \text{and } -14 + (-8)\)
- תשובה
-
- \(8\)
- \(-22\)
תראו מה קורה כשאנחנו מפחיתים שלילי.

חיסור מספר שלילי זה כמו להוסיף חיובי!
לעתים קרובות תראה את זה כתוב כ\(a−(−b)=a+b\).
האם זה עובד גם למספרים אחרים? בואו נעשה את הדוגמה הבאה ונראה.
פשט:
- \(9 - (-15) \space \text{and } 9 + 15\)
- \(-7 - (-4) \space \text{and } -7 + 4\)
פתרון:
- \(\begin{array} {lll} {} &{9 - (-15)} &{9 + 15} \\ {\text{Subtract}} &{24} &{24} \end{array}\)
- \(\begin{array} {lll} {} &{-7 - (-4)} &{-7 + 4} \\ {\text{Subtract}} &{-3} &{-3} \end{array}\)
פשט:
- \(6 - (-13) \space \text{and } 6 + 13\)
- \(-5 - (-1) \space \text{and } -5 + 1\)
- Answer
-
- \(19\)
- \(-4\)
פשט:
- \(4 - (-19) \space \text{and } 4 + 19\)
- \(-4 - (-7) \space \text{and } -4 + 7\)
- תשובה
-
- \(23\)
- \(3\)
בואו נסתכל שוב על התוצאות של חיסור השילובים השונים של \(5,−5\) ו. \(3,−3\)
\[\begin{array} {l} {5 - 3} &{-5 - (-3)} \\ {2} &{-2} \\ {5\space\text{positives take away }3\space\text{positives}} &{5\space\text{negatives take away }3\space\text{negatives}} \\ {2\space\text{positives}} &{2\space\text{negatives}} \end{array}\nonumber\]
כאשר יהיו מספיק מונים של צבע לקחת, לחסר.
\[\begin{array} {l} {-5 - 3} &{5 - (-3)} \\ {-8} &{8} \\ {5\space\text{negatives, want to take away }3\space\text{positives}} &{5\space\text{positives, want to take away }3\space\text{negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}} \end{array}\nonumber\]
כאשר לא יהיו מספיק מונים של צבע לקחת, להוסיף.
מה קורה כשיש יותר משלושה מספרים שלמים? אנחנו פשוט משתמשים בסדר הפעולות כרגיל.
פשט:
\(7 - (-4 -3) - 9\)
פתרון:
\[ \begin{array} {ll} {} &{7 - (-4 - 3) - 9} \\ {\text{Simplify inside the parenthesis first.}} &{7 - (-7) - 9} \\ {\text{Subtract left to right.}} &{14 - 9} \\ {\text{Subtract}} &{5} \end{array}\nonumber\]
פשט:
\(8−(−3−1)−9\)
- Answer
-
\(3\)
פשט:
\(12−(−9−6)−14\)
- תשובה
-
\(12\)
גש למשאבים מקוונים אלה לקבלת הדרכה ותרגול נוספים עם הוספה וחיסור של מספרים שלמים. יהיה עליך להפעיל Java בדפדפן האינטרנט שלך כדי להשתמש ביישומים.
מושגי מפתח
- הוספת מספרים שלמים חיוביים ושליליים
\[\begin{array} {ll} {5 + 3} &{-5+(-3)} \\ {8} &{-8} \\ {\text{both positive,}} &{\text{both negative,}} \\ {\text{sum positive}} &{\text{sum negative}} \end{array}\nonumber\]
\[\begin{array} {ll} {-5 + 3} &{5+(-3)} \\ {-2} &{2} \\ {\text{different signs,}} &{\text{different signs,}} \\ {\text{more negatives}} &{\text{more positives}} \\ {\text{sum negative}} &{\text{sum positive}} \end{array}\nonumber\]
- נכס בעל ערך מוחלט:
\(|n| \geq 0\)לכל המספרים. ערכים מוחלטים תמיד גדולים או שווים לאפס!
- חיסור מספרים שלמים
\[\begin{array} {ll} {5 - 3} &{-5-(-3)} \\ {2} &{-2} \\ {5\space\text{positives}} &{5\space\text{negatives}} \\ {\text{take away 3 positives}} &{\text{take away 3 negatives}} \\ {\text{2 positives}} &{\text{2 negatives}} \end{array}\nonumber\]
\[\begin{array} {ll} {-5 - 3} &{5-(-3)} \\ {-8} &{8} \\ {\text{5 negatives, want to}} &{\text{5 positives, want to}} \\ {\text{subtract 3 positives}} &{\text{subtract 3 negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}}\end{array}\nonumber\]
- מאפיין חיסור: חיסור מספר זהה להוספת ההפך.
רשימת מילים
- ערך מוחלט
- הערך המוחלט של מספר הוא המרחק שלו מ- 0 בשורת המספרים. הערך המוחלט של מספר nn כתוב כ- |n |.
- מספרים שלמים
- המספרים השלמים והניגודים שלהם נקראים מספרים שלמים: \(...−3, −2, −1, 0, 1, 2, 3...\)
- ממול
- ההפך ממספר הוא המספר שנמצא באותו מרחק מאפס בשורת המספרים אך בצד הנגדי של אפס: - \(a\) פירושו ההפך מהמספר. הסימון - \(a\) נקרא "ההפך מ\(a\)."


