1.3: השתמש בשפת האלגברה
- Page ID
- 205688
בסוף פרק זה תוכל:
- השתמש במשתנים ובסמלים אלגבריים
- פשט ביטויים לפי סדר הפעולות
- הערך ביטוי
- זהה ושלב מונחים דומים
- תרגם ביטוי באנגלית לביטוי אלגברי
השתמש במשתנים ובסמלים אלגבריים
נניח שהשנה גרג בן \(20\) שנים ואלכס הוא\(23\). אתה יודע שאלכס מבוגר מגרג \(3\) בשנים. כשגרג היה\(12\), אלכס היה\(15\). כאשר גרג יהיה\(35\), אלכס יהיה\(38\). לא משנה מה גילו של גרג, הגיל של אלכס תמיד יהיה 3 שנים יותר, נכון? בשפת האלגברה אנו אומרים שגילו של גרג וגילו של אלכס הם משתנים \(3\) וזה קבוע. הגילאים משתנים ("משתנים") אך \(3\) השנים ביניהם תמיד נשארות זהות ("קבועות"). מכיוון שגילו של גרג וגילו של אלכס תמיד יהיו שונים \(3\) בשנים, \(3\) הוא הקבוע. באלגברה אנו משתמשים באותיות האלף-בית כדי לייצג משתנים. אז אם נקרא לגילו של גרג\(g\), נוכל לייצג \(g + 3g + 3\) את גילו של אלכס. ראה טבלה\(\PageIndex{1}\).
| גילו של גרג | הגיל של אלכס |
|---|---|
| \(12\) | \(15\) |
| \(20\) | \(23\) |
| \(35\) | \(38\) |
| \(g\) | \(g+3\) |
האותיות המשמשות לייצוג הגילאים המשתנים הללו נקראות משתנים. האותיות הנפוצות ביותר עבור משתנים הן \(x, y, a, b,\) ו\(c\).
משתנה הוא אות המייצגת מספר שערכו עשוי להשתנות.
קבוע הוא מספר שערכו תמיד נשאר זהה.
כדי לכתוב אלגברית, אנו זקוקים לכמה סמלי פעולה כמו גם מספרים ומשתנים. ישנם מספר סוגים של סמלים בהם נשתמש.
ישנן ארבע פעולות חשבון בסיסיות: חיבור, חיסור, כפל וחילוק. נפרט את הסמלים המשמשים לציון פעולות אלה להלן (טבלה\(\PageIndex{2}\)). סביר להניח שתזהו כמה מהם. \(\require{enclose}\)
| מבצע | סימון | תגיד: | התוצאה היא... |
|---|---|---|---|
| תוספת | \(a+b\) | \(a\)פלוס \(b\) | סכום \(a\) ו \(b\) |
| חיסור | \(a−b\) | \(a\)מינוס \(b\) | ההבדל של \(a\) ו \(b\) |
| כפל | \(a·b,ab,(a)(b),(a)b,a(b)\) | \(a\)פעמים \(b\) | המוצר של \(a\) ו \(b\) |
| חטיבה | \(a\div{b}, a/b,\dfrac{a}{b}, b \enclose{longdiv}{a}\) | \(a\)מחולק על ידי \(b\) | המנה של \(a\) ו\(b\), \(a\) נקרא דיבידנד, והוא \(b\) נקרא המחלק |
אנו מבצעים פעולות אלה בשני מספרים. כאשר מתרגמים מצורה סמלית לאנגלית, או מאנגלית לצורה סמלית, שימו לב למילים "של" ו- "ו".
- ההבדל בין \(2\) פירושו לחסר\(2\), \(9\) ובמילים אחרות, \(9\) מינוס\(2\), אשר אנו כותבים באופן סמלי כמו. \(9\) \(9−2\)
- התוצר של \(4\) \(8\) ואמצעים מתרבים\(8\), \(4\) ובמילים אחרות \(4\) פעמים\(8\), שאנו כותבים באופן סמלי כ. \(4\cdot 8\)
באלגברה, סמל הצלב\(\times\), אינו משמש להצגת כפל מכיוון שסמל זה עלול לגרום לבלבול. האם \(3xy\) הכוונה \(3\times y\) ('שלוש \(y\) פעמים') או \(3\cdot x \cdot y\) (שלוש \(x\) פעמים\(y\))? כדי להבהיר, השתמש \(\cdot\) או בסוגריים לכפל.
כאשר לשני כמויות יש אותו ערך, אנו אומרים שהם שווים ומחברים אותם עם סימן שווה.
\(a = b\)נקרא "\(a\)שווה ל\(b\)"
הסמל \(“=”\) נקרא סימן שווה.
בשורת המספרים המספרים גדלים ככל שהם עוברים משמאל לימין. ניתן להשתמש בשורת המספרים כדי להסביר את הסמלים \(“<”\) ו\(“>"\).
\(a<b\)נקרא "\(a\)הוא פחות מ\(b\)"
\(a\)נמצא \(b\) משמאל לשורת המספרים
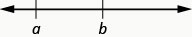
\(a>b\)נקרא "\(a\)הוא גדול מ\(b\)"
\(a\)נמצא \(b\) מימין לשורת המספרים
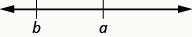
הביטויים \(a < b\) או \(a > b\) ניתן לקרוא משמאל לימין או מימין לשמאל, אם כי באנגלית אנו קוראים בדרך כלל משמאל לימין טבלה\(\PageIndex{3}\). באופן כללי, \(a < b\) שווה ערך ל\(b > a\). לדוגמה \(7 < 11\) שווה ערך ל\(11 > 7\). והוא \(a > b\) שווה ערך ל\(b < a\). לדוגמה \(17 > 4\) שווה ערך ל\(4 < 17\).
| סמלי אי שוויון | מילים |
|---|---|
| \(a \neq b\) | \(a\)אינו שווה ל \(b\) |
| \(a < b\) | \(a\)הוא פחות מ \(b\) |
| \(a \leq b\) | \(a\)הוא פחות או שווה ל \(b\) |
| \(a > b\) | \(a\)הוא גדול מ \(b\) |
| \(a \geq b\) | \(a\)גדול או לא שווה \(b\) |
תרגם מאלגברה לאנגלית:
- \(17 \leq 26\)
- \(8 \neq 17 - 3\)
- \(12 > 27 \div 3\)
- \(y + 7 < 19\)
- תשובה
-
- \(17 \leq 26\), \(17\) הוא פחות או שווה ל \(26\)
- \(8 \neq 17 - 3\), \(8\) אינו שווה \(17\) למינוס \(3\)
- \(12 > 27 \div 3\), \(12\) הוא גדול יותר מאשר \(27\) מחולק על ידי \(3\)
- \(y + 7 < 19\), \(y\) פלוס \(7\) הוא פחות מ \(19\)
תרגם מאלגברה לאנגלית:
- \(14 \leq 27\)
- \(19 - 2 \neq 8\)
- \(12 > 4 \div 2\)
- \(x - 7 < 1\)
- תשובה
-
- \(14\)הוא פחות או שווה ל \(27\)
- \(19\)מינוס \(2\) אינו שווה ל \(8\)
- \(12\)הוא גדול יותר מאשר \(4\) מחולק על ידי \(2\)
- \(x\)מינוס \(7\) הוא פחות מ \(1\)
תרגם מאלגברה לאנגלית:
- \(19 \leq 15\)
- \(7 = 12 - 5\)
- \(15 \div 3 < 8\)
- \(y + 3 < 6\)
- תשובה
-
- \(19\)גדול אז או שווה ל \(15\)
- \(7\)שווה \(12\) למינוס \(5\)
- \(15\)מחולק על ידי \(3\) הוא פחות מ \(8\)
- \(y\)פלוס \(3\) גדול מ \(6\)
סמלי קיבוץ באלגברה דומים מאוד לפסיקים, נקודתיים וסימני פיסוק אחרים באנגלית. הם עוזרים להבהיר אילו ביטויים יש לשמור יחד ולהפריד מביטויים אחרים. נציג כעת שלושה סוגים.
\[\begin{align*} & \text{Parentheses} & & ( ) \\ & \text{Brackets} & & [ ] \\ & \text{Braces} & & \{ \} \end{align*}\]
להלן מספר דוגמאות לביטויים הכוללים סמלי קיבוץ. אנו נפשט ביטויים כאלה בהמשך פרק זה.
\[8(14−8) \qquad 21−3[2 + 4(9−8)] \qquad 24\div \{ 13−2[1(6−5)+4] \nonumber\}\]
מה ההבדל באנגלית בין משפט למשפט? ביטוי מבטא מחשבה אחת שאינה שלמה בפני עצמה, אבל משפט עושה הצהרה מלאה. "לרוץ מהר מאוד" הוא ביטוי, אבל "שחקן הכדורגל רץ מהר מאוד" הוא משפט. למשפט יש נושא ופועל. באלגברה יש לנו ביטויים ומשוואות.
ביטוי הוא מספר, משתנה או שילוב של מספרים ומשתנים המשתמשים בסמלי פעולה.
ביטוי הוא כמו ביטוי באנגלית. הנה כמה דוגמאות לביטויים:
| ביטוי | מילים | ביטוי באנגלית |
|---|---|---|
| \(3 + 5\) | \(3\)פלוס \(5\) | סכום של שלוש וחמש |
| \(n − 1\) | \(n\)מינוס אחד | ההבדל של \(n\) ואחד |
| \(6\cdot 7\) | \(6\)פעמים \(7\) | תוצר של שש ושבע |
| \(\dfrac{x}{y}\) | \(x\)מחולק על ידי \(y\) | המנה של ו \(x\) \(y\) |
שימו לב שהביטויים באנגלית אינם יוצרים משפט שלם מכיוון שלביטוי אין פועל. משוואה היא שני ביטויים המקושרים לסימן שווה. כשאתה קורא את המילים שהסמלים מייצגים במשוואה, יש לך משפט שלם באנגלית. הסימן השווה נותן את הפועל.
משוואה היא שני ביטויים המחוברים בסימן שווה.
הנה כמה דוגמאות למשוואות.
| משוואה | משפט באנגלית |
|---|---|
| \(3+5=8\) | הסכום של שלוש וחמש שווה לשמונה |
| \(n−1=14\) | \(n\)מינוס אחד שווה ארבע עשרה |
| \(6 \cdot 7=42\) | התוצר של שש ושבע שווה לארבעים ושתיים |
| \(x=53\) | \(x\)שווה לחמישים ושלוש |
| \(y+9=2y−3\) | \(y\)פלוס תשע שווה לשניים \(y\) מינוס שלוש |
קבע אם כל אחד מהם הוא ביטוי או משוואה:
- \(2(x + 3) = 10\)
- \(4(y - 1) + 1\)
- \(x \div 25\)
- \(y + 8 = 40\)
- תשובה
-
- \(2(x + 3) = 10\). זו משוואה - שני ביטויים קשורים בסימן שווה.
- \(4(y - 1) + 1\). זהו ביטוי - אין סימן שווה.
- \(x \div 25\). זהו ביטוי - אין סימן שווה.
- \(y + 8 = 40\). זו משוואה - שני ביטויים קשורים בסימן שווה.
קבע אם כל אחד מהם הוא ביטוי או משוואה:
- \(3(x - 7) = 27\)
- \(5(4y - 2) - 7\)
- תשובה
-
- משוואה
- ביטוי
קבע אם כל אחד מהם הוא ביטוי או משוואה:
- \(y^{3} \div 14\)
- \(4x - 6 = 22\)
- תשובה
-
- ביטוי
- משוואה
נניח שאנחנו צריכים להכפיל תשעה גורמים של\(2\). אנחנו יכולים לכתוב את זה כ\(2\cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\). זה מייגע וזה יכול להיות קשה לעקוב אחר כל אותם 2s, אז אנחנו משתמשים במעריכים. אנחנו כותבים \(2\cdot 2 \cdot 2\) כמו \(2^{3}\) \(2\cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\) וכמו\(2^{9}\). בביטויים כמו\(2^{3}\), \(2\) נקרא הבסיס וה \(3\) נקרא המעריך. המעריך אומר לנו כמה פעמים אנחנו צריכים להכפיל את הבסיס.

אנו קוראים \(2^{3}\) כ"שניים לכוח השלישי "או" שני קוביות".
אנו אומרים \(2^{3}\) שהוא בסימון אקספוננציאלי \(2\cdot 2 \cdot 2\) ונמצא בסימון מורחב.
\(a^{n}\)פירושו תוצר של \(n\) גורמים של\(a\).
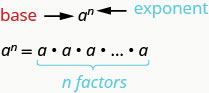
הביטוי \(a^{n}\) נקרא \(a\) \(n^{th}\) לכוח.
בעוד אנו קוראים \(a^{n}\) \(n^{th}\) כ"כוח "\(a\), אנו קוראים בדרך כלל:
- \(a^{2}\)"בריבוע"
- \(a^{3}\)"קוביות"
נראה מאוחר יותר מדוע \(a^{2}\) ויש \(a^{3}\) לנו שמות מיוחדים.
הטבלה \(\PageIndex{6}\) מראה כיצד אנו קוראים כמה ביטויים עם מעריכים.
| ביטוי | במילים |
|---|---|
| \(7^{2}\) | \(7\)לכוח השני או \(7\) בריבוע |
| \(5^{3}\) | \(5\)לכוח השלישי או \(5\) לקוביות |
| \(9^{4}\) | \(9\)לכוח הרביעי |
| \(12^{5}\) | \(12\)אל הכוח החמישי |
פשט: \(3^{4}\)
- תשובה
-
\[\quad 3^{4}\nonumber\]
\ [\ התחל {align*} &\ text {הרחב את הביטוי} & & 3\ cdot 3\ cdot 3\ cdot 3\\\ טקסט {הכפל משמאל לימין} & & 9\ cdot 3\ cdot 3\\ cdot 3\ cdot 3\\ טקסט {כפל}
& 81\ סיום {יישור *}\]
פשט:
- \(5^{3}\)
- \(1^{7}\)
- תשובה
-
- \(125\)
- \(1\)
- \(7^{2}\)
- \(0^{5}\)
- תשובה
-
- \(49\)
- \(0\)
פשט ביטויים באמצעות סדר הפעולות
לפשט ביטוי פירושו לעשות את כל המתמטיקה האפשרית. לדוגמה, כדי לפשט \(4\cdot 2 + 1\) היינו קודם כל להכפיל \(4\cdot 2\) כדי לקבל \(8\) ולאחר מכן להוסיף את \(1\) כדי לקבל\(9\). הרגל טוב להתפתח הוא לעבוד לאורך הדף, לכתוב כל שלב בתהליך מתחת לשלב הקודם. הדוגמה שתוארה זה עתה תיראה כך:
\[4\cdot 2 + 1\nonumber\]
\[8 + 1\nonumber\]
\[9\nonumber\]
על ידי אי שימוש בסימן שווה כשאתה מפשט ביטוי, אתה יכול להימנע מבלבול ביטויים עם משוואות.
כדי לפשט ביטוי, בצע את כל הפעולות בביטוי.
הצגנו את רוב הסמלים והסימונים המשמשים באלגברה, אך כעת עלינו להבהיר את סדר הפעולות. אחרת, לביטויים עשויות להיות משמעויות שונות, והן עלולות לגרום לערכים שונים. לדוגמה, שקול את הביטוי:
\[4 + 3\cdot 7\nonumber\]
אם אתה מפשט את הביטוי הזה, מה אתה מקבל?
חלק מהתלמידים אומרים\(49\),
\[4 + 3\cdot 7\nonumber\]
מאז \(4+3\) נותן\(7\).
\[7 \cdot 7\nonumber\]
\(7\cdot 7\)והוא \(49\) \[49\nonumber\]
אחרים אומרים\(25\),
\[4 + 3\cdot 7\nonumber\]
מאז \(3\cdot 7\) הוא\(21\).
\[4 + 21\nonumber\]
\(21 + 4\)ועושה\(25\).
\[25\nonumber\]
תארו לעצמכם את הבלבול במערכת הבנקאית שלנו אם לכל בעיה היו כמה תשובות נכונות שונות!
אותו ביטוי צריך לתת את אותה תוצאה. אז מתמטיקאים קבעו בשלב מוקדם כמה הנחיות הנקראות סדר הפעולות.
- סוגריים וסמלי קיבוץ אחרים
- פשט את כל הביטויים בתוך הסוגריים או סמלי קיבוץ אחרים, ועבד תחילה על הסוגריים הפנימיים ביותר.
- מעריכים
- פשט את כל הביטויים בעזרת אקספוננטים.
- כפל וחילוק
- בצע את כל הכפל והחלוקה לפי הסדר משמאל לימין. לפעולות אלה יש עדיפות שווה.
- חיבור וחיסור
- בצע את כל ההוספה והחיסור לפי הסדר משמאל לימין. לפעולות אלה יש עדיפות שווה.
ביצוע פעילות המתמטיקה המניפולטיבית "משחק 24" יעניק לך תרגול לפי סדר הפעולות.
התלמידים שואלים לעתים קרובות, "איך אזכור את ההזמנה?" הנה דרך לעזור לך לזכור: קח את האות הראשונה של כל מילת מפתח והחלף את הביטוי המטופש: "אנא סלח לדודתי היקרה סאלי."
\ [\ התחל {יישור*} &\ טקסט {P}\ טקסט {ארנתזות} & &\ טקסט {P}\ טקסט {חכירה}\\ [5pt]
&\ טקסט {E}\ טקסט {xponents} & &\ טקסט {E}\ טקסט {xcuse}\\ [5pt]
&\ textbf {M}\ שטח\ טקסט {D}\ טקסט {ivision} & &\ טקסט {M}\ טקסט {y}\ טקסט\ טקסט {D}\ טקסט {D}\ טקסט {אוזן}\ [5pt] &\ טקסט {A}\ טקסט {ddition}\ טקסט {S}\ טקסט {משיכה}
& &\ טקסט רווח\ טקסט {S}\ טקסט {ברית}\ סוף {יישור*}\]
זה טוב ש- "\(\textbf{M}\text{y}\space\textbf{D}\text{ear}\)" הולך ביחד, מכיוון שזה מזכיר לנו כי ל- m ultiplication ו - d ivision יש עדיפות שווה. אנחנו לא תמיד עושים כפל לפני חלוקה או תמיד עושים חלוקה לפני הכפל. אנחנו עושים אותם לפי הסדר משמאל לימין.
באופן דומה, "\(\textbf{A}\text{unt}\space\textbf{S}\text{ally}\)" הולך יחד וכך מזכיר לנו שלדיטציה ו- s ubtraction יש גם עדיפות שווה ואנחנו עושים אותם לפי סדר משמאל לימין.
בואו ננסה דוגמה.
פשט:
- \(4 + 3\cdot 7\)
- \((4 + 3)\cdot 7\)
- תשובה
- 1.
\(4 + 3 \cdot 7\) האם יש p arentheses? לא. האם יש אקספונטים? לא. האם יש m אולטיקציה או d ivision? כן. הכפל תחילה. \(4 + {\color{red}{3 \cdot 7}}\) להוסיף. \(4+21\) \(25\) 2.
\((4 + 3)\cdot 7\) האם יש p arentheses? כן. \({\color{red}{(4 + 3)}}\cdot 7\) פשט בתוך הסוגריים. \(({\color{red}{7}})7\) האם יש אקספונטים? לא. האם יש m אולטיקציה או d ivision? כן. להכפיל. \(49\)
פשט:
- \(12 - 5\cdot 2\)
- \((12 - 5)\cdot 2\)
- תשובה
-
- \(2\)
- \(14\)
פשט:
- \(8 + 3\cdot 9\)
- \((8 + 3)\cdot 9\)
- תשובה
-
- \(35\)
- \(99\)
פשט: \(18\div 6 + 4(5 - 2)\)
- תשובה
-
סוגריים? כן, תחסר קודם. \(18\div 6 + 4(5 - 2)\)
\(18\div 6 + 4(3)\)אקספונסנטים? לא. כפל או חלוקה? כן. \({\color{red}{18\div 6}} + {\color{red}{4(3)}}\) חלקו תחילה מכיוון שאנו מכפילים ומחלקים משמאל לימין. \(3+{\color{red}{4(3)}}\) כל כפל או חלוקה אחרים? כן. להכפיל. \(3 + 12\) כל כפל או חלוקה אחרים? לא. כל תוספת או חיסור? כן. \(15\)
פשט: \(30\div 5 + 10(3 - 2)\)
- תשובה
-
\(16\)
פשט: \(70\div 10 + 4(6 - 2)\)
- תשובה
-
\(23\)
כאשר ישנם סמלי קיבוץ מרובים, אנו מפשטים תחילה את הסוגריים הפנימיים ביותר ועובדים כלפי חוץ.
פשט:\(5 + 2^{3} + 3[6 - 3(4 - 2)]\).
- תשובה
-
\(5 + 2^{3} + 3[6 - 3(4 - 2)]\) האם יש סוגריים (או סמל קיבוץ אחר)? כן. התמקדו בסוגריים שנמצאים בתוך הסוגריים. \(5 + 2^{3} + 3[6 - 3{\color{red}{(4 - 2)}}]\) לחסר. \(5 + 2^{3} + 3[6 - {\color{red}{3(2)}}]\) המשך בתוך הסוגריים והכפיל. \(5 + 2^{3} + 3[{\color{red}{6 - 6}}]\) המשך בתוך הסוגריים וחסר. \(5 + 2^{3} + 3[{\color{red}{0}}]\) הביטוי בתוך הסוגריים אינו דורש פישוט נוסף. האם יש אקספונסנטים? כן. \(5 + {\color{red}{2^{3}}}+ 3[0]\) פשט את המעריכים. \(5 + 8 + {\color{red}{3[0]}}\) האם יש כפל או חלוקה? כן. להכפיל. \({\color{red}{5 + 8}}+0\) האם יש חיבור או חיסור? כן. להוסיף. \({\color{red}{13 + 0}}\) להוסיף. \(13\)
פשט:\(9 + 5^{3} - [4(9 + 3)]\).
- תשובה
-
\(86\)
פשט:\(7^{2} - 2[4(5 + 1)]\).
- תשובה
-
\(1\)
הערך ביטוי
בדוגמאות האחרונות פשטנו ביטויים לפי סדר הפעולות. כעת נעריך כמה ביטויים - שוב בעקבות סדר הפעולות. הערכת ביטוי פירושה למצוא את ערך הביטוי כאשר המשתנה מוחלף במספר נתון.
הערכת ביטוי פירושה למצוא את ערך הביטוי כאשר המשתנה מוחלף במספר נתון.
כדי להעריך ביטוי, החלף את המספר הזה במשתנה בביטוי ואז פשט את הביטוי.
להעריך\(7x - 4\), מתי
- \(x = 5\)
- \(x = 1\)
- תשובה
-
1.
מתי \(x = {\color{red}{5}}\) \(7x - 4\) \(7({\color{red}{5}}) - 4\) להכפיל. \(35 - 4\) לחסר. \(31\) 2.
מתי \(x = {\color{red}{1}}\) \(7x - 4\) \(7({\color{red}{1}}) - 4\) להכפיל. \(7 - 4\) לחסר. \(3\)
להעריך\(8x - 3\), מתי
- \(x = 2\)
- \(x = 1\)
- תשובה
-
- \(13\)
- \(5\)
להעריך\(4y - 4\), מתי
- \(y = 3\)
- \(y = 5\)
- תשובה
-
- \(8\)
- \(16\)
להעריך\(x = 4\), מתי
- \(x^{2}\)
- \(3^{x}\)
- תשובה
-
1.
\(x^{2}\) החלף \(x\) עם\({\color{red}{4}}\). \(({\color{red}{4}})^{2}\) השתמש בהגדרה של מעריך. \(4\cdot 4\) לפשט. \(16\) 2.
\(3^{x}\) החלף \(x\) עם\({\color{red}{4}}\). \(3^ (click for details)\)Callstack: at (עברית/אלגברה_יסודית_1e_(OpenStax)/01:_יסודות/1.03:_השתמש_בשפת_האלגברה), /content/body/div[4]/div[5]/div/dl/dd/table[2]/tbody/tr[2]/td[2]/span/span, line 1, column 1השתמש בהגדרה של מעריך. \(3\cdot3\cdot3\cdot3\) לפשט. \(81\)
להעריך\(x = 3\), מתי
- \(x^{2}\)
- \(4^{x}\)
- תשובה
-
- \(9\)
- \(64\)
להעריך\(x = 6\), מתי
- \(x^{3}\)
- \(2^{x}\)
- תשובה
-
- \(216\)
- \(64\)
להעריך \(2x^{2} + 3x + 8\) מתי\(x = 4\).
- תשובה
-
\(2x^{2} + 3x + 8\) תחליף\(x = {\color{red}{4}}\). \(\small{2x^{2} + 3x + 8}\)
\(2({\color{red}{4}})^{2} + 3({\color{red}{4}}) + 8\)בצע את סדר הפעולות. \(2(16)+3(4)+8\) \(32+12+8\) \(52\)
להעריך \(3x^{2} + 4x + 1\) מתי\(x = 3\).
- תשובה
-
\(40\)
להעריך \(6x^{2} - 4x - 7\) מתי\(x = 2\).
- תשובה
-
\(9\)
זהה ושלב מונחים דומים
ביטויים אלגבריים מורכבים ממונחים. מונח הוא קבוע, או תוצר של משתנה קבוע ואחד או יותר.
מונח הוא קבוע, או תוצר של משתנה קבוע ואחד או יותר.
דוגמאות למונחים הן\(7, y, 5x^{2}, 9a\), ו\(b^{5}\).
הקבוע שמכפיל את המשתנה נקרא מקדם.
המקדם של מונח הוא הקבוע שמכפיל את המשתנה במונח.
חשבו על המקדם כמספר מול המשתנה. המקדם של המונח \(3x\) הוא\(3\). כאשר אנו כותבים\(x\), המקדם הוא\(1\), שכן\(x=1\cdot x\).
זהה את המקדם של כל מונח:
- \(14y\)
- \(15x^{2}\)
- \(a\)
- תשובה
-
- המקדם של \(14y\) הוא \(14\)
- המקדם של \(15x^{2}\) הוא \(15\)
- המקדם של \(a\) הוא \(1\) מאז\(a=1a\).
זהה את המקדם של כל מונח:
- \(17x\)
- \(41b^{2}\)
- \(z\)
- תשובה
-
- \(14\)
- \(41\)
- \(1\)
זהה את המקדם של כל מונח:
- \(9p\)
- \(13a^{2}\)
- \(y^{3}\)
- תשובה
-
- \(9\)
- \(13\)
- \(1\)
מונחים מסוימים חולקים תכונות משותפות. תסתכל על 6 המונחים הבאים. לאילו מהם יש תכונות משותפות?
\[5x \qquad 7 \qquad n^{2} \qquad 4 \qquad 3x \qquad 9n^{2}\nonumber\]
ה \(7\) ו- שניהם \(4\) מונחים קבועים.
ה \(5x\) ו שניהם \(3x\) מונחים עם\(x\).
ה \(n^{2}\) ו שניהם \(9n^{2}\) מונחים עם\(n^{2}\).
כאשר שני מונחים הם קבועים או שיש להם אותו משתנה ומעריך, אנו אומרים שהם כמו מונחים.
- \(7\)\(4\)והם כמו תנאים.
- \(5x\)\(3x\)והם כמו תנאים.
- \(x^{2}\)\(9x^{2}\)והם כמו תנאים.
מונחים שהם קבועים או שיש להם אותם משתנים המועלים לאותם כוחות נקראים כמו מונחים.
זהה את המונחים הדומים:\(y^{3},7x^{2}, 14, 23, 4y^{3}, 9x, 5x^{2}\).
- תשובה
-
\(y^{3}\)\(4y^{3}\)והם כמו מונחים מכיוון שלשניהם יש\(y^{3}\); המשתנה והתאמה המעריך.
\(7x^{2}\)\(5x^{2}\)והם כמו מונחים מכיוון שלשניהם יש\(x^{2}\); המשתנה והתאמה המעריך.
\(14\)\(23\)והם כמו מונחים כי שניהם קבועים.
אין מונח אחר כמו\(9x\).
זהה את המונחים הדומים:\(9, 2x^{3},y^{2}, 8x^{3}, 15, 9y, 11y^{2}\).
- תשובה
-
\(9\)ו\(15\), \(y^{2}\) ו\(11y^{2}\), \(2x^{3}\) ו \(8x^{3}\)
זהה את המונחים הדומים:\(4x^{3},8x^{2}, 19, 3x^{3}, 24, 6x^{3}\).
- תשובה
-
\(19\)ו\(24\), \(8x^{2}\) ו\(3x^{2}\), \(4x^{3}\) ו \(6x^{3}\)
זהה את המונחים בכל ביטוי.
- \(9x^{2}+7x+12\)
- \(8x+3y\)
- תשובה
-
- התנאים של \(9x^{2}+7x+12\) הם\(9x^{2}, 7x\), ו\(12\).
- התנאים של \(8x+3y\) הם \(8x\) ו\(3y\).
זהה את המונחים בביטוי\(4x^{2}+5x+17\).
- תשובה
-
\(4x^{2}, 5x, 17\)
זהה את המונחים בביטוי\(5x+2y\).
- תשובה
-
\(5x, 2y\)
אם יש מונחים דומים בביטוי, אתה יכול לפשט את הביטוי על ידי שילוב של מונחים דומים. מה לדעתך \(4x+7x+x\) יפשט? אם היית חושב\(12x\), היית צודק!
\[\begin{array} { c } { 4 x + 7 x + x } \\ { x + x + x + x \quad + x + x + x + x + x + x + x \quad+ x } \\ { 12 x } \end{array}\]
הוסף את המקדמים ושמור על אותו משתנה. לא משנה מה זה x - אם יש לך 4 ממשהו ותוסיף עוד 7 מאותו הדבר ואז הוסף עוד 1, התוצאה היא 12 מהם. לדוגמא, 4 תפוזים פלוס 7 תפוזים פלוס תפוז אחד הם 12 תפוזים. נדון בתכונות המתמטיות העומדות מאחורי זה בהמשך.
פשט: \(4x+7x+x\)
הוסף את המקדמים. \(12x\)
פשט: \(2x^{2} + 3x + 7 + x^{2} + 4x + 5\)
- תשובה
-


פשט:\(3x^{2} + 7x + 9 + 7x^{2} + 9x + 8\).
- תשובה
-
\(10x^{2}+16x+17\)
פשט:\(4y^{2} + 5y + 2 + 8y^{2} + 4y + 5\).
- תשובה
-
\(12y^{2}+9y+7\)
- זהה מונחים דומים.
- סדר מחדש את הביטוי כך שמונחים יהיו ביחד.
- הוסף או הפחת את המקדמים ושמור על אותו משתנה עבור כל קבוצה של מונחים דומים.
תרגם ביטוי באנגלית לביטוי אלגברי
בחלק האחרון פירטנו סמלי פעולה רבים המשמשים באלגברה, ואז תרגמנו ביטויים ומשוואות לביטויים ומשפטים באנגלית. עכשיו נהפוך את התהליך. נתרגם ביטויים באנגלית לביטויים אלגבריים. הסמלים והמשתנים עליהם דיברנו יעזרו לנו לעשות זאת. הטבלה \(\PageIndex{7}\) מסכמת אותם.
| מבצע | ביטוי | הבעה |
|---|---|---|
| תוספת | \(a\)בתוספת \(b\) הסכום \(a\) \(b\) \(a\) והגדיל ביותר \(a\) מהסך הכולל \(a\) \(b\) \(b\) והוסיף ל \(b\) \(b\) \(a\) |
\[a+b\] |
| חיסור | \(a\)מינוס \(b\) ההפרש של \(a\) \(b\) \(a\) וירד \(b\) \(b\) בפחות \(a\) \(b\) מהפחתת \(a\) |
\[a−b\] |
| כפל | \(a\)פעמים \(b\) המוצר של \(a\) \(b\) ופעמיים \(a\) |
\[a\cdot b, ab, a(b), (a)(b)\] \[2a\] |
| חטיבה | \(a\)מחולק \(b\) על ידי המנה של \(a\) והיחס \(b\) של \(a\) \(b\) \(b\) ומחולק \(a\) |
\[a\div b, a/b, \frac{a}{b}, b \enclose{longdiv}{a}\] |
התבונן מקרוב בביטויים אלה באמצעות ארבע הפעולות:

כל ביטוי אומר לנו לפעול על שני מספרים. חפש את המילים של ולמצוא את המספרים.
תרגם כל ביטוי באנגלית לביטוי אלגברי:
- ההבדל של \(17x\) ו \(5\)
- המנה של \(10x^{2}\) ו. \(7\)
- תשובה
-
- מילת המפתח היא הבדל, שאומר לנו שהפעולה היא חיסור. חפש את המילים של ו ו- t o מצא את המספרים שיש לחסר.
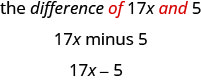
- מילת המפתח היא "מנה", שאומרת לנו שהמבצע הוא חלוקה.
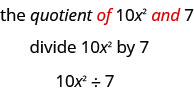
זה יכול להיות גם כתוב \(10x^{2}/7\) או\(\dfrac{10x^{2}}{7}\).
- מילת המפתח היא הבדל, שאומר לנו שהפעולה היא חיסור. חפש את המילים של ו ו- t o מצא את המספרים שיש לחסר.
תרגם כל ביטוי באנגלית לביטוי אלגברי:
- ההבדל של \(14x^{2}\) ו \(13\)
- המנה של \(12x\) ו. \(2\)
- תשובה
-
- \(14x^{2} - 13\)
- \(12x \div 2\)
תרגם כל ביטוי באנגלית לביטוי אלגברי:
- סכום \(17y^{2}\) ו \(19\)
- המוצר של \(7\) ו\(y\).
- תשובה
-
- \(17y^{2} + 19\)
- \(7y\)
בן כמה תהיה בעוד שמונה שנים? איזה גיל הוא שמונה שנים יותר מגילך עכשיו? האם הוספת 8 לגילך הנוכחי? שמונה "יותר מ" פירושו 8 שנוספו לגילך הנוכחי. בן כמה היית לפני שבע שנים? זה 7 שנים פחות מגילך עכשיו. אתה מחסיר 7 מגילך הנוכחי. שבעה "פחות מ" פירושו 7 מופחת מגילך הנוכחי.
תרגם את הביטוי האנגלי לביטוי אלגברי:
- שבע עשרה יותר מ \(y\)
- תשע פחות מ\(9x^{2}\).
- תשובה
-
- מילות המפתח הן יותר מ. הם אומרים לנו שהמבצע הוא תוספת. יותר מאשר פירושו "להוסיף ל".
\(\begin{array} { c } { \text { Seventeen more than } y } \\ { \text { Seventeen added to } y } \\ { y + 17 } \end{array}\)
- מילות המפתח הן פחות מ. הם אומרים לנו לחסר. פחות מ פירושו "מופחת מ."
\(\begin{array} { c } { \text { Nine less than } 9 x ^ { 2 } } \\ { \text { Nine subtracted from } 9 x ^ { 2 } } \\ { 9 x ^ { 2 } - 9 } \end{array}\)
- מילות המפתח הן יותר מ. הם אומרים לנו שהמבצע הוא תוספת. יותר מאשר פירושו "להוסיף ל".
תרגם את הביטוי האנגלי לביטוי אלגברי:
- 11 יותר מ- x
- ארבע עשרה פחות\(11a\).
- תשובה
-
- \(x+11\)
- \(11a−14\)
תרגם את הביטוי האנגלי לביטוי אלגברי:
- \(13\)יותר מ \(z\)
- \(18\)פחות מ\(8x\).
- תשובה
-
1. \(z+13\)
2. \(8x−18\)
תרגם את הביטוי האנגלי לביטוי אלגברי:
- חמש פעמים את הסכום של \(m\) ו \(n\)
- סכום של חמש פעמים \(m\) ו\(n\).
- תשובה
-
ישנן שתי מילות פעולה - הזמנים אומרים לנו להכפיל והסכום אומר לנו להוסיף.
1. מכיוון שאנו מכפילים \(5\) כפול הסכום שאנו זקוקים לסוגריים סביב סכום \(m\) ו\(n\),\((m+n)\). זה מכריח אותנו לקבוע תחילה את הסכום. (זכור את סדר הפעולות.)\[\begin{array} { c } { \text { five times the sum of } m \text { and } n } \\ { 5 ( m + n ) } \end{array}\]
2. כדי לקחת סכום, אנו מחפשים את המילים "של" ו- "ו-" כדי לראות מה מתווסף. כאן אנו לוקחים את הסכום של חמש פעמים \(m\) ו\ (n\.)\[\begin{array} { c } { \text { the sum of five times } m \text { and } n } \\ { 5 m + n } \end{array}\]
תרגם את הביטוי האנגלי לביטוי אלגברי:
- ארבע פעמים את הסכום של \(p\) ו \(q\)
- סכום של ארבע פעמים \(p\) ו\(q\).
- תשובה
-
- \(4(p+q)\)
- \(4p+q\)
תרגם את הביטוי האנגלי לביטוי אלגברי:
- ההבדל של פעמיים x ו\(8\),
- פי שניים מההפרש של x ו-\(8\).
- תשובה
-
- \(2x−8\)
- \(2(x−8)\)
בהמשך קורס זה, ניישם את כישורינו באלגברה לפתרון יישומים. השלב הראשון יהיה לתרגם ביטוי באנגלית לביטוי אלגברי. נראה כיצד לעשות זאת בשתי הדוגמאות הבאות.
אורכו של מלבן \(6\) קטן מהרוחב. בואו \(w\) לייצג את רוחב המלבן. כתוב ביטוי לאורך המלבן.
- תשובה
-
\[\begin{array} { l l } { \text { Write a phrase about the length of the rectangle. } } &{ 6 \text { less than the width } } \\ { \text { Substitute } w \text { for "the width." } } &{\text{6 less then w}} \\ { \text { Rewrite "less than" as "subtracted from." } } &{\text{6 subtracted from w}} \\ { \text { Translate the phrase into algebra. } } &{w - 6} \end{array}\]
אורכו של מלבן \(7\) קטן מהרוחב. בואו \(w\) לייצג את רוחב המלבן. כתוב ביטוי לאורך המלבן.
- תשובה
-
\(w - 7\)
רוחב המלבן \(6\) קטן מהאורך. בואו \(l\) לייצג את אורך המלבן. כתוב ביטוי לרוחב המלבן.
- תשובה
-
\(l - 6\)
לג'ון יש מטבעות ורבעים בארנקה. מספר הפרוטות הוא שלוש פחות מארבע פעמים ממספר הרבעונים. בואו \(q\) לייצג את מספר הרבעונים. כתוב ביטוי למספר הפרוטות.
- תשובה
-
\[\begin{array} { ll } { \text { Write the phrase about the number of dimes. } } &{\text{three less than four times the number of quarters}} \\ { \text { Substitute } q \text { for the number of quarters. } } &{\text{3 less than 4 times q}} \\ { \text { Translate "4 times } q \text { ." } } &{\text{3 less than 4q}} \\ { \text { Translate the phrase into algebra. } } &{\text{4q - 3}} \end{array}\]
לג'פרי יש מטבעות ורבעים בכיס. מספר הפרוטות הוא שמונה פחות מארבע פעמים ממספר הרבעונים. בואו \(q\) לייצג את מספר הרבעונים. כתוב ביטוי למספר הפרוטות.
- תשובה
-
\(4q - 8\)
ללורן יש מטבעות וניקלים בארנק. מספר הפרוטות הוא פי שלושה יותר משבעה ממספר הניקלים. בואו \(n\) לייצג את מספר הניקלים. כתוב ביטוי למספר הפרוטות.
- תשובה
-
\(7n + 3\)
מושגי מפתח
- סימון התוצאה היא...
\(\begin{array} { l l } {\bullet \space a + b } &{ \text { the sum of } a \text { and } b } \\ { \bullet \space a - b } &{ \text { the difference of } a \text { and } b } \\ {\bullet\space a \cdot b , a b , ( a ) ( b ) ( a ) b , a ( b ) } &{ \text { the product of } a \text { and } b } \\ {\bullet\space a \div b , a / b , \frac { a } { b } , b ) \overline{a} } &{ \text { the quotient of } a \text { and } b } \end{array}\) - אי שוויון
\(\begin{array} { l l } { \bullet \space a < b \text { is read "a is less than } b ^ { \prime \prime } } &{a \text { is to the left of } b \text { on the number line } } \\ { \bullet \space a > b \text { is read "a is greater than } b ^ { \prime \prime } } & { a \text { is to the right of } b \text { on the number line } } \end{array}\) - אי שוויון סמלים מילים
\(\begin{array} {ll} { \bullet a \neq b } &{ a \text { is not equal to } b } \\ { \bullet a < b } &{ a \text { is less than } b } \\ { \bullet a \leq b } &{ a \text { is less than or equal to } b } \\ { \bullet a > b } & { a \text { is greater than } b } \\ { \bullet a \geq b } & { a \text { is greater than or equal to } b } \end{array}\) - קיבוץ סמלים
- סוגריים ()
- סוגריים []
- גשר בשיניים {}
- סימון אקספוננציאלי
- \(a^{n}\)פירושו תוצר של \(n\) גורמים של\(a\). הביטוי \(a^{n}\) נקרא \(a\) \(n^{th}\) לכוח.
- סדר הפעולות: בעת פישוט ביטויים מתמטיים בצע את הפעולות בסדר הבא:
- סוגריים וסמלי קיבוץ אחרים: פשט את כל הביטויים בתוך הסוגריים או סמלי קיבוץ אחרים, ועבד תחילה על הסוגריים הפנימיים ביותר.
- אקספונסנטים: פשט את כל הביטויים בעזרת אקספונסנטים.
- כפל וחילוק: בצע את כל הכפל והחלוקה לפי סדר משמאל לימין. לפעולות אלה יש עדיפות שווה.
- חיבור וחיסור: בצע את כל החיבור והחיסור לפי הסדר משמאל לימין. לפעולות אלה יש עדיפות שווה.
- שילוב מונחים כמו
- זהה מונחים דומים.
- סדר מחדש את הביטוי כך שמונחים יהיו ביחד.
- הוסף או הפחת את המקדמים ושמור על אותו משתנה עבור כל קבוצה של מונחים דומים.
רשימת מילים
- מקדם
- המקדם של מונח הוא הקבוע שמכפיל את המשתנה במונח.
- קבוע
- קבוע הוא מספר שערכו תמיד נשאר זהה.
- סמל שוויון
- הסמל "\(=\)" נקרא סימן שווה. אנו קוראים \(a=b\) כמו "\(a\)שווה ל\(b\)."
- משוואה
- משוואה היא שני ביטויים המחוברים בסימן שווה.
- להעריך ביטוי
- הערכת ביטוי פירושה למצוא את ערך הביטוי כאשר המשתנה מוחלף במספר נתון.
- ביטוי
- ביטוי הוא מספר, משתנה או שילוב של מספרים ומשתנים המשתמשים בסמלי פעולה.
- כמו מונחים
- מונחים שהם קבועים או שיש להם אותם משתנים המועלים לאותם כוחות נקראים כמו מונחים.
- לפשט ביטוי
- כדי לפשט ביטוי, בצע את כל הפעולות בביטוי.
- מונח
- מונח הוא קבוע או תוצר של משתנה קבוע ואחד או יותר.
- משתנה
- משתנה הוא אות המייצגת מספר שערכו עשוי להשתנות.


