2.7: Aina nyingine za Equations
- Page ID
- 180775
- Kutatua milinganyo kuwashirikisha exponents busara.
- Tatua equations kwa kutumia factoring.
- Tatua equations radical.
- Tatua milinganyo ya thamani kamili.
- Tatua aina nyingine za equations.
Tumetatua equations linear, equations busara, na equations quadratic kutumia mbinu kadhaa. Hata hivyo, kuna aina nyingine nyingi za milinganyo, na tutachunguza aina chache zaidi katika sehemu hii. Tutaangalia equations kuwashirikisha exponents busara, milinganyo polynomial, equations radical, equations thamani kamili, equations katika quadratic fomu, na baadhi ya milinganyo ya busara ambayo inaweza kubadilishwa katika quadratics. Kutatua equation yoyote, hata hivyo, inaajiri sheria sawa za msingi za algebraic. Tutajifunza baadhi ya mbinu mpya kama wao kuomba kwa equations fulani, lakini algebra kamwe mabadiliko.
Kutatua Equations Kuhusisha Watazamaji wa busara
Maonyesho ya busara ni vielelezo ambavyo ni sehemu ndogo, ambapo namba ni nguvu na denominator ni mizizi. Kwa mfano,\({16}^{\tfrac{1}{2}}\) ni njia nyingine ya kuandika\(\sqrt{16}\);\(8^{\tfrac{1}{3}}\) ni njia nyingine ya kuandika\(\sqrt[3]{8}\). Uwezo wa kufanya kazi na watazamaji wa busara ni ujuzi muhimu, kwa kuwa unatumika sana katika calculus.
Tunaweza kutatua milinganyo ambayo variable hufufuliwa kwa exponent busara kwa kuinua pande zote mbili za equation kwa usawa wa exponent. Sababu tunayoinua equation kwa usawa wa exponent ni kwa sababu tunataka kuondokana na exponent juu ya muda kutofautiana, na idadi imeongezeka kwa sawa yake ya usawa\(1\). Kwa mfano,
\[\dfrac{2}{3}\left (\dfrac{3}{2} \right )=1 \nonumber\]
\[3\left (\dfrac{1}{3} \right )=1, \nonumber\]
na kadhalika.
Mtazamo wa busara unaonyesha nguvu katika nambari na mizizi katika denominator. Kuna njia nyingi za kuandika maneno, kutofautiana, au nambari yenye kielelezo cha busara:
\[a^{\tfrac{m}{n}}={\left (a^{\tfrac{1}{n}} \right )}^m={a^m}^{\tfrac{1}{n}}=\sqrt[n]{a^m}={(\sqrt[n]{a})}^m\]
Tathmini\(8^{\tfrac{2}{3}}\)
Suluhisho
Ikiwa tunachukua mizizi kwanza au nguvu ya kwanza inategemea idadi. Ni rahisi kupata mchemraba mzizi wa\(8\), hivyo kuandika upya\(8^{\tfrac{2}{3}}\) kama\({\left (8^{\tfrac{1}{3}} \right )}^2\).
\[\begin{align*} {\left (8^{\tfrac{1}{3}} \right )}^2&= {(2)}^2\\ &= 4 \end{align*}\]
Tathmini\({64}^{-\tfrac{1}{3}}\)
- Jibu
-
\(\dfrac{1}{4}\)
Kutatua equation ambayo variable hufufuliwa kwa exponent busara:\(x^{\tfrac{5}{4}} = 32\).
Suluhisho
Njia ya kuondoa exponent juu\(x\) ni kwa kuinua pande zote mbili za equation kwa nguvu ambayo ni ya kawaida ya\(\dfrac{5}{4}\), yaani\(\dfrac{4}{5}\).
\[\begin{align*} x^{\tfrac{5}{4}}&= 32\\ {\left(x^{\tfrac{5}{4}}\right)}^{\tfrac{4}{5}}&= {\left(32\right)}^{\tfrac{4}{5}}\\ x&= (2)^4\\ &= 16 \end{align*}\]
Kutatua equation\(x^{\tfrac{3}{2}} = 125\).
- Jibu
-
\(25\)
Kutatua\(3x^{\tfrac{3}{4}} = x^{\tfrac{1}{2}}\).
Suluhisho
Equation hii inahusisha exponents busara kama vile factoring exponents busara. Hebu tuchukue hatua hii moja kwa wakati. Kwanza, weka maneno ya kutofautiana upande mmoja wa ishara sawa na kuweka equation sawa na sifuri.
\[\begin{align*} 3x^{\tfrac{3}{4}}-\left(x^{\tfrac{1}{2}}\right)&= x^{\tfrac{1}{2}}-\left(x^{\tfrac{1}{2}}\right)\\ 3x^{\tfrac{3}{4}}-x^{\tfrac{1}{2}}&= 0 \end{align*}\]
Sasa, inaonekana kama tunapaswa kuzingatia upande wa kushoto, lakini tunafanya nini? Tunaweza daima sababu mrefu na exponent chini. Andika upya\(x^{\tfrac{1}{2}}\) kama\(x^{\tfrac{2}{4}}\). Kisha, fikiria\(x^{\tfrac{2}{4}}\) kutoka kwa maneno yote upande wa kushoto.
\[\begin{align*} 3x^{\tfrac{3}{4}}-x^{\tfrac{1}{2}}&= 0\\ x^{\tfrac{2}{4}}\left (3x^{\tfrac{1}{4}}-1 \right )&= 0 \end{align*}\]
Ambapo\(x^{\tfrac{1}{4}}\) walitoka wapi? Kumbuka, wakati sisi kuzidisha namba mbili na msingi huo, sisi kuongeza exponents. Kwa hiyo, kama sisi kuzidisha\(x^{\tfrac{2}{4}}\) nyuma katika kutumia mali distributive, sisi kupata kujieleza tulikuwa kabla factoring, ambayo ni nini lazima kutokea. Tunahitaji exponent vile kwamba wakati aliongeza kwa\(\dfrac{2}{4}\) sawa\(\dfrac{3}{4}\). Hivyo, exponent juu\(x\) katika mabano ni\(\dfrac{1}{4}\).
Hebu tuendelee. Sasa tuna mambo mawili na tunaweza kutumia theorem ya sababu ya sifuri.
\ [kuanza {align*}
x^ {\ tfrac {2} {4}}\ kushoto (3x^ {\ tfrac {1} {4}} -1\ haki) &= 0\\
x^ {\ tfrac {2} {4}} {4}} &= 0\\ x&= 0\\
3x^ {\ tfrac {1} 4}} -1 & = 0\\ x&= 0\\ 3x^ {1} 4} -1 & = 0\\ x\\
3x^ {\ tfrac {1} {4}} &= 1\\
x^ {\ tfrac {1} {4}} &=\ dfrac {1} {3},\ quad\ maandishi {Gawanya pande zote mbili kwa 3.} \\
{kushoto (x^ {\ tfrac {1} {4}}\ kulia)} ^4&= {\ kushoto (\ dfrac {1} {3}\ haki)} ^4,\ qquad\ maandishi {Panda pande zote mbili kwa usawa wa}\ dfrac {1} {4}\
x&=\ dfrac {1} {81}
\ mwisho {}\]
Ufumbuzi mbili ni\(0\) na\(\dfrac{1}{81}\).
Kutatua:\({\left(x+5\right)}^{\tfrac{3}{2}}=8\).
- Jibu
-
\(-1\)
Kutatua equations Kutumia factoring
Tumetumia factoring kutatua equations quadratic, lakini ni mbinu ambayo tunaweza kutumia na aina nyingi za milinganyo polynomial, ambayo ni milinganyo ambayo yana kamba ya maneno ikiwa ni pamoja na coefficients namba na vigezo. Wakati sisi ni wanakabiliwa na equation zenye polynomials ya shahada ya juu kuliko\(2\), tunaweza mara nyingi kutatua yao kwa factoring.
Polynomial ya shahada\(n\) ni usemi wa aina
\[a_nx^n+a_{n−1}x^{n−1}+⋅⋅⋅+a_2x^2+a_1x+a_0\]
wapi\(n\) is a positive integer and \(a_n ,…, a_0\) are real numbers and \(a_n≠0\).
Kuweka polynomial sawa na sifuri hutoa equation polynomial. Idadi ya ufumbuzi (halisi na ngumu) kwa equation polynomial ni sawa na exponent ya juu\(n\).
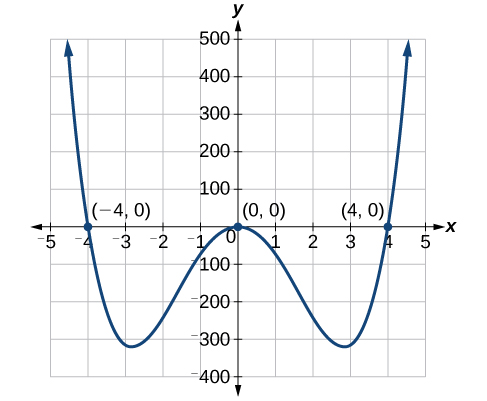
Tatua polynomial kwa kuzingatia:\(5x^4 = 80x^2\).
Suluhisho
Kwanza, weka equation sawa na sifuri. Kisha sababu nje nini ni kawaida kwa maneno yote, GCF.
\[\begin{align*} 5x^4-80x^2&= 0\\ 5x^2(x^2-16)&= 0 \end{align*}\]
Angalia kwamba tuna tofauti ya mraba katika sababu\(x^2−16\), ambayo tutaendelea kuzingatia na kupata ufumbuzi mbili. Muda wa kwanza\(5x^2\),, inazalisha, kitaalam, ufumbuzi mbili kama exponent ni\(2\), lakini ni suluhisho moja.
\[\begin{align*} 5x^2&= 0\\ x&=0\\ x^2-16&= 0\\ (x+4)(x-4)&= 0\\ x&= 4\\ x&= -4 \end{align*}\]
Ufumbuzi ni\(0\) (ufumbuzi mara mbili),\(4\), na\(−4\).
Uchambuzi
Tunaweza kuona ufumbuzi kwenye grafu katika Kielelezo\(\PageIndex{1}\). Kuratibu x-ya pointi ambapo grafu huvuka\(x\) -axis ni ufumbuzi\(x\) -the -intercepts. Angalia kwenye grafu kwamba katika suluhisho\(0\), grafu inagusa\(x\) -axis na inarudi nyuma. Haivuka msalaba\(x\) -axis. Hii ni mfano wa ufumbuzi mara mbili.
Kutatua kwa factoring:\(12x^4 = 3x^2\).
- Jibu
-
\(x=0, x=12, x=−12\)
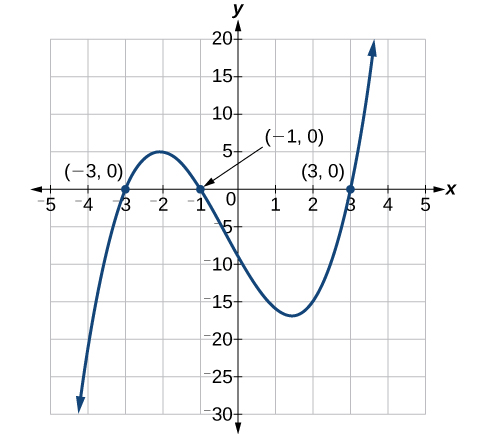
Tatua polynomial kwa kikundi:\(x^3+x^2−9x−9=0\).
Suluhisho
Polynomial hii ina\(4\) maneno, ambayo tunaweza kutatua kwa kikundi. Taratibu za makundi zinahitaji kuzingatia masharti mawili ya kwanza na kisha kuzingatia masharti mawili ya mwisho. Ikiwa mambo katika mabano yanafanana, tunaweza kuendelea na mchakato na kutatua, isipokuwa factoring zaidi inapendekezwa.
\[\begin{align*} x^3+x^2-9x-9&= 0\\ x^2(x+1)-9(x+1)&= 0\\ (x^2-9)(x+1)&= 0 \end{align*}\]
Mchakato wa makundi unamalizika hapa, kwa kuwa tunaweza kuzingatia\(x^2−9\) kutumia tofauti ya formula ya mraba.
\[\begin{align*} (x^2-9)(x+1)&= 0\\ (x-3)(x+3)(x+1)&= 0\\ x&= 3\\ x&= -3\\ x&= -1 \end{align*}\]
Ufumbuzi ni\(3\),\(−3\), na\(−1\). Kumbuka kuwa exponent juu ni\(3\) na sisi kupatikana\(3\) ufumbuzi. Tunaweza kuona ufumbuzi, x-intercepts, kwenye grafu katika Kielelezo\(\PageIndex{2}\).
Uchambuzi
Tuliangalia kutatua equations quadratic kwa kuzingatia wakati mgawo wa kuongoza ni\(1\). Wakati mgawo wa kuongoza sio\(1\), tulitatuliwa kwa kikundi. Kundi linahitaji maneno manne, ambayo tulipata kwa kugawanya muda wa mstari wa equations quadratic. Tunaweza pia kutumia kikundi kwa baadhi ya polynomials ya shahada ya juu kuliko\(2\), kama tulivyoona hapa, kwa kuwa kulikuwa na maneno manne tayari.
Kutatua equations radical
Ulinganifu mkubwa ni milinganyo ambayo yana vigezo katika radicand (maneno chini ya ishara kali), kama vile
\[\sqrt{3x+18}=x \nonumber\]
\[\sqrt{x+3}=x-3 \nonumber\]
\[\sqrt{x+5}-\sqrt{x-3}=2 \nonumber\]
Ulinganifu mkubwa unaweza kuwa na maneno moja au zaidi, na hutatuliwa kwa kuondoa kila radical, moja kwa wakati. Tunapaswa kuwa makini wakati wa kutatua equations radical, kama si kawaida kupata ufumbuzi extraneous, mizizi ambayo si, kwa kweli, ufumbuzi wa equation. Ufumbuzi huu sio kutokana na kosa katika njia ya kutatua, lakini matokeo ya mchakato wa kuinua pande zote mbili za equation kwa nguvu. Hata hivyo, kuangalia kila jibu katika equation ya awali itathibitisha ufumbuzi wa kweli.
Equation iliyo na maneno na variable katika radicand inaitwa equation radical.
- Sulua kujieleza kwa upande mmoja wa ishara sawa. Weka masharti yote yaliyobaki upande mwingine.
- Ikiwa radical ni mizizi ya mraba, basi mraba pande zote mbili za equation. Ikiwa ni mizizi ya mchemraba, kisha uinua pande zote mbili za equation kwa nguvu ya tatu. Kwa maneno mengine, kwa\(n^{th}\) mizizi ya mizizi, ongeza pande zote mbili kwa\(n^{th}\) nguvu. Kufanya hivyo hupunguza ishara kali.
- Tatua equation iliyobaki.
- Kama neno radical bado, kurudia hatua 1—2.
- Thibitisha ufumbuzi kwa kuwabadilisha katika equation ya awali.
Kutatua\(\sqrt{15−2x}=x\).
Suluhisho
Ya radical tayari imetengwa upande wa kushoto wa upande sawa, hivyo endelea mraba pande zote mbili.
\[\begin{align*} \sqrt{15-2x}&= x\\ {\left (\sqrt{15-2x} \right )}^2&= {(x)}^2\\ 15-2x&= x^2 \end{align*}\]
Tunaona kwamba equation iliyobaki ni quadratic. Weka sawa na sifuri na kutatua.
\[\begin{align*} 0&= x^2+2x-15\\ 0&= (x+5)(x-3)\\ x&= -5\\ x&= 3 \end{align*}\]
Ufumbuzi uliopendekezwa ni\(−5\) na\(3\). Hebu angalia kila ufumbuzi nyuma katika equation awali. Kwanza, angalia\(x=−5\).
\[\begin{align*} \sqrt{15-2x}&= x\\ \sqrt{15-2(-5)}&=-5\\ \sqrt{25}&= -5\\ 5&\neq -5 \end{align*}\]
Hii ni suluhisho la nje. Wakati hakuna kosa lilifanywa kutatua equation, tuligundua ufumbuzi kwamba haina kukidhi equation awali.
Angalia\(x=3\).
\[\begin{align*} \sqrt{15-2x}&= x\\ \sqrt{15-2(3)}&= 3\\ \sqrt{9}&= 3\\ 3&= 3 \end{align*}\]
Suluhisho ni\(3\).
Tatua equation radical:\(\sqrt{x+3}=3x-1\)
- Jibu
-
\(x=1\), ufumbuzi wa nje\(x=−\dfrac{2}{9}\)
Kutatua\(\sqrt{2x+3}+\sqrt{x-2}=4\)
Suluhisho
Kama equation hii ina radicals mbili, sisi kutenganisha radical moja, kuondoa hiyo, na kisha kutenganisha radical pili.
\[\sqrt{2x+3}+\sqrt{x-2}=4 \nonumber\]
\[\begin{align*} \sqrt{2x+3}&= 4-\sqrt{x-2} \qquad \text{Subtract } \sqrt{x-2} \text{ from both sides}\\ {\left (\sqrt{2x+3} \right )}^2&= {\left (4-\sqrt{x-2} \right )}^2\qquad \text{Square both sides} \end{align*}\]
Tumia formula kamili ya mraba kupanua upande wa kulia:\({(a−b)}^2=a^2−2ab+b^2\).
\[\begin{align*} 2x+3&= {(4)}^2-2(4)\sqrt{x-2}+{(\sqrt{x-2})}^2\\ 2x+3&= 16-8\sqrt{x-2}+(x-2)\\ 2x+3&= 14+x-8\sqrt{x-2} \qquad \text{Combine like terms}\\ x-11&= -8\sqrt{x-2} \qquad \text{Isolate the second radical}\\ {(x-11)}^2&= {(-8\sqrt{x-2})}^2 \qquad \text{Square both sides}\\ x^2-22x+121&= 64(x-2) \end{align*}\]
Sasa kwamba radicals wote wameondolewa, kuweka quadratic sawa na sifuri na kutatua.
\[\begin{align*} x^2-22x+121&= 64x-128\\ x^2-86x+249&= 0\\ (x-3)(x-83)&= 0\\ x&= 3\\ x&= 83 \end{align*}\]
Ufumbuzi uliopendekezwa ni\(3\) na\(83\). Angalia kila suluhisho katika equation ya awali.
\[\begin{align*} \sqrt{2x+3}+\sqrt{x-2}&= 4\\ \sqrt{2x+3}&= 4-\sqrt{x-2}\\ \sqrt{2(3)+3}&= 4-\sqrt{(3)-2}\\ \sqrt{9}&= 4-\sqrt{1}\\ 3&= 3 \end{align*}\]
Suluhisho moja ni\(3\).
Angalia\(x=83\).
\[\begin{align*} \sqrt{2x+3}+\sqrt{x-2}&= 4\\ \sqrt{2x+3}&= 4-\sqrt{x-2}\\ \sqrt{2(83)+3}&= 4-\sqrt{(83)-2}\\ \sqrt{169}&= 4-\sqrt{81}\\ 13&\neq -5 \end{align*}\]
Suluhisho pekee ni\(3\). Tunaona kwamba\(x=83\) ni suluhisho la nje.
Tatua equation na radicals mbili:\(\sqrt{3x+7}+\sqrt{x+2}=1\)
- Jibu
-
\(x=−2\), ufumbuzi wa nje\(x=−1\)
Kutatua Equation ya Thamani kamili
Ifuatayo, tutajifunza jinsi ya kutatua usawa wa thamani kabisa. Ili kutatua equation kama vile\(|2x−6|=8\), tunaona kwamba thamani kamili itakuwa sawa na\(8\) kama kiasi ndani ya baa thamani kamili ni\(8\) au\(−8\). Hii inasababisha equations mbili tofauti tunaweza kutatua kwa kujitegemea.
\[\begin{align*} 2x-6&= 8\\ 2x&= 14\\ x&= 7 \end{align*}\]
AU
\[\begin{align*} 2x-6&= -8\\ 2x&= -2\\ x&= -1 \end{align*}\]
Kujua jinsi ya kutatua matatizo yanayohusisha kazi za thamani kamili ni muhimu. Kwa mfano, tunaweza kuhitaji kutambua namba au pointi kwenye mstari ulio umbali maalum kutoka kwenye hatua ya kumbukumbu iliyotolewa.
Thamani kamili ya\(x\) imeandikwa kama\(|x|\). Ina mali zifuatazo:
Ikiwa\(x≥0\), basi,\(|x|=x\) .Ikiwa\(x<0\), basi\(x=−x\).
Kwa idadi halisi\(A\) na\(B\), equation ya fomu\(|A|=B\), na\(B≥0\), itakuwa na ufumbuzi wakati\(A=B\) au\(A=−B\). Kama\(B<0\), equation\(|A|=B\) haina ufumbuzi.
Equation ya thamani kamili katika fomu\(|ax+b|=c\) ina mali zifuatazo:
- Kama\(c<0\),\(|ax+b|=c\) haina ufumbuzi.
- Ikiwa\(c=0\),\(|ax+b|=c\) ina suluhisho moja.
- Ikiwa\(c>0\),\(|ax+b|=c\) ina ufumbuzi mbili.
Kutokana na usawa wa thamani kamili, tatua.
- Sulua kujieleza thamani kamili kwa upande mmoja wa ishara sawa.
- Kama\(c>0\), kuandika na kutatua equations mbili:\(ax+b=c\) na\(ax+b=−c\).
Tatua milinganyo ya thamani kamili yafuatayo:
- \(|6x+4|=8\)
- \(|3x+4|=−9\)
- \(|3x−5|−4=6\)
- \(|−5x+10|=0\)
Suluhisho
- \(|6x+4|=8\)
Andika equations mbili na kutatua kila:
\[\begin{align*} 6x+4&= 8\\ 6x&= 4\\ x&= \dfrac{2}{3} \end{align*}\]
AU
\[\begin{align*} 6x+4&= -8\\ 6x&= -12\\ x&= -2 \end{align*}\]
Ufumbuzi mbili ni\(\dfrac{2}{3}\) na\(−2\).
- \(|3x+4|=−9\)
Hakuna suluhisho kama thamani kamili haiwezi kuwa hasi.
- \(|3x−5|−4=6\)
Sulua kujieleza thamani kamili na kisha kuandika equations mbili.
\[\begin{align*} |3x-5|-4&= 6\\ |3x-5|&= 10\\ 3x-5&= 10\\ 3x&= 15\\ x&= 5 \end{align*}\]
AU
\[\begin{align*} 3x-5&= -10\\ 3x=-5\\ x=\dfrac{5}{3} \end{align*}\]
Kuna ufumbuzi mbili:\(5\), na\(-\dfrac{5}{3}\).
- \(|−5x+10|=0\)
equation ni kuweka sawa na sifuri, hivyo tuna kuandika equation moja tu.
\[\begin{align*} -5x+10&= 0\\ -5x&= -10\\ x&= 2 \end{align*}\]
Kuna suluhisho moja:\ (2\).
Kutatua kabisa thamani equation:\(|1−4x|+8=13\).
- Jibu
-
\(x=−1, x=\dfrac{3}{2}\)
Kutatua Aina nyingine za equations
Kuna aina nyingine nyingi za equations pamoja na zile ambazo tumejadili hadi sasa. Tutaona zaidi yao katika maandiko. Hapa, tutajadili usawa ulio katika fomu ya quadratic, na usawa wa busara unaosababisha quadratic.
Kutatua Ulinganifu katika Fomu ya Quadratic
Ulinganisho katika fomu ya quadratic ni equations na maneno matatu. Muda wa kwanza una nguvu zaidi ya\(2\). Muda wa kati una exponent ambayo ni nusu ya exponent ya muda wa kuongoza. Muda wa tatu ni mara kwa mara. Tunaweza kutatua equations katika fomu hii kama kwamba walikuwa quadratic. Mifano michache ya milinganyo haya ni pamoja na\(x^4−5x^2+4=0\)\(x^6+7x^3−8=0\),, na\(x^{\tfrac{2}{3}} +4x^{\tfrac{1}{3}}+2=0\). Katika kila mmoja, mara mbili exponent ya muda wa kati ni sawa exponent juu ya muda wa kuongoza. Tunaweza kutatua equations hizi kwa kubadilisha variable kwa muda wa kati.
Kama exponent juu ya muda wa kati ni nusu ya exponent juu ya muda wa kuongoza, tuna equation katika fomu quadratic, ambayo tunaweza kutatua kama ni quadratic. Sisi badala ya kutofautiana kwa muda wa kati ili kutatua equations katika fomu quadratic.
- Kutambua exponent juu ya muda wa kuongoza na kuamua kama ni mara mbili exponent juu ya muda wa kati.
- Kama ni, mbadala variable, kama vile\(u\), kwa ajili ya sehemu variable ya muda wa kati.
- Andika upya equation ili inachukua fomu ya kawaida ya quadratic.
- Tatua kutumia njia moja ya kawaida ya kutatua quadratic.
- Badilisha nafasi ya kubadilisha na muda wa awali.
- Tatua equation iliyobaki.
Kutatua hii ya nne shahada equation:\(3x^4−2x^2−1=0\).
Suluhisho
equation hii inafaa vigezo kuu, kwamba nguvu juu ya muda wa kuongoza ni mara mbili ya nguvu juu ya muda wa kati. Kisha, tutafanya badala ya muda wa kutofautiana katikati. Hebu\(u =x^2\). Andika upya equation katika\(u\).
\[3u^2−2u−1=0 \nonumber\]
Sasa tatua quadratic.
\[\begin{align*} 3u^2-2u-1&= 0\\ (3u+1)(u-1)&= 0 \end{align*}\]
Kutatua kila sababu na kuchukua nafasi ya muda wa awali kwa ajili ya\(u\).
\[\begin{align*} 3u+1&= 0\\ 3u&= -1\\ u&= -\dfrac{1}{3}\\ x^2&= -\dfrac{1}{3}\\ x&= \pm i\sqrt{\dfrac{1}{3}}\\ u-1&= 0\\ u&= 1\\ x^2&= 1\\ x&= \pm 1 \end{align*}\]
Ufumbuzi ni\(x=±i\sqrt{\dfrac{1}{3}}\) na\(x=±1\)
Tatua kutumia mbadala:\(x^4−8x^2−9=0\).
- Jibu
-
\(x=−3,3,−i,i\)
Tatua equation katika fomu ya quadratic:\({(x+2)}^2+11(x+2)−12=0\).
Suluhisho
Equation hii ina binomial badala ya variable moja. Tabia ni kupanua kile kilichowasilishwa. Hata hivyo, kutambua kwamba inafaa vigezo vya kuwa katika fomu ya quadratic hufanya tofauti zote katika mchakato wa kutatua. Kwanza, fanya badala, kuruhusu\(u =x+2\). Kisha kuandika upya equation katika\(u\).
\[\begin{align*} u^2+11u-12&= 0\\ (u+12)(u-1)&= 0 \end{align*}\]
Tatua kutumia mali ya sifuri na kisha\(u\) ubadilishe na kujieleza awali.
\[\begin{align*} u+12&= 0\\ u&= -12\\ x+2&= -12\\ x&= -14 \end{align*}\]
Sababu ya pili inaongoza
\[\begin{align*} u-1&= 0\\ u&= 1\\ x+2&= 1\\ x&= -1 \end{align*}\]
Tuna ufumbuzi mbili:\(−14\), na\(−1\).
Kutatua:\({(x−5)}^2−4(x−5)−21=0\).
- Jibu
-
\(x=2,x=12\)
Kutatua Equations Mantiki Kusababisha Quadratic
Mapema, tulitatua usawa wa busara. Wakati mwingine, kutatua matokeo ya usawa wa busara katika quadratic. Wakati hii itatokea, tunaendelea suluhisho kwa kurahisisha equation quadratic kwa njia moja tuliyoyaona. Inaweza kugeuka kuwa hakuna suluhisho.
Tatua usawa wa busara wafuatayo:\(\dfrac{-4x}{x-1}+\dfrac{4}{x+1}=\dfrac{-8}{x^2-1}\)
Suluhisho
Tunataka denominators wote katika fomu factored kupata LCD. Denominators mbili haziwezi kuhesabiwa zaidi. Hata hivyo,\(x^2−1=(x+1)(x−1)\). Kisha, LCD ni\((x+1)(x−1)\). Kisha, tunazidisha equation nzima na LCD.
\ [kuanza {align*} (x+1) (x-1)\ kushoto (\ dfrac {-4x} {x-1} +\ dfrac {4} {x+1}\ haki) &=\ kushoto (\ dfrac {-8} {x ^ 2-1}\ haki) (x-1) (x-1)\\ -4x (x+1) +4 (x-1) &= -8\\ -4x^ 2-4x+4x-4 & = -8\\ -4x^2+4&= 0\\
-4 (x ^ 2-1) &= 0\\ -4 (x+1) (x-1) &= 0\\ x&= -1\\ x & = 1\\ x & = 1\ mwisho {align*}\]
Katika kesi hii, suluhisho ama hutoa sifuri katika denominator katika equation ya awali. Hivyo, hakuna suluhisho.
Kutatua\(\dfrac{3x+2}{x-2}+\dfrac{1}{x}=\dfrac{-2}{x^2-2x}\)
- Jibu
-
\(x=−1, x= 0\)si ufumbuzi.
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na aina tofauti za equations.
- Equation ya busara na hakuna Suluhisho
- Kutatua equations na watazamaji wa busara kutumia nguvu za usawa
- Kutatua equations radical sehemu ya 1 ya 2
- Kutatua equations radical sehemu ya 2 ya 2
Dhana muhimu
- Watazamaji wa busara wanaweza kuandikwa upya njia kadhaa kulingana na kile ambacho ni rahisi zaidi kwa tatizo. Ili kutatua, pande zote mbili za equation hufufuliwa kwa nguvu ambayo itatoa exponent juu ya kutofautiana sawa na\(1\). Angalia Mfano, Mfano, na Mfano.
- Factoring inaenea kwa polynomials ya juu-ili wakati inahusisha factoring nje GCF au factoring kwa kambi. Angalia Mfano na Mfano.
- Tunaweza kutatua equations radical kwa kutenganisha radical na kuongeza pande zote mbili za equation kwa nguvu inayolingana index. Angalia Mfano na Mfano.
- Ili kutatua usawa wa thamani kamili, tunahitaji kuandika equations mbili, moja kwa thamani nzuri na moja kwa thamani hasi. Angalia Mfano.
- Equations katika fomu quadratic ni rahisi doa, kama exponent juu ya muda wa kwanza ni mara mbili exponent juu ya muda wa pili na muda wa tatu ni mara kwa mara. Tunaweza pia kuona binomial katika nafasi ya variable moja. Tunatumia badala ya kutatua. Angalia Mfano na Mfano.
- Kutatua equation ya busara inaweza pia kusababisha equation quadratic au equation katika fomu quadratic. Angalia Mfano.


