2.6: Ulinganifu wa Quadratic

Malengo ya kujifunza

• Tatua equations quadratic kwa factoring.
• Tatua usawa wa quadratic na mali ya mizizi ya mraba.
• Tatua equations quadratic kwa kukamilisha mraba.
• Tatua usawa wa quadratic kwa kutumia formula ya quadratic.

Mfuatiliaji wa kompyuta upande wa kushoto katika Kielelezo\(\PageIndex{1}\) ni mfano wa\(23.6\) inchi na moja ya kulia ni mfano wa\(27\) inchi. Kwa kiasi kikubwa, wachunguzi wanaonekana sawa. Ikiwa kuna kiasi kidogo cha nafasi na tunataka kufuatilia kubwa iwezekanavyo, tunaamuaje ni nani atakayechagua? Katika sehemu hii, tutajifunza jinsi ya kutatua matatizo kama haya kwa kutumia mbinu nne tofauti.

Kielelezo\(\PageIndex{1}\)

Kutatua equations Quadratic kwa factoring

Equation iliyo na polynomial ya shahada ya pili inaitwa equation quadratic. Kwa mfano, equations kama vile\(2x^2 +3x−1=0\) na\(x^2−4= 0\) ni equations quadratic. Wao hutumiwa kwa njia nyingi katika nyanja za uhandisi, usanifu, fedha, sayansi ya kibaiolojia, na, bila shaka, hisabati.

Mara nyingi njia rahisi ya kutatua equation quadratic ni factoring. Factoring inamaanisha kutafuta maneno ambayo yanaweza kuzidishwa pamoja ili kutoa usemi upande mmoja wa equation.

Ikiwa equation ya quadratic inaweza kuhesabiwa, imeandikwa kama bidhaa ya maneno ya mstari. Kutatua kwa kuzingatia inategemea mali ya sifuri, ambayo inasema kwamba ikiwa\(a⋅b=0\), basi\(a = 0\) au\(b =0\), ambapo a na b ni namba halisi au maneno ya algebraic. Kwa maneno mengine, kama bidhaa ya namba mbili au maneno mawili ni sawa na sifuri, basi moja ya namba au moja ya maneno lazima sawa sifuri kwa sababu sifuri kuongezeka kwa kitu chochote sawa na sifuri.

Kuzidisha sababu huongeza equation kwa kamba ya maneno yaliyotengwa na ishara pamoja au ndogo. Kwa hiyo, kwa maana hiyo, uendeshaji wa kuzidisha hupunguza uendeshaji wa factoring. Kwa mfano, kupanua kujieleza\((x−2)(x+3)\) kwa kuzidisha mambo mawili pamoja.

\[\begin{align*} (x-2)(x+3)&= x^2+3x-2x-6\\ &= x^2+x-6\\ \end{align*}\]

Bidhaa ni kujieleza kwa quadratic. Kuweka sawa na sifuri,\(x^2+x−6= 0\) ni equation quadratic. Kama tulikuwa na sababu equation, tunataka kupata nyuma sababu sisi tele.

Mchakato wa kuzingatia equation ya quadratic inategemea mgawo wa kuongoza, iwe ni\(1\) au integer nyingine. Tutaangalia hali zote mbili; lakini kwanza, tunataka kuthibitisha kwamba equation imeandikwa katika hali ya kawaida\(ax^2+bx+c=0\), ambapo\(a\),\(b\), na\(c\) ni idadi halisi, na\(a≠0\). Equation\(x^2 +x−6= 0\) iko katika fomu ya kawaida.

Tunaweza kutumia mali sifuri-bidhaa kutatua equations quadratic ambayo sisi kwanza kuwa na sababu nje kubwa ya kawaida sababu (GCF), na kwa equations kwamba kuwa maalum factoring formula pia, kama vile tofauti ya mraba, wote ambao tutaona baadaye katika sehemu hii.

MALI YA BIDHAA ZA SIFURI NA USAWA WA QUADRATIC

Zero-bidhaa mali inasema

Ikiwa\(a⋅b=0\), basi\(a=0\) au\(b=0\),

wapi\(a\) na\(b\) ni namba halisi au maneno ya algebraic.

Equation quadratic ni equation iliyo na polynomial ya shahada ya pili; kwa mfano

\[ax^2+bx+c=0\]

ambapo\(a\),\(b\), na\(c\) ni idadi halisi, na kama\(a≠0\), ni katika hali ya kiwango.

Kutatua Quadratics na mgawo wa Uongozi wa\(1\)

Katika equation quadratic\(x^2 +x−6=0\), mgawo wa kuongoza, au mgawo wa\(x^2\), ni\(1\). Tuna njia moja ya kuzingatia equations quadratic katika fomu hii.

Jinsi ya: Fanya equation quadratic na mgawo wa kuongoza wa 1

1. Kupata namba mbili ambazo bidhaa ni sawa\(c\) na ambao jumla ni sawa\(b\).
2. Tumia namba hizo kuandika mambo mawili ya fomu\((x+k)\) au\((x−k)\), ambapo k ni moja ya namba zilizopatikana katika hatua ya 1. Tumia namba hasa kama ilivyo. Kwa maneno mengine, kama namba mbili ni\(1\) na\(−2\), sababu ni\((x+1)(x−2)\).
3. Tatua kutumia mali ya sifuri kwa kuweka kila sababu sawa na sifuri na kutatua kwa kutofautiana.

Mfano\(\PageIndex{1}\): Solving a Quadratic with Leading Coefficient of \(1\)

Sababu na kutatua equation:\(x^2+x−6=0\).

Suluhisho

Kwa sababu\(x^2 +x−6=0\), tunatafuta namba mbili ambazo bidhaa zinalingana\(−6\) na ambazo jumla yake ni sawa\(1\). Anza kwa kuangalia mambo ya uwezekano wa\(−6\).

\[1⋅(−6) \nonumber \]

\[(−6)⋅1 \nonumber \]

\[2⋅(−3) \nonumber \]

\[3⋅(−2) \nonumber \]

jozi ya mwisho\(3⋅(−2)\), jumla kwa\(1\), hivyo hizi ni idadi. Kumbuka kwamba jozi moja tu ya namba itafanya kazi. Kisha, andika mambo.

\[(x−2)(x+3)=0 \nonumber \]

Ili kutatua equation hii, tunatumia mali ya sifuri. Weka kila sababu sawa na sifuri na kutatua.

\[\begin{align*} (x-2)(x+3)&= 0\\ (x-2)&= 0\\ x&= 2\\ (x+3)&= 0\\ x&= -3 \end{align*}\]

Ufumbuzi mbili ni\(2\) na\(−3\). Tunaweza kuona jinsi ufumbuzi unahusiana na grafu katika Kielelezo\(\PageIndex{2}\). Ufumbuzi ni x-intercepts ya\(x^2 +x−6=0\).

Kielelezo\(\PageIndex{2}\)

Zoezi\(\PageIndex{1}\)

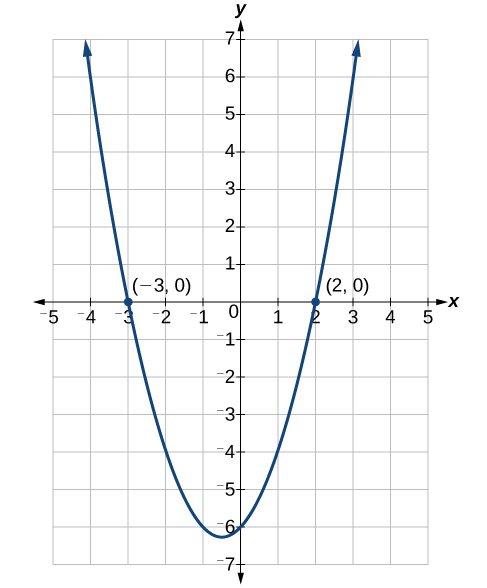
Sababu na kutatua equation quadratic:\(x^2−5x−6=0\).

Jibu

\((x−6)(x+1)=0\),\(x=6\),\(x=−1\)

Mfano\(\PageIndex{2}\): Solve the Quadratic Equation by Factoring

Kutatua equation quadratic kwa factoring:\(x^2+8x+15=0\).

Suluhisho

Kupata namba mbili ambazo bidhaa ni sawa\(15\) na ambao jumla ni sawa\(8\). Orodha ya mambo ya\(15\).

\[1⋅15 \nonumber \]

\[3⋅5 \nonumber \]

\[(−1)⋅(−15) \nonumber \]

\[(−3)⋅(−5) \nonumber \]

Nambari zinazoongeza\(8\) ni\(3\) na\(5\). Kisha, weka mambo, weka kila jambo sawa na sifuri, na usuluhishe.

\[\begin{align*} (x+3)(x+5)&= 0\\ (x+3)&= 0\\ x&= -3\\ (x+5)&= 0\\ x&= -5 \end{align*}\]

Ufumbuzi ni\(−3\) na\(−5\).

Zoezi\(\PageIndex{2}\)

Kutatua equation quadratic kwa factoring:\(x^2−4x−21=0\).

Jibu

\((x−7)(x+3)=0\),\(x=7\),\(x=−3\)

Mfano\(\PageIndex{3}\): Using Zero-Product Property to Solve a Quadratic Equation

Kutatua tofauti ya mraba equation kutumia mali sifuri-bidhaa:\(x^2−9=0\).

Suluhisho

Kutambua kwamba equation inawakilisha tofauti ya mraba, tunaweza kuandika mambo mawili kwa kuchukua mizizi ya mraba ya kila neno, kwa kutumia ishara minus kama operator katika sababu moja na ishara pamoja kama operator katika nyingine. Tatua kutumia mali ya sifuri.

\[\begin{align*} x^2-9&= 0\\ (x-3)(x+3)&= 0\\ x-3&= 0\\ x&= 3\\ (x+3)&= 0\\ x&= -3 \end{align*}\]

Ufumbuzi ni\(3\) na\(−3\).

Zoezi\(\PageIndex{3}\)

Kutatua kwa factoring:\(x^2−25=0\).

Jibu

\((x+5)(x−5)=0, x=−5, x=5\)

Kuzingatia na Kutatua Equation ya Quadratic ya Amri ya Juu

Wakati mgawo wa kuongoza sio\(1\), tunazingatia equation ya quadratic kwa kutumia njia inayoitwa kikundi, ambayo inahitaji maneno manne.

Kundi: Hatua za kuzingatia usawa wa quadratic

Kwa usawa katika fomu ya kawaida, hebu tupate taratibu za makundi

1. Kwa quadratic katika fomu ya kawaida,\(ax^2+bx+c=0\), kuzidisha\(a⋅c\).
2. Pata namba mbili ambazo bidhaa ni sawa na ac na ambao jumla ni sawa\(b\).
3. Andika upya equation kuchukua nafasi ya\(bx\) muda na maneno mawili kwa kutumia namba kupatikana katika hatua\(1\) kama coefficients ya\(x\).
4. Fanya masharti mawili ya kwanza na kisha ueleze masharti mawili ya mwisho. Maneno katika mabano yanapaswa kuwa sawa na kutumia kikundi.
5. Fanya nje ya maneno katika mabano.
6. Weka maneno sawa na sifuri na kutatua kwa kutofautiana.

Mfano\(\PageIndex{4}\): Solving a Quadratic Equation Using Grouping

Tumia kikundi kwa sababu na kutatua equation quadratic:\(4x^2+15x+9=0\).

Suluhisho

Kwanza, ongeze\(ac:4(9)=36\). Kisha orodha ya mambo ya\(36\).

\[1⋅36 \nonumber\]

\[2⋅18 \nonumber\]

\[3⋅12 \nonumber\]

\[4⋅9 \nonumber\]

\[6⋅6 \nonumber\]

jozi tu ya mambo ambayo ni kiasi kwa\(15\) ni\(3+12\). Andika upya equation kuondoa b mrefu,\(15x\), na maneno mawili kutumia\(3\) na\(12\) kama coefficients ya\(x\). Fanya masharti mawili ya kwanza, na kisha ueleze masharti mawili ya mwisho.

\[\begin{align*} 4x^2+3x+12x+9&= 0\\ x(4x+3)+3(4x+3)&= 0\\ (4x+3)(x+3)&= 0 \qquad \text{Solve using the zero-product property}\\ (4x+3)&= 3\\ x&= -\dfrac{3}{4}\\ (x+3)&= 0\\ x&= -3 \end{align*}\]

Ufumbuzi ni\(−\dfrac{3}{4}\), na\(−3\). Angalia Kielelezo\(\PageIndex{3}\).

Kielelezo\(\PageIndex{3}\)

Zoezi\(\PageIndex{4}\)

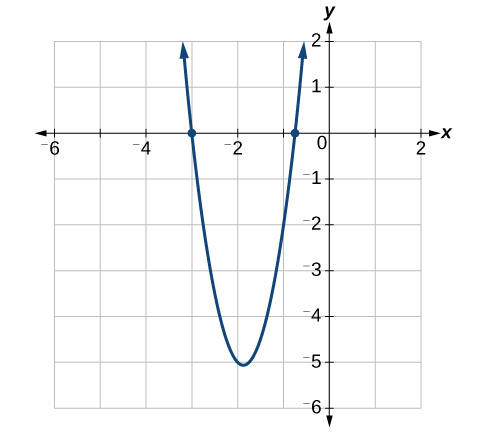
Tatua kutumia factoring kwa kikundi:\(12x^2+11x+2=0\).

Jibu

\((3x+2)(4x+1)=0\),\(x=−\dfrac{2}{3}\),\(x=−\dfrac{1}{4}\)

Mfano\(\PageIndex{5}\): Solving a Higher Degree Quadratic Equation by Factoring

Kutatua equation kwa factoring:\(−3x^3−5x^2−2x=0\).

Suluhisho

Equation hii haionekani kama quadratic, kama nguvu ya juu ni\(3\), si\(2\). Kumbuka kwamba jambo la kwanza tunataka kufanya wakati kutatua equation yoyote ni sababu nje GCF, kama moja ipo. Na inafanya hapa. Tunaweza kuzingatia\(−x\) kutoka kwa maneno yote na kisha kuendelea na kikundi.

\ [kuanza {align*}
-3x ^ 3-5x ^ 2-2x&= 0\\
-x (3x ^ 2+5x+2) &= 0\\
-x (3x ^ 2+3x+2x+2) &= 0\ qquad\ maandishi {Matumizi kikundi juu ya kujieleza katika mabano}\\
-x [3x (x+1) +2 (x+1)] &= 0\\
-x (3x+2) (x+1) &= 0\\
\ maandishi {Sasa, tunatumia mali sifuri-bidhaa. Angalia kwamba tuna mambo matatu.} \\
-x&= 0\\
x&= 0\\
3x+2&= 0\\
x&= -\ dfrac {2} {3}\\
x+1&= 0\\
x&= -1
\\ mwisho {align*}\]

Ufumbuzi ni\(0\),\(−\dfrac{2}{3}\), na\(−1\).

Zoezi\(\PageIndex{5}\)

Kutatua kwa factoring:\(x^3+11x^2+10x=0\).

Jibu

\(x=0, x=−10, x=−1\)

Kutumia Mali ya Mizizi ya Mraba

Wakati hakuna neno linear katika equation, njia nyingine ya kutatua equation quadratic ni kwa kutumia mali ya mizizi ya mraba, ambayo sisi kutenganisha\(x^2\) mrefu na kuchukua mizizi mraba wa idadi upande wa pili wa ishara sawa. Kumbuka kwamba wakati mwingine tunaweza kuwa na kuendesha equation kujitenga\(x^2\) mrefu ili mali mizizi mraba inaweza kutumika.

MIZIZI YA MRABA MALI

Kwa\(x^2\) neno pekee, mali ya mizizi ya mraba inasema kwamba:

kama\(x^2=k\), basi\(x=±\sqrt{k}\)

wapi\(k\) nambari halisi ya nonzero.

Jinsi ya: Kutokana na equation quadratic na\(x^2\) term but no \(x\) term, use the square root property to solve it

1. Sulua\(x^2\) neno kwa upande mmoja wa ishara sawa.
2. Kuchukua mizizi ya mraba ya pande zote mbili za equation, kuweka\(±\) ishara kabla ya kujieleza upande kinyume na muda wa mraba.
3. Kurahisisha idadi upande na\(±\) ishara.

Mfano\(\PageIndex{6}\): Solving a Simple Quadratic Equation Using the Square Root Property

Tatua quadratic kutumia mali ya mizizi ya mraba:\(x^2=8\).

Suluhisho

Kuchukua mizizi ya mraba ya pande zote mbili, na kisha urahisishe radical. Kumbuka kutumia\(±\) ishara kabla ya ishara kali.

\[\begin{align*} x^2&= 8\\ x&= \pm \sqrt{8}\\ &= \pm 2\sqrt{2} \end{align*}\]

Ufumbuzi ni\(2\sqrt{2}\),\(-2\sqrt{2}\)

Mfano\(\PageIndex{7}\): Solving a Quadratic Equation Using the Square Root Property

Tatua equation ya quadratic:\(4x^2+1=7\).

Suluhisho

Kwanza, jitenga\(x^2\) neno. Kisha kuchukua mizizi ya mraba ya pande zote mbili.

\[\begin{align*} 4x^2+1&= 7\\ 4x^2&= 6\\ x^2&= \dfrac{6}{4}\\ x&= \pm \dfrac{\sqrt{6}}{2} \end{align*}\]

Ufumbuzi ni\(\dfrac{\sqrt{6}}{2}\), na\(-\dfrac{\sqrt{6}}{2}\).

Zoezi\(\PageIndex{6}\)

Tatua equation ya quadratic kwa kutumia mali ya mizizi ya mraba:\(3{(x−4)}^2=15\).

Jibu

\(x=4±\sqrt{5}\)

Kukamilisha Square

Sio equations zote za quadratic zinaweza kuzingatiwa au zinaweza kutatuliwa katika fomu yao ya awali kwa kutumia mali ya mizizi ya mraba. Katika kesi hizi, tunaweza kutumia njia ya kutatua equation quadratic inayojulikana kama kukamilisha mraba. Kutumia njia hii, tunaongeza au kuondoa maneno kwa pande zote mbili za equation mpaka tuwe na trinomial mraba kamili upande mmoja wa ishara sawa. Kisha tunatumia mali ya mizizi ya mraba. Ili kukamilisha mraba, mgawo wa kuongoza\(a\), lazima iwe sawa\(1\). Ikiwa haifai, basi ugawanye equation nzima na\(a\). Kisha, tunaweza kutumia taratibu zifuatazo kutatua equation quadratic kwa kukamilisha mraba.

Tutatumia mfano\(x^2+4x+1=0\) kuonyesha kila hatua.

Kutokana na equation quadratic ambayo haiwezi kuhesabiwa, na kwa\(a=1\), first add or subtract the constant term to the right sign of the equal sign.

\ [kuanza {align*}
x ^ 2+4x+1&= 0\\
x ^ 2+4x&= -1\ qquad\ maandishi {Kuzidisha b}\ maandishi {neno kwa}\ dfrac {1} {2}\ maandishi {na mraba yake.} \
\ dfrac {1} {2} (4) &= 2\\ 2
^2&= 4\ qquad\ maandishi {Ongeza}\ kushoto ({\ dfrac {1} {2}}\ haki) ^2\ maandishi {kwa pande zote mbili za ishara sawa na kurahisisha upande wa kulia. Tuna}\\
x ^ 2+4x+4&= -1+4\\
x ^ 2+4x+4&= 3\ qquad\ Nakala {Upande wa kushoto wa equation sasa unaweza kuhesabiwa kama mraba kamilifu.} \\
{(x+2)} ^2&=3\
\ sqrt {{(x+2)} ^2} &=\ pm\ sqrt {3}\ qquad\ maandishi {Tumia mali ya mizizi ya mraba na kutatua.} \
\ sqrt {{(x+2)} ^2} &=\ pm\ sqrt {3}\
x+2&=\ pm\ sqrt {3}\
x&= -2\ pm\ sqrt {3}
\ mwisho {align*}\]

Ufumbuzi ni\(−2+\sqrt{3}\), na\(−2−\sqrt{3}\).

Mfano\(\PageIndex{8}\): Solving a Quadratic by Completing the Square

Tatua equation quadratic kwa kukamilisha mraba:\(x^2−3x−5=0\).

Suluhisho

Kwanza, fanya muda wa mara kwa mara upande wa kulia wa ishara sawa.

\ [kuanza {align*}
x ^ 2-3x&= 5\ qquad\ maandishi {Kisha, chukua}\ dfrac {1} {2}\ maandishi {ya b mrefu na mraba yake.} \
\ dfrac {1} {2} (-3) &= -\ dfrac {3} {2}\\
{kushoto (-\ dfrac {3} {2}\ haki)} ^2=\ dfrac {9} {4}\
x ^ 2-3x+ {kushoto (-\ dfrac {3} {2}\ haki)} ^2&= 5+ {\ kushoto (-\ dfrac {3} {2}\ kulia)} ^2\ qquad\ maandishi {Ongeza matokeo kwa pande zote mbili za ishara sawa.} \\
x^2-3x+\ dfrac {9} {4} &= 5+\ dfrac {9} {4}\
\ Nakala {Fanya upande wa kushoto kama mraba kamilifu na kurahisisha upande wa kulia.} \\
{kushoto (x-\ dfrac {3} {2}\ haki)} ^2&=\ dfrac {29} {4}\\
(x-\ dfrac {3} {2}) &=\ pm\ dfrac {\ sqrt {29}} {2}\ qquad\ maandishi {Tumia mali ya mizizi ya mraba na kutatua.} \\
x&=\ dfrac {3} {2}\ pm\ dfrac {\ sqrt {29}} {2}\
\ mwisho {align*}\]

Ufumbuzi ni\(\dfrac{3}{2}+\dfrac{\sqrt{29}}{2}\), na\(\dfrac{3}{2}-\dfrac{\sqrt{29}}{2}\)

Zoezi\(\PageIndex{7}\)

Tatua kwa kukamilisha mraba:\(x^2−6x=13\).

Jibu

\(x=3±\sqrt{22}\)

Kutumia Mfumo wa Quadratic

Njia ya nne ya kutatua equation ya quadratic ni kwa kutumia formula ya quadratic, formula ambayo itasuluhisha equations zote za quadratic. Ingawa formula ya quadratic inafanya kazi kwenye equation yoyote ya quadratic katika fomu ya kawaida, ni rahisi kufanya makosa katika kubadilisha maadili katika formula. Jihadharini sana wakati wa kubadilisha, na utumie mabano wakati wa kuingiza namba hasi.

Tunaweza kupata formula ya quadratic kwa kukamilisha mraba. Sisi kudhani kwamba mgawo wa kuongoza ni chanya; kama ni hasi, tunaweza kuzidisha equation\(−1\) na kupata chanya. kutokana\(ax^2+bx+c=0, a≠0\), sisi kukamilisha mraba kama ifuatavyo:

Kwanza, fanya muda wa mara kwa mara upande wa kulia wa ishara sawa:

\[ax^2+bx=−c \nonumber \]

Kama tunataka mgawo wa kuongoza kuwa sawa\(1\), ugawanye kupitia kwa\(a\):

\[x^2+\dfrac{b}{a}x=−\dfrac{c}{a} \nonumber \]

Kisha,\(\dfrac{1}{2}\) tafuta muda wa kati, na\({(\dfrac{1}{2}\dfrac{b}{a})}^2=\dfrac{b^2}{4a^2}\) uongeze pande zote mbili za ishara sawa:

\[x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}=\dfrac{b^2}{4a^2}-\dfrac{c}{a} \nonumber \]

Kisha, weka upande wa kushoto kama mraba kamilifu. Pata denominator ya kawaida ya upande wa kulia na uandike kama sehemu moja:

\[{(x+\dfrac{b}{2a})}^2=\dfrac{b^2-4ac}{4a^2} \nonumber \]

Sasa, kutumia mizizi ya mraba mali, ambayo inatoa

\[x+\dfrac{b}{2a}=±\sqrt{\dfrac{b^2-4ac}{4a^2}} \nonumber \]

\[x+\dfrac{b}{2a}=\dfrac{±\sqrt{b^2-4ac}}{2a} \nonumber \]

Hatimaye,\(-\dfrac{b}{2a}\) kuongeza pande zote mbili za equation na kuchanganya maneno upande wa kulia. Hivyo,

\[x=\dfrac{-b±\sqrt{b^2-4ac}}{2a} \nonumber \]

FORMULA YA QUADRATIC

Imeandikwa kwa fomu ya kawaida,\(ax^2+bx+c=0\), equation yoyote ya quadratic inaweza kutatuliwa kwa kutumia formula quadratic:

\[x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}\]

ambapo\(a\),\(b\), na\(c\) ni idadi halisi na\(a≠0\).

Jinsi ya

Kutokana na equation quadratic, kutatua kwa kutumia formula quadratic

1. Hakikisha equation iko katika hali ya kawaida:\(ax^2+bx+c=0\).
2. Tambua maadili ya coefficients na muda wa mara kwa mara,\(a\),\(b\), na\(c\).
3. Makini badala ya maadili alibainisha katika hatua ya 2 katika equation. Ili kuepuka makosa yasiyo na maana, tumia mabano karibu na kila pembejeo ya namba kwenye fomu.
4. Tumia na kutatua.

Mfano\(\PageIndex{9}\): Solve the Quadratic Equation Using the Quadratic Formula

Tatua equation ya quadratic:\(x^2+5x+1=0\).

Suluhisho

Tambua coefficients:\(a=1,b=5,c=1\). Kisha tumia formula ya quadratic.

\[\begin{align*} x&= \dfrac{-(5) \pm \sqrt{(5)^2-4(1)(1)}}{2(1)}\\ &= \dfrac{-5 \pm \sqrt{25-4}}{2}\\ &= \dfrac{-5 \pm \sqrt{21}}{2} \end{align*}\]

Mfano\(\PageIndex{10}\): Solving a Quadratic Equation with the Quadratic Formula

Tumia formula ya quadratic kutatua\(x^2+x+2=0\).

Suluhisho

Kwanza, tunatambua coefficients:\(a=1\),\(b=1\), na\(c=2\).

Weka maadili haya katika formula ya quadratic.

\[\begin{align*} x&= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\\ &= \dfrac{-(1) \pm \sqrt{(1)^2-4(1)(2)}}{2(1)}\\ &= \dfrac{-1 \pm \sqrt{1-8}}{2}\\ &= \dfrac{-1 \pm \sqrt{-7}}{2}\\ &= \dfrac{-1 \pm i\sqrt{7}}{2} \end{align*}\]

Zoezi\(\PageIndex{8}\)

Tatua equation ya quadratic kwa kutumia formula ya quadratic:\(9x^2+3x−2=0\).

Jibu

\(x=-\dfrac{2}{3},x=\dfrac{1}{3}\)

Wabaguzi

Fomu ya quadratic sio tu inazalisha ufumbuzi wa equation ya quadratic, inatuambia kuhusu hali ya ufumbuzi wakati tunazingatia ubaguzi, au maneno chini ya radical,\(b^2−4ac\). Mbaguzi hutuambia kama ufumbuzi ni namba halisi au namba ngumu, na ni ufumbuzi wangapi wa kila aina ya kutarajia. Jedwali\(\PageIndex{1}\) linahusiana na thamani ya wabaguzi kwa ufumbuzi wa equation quadratic.

Jedwali\(\PageIndex{1}\)

Thamani ya Ubaguzi	Matokeo
\(b^2−4ac=0\)	Suluhisho moja la busara (ufumbuzi mara mbili)
\(b^2−4ac>0\), mraba kamili	Ufumbuzi mbili wa busara
\(b^2−4ac>0\), si mraba kamili	Mbili ufumbuzi irrational
\(b^2−4ac<0\)	Ufumbuzi mbili tata

WABAGUZI

Kwa\(ax^2+bx+c=0\), wapi\(a\)\(b\), na\(c\) ni namba halisi, ubaguzi ni usemi chini ya radical katika formula quadratic:\(b^2−4ac\). Inatuambia kama ufumbuzi ni namba halisi au namba ngumu na jinsi ufumbuzi wengi wa kila aina ya kutarajia.

Mfano\(\PageIndex{11}\): Using the Discriminant to Find the Nature of the Solutions to a Quadratic Equation

Tumia ubaguzi ili kupata asili ya ufumbuzi wa equations zifuatazo za quadratic:

1. \(x^2+4x+4=0\)
2. \(8x^2+14x+3=0\)
3. \(3x^2−5x−2=0\)
4. \(3x^2−10x+15=0\)

Suluhisho

Tumia mabaguzi\(b^2−4ac\) kwa kila equation na ueleze aina inayotarajiwa ya ufumbuzi.

a.

\(x^2+4x+4=0\)

\(b^2-4ac={(4)}^2-4(1)(4)=0\)Kutakuwa na suluhisho moja la busara mara mbili.

b.

\(8x^2+14x+3=0\)

\(b^2-4ac={(14)}^2-4(8)(3)=100\)Kama\(100\) ni mraba kamili, kutakuwa na ufumbuzi wa busara mbili.

c.

\(3x^2−5x−2=0\)

\(b^2-4ac={(-5)}^2-4(3)(-2)=49\)Kama\(49\) ni mraba kamili, kutakuwa na ufumbuzi wa busara mbili.

d.

\(3x^2−10x+15=0\)

\(b^2-4ac={(-10)}^2-4(3)(15)=-80\)Kutakuwa na ufumbuzi wawili tata.

Kutumia Theorem ya Pythagorean

Moja ya formula maarufu zaidi katika hisabati ni Theorem ya Pythagorean. Inategemea pembetatu ya kulia, na inasema uhusiano kati ya urefu wa pande kama\(a^2+b^2=c^2\), wapi\(a\) na\(b\) kutaja miguu ya pembetatu ya kulia karibu na\(90°\) angle, na\(c\) inahusu hypotenuse. Ina matumizi yasiyopimika katika usanifu, uhandisi, sayansi, jiometri, trigonometry, na algebra, na katika maombi ya kila siku.

Tunatumia Theorem ya Pythagorean kutatua kwa urefu wa upande mmoja wa pembetatu wakati tuna urefu wa wengine wawili. Kwa sababu kila moja ya maneno ni mraba katika theorem, wakati sisi ni kutatua kwa upande wa pembetatu, tuna equation quadratic. Tunaweza kutumia mbinu za kutatua equations quadratic ambayo tulijifunza katika sehemu hii kutatua kwa upande kukosa.

Theorem ya Pythagorean inapewa kama

\[a^2+b^2=c^2\]

wapi\(a\) na\(b\) rejea miguu ya pembetatu ya kulia karibu na\(90°\) angle, na\(c\) inahusu hypotenuse, kama inavyoonekana.

Kielelezo\(\PageIndex{4}\)

Mfano\(\PageIndex{12}\): Finding the Length of the Missing Side of a Right Triangle

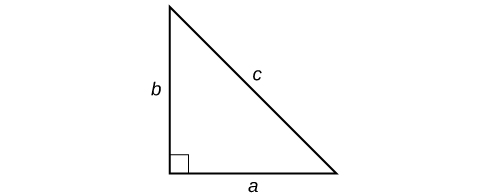
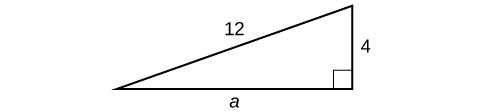
Pata urefu wa upande usiopotea wa pembetatu sahihi katika Kielelezo\(\PageIndex{5}\).

Kielelezo\(\PageIndex{5}\)

Suluhisho

Kama tuna vipimo kwa upande\(b\) na hypotenuse, upande wa kukosa ni\(a\).

\[\begin{align*} a^2+b^2&= c^2\\ a^2+{(4)}^2&= {(12)}^2\\ a^2+16&= 144\\ a^2&= 128\\ a&= \sqrt{128}\\ &= 8\sqrt{2} \end{align*}\]

Zoezi\(\PageIndex{9}\)

Tumia Theorem ya Pythagorean kutatua tatizo la pembetatu sahihi: Mguu hatua 4 vitengo, mguu b hatua 3 vitengo. Pata urefu wa hypotenuse.

Jibu

\(5\)vitengo

Media

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na usawa wa quadratic.

1. Kutatua equations Quadratic kwa factoring
2. Zero-Bidhaa Mali
3. Kukamilisha Square
4. Mfumo wa Quadratic na Suluhisho mbili za busara
5. Urefu wa mguu wa pembetatu ya kulia

Mlinganyo muhimu

formula ya quadratic

\(x=\dfrac{−b±\sqrt{b^2-4ac}}{2a}\)

Dhana muhimu

• Wengi equations quadratic inaweza kutatuliwa kwa factoring wakati equation ina mgawo wa kuongoza wa\(1\) au kama equation ni tofauti ya mraba. Mali ya sifuri hutumiwa kutafuta ufumbuzi. Angalia Mfano, Mfano, na Mfano.
• Equations nyingi za quadratic na mgawo wa kuongoza zaidi ya\(1\) inaweza kutatuliwa kwa kuzingatia kutumia njia ya kikundi. Angalia Mfano na Mfano.
• Njia nyingine ya kutatua quadratics ni mali ya mizizi ya mraba. Tofauti ni mraba. Tunajitenga muda wa mraba na kuchukua mizizi ya mraba ya pande zote mbili za equation. Suluhisho litazalisha suluhisho chanya na hasi. Angalia Mfano na Mfano.
• Kukamilisha mraba ni njia ya kutatua equations quadratic wakati equation haiwezi kuhesabiwa. Angalia Mfano.
• Njia yenye kutegemewa sana ya kutatua equations quadratic ni formula ya quadratic, kulingana na coefficients na muda wa mara kwa mara katika equation. Angalia Mfano.
• Ubaguzi hutumiwa kuonyesha asili ya mizizi ambayo equation ya quadratic itazaa: halisi au ngumu, busara au isiyo ya maana, na ni wangapi kila mmoja. Angalia Mfano.
• Theorem ya Pythagorean, kati ya theorems maarufu zaidi katika historia, hutumiwa kutatua matatizo ya pembetatu ya kulia na ina maombi katika maeneo mengi. Kutatua kwa urefu wa upande mmoja wa pembetatu sahihi inahitaji kutatua equation quadratic. Angalia Mfano.