2.5: Idadi tata

Malengo ya kujifunza

• Ongeza na uondoe namba tata.
• Panua na ugawanye namba tata.
• Tatua equations quadratic na idadi tata

Iligunduliwa na Benoit Mandelbrot karibu 1980, Mandelbrot Kuweka ni moja ya picha za fractal zinazotambulika. Picha imejengwa juu ya nadharia ya kufanana na uendeshaji wa iteration. Kuzunguka kwenye picha ya fractal huleta mshangao wengi, hasa katika kiwango cha juu cha kurudia kwa undani inayoonekana kama ongezeko la ukuzaji. Equation inayozalisha picha hii inakuwa rahisi sana.

Kielelezo$\PageIndex{1}$: Kuweka Mandelbrot inaonyesha kufanana, ambayo ni bora inavyoonekana katika uhuishaji.

Ili kuelewa vizuri, tunahitaji kuwa na ujuzi na seti mpya ya namba. Kumbuka kwamba utafiti wa hisabati unaendelea kujengwa juu ya yenyewe. Integers hasi, kwa mfano, kujaza tupu kushoto na seti ya integers chanya. Seti ya namba za busara, kwa upande wake, hujaza tupu iliyoachwa na seti ya integers. Seti ya namba halisi hujaza tupu iliyoachwa na seti ya namba za busara. Haishangazi, seti ya namba halisi ina voids pia. Katika sehemu hii, tutazingatia seti ya namba zinazojaza voids katika seti ya namba halisi na kujua jinsi ya kufanya kazi ndani yake.

Kuonyesha Mizizi ya Mraba ya Hesabu Hasi kama Mizigo ya$i$

Tunajua jinsi ya kupata mizizi ya mraba ya nambari yoyote halisi. Kwa namna hiyo, tunaweza kupata mizizi ya mraba ya idadi yoyote hasi. Tofauti ni kwamba mizizi si halisi. Ikiwa thamani katika radicand ni hasi, mizizi inasemekana kuwa nambari ya kufikiri.Nambari ya kufikiri$i$ inaelezwa kama mizizi ya mraba ya$−1$.

$$\sqrt{-1}=i$$

Hivyo, kwa kutumia mali ya radicals,

$$i^2=(\sqrt{-1})^2=-1$$

Tunaweza kuandika mizizi mraba wa idadi yoyote hasi kama nyingi ya$i$. Fikiria mizizi ya mraba ya$−49$.

$$\begin{align*} \sqrt{-49}&= \sqrt{49\times(-1)}\\[4pt] &= \sqrt{49}\sqrt{-1}\\[4pt] &= 7i \end{align*}$$

Tunatumia$7i$ na si$−7i$ kwa sababu mizizi kuu ya$49$ ni mizizi chanya.

Nambari ngumu ni jumla ya nambari halisi na nambari ya kufikiri. Nambari ngumu inaonyeshwa kwa fomu ya kawaida wakati imeandikwa$a+bi$ ambapo$a$ ni sehemu halisi na$b$ ni sehemu ya kufikiri. Kwa mfano,$5+2i$ ni idadi tata. Hivyo, pia, ni$3+4i\sqrt{3}$.

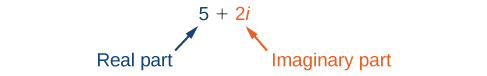
Nambari za kufikiri zinatofautiana na namba halisi kwa kuwa nambari ya kufikiri ya mraba inazalisha nambari halisi ya hasi. Kumbuka kwamba wakati nambari halisi nzuri ni mraba, matokeo ni nambari halisi halisi na wakati nambari halisi ya mraba, matokeo pia ni nambari halisi ya kweli. Nambari tata zinajumuisha namba halisi na za kufikiri.

Ufafanuzi: IMAGINARY NA COMPLEX IDADI

Nambari tata ni idadi ya fomu$a+bi$ ambapo

1. $a$ni sehemu halisi ya idadi tata.
2. $b$ni sehemu ya kufikiri ya idadi tata.

Ikiwa$b=0$, basi$a+bi$ ni namba halisi. Ikiwa$a=0$ na$b$ si sawa na$0$, nambari tata inaitwa nambari safi ya kufikiri. Nambari ya kufikiri ni hata mizizi ya namba hasi.

Jinsi ya: Kutokana na idadi ya kufikiri, kuelezea kwa fomu ya kawaida ya idadi tata

1. Andika$\sqrt{-a}$ kama$\sqrt{a}\sqrt{-1}$.
2. Express$\sqrt{-1}$ kama$i$.
3. Andika$\sqrt{a}\times i$ kwa fomu rahisi.

Mfano$\PageIndex{1}$: Expressing an Imaginary Number in Standard Form

Eleza$\sqrt{-9}$ kwa fomu ya kawaida.

Suluhisho

$$\begin{align*} \sqrt{-9}&= \sqrt{9}\sqrt{-1)}\\[4pt] &= 3i\\[4pt] \end{align*}$$

Kwa fomu ya kawaida, hii ni$0+3i$.

Zoezi$\PageIndex{1}$

Eleza$\sqrt{-24}$ kwa fomu ya kawaida.

Jibu

$\sqrt{-24}=0+2i\sqrt{6}$

Kupanga Nambari Complex juu ya Ndege Complex

Hatuwezi kupanga namba tata kwenye mstari wa namba kama tunaweza namba halisi. Hata hivyo, bado tunaweza kuwawakilisha graphically. Ili kuwakilisha namba tata, tunahitaji kushughulikia vipengele viwili vya nambari. Tunatumia ndege tata, ambayo ni mfumo wa kuratibu ambao mhimili usio na usawa unawakilisha sehemu halisi na mhimili wima inawakilisha sehemu ya kufikiri. Nambari tata ni pointi kwenye ndege, zilizoelezwa kama jozi zilizoamriwa$(a,b)$, ambapo$a$ inawakilisha kuratibu kwa mhimili usio na usawa na$b$ inawakilisha kuratibu kwa mhimili wima.

Hebu fikiria idadi$−2+3i$. Sehemu halisi ya idadi tata ni$−2$ na sehemu ya kufikiri ni$3$. Tunapanga jozi iliyoamriwa$(−2,3)$ ili kuwakilisha namba tata$−2+3i$, kama inavyoonekana kwenye Mchoro$\PageIndex{2}$.

Kielelezo$\PageIndex{2}$

NDEGE TATA

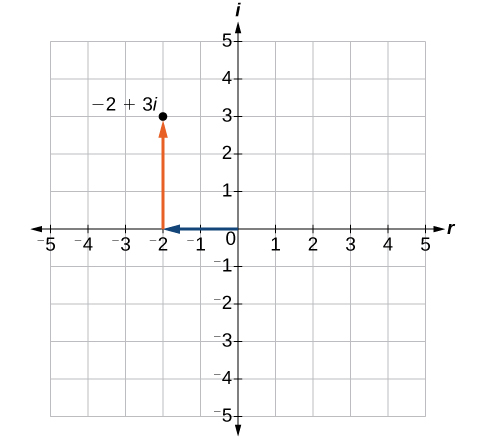
Katika ndege ngumu, mhimili usio na usawa ni mhimili halisi, na mhimili wima ni mhimili wa kufikiri, kama inavyoonekana kwenye Mchoro$\PageIndex{3}$.

Kielelezo$\PageIndex{3}$

Jinsi ya: Kutokana na idadi tata, kuwakilisha vipengele vyake kwenye ndege tata

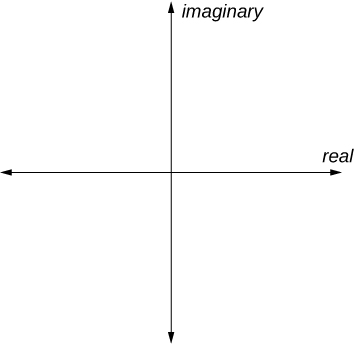
1. Kuamua sehemu halisi na sehemu ya kufikiri ya idadi tata.
2. Hoja kando ya mhimili usio na usawa ili kuonyesha sehemu halisi ya namba.
3. Hoja sambamba na mhimili wima kuonyesha sehemu imaginary ya idadi.
4. Plot uhakika.

Mfano$\PageIndex{2}$: Plotting a Complex Number on the Complex Plane

Panda idadi tata$3−4i$ kwenye ndege tata.

Suluhisho

Sehemu halisi ya idadi tata ni$3$, na sehemu ya kufikiri ni$–4$. Tunapanga jozi iliyoamriwa$(3,−4)$ kama inavyoonekana kwenye Mchoro$\PageIndex{4}$.

Kielelezo$\PageIndex{4}$

Zoezi$\PageIndex{2}$

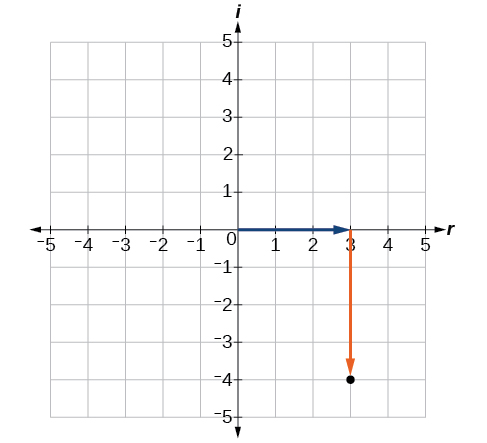
Panda idadi tata$−4−i$ kwenye ndege tata.

Jibu

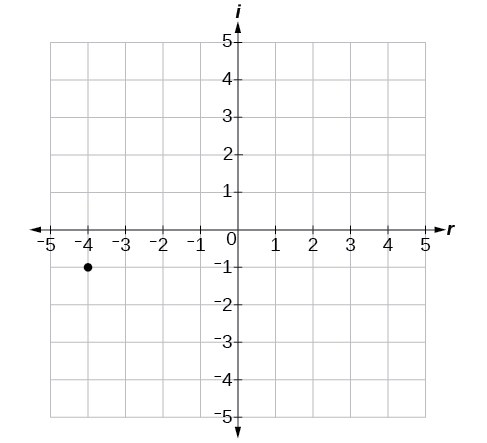
Kielelezo$\PageIndex{5}$

Kuongeza na Kutoa Hesabu Complex

Kama ilivyo na idadi halisi, tunaweza kufanya shughuli za hesabu kwenye namba tata. Ili kuongeza au kuondoa namba tata, tunachanganya sehemu halisi na kisha kuchanganya sehemu za kufikiri.

IDADI TATA: KUONGEZA NA KUONDOA

Kuongeza namba tata:

$$(a+bi)+(c+di)=(a+c)+(b+d)i$$

Kuondoa namba tata:

$$(a+bi)−(c+di)=(a−c)+(b−d)i$$

Howto: Kutokana na namba mbili ngumu, pata jumla au tofauti

1. Tambua sehemu halisi na za kufikiri za kila nambari.
2. Ongeza au uondoe sehemu halisi.
3. Ongeza au uondoe sehemu za kufikiri.

Mfano$\PageIndex{3}$: Adding and Subtracting Complex Numbers

Ongeza au uondoe kama ilivyoonyeshwa.

1. $(3−4i)+(2+5i)$
2. $(−5+7i)−(−11+2i)$

Suluhisho

1. $$\begin{align*} (3-4i)+(2+5i)&= 3-4i+2+5i\\[4pt] &= 3+2+(-4i)+5i\\[4pt] &= (3+2)+(-4+5)i\\[4pt] &= 5+i \end{align*}$$
2. $$\begin{align*} (-5+7i)-(-11+2i)&= -5+7i+11-2i\\[4pt] &= -5+11+7i-2i\\[4pt] &= (-5+11)+(7-2)i\\[4pt] &= 6+5i \end{align*}$$

Zoezi$\PageIndex{3}$

Ondoa$2+5i$ kutoka$3–4i$.

Jibu

$(3−4i)−(2+5i)=1−9i$

Kuzidisha Idadi tata

Kuzidisha idadi tata ni sawa na kuzidisha binomials. Tofauti kubwa ni kwamba tunafanya kazi na sehemu halisi na za kufikiri tofauti.

Kuzidisha Nambari Tata kwa Nambari halisi

Hebu tuanze kwa kuzidisha idadi tata kwa idadi halisi. Sisi kusambaza idadi halisi kama sisi ingekuwa na binomial. Fikiria, kwa mfano,$3(6+2i)$:

Jinsi ya: Kutokana na idadi tata na idadi halisi, kuzidisha ili kupata bidhaa

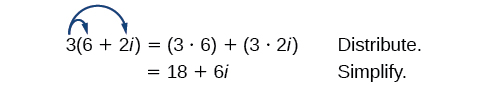
1. Tumia mali ya usambazaji.
2. Kurahisisha.

Mfano$\PageIndex{4}$: Multiplying a Complex Number by a Real Number

Pata bidhaa$4(2+5i)$.

Suluhisho

Kusambaza$4$.

$$\begin{align*} 4(2+5i)&= (4\cdot 2)+(4\cdot 5i)\\[4pt] &= 8+20i \end{align*}$$

Zoezi$\PageIndex{4}$

Pata bidhaa:$\dfrac{1}{2}(5−2i)$.

Jibu

$\dfrac{5}{2}-i$

Kuzidisha Idadi Tata Pamoja

Sasa, hebu tuzidishe namba mbili ngumu. Tunaweza kutumia ama mali ya kusambaza au zaidi hasa njia ya FOIL kwa sababu tunashughulika na binomials. Kumbuka kwamba FOIL ni kifupi cha kuzidisha maneno ya Kwanza, ya ndani, ya nje, na ya mwisho pamoja. Tofauti na idadi tata ni kwamba wakati sisi kupata muda squared,$i^2$, ni sawa$-1$.

$$\begin{align*} (a+bi)(c+di)&= ac+adi+bci+bdi^2\\[4pt] &= ac+adi+bci-bd(-1)\qquad i^2 = -1\\[4pt] &= ac+adi+bci-bd\\[4pt] &= (ac-bd)+(ad+bc)i \end{align*}$$

Masharti halisi ya kikundi na maneno ya kufikiri.

Jinsi ya: Kutokana na namba mbili ngumu, kuzidisha ili kupata bidhaa

1. Tumia mali ya usambazaji au njia ya FOIL.
2. Kumbuka hilo$i^2=-1$.
3. Kundi pamoja maneno halisi na masharti imaginary

Mfano$\PageIndex{5}$: Multiplying a Complex Number by a Complex Number

Kuzidisha$(4+3i)(2−5i)$.

Suluhisho

$$\begin{align*} (4+3i)(2-5i)&= 4(2)-4(5i)+3i(2)-(3i)(5i)\\[4pt] &= 8-20i+6i-15(i^2)\\[4pt] &= (8+15)+(-20+6)i\\[4pt] &= 23-14i \end{align*}$$

Zoezi$\PageIndex{5}$

Kuzidisha:$(3−4i)(2+3i)$.

Jibu

$18+i$

Kugawanya idadi Complex

Kugawanya namba mbili ngumu ni ngumu zaidi kuliko kuongeza, kutoa, au kuzidisha kwa sababu hatuwezi kugawanya na idadi imaginary, maana kwamba sehemu yoyote lazima iwe na denominator halisi ya nambari kuandika jibu kwa fomu ya kawaida$a+bi$. Tunahitaji kupata muda ambao tunaweza kuzidisha nambari na denominator ambayo itaondoa sehemu ya kufikiri ya denominator ili tuweze kuishia na idadi halisi kama denominator. Neno hili linaitwa conjugate tata ya denominator, ambayo hupatikana kwa kubadilisha ishara ya sehemu ya kufikiri ya idadi tata. Kwa maneno mengine, conjugate tata ya$a+bi$ ni$a−bi$. Kwa mfano, bidhaa ya$a+bi$ na$a−bi$ ni

$$\begin{align*} (a+bi)(a-bi)&= a^2-abi+abi-b^2i^2\\[4pt] &= a^2+b^2 \end{align*}$$

Matokeo ni idadi halisi.

Kumbuka kuwa conjugates tata zina uhusiano tofauti: Mchanganyiko mgumu wa$a+bi$ ni$a−bi$, na mchanganyiko tata wa$a−bi$ ni$a+bi$. Zaidi ya hayo, wakati equation quadratic na coefficients halisi ina ufumbuzi tata, ufumbuzi daima ni conjugates tata ya mtu mwingine.

Tuseme tunataka kugawanya$c+di$ na$a+bi$, ambapo wala$a$ wala$b$ sawa sifuri. Sisi kwanza kuandika mgawanyiko kama sehemu, kisha kupata conjugate tata ya denominator, na kuzidisha.

$\dfrac{c+di}{a+bi}$wapi$a≠0$ na$b≠0$

Panua namba na denominator kwa conjugate tata ya denominator.

$$\begin{align*} \dfrac{(c+di)}{(a+bi)}\cdot \dfrac{(a-bi)}{(a-bi)}&= \dfrac{(c+di)(a-bi)}{(a+bi)(a-bi)}\\[4pt] &= \dfrac{ca-cbi+adi-bdi^2}{a^2-abi+abi-b^2i^2} \qquad \text{Apply the distributive property}\\[4pt] &= \dfrac{ca-cbi+adi-bd(-1)}{a^2-abi+abi-b^2(-1)} \qquad \text{Simplify, remembering that } i^2=-1\\[4pt] &= \dfrac{(ca+bd)+(ad-cb)i}{a^2+b^2} \end{align*}$$

Ufafanuzi: CONJUGATE COMPLEX

Mchanganyiko mgumu wa idadi tata$a+bi$ ni$a−bi$. Inapatikana kwa kubadilisha ishara ya sehemu ya kufikiri ya idadi tata. Sehemu halisi ya nambari imesalia bila kubadilika.

1. Wakati nambari tata imeongezeka kwa mchanganyiko wake mgumu, matokeo ni namba halisi.
2. Wakati nambari tata imeongezwa kwenye mchanganyiko wake mgumu, matokeo ni namba halisi.

Mfano$\PageIndex{6}$: Finding Complex Conjugates

Pata mchanganyiko tata wa kila nambari.

1. $2+i\sqrt{5}$
2. $-\dfrac{1}{2}i$

Suluhisho

1. Nambari tayari iko katika fomu$a+bi$. Mchanganyiko mgumu ni$a−bi$, au$2−i\sqrt{5}$.
2. Tunaweza kuandika upya idadi hii katika fomu$a+bi$ kama$0−\dfrac{1}{2}i$. Mchanganyiko mgumu ni$a−bi$, au$0+\dfrac{1}{2}i$. Hii inaweza kuandikwa tu kama$\dfrac{1}{2}i$.

Uchambuzi

Ingawa tumeona kwamba tunaweza kupata conjugate tata ya idadi ya kufikiri, katika mazoezi sisi kwa ujumla kupata conjugates tata ya idadi tata tu na sehemu halisi na imaginary. Ili kupata namba halisi kutoka kwa nambari ya kufikiri, tunaweza tu kuzidisha na$i$.

Zoezi$\PageIndex{6}$

Kupata conjugate tata ya$−3+4i$.

Jibu

$−3−4i$

Jinsi ya: Kutokana na namba mbili ngumu, ugawanye moja kwa moja

1. Andika tatizo la mgawanyiko kama sehemu.
2. Kuamua conjugate tata ya denominator.
3. Kuzidisha nambari na denominator ya sehemu na conjugate tata ya denominator.
4. Kurahisisha.

Mfano$\PageIndex{7}$: Dividing Complex Numbers

Gawanya$(2+5i)$ na$(4−i)$.

Suluhisho

Tunaanza kwa kuandika tatizo kama sehemu.

$$\dfrac{(2+5i)}{(4−i)} \nonumber$$

Kisha sisi huzidisha nambari na denominator kwa conjugate tata ya denominator.

$$\dfrac{(2+5i)}{(4−i)}⋅\dfrac{(4+i)}{(4+i)} \nonumber$$

Ili kuzidisha namba mbili ngumu, tunapanua bidhaa kama tunavyopenda na polynomials (kwa kutumia FOIL).

$$\begin{align*} \dfrac{(2+5i)}{(4-i)}\cdot \dfrac{(4+i)}{(4+i)}&= \dfrac{8+2i+20i+5i^2}{16+4i-4i-i^2}\\[4pt] &= \dfrac{8+2i+20i+5(-1)}{16+4i-4i-(-1)}\; i^2=-1 \\[4pt] &= \dfrac{3+22i}{17}\\[4pt] &= \dfrac{3}{17}+\dfrac{22}{17i} \end{align*}$$

Toa sehemu halisi na za kufikiri.

Kumbuka kwamba hii inaonyesha quotient katika fomu ya kawaida.

Kurahisisha Mamlaka ya$i$

Nguvu za$i$ ni za mzunguko. Hebu tuangalie kile kinachotokea tunapoinua$i$ kwa nguvu zinazoongezeka.

$$i^1=i \nonumber$$ $$i^2=-1 \nonumber$$ $$i^3=i^2⋅i=-1⋅i=-i \nonumber$$ $$i^4=i^3⋅i=-i⋅i=-i^2=-(-1)=1 \nonumber$$ $$i^5=i^4⋅i=1⋅i=i \nonumber$$

Tunaweza kuona kwamba tunapofika nguvu ya tano ya i, ni sawa na nguvu ya kwanza. Tunapoendelea kuongezeka$i$ kwa nguvu zinazoongezeka, tutaona mzunguko wa nne. Hebu kuchunguza ijayo nguvu nne za$i$.

$$i^6=i^5⋅i=i⋅i=i^2=-1 \nonumber$$ $$i^7=i^6⋅i=i^2⋅i=i^3=-i \nonumber$$ $$i^8=i^7⋅i=i^3⋅i=i^4=1 \nonumber$$ $$i^9=i^8⋅i=i^4⋅i=i^5=i \nonumber$$

Mzunguko unarudiwa kwa kuendelea:$i,−1,−i,1,$ kila nguvu nne.

Mfano$\PageIndex{8}$: Simplifying Powers of $i$

Tathmini:$i^{35}$.

Suluhisho

Tangu$i^4=1$, tunaweza kurahisisha tatizo kwa kuzingatia mambo mengi ya$i^4$ iwezekanavyo. Kwa kufanya hivyo, kwanza onyesha mara ngapi$4$ huingia$35: 35=4⋅8+3$.

$$i^{35}=i^{4⋅8+3}=i^{4⋅8}⋅i^3={(i^4)}^8⋅i^3=i^8⋅i^3=i^3=−i \nonumber$$

Zoezi$\PageIndex{7}$

Tathmini:$i^{18}$

Jibu

$−1$

Q & A

Je, tunaweza kuandika$i^{35}$ kwa njia nyingine muhimu?

Kama tulivyoona katika Mfano$\PageIndex{8}$, sisi kupunguzwa$i^{35}$ kwa$i^3$ kwa kugawa exponent na$4$ na kutumia salio kupata fomu kilichorahisishwa. Lakini labda mwingine factorization ya$i^{35}$ inaweza kuwa na manufaa zaidi. Jedwali$\PageIndex{1}$ linaonyesha baadhi factorizations nyingine iwezekanavyo.

Jedwali$\PageIndex{1}$

Factorization ya$i^{35}$	$i^{34}⋅i$	$i^{33}⋅i^2$	$i^{31}⋅i^4$	$i^{19}⋅i^{16}$
Fomu iliyopunguzwa	${(i^2)}^{17}⋅i$	$i^{33}⋅(−1)$	$i^{31}⋅1$	$i^{19}⋅{(i^4)}^4$
Fomu rahisi	${(−1)}^{17}⋅i$	$−i^{33}$	$i^{31}$	$i^{19}$

Kila moja ya haya hatimaye itasababisha jibu tulilopata hapo juu lakini inaweza kuhitaji hatua kadhaa zaidi kuliko njia yetu ya awali.

vyombo vya habari

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na namba ngumu.

1. Kuongeza na Kutoa Hesabu Complex
2. Kuzidisha idadi tata
3. Kuzidisha conjugates Complex
4. Kuinua kwa Mamlaka

Dhana muhimu

• Mizizi ya mraba ya idadi yoyote hasi inaweza kuandikwa kama nyingi ya \(i\). Angalia Mfano.
• Ili kupanga namba tata, tunatumia mistari miwili ya namba, tulivuka ili kuunda ndege tata. Mhimili usio na usawa ni mhimili halisi, na mhimili wima ni mhimili wa kufikiri. Angalia Mfano.
• Nambari tata zinaweza kuongezwa na kuondolewa kwa kuchanganya sehemu halisi na kuchanganya sehemu za kufikiri. Angalia Mfano.
• Nambari tata zinaweza kuongezeka na kugawanywa.
  • Ili kuzidisha idadi tata, usambaze kama vile kwa polynomials. Angalia Mfano na Mfano.
  • Ili kugawanya namba tata, kuzidisha namba zote mbili na denominator kwa conjugate tata ya denominator ili kuondoa idadi tata kutoka kwa denominator. Angalia Mfano na Mfano.
• Nguvu zake ni za mzunguko, kurudia kila nne. Angalia Mfano.