2.4: Mifano na Matumizi
- Page ID
- 180776
- Weka equation linear kutatua maombi halisi ya dunia.
- Tumia formula ili kutatua programu halisi ya ulimwengu.
Josh ni matumaini ya kupata\(A\) katika darasa lake algebra chuo. Ana alama ya\(75\),,\(82\),\(95\)\(91\), na\(94\) juu ya vipimo vyake vya kwanza vya tano. Mtihani wa mwisho tu unabaki, na kiwango cha juu cha pointi ambazo zinaweza kupatikana ni\(100\). Je, inawezekana kwa Josh kumaliza kozi na\(A\)? Equation rahisi ya mstari itatoa Josh jibu lake.

Maombi mengi ya ulimwengu halisi yanaweza kutokana na equations linear. Kwa mfano, mfuko wa simu ya mkononi unaweza kujumuisha ada ya huduma ya kila mwezi pamoja na malipo kwa dakika ya muda wa majadiliano; inagharimu mtengenezaji wa widget kiasi fulani cha kuzalisha x vilivyoandikwa kwa mwezi pamoja na mashtaka ya kila mwezi ya uendeshaji; kampuni ya kukodisha gari inadai ada ya kila siku pamoja na kiasi kwa kila maili inayotokana. Hizi ni mifano ya maombi tunayopata kila siku ambayo inatokana na equations linear. Katika sehemu hii, tutaanzisha na kutumia equations linear kutatua matatizo kama hayo.
Kuanzisha Equation ya Linear ili Kutatua Maombi halisi ya Ulimwenguni
Kuanzisha au mfano equation linear kifafa maombi halisi ya dunia, ni lazima kwanza kuamua kiasi inayojulikana na kufafanua kiasi haijulikani kama variable. Kisha, tunaanza kutafsiri maneno kama maneno ya hisabati kwa kutumia alama za hisabati. Tutumie mfano wa kukodisha gari hapo juu. Katika kesi hiyo, gharama inayojulikana, kama vile\($0.10/mi\), imeongezeka kwa kiasi kisichojulikana, idadi ya maili inayotokana. Kwa hiyo, tunaweza kuandika\(0.10x\). Maneno haya yanawakilisha gharama ya kutofautiana kwa sababu inabadilika kulingana na idadi ya maili inayotokana.
Kama wingi ni huru ya variable, sisi kawaida tu kuongeza au Ondoa ni, kulingana na tatizo. Kama kiasi hiki hazibadilika, tunawaita gharama za kudumu. Fikiria shirika la kukodisha gari ambalo lina gharama\($0.10/mi\) pamoja na ada ya kila siku ya\($50\). Tunaweza kutumia kiasi hiki kutengeneza equation ambayo inaweza kutumika kupata gharama ya kukodisha gari kila siku\(C\).
\(C=0.10x+50 \tag{2.4.1}\)
Wakati wa kushughulika na maombi halisi ya ulimwengu, kuna maneno fulani ambayo tunaweza kutafsiri moja kwa moja kwenye hesabu. Jedwali\(\PageIndex{1}\) linaorodhesha maneno ya kawaida ya matusi na maneno yao sawa ya hisabati.
| Maneno | Tafsiri ya Math Operesheni |
|---|---|
| Nambari moja unazidi mwingine kwa | \(x,x+a\) |
| Mara mbili kwa idadi | \(2x\) |
| Nambari moja ni\(a\) zaidi ya namba nyingine | \(x,x+a\) |
| Nambari moja ni chini ya mara mbili namba nyingine | \(x,2x−a\) |
| Bidhaa ya idadi na\(a\), ilipungua kwa\(b\) | \(ax−b\) |
| Quotient ya idadi na idadi pamoja\(a\) ni mara tatu idadi | \(\dfrac{x}{x+a}=3x\) |
| bidhaa ya mara tatu idadi na idadi ilipungua kwa\(b\) ni\(c\) | \(3x(x−b)=c\) |
- Tambua kiasi kinachojulikana.
- Weka variable kuwakilisha kiasi haijulikani.
- Ikiwa kuna kiasi zaidi ya moja haijulikani, tafuta njia ya kuandika pili haijulikani kwa suala la kwanza.
- Andika equation kutafsiri maneno kama shughuli za hisabati.
- Kutatua equation. Hakikisha ufumbuzi unaweza kuelezewa kwa maneno, ikiwa ni pamoja na vitengo vya kipimo.
Kupata equation linear kutatua kwa yafuatayo kiasi haijulikani: Nambari moja unazidi idadi nyingine\( 17\) na na jumla yao ni\( 31\). Kupata namba mbili.
Suluhisho
Hebu\( x\) sawa namba ya kwanza. Kisha, kama namba ya pili unazidi kwanza na\(17\), tunaweza kuandika namba ya pili kama\( x +17\). Jumla ya namba mbili ni\(31\). Sisi kawaida kutafsiri neno ni kama ishara sawa.
\[\begin{align*} x+(x+17)&= 31\\ 2x+17&= 31\\ 2x&= 14\\ x&= 7 \end{align*}\]
\[\begin{align*} x+17&= 7 + 17\\ &= 24\\ \end{align*}\]
Nambari mbili ni\(7\) na\(24\).
Kupata equation linear kutatua kwa yafuatayo kiasi haijulikani: Nambari moja ni tatu zaidi ya mara mbili idadi nyingine. Kama jumla ya namba mbili ni\(36\), kupata idadi.
- Jibu
-
\(11\)na\(25\)
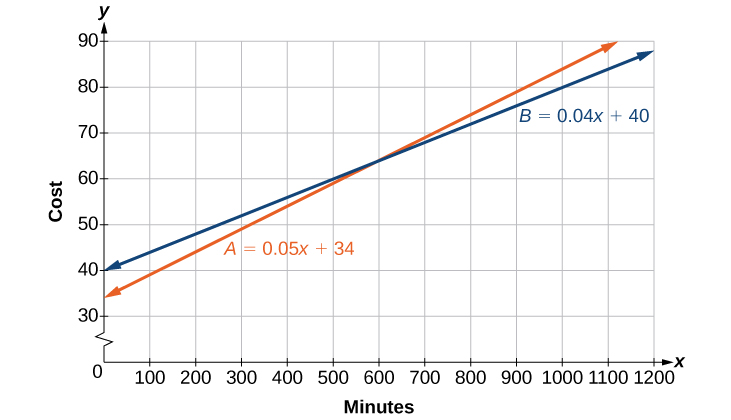
Kuna makampuni mawili ya simu ya mkononi ambayo hutoa paket tofauti. Kampuni A inadai ada ya huduma ya kila mwezi ya\($34\) pamoja na\($.05/min\) wakati wa majadiliano. Kampuni B inadai ada ya huduma ya kila mwezi ya\($40\) pamoja na\($.04/min\) wakati wa majadiliano.
- Andika equation linear kwamba mifano ya paket inayotolewa na makampuni yote mawili.
- Kama wastani wa idadi ya dakika kutumika kila mwezi ni\(1,160\), ambayo kampuni inatoa mpango bora?
- Kama wastani wa idadi ya dakika kutumika kila mwezi ni\(420\), ambayo kampuni inatoa mpango bora?
- Ni dakika ngapi za muda wa kuzungumza zingeweza kutoa taarifa sawa za kila mwezi kutoka kwa makampuni yote mawili?
Suluhisho
a.
Mfano wa Kampuni A unaweza kuandikwa kama\( A =0.05x+34\). Hii ni pamoja na gharama variable ya\( 0.05x\) pamoja malipo ya kila mwezi huduma ya\($34\). Kampuni B ya mfuko mashtaka ya juu ya ada ya kila mwezi ya\($40\), lakini gharama ya chini variable ya\( 0.04x\). Mfano wa Kampuni B inaweza kuandikwa kama\( B =0.04x+$40\).
b.
Kama wastani wa idadi ya dakika kutumika kila mwezi ni\(1,160\), tuna zifuatazo:
\[\begin{align*} \text{Company A}&= 0.05(1.160)+34\\ &= 58+34\\ &= 92 \end{align*}\]
\[\begin{align*} \text{Company B}&= 0.04(1,1600)+40\\ &= 46.4+40\\ &= 86.4 \end{align*}\]
Hivyo, Kampuni B inatoa gharama ya chini ya\($86.40\) kila mwezi ikilinganishwa na gharama ya\($92\) kila mwezi inayotolewa na Kampuni A wakati wastani wa idadi ya dakika kutumika kila mwezi ni\(1,160\).
c.
Kama wastani wa idadi ya dakika kutumika kila mwezi ni\(420\), tuna zifuatazo:
\[\begin{align*} \text{Company A}&= 0.05(420)+34\\ &= 21+34\\ &= 55 \end{align*}\]
\[\begin{align*} \text{Company B}&= 0.04(420)+40\\ &= 16.8+40\\ &= 56.8 \end{align*}\]
Kama wastani wa idadi ya dakika kutumika kila mwezi ni\(420\), basi Kampuni A inatoa gharama ya chini ya kila mwezi ya\($55\) ikilinganishwa na Kampuni B ya gharama ya kila mwezi ya\($56.80\).
d.
Ili kujibu swali la jinsi wengi majadiliano wakati dakika bila mavuno muswada huo kutoka makampuni yote, tunapaswa kufikiri juu ya tatizo katika suala la\((x,y)\) kuratibu: Katika hatua gani ni wote\(x\) -thamani na\(y\) -value sawa? Tunaweza kupata hatua hii kwa kuweka equations sawa na kila mmoja na kutatua kwa\(x\).
\[\begin{align*} 0.05x+34&= 0.04x+40\\ 0.01x&= 6\\ x&= 600 \end{align*}\]Angalia\(x\) -thamani katika kila equation.
\(0.05(600)+34=64\)
\(0.04(600)+40=64\)
Kwa hiyo, wastani wa kila\(600\) mwezi wa dakika ya kuzungumza hufanya mipango sawa. Angalia Kielelezo\(\PageIndex{2}\).
Pata usawa wa mstari ili kuiga programu hii halisi ya ulimwengu: Inapunguza kampuni ya umeme ya ABC\($2.50\) kwa kila kitengo ili kuzalisha sehemu inayotumiwa katika brand maarufu ya kompyuta za kompyuta. Kampuni ina gharama za kila mwezi za uendeshaji wa\($350\) huduma na\($3,300\) kwa mishahara. Gharama za kila mwezi za kampuni ni nini?
- Jibu
-
\(C=2.5x+3,650\)
Kutumia Mfumo wa Kutatua Maombi halisi ya Dunia
Maombi mengi yanatatuliwa kwa kutumia fomu zinazojulikana. Tatizo linasemwa, formula ni kutambuliwa, kiasi kinachojulikana kinabadilishwa katika formula, equation hutatuliwa kwa haijulikani, na swali la tatizo linajibu. Kwa kawaida, matatizo haya yanahusisha equations mbili zinazowakilisha safari mbili, uwekezaji wawili, maeneo mawili, na kadhalika. Mifano ya formula ni pamoja na eneo la mkoa wa mstatili,
\[A=LW \tag{2.4.2}\]
mzunguko wa mstatili,
\[P=2L+2W \tag{2.4.3}\]
na kiasi cha imara ya mstatili,
\[V=LWH. \tag{2.4.4}\]
Wakati kuna haijulikani mbili, tunapata njia ya kuandika moja kwa upande wa nyingine kwa sababu tunaweza kutatua kwa kutofautiana moja tu kwa wakati mmoja.
Inachukua Andrew\(30\; min\) kuendesha gari ili kufanya kazi asubuhi. Yeye anatoa nyumbani kwa kutumia njia hiyo, lakini inachukua\(10\; min\) muda mrefu, na yeye wastani\(10\; mi/h\) chini ya asubuhi. Je, Andrew anaendesha gari kwa kazi?
Suluhisho
Hili ni tatizo umbali, ili tuweze kutumia formula\(d =rt\), ambapo umbali sawa na kiwango cha kuzidisha kwa wakati. Kumbuka kwamba wakati kiwango kinapotolewa\(mi/h\), wakati lazima uelezwe kwa masaa. Vitengo vyema vya kipimo ni muhimu kwa kupata suluhisho sahihi.
Kwanza, tunatambua kiasi kinachojulikana na haijulikani. Andrew asubuhi gari kwa kazi inachukua\(30\; min\), au\(12\; h\) kwa kiwango cha\(r\). Gari lake nyumbani inachukua\(40\; min\)\(23\; h\), au, na kasi yake wastani\(10\; mi/h\) chini ya gari asubuhi. Safari zote mbili hufunika umbali\(d\). Jedwali, kama vile Jedwali\(\PageIndex{2}\), mara nyingi husaidia kwa kuweka wimbo wa habari katika aina hizi za matatizo.
| \(d\) | \(r\) | \(t\) | |
|---|---|---|---|
| Kufanya Kazi | \ (d\)” style="text-align:katikati;” class="lt-math-1632">\(d\) | \ (r\)” style="text-align:center;” class="lt-math-1632">\(r\) | \ (t\)” style="text-align:center;” class="lt-math-1632">\(12\) |
| Kwa Nyumbani | \ (d\)” style="text-align:katikati;” class="lt-math-1632">\(d\) | \ (r\)” style="text-align:center;” class="lt-math-1632">\(r−10\) | \ (t\)” style="text-align:center;” class="lt-math-1632">\(23\) |
Andika equations mbili, moja kwa kila safari.
\[d=r\left(\dfrac{1}{2}\right) \qquad \text{To work} \nonumber\]
\[d=(r-10)\left(\dfrac{2}{3}\right) \qquad \text{To home} \nonumber\]
Kama equations zote mbili sawa umbali huo, tunawaweka sawa na kila mmoja na kutatua\(r\).
\[\begin{align*} r\left (\dfrac{1}{2} \right )&= (r-10)\left (\dfrac{2}{3} \right )\\ \dfrac{1}{2r}&= \dfrac{2}{3}r-\dfrac{20}{3}\\ \dfrac{1}{2}r-\dfrac{2}{3}r&= -\dfrac{20}{3}\\ -\dfrac{1}{6}r&= -\dfrac{20}{3}\\ r&= -\dfrac{20}{3}(-6)\\ r&= 40 \end{align*}\]
Sisi kutatuliwa kwa kiwango cha kasi ya kufanya kazi,\(40\; mph\). Kubadilisha\(40\) katika kiwango cha juu ya safari ya kurudi mavuno\(30 mi/h\). Sasa tunaweza kujibu swali. Badala ya kiwango cha nyuma katika equation ama na kutatua kwa\(d\).
\[\begin{align*}d&= 40\left (\dfrac{1}{2} \right )\\ &= 20 \end{align*}\]
Umbali kati ya nyumba na kazi ni\(20\; mi\).
Uchambuzi
Kumbuka kwamba tunaweza kuwa akalipa FRACTIONS katika equation kwa kuzidisha pande zote mbili za equation na LCD kutatua kwa\(r\).
\[\begin{align*} r\left (\dfrac{1}{2} \right)&= (r-10)\left (\dfrac{2}{3} \right )\\ 6\times r\left (\dfrac{1}{2} \right)&= 6\times (r-10)\left (\dfrac{2}{3} \right )\\ 3r&= 4(r-10)\\ 3r&= 4r-40\\ r&= 40 \end{align*}\]
Jumamosi asubuhi, ilichukua Jennifer\(3.6\; h\) kuendesha gari nyumbani kwa mama yake mwishoni mwa wiki. Jumapili jioni, kutokana na trafiki nzito, ilichukua Jennifer\(4\; h\) kurudi nyumbani. Kasi yake ilikuwa\(5\; mi/h\) polepole Jumapili kuliko Jumamosi. Je, kasi yake ilikuwa siku ya Jumapili?
- Jibu
-
\(45\; mi/h\)
Mzunguko wa patio ya nje ya mstatili ni\(54\; ft\). Urefu ni\(3\; ft\) mkubwa kuliko upana. Je! Ni vipimo gani vya patio?
Suluhisho
Fomu ya mzunguko ni ya kawaida:\(P=2L+2W\). Tuna kiasi mbili haijulikani, urefu na upana. Hata hivyo, tunaweza kuandika urefu katika suala la upana kama\(L =W+3\). Weka thamani ya mzunguko na kujieleza kwa urefu ndani ya formula. Ni mara nyingi kusaidia kufanya mchoro na studio pande kama katika Kielelezo\(\PageIndex{3}\).
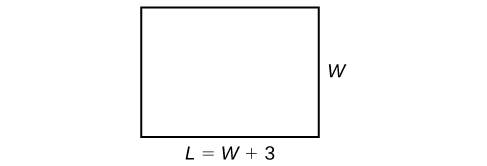
Sasa tunaweza kutatua kwa upana na kisha tuhesabu urefu.
\[\begin{align*} P&= 2L + 2W\\ 54&= 2(W+3)+2W\\ 54&= 2W+6+2W\\ 54&= 4W+6\\ 48&= 4W\\ W&= 12 \end{align*}\]
\[\begin{align*} L&= 12+3\\ L&= 15 \end{align*}\]
Vipimo ni\(L = 15\; ft\) na\(W = 12\; ft\).
Pata vipimo vya mstatili kutokana na kwamba mzunguko ni\(110\; cm\) na urefu ni\(1\; cm\) zaidi ya mara mbili upana.
- Jibu
-
\(L=37\; cm\),\(W=18\; cm\)
Mzunguko wa kibao cha karatasi ya grafu ni\(48\space{in.}^2\). Urefu\(6\; in\) ni. zaidi ya upana. Pata eneo la karatasi ya grafu.
Suluhisho
Fomu ya kawaida ya eneo ni\(A =LW\); hata hivyo, tutasuluhisha tatizo kwa kutumia formula ya mzunguko. Sababu tunayotumia formula ya mzunguko ni kwa sababu tunajua habari za kutosha kuhusu mzunguko ambao formula itatuwezesha kutatua kwa moja ya haijulikani. Kama mzunguko na eneo hutumia urefu na upana kama vipimo, mara nyingi hutumiwa pamoja ili kutatua tatizo kama hili.
Tunajua kwamba urefu\(6\; in\) ni. zaidi ya upana, ili tuweze kuandika urefu kama\(L =W+6\). Weka thamani ya mzunguko na kujieleza kwa urefu ndani ya formula ya mzunguko na kupata urefu.
\[\begin{align*} P&= 2L + 2W\\ 48&= 2(W+6)+2W\\ 48&= 2W+12+2W\\ 48&= 4W+12\\ 36&= 4W\\ W&= 9 \end{align*}\]
\[\begin{align*}L&= 9+6\\ L&= 15 \end{align*}\]
Sasa, tunapata eneo lililopewa vipimo vya\(L = 15\; in\). na\(W = 9\; in\).
\[\begin{align*} A&= LW\\ A&=15(9)\\ A&= 135\space{in.}^2 \end{align*}\]
Eneo hilo ni\(135\space{in.}^2\).
mchezo chumba ina mzunguko wa\(70\; ft\). Urefu ni tano zaidi ya mara mbili upana. Ni\(ft^2\) ngapi ya carpeting mpya inapaswa kuamuru?
- Jibu
-
\(250\space{ft}^2\)
Kupata vipimo ya sanduku meli kutokana na kwamba urefu ni mara mbili upana, urefu ni\(8\; \) katika, na kiasi ni\(1,600\space{in.}^3\).
Suluhisho
Fomu ya kiasi cha sanduku hutolewa kama\(V =LWH\), bidhaa ya urefu, upana, na urefu. Sisi ni kutokana na kwamba\(L =2W\), na\(H =8\). Kiasi ni\(1,600\; \text{cubic inches}\).
\[\begin{align*} V&= LWH\\ 1600&= (2W)W(8)\\ 1600&= 16W^2\\ 100&= W^2\\ 10&= W \end{align*}\]Vipimo ni\(L = 20\; in\),\(W= 10\; in\), na\(H = 8\; in\).
Uchambuzi
Kumbuka kuwa mizizi mraba ya\(W^2\) ingekuwa kusababisha thamani chanya na hasi. Hata hivyo, kwa sababu tunaelezea upana, tunaweza kutumia tu matokeo mazuri.
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na mifano na matumizi ya usawa wa mstari.
- Kutatua tatizo kwa kutumia equations linear
- Tatizo kutatua kwa kutumia equations
- Kupata vipimo vya eneo lililopewa mzunguko
- Find umbali kati ya miji kwa kutumia umbali = kiwango * wakati formula
- Maombi ya usawa wa mstari (Andika equation ya gharama)
Dhana muhimu
- equation linear inaweza kutumika kutatua kwa haijulikani katika tatizo idadi. Angalia Mfano.
- Maombi yanaweza kuandikwa kama matatizo ya hisabati kwa kutambua kiasi kinachojulikana na kumshirikisha variable kwa kiasi kisichojulikana. Angalia Mfano.
- Kuna aina nyingi zinazojulikana ambazo zinaweza kutumika kutatua programu. Matatizo ya umbali, kwa mfano, yanatatuliwa kwa kutumia\(d = rt\) formula. Angalia Mfano.
- Matatizo mengi ya jiometri yanatatuliwa kwa kutumia formula ya mzunguko\(P =2L+2W\), formula ya eneo\(A =LW\), au formula ya kiasi\(V =LWH\). Angalia Mfano, Mfano, na Mfano.


