12.R: Utangulizi wa Calculus (Tathmini)

Last updated
Save as PDF

Page ID: 181338

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

12.1: Kupata Mipaka - Njia za Nambari na za kielelezo

Kwa mazoezi 1-6, tumia Kielelezo hapa chini.

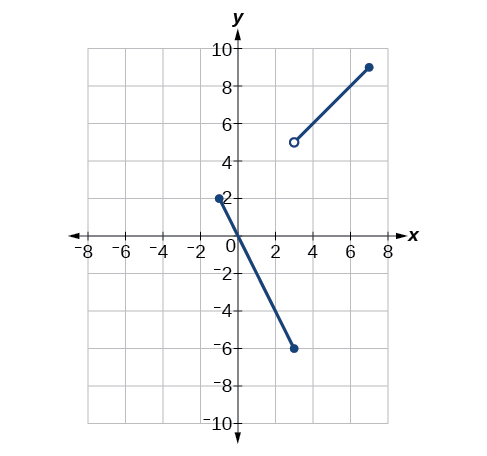
$R 12.1.1.png$

1)$\lim \limits_{x \to -1^+}f(x)$

Jibu: $2$

2)$\lim \limits_{x \to -1^-}f(x)$

3)$\lim \limits_{x \to -1}f(x)$

Jibu: haipo

4)$\lim \limits_{x \to 3}f(x)$

5) Ni maadili gani ya$x$ kazi ya kuacha? Ni hali gani ya kuendelea inavunjwa?

Jibu: Discontinuous katika$x=-1\left (\lim \limits_{x \to a}f(x) \text{ does not exist} \right )$$x=3\left (\text{ jump discontinuity} \right )$,, na$x=7\left (\lim \limits_{x \to a}f(x) \text{ does not exist} \right )$.

6) Kutumia Jedwali hapa chini, makadirio$\lim \limits_{x \to 0}f(x)$.

$x$	$F(x)$
\ (x\) "> -0.1	\ (F (x)\) "> 2.875
\ (x\) ">-0.01	\ (F (x)\) "> 2.92
\ (x\) "> -0.001	\ (F (x)\) "> 2.998
\ (x\) "> 0	\ (F (x)\) "> Haijafafanuliwa
\ (x\) ">0.001	\ (F (x)\) "> 2.9987
\ (x\) ">0.01	\ (F (x)\) "> 2.865
\ (x\) "> 0.1	\ (F (x)\) "> 2.78145
\ (x\) ">0.15	\ (F (x)\) "> 2.678

Jibu: $3$

Kwa mazoezi 7-9, pamoja na matumizi ya matumizi ya graphing, tumia ushahidi wa namba au wa kielelezo ili kuamua mipaka ya kushoto na ya kulia ya kazi iliyotolewa kama$x$ mbinu$a$. Kama kazi ina kikomo kama$x$ mbinu$a$, hali yake. Ikiwa sio, jadili kwa nini hakuna kikomo.

7)$f(x)=\begin{cases} \left | x \right |-1 & \text{ if } x\neq 1 \\ x^3 & \text{ if } x= 1 \end{cases} a=1$

8)$f(x)=\begin{cases} \dfrac{1}{x+1} & \text{ if } x= -2 \\ (x+1)^2 & \text{ if } x\neq -2 \end{cases} a=-2$

Jibu: $\lim \limits_{x \to -2}f(x)=1$

9)$f(x)=\begin{cases} \sqrt{x+3} & \text{ if } x<1 \\ -\sqrt[3]{x} & \text{ if } x>1 \end{cases} a=1$

12.2: Kupata Mipaka - Mali ya Mipaka

Kwa mazoezi 1-6, pata mipaka ikiwa$\lim \limits_{x \to c} f(x)=-3$ na$\lim \limits_{x \to c} g(x)=5$.

1)$\lim \limits_{x \to c} (f(x)+g(x))$

Jibu: $2$

2)$\lim \limits_{x \to c} \dfrac{f(x)}{g(x)}$

3)$\underset{x \to c}{\lim } (f(x)\cdot g(x))$

Jibu: $-15$

4)$\lim \limits_{x \to 0^+} f(x), f(x)=\begin{cases} 3x^2+2x+1 & x>0 \\ 5x+3 & x<0 \end{cases}$

5)$\lim \limits_{x \to 0^-} f(x), f(x)=\begin{cases} 3x^2+2x+1 & x>0 \\ 5x+3 & x<0 \end{cases}$

Jibu: $3$

6)$\lim \limits_{x \to 3^+} (3x-〚x〛)$

Kwa mazoezi 7-11, tathmini mipaka kwa kutumia mbinu za algebraic.

7)$\lim \limits_{h \to 0} \left ( \dfrac{(h+6)^2-36}{h} \right )$

Jibu: $12$

8)$\lim \limits_{x \to 25} \left ( \dfrac{x^2-625}{\sqrt{x}-5} \right )$

9)$\lim \limits_{x \to 1} \left ( \dfrac{-x^2-9x}{x} \right )$

Jibu: $-10$

10)$\lim \limits_{x \to 4} \left ( \dfrac{7-\sqrt{12x+1}}{x-4} \right )$

11)$\lim \limits_{x \to 3} \left ( \dfrac{\frac{1}{3}+\frac{1}{x}}{3+x} \right )$

Jibu: $-\dfrac{1}{9}$

12.3: Mwendelezo

Kwa mazoezi 1-5, tumia ushahidi wa namba ili uone kama kikomo kipo$x=a$. Ikiwa sio, kuelezea tabia ya grafu ya kazi$x=a$.

1)$f(x)=\dfrac{-2}{x-4};\; a=4$

2)$f(x)=\dfrac{-2}{(x-4)^2};\; a=4$

Jibu: Kwa$x=4$, kazi ina asymptote ya wima.

3)$f(x)=\dfrac{-x}{x^2-x-6};\; a=3$

4)$f(x)=\dfrac{6x^2+23x+20}{4x^2-25};\; a=-\dfrac{5}{2}$

Jibu: discontinuity kutolewa katika$a=-\dfrac{5}{2}$

5)$f(x)=\dfrac{\sqrt{x}-3}{9-x};\; a=9$

Kwa mazoezi 6-12, tambua wapi kazi iliyotolewa$f(x)$ inaendelea. Ambapo sio kuendelea, hali ambayo hali inashindwa, na uainishe discontinuities yoyote.

6)$f(x)=x^2-2x-15$

Jibu: kuendelea$(-\infty, \infty)$

7)$f(x)=\dfrac{x^2-2x-15}{x-5}$

8)$f(x)=\dfrac{x^2-2x}{x^2-4x+4}$

Jibu: kutolewa discontinuity katika$x=2$. $f(2)$si defined, lakini mipaka zipo.

9)$f(x)=\dfrac{x^3-125}{2x^2-12x+10}$

10)$f(x)=\dfrac{x^2-\frac{1}{x}}{2-x}$

Jibu: kukomesha saa$x=0$ na$x=2$. Wote$f(0)$ na$f(2)$ si defined.

11)$f(x)=\dfrac{x+2}{x^2-3x-10}$

12)$f(x)=\dfrac{x+2}{x^3+8}$

Jibu: kutolewa discontinuity katika$x=-2$. $f(-2)$si defined.

12.4: Derivatives

Kwa mazoezi 1-5, pata kiwango cha wastani cha mabadiliko$f(x)=\dfrac{f(x+h)-f(x)}{h}$.

1)$f(x)=3x+2$

2)$f(x)=5$

Jibu: $0$

3)$f(x)=\dfrac{1}{x+1}$

4)$f(x)=\ln (x)$

Jibu: $f(x)=\dfrac{\ln (x+h)-\ln (x)}{h}$

5)$f(x)=e^{2x}$

Kwa mazoezi 6-7, tafuta derivative ya kazi.

6)$f(x)=4x-6$

Jibu: $4$

7)$f(x)=5x^2-3x$

8) Pata usawa wa mstari wa tangent kwenye grafu ya$f(x)$$x$ thamani iliyoonyeshwa. \[f(x)=-x^3+4x;\; x=2 \nonumber \]

Jibu: $y=-8x+16$

9) Kwa zoezi zifuatazo, kwa msaada wa matumizi ya graphing, kuelezea kwa nini kazi haijulikani kila mahali kwenye uwanja wake. Taja pointi ambapo kazi haijulikani. \[f(x)=\dfrac{x}{\left | x \right |} \nonumber \]

10) Kutokana na kwamba kiasi cha koni ya mviringo ya kulia ni$V=\dfrac{1}{3}\pi r^2h$ na kwamba koni iliyotolewa ina urefu wa urefu wa$9$ cm na urefu wa radius ya kutofautiana, kupata kiwango cha instantaneous cha mabadiliko ya kiasi kuhusiana na urefu wa radius wakati radius ni$2$ cm. Kutoa jibu halisi katika suala la$π$.

Jibu: $12\pi $

Mazoezi mtihani

Kwa mazoezi 1-6, tumia grafu ya$f$ kwenye Kielelezo hapa chini.

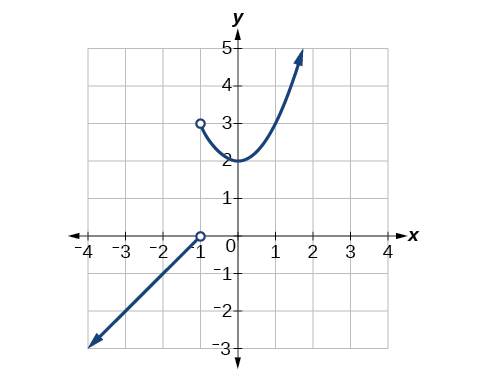
$R Practice.png$

1)$f(1)$

Jibu: $3$

2)$\lim \limits_{x \to -1^+} f(x)$

3)$\lim \limits_{x \to -1^-} f(x)$

Jibu: $0$

4)$\lim \limits_{x \to -1} f(x)$

5)$\lim \limits_{x \to -2} f(x)$

Jibu: $-1$

6) Ni maadili gani ya$x$$f$ kuacha? Ni mali gani ya kuendelea inavunjwa?

7)$f(x)=\begin{cases} \dfrac{1}{3}-3 & \text{ if } x\leq 2 \\ x^3+1 & \text{ if } x>2 \end{cases} a=2$

Jibu

$\lim \limits_{x \to 2^-} f(x)=-\dfrac{5}{2}a$na$\lim \limits_{x \to 2^+} f(x)=9$

Hivyo, kikomo cha kazi kama$x$ mbinu$2$ haipo.

8)$f(x)=\begin{cases} x^3+1 & \text{ if } x<1 \\ 3x^2-1 & \text{ if } x=1\; a=1 \\ -\sqrt{x+3}+4 & \text{ if } x>1 \end{cases}$

Kwa mazoezi 9-11, tathmini kila kikomo kwa kutumia mbinu za algebraic.

9)$\lim \limits_{x \to -5} \left ( \dfrac{\frac{1}{5}+\frac{1}{x}}{10+2x} \right )$

Jibu: $-\dfrac{1}{50}$

10)$\lim \limits_{h \to 0} \left ( \dfrac{\sqrt{h^2+25}-5}{h^2} \right )$

11)$\lim \limits_{h \to 0} \left ( \dfrac{1}{h}-\dfrac{1}{h^2+h} \right )$

Jibu: $1$

Kwa mazoezi 12-13, onyesha kama kazi iliyopewa$f$ inaendelea. Ikiwa inaendelea, onyesha kwa nini. Ikiwa haiendelei, hali ambayo hali inashindwa.

12)$f(x)=\sqrt{x^2-4}$

13)$f(x)=\dfrac{x^3-4x^2-9x+36}{x^3-3x^2+2x-6}$

Jibu: discontinuity kutolewa katika$x=3$

Kwa mazoezi 14-16, tumia ufafanuzi wa derivative ili kupata derivative ya kazi iliyotolewa$x=a$.

14)$f(x)=\dfrac{3}{5+2x}$

15)$f(x)=\dfrac{3}{\sqrt{x}}$

Jibu: $f'(x)=-\dfrac{3}{2a^{\frac{3}{2}}}$

16)$f(x)=2x^2+9x$

17) Kwa grafu katika Kielelezo hapa chini, onyesha ambapo kazi inaendelea/kuacha na kutofautishwa/haijulikani.

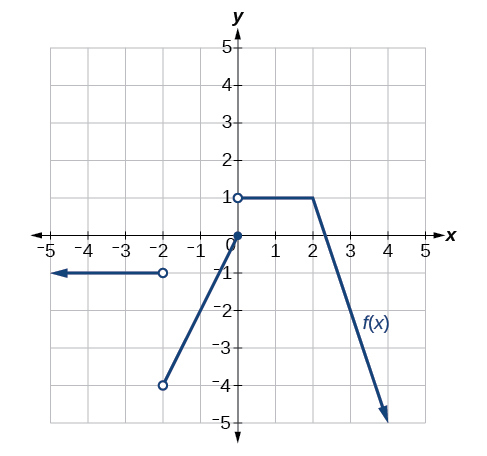
$R Mazoezi 17.png$

Jibu: discontinuous katika$-2,0$, si differentiable katika$-2,0, 2$.

Kwa mazoezi 18-19, kwa msaada wa matumizi ya graphing, kuelezea kwa nini kazi haijulikani kila mahali kwenye uwanja wake. Taja pointi ambapo kazi haijulikani.

18)$f(x)=\left | x-2 \right | - \left | x+2 \right |$

19)$f(x)=\dfrac{2}{1+e^{\frac{2}{x}}}$

Jibu: si differentiable katika$x=0$ (hakuna kikomo)

Kwa mazoezi 20-24, kueleza notation kwa maneno wakati urefu wa projectile kwa miguu$s$, ni kazi ya muda$t$ katika sekunde baada ya uzinduzi na hutolewa na kazi$s(t)$.

20)$s(0)$

21)$s(2)$

Jibu: urefu wa projectile kwa$t=2$ sekunde

22)$s'(2)$

23)$\dfrac{s(2)-s(1)}{2-1}$

Jibu: kasi ya wastani kutoka$t=1$ kwa$t=2$

24)$s(t)=0$

Kwa mazoezi 25-28, tumia teknolojia ili kutathmini kikomo.

25)$\lim \limits_{x \to 0}\dfrac{\sin (x)}{3x}$

Jibu: $\dfrac{1}{3}$

26)$\lim \limits_{x \to 0}\dfrac{\tan ^2(x)}{2x}$

27)$\lim \limits_{x \to 0}\dfrac{\sin (x)(1-\cos (x))}{2x^2}$

Jibu: $0$

28) Tathmini kikomo kwa mkono.

\[\lim \limits_{x \to 1}f(x), \text{ where } f(x)=\begin{cases} 4x-7 & x\neq 1 \\ x^2-4 & x= 1 \end{cases} \nonumber \]

Kwa thamani gani (s) ya$x$ ni kazi chini ya kuacha?

\[f(x)=\begin{cases} 4x-7 & x\neq 1 \\ x^2-4 & x= 1 \end{cases} \nonumber \]

Kwa mazoezi 29-32, fikiria kazi ambayo grafu inaonekana kwenye Kielelezo.

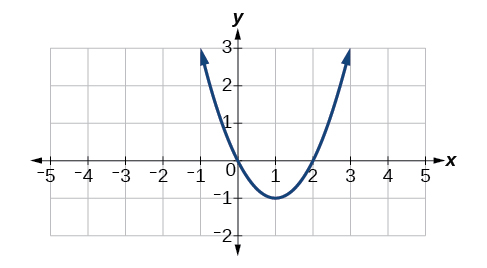
$R Mazoezi 29-32.png$

29) Kupata kiwango cha wastani wa mabadiliko ya kazi kutoka$x=1$ kwa$x=3$.

Jibu: $2$

30) Kupata maadili yote ya$x$ saa ambayo$f'(x)=0$.

Jibu: $x=1$

31) Pata maadili yote ambayo$f'(x)$ haipo.$x$

32) Pata usawa wa mstari wa tangent kwenye grafu$f$ ya hatua iliyoonyeshwa:$f(x)=3x^2-2x-6,\; x=-2$

Jibu: $y=-14x-18$

Kwa mazoezi 33-34, tumia kazi$f(x)=x(1-x)^{\frac{2}{5}}$

33) Graph kazi$f(x)=x(1-x)^{\tfrac{2}{5}}$ kwa kuingia$f(x)=x\left ((1-x)^2 \right )^{\tfrac{1}{5}}$ na kisha kwa kuingia$f(x)=x\left ((1-x)^{\tfrac{1}{5}} \right )^2$.

34) Kuchunguza tabia ya grafu ya$f(x)$ karibu$x=1$ na kuchora kazi kwenye nyanja zifuatazo,$[0.9, 1.1], [0.99, 1.01], [0.999, 1.001]$, na$[0.9999, 1.0001]$. Tumia habari hii ili kuamua kama kazi inaonekana kuwa tofauti katika$x=1$.

Jibu: Grafu haipatikani katika$x=1$ (cusp).

Kwa mazoezi 35-42, tafuta derivative ya kila kazi kwa kutumia ufafanuzi: $\lim \limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$

35)$f(x)=2x-8$

36)$f(x)=4x^2-7$

Jibu: $f'(x)=8x$

37)$f(x)=x-\dfrac{1}{2}x^2$

38)$f(x)=\dfrac{1}{x+2}$

Jibu: $f'(x)=-\dfrac{1}{(2+x)^2}$

39)$f(x)=\dfrac{3}{x-1}$

40)$f(x)=-x^3+1$

Jibu: $f'(x)=-3x^2$

41)$f(x)=x^2+x^3$

42)$f(x)=\sqrt{x-1}$

Jibu: $f'(x)=-\dfrac{1}{2\sqrt{x-1}}$

Wachangiaji na Majina

Template:OpenStaxPreCalc