12.E: Utangulizi wa Calculus (Mazoezi)

12.1: Kupata Mipaka - Njia za Nambari na za kielelezo

Katika sehemu hii, tutachunguza mbinu za namba na za kielelezo za kutambua mipaka.

Maneno

1) Eleza tofauti kati ya thamani katika\(x=a\) na kikomo kama\(x\) mbinu\(a\).

Jibu

Thamani ya kazi, pato, katika\(x=a\) ni\(f(a)\). Wakati\(\lim \limits_{x \to a}f(x)\) ni kuchukuliwa, maadili ya\(x\) kupata kubwa karibu na\(a\) lakini kamwe sawa\(a\). Kama maadili ya\(x\) mbinu\(a\) kutoka kushoto na kulia, kikomo ni thamani ambayo kazi inakaribia.

2) Eleza kwa nini tunasema kazi haina kikomo kama\(x\) mbinu\(a\) ikiwa, kama\(x\) mbinu\(a\), kikomo cha mkono wa kushoto si sawa na kikomo cha mkono wa kulia.

Graphic

Kwa mazoezi 3-14, tathmini maadili ya kazi na mipaka kutoka kwenye grafu ya kazi\(f\) iliyotolewa katika Kielelezo hapa chini.

3)\(\lim \limits_{x \to −2^−} f(x)\)

Jibu

\(-4\)

4)\(\lim \limits_{x \to −2^+ }f(x)\)

5)\(\lim \limits_{x \to −2 f(x)}\)

Jibu

\(-4\)

6)\(f(−2)\)

7)\(\lim \limits_{x \to −1^− f(x)}\)

Jibu

\(2\)

8)\(\lim \limits_{x \to 1^+} f(x)\)

9)\(\lim \limits_{x \to 1} f(x)\)

Jibu

haipo

10)\(f(1)\)

11)\(\lim \limits_{x \to 4^−} f(x)\)

Jibu

\(4\)

12)\(\lim \limits_{x \to 4^+} f(x)\)

13)\(\lim \limits_{x \to 4} f(x)\)

Jibu

haipo

14)\(f(4)\)

Kwa mazoezi 15-21, futa grafu ya kazi kutoka kwa maadili ya kazi na mipaka iliyotolewa.

15)\(\lim \limits_{x \to 0^−} f(x)=2, \lim \limits_{x \to 0^+} f(x)=–3, \lim \limits_{x \to 2} f(x)=2, f(0)=4, f(2)=–1, f(–3) \text{ does not exist.}\)

Jibu

Majibu yatatofautiana.

16)\(\lim \limits_{x \to 2^−} f(x)=0,\lim \limits_{x \to 2^+} =–2,\lim \limits_{x \to 0} f(x)=3, f(2)=5, f(0)\)

Jibu

Majibu yatatofautiana.

17)\(\lim \limits_{ x \to 2^−} f(x)=2, \lim \limits_{ x \to 2^+} f(x)=−3, \lim \limits_{x \to 0} f(x)=5, f(0)=1, f(1)=0\)

Jibu

Majibu yatatofautiana.

18)\(\lim \limits_{x \to 3^−} f(x)=0, \lim \limits_{x \to 3^+} f(x)=5, \lim \limits_{x \to 5} f(x)=0, f(5)=4, f(3) \text{ does not exist.}\)

Jibu

Majibu yatatofautiana.

19)\( \lim \limits_{ x \to 4} f(x)=6, \lim \limits_{ x \to 6^+} f(x)=−1, \lim \limits_{ x \to 0} f(x)=5, f(4)=6, f(2)=6\)

Jibu

Majibu yatatofautiana.

20)\( \lim \limits_{ x \to −3} f(x)=2, \lim \limits_{ x \to 1^+} f(x)=−2, \lim \limits_{ x \to 3} f(x)=–4, f(–3)=0, f(0)=0\)

Jibu

Majibu yatatofautiana.

21)\( \lim \limits_{ x \to π} f(x)=π^2, \lim \limits_{ x \to –π} f(x)=\dfrac{π}{2}, \lim \limits_{ x \to 1^-} f(x)=0, f(π)=\sqrt{2}, f(0) \text{ does not exist}.\)

Jibu

Majibu yatatofautiana.

Kwa mazoezi 22-26, tumia calculator ya graphing kuamua kikomo kwa maeneo ya\(5\) decimal kama\(x\) mbinu\(0\).

22)\(f(x)=(1+x)^{\frac{1}{x}}\)

23)\(g(x)=(1+x)^{\frac{2}{x}}\)

Jibu

\(7.38906\)

24)\(h(x)=(1+x)^{\frac{3}{x}}\)

25)\(i(x)=(1+x)^{\frac{4}{x}}\)

Jibu

\(54.59815\)

26)\(j(x)=(1+x)^{\frac{5}{x}}\)

27) Kulingana na muundo ulioona katika mazoezi hapo juu, fanya dhana kuhusu kikomo cha\(f(x)=(1+x)^{\frac{6}{x}}, g(x)=(1+x)^{\frac{7}{x}},\) na\(h(x)=(1+x)^{\frac{n}{x}}.\)

Jibu

\(e^6≈403.428794,e^7≈1096.633158, e^n\)

Kwa mazoezi 28-29, tumia matumizi ya graphing ili kupata ushahidi wa kielelezo ili kuamua mipaka ya kushoto na ya kulia ya kazi iliyotolewa kama\(x\) mbinu\(a\). Kama kazi ina kikomo kama\(x\) mbinu\(a\), hali yake. Ikiwa sio, jadili kwa nini hakuna kikomo.

28)\((x)= \begin{cases} |x|−1, && \text{if }x≠1 \\ x^3, && \text{if }x=1 \end{cases} a=1 \)

29)\((x)= \begin{cases} \frac{1}{x+1}, && \text{if } x=−2 \\ (x+1)^2, && \text{if } x≠−2 \end{cases} a=−2 \)

Jibu

\(\lim \limits_{x \to −2} f(x)=1\)

Numeric

Kwa mazoezi 30-38, tumia ushahidi wa namba ili uone kama kikomo kipo\(x=a\). Ikiwa sio, kuelezea tabia ya grafu ya kazi karibu\(x=a\). Majibu ya pande zote kwa maeneo mawili ya decimal.

30)\(f(x)=\dfrac{x^2−4x}{16−x^2};a=4\)

31)\(f(x)=\dfrac{x^2−x−6}{x^2−9};a=3\)

Jibu

\(\lim \limits_{x \to 3} \left (\dfrac{x^2−x−6}{x^2−9} \right )=\dfrac{5}{6}≈0.83\)

32)\(f(x)=\dfrac{x^2−6x−7}{x^2– 7x};a=7\)

33)\(f(x)=\dfrac{x^2–1}{x^2–3x+2};a=1\)

Jibu

\(\lim \limits_{x \to 1} \left (\dfrac{x^2−1}{x^2−3x+2} \right )=−2.00\)

34)\(f(x)=\dfrac{1−x^2}{x^2−3x+2};a=1\)

35)\(f(x)=\dfrac{10−10x^2}{x^2−3x+2};a=1\)

Jibu

\(\lim \limits_{x \to 1} \left (\dfrac{10−10x^2}{x^2−3x+2} \right )=20.00\)

36)\(f(x)=\dfrac{x}{6x^2−5x−6};a=\dfrac{3}{2}\)

37)\(f(x)=\dfrac{x}{4x^2+4x+1};a=−\dfrac{1}{2}\)

Jibu

\(\lim \limits_{x \to \frac{−1}{2}} \left (\dfrac{x}{4x^2+4x+1} \right )\)haipo. Kazi maadili kupungua bila amefungwa kama\(x\) mbinu\(-0.5\) kutoka ama kushoto au kulia.

38)\(f(x)=\frac{2}{x−4}; a=4\)

Kwa mazoezi 39-41, tumia calculator kukadiria kikomo kwa kuandaa meza ya maadili. Ikiwa hakuna kikomo, kuelezea tabia ya kazi kama\(x\) inakaribia thamani iliyotolewa.

39)\(\lim \limits_{x \to 0} \dfrac{7 \tan x}{3x}\)

Jibu

\(\lim \limits_{x \to 0} \dfrac{7 \tan x}{3x}=\dfrac{7}{3}\)

40)\(\lim \limits_{x \to 4} \dfrac{x^2}{x−4}\)

Jibu

41)\(\lim \limits_{x \to 0}\dfrac{2 \sin x}{4 \tan x}\)

Jibu

\(\lim \limits_{x \to 0} \dfrac{2 \sin x}{4 \tan x}=\dfrac{1}{2}\)

Kwa mazoezi 42-49, tumia matumizi ya graphing ili kupata ushahidi wa nambari au wa kielelezo ili kuamua mipaka ya kushoto na ya kulia ya kazi iliyotolewa kama\(x\) mbinu\(a\). Kama kazi ina kikomo kama\(x\) mbinu\(a\), hali yake. Ikiwa sio, jadili kwa nini hakuna kikomo.

42)\(\lim \limits_{x \to 0}e^{e^{\frac{1}{x}}}\)

43)\(\lim \limits_{x \to 0}e^{e^{− \frac{1}{x^2}}}\)

Jibu

\(\lim \limits_{x \to 0}e^{e^{− \frac{1}{x^2}}}=1.0\)

44)\(\lim \limits_{x \to 0} \dfrac{|x|}{x}\)

45)\(\lim \limits_{x \to −1} \dfrac{|x+1|}{x+1}\)

Jibu

\(\lim \limits_{ x→−1^−}\dfrac{| x+1 |}{x+1}=\dfrac{−(x+1)}{(x+1)}=−1\)na\(\lim \limits_{ x \to −1^+}\dfrac{| x+1 |}{x+1}=\dfrac{(x+1)}{(x+1)}=1\); tangu kikomo cha mkono wa kulia haufanani kikomo cha mkono wa kushoto,\(\lim \limits_{ x \to −1}\dfrac{|x+1|}{x+1}\) haipo.

46)\(\lim \limits_{ x \to 5} \dfrac{| x−5 |}{5−x}\)

47)\(\lim \limits_{ x \to −1}\dfrac{1}{(x+1)^2}\)

Jibu

\(\lim \limits_{ x \to −1} \dfrac{1}{(x+1)^2}\)haipo. Kazi huongezeka bila kufungwa kama\(x\) mbinu\(−1\) kutoka upande wowote.

48)\(\lim \limits_{ x \to 1} \dfrac{1}{(x−1)^3}\)

49)\(\lim \limits_{ x \to 0} \dfrac{5}{1−e^{\frac{2}{x}}}\)

Jibu

\(\lim \limits_{ x \to 0} \dfrac{5}{1−e^{\frac{2}{x}}}\)haipo. Maadili ya kazi mbinu\(5\) kutoka upande wa kushoto na mbinu\(0\) kutoka kulia.

50) Tumia ushahidi wa nambari na wa kielelezo kulinganisha na kulinganisha mipaka ya kazi mbili ambazo fomu zinaonekana sawa:\(f(x)=\left | \dfrac{1−x}{x} \right |\) na\(g(x)=\left | \dfrac{1+x}{x} \right |\) kama\(x\) mbinu\(0\). Tumia matumizi ya graphing, ikiwa inawezekana, kuamua mipaka ya kushoto na ya kulia ya kazi\(f(x)\) na\(g(x)\) kama\(x\) mbinu\(0\). Ikiwa kazi zina kikomo kama\(x\) mbinu\(0\), sema. Ikiwa sio, jadili kwa nini hakuna kikomo.

Upanuzi

51) Kwa mujibu wa Nadharia ya Relativity, molekuli m m ya chembe inategemea kasi yake\(v\). Hiyo ni

\[m=\dfrac{m_o}{\sqrt{1−(v^2/c^2)}} \nonumber \]

\(m_o\)wapi wingi wakati chembe inapumzika na\(c\) ni kasi ya mwanga. Pata kikomo cha wingi\(m\), kama\(v\) mbinu\(c^−.\)

Jibu

Kupitia uchunguzi wa postulates na uelewa wa fizikia relativistic, kama\(v→c, m→∞. \) Chukua hatua hii moja zaidi kwa suluhisho,\[\lim \limits_{v \to c^−}m=\lim \limits_{v \to c^−} \dfrac{m_o}{\sqrt{1−(v^2/c^2)}}=∞ \nonumber \]

52) Ruhusu kasi ya mwanga\(c\),, kuwa sawa na\(1.0\). Ikiwa wingi,\(m\)\(1\), ni nini kinachotokea\(m\) kama\(v \to c\)? Kutumia maadili yaliyoorodheshwa katika Jedwali hapa chini, fanya dhana kuhusu nini umati ni kama\(v\) mbinu\(1.00\).

\(v\)	\(m\)
\ (v\) "> 0.5	\ (m\) ">1.15
\ (v\) ">0.9	\ (m\) ">2.29
\ (v\) ">0.95	\ (m\) ">3.20
\ (v\) ">0.99	\ (m\) ">7.09
\ (v\) ">0.999	\ (m\) "> 22.36
\ (v\) "> 0.99999	\ (m\) ">223.61

12.2: Kupata Mipaka - Mali ya Mipaka

Kuweka kazi au kuchunguza meza ya maadili ili kuamua kikomo inaweza kuwa mbaya na ya muda. Ikiwezekana, ni ufanisi zaidi kutumia mali ya mipaka, ambayo ni mkusanyiko wa theorems ya kutafuta mipaka. Kujua mali ya mipaka inatuwezesha kuhesabu mipaka moja kwa moja.

Maneno

1) Kutoa mfano wa aina ya kazi\(f\) ambayo kikomo, kama\(x\) mbinu\(a,\) ni\(f(a)\).

Jibu

Ikiwa\(f\) ni kazi ya polynomial, kikomo cha kazi ya polynomial kama\(x\) mbinu\(a\) zitakuwa daima\(f(a)\).

2) Wakati badala ya moja kwa moja hutumiwa kutathmini kikomo cha kazi ya busara kama\(x\) mbinu\(a\) na matokeo ni\(f(a)=\dfrac{0}{0}\), je, hii inamaanisha kuwa kikomo cha\(f\) haipo?

3) Ina maana gani kusema kikomo cha\(f(x)\), kama\(x\) mbinu\(c\), haijulikani?

Jibu

Inaweza kumaanisha ama (1) maadili ya ongezeko la kazi au kupungua bila kufungwa kama\(x\) mbinu\(c,\) au (2) mipaka ya kushoto na ya kulia si sawa.

Kialjebra

Kwa mazoezi 4-30, tathmini mipaka algebraically.

4)\(\lim \limits_{x \to 0} (3)\)

5)\(\lim \limits_{x \to 2} \left (\dfrac{−5x}{x^2−1} \right )\)

Jibu

\(\dfrac{−10}{3}\)

6)\(\lim \limits_{x \to 2} \left (\dfrac{x^2−5x+6}{x+2} \right )\)

7)\(\lim \limits_{x \to 3} \left (\dfrac{x^2−9}{x−3} \right )\)

Jibu

\(6\)

8)\(\lim \limits_{x \to −1} \left (\dfrac{x^2−2x−3}{x+1} \right )\)

9)\(\lim \limits_{x \to \frac{3}{2}} \left (\dfrac{6x^2−17x+12}{2x−3} \right )\)

Jibu

\(\dfrac{1}{2}\)

10)\(\lim \limits_{ x \to −\frac{7}{2}} \left (\dfrac{8x^2+18x−35}{2x+7} \right )\)

11)\(\lim \limits_{ x \to 3} \left (\dfrac{x^2−9}{x−5x+6} \right )\)

Jibu

\(6\)

12)\(\lim \limits_{ x \to −3} \left (\dfrac{−7x^4−21x^3}{−12x^4+108x^2} \right )\)

13)\(\lim \limits_{ x \to 3} \left (\dfrac{x^2+2x−3}{x−3} \right )\)

Jibu

haipo

14)\(\lim \limits_{ h \to 0} \left (\dfrac{(3+h)^3−27}{h} \right )\)

15)\(\lim \limits_{ h \to 0} \left (\dfrac{(2−h)^3−8}{h} \right )\)

Jibu

\(−12\)

16)\(\lim \limits_{ h \to 0} \left (\dfrac{(h+3)^2−9}{h} \right )\)

17)\(\lim \limits_{ h \to 0} \left (\dfrac{\sqrt{5−h}−\sqrt{5}}{h} \right )\)

Jibu

\(−\dfrac{\sqrt{5}}{10}\)

18)\(\lim \limits_{ x \to 0} \left (\dfrac{\sqrt{3−x}−\sqrt{3}}{x} \right )\)

19)\(\lim \limits_{ x \to 9} \left (\dfrac{x^2−81}{3−x} \right )\)

Jibu

\(−108\)

20)\(\lim \limits_{ x \to 1} \left (\dfrac{\sqrt{x}−x^2}{1−\sqrt{x}} \right )\)

21)\(\lim \limits_{ x \to 0}\left ( \dfrac{x}{\sqrt{1+2x}-1} \right )\)

Jibu

\(1\)

22)\(\lim \limits_{ x \to \frac{1}{2}} \left (\dfrac{x^2−\tfrac{1}{4}}{2x−1} \right )\)

23)\(\lim \limits_{ x \to 4} \left (\dfrac{x^3−64}{x^2−16} \right )\)

Jibu

\(6\)

24)\(\lim \limits_{ x \to 2^−} \left (\dfrac{|x−2|}{x−2} \right )\)

25)\(\lim \limits_{ x \to 2^+} \left (\dfrac{| x−2 |}{x−2} \right )\)

Jibu

\(1\)

26)\(\lim \limits_{ x \to 2} \left (\dfrac{| x−2 |}{x−2} \right )\)

27)\(\lim \limits_{ x \to 4^−} \left (\dfrac{| x−4 |}{4−x} \right )\)

Jibu

\(1\)

28)\(\lim \limits_{ x \to 4^+} \left (\dfrac{| x−4 |}{4−x} \right )\)

29)\(\lim \limits_{ x \to 4} \left (\dfrac{| x−4 |}{4−x} \right )\)

Jibu

haipo

30)\(\lim \limits_{ x \to 2} \left (\dfrac{−8+6x−x^2}{x−2} \right )\)

Kwa mazoezi 31-33, tumia taarifa iliyotolewa ili kutathmini mipaka:\(\lim \limits_{x \to c}f(x)=3, \lim \limits_{x \to c} g(x)=5\)

31)\(\lim \limits_{x \to c} [ 2f(x)+\sqrt{g(x)} ]\)

Jibu

\(6+\sqrt{5}\)

32)\(\lim \limits_{x \to c} [ 3f(x)+\sqrt{g(x)} ]\)

33)\(\lim \limits_{x \to c}\dfrac{f(x)}{g(x)}\)

Jibu

\(\dfrac{3}{5}\)

Kwa mazoezi 34-43, tathmini mipaka ifuatayo.

34)\(\lim \limits_{x \to 2} \cos (πx)\)

35)\(\lim \limits_{x \to 2} \sin (πx)\)

Jibu

\(0\)

36)\(\lim \limits_{x \to 2} \sin \left (\dfrac{π}{x} \right )\)

37)\(f(x)= \begin{cases} 2x^2+2x+1, && x≤0 \\ x−3, && x>0 ; \end{cases} \lim \limits_{x \to 0^+}f(x)\)

Jibu

\(−3\)

38)\(f(x)= \begin{cases} 2x^2+2x+1, && x≤0 \\ x−3, && x>0 ; \end{cases} \lim \limits_{x \to 0^−} f(x)\)

39)\(f(x)= \begin{cases} 2x^2+2x+1, && x≤0 \\ x−3, && x>0 ; \end{cases} \lim \limits_{x \to 0}f(x)\)

Jibu

haipo; kikomo cha mkono wa kulia si sawa na kikomo cha mkono wa kushoto.

40)\(\lim \limits_{x \to 4} \dfrac{\sqrt{x+5}−3}{x−4}\)

41)\(\lim \limits_{x \to 2^+} (2x−〚x〛)\)

Jibu

\(2\)

42)\(\lim \limits_{x \to 2} \dfrac{\sqrt{x+7}−3}{x^2−x−2}\)

43)\(\lim \limits_{x \to 3^+}\dfrac{x^2}{x^2−9}\)

Jibu

Limit haipo; kikomo mbinu infinity.

Kwa mazoezi 44-53, pata kiwango cha wastani cha mabadiliko\(\dfrac{f(x+h)−f(x)}{h}\).

44)\(f(x)=x+1\)

45)\(f(x)=2x^2−1\)

Jibu

\(4x+2h\)

46)\(f(x)=x^2+3x+4\)

47)\(f(x)=x^2+4x−100\)

Jibu

\(2x+h+4\)

48)\(f(x)=3x^2+1\)

49)\(f(x)= \cos (x)\)

Jibu

\(\dfrac{\cos (x+h)− \cos (x)}{h}\)

50)\(f(x)=2x^3−4x\)

51)\(f(x)=\dfrac{1}{x}\)

Jibu

\(\dfrac{−1}{x(x+h)}\)

52)\(f(x)=\dfrac{1}{x^2}\)

53)\(f(x)=\sqrt{x}\)

Jibu

\(\dfrac{−1}{\sqrt{x+h}+\sqrt{x}}\)

Graphic

54) Kupata equation ambayo inaweza kuwakilishwa na Kielelezo hapa chini.

Kielelezo hapa chini.

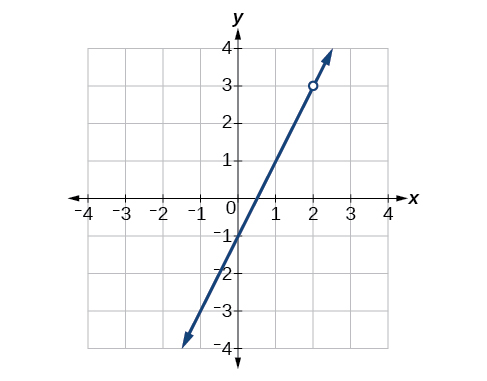
Jibu

\(f(x)=\dfrac{x^2+5x+6}{x+3}\)

Kwa mazoezi 56-57, rejea kwenye Kielelezo hapa chini.

56) Kikomo cha mkono wa kulia wa kazi kama\(x\) mbinu ni\(0\) nini?

57) Kikomo cha mkono wa kushoto cha kazi kama\(x\) mbinu ni\(0\) nini?

Jibu

haipo

Real-World Matumizi

58) Kazi ya msimamo\(s(t)=−16t^2+144t\) inatoa nafasi ya projectile kama kazi ya wakati. Pata kasi ya wastani (wastani wa kiwango cha mabadiliko) kwa muda\([ 1,2 ]\).

59) Urefu wa projectile hutolewa na\(s(t)=−64t^2+192t\) Kupata kiwango cha wastani cha mabadiliko ya urefu kutoka\(t=1\) pili hadi\(t=1.5\) sekunde.

Jibu

\(52\)

60) Kiasi cha fedha katika akaunti baada ya\(t\) miaka iliyozidi kuendelea kwa\(4.25\%\) riba hutolewa na formula\(A=A_0e^{0.0425t}\), ambapo kiasi cha awali\(A_0\) kiliwekeza. Pata kiwango cha wastani cha mabadiliko ya usawa wa akaunti kutoka\(t=1\) mwaka hadi\(t=2\) miaka ikiwa kiasi cha awali kiliwekeza ni\(\$1,000.00.\)

12.3: Kuendelea

Kazi ambayo inabakia ngazi kwa muda na kisha inaruka mara moja kwa thamani ya juu inaitwa kazi ya hatua kwa hatua. Kazi hii ni mfano. Kazi ambayo ina shimo lolote au kuvunja katika grafu yake inajulikana kama kazi ya kuacha. Kazi ya hatua kwa hatua, kama vile mashtaka ya maegesho ya karakana kama kazi ya masaa yaliyowekwa, ni mfano wa kazi ya kuacha. Tunaweza kuangalia hali tatu tofauti kuamua kama kazi ni kuendelea katika idadi fulani.

Maneno

1) Hali kwa maneno yako mwenyewe nini maana kwa ajili ya kazi\(f\) ya kuendelea katika\(x=c\).

Jibu

Kwa kawaida, ikiwa kazi inaendelea\(x=c\), basi hakuna mapumziko katika grafu ya kazi\(f(c)\), na\(f(c)\) inaelezwa.

2) Hali kwa maneno yako mwenyewe nini maana kwa ajili ya kazi ya kuendelea juu ya muda\((a,b)\).

Kialjebra

Kwa mazoezi 3-22, onyesha kwa nini kazi hiyo\(f\) imekoma kwa hatua fulani\(a\) kwenye grafu. Hali ambayo hali inashindwa.

3)\(f(x)=\ln | x+3 |,a=−3\)

Jibu

kuacha saa\(a=−3\);\(f(−3)\) haipo

4)\(f(x)= \ln | 5x−2 |,a=\dfrac{2}{5}\)

5)\(f(x)=\dfrac{x^2−16}{x+4},a=−4\)

Jibu

discontinuity kutolewa katika\(a=−4; f(−4)\) si defined

6)\(f(x)=\dfrac{x^2−16x}{x},a=0\)

7)\(f(x)= \begin{cases} x, && x≠3 \\ 2x, && x=3 \end{cases} a=3\)

Jibu

\(a=3; \lim \limits_{x \to 3} f(x)=3,\)Discontinuous saa lakini\(f(3)=6,\) ambayo si sawa na kikomo.

8)\(f(x) = \begin{cases} 5, &&x≠0 \\ 3, && x=0 \end{cases} a=0\)

9)\(f(x)= \begin{cases} \dfrac{1}{2−x}, && x≠2 \\ 3, &&x=2 \end{cases} a=2\)

Jibu

\(\lim \limits_{x \to 2}f(x)\)haipo.

10)\(f(x)= \begin{cases} \dfrac{1}{x+6}, && x=−6 \\ x^2, && x≠−6 \end{cases} a=−6\)

11)\(f(x)=\begin{cases} 3+x, &&x<1 \\ x, &&x=1 \\ x^2, && x>1 \end{cases} a=1\)

Jibu

\(\lim \limits_{x \to 1^−}f(x)=4;\lim \limits_{x \to 1^+}f(x)=1.\)Kwa hiyo,\(\lim \limits_{x \to 1}f(x)\) haipo.

12)\(f(x)= \begin{cases} 3−x, && x<1 \\ x, && x=1 \\ 2x^2, && x>1 \end{cases} a=1\)

13)\(f(x)= \begin{cases} 3+2x, && x<1 \\ x, && x=1 \\ −x^2, && x>1 \end{cases} a=1\)

Jibu

\(\lim \limits_{x \to 1^−} f(x)=5≠ \lim \limits_{x \to 1^+}f(x)=−1\). Hivyo\(\lim \limits_{x \to 1}f(x)\) haipo.

14)\(f(x)= \begin{cases} x^2, &&x<−2 \\ 2x+1, && x=−2 \\ x^3, && x>−2 \end{cases} a=−2\)

15)\(f(x)= \begin{cases} \dfrac{x^2−9}{x+3}, && x<−3 \\ x−9, && x=−3 \\ \dfrac{1}{x}, && x>−3 \end{cases} a=−3\)

Jibu

\(\lim \limits_{x to −3^+}f(x)=−\dfrac{1}{3}\)

Kwa hiyo,\(\lim \limits_{x \to −3} f(x)\) haipo.

16)\(f(x)= \begin{cases} \dfrac{x^2−9}{x+3}, && x<−3 \\ x−9, && x=−3\\ −6, && x>−3 \end{cases} a=3\)

17)\(f(x)=\dfrac{x^2−4}{x−2}, a=2\)

Jibu

\(f(2)\)si defined.

18)\(f(x)=\dfrac{25−x^2}{x^2−10x+25}, a=5\)

19)\(f(x)=\dfrac{x^3−9x}{x^2+11x+24}, a=−3\)

Jibu

\(f(−3)\)si defined.

20)\(f(x)=\dfrac{x^3−27}{x^2−3x}, a=3\)

21)\(f(x)=\dfrac{x}{|x|}, a=0\)

Jibu

\(f(0)\)si defined.

22)\(f(x)=\dfrac{2|x+2|}{x+2}, a=−2\)

Kwa mazoezi 23-35, onyesha kama kazi iliyopewa\(f\) inaendelea kila mahali. Kama ni kuendelea kila mahali ni defined, hali kwa nini mbalimbali ni kuendelea. Kama ni discontinuous, hali ambapo ni discontinuous.

23)\(f(x)=x^3−2x−15\)

Jibu

Kuendelea\((−∞,∞)\)

24)\(f(x)=\dfrac{x^2−2x−15}{x−5}\)

25)\(f(x)=2⋅3^{x+4}\)

Jibu

Kuendelea\((−∞,∞)\)

26)\(f(x)=− \sin (3x)\)

27)\(f(x)=\dfrac{|x−2|}{x^2−2x}\)

Jibu

Discontinuous katika\(x=0\) na\(x=2\)

28)\(f(x)= \tan (x)+2\)

29)\(f(x)=2x+\dfrac{5}{x}\)

Jibu

Discontinuous katika\(x=0\)

30)\(f(x)=\log _2 (x)\)

31)\(f(x)= \ln x^2 \)

Jibu

Kuendelea\((0,∞)\)

32)\(f(x)=e^{2x}\)

33)\(f(x)=\sqrt{x−4}\)

Jibu

Kuendelea\([4,∞)\)

34)\(f(x)= \sec (x)−3\)

35)\(f(x)=x^2+ \sin (x)\)

Jibu

Kuendelea juu\((−∞,∞)\).

36) Kuamua maadili ya\(b\) na\(c\) kama kwamba kazi zifuatazo ni kuendelea kwenye nzima halisi idadi line.

\[f(x)= \begin{cases}x+1, && 1<x<3 \\ x^2+bx+c, &&|x−2|≥1 \end{cases} \nonumber \]

Graphic

Kwa mazoezi 37-39, rejea kwenye Kielelezo hapa chini. Kila mraba inawakilisha kitengo kimoja cha mraba. Kwa kila thamani ya\(a\), kuamua ni ya masharti matatu ya mwendelezo ni kuridhika katika\(x=a\) na ambayo si.

37)\(x=−3\)

Jibu

\(1\), lakini si\(2\) au\(3\)

38)\(x=2\)

39)\(x=4\)

Jibu

\(1\)na\(2\), lakini si\(3\)

Kwa mazoezi 40-43, tumia matumizi ya graphing ili kuunda kazi\(f(x)= \sin \left (\dfrac{12π}{x} \right )\) kama kwenye Mchoro. Weka\(x\) -axis umbali mfupi kabla na baada\(0\) ya kuonyesha hatua ya kukomesha.

40) Ni masharti gani ya kuendelea yanashindwa wakati wa kuacha?

41) Tathmini\(f(0)\).

Jibu

\(f(0)\)haijafafanuliwa.

42) Kutatua kwa ajili ya\(x\) kama\(f(x)=0\).

43) Ni uwanja wa\(f(x)\) nini?

Jibu

\((−∞,0)∪(0,∞)\)

Kwa mazoezi 44-45, fikiria kazi iliyoonyeshwa kwenye Kielelezo hapa chini.

44) Kwa nini\(x\) -kuratibu ni kazi discontinuous?

45) Ni hali gani ya kuendelea inavunjwa katika pointi hizi?

Jibu

Katika\(x=−1\), kikomo haipo. Katika\(x=1, f(1)\) haipo.

Kwa\(x=2\), inaonekana kuwa na asymptote ya wima, na kikomo haipo.

46) Fikiria kazi iliyoonyeshwa kwenye Kielelezo hapa chini. Kwa nini\(x\) -kuratibu ni kazi discontinuous? Ni hali gani ya kuendelea ilivunjwa?

47) Kujenga kazi ambayo hupita kwa njia ya asili na mteremko mara kwa mara ya\(1\), na discontinuities kutolewa katika\(x=−7\) na\(x=1\).

Jibu

\(\dfrac{x^3+6x^2−7x}{(x+7)(x−1)}\)

48) Kazi\(f(x)=\dfrac{x^3−1}{x−1}\) imewekwa kwenye Kielelezo hapa chini. Inaonekana kuwa inaendelea kwa muda\([−3,3]\), lakini kuna\(x\) -thamani kwenye kipindi hicho ambacho kazi hiyo imekoma. Kuamua thamani ya\(x\) ambayo kazi ni discontinuous, na kueleza pitfall ya kutumia teknolojia wakati wa kuzingatia mwendelezo wa kazi kwa kuchunguza grafu yake.

49) Kupata kikomo\(\lim \limits_{ x \to 1}f(x)\) na kuamua kama kazi zifuatazo ni kuendelea katika\(x=1\):

\[fx= \begin{cases} x^2+4 && x≠1 \\ 2 && x=1\end{cases} \nonumber \]

Jibu

kazi ni discontinuous kwa\(x=1\) sababu kikomo kama\(x\) mbinu\(1\) ni\(5\) na\(f(1)=2\).

50) Grafu ya\(f(x)= \dfrac{\sin (2x)}{x}\) inavyoonekana kwenye Kielelezo hapa chini. Je, kazi\(f(x)\) inaendelea kwa\(x=0?\) nini au kwa nini?

12.4: Derivatives

Mabadiliko kugawanywa na wakati ni mfano mmoja wa kiwango. Viwango vya mabadiliko katika mifano ya awali ni tofauti. Kwa maneno mengine, baadhi yamebadilika kwa kasi zaidi kuliko wengine. Ikiwa tungekuwa na graph kazi, tunaweza kulinganisha viwango kwa kuamua mteremko wa grafu.

Maneno

1) Je, mteremko wa kazi ya mstari ni sawa na derivative?

Jibu

Mteremko wa kazi ya mstari unakaa sawa. Derivative ya kazi ya jumla inatofautiana kulingana na\(x\). Wote mteremko wa mstari na derivative kwa hatua kupima kiwango cha mabadiliko ya kazi.

2) Ni tofauti gani kati ya kiwango cha wastani cha mabadiliko ya kazi kwenye muda\([x,x+h]\) na derivative ya kazi katika\(x\)?

3) gari alisafiri\(110\) maili katika kipindi cha muda kutoka 2:00 P.M. kwa 4:00 P.M. ilikuwa gari wastani kasi gani? Katika hasa 2:30 P.M., kasi ya gari imesajiliwa hasa\(62\) maili kwa saa. Jina lingine la kasi ya gari saa 2:30 P.M.? Kwa nini kasi hii inatofautiana na kasi ya wastani?

Jibu

Wastani kasi ni\(55\) maili kwa saa. Kasi ya instantaneous saa 2:30 p.m. ni\(62\) maili kwa saa. Kasi ya instantaneous inapima kasi ya gari kwa papo hapo wakati ambapo kasi ya wastani inatoa kasi ya gari juu ya muda.

4) Eleza dhana ya mteremko wa curve kwa uhakika\(x\).

5) Tuseme maji yanaingia ndani ya tangi kwa kiwango cha wastani cha\(45\) galoni kwa dakika. Tafsiri kauli hii katika lugha ya hisabati.

Jibu

Kiwango cha wastani cha mabadiliko ya kiasi cha maji katika tangi ni\(45\) galoni kwa dakika. Ikiwa\(f(x)\) ni kazi ya kutoa kiasi cha maji katika tangi wakati wowote\(t\), basi kiwango cha wastani cha mabadiliko ya\(f(x)\) kati\(t=a\) na\(t=b\) ni\(f(a)+45(b−a)\).

Kialjebra

Kwa mazoezi 6-17, tumia ufafanuzi wa derivative\(\lim \limits_{ h \to 0}\dfrac{f(x+h)-f(x)}{h}\) ili kuhesabu derivative ya kila kazi.

6)\(f(x)=3x-4\)

7)\(f(x)=-2x+1\)

Jibu

\(f'(x)=-2\)

8)\(f(x)=x^2-2x+1\)

9)\(f(x)=2x^2+x-3\)

Jibu

\(f'(x)=4x+1\)

10)\(f(x)=2x^2+5\)

11)\(f(x)=\dfrac{-1}{x-2}\)

Jibu

\(f'(x)=\dfrac{1}{(x-2)^2}\)

12)\(f(x)=\dfrac{2+x}{1-x}\)

13)\(f(x)=\dfrac{5-2x}{3+2x}\)

Jibu

\(\dfrac{-16}{(3+2x)^2}\)

14)\(f(x)=\sqrt{1+3x}\)

15)\(f(x)=3x^3-x^2+2x+5\)

Jibu

\(f'(x)=9x^2-2x+2\)

16)\(f(x)=5\)

17)\(f(x)=5\pi\)

Jibu

\(f'(x)=0\)

Kwa mazoezi 18-21, pata kiwango cha wastani cha mabadiliko kati ya pointi mbili.

18)\((-2,0)\) na\((-4,5)\)

19)\((4,-3)\) na\((-2,-1)\)

Jibu

\(-\dfrac{1}{3}\)

20)\((0,5)\) na\((6,5)\)

21)\((7,-2)\) na\((7,10)\)

Jibu

haijafafanuliwa

Kwa kazi za polynomial 22-25, pata derivatives.

22)\(f(x)=x^3+1\)

23)\(f(x)=-3x^2-7x=6\)

Jibu

\(f'(x)=-6x-7\)

24)\(f(x)=7x^2\)

25)\(f(x)=3x^3+2x^2+x-26\)

Jibu

\(f'(x)=9x^2+4x+1\)

Kwa kazi 26-28, pata equation ya mstari wa tangent kwenye safu\(x\) kwenye hatua iliyotolewa kwenye safu.

26)\(f(x)=2x^2-3x\; \; x=3\)

27)\(f(x)=x^2+1\; \; x=2\)

Jibu

\(y=12x-15\)

28)\(f(x)=\sqrt{x}\; \; x=9\)

29) Kwa zoezi zifuatazo, tafuta\(k\) vile kwamba mstari uliopewa ni tangent kwa grafu ya kazi.

\[f(x)=x^2-kx\; \; y=4x-9 \nonumber \]

Jibu

\(k=-10\)au\(k=2\)

Graphic

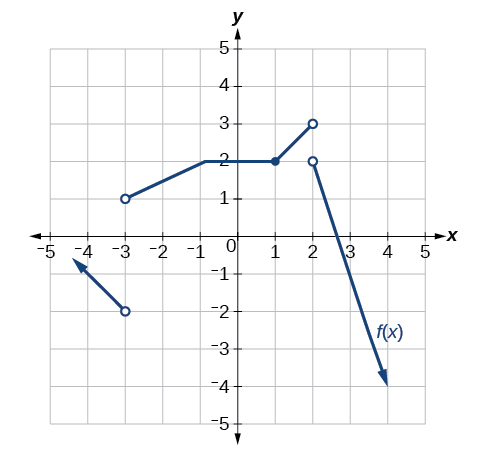
Kwa mazoezi 30-33, fikiria grafu ya kazi\(f\) na ueleze ambapo kazi inaendelea/kuacha na kutofautishwa/isiyofahamika.

30)

31)

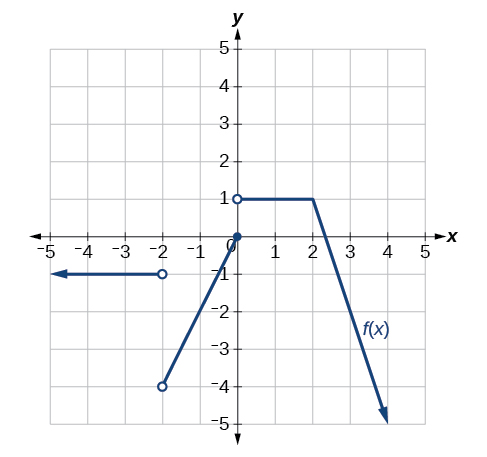
Jibu

Discontinuous katika\(x=-2\) na\(x=0\). Si differentiable katika\(-2, 0, 2\).

32)

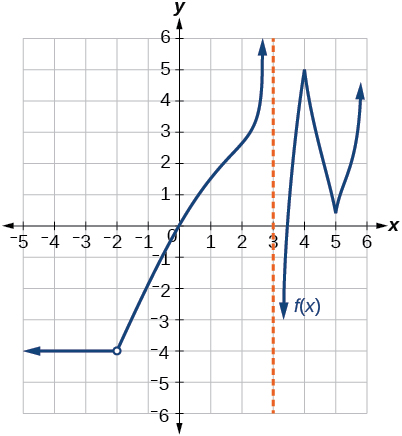
33)

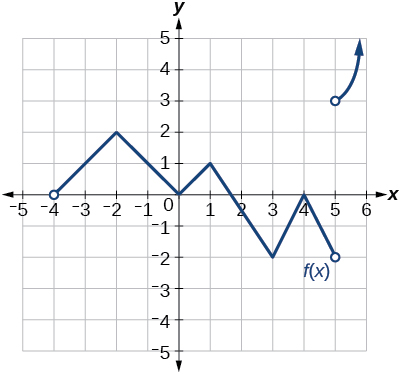
Jibu

Discontinuous katika\(x=5\). Si differentiable katika\(-4, -2, 0, 1, 3, 4, 5\).

Kwa mazoezi 34-43, tumia Kielelezo hapa chini ili kukadiria ama kazi kwa thamani fulani ya\(x\) au derivative kwa thamani fulani ya\(x\), kama ilivyoonyeshwa.

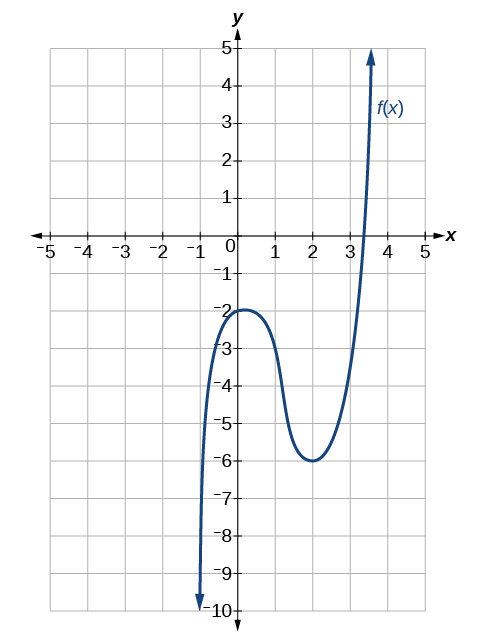
34)\(f(-1)\)

35)\(f(0)\)

Jibu

\(f(0)=-2\)

36)\(f(1)\)

37)\(f(2)\)

Jibu

\(f(2)=-6\)

38)\(f(3)\)

39)\(f'(-1)\)

Jibu

\(f'(-1)=9\)

40)\(f'(0)\)

41)\(f'(1)\)

Jibu

\(f'(1)=-3\)

42)\(f'(2)\)

43)\(f'(3)\)

Jibu

\(f'(3)=9\)

44) Mchoro kazi kulingana na maelezo hapa chini:

\[f'(x)=2x, f(2)=4 \nonumber \]

Teknolojia

45) Numerically kutathmini derivative. Kuchunguza tabia ya grafu ya\(f(x)=x^2\) karibu\(x=1\) na graphing kazi kwenye nyanja zifuatazo:\([0.9,1.1], [0.99,1.01], [0.999,1.001], [0.9999, 1.0001]\). Tunaweza kutumia kipengele kwenye calculator yetu kwamba moja kwa moja seti Ymin na Ymax kwa Xmin na Xmax maadili sisi preset. (Katika baadhi ya mahesabu ya kawaida ya graphing, kipengele hiki kinaweza kuitwa ZOOM FIT au ZOOM AUTO). Kwa kuchunguza maadili ya aina mbalimbali kwa dirisha hili la kutazama, takriban jinsi safu inavyobadilika\(x=1\), yaani, takriban derivative saa\(x=1\).

Jibu

Majibu hutofautiana. Mteremko wa mstari wa tangent karibu\(x=1\) ni\(2\).

Real-World Matumizi

Kwa mazoezi 46-50, kuelezea notation kwa maneno. Kiasi\(f(t)\) cha tank ya petroli, katika galoni,\(t\) dakika baada ya mchana.

46)\(f(0)=600\)

47)\(f'(30)=-20\)

Jibu

Saa 12:30 p.m., kiwango cha mabadiliko ya idadi ya galoni katika tangi ni\(-20\) galoni kwa dakika. Hiyo ni, tank inapoteza\(20\) galoni kwa dakika.

48)\(f(30)=0\)

49)\(f'(200)=30\)

Jibu

Kwa\(200\) dakika baada ya mchana, kiasi cha galoni katika tangi kinabadilika kwa kiwango cha\(30\) galoni kwa dakika.

50)\(f(240)=500\)

Kwa mazoezi 51-55, kuelezea kazi kwa maneno. Urefu,\(s\), wa projectile baada ya\(t\) sekunde hutolewa na\(s(t)=-16t^2+80t\).

51)\(s(2)=96\)

Jibu

Urefu wa projectile baada ya\(2\) sekunde ni\(96\) miguu.

52)\(s'(2)=16\)

53)\(s(3)=96\)

Jibu

Urefu wa projectile kwa\(t=3\) sekunde ni\(96\) miguu.

54)\(s'(3)=-16\)

55)\(s(0)=0, s(5)=0\)

Jibu

Urefu wa projectile ni sifuri\(t=0\) na tena\(t=5\). Kwa maneno mengine, projectile huanza chini na kuanguka duniani tena baada ya\(5\) sekunde.

Kwa mazoezi 56-57, kiasi\(V\) cha nyanja kwa heshima na radius yake\(r\) hutolewa na\(V=\dfrac{4}{3}\pi r^3\).

56) Pata kiwango cha wastani cha mabadiliko ya\(V\)\(r\) mabadiliko kutoka\(1\) cm hadi\(2\) cm.

57) Kupata kiwango instantaneous ya mabadiliko ya\(V\) wakati\(r=3\) cm.

Jibu

\(36\pi \)

Kwa mazoezi 58-60, mapato yanayotokana na kuuza\(x\) vitu hutolewa na\(R(x)=2x^2+10x\).

58) Kupata mabadiliko ya wastani wa kazi ya mapato kama\(x\) mabadiliko kutoka\(x=10\) kwa\(x=20\).

59) Tafuta\(R'(10)\) na kutafsiri.

Jibu

\(\$50.00\)kwa kila kitengo, ambayo ni kiwango cha instantaneous ya mabadiliko ya mapato wakati hasa\(10\) vitengo ni kuuzwa.

60) Tafuta\(R'(15)\) na kutafsiri. Linganisha\(R'(15)\) na\(R'(10)\), na kueleza tofauti.

Kwa mazoezi 61-63, gharama ya kuzalisha\(x\) simu za mkononi inaelezwa na kazi\(C(x)=x^2-4x+1000\).

61) Pata kiwango cha wastani cha mabadiliko katika gharama ya jumla kama\(x\) mabadiliko kutoka\(x=10\) kwa\(x=15\).

Jibu

\(\$21\)kwa kila kitengo

62) Kupata takriban gharama pembezoni, wakati\(15\) simu za mkononi kuwa zinazozalishwa, ya kuzalisha\(16^{th}\) simu za mkononi.

63) Kupata takriban gharama pembezoni, wakati\(20\) simu za mkononi kuwa zinazozalishwa, ya kuzalisha\(21^{st}\) simu za mkononi.

Jibu

\(\$36\)

Ugani

Kwa mazoezi 64-67, tumia ufafanuzi wa derivative kwa uhakika\(x=a\)\(\lim \limits_{x \to a}\dfrac{f(x)-f(a)}{x-a}\), ili kupata derivative ya kazi.

64)\(f(x)=\dfrac{1}{x^2}\)

65)\(f(x)=5x^2-x+4\)

Jibu

\(f'(x)=10a-1\)

66)\(f(x)=-x^2+4x+7\)

67)\(f(x)=\dfrac{-4}{3-x^2}\)

Jibu

\(\dfrac{4}{(3-x)^2}\)

Wachangiaji na Majina

• Template:OpenStaxPreCalc