12.4: Derivatives
- Page ID
- 181369
Kijana wastani nchini Marekani anafungua mlango wa jokofu inakadiriwa mara 25 kwa siku. Inadhaniwa, wastani huu umeongezeka kutoka miaka 10 iliyopita wakati kijana wastani alifungua mlango wa jokofu mara 20 kwa siku 1. Inakadiriwa kuwa televisheni iko nyumbani masaa 6.75 kwa siku, ambapo wazazi hutumia takribani dakika 5.5 kwa siku wakiwa na mazungumzo yenye maana na watoto wao. Wastani huu, pia, si sawa na walivyokuwa miaka 10 iliyopita, wakati televisheni ilikuwa inakadiriwa saa 6 kwa siku katika kaya ya kawaida, na wazazi walitumia dakika 12 kwa siku katika mazungumzo yenye maana na watoto wao. Je, matukio haya yanafanana nini? Kazi zinazowakilisha zimebadilika kwa muda. Katika sehemu hii, tutazingatia njia za kompyuta mabadiliko hayo kwa muda.
Kutafuta Kiwango cha Wastani cha Mabadiliko ya Kazi
Kazi zinazoelezea mifano hapo juu zinahusisha mabadiliko baada ya muda. Mabadiliko ya kugawanywa na wakati ni mfano mmoja wa kiwango. Viwango vya mabadiliko katika mifano ya awali ni tofauti. Kwa maneno mengine, baadhi yamebadilika kwa kasi zaidi kuliko wengine. Ikiwa tungekuwa na graph kazi, tunaweza kulinganisha viwango kwa kuamua mteremko wa grafu.
Mstari wa tangent kwa curve ni mstari unaozunguka pembe kwa hatua moja tu lakini hauuvuka huko. (Line tangent inaweza intersect Curve katika hatua nyingine mbali na hatua ya riba.) Kama sisi zoom katika Curve katika hatua hiyo, Curve inaonekana linear, na mteremko wa Curve katika hatua hiyo ni karibu na mteremko wa mstari tangent katika hatua hiyo.
Kielelezo\(\PageIndex{1}\) inawakilisha kazi\(f(x)=x^3−4x\). Tunaweza kuona mteremko kwa pointi mbalimbali kando ya pembe.
- mteremko katika\(x=−2\) ni 8
- mteremko katika\(x=−1\) ni -1
- mteremko katika\(x=2\) ni 8
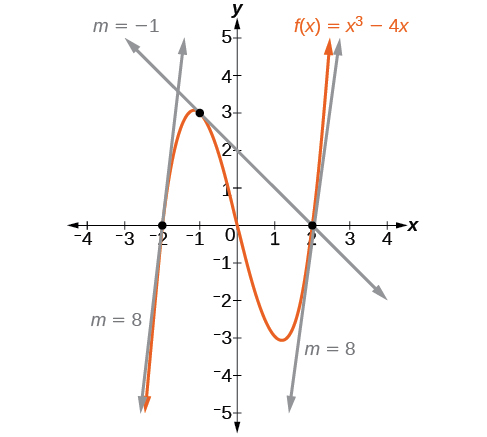
Hebu fikiria hatua juu ya Curve ya kazi\(f\) katika\(x=a\) kama inavyoonekana katika Kielelezo\(\PageIndex{1}\). Kuratibu ya uhakika ni\((a,f(a))\). Unganisha hatua hii na hatua ya pili juu ya Curve kidogo na haki ya\(x=a\), na x -thamani iliongezeka kwa baadhi ndogo idadi halisi\(h\). Kuratibu za hatua hii ya pili ni\((a+h,f(a+h))\) kwa thamani nzuri\(h\).
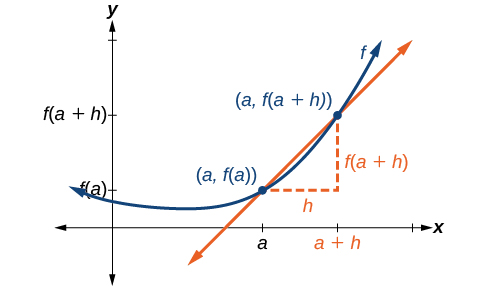
Tunaweza kuhesabu mteremko wa mstari unaounganisha pointi mbili\((a,f(a))\) na\((a+h,f(a+h))\), inayoitwa mstari wa salama, kwa kutumia formula ya mteremko,
\[ \mathrm{slope = \dfrac{change \; in \; y}{change \; in \; x}} \]
Tunatumia notation\(m_{sec}\) kuwakilisha mteremko wa mstari wa salama kuunganisha pointi mbili.
\[\begin{align} m_{sec} &= \dfrac{f(a+h)−f(a)}{(a+h)−(a) } \\ &= \dfrac{f(a+h)−f(a)}{\cancel{a}+h−\cancel{a}} \end{align}\]
\(m_{sec}\)Mteremko unafanana na kiwango cha wastani cha mabadiliko kati ya pointi mbili\((a,f(a))\) na\((a+h,f(a+h)).\)
\[m_{sec}=\dfrac{f(a+h)−f(a)}{h}\]
KIWANGO CHA WASTANI WA MABADILIKO KATI YA POINTI MBILI KWENYE CURVE
Kiwango cha wastani cha mabadiliko (AROC) kati ya pointi mbili\((a,f(a))\) na\((a+h,f(a+h))\) kwenye pembe ya\(f\) ni mteremko wa mstari unaounganisha pointi mbili na hutolewa na
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}\]
Mfano\(\PageIndex{1}\): Finding the Average Rate of Change
Pata kiwango cha wastani cha mabadiliko ya kuunganisha pointi\((2,−6)\) na\((−1,5)\).
Suluhisho
Tunajua kiwango cha wastani cha mabadiliko ya kuunganisha pointi mbili inaweza kutolewa na
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}\]
Ikiwa hatua moja ni\((2,−6)\), au\((2,f(2))\), basi\(f(2)=−6.\)
Thamani\(h\) ni uhamisho kutoka\(2\) kwa\(−1\), ambayo ni sawa\(−1−2=−3.\)
Kwa upande mwingine,\(f(a+h)\) ni y -kuratibu katika\(a+h\), ambayo ni\(2+(−3)\) au\(−1,\) hivyo\(f(a+h)=f(−1)=5\).
\[\begin{align} \text{AROC} &= \dfrac{f(a+h)−f(a)}{h} \\ &=\dfrac{5−(−6)}{−3} \\&=\dfrac{11}{−3} \\ &=−\dfrac{11}{3} \end{align}\]
Zoezi\(\PageIndex{1}\)
Pata kiwango cha wastani cha mabadiliko ya kuunganisha pointi\((−5,1.5)\) na\((−2.5,9)\)
Suluhisho
3
Kuelewa Kiwango cha Mabadiliko ya Instantaneous
Sasa kwa kuwa tunaweza kupata kiwango cha wastani wa mabadiliko, tuseme sisi kufanya\(h\) katika Kielelezo\(\PageIndex{2}\) ndogo na ndogo. Kisha\(a+h\) itakuwa mbinu\(a\) kama\(h\) anapata ndogo, kupata karibu na karibu na 0. Vivyo hivyo, hatua ya pili\((a+h,f(a+h))\) itakaribia hatua ya kwanza,\((a,f(a))\). Kwa hiyo, mstari wa kuunganisha kati ya pointi mbili, inayoitwa mstari wa secant, utapata karibu na karibu na kuwa tangent kwa kazi\(x=a\), na mteremko wa mstari wa secant utapata karibu na karibu na mteremko wa tangent\(x=a\) (Kielelezo\(\PageIndex{3}\)).
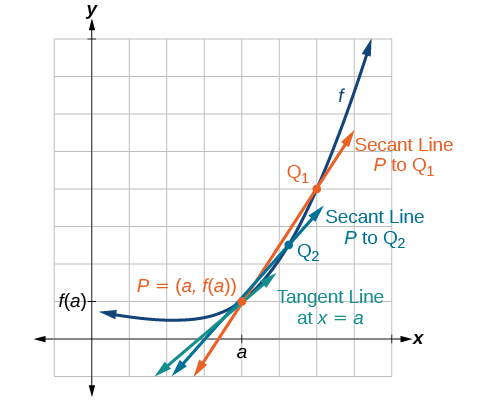
Kwa sababu sisi ni kuangalia kwa mteremko wa tangent katika\(x=a\), tunaweza kufikiria kipimo cha mteremko wa Curve ya kazi\(f\) katika hatua fulani kama kiwango cha mabadiliko katika papo fulani. Tunaita mteremko huu kiwango cha mabadiliko ya papo hapo, au derivative ya kazi katika\(x=a.\) Wote wanaweza kupatikana kwa kutafuta kikomo cha mteremko wa mstari unaounganisha uhakika\(x=a\) na hatua ya pili karibu sana kwenye pembe. Kwa kazi\(f\) wote kiwango instantaneous ya mabadiliko ya kazi na derivative ya kazi katika\(x=a\) yameandikwa kama\(f'(a),\) na tunaweza kufafanua yao kama kikomo mbili upande mmoja ambayo ina thamani sawa kama akakaribia kutoka kushoto au kulia.
\[f′(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
Maneno ambayo kikomo kinapatikana hujulikana kama quotient tofauti.
UFAFANUZI WA KIWANGO CHA MABADILIKO YA INSTANTANEOUS
derivative, au kiwango cha instantaneous ya mabadiliko, ya kazi\(f\) katika\(x=a\), ni iliyotolewa na
\[ f'(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
Maneno\(\frac{f(a+h)−f(a)}{h}\) huitwa quotient tofauti.
Tunatumia tofauti quotient kutathmini kikomo cha kiwango cha mabadiliko ya kazi kama\(h\) mbinu 0.
Derivatives: Tafsiri na Uthibit
Derivative ya kazi inaweza kutafsiriwa kwa njia tofauti. Inaweza kuzingatiwa kama tabia ya grafu ya kazi au mahesabu kama kiwango cha namba ya mabadiliko ya kazi.
- Derivative ya kazi\(f(x)\) katika hatua\(x=a\) ni mteremko wa mstari tangent kwa Curve\(f(x)\) saa\(x=a\). Derivative ya\(f(x)\) saa\(x=a\) imeandikwa\(f′(a)\).
- \(f′(a)\)Hatua za derivative jinsi Curve inavyobadilika kwa hatua\((a,f(a))\).
- derivative\(f′(a)\) inaweza kuwa mawazo ya kama kiwango instantaneous ya mabadiliko ya kazi\(f(x)\) katika\(x=a\).
- Ikiwa kazi inachukua umbali kama kazi ya muda, basi derivative inachukua kasi ya papo hapo kwa wakati\(t=a\).
MAELEZO KWA AJILI YA DERIVATIVE
equation ya derivative ya kazi\(f(x)\) imeandikwa kama\(y′=f′(x)\), ambapo\(y=f(x)\). nukuu\(f′(x)\) ni kusoma kama “\(f\)mkuu wa\(x\).” Maelezo mbadala ya derivative ni pamoja na yafuatayo:
\[f′(x)=y′=\dfrac{dy}{dx}=\dfrac{df}{dx}=\dfrac{d}{dx} f(x)=Df(x)\]
kujieleza sasa\(f′(x)\) ni kazi ya\(x\); kazi hii inatoa mteremko wa Curve\(y=f(x)\) katika thamani yoyote ya\(x\). Derivative ya kazi kwa\(f(x)\) hatua\(x=a\) inaashiria\(f′(a)\).
jinsi ya: Kutokana na kazi\(f\), find the derivative by applying the definition of the derivative.
- Tumia\(f(a+h)\).
- Tumia\(f(a)\).
- Mbadala na kurahisisha\(\frac{f(a+h)−f(a)}{h}\).
- Tathmini kikomo ikiwa ipo:\(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\).
Mfano\(\PageIndex{1}\): Finding the Derivative of a Polynomial Function
Pata derivative ya\(f(x)=x^2−3x+5\) kazi\(x=a.\)
Suluhisho
Tuna:
\[ f′(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \;\;\;\;\;\;\;\; \text{Definition of a derivative}\]
Mbadala\(f(a+h)=(a+h)^2−3(a+h)+5\) na\(f(a)=a^2−3a+5.\)
\[ \begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{(a+h)(a+h)−3(a+h)+5−(a^2−3a+5)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{a^2+2ah+h^2−3a−3h+5−a^2+3a−5}{h} && \text{Evaluate to remove parentheses.} \\ & = \lim \limits_{h \to 0} \dfrac{\cancel{a^2}+2ah+h^2−\cancel{3a}−3h+\cancel{5}−\cancel{a^2}+\cancel{3a}−\cancel{5}}{h} && \text{Simplify.} \\ & = \lim \limits_{h \to 0} \dfrac{2ah+h^2−3h}{h} && \text{Factor out an }h. \\ & =2a+0−3 && \text{Evaluate the limit.} \\ &=2a−3 \end{align} \]
Zoezi\(\PageIndex{1}\)
Pata derivative ya\(f(x)=3x^2+7x\) kazi\(x=a\)
Suluhisho
\(f′(a)=6a+7\)
Kutafuta Derivatives ya Kazi nzuri
Ili kupata derivative ya kazi ya busara, wakati mwingine tutawezesha kujieleza kwa kutumia mbinu za algebraic ambazo tayari tumejifunza.
Mfano\(\PageIndex{1}\): Finding the Derivative of a Rational Function
Pata derivative ya kazi\(f(x)=\dfrac{3+x}{2−x}\) katika\(x=a.\)
\[\begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{\frac{3+(a+h)}{2−(a+h)}−(\frac{3+a}{2−a})}{h} && \text{Substitute }f(a+h) \text{ and }f(a) \\ &= \lim \limits_{h \to 0} \dfrac{(2−(a+h))(2−a)[ \frac{3+(a+h)}{2−(a+h)}−(\frac{3+a}{2−a}) ]}{(2−(a+h))(2−a)(h)} && \text{Multiply numerator and denominator by } (2−(a+h))(2−a) \\ & =\lim \limits_{h \to 0}\dfrac{(\cancel{2−(a+h)})(2−a)(\frac{3+(a+h)}{\cancel{(2−(a+h))}})−(2−(a+h))\cancel{(2−a)}(\frac{3+a}{\cancel{2−a}})}{(2−(a+h))(2−a)(h)} && \text{Distribute} \\ & =\lim \limits_{h \to 0} \dfrac{6−3a+2a−a^2+2h−ah−6+3a+3h−2a+a^2+ah}{(2−(a+h))(2−a)(h)} && \text{Multiply} \\ &=\lim \limits_{h \to 0} \dfrac{5 \cancel{h}}{(2−(a+h))(2−a)(\cancel{h})} && \text{Combine like terms} \\ & = \lim \limits_{h \to 0} \dfrac{5}{(2−(a+h))(2−a)} && \text{Cancel like factors} \\ & =\dfrac{5}{(2−(a+0))(2−a)}=\dfrac{5}{(2−a)(2−a)}=\dfrac{5}{(2−a)^2} && \text{Evaluate the limit} \end{align}\]
Zoezi\(\PageIndex{1}\):
Kupata derivative ya kazi\(f(x)=\frac{10x+11}{5x+4}\) katika\(x=a\).
\[f′(a)=\dfrac{−15}{(5a+4)^2}\]
Kutafuta derivatives ya Kazi na Mizizi
Ili kupata derivatives ya kazi na mizizi, tunatumia mbinu ambazo tumejifunza kupata mipaka ya kazi na mizizi, ikiwa ni pamoja na kuzidisha kwa conjugate.
Mfano\(\PageIndex{1}\): Finding the Derivative of a Function with a Root
Pata derivative ya\(f(x)=4\sqrt{x}\) kazi\(x=36.\)
Tuna
\[\begin{align} f′(a) &=\lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{4\sqrt{a+h}−4\sqrt{a}}{h} && \text{Substitute }f(a+h) \text{ and }f(a) \end{align}\]
Panua nambari na denominator kwa conjugate:\(\frac{4\sqrt{a+h}+4\sqrt{a}}{4\sqrt{a+h}+4\sqrt{a}}\).
\[\begin{align} f′(a) &= \lim \limits_{h \to 0}\bigg( \dfrac{4\sqrt{a+h}−4\sqrt{a}}{h} \bigg)⋅ \bigg(\dfrac{4\sqrt{a+h}+4\sqrt{a}}{4\sqrt{a+h}+4\sqrt{a}} \bigg) \\ &=\lim \limits_{h \to 0} \bigg( \dfrac{16(a+h)−16a}{h4(\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Multiply.} \\ &=\lim \limits_{ h \to 0} \bigg( \dfrac{\cancel{16a}+16h\cancel{−16a}}{h4(\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Distribute and combine like terms.} \\ &= \lim \limits_{h \to 0}\bigg(\dfrac{16\cancel{h}}{\cancel{h}(4\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Simplify.} \\ & = \lim \limits_{h \to 0} \bigg( \dfrac{16}{4\sqrt{a+h}+4\sqrt{a}} \bigg) && \text{Evaluate the limit by letting } h=0. \\ & =\dfrac{16}{8\sqrt{a}}=\dfrac{2}{\sqrt{a}} \\ f′(36) &= \dfrac{2}{\sqrt{36}} && \text{Evaluate the derivative at } x=36. \\ &=\dfrac{2}{6} \\ & =\dfrac{1}{3} \end{align}\]
Zoezi\(\PageIndex{1}\):
Pata derivative ya\(f(x)=9\sqrt{x}\) kazi\(x=9.\)
\(\frac{3}{2}\)
Kupata Viwango vya Mabadiliko ya Instantaneous
Maombi mengi ya derivative kuhusisha kuamua kiwango cha mabadiliko katika papo fulani ya kazi na kujitegemea variable wakati-ambayo ni kwa nini neno instantaneous ni kutumika. Fikiria urefu wa mpira kuchafuka juu na kasi ya awali ya 64 miguu kwa sekunde, iliyotolewa na\(s(t)=−16t^2+64t+6\), ambapo\(t\) ni kipimo katika sekunde na\(s(t)\) ni kipimo kwa miguu. Tunajua njia ni ile ya parabola. Derivative itatuambia jinsi urefu unavyobadilika wakati wowote kwa wakati. Urefu wa mpira umeonyeshwa kwenye Kielelezo kama kazi ya muda. Katika fizikia, tunaita hii “s - t grafu.”
Mfano\(\PageIndex{1}\): Finding the Instantaneous Rate of Change
Kwa kutumia kazi hapo juu,\(s(t)=−16t^2+64t+6\), ni nini kasi instantaneous ya mpira katika 1 pili na 3 sekunde katika ndege yake?
Kasi katika\(t=1\) na\(t=3\) ni kiwango cha instantaneous ya mabadiliko ya umbali kwa wakati, au kasi. Angalia kwamba urefu wa awali ni miguu 6. Ili kupata kasi ya papo hapo, tunapata derivative na tathmini yake\(t=1\) na\(t=3\):
\[\begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{−16(t+h)^2+64(t+h)+6−(−16t^2+64t+6)}{h} && \text{Substitute } s(t+h) \text{ and } s(t). \\ &= \lim \limits_{h \to 0} \dfrac{−16t^2−32ht−h^2+64t+64h+6+16t^2−64t−6}{h} && \text{Distribute} \\ & =\lim \limits_{h \to 0} \dfrac{−32ht−h^2+64h}{h} && \text{Simplify.} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{h}(−32t−h+64)}{\cancel{h}} && \text{Factor the numerator.} \\ & =\lim \limits_{h \to 0}−32t−h+64 && \text{ Cancel out the common factor} h. \\ s′(t) &=−32t+64 && \text{Evaluate the limit by letting} h=0. \end{align}\]
Kwa thamani yoyote ya\(t\),\(s′(t)\) inatuambia kasi kwa kuwa thamani ya\(t\).
Tathmini\(t=1\) na\(t=3\).
\[\begin{align}s′(1) &=−32(1)+64=32 \\ s′(3) &=−32(3)+64=−32 \end{align}\]
Kasi ya mpira baada ya pili ya pili ni futi 32 kwa pili, kama ilivyo njiani.
Kasi ya mpira baada ya sekunde 3 ni futi -32 kwa sekunde, kama ilivyo njiani chini.
Zoezi\(\PageIndex{1}\):
Msimamo wa mpira hutolewa na kasi\(s(t)=−16t^2+64t+6.\) yake ya sekunde 2 katika kukimbia?
0
Kutumia Grafu ili Kupata Viwango vya Mabadiliko ya papo hapo
Tunaweza kukadiria kiwango cha instantaneous ya mabadiliko katika\(x=a\) kwa kuchunguza mteremko wa Curve ya kazi\(f(x)\) katika\(x=a\). Tunafanya hivyo kwa kuchora mstari wa mstari kwenye kazi\(x=a\) na kutafuta mteremko wake.
jinsi ya: Kutokana na grafu ya kazi\(f( x )\), find the instantaneous rate of change of the function at \(x=a\).
- Pata\(x=a\) kwenye grafu ya kazi\(f(x)\).
- Chora mstari wa tangent, mstari unaoendelea kwa njia ya\(x=a\) saa\(a\) na hakuna hatua nyingine katika sehemu hiyo ya Curve. Kupanua mstari mbali kutosha mahesabu ya mteremko wake kama
\[\dfrac{\text{change in }y}{\text{change in }x.}\]
Mfano\(\PageIndex{1}\): Estimating the Derivative at a Point on the Graph of a Function
Kutoka kwenye grafu ya kazi\(y=f(x)\) iliyotolewa kwenye Kielelezo, tathmini kila moja ya yafuatayo:
\(f(0) ; f(2) ; f'(0) ; f'(2)\)
Ili kupata thamani ya kazi\(f(a)\), tafuta y -kuratibu katika\(x=a\).
Ili kupata derivative katika\(x=a, f′(a),\) kuteka mstari wa tangent saa\(x=a,\) na kukadiria mteremko wa mstari huo wa tangent. Angalia Kielelezo.
- \(f(0)\)ni y -kuratibu katika\(x=0\). Hatua ina kuratibu\((0,1)\), hivyo\(f(0)=1\).
- \(f(2)\)ni y -kuratibu katika\(x=2\). Hatua ina kuratibu\((2,1)\), hivyo\(f(2)=1\).
- \(f′(0)\)hupatikana kwa kukadiria mteremko wa mstari wa tangent kwa Curve saa\(x=0\). Mstari wa tangent kwa curve\(x=0\) inaonekana usawa. Mstari wa usawa una mteremko wa 0, hivyo\(f′(0)=0\).
- \(f′(2)\)hupatikana kwa kukadiria mteremko wa mstari wa tangent kwa Curve saa\(x=2\). Kuzingatia njia ya mstari tangent kwa Curve saa\(x=2\). Kama\(x\) thamani inapohamisha kitengo kimoja upande wa kulia,\(y\) thamani inakwenda vitengo vinne hadi hatua nyingine kwenye mstari. Hivyo, mteremko ni 4, hivyo\(f′(2)=4\).
Zoezi\(\PageIndex{1}\):
Kutumia grafu ya kazi\(f(x)=x^3−3x\) iliyoonyeshwa kwenye Kielelezo, makadirio:\(f(1), f′(1), f(0)\), na\(f′(0)\).
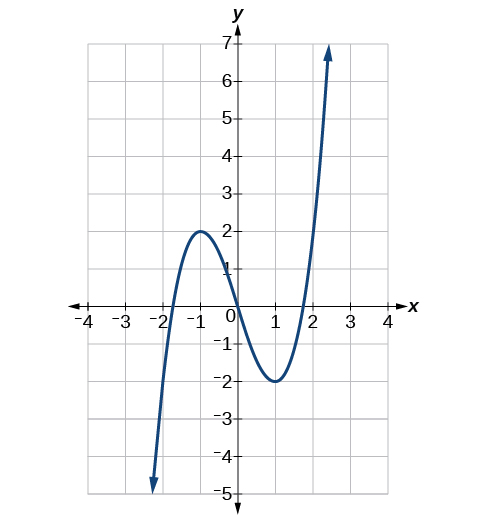
-2, -2,0, 0, -3
Kutumia Viwango vya Mabadiliko ya Instantaneous Kutatua Matatizo halisi ya Dunia
Njia nyingine ya kutafsiri kiwango cha instantaneous cha mabadiliko katika\(x=a\) ni kuchunguza kazi katika mazingira halisi ya ulimwengu. Kitengo cha derivative ya kazi\(f(x)\) ni
\[\dfrac{\text{output units}}{\text{input unit}}\]
Kitengo hicho kinaonyesha kwa vitengo vingi vya pato hubadilika kwa kila mabadiliko ya kitengo kimoja cha pembejeo. Kiwango cha mabadiliko ya papo hapo kinaonyesha kitu kimoja: vitengo vya mabadiliko ya pato kwa mabadiliko ya kitengo kimoja cha pembejeo.
Mfano mmoja wa kiwango cha mabadiliko ya papo hapo ni gharama ndogo. Kwa mfano, tuseme gharama za uzalishaji kwa kampuni ya kuzalisha\(x\) vitu hutolewa na\(C(x)\), kwa maelfu ya dola. Kazi ya derivative inatuambia jinsi gharama inabadilika kwa thamani yoyote ya\(x\) katika uwanja wa kazi. Kwa maneno mengine,\(C′(x)\) ni kufasiriwa kama gharama ndogo, gharama ya ziada katika maelfu ya dola ya kuzalisha bidhaa moja zaidi wakati\(x\) vitu kuwa zinazozalishwa. Kwa mfano,\(C′(11)\) ni takriban gharama za ziada katika maelfu ya dola ya kuzalisha bidhaa 12 th baada ya vitu 11 kuwa zinazozalishwa. \(C′(11)=2.50\)ina maana kwamba wakati 11 vitu kuwa zinazozalishwa, kuzalisha 12 th bidhaa bila kuongeza gharama ya jumla kwa takriban $2,500.00.
Mfano\(\PageIndex{1}\): Finding a Marginal Cost
Gharama kwa dola za kuzalisha\(x\) kompyuta za kompyuta kwa dola ni\(f(x)=x^2−100x.\) Wakati ambapo kompyuta 200 zimezalishwa, ni gharama gani ya karibu ya kuzalisha kitengo cha 201 st?
Kama\(f(x)=x^2−100x\) inaelezea gharama ya kuzalisha\(x\) kompyuta,\(f′(x)\) kuelezea gharama ndogo. Tunahitaji kupata derivative. Kwa madhumuni ya kuhesabu derivative, tunaweza kutumia kazi zifuatazo:
\[\begin{align} f(a+b) &=(x+h)^2−100(x+h) \\ f(a) &=a ^2−100a \end{align}\]
\[\begin{align} f′(x) &=\dfrac{f(a+h)−f(a)}{h} && \text{Formula for a derivative} \\ &=\dfrac{(x+h)^2−100(x+h)−(x^2−100x)}{h} \\ \text{Substitute }f(a+h) \text{ and }f(a). \\ & =\dfrac{x^2+2xh+h^2−100x−100h−x^2+100x}{h} && \text{Multiply polynomials, distribute.} \\ &= \text{2xh+h^2−100h}{h} && \text{Collect like terms.} \\ &=\dfrac{\cancel{h}(2x+h−100)}{\cancel{h}} && \text{Factor and cancel like terms.} \\ &=2x+h−100 && \text{Simplify.} \\ &=2x−100 && \text{Evaluate when }h=0. \\ f′(x) &=2x−100 && \text{Formula for marginal cost} \\ f′(200) &=2(200)−100=300 && \text{Evaluate for 200 units.} \end{align}\]
Gharama ndogo ya kuzalisha kitengo cha 201 itakuwa takriban $300.
Mfano\(\PageIndex{1}\):Interpreting a Derivative in Context
Gari linaacha makutano. Umbali unaotembea kwa maili hutolewa na kazi\( f(t)\), ambapo\(t\) inawakilisha masaa. Eleza maelezo yafuatayo:
\(f(0)=0 f′(1)=60 f(1)=70 f(2.5)=150\)
Kwanza tunahitaji kutathmini kazi\(f(t)\) na derivative ya kazi\(f′(t)\), na kutofautisha kati ya mbili. Tunapotathmini kazi\(f(t)\), tunapata umbali ambao gari limesafiri kwa\(t\) masaa. Tunapotathmini derivative f′ (t), f (t), tunapata kasi ya gari baada ya\(t\) masaa.
- \(f(0)=0\)ina maana kwamba katika masaa sifuri, gari ina alisafiri maili sifuri.
- \(f′(1)=60\)ina maana kwamba saa moja katika safari, gari ni kusafiri 60 maili kwa saa.
- \(f(1)=70\)ina maana kwamba saa moja katika safari, gari ina alisafiri 70 maili. Wakati fulani wakati wa saa ya kwanza, basi, gari lazima limesafiri kwa kasi zaidi kuliko ilivyokuwa kwenye alama ya saa 1.
- \(f(2.5)=150\)ina maana kwamba saa mbili na dakika thelathini katika safari, gari ina alisafiri 150 maili.
Zoezi\(\PageIndex{1}\)
Mkimbiaji anaendesha kando ya barabara moja kwa moja mashariki-magharibi. kazi\(f(t)\) anatoa ngapi miguu upande wa mashariki ya hatua yake ya kuanzia yeye ni baada ya\(t\) sekunde. Tafsiri kila moja ya yafuatayo kama inahusiana na mkimbiaji.
\(f(0)=0 ; f(10)=150 ; f′(10)=15 ; f′(20)=−10 ; f(40)=−100\)
- Baada ya sekunde sifuri, amesafiri miguu 0.
- Baada ya sekunde 10, amesafiri miguu 150 mashariki.
- Baada ya sekunde 10, anahamia upande wa mashariki kwa kiwango cha 15 ft/sec.
- Baada ya sekunde 20, anahamia upande wa magharibi kwa kiwango cha 10 ft/sec.
- Baada ya sekunde 40, yeye ni miguu 100 upande wa magharibi wa hatua yake ya kuanzia.
Kutafuta Pointi Ambapo Derivative ya Kazi Haipo
Ili kuelewa ambapo derivative ya kazi haipo, tunahitaji kukumbuka kile kinachotokea wakati kazi\(f(x)\) ina derivative katika\(x=a\). Tuseme tunatumia matumizi ya graphing ili kuvuta\(x=a\). Ikiwa kazi\(f(x)\) ni tofauti, yaani, ikiwa ni kazi ambayo inaweza kutofautishwa, basi karibu huingia, karibu zaidi grafu inakaribia mstari wa moja kwa moja. Tabia hii inaitwa linearity.
Angalia grafu katika Kielelezo. Karibu tunakaribia juu ya hatua, zaidi ya mstari inaonekana.
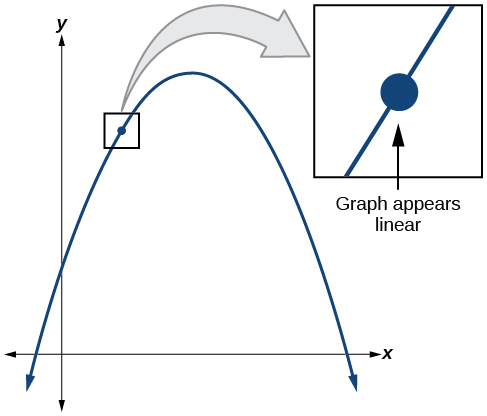
Grafu ya kazi\(f(x)=| x |\), na x -axis kutoka -0.1 hadi 0.1 na y -axis kutoka -0.1 hadi 0.1.
Je! Ni sifa gani za grafu ambayo haijulikani kwa hatua? Hapa ni baadhi ya mifano ambayo kazi\(f(x)\) si tofauti katika\(x=a\).
Katika Kielelezo, tunaona grafu ya
\[f(x)=\begin{cases} x^2, &&x≤2 \\ 8−x, &&x>2.\end{cases} .\]
Kumbuka kwamba, kama\(x\) inakaribia 2 kutoka upande wa kushoto, kikomo cha mkono wa kushoto kinaweza kuzingatiwa kuwa 4, wakati kama\(x\) inakaribia 2 kutoka kulia, kikomo cha mkono wa kulia kinaweza kuzingatiwa kuwa 6. Tunaona kwamba ina discontinuity katika\(x=2\).
Grafu ya\(f(x)\) ina discontinuity katika\(x=2\).
Katika Kielelezo, tunaona grafu ya\(f(x)=|x|\). Tunaona kwamba grafu ina hatua ya kona\(x=0\).
Grafu ya\(f(x)=| x |\) ina hatua ya kona\(x=0\).
Katika Kielelezo, tunaona kwamba grafu ya\(f(x)=x^{\frac{2}{3}}\) ina cusp saa\(x=0\). Cusp ina kipengele kipekee. Kuondoka mbali na cusp, mipaka ya mkono wa kushoto na wa kulia inakaribia ama infinity au infinity hasi. Angalia mistari ya tangent kama\(x\) inakaribia 0 kutoka kwa kushoto na kulia inaonekana kuongezeka kwa kasi, lakini moja ina mteremko hasi, mwingine ana mteremko mzuri.
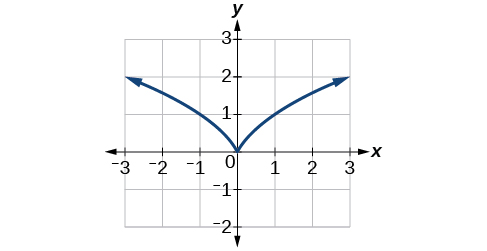
Grafu ya\(f(x)=x^\frac{2}{3}\) ina cusp saa\(x=0\).
Katika Kielelezo, tunaona kwamba grafu ya\(f(x)=x^{frac{1}{3}}\) ina tangent wima katika\(x=0\). Kumbuka kwamba tangents wima ni mistari ya wima, hivyo ambapo tangent wima ipo, mteremko wa mstari haujulikani. Hii ndiyo sababu derivative, ambayo inachukua mteremko, haipo huko.

Grafu ya\(f(x)=x^\frac{1}{3}\) ina tangent wima katika\(x=0\).
kutofautisha
kazi\(f(x)\) ni kutofautishwa katika\(x=a\) kama derivative ipo katika\(x=a\), ambayo ina maana kwamba\(f′(a)\) ipo.
Kuna matukio manne ambayo kazi\(f(x)\) haijulikani kwa uhakika\(x=a\).
- Wakati kuna discontinuity katika\(x=a\).
- Wakati kuna hatua ya kona saa\(x=a\).
- Wakati kuna cusp katika\(x=a\).
- Wakati wowote mwingine wakati kuna tangent wima saa\(x=a\).
Mfano\(\PageIndex{1}\): Determining Where a Function Is Continuous and Differentiable from a Graph
Kutumia Kielelezo, tambua ambapo kazi ni
- endelevu
- kukomeshwa
- inayoweza kutofautishwa
- si kutofautishwa
Katika pointi ambapo grafu imekoma au haijulikani, sema kwa nini.
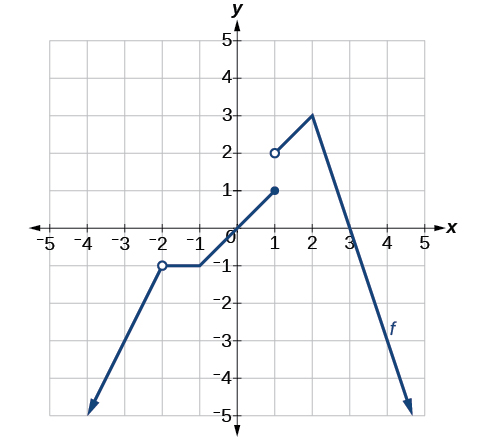
Vipindi vitatu ambapo kazi inaendelea
Grafu ya ni tofauti juu ya\((−∞,−2)∪(−2,−1)∪(−1,1)∪(1,2)∪(2,∞)\). Grafu ya\(f(x)\) haipatikani\(x=−2\) kwa sababu ni hatua ya kuacha,\(x=−1\) kwa sababu ya kona kali,\(x=1\) kwa sababu ni hatua ya kuacha, na\(x=2\) kwa sababu ya kona kali. Angalia Kielelezo.
Tano vipindi ambapo kazi ni differentiable
Zoezi\(\PageIndex{1}\):
Kuamua ambapo kazi\(y=f(x)\) inavyoonekana katika Kielelezo ni kuendelea na kutofautishwa kutoka grafu.
Grafu ya\(f\) inaendelea\((−∞,1)∪(1,3)∪(3,∞).\) kwenye Grafu ya f f imekoma\(x=1\) na\(x=3\). Grafu ya\(f\) ni tofauti juu ya\((−∞,1)∪(1,3)∪(3,∞)\). Grafu ya\(f\) haijulikani\(x=1\) na\(x=3\).
Kutafuta Equation ya Tangent Line kwa Grafu ya Kazi
equation ya mstari tangent kwa Curve ya kazi\(f(x)\) katika\(x=a\) ni inayotokana na hatua mteremko aina ya mstari,\(y=m(x−x_1)+y_1\). Mteremko wa mstari ni mteremko wa Curve saa\(x=a\) na kwa hiyo ni sawa na derivative ya\(f(x)\)\(x=a.\) katika. jozi kuratibu ya uhakika juu ya mstari katika\(x=a\) ni\((a,f(a))\).\(f′(a),\)
Kama sisi badala katika fomu hatua-mteremko, tuna
Equation ya mstari wa tangent ni
\[y=f'(a)(x−a)+f(a)\]
F
equation ya mstari tangent kwa Curve ya kazi\(f\) katika hatua\(x=a\) ni
\[y=f'(a)(x−a)+f(a)\]
jinsi ya: Kutokana na kazi\(f\), find the equation of a line tangent to the function at \(x=a\).
- Kupata derivative ya\(f(x)\) saa\(x=a\) kutumia\(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}.\)
- Tathmini kazi katika\(x=a\). Hii ni\(f(a)\).
- Mbadala\((a,f(a))\) na\(f′(a)\) katika\(y=f'(a)(x−a)+f(a)\).
- Andika equation ya mstari wa tangent katika fomu\(y=mx+b\).
Mfano\(\PageIndex{1}\): Finding the Equation of a Line Tangent to a Function at a Point
Find equation ya tangent line Curve\(f(x)=x^2−4x\) katika\(x=3.\)
Kutumia:
\[f'(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
Mbadala\(f(a+h)=(a+h)^2−4(a+h)\) na\(f(a)=a^2−4a.\)
\[\begin{align} f′(a) &= \lim \limits_{h \to 0}\dfrac{(a+h)(a+h)−4(a+h)−(a2−4a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{a^2+2ah+h^2−4a−4h−a^2+4a}{h} && \text{Remove parentheses.} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{a^2}+2ah+h^2−\cancel{4a}−4h−\cancel{a^2}+\cancel{4a}}{h} && \text{Combine like terms.} \\ &= \lim \limits_{h \to 0} \dfrac{2ah+h^2−4h}{h} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{h}(2a+h−4)}{h} && \text{Factor out }h. \\ &=2a+0−4 \\ f′(a)&=2a−4 && \text{Evaluate the limit.} \\ f′(3)&=2(3)−4=2 \end{align}\]
Equation ya mstari tangent katika\(x=3\):
\[\begin{align} y &= f'(a)(x−a)+f(a) \\ y &=f'(3)(x−3)+f(3) \\ y &=2(x−3)+(−3) \\ y &=2x−9 \end{align}\]
Uchambuzi
Tunaweza kutumia matumizi ya graphing kwa grafu kazi na mstari wa tangent. Kwa kufanya hivyo, tunaweza kuchunguza hatua ya tangency katika\(x=3\) kama inavyoonekana katika Kielelezo.
Grafu inathibitisha hatua ya tangency katika\(x=3\).
Zoezi\(\PageIndex{1}\):
Find equation ya mstari tangent kwa Curve ya kazi\(f(x)=5x^2−x+4\) katika\(x=2\).
\(y=19x−16\)
Kutafuta kasi ya papo hapo ya Chembe
Kama kazi hatua nafasi dhidi ya wakati, hatua derivative makazi yao dhidi ya wakati, au kasi ya kitu. Mabadiliko katika kasi au mwelekeo kuhusiana na mabadiliko ya wakati hujulikana kama kasi. Kasi katika papo fulani inajulikana kama kasi ya papo hapo.
Katika kujaribu kupata kasi au kasi ya kitu kwa papo hapo, tunaonekana kukutana na utata. Sisi kawaida kufafanua kasi kama umbali alisafiri kugawanywa na muda uliopita. Lakini kwa papo hapo, hakuna umbali unaosafiri, na hakuna muda unaopita. Tutagawanaje sifuri na sifuri? Matumizi ya derivative hutatua tatizo hili. Derivative inatuwezesha kusema kwamba hata wakati kasi ya kitu inabadilika, ina kasi fulani kwa papo hapo. Hiyo ina maana kwamba kama kitu alisafiri katika kasi kwamba halisi kwa kitengo cha muda, ingekuwa kusafiri umbali maalum.
KASI YA HARAKA
Hebu kazi\(s(t)\) inawakilisha nafasi ya kitu\(t.\) kwa wakati Kasi ya papo hapo au kasi ya kitu kwa wakati\(t=a\) hutolewa na
\[s′(a)= \lim \limits_{h \to 0} \dfrac{s(a+h)−s(a)}{h}\]
Mfano\(\PageIndex{1}\): Finding the Instantaneous Velocity
Mpira hupigwa juu kutoka kimo cha miguu 200 na kasi ya awali ya 36 ft/sec. Kama urefu wa mpira katika miguu baada ya\(t\) sekunde ni kutolewa kwa\(s(t)=−16t^2+36t+200,\) kupata kasi instantaneous ya mpira katika\( t=2\).
Kwanza, tunapaswa kupata derivative\(s′(t)\). Kisha sisi kutathmini derivative katika\(t=2\), kutumia\(s(a+h)=−16(a+h)^2+36(a+h)+200\) na\(s(a)=−16a^2+36a+200.\)
\[\begin{align} s′(a)= \lim \limits_{h \to 0} \dfrac{s(a+h)−s(a)}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−16(a+h)^2+36(a+h)+200−(−16a^2+36a+200)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{−16(a^2+2ah+h^2)+36(a+h)+200−(−16a^2+36a+200)}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−16a^2−32ah−16h^2+36a+36h+200+16a^2−36a−200}{h} \\ &= \lim \limits_{h \to 0}\dfrac{\cancel{−16a^2}−32ah−16h^2+\cancel{36a}+36h+\cancel{200}+\cancel{16a^2}−\cancel{36a}−\cancel{200}}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−32ah−16h^2+36h}{h} \\ &= \lim \limits_{h \to 0}\dfrac{\cancel{h}(−32a−16h+36)}{\cancel{h}} \\ &= \lim \limits_{h \to 0}(−32a−16h+36) \\&=−32a−16⋅0+36 \\ s′(a) &=−32a+36 \\ s′(2) &=−32(2)+36 \\ & =−28 \end{align}\]
Uchambuzi
Matokeo haya ina maana kwamba wakati wa\(t=2\) sekunde, mpira unashuka kwa kiwango cha 28 ft/sec.
Zoezi\(\PageIndex{1}\):
roketi fireworks ni risasi zaidi nje ya shimo 12 ft chini ya ardhi kwa kasi ya 60 ft/sec. Urefu wake kwa miguu baada ya\(t\) sekunde hutolewa\(s=−16t^2+60t−12.\) na kasi yake ya haraka baada ya sekunde 4?
—68 ft/sec, ni kuacha nyuma duniani kwa kiwango cha 68 ft/s.
Fikia rasilimali hizi mtandaoni kwa maelekezo ya ziada na mazoezi na derivatives.
Ziara tovuti hii kwa maswali ya ziada mazoezi kutoka Learningpod.
Mlinganyo muhimu
| wastani wa kiwango cha mabadiliko | \(\text{AROC}=\frac{f(a+h)−f(a)}{h}\) |
| derivative ya kazi | \(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\) |
Dhana muhimu
- Mteremko wa mstari wa salama unaounganisha pointi mbili ni kiwango cha wastani cha mabadiliko ya kazi kati ya pointi hizo. Angalia Mfano.
- Kiwango cha derivative, au instantaneous ya mabadiliko, ni kipimo cha mteremko wa curve ya kazi kwa hatua fulani, au mteremko wa mstari wa tangent kwa curve wakati huo. Angalia Mfano, Mfano, na Mfano.
- Quotient tofauti ni quotient katika formula kwa kiwango cha instantaneous ya mabadiliko:
\(\frac{f(a+h)−f(a)}{h}\)
- Viwango vya haraka vya mabadiliko vinaweza kutumika kutafuta ufumbuzi wa matatizo mengi ya ulimwengu halisi. Angalia Mfano.
- Kiwango cha mabadiliko ya papo hapo kinaweza kupatikana kwa kuchunguza mteremko wa kazi kwa hatua kwenye grafu kwa kuchora mstari wa tangent kwa kazi wakati huo. Angalia Mfano.
- Viwango vya instantaneous vya mabadiliko vinaweza kutafsiriwa kuelezea hali halisi ya ulimwengu. Angalia Mfano na Mfano.
- Baadhi ya kazi si kutofautishwa katika hatua au pointi. Angalia Mfano.
- Aina ya mteremko wa mstari inaweza kutumika kupata equation ya mstari tangent kwa Curve ya kazi. Angalia Mfano.
- Velocity ni mabadiliko katika nafasi jamaa na wakati. Kasi ya papo hapo inaelezea kasi ya kitu kwa papo hapo. Wastani kasi inaeleza kasi iimarishwe juu ya muda wa muda.
- Kutumia derivative inafanya uwezekano wa kuhesabu kasi instantaneous hata kama hakuna muda uliopita. Angalia Mfano.
Mazoezi ya sehemu
Maneno
Je! Mteremko wa kazi ya mstari ni sawa na derivative?
Mteremko wa kazi ya mstari unakaa sawa. Derivative ya kazi ya jumla inatofautiana kulingana na\(x\). Wote mteremko wa mstari na derivative kwa hatua kupima kiwango cha mabadiliko ya kazi.
Ni tofauti gani kati ya kiwango cha wastani cha mabadiliko ya kazi kwenye muda\([ x,x+h ]\) na derivative ya kazi katika\(x\)?
gari alisafiri 110 maili katika kipindi cha muda kutoka 2:00 P.M. kwa 4:00 P.M. ilikuwa gari wastani kasi gani? Katika hasa 2:30 P.M., kasi ya gari imesajiliwa hasa maili 62 kwa saa. Jina lingine la kasi ya gari saa 2:30 P.M.? Kwa nini kasi hii inatofautiana na kasi ya wastani?
Wastani kasi ni 55 maili kwa saa. Kasi ya instantaneous saa 2:30 p.m ni maili 62 kwa saa. Kasi ya instantaneous inapima kasi ya gari kwa papo hapo wakati ambapo kasi ya wastani inatoa kasi ya gari juu ya muda.
Eleza dhana ya mteremko wa curve kwa uhakika\(x\).
Tuseme maji yanaingia ndani ya tangi kwa kiwango cha wastani cha galoni 45 kwa dakika. Tafsiri kauli hii katika lugha ya hisabati.
Kiwango cha wastani cha mabadiliko ya kiasi cha maji katika tangi ni galoni 45 kwa dakika. Ikiwa\(f(x)\) ni kazi ya kutoa kiasi cha maji katika tangi wakati wowote\(t\), basi kiwango cha wastani cha mabadiliko ya\(f(x)\) kati\(t=a\) na\(t=b\) ni\(f(a)+45(b−a).\)
Kialjebra
Kwa mazoezi yafuatayo, tumia ufafanuzi wa derivative\(\lim \limits_{h to 0} \frac{f(x+h)−f(x)}{h}\) ili kuhesabu derivative ya kila kazi.
\(f(x)=3x−4\)
\(f(x)=−2x+1\)
\(f′(x)=−2\)
\(f(x)=x^2−2x+1\)
\ (f (x) =2x^2+x-3
\(f′(x)=4x+1\)
\(f(x)=2x^2+5\)
\(f(x)=\frac{−1}{x−2}\)
\(f′(x)=\frac{1}{(x−2)^2}\)
\(f(x)=\frac{2+x}{1−x}\)
\(f(x)=\frac{5−2x}{3+2x}\)
\(\frac{−16(}{3+2x)^2}\)
\(f(x)=\sqrt{1+3x}\)
\(f(x)=3x^3−x^2+2x+5\)
\(f′(x)=9x^2−2x+2\)
\(f(x)=5\)
\(f(x)=5π\)
\(f′(x)=0\)
Kwa mazoezi yafuatayo, pata kiwango cha wastani cha mabadiliko kati ya pointi mbili.
\((−2,0)\)na\((−4,5)\)
\((4,−3)\)na\((−2,−1)\)
\(−\frac{1}{3}\)
\((0,5)\)na\((6,5)\)
\((7,−2)\)na\((7,10)\)
haijafafanuliwa
Kwa kazi zifuatazo za polynomial, pata derivatives.
\(f(x)=x^3+1\)
\(f(x)=−3x^2−7x=6\)
\(f′(x)=−6x−7\)
\(f(x)=7x^2\)
\(f(x)=3x^3+2x^2+x−26\)
\(f′(x)=9x^2+4x+1\)
Kwa kazi zifuatazo, kupata equation ya mstari tangent kwa Curve katika hatua fulani\(x\) juu ya Curve.
\(f(x)=2x^2−3x \;\;\; x=3\)
\(f(x)=x^3+1 \;\;\;\; x=2\)
\(y=12x−15\)
\(f(x)=\sqrt{x} \;\;\;\; x=9\)
Kwa zoezi zifuatazo, tafuta\(k\) vile kwamba mstari uliopewa ni tangent kwa grafu ya kazi.
\(f(x)=x^2−kx, \;\;\; y=4x−9\)
\(k=−10\)au\(k=2\)
Picha
Kwa mazoezi yafuatayo, fikiria grafu ya kazi\(f\) na ueleze ambapo kazi inaendelea/kuacha na kutofautishwa/isiyofahamika.
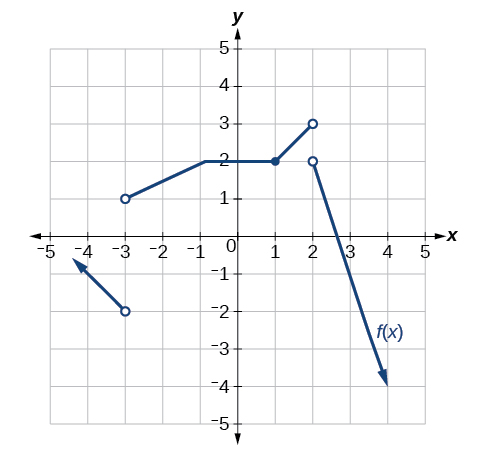
Discontinuous katika\(x=−2\) na\(x=0\). Si differentiable katika —2, 0, 2.
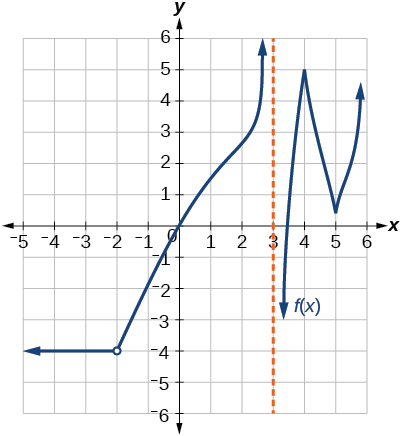
Discontinuous katika\(x=5\). Si differentiable katika -4, -2, 0, 1, 3, 4, 5.
Kwa mazoezi yafuatayo, kutumia Kielelezo kukadiria ama kazi katika thamani fulani ya\(x\) au derivative katika thamani fulani ya\(x\), kama ilivyoonyeshwa.
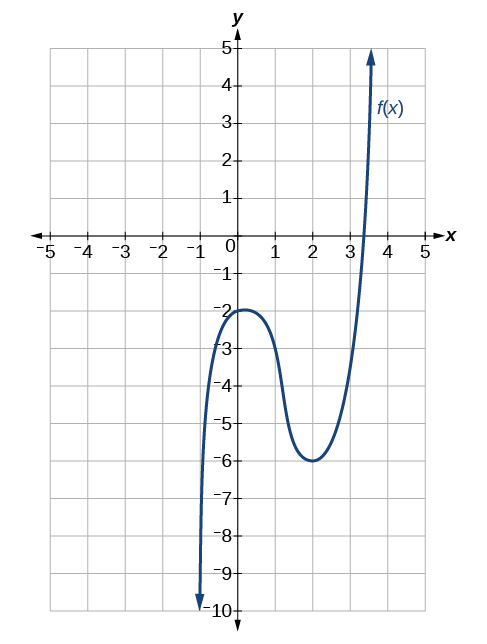
\(f(−1)\)
\(f(0)\)
\(f(0)=−2\)
\(f(1)\)
\(f(2)\)
\ (f (2) =-6f (2) =-6
\(f(3)\)
\(f′(−1)\)
\(f′(−1)=9\)
\(f′(0)\)
\(f′(1)\)
\(f′(1)=−3\)
\(f′(2)\)
\(f′(3)\)
\(f′(3)=9\)
Mchoro kazi kulingana na maelezo hapa chini:
\(f′(x)=2x, f(2)=4\)
Teknolojia
Numerically kutathmini derivative. Kuchunguza tabia ya grafu ya\(f(x)=x^2\) karibu\(x=1\) na graphing kazi kwenye nyanja zifuatazo:\([ 0.9,1.1 ], [ 0.99,1.01 ], [ 0.999,1.001 ],\) na\([0.9999, 1.0001]\). Tunaweza kutumia kipengele kwenye calculator yetu kwamba moja kwa moja seti Ymin na Ymax kwa Xmin na Xmax maadili sisi preset. (Katika baadhi ya mahesabu ya kawaida ya graphing, kipengele hiki kinaweza kuitwa ZOOM FIT au ZOOM AUTO). Kwa kuchunguza maadili ya kiwango cha sambamba kwa dirisha hili la kutazama, takriban jinsi safu inavyobadilika kwa\(x=1,\) hiyo, takriban derivative\(x=1.\)
Majibu hutofautiana. Mteremko wa mstari wa tangent karibu\(x=1\) ni 2.
Real-World Matumizi
Kwa mazoezi yafuatayo, kuelezea notation kwa maneno. Kiasi\(f(t)\) cha tank ya petroli, katika galoni,\(t\) dakika baada ya mchana.
\(f(0)=600\)
\(f'(30)=−20\)
Saa 12:30 p.m., kiwango cha mabadiliko ya idadi ya galoni katika tangi ni -20 galoni kwa dakika. Hiyo ni, tank inapoteza galoni 20 kwa dakika.
\(f(30)=0\)
\(f'(200)=30\)
Katika dakika 200 baada ya mchana, kiasi cha galoni katika tangi kinabadilika kwa kiwango cha galoni 30 kwa dakika.
\(f(240)=500\)
Kwa mazoezi yafuatayo, kuelezea kazi kwa maneno. Urefu\(s\), wa projectile baada ya\(t\) sekunde hutolewa na\(s(t)=−16t^2+80t.\)
\(s(2)=96\)
Urefu wa projectile baada ya sekunde 2 ni miguu 96.
\(s'(2)=16\)
\(s(3)=96\)
Urefu wa projectile kwa\(t=3\) sekunde ni miguu 96.
\(s'(3)=−16\)
\(s(0)=0,s(5)=0.\)
Urefu wa projectile ni sifuri\(t=0\) na tena\(t=5\). Kwa maneno mengine, projectile huanza chini na kuanguka duniani tena baada ya sekunde 5.
Kwa mazoezi yafuatayo, kiasi\(V\) cha nyanja kwa heshima na radius yake\(r\) hutolewa na\(V=\frac{4}{3}πr^3.\)
Pata kiwango cha wastani cha mabadiliko ya\(V\)\(r\) mabadiliko kutoka 1 cm hadi 2 cm.
Pata kiwango cha instantaneous cha mabadiliko ya\(V\) wakati r=3 cm. r=3 cm.
\(36π\)
Kwa mazoezi yafuatayo, mapato yanayotokana na kuuza\(x\) vitu hutolewa na\(R(x)=2x^2+10x\).
Pata mabadiliko ya wastani ya kazi ya mapato kama\(x\) mabadiliko kutoka\(x=10\) kwa\(x=20\).
Pata\(R'(10)\) na kutafsiri.
$50.00 kwa kila kitengo, ambayo ni kiwango cha instantaneous cha mabadiliko ya mapato wakati vitengo 10 vinauzwa.
Pata\(R'(15)\) na kutafsiri. Linganisha\(R'(10),\) na\(R'(15)\) kuelezea tofauti.
Kwa mazoezi yafuatayo, gharama za\(x\) kuzalisha simu za mkononi zinaelezwa na kazi\(C(x)=x^2−4x+1000.\)
Pata kiwango cha wastani cha mabadiliko katika gharama ya jumla kama\(x\) mabadiliko kutoka\(x=10\) kwa\(x=15.\)
$21 kwa kila kitengo
Kupata takriban gharama pembezoni, wakati 15 simu za mkononi kuwa zinazozalishwa, ya kuzalisha 16 th Mkono.
Kupata takriban gharama pembezoni, wakati 20 simu za mkononi kuwa zinazozalishwa, ya kuzalisha 21 st Mkono.
$36
Ugani
Kwa mazoezi yafuatayo, tumia ufafanuzi wa derivative kwa uhakika\(x=a\),\(\lim \limits_{x \to a}\frac{f(x)−f(a)}{x−a},\) ili kupata derivative ya kazi.
\(f(x)=\frac{1}{x^2}\)
\(f(x)=5x^2−x+4\)
\(f'(x)=10a−1\)
\(f(x)=−x^2+4x+7\)
\(f(x)=\frac{−4}{3−x^2}\)
\(\frac{4}{(3−x)^2}\)
Sura ya Mapitio ya mazoezi
Kupata mipaka: Njia ya Nambari na Graphical
Kwa mazoezi yafuatayo, tumia Kielelezo.
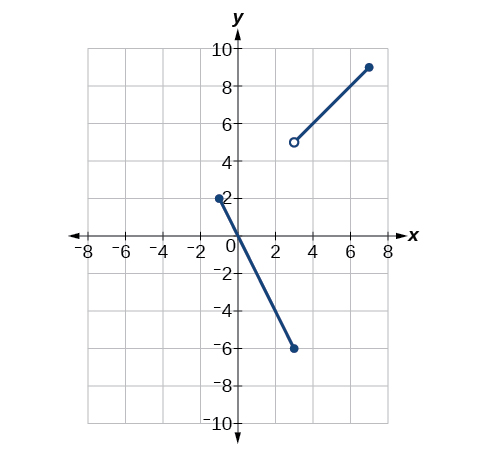
\(\lim \limits_{x \to −1^+}f(x)\)
2
\(\lim \limits_{x \to −1^−}f(x)\)
\(\lim \limits_{x \to −1} f(x)\)
haipo
\(\lim \limits_{x \to 3}f(x)\)
Ni maadili gani\(x\) ya kazi ya kuacha? Ni hali gani ya kuendelea inavunjwa?
Kuacha katika\(x=−1\) (\(\lim \limits_{x \to a} f(x)\)haipo),\(x=3\) (kuruka kuacha), na\(x=7\) (\ lim\ mipaka _ {x\ kwa} f (x)\) haipo).
Kutumia Jedwali, makisio\(\lim \limits_{x \to 0}f(x).\)
| \(x\) | \(F(x)\) |
| -0.1 | 2.875 |
| -0.01 | 2.92 |
| -0.001 | 2.998 |
| 0 | Haijafafanuliwa |
| 0.001 | 2.9987 |
| 0.01 | 2.865 |
| 0.1 | 2.78145 |
| 0.15 | 2.678 |
3
Kwa mazoezi yafuatayo, pamoja na matumizi ya matumizi ya graphing, tumia ushahidi wa namba au wa kielelezo ili kuamua mipaka ya kushoto na ya kulia ya kazi iliyotolewa kama\(x\) mbinu\(a\). Kama kazi ina kikomo kama\(x\) mbinu\(a\), hali yake. Ikiwa sio, jadili kwa nini hakuna kikomo.
\(f(x)=\begin{cases} | x |−1, && \text{if }x≠1 \\ x^3, \text{if }x=1 \end{cases} a=1\)
\(f(x)=\begin{cases} \frac{1}{x+1}, && \text{if }x=−2 \\ (x+1)^2, && \text{if }x≠−2 \end{cases} a=−2\)
\(\lim \limits_{x \to −2} f(x)=1\)
\(f(x)= \begin{cases} \sqrt{x+3} && \text{if } x < 1 \\ −\sqrt[3]{x} && \text{if }x>1 \end{cases} a=1\)
Kupata mipaka: Mali ya Mipaka
Kwa mazoezi yafuatayo, pata mipaka ikiwa\(\lim \limits_{x \to c} f(x)=−3\) na\(\lim \limits_{x \to c} g(x)=5\).
\(\lim \limits_{x \to c} (f(x)+g(x))\)
2
\(\lim \limits_{x \to c} \frac{f(x)}{g(x)}\)
\(\lim \limits_{x to c}(f(x)⋅g(x))\)
\(−15\)
\(\lim \limits_{x \to 0^+}f(x),f(x)= \begin{cases} 3x^2+2x+1 && x>0 \\ 5x+3 && x<0 \end{cases}\)
\(\lim \limits_{x \to 0^-}f(x),f(x)= \begin{cases} 3x^2+2x+1 && x>0 \\ 5x+3 && x<0 \end{cases}\)
3
\(\lim \limits_{x \to 3^+}(3x−〚x〛)\)
Kwa mazoezi yafuatayo, tathmini mipaka kwa kutumia mbinu za algebraic.
\(\lim \limits_{h \to 0}(\frac{(h+6)^2−36}{h})\)
12
\(\lim \limits_{x \to 25}(\frac{x^2−625}{\sqrt{x}−5)}\)
\(\lim \limits_{x \to 1}(\frac{−x^2−9x}{x})\)
-10
\(\lim \limits_{x \to 4}\frac{7−\sqrt{12x+1}}{x−4}\)
\(\lim \limits_{x \to −3}(\frac{\frac{1}{3}+\frac{1}{x}}{3+x})\)
\(−\frac{1}{9}\)
Mwendelezo
Kwa mazoezi yafuatayo, tumia ushahidi wa namba ili uone kama kikomo kipo\(x=a\). Ikiwa sio, kuelezea tabia ya grafu ya kazi\(x=a\).
\(f(x)=\frac{−2}{x−4}; a=4\)
\(f(x)=\frac{−2}{(x−4)^2}; a=4\)
Kwa\(x=4\), kazi ina asymptote ya wima.
\(f(x)=\frac{−x}{x^2−x−6}; a=3\)
\(f(x)=\frac{6x^2+23x+20}{4x^2−25}; a=−\frac{5}{2}\)
discontinuity kutolewa katika\(a=−\frac{5}{2}\)
\(f(x)=\frac{\sqrt{x}−3}{9−x}; a=9\)
Kwa mazoezi yafuatayo, tambua wapi kazi iliyotolewa\(f(x)\) inaendelea. Ambapo sio kuendelea, hali ambayo hali inashindwa, na uainishe discontinuities yoyote.
\(f(x)=x^2−2x−15\)
kuendelea\((−∞,∞)\)
\(f(x)=\frac{x^2−2x−15}{x−5}\)
\(f(x)=\frac{x^2−2x}{x^2−4x+4}\)
removable\(x=2. f(2)\) discontinuity katika si defined, lakini mipaka zipo.
\(f(x)=\frac{x^3−125}{2x^2−12x+10}\)
\(f(x)=\frac{x^2−\frac{1}{x}}{2−x}\)
discontinuity katika\(x=0\) na\(x=2\). Wote\(f(0)\) na\(f(2)\) si defined.
\(f(x)=\frac{x+2}{x^2−3x−10}\)
\(f(x)=\frac{x+2}{x^3+8}\)
discontinuity kutolewa katika\(x=–2. f(–2)\) si defined.
Derivat
Kwa mazoezi yafuatayo, pata kiwango cha wastani cha mabadiliko\(\frac{f(x+h)−f(x)}{h}\).
\(f(x)=3x+2\)
\(f(x)=5\)
0
\(f(x)=\frac{1}{x+1}\)
\(f(x)= \ln (x)\)
\(\frac{\ln (x+h)− \ln (x)}{h}\)
\(f(x)=e^{2x}\)
Kwa mazoezi yafuatayo, pata derivative ya kazi.
\(f(x)=4x−6\)
\(=4\)
\(f(x)=5x^2−3x\)
Pata usawa wa mstari wa tangent kwenye grafu ya\(f(x)\)\(x\) thamani iliyoonyeshwa.
\(f(x)=−x^3+4x; x=2.\)
\(y=−8x+16\)
Kwa mazoezi yafuatayo, kwa msaada wa matumizi ya graphing, kuelezea kwa nini kazi haijulikani kila mahali kwenye uwanja wake. Taja pointi ambapo kazi haijulikani.
\(f(x)=\frac{x}{| x |}\)
Kutokana na kwamba kiasi cha koni ya mviringo ya haki ni\(V=\frac{1}{3}πr^2h\) na kwamba koni iliyotolewa ina urefu fasta ya cm 9 na urefu wa radius kutofautiana, kupata kiwango cha instantaneous cha mabadiliko ya kiasi kuhusiana na urefu wa radius wakati radius ni 2 cm. Kutoa jibu halisi katika suala la\(π\)
\(12π\)
Mazoezi mtihani
Kwa mazoezi yafuatayo, tumia grafu ya\(f\) katika Kielelezo.
\(f(1)\)
3
\(\lim \limits_{x \to −1^+}f(x)\)
\(\lim \limits_{x \to −1^-}f(x)\)
0
\(\lim \limits_{x \to −1}f(x)\)
\(\lim \limits_{x \to −2}f(x)\)
\(−1\)
Ni maadili gani\(x\) ya\(f\) kuacha? Ni mali gani ya kuendelea inavunjwa?
Kwa mazoezi yafuatayo, pamoja na matumizi ya matumizi ya graphing, tumia ushahidi wa namba au wa kielelezo ili kuamua mipaka ya kushoto na ya kulia ya kazi iliyotolewa kama\(x\) mbinu\(a\). Kama kazi ina kikomo kama\(x\) mbinu\(a\), hali yake. Kama siyo, kujadili kwa nini hakuna kikomo
\(f(x)=\begin{cases} \frac{1}{x}−3, && \text{if }x≤2 \\ x^3+1, && \text{if } x>2 \end{cases} a=2\)
\(\lim \limits_{x \to 2^−} f(x)=−\frac{5}{2}a\)na\(\lim \limits_{x \to 2^+} f(x)=9\) Hivyo, kikomo cha kazi kama\(x\) mbinu 2 haipo.
\(f(x)=\begin{cases} x^3+1, && \text{if }x<1 \\ 3x^2−1, && \text{if } x=1 \\ −\sqrt{x+3}+4, && \text{if } x>1 \end{cases} a=1\)
Kwa mazoezi yafuatayo, tathmini kila kikomo kwa kutumia mbinu za algebraic.
\(\lim \limits_{x \to −5}(\frac{\frac{1}{5}+\frac{1}{x}}{10+2x})\)
\(−\frac{1}{50}\)
\(\lim \limits_{h \to 0} (\frac{\sqrt{h^2+25}−5}{h^2})\)
\(\lim \limits_{h \to 0} (\frac{1}{h}−\frac{1}{h^2+h})\)
1
Kwa mazoezi yafuatayo, onyesha kama kazi iliyopewa\(f\) inaendelea. Ikiwa inaendelea, onyesha kwa nini. Kama si kuendelea, hali ambayo hali ya kushindwa.
\(f(x)=\sqrt{x^2−4}\)
\(f(x)=\frac{x^3−4x^2−9x+36}{x^3−3x^2+2x−6}\)
discontinuity kutolewa katika\(x=3\)
Kwa mazoezi yafuatayo, tumia ufafanuzi wa derivative ili kupata derivative ya kazi iliyotolewa\(x=a\).
\(f(x)=\frac{3}{5+2x}\)
\(f(x)=\frac{3}{\sqrt{x}}\)
\(f'(x)=−\frac{3}{2a^{\frac{3}{2}}}\)
\(f(x)=2x^2+9x\)
discontinuous katika -2,0, si kutofautisha katika -2,0, 2.
Kwa mazoezi yafuatayo, kwa msaada wa matumizi ya graphing, kuelezea kwa nini kazi haijulikani kila mahali kwenye uwanja wake. Taja pointi ambapo kazi haijulikani.
\(f(x)=| x−2 |−| x+2 |\)
\(f(x)=\frac{2}{1+e^{\frac{2}{x}}}\)
si differentiable katika\(x=0\) (hakuna kikomo)
Kwa mazoezi yafuatayo, kueleza nukuu kwa maneno wakati urefu wa projectile kwa miguu,\(s\), ni kazi ya muda t t katika sekunde baada ya uzinduzi na hutolewa na kazi\(s(t)\).
\(s(0)\)
\(s(2)\)
urefu wa projectile kwa\(t=2\) sekunde
\(s'(2)\)
\(\frac{s(2)−s(1)}{2−1}\)
kasi ya wastani kutoka\(t=1\) kwa\(t=2\)
\(s(t)=0\)
Kwa mazoezi yafuatayo, tumia teknolojia ili kutathmini kikomo.
\(\lim \limits_{x \to 0} \frac{\sin (x)}{3x}\)
\(\frac{1}{3}\)
\(\lim \limits_{x \to 0} \frac{\tan ^2 (x)}{2x}\)
\(\lim \limits_{x \to 0}\frac{\sin (x)(1−\cos (x))}{2x^2}\)
0
Tathmini kikomo kwa mkono.
\(\lim \limits_{x \to 1}f(x), \text{where } f(x)= \begin{cases} 4x−7 && x≠1 \\ x^2−4 &&x=1 \end{cases}\)
Kwa thamani gani (s) ya\(x\) ni kazi chini ya kuacha?
\(f(x)= \begin{cases} 4x−7 && x≠1 \\ x^2−4 &&x=1 \end{cases}\)
Kwa mazoezi yafuatayo, fikiria kazi ambayo grafu inaonekana kwenye Kielelezo.
Pata kiwango cha wastani cha mabadiliko ya kazi kutoka\(x=1\) kwa\(x=3\).
2
Kupata maadili yote ya\(x\) saa ambayo\(f'(x)=0\).
\(x=1\)
Pata maadili yote ambayo\(f'(x)\) haipo.\(x\)
Pata usawa wa mstari wa tangent kwenye grafu\(f\) ya hatua iliyoonyeshwa:\(f(x)=3x^2−2x−6, x=−2\)
\(y=−14x−18\)
Kwa mazoezi yafuatayo, tumia kazi\(f(x)=x(1−x)^{\frac{2}{5}}\).
Graph kazi\(f(x)=x(1−x)^{\frac{2}{5}}\) kwa kuingia\(f(x)=x((1−x)^2)^{\frac{1}{5}}\) na kisha kwa kuingia\(f(x)=x((1−x)^{\frac{1}{5}})^2\).
Kuchunguza tabia ya grafu ya\(f(x)\) karibu\(x=1\) na kuchora kazi kwenye vikoa vifuatavyo, [0.9, 1.1], [0.99, 1.01], [0.999, 1.001], na [0.9999, 1.0001]. Tumia habari hii ili kuamua kama kazi inaonekana kuwa tofauti katika\(x=1\).
Grafu haipatikani katika\(x=1\) (cusp).
Kwa mazoezi yafuatayo, tafuta derivative ya kila kazi kwa kutumia ufafanuzi:\(\lim \limits_{h \to 0} \frac{f(x+h)−f(x)}{h}\)
\(f(x)=2x−8\)
\(f(x)=4x^2−7\)
\(f′(x)=8x\)
\(f(x)=x−\frac{1}{2}x^2\)
\(f(x)=\frac{1}{x+2}\)
\(f'(x)=−\frac{1}{(2+x)^2}\)
\(f(x)=\frac{3}{x−1}\)
\(f(x)=−x^3+1\)
\(f′(x)=−3^x2\)
\(f(x)=x^2+x^3\)
\(f(x)=\sqrt{x−1}\)
\(f'(x)=\frac{1}{2\sqrt{x−1}}\)
maelezo ya chini
- 1 www.csun.edu/science/health/d... tv&health.html Chanzo zinazotolewa.
faharasa
- wastani wa kiwango cha mabadiliko
- mteremko wa mstari kuunganisha pointi mbili\((a,f(a))\) na\((a+h,f(a+h))\) juu ya Curve ya\(f(x)\); ni iliyotolewa na
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}.\]
- derivative
- mteremko wa kazi kwa hatua fulani; imeashiria\(f′(a)\),\(x=a\) kwa uhakika\(f′(a)=\lim \limits_{h \to 0}\frac{f(a+h)−f(a)}{h}\), kutoa kikomo ipo.
- inayoweza kutofautishwa
- kazi\(f(x)\) ambayo derivative ipo\(x=a.\) katika Kwa maneno mengine, kama f′ (a) f′ (a) ipo.
- instantaneous kiwango cha mabadiliko
- mteremko wa kazi kwa hatua fulani;\(x=a\) kwa hiyo hutolewa na\(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\).
- kasi ya papo hapo
- mabadiliko katika kasi au mwelekeo kwa papo fulani; kazi\(s(t)\) inawakilisha nafasi ya kitu kwa wakati\(t\), na kasi ya instantaneous au kasi ya kitu kwa wakati\(t=a\) hutolewa na\(s′(a)=\lim \limits_{h \to 0}\frac{s(a+h)−s(a)}{h}\).
- mstari wa secant
- line kwamba intersects pointi mbili juu ya Curve
- mstari wa tangent
- line kwamba intersects Curve katika hatua moja


