12.3: Mwendelezo

Arizona inajulikana kwa joto lake kavu. Katika siku fulani, joto inaweza kupanda kama juu kama$118^∘F$ na kushuka chini tu kwa$95^∘F.$ Kielelezo brisk$\PageIndex{1}$ inaonyesha kazi$T$, ambapo pato la$T(x)$ ni joto katika digrii Fahrenheit na pembejeo$x$ ni wakati wa siku, kutumia saa 24 saa juu ya hasa majira ya siku.

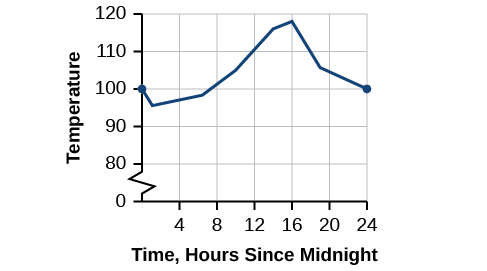
Kielelezo$\PageIndex{1}$: Joto kama kazi ya muda hufanya kazi inayoendelea.

Tunapochambua grafu hii, tunaona tabia maalum. Hakuna mapumziko katika grafu. Tunaweza kufuatilia grafu bila kuokota penseli yetu. Uchunguzi huu single inatuambia mpango mkubwa kuhusu kazi. Katika sehemu hii, tutachunguza kazi na bila mapumziko.

Kuamua Kama Kazi Inaendelea kwa Nambari

Hebu fikiria mfano maalum wa joto kwa suala la tarehe na mahali, kama vile Juni 27, 2013, huko Phoenix, AZ. Grafu katika Kielelezo$\PageIndex{1}$ inaonyesha kwamba, saa 2 asubuhi, joto lilikuwa$96 ^∘F$. By 2 p.m. joto alikuwa imeongezeka$116^∘F,$ na kwa saa 4 p.m. ilikuwa$118 ^∘F.$ Wakati mwingine kati ya 2 a.m. na 4 p.m., joto nje lazima kuwa hasa$110.5 ^∘ F$. Kwa kweli, joto lolote kati$96 ^∘ F$ na$118 ^∘ F$ lilitokea wakati fulani siku hiyo. Hii inamaanisha namba zote halisi katika pato kati$96 ^∘ F$ na$118 ^∘ F$ zinazalishwa wakati fulani na kazi kulingana na theorem ya thamani ya kati,

Angalia tena kwenye Kielelezo$\PageIndex{1}$. Hakuna mapumziko katika grafu ya kazi kwa kipindi hiki cha saa 24. Kwa wakati wowote joto haliacha kuwepo, wala hapakuwa na hatua ambayo joto lilipuka mara moja na digrii kadhaa. Kazi isiyo na mashimo au mapumziko katika grafu yake inajulikana kama kazi inayoendelea. Joto kama kazi ya muda ni mfano wa kazi inayoendelea.

Ikiwa joto linawakilisha kazi inayoendelea, ni aina gani ya kazi haiwezi kuendelea? Fikiria mfano wa dola walionyesha kama kazi ya masaa ya maegesho. Hebu kujenga kazi$D$, ambapo$D(x)$ ni pato anayewakilisha gharama katika dola kwa ajili ya maegesho$x$ idadi ya masaa (Kielelezo$\PageIndex{2}$).

Tuseme maegesho karakana mashtaka $4.00 kwa saa au sehemu ya saa, kwa $25 kwa siku malipo ya kiwango cha juu. Park kwa saa mbili na dakika tano na malipo ni $12. Park saa ya ziada na malipo ni $16. Hatuwezi kamwe kushtakiwa $13, $14, au $15. Kuna idadi halisi kati ya 12 na 16 kwamba kazi kamwe matokeo. Kuna mapumziko katika grafu ya kazi kwa kipindi hiki cha saa 24, pointi ambayo bei ya maegesho inaruka mara moja na dola kadhaa.

Kielelezo$\PageIndex{2}$: Mashtaka ya maegesho ya karakana huunda kazi ya kuacha.

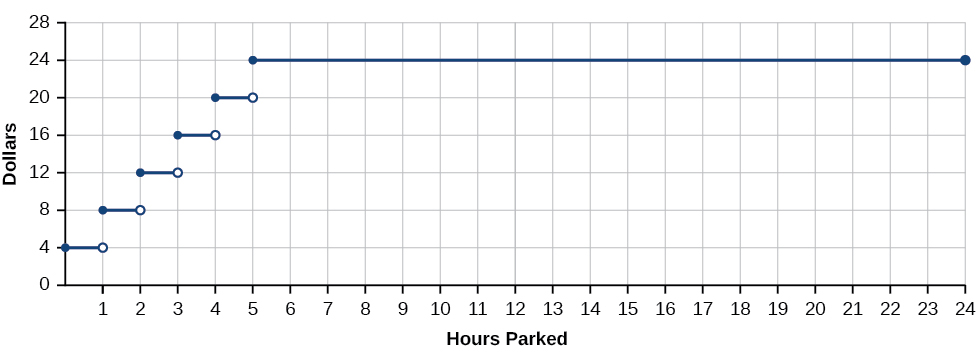
Kazi ambayo inabakia ngazi kwa muda na kisha inaruka mara moja kwa thamani ya juu inaitwa kazi ya hatua kwa hatua. Kazi hii ni mfano.

Kazi ambayo ina shimo lolote au kuvunja katika grafu yake inajulikana kama kazi ya kuacha. Kazi ya hatua kwa hatua, kama vile mashtaka ya maegesho ya karakana kama kazi ya masaa yaliyowekwa, ni mfano wa kazi ya kuacha.

Hivyo jinsi gani tunaweza kuamua kama kazi ni kuendelea katika idadi fulani? Tunaweza kuangalia hali tatu tofauti. Hebu kutumia kazi$y=f(x)$ kuwakilishwa katika Kielelezo kama mfano.

Kielelezo _12_03_004">Kielelezo.

Figure_12_03_003">Kielelezo$x=a$ kinakaribia kutoka kushoto na kulia, sawa y -kuratibu inakaribia. Kwa hiyo, Hali ya 2 imeridhika. Hata hivyo, bado kunaweza kuwa na shimo kwenye grafu$x=a$.

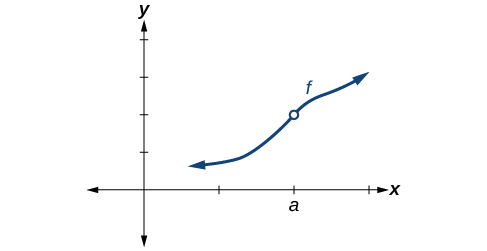
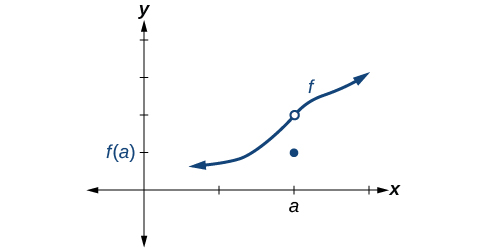
Hali 3 Kwa mujibu wa Hali 3, sambamba y y kuratibu katika$x=a$ hujaza shimo katika grafu ya$f$. Hii imeandikwa$\lim \limits_{x \to a} f(x)=f(a)$.

Kutosheleza hali zote tatu inamaanisha kuwa kazi inaendelea. Masharti yote matatu ni kuridhika kwa ajili ya kazi kuwakilishwa katika Kielelezo hivyo kazi ni kuendelea kama$x=a$.

Masharti yote matatu yanatidhika. kazi ni kuendelea katika$x=a$.

Kielelezo kupitia Kielelezo kutoa mifano kadhaa ya grafu ya kazi ambazo si kuendelea katika$x=a$ na hali au hali ambayo kushindwa.

Hali ya 2 imeridhika. Masharti 1 na 3 wote wanashindwa.

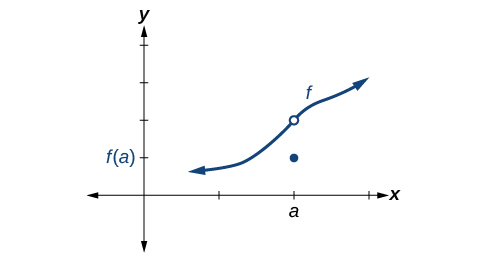
Masharti ya 1 na 2 ni wote kuridhika. Hali 3 inashindwa.

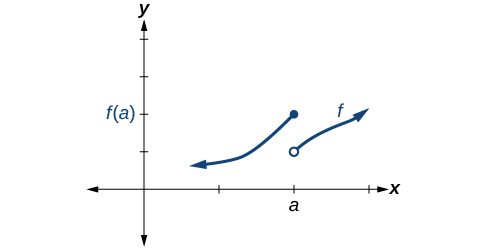
Hali ya 1 imeridhika. Masharti 2 na 3 kushindwa.

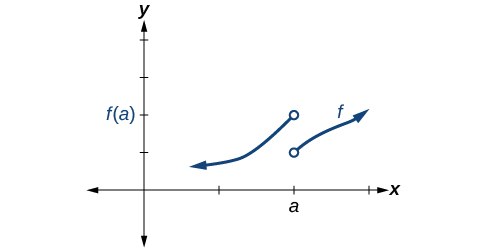
Masharti ya 1, 2, na 3 yote yanashindwa.

Ufafanuzi wa kuendelea

kazi$f(x)$ ni kuendelea katika$x=a$ zinazotolewa zote tatu ya masharti yafuatayo kushikilia kweli:

• Hali ya 1:$f(a)$ ipo.
• mode 2:$\lim \limits_{x \to a} f(x)$ ipo katika$x=a$.
• Hali ya 3:$\lim \limits_{x \to a} f(x)=f(a)$

Kama kazi$f(x)$ si kuendelea katika$x=a$, kazi ni discontinuous katika$x=a$.

Kutambua kukomesha Rukia

Kuondoka kunaweza kutokea kwa njia tofauti. Tuliona katika sehemu iliyopita kwamba kazi inaweza kuwa na kikomo cha mkono wa kushoto na kikomo cha mkono wa kulia hata kama si sawa. Kama kushoto- na kulia mipaka zipo lakini ni tofauti, grafu “anaruka” katika$x=a$. Kazi inasemekana kuwa na kuacha kuruka.

Kwa mfano, angalia grafu ya kazi$y=f(x)$ katika Kielelezo. Angalia kama$x$ mbinu$a$ jinsi pato inakaribia maadili tofauti kutoka kushoto na kutoka kulia.

Grafu ya kazi na kuacha kuruka.

KURUKA KUACHA

kazi$f(x)$ ina kuruka discontinuity katika$x=a$ kama kushoto- na mkono wa kulia mipaka zote zipo lakini si sawa:$\lim \limits_{x \to a^−} f(x)≠ \lim \limits_{x \to a^+} f(x)$

Kutambua Kuondolewa Kuondolewa

Baadhi ya kazi na discontinuity, lakini inawezekana kufafanua upya kazi katika hatua hiyo ili kufanya hivyo kuendelea. Aina hii ya kazi inasemekana kuwa na discontinuity inayoondolewa. Hebu tuangalie kazi$y=f(x)$ iliyowakilishwa na grafu katika Kielelezo. Kazi ina kikomo. Hata hivyo, kuna shimo katika$x=a$. Shimo linaweza kujazwa kwa kupanua kikoa ili kuingiza pembejeo$x=a$ na kufafanua pato linalofanana la kazi kwa thamani hiyo kama kikomo cha kazi$x=a$.

Grafu ya kazi$f$ na discontinuity removable katika$x=a$.

kukomesha kutolewa

kazi f (x) f (x) ina discontinuity kutolewa katika$x=a$ kama kikomo,$\lim \limits_{x \to a} f(x),$ ipo, lakini ama

1. $f(a)$haipo au
2. $f(a)$, thamani ya kazi katika$x=a$ haina sawa na kikomo,$f(a)≠ \lim \limits_{x \to a} f(x)$.

Mfano$\PageIndex{1}$: Identifying Discontinuities

Kutambua discontinuities wote kwa ajili ya kazi zifuatazo kama ama kuruka au discontinuities kutolewa.

1. $f(x)=\frac{x^2−2x−15}{x−5}$
2. $$g(x)= \begin{cases} x+1, & x<2 \\ −x, & x≥2 \end{cases}$$

1. Kumbuka kwamba kazi hufafanuliwa kila mahali isipokuwa saa$x=5$.

   Hivyo,$f(5)$ haipo, Hali 2 si kuridhika. Kwa kuwa Hali ya 1 imeridhika, kikomo kama$x$ mbinu 5 ni 8, na Hali ya 2 haijatoshi.Hii inamaanisha kuwa kuna kutokuwepo kwa kutolewa$x=5$.

2. Hali ya 2 imeridhika kwa sababu$g(2)=−2.$

   Kumbuka kwamba kazi ni kazi ya kipande, na kwa kila kipande, kazi inafafanuliwa kila mahali kwenye uwanja wake. Hebu tuchunguze Hali 1 kwa kuamua kushoto- na mipaka ya mkono wa kulia kama$x$ mbinu 2.

   Kikomo cha mkono wa kushoto:$\lim \limits_{x \to 2^−} (x+1)=2+1=3$. Kikomo cha mkono wa kushoto kipo.

   Mkono wa kulia kikomo:$\lim \limits_{x \to 2^+} (−x)=−2$. Kikomo cha mkono wa kulia kipo. Lakini

   $$\lim \limits_{x \to 2^−} f(x)≠ \lim \limits_{x \to 2^+} f(x).$$

   Kwa hivyo,$\lim \limits_{x \to 2} f(x)$ haipo, na Hali ya 2 inashindwa: Hakuna kuacha kutolewa. Hata hivyo, tangu wote kushoto- na mipaka ya mkono wa kulia zipo lakini si sawa, hali ni kuridhika kwa kuruka kuacha katika$x=2$.

Zoezi$\PageIndex{1}$:

Kutambua discontinuities wote kwa ajili ya kazi zifuatazo kama ama kuruka au discontinuities kutolewa.

1. $f(x)=\frac{x^2−6x}{x−6}$
2. $g(x)= \begin{cases} \sqrt{x}, & 0≤x<4 \\ 2x, & x≥4 \end{cases}$

1. kukomesha kutolewa katika$x=6$;
2. kuruka kuacha$x=4$

Kutambua Kazi za Nambari halisi za Kuendelea na zisizoendelea

Kazi nyingi ambazo tumekutana katika sura za awali zinaendelea kila mahali. Hawana shimo ndani yao, na hawajawahi kuruka kutoka thamani moja hadi ijayo. Kwa wote wa kazi hizi, kikomo cha$f(x)$ kama$x$ mbinu a ni sawa na thamani ya$f(x)$ wakati$x=a$. Hivyo$\lim \limits_{x \to a} f(x)=f(a)$. Kuna baadhi ya kazi ambazo zinaendelea kila mahali na baadhi ambazo zinaendelea tu ambapo zinaelezwa kwenye uwanja wao kwa sababu hazifafanuliwa kwa namba zote halisi.

MIFANO YA KAZI ZINAZOENDELEA

Kazi zifuatazo zinaendelea kila mahali:

Kazi nyingi	Ex:$f(x)=x^4−9x^2$
Kazi za kielelezo	Ex:$f(x)=4^{x+2}−5$
Sine kazi	Ex:$f(x)=\sin (2x)−4$
Kazi za Cosine	Ex:$f(x)=− \cos (x+\frac{π}{3})$

Kazi zifuatazo zinaendelea kila mahali zinafafanuliwa kwenye uwanja wao:

Kazi za Logarithmic	Ex:$f(x)=2 \ln (x), x>0$
Tangent kazi	Ex:$f(x)= \tan (x)+2, x≠ \frac{π}{2}+kπ, k$ ni integer
Kazi za busara	Ex:$f(x)=\frac{x^2−25}{x−7}, x≠7$

jinsi ya:Kutokana na kazi$f(x)$, determine if the function is continuous at $x=a$.

1. Angalia Hali 1:$f(a)$ ipo.
2. Angalia Hali 2:$\lim \limits_{x \to a} f(x)$ ipo katika$x=a$.
3. Angalia Hali 3:$\lim \limits_{x \to a} f(x)=f(a).$
4. Kama hali zote tatu ni kuridhika, kazi ni kuendelea katika$x=a$. Kama moja ya masharti si kuridhika, kazi si kuendelea katika$x=a$.

Mfano$\PageIndex{2}$: Determining Whether a Piecewise Function is Continuous at a Given Number

Kuamua kama kazi$f(x)= \begin{cases} 4x, & x≤3 \\ 8+x, & x>3 \end{cases}$ inaendelea

1. $x=3$
2. $x=\frac{8}{3}$

Kuamua kama kazi$f$ ni kuendelea katika$x=a,$ sisi kuamua kama hali tatu ya kuendelea ni kuridhika katika$x=a$.

1. Hali ya 1: Je,$f(a)$ zipo?

   $$\begin{align} f(3)=4(3)=12 \\ ⇒ \text{Condition 1 is satisfied.} \end{align}$$

   Hali 2: Je,$\lim \limits_{x \to 3} f(x)$ zipo?

   Kwa upande wa kushoto wa$x=3, f(x)=4x;$ kulia wa$x=3, f(x)=8+x.$ Tunahitaji kutathmini kushoto- na mipaka ya mkono wa kulia kama$x$ mbinu 1.

   • Kikomo cha mkono wa kushoto:$\lim \limits_{x \to 3^−} f(x)= \lim \limits_{x \to 3^−} 4(3)=12$
   • Kikomo cha mkono wa kulia:$\lim \limits_{x \to 3^+} f(x)= \lim \limits_{x \to 3^+}(8+x)=8+3=11$

   Kwa sababu$\lim \limits_{x \to 1^−} f(x)≠ \lim \limits_{x \to 1^+} f(x), \lim \limits_{x \to 1} f(x)$ haipo.

   $$⇒ \text{Condition 2 fails.}$$

   Hakuna haja ya kuendelea zaidi. hali 2 inashindwa katika$x=3$. Kama yoyote ya masharti ya mwendelezo si kuridhika katika$x=3$, kazi$f(x)$ si kuendelea katika$x=3$.

2. $x=\frac{8}{3}$

   Hali ya 1: Je,$f(\frac{8}{3})$ zipo?

   $$\begin{align} f(\frac{8}{3})=4(\frac{8}{3})=\frac{32}{3} \\ ⇒\text{Condition 1 is satisfied.} \end{align}$$

   Hali 2: Je,$\lim \limits_{x \to \frac{8}{3}} f(x)$ zipo?

   Kwa upande wa kushoto wa$x=\frac{8}{3}$,$f(x)=4x$; na haki ya$x=\frac{8}{3}, f(x)=8+x$. Tunahitaji kutathmini mipaka ya kushoto na ya kulia kama$x$ mbinu$\frac{8}{3}$.

   • Kikomo cha mkono wa kushoto:$\lim \limits_{x \to \frac{8}{3}^−} f(x)= \lim \limits_{x \to \frac{8}{3}^−} 4(\frac{8}{3})=\frac{32}{3}$
   • Kikomo cha mkono wa kulia:$\lim \limits_{x \to \frac{8}{3}^+} f(x)= \lim \limits_{x \to \frac{8}{3}^+} (8+x)=8+\frac{8}{3}=\frac{32}{3}$

   Kwa sababu$\lim \limits_{x \to \frac{8}{3}} f(x)$ ipo,

   $$⇒ \text{Condition 2 is satisfied.}$$

   Hali 3: Je$f(\frac{8}{3})=\lim \limits_{x \to \frac{8}{3}} f(x)$?

   $$\begin{align} f(\frac{32}{3})=\frac{32}{3}=\lim \limits_{x \to \frac{8}{3}} f(x) \\ ⇒ \text{Condition 3 is satisfied.} \end{align}$$

   Kwa sababu hali zote tatu za mwendelezo ni kuridhika katika$x=\frac{8}{3}$, kazi$f(x)$ ni kuendelea katika$x=\frac{8}{3}$.

Zoezi$\PageIndex{2}$:

Kuamua kama kazi$f(x)= \begin{cases} & \frac{1}{x}, && x≤2 \\ & 9x−11.5, && x>2 \end{cases}$ inaendelea$x=2$.

ndiyo

Mfano$\PageIndex{3}$: Determining Whether a Rational Function is Continuous at a Given Number

Kuamua kama kazi$f(x)=\frac{x^2−25}{x−5}$ inaendelea$x=5$.

Kuamua kama kazi$f$ inaendelea$x=5$, tutaamua ikiwa hali tatu za kuendelea zinaridhika$x=5$.

Hali ya 1:

$$\begin{align} f(5) \text{ does not exist.} \\ ⇒ \text{Condition 1 fails.} \end{align}$$

Hakuna haja ya kuendelea zaidi. hali 2 inashindwa katika$x=5$. Kama yoyote ya masharti ya mwendelezo si kuridhika katika$x=5$, kazi f f si kuendelea katika$x=5$.

Uchambuzi

Angalia Kielelezo. Kumbuka kwamba kwa Hali 2 tuna

$$\begin{align} \lim \limits_{x \to 5} \dfrac{x^2−25}{x−5} &= \lim \limits_{x \to 3} \dfrac{\cancel{(x−5)}(x+5)}{\cancel{x−5}} \\ &= \lim \limits_{x \to 5}(x+5) \\ &=5+5=10 \\ &⇒ \text{Condition 2 is satisfied.} \end{align}$$

Katika x=5, x=5, kuna discontinuity removable. Angalia Kielelezo.

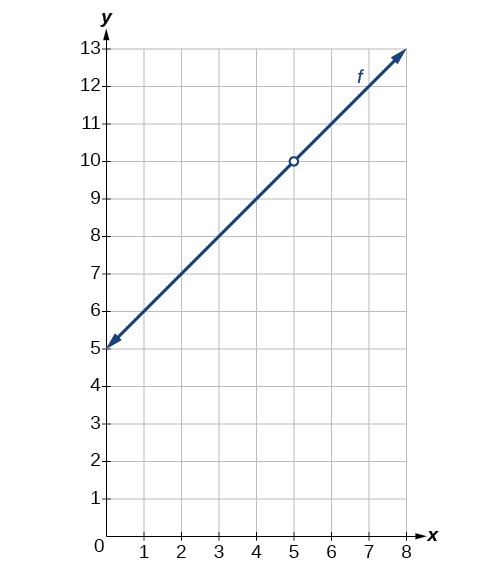
Zoezi$\PageIndex{3}$:

Kuamua kama kazi$f(x)=\frac{9−x^2}{x^2−3x}$ inaendelea$x=3$. Ikiwa sio, sema aina ya kuacha.

Hapana, kazi haiendelei$x=3$. Kuna discontinuity removable katika$x=3$.

Kuamua Maadili ya Pembejeo ambayo Kazi Inakoma

Sasa kwa kuwa tunaweza kutambua kazi zinazoendelea, kuruka discontinuities, na discontinuities zinazoondolewa, tutaangalia kazi ngumu zaidi ili kupata discontinuities. Hapa, sisi kuchambua kazi piecewise kuamua kama idadi yoyote halisi zipo ambapo kazi si kuendelea. Kazi ya kipande inaweza kuwa na discontinuities kwenye pointi za mipaka ya kazi na pia ndani ya kazi zinazoifanya.

Kuamua idadi halisi ambayo kazi ya kipande inayojumuisha kazi ya polynomial haiendelei, kumbuka kwamba kazi za polynomial wenyewe zinaendelea kwenye seti ya namba halisi. Discontinuity yoyote itakuwa katika pointi mipaka. Hivyo tunahitaji kuchunguza hali tatu ya mwendelezo katika pointi mipaka ya kazi piecewise.

jinsi ya: Kutokana na kazi piecewise, kuamua kama ni kuendelea katika pointi mipaka

1. Kwa kila hatua$a$ ya mipaka ya kazi piecewise, kuamua kushoto- na mipaka ya mkono wa kulia$a,$ kama$x$ mbinu pamoja na thamani ya kazi katika$a$.
2. Angalia kila hali kwa kila thamani kuamua kama hali zote tatu ni kuridhika.
3. Kuamua kama kila thamani inatimiza hali 1:$f(a)$ ipo.
4. Kuamua kama kila thamani inatimiza hali 2:$\lim \limits_{x \to a} f(x)$ ipo.
5. Kuamua kama kila thamani inatimiza hali 3:$\lim \limits_{x \to a} f(x)=f(a).$
6. Kama hali zote tatu ni kuridhika, kazi ni kuendelea katika$x=a$. Ikiwa mojawapo ya masharti inashindwa, kazi haiendelei$x=a$.

Mfano$\PageIndex{4}$: Determining the Input Values for Which a Piecewise Function Is Discontinuous

Kuamua kama kazi f f ni discontinuous kwa idadi yoyote halisi.

$$fx= \begin{cases} x+1, &x<2 \\ 3, &2≤x<4 \\ x^2−11, & x≥4 \end{cases}$$

Uchambuzi

Angalia Kielelezo. Katika$x=4$, kuna kuacha kuruka. Kumbuka kwamba kazi ni kuendelea katika$x=2$.

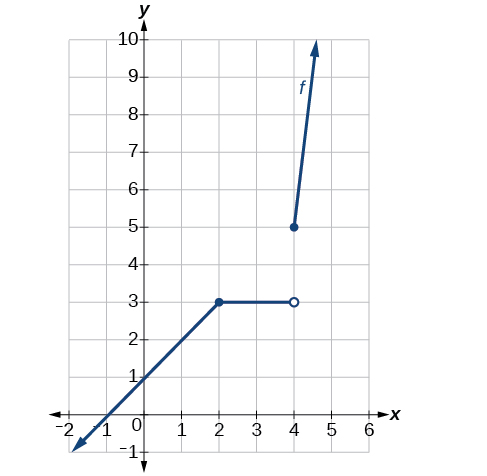
Grafu inaendelea$x=2$ but shows a jump discontinuity at $x=4$.

Zoezi$\PageIndex{4}$:

Tambua ambapo kazi hiyo$f(x)= \begin{cases} \frac{πx}{4}, &x<2 \\ \frac{π}{x}, & 2≤x≤6 \\ 2πx, &x>6 \end{cases}$ imekoma.

$x=6$

Kuamua Kama Kazi Inaendelea

Kuamua kama kazi ya kipande ni ya kuendelea au kuacha, pamoja na kuangalia pointi za mipaka, lazima pia tuangalie kama kila kazi zinazofanya kazi ya kipande kinaendelea.

jinsi ya: Kutokana na kazi piecewise, kuamua kama ni kuendelea.

1. Kuamua kama kila kazi ya sehemu ya kazi ya kipande ni kuendelea. Ikiwa kuna discontinuities, je, hutokea ndani ya uwanja ambapo kazi hiyo ya sehemu inatumiwa?
2. Kwa kila hatua$x=a$ ya mipaka ya kazi piecewise, kuamua kama kila moja ya hali tatu kushikilia.

Mfano$\PageIndex{5}$: Determining Whether a Piecewise Function Is Continuous

Kuamua kama kazi hapa chini inaendelea. Ikiwa sivyo, sema eneo na aina ya kila kuacha.

$$fx= \begin{cases} \sin (x), &x<0 \\ x^3, & x>0 \end{cases}$$

Kazi mbili zinazojumuisha kazi hii ya kipande ni$f(x)=\sin (x)$$f(x)=x^3$ juu$x<0$ na kuendelea$x>0$. Kazi ya sine na kazi zote za polynomial zinaendelea kila mahali. Discontinuities yoyote itakuwa katika hatua ya mipaka,

Katika$x=0$, hebu angalia hali tatu za kuendelea.

Hali ya 1:

$$\begin{align} f(0) \text{ does not exist.} \\ ⇒ \text{Condition 1 fails.} \end{align}$$

Kwa sababu hali zote tatu si kuridhika katika$x=0$, kazi$f(x)$ ni discontinuous katika$x=0$.

Uchambuzi

Angalia Kielelezo. Kuna discontinuity kutolewa katika$x=0$;$\lim \limits_{x \to 0} f(x)=0$, hivyo kikomo ipo na ni ya mwisho, lakini$f(a)$ haipo.

Kazi ina discontinuity kutolewa katika 0.

Media

Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na mwendelezo.

• Mwendelezo katika Point
• Kuendelea kwa Point: Dhana Angalia

Dhana muhimu

• Kazi inayoendelea inaweza kuwakilishwa na grafu bila mashimo au mapumziko.
• Kazi ambayo grafu ina mashimo ni kazi ya kuacha.
• Kazi inaendelea kwa idadi fulani ikiwa hali tatu zinakabiliwa:
  • Hali ya 1:$f(a)$ ipo.
  • mode 2:$\lim \limits_{x \to a} f(x)$ ipo katika$x=a$.
  • Hali ya 3:$\lim \limits_{x \to a} f(x)=f(a)$.
• Kazi ina kuacha kuruka ikiwa mipaka ya kushoto na ya kulia ni tofauti, na kusababisha grafu “kuruka.”
• Kazi ina discontinuity inayoondolewa ikiwa inaweza kufafanuliwa upya katika hatua yake ya kuacha ili kuifanya kuendelea. Angalia Mfano.
• Kazi zingine, kama vile kazi za polynomial, zinaendelea kila mahali. Kazi nyingine, kama kazi za logarithmic, zinaendelea kwenye uwanja wao. Angalia Mfano na Mfano.
• Kwa kazi ya kipande ili kuendelea kila kipande lazima iendelee kwa sehemu yake ya kikoa na kazi kwa ujumla lazima iendelee kwenye mipaka. Angalia Mfano na Mfano.

faharasa

kazi inayoendelea

kazi ambayo haina mashimo au mapumziko katika grafu yake

kazi ya kukomesha

kazi ambayo haiendelei$x=a$

kuruka kukomesha

hatua ya kuacha$f(x)$ katika kazi$x=a$ ambapo mipaka yote ya kushoto na ya kulia iko, lakini$\lim \limits_{x \to a^−} f(x)≠ \lim \limits_{x \to a^+} f(x)$

kukomesha kutolewa

hatua ya kutokuwepo katika kazi$f(x)$ ambapo kazi imekoma, lakini inaweza kufafanuliwa upya ili iendelee