12.2: Kupata Mipaka - Mali ya Mipaka

Last updated
Save as PDF

Page ID: 181352

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Fikiria kazi ya busara

\[f(x)=\dfrac{x^2−6x−7}{x−7} \nonumber \]

Kazi inaweza kuzingatiwa kama ifuatavyo:

\[f(x)=\dfrac{\cancel{(x−7)}(x+1)}{\cancel{x−7}} \nonumber \]

ambayo inatupa

\[f(x)=x+1,x≠7. \nonumber \]

Je, hii inamaanisha kazi$f(x)$ ni sawa na kazi$g(x)=x+1?$

Jibu ni hapana. Kazi$f(x)$ haina$x=7$ katika uwanja wake, lakini$g(x)$ inafanya. Graphically, tunaona kuna shimo katika grafu ya$f(x)$ saa$x=7$, kama inavyoonekana katika Kielelezo na hakuna shimo kama katika grafu ya$g(x)$, kama inavyoonekana katika Kielelezo.

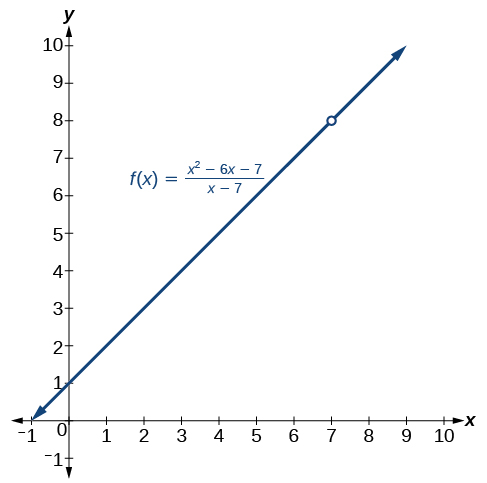
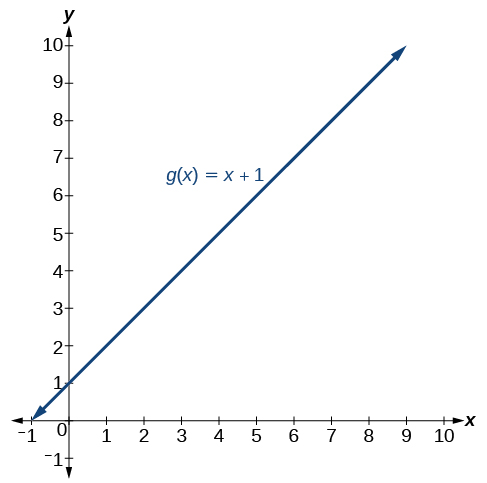
$CNX_Precalc_Figure_12_02_001.jpg$ $CNX_Precalc_Figure_12_02_002.jpg$

(kushoto) graph ya kazi$f$ ina mapumziko katika$x=7$ na kwa hiyo si kuendelea katika$x=7$. (Haki) Grafu ya kazi$g$ inaendelea.

Kwa hiyo, je, kazi hizi mbili tofauti pia zina mipaka tofauti kama$x$ mbinu 7? Si lazima. Kumbuka, katika kuamua kikomo cha kazi kama$x$ mbinu$a$, mambo muhimu ni kama pato inakaribia idadi halisi kama sisi kupata karibu na$x=a$. Kuwepo kwa kikomo hautegemei kile kinachotokea wakati$x$ sawa$a$.

Angalia tena kwenye Kielelezo na Kielelezo. Angalia kwamba katika grafu zote mbili, kama$x$ mbinu 7, maadili ya pato yanafikia 8. Hii ina maana

\[ \lim \limits_{x \to 7} f(x)= \lim \limits_{x \to 7} g(x). \nonumber \]

Kumbuka kwamba wakati wa kuamua kikomo, wasiwasi ni nini kinachotokea karibu$x=a$, sio$x=a$. Katika sehemu hii, tutatumia mbinu mbalimbali, kama vile kazi za kuandika upya kwa kuzingatia, kutathmini kikomo. Mbinu hizi zitatupa uthibitisho rasmi kwa kile tulichotimizwa na intuition.

Kutafuta Kikomo cha Jumla, Tofauti, na Bidhaa

Kuweka kazi au kuchunguza meza ya maadili ili kuamua kikomo inaweza kuwa mbaya na ya muda. Ikiwezekana, ni ufanisi zaidi kutumia mali ya mipaka, ambayo ni mkusanyiko wa theorems ya kutafuta mipaka.

Kujua mali ya mipaka inatuwezesha kuhesabu mipaka moja kwa moja. Tunaweza kuongeza, kuondoa, kuzidisha, na kugawanya mipaka ya kazi kama tulikuwa tukifanya shughuli kwenye kazi wenyewe ili kupata kikomo cha matokeo. Vilevile, tunaweza kupata kikomo cha kazi iliyoinuliwa kwa nguvu kwa kuongeza kikomo kwa nguvu hiyo. Pia unaweza kupata kikomo cha mzizi wa kazi kwa kuchukua mzizi wa kikomo. Kutumia shughuli hizi kwa mipaka, tunaweza kupata mipaka ya kazi ngumu zaidi kwa kutafuta mipaka ya kazi zao za sehemu rahisi.

mali ya mipaka

Hebu$a, k, A,$ na$B$ uwakilisha namba halisi,$f$ na$g$ uwe na kazi, kama hiyo$\lim \limits_{x \to a} f(x)=A$ na$ \lim \limits_{x \to a}g(x)=B.$ Kwa mipaka iliyopo na ni ya mwisho, mali ya mipaka ni muhtasari katika Jedwali

Mara kwa mara, k	$\lim \limits_{x \to a} k=k $
Mara kwa mara kazi	$\lim \limits_{x \to a} [k⋅f(x)]=k \lim \limits_{x \to a} f(x)=kA$
Jumla ya kazi	$\lim \limits_{x \to a} [f(x)+g(x)]= \lim \limits_{x \to a}f(x)+ \lim \limits_{x to a} g(x)=A+B$
Tofauti ya kazi	$\lim \limits_{x \to a} [f(x)−g(x)]= \lim \limits_{x \to a} f(x)− \lim \limits_{x \to a} g(x)=A−B$
Bidhaa ya kazi	$ \lim \limits _{x \to a}[f(x)⋅g(x)]= \lim \limits _{x \to a}f(x)⋅ \lim \limits_{x \to a} g(x)=A⋅B$
Quotient ya kazi	$\lim \limits _{x \to a} \frac{f(x)}{g(x)}= \frac{\lim \limits _{x \to a}f(x) }{\lim \limits _{x \to a}g(x)}=\frac{A}{B},B≠0$
Kazi alimfufua kwa exponent	$\lim \limits _{x \to a}[f(x)]^n=[\lim \limits _{x \to ∞}f(x)]^n=A^n$,$n$ wapi integer chanya
Katika mizizi ya kazi, ambapo n ni integer chanya	$\lim \limits _{x \to a}f(x) \sqrt[n]{f(x)} = \sqrt[n]{ \lim \limits _{x \to a}[ f(x) ]}=\sqrt[n]{A}$
Kazi ya polynomial	$ \lim \limits _{x \to a} p(x)=p(a)$

Mfano$\PageIndex{1}$: Evaluating the Limit of a Function Algebraically

Tathmini\[\lim \limits _{x \to 3}(2x+5). \nonumber \]

Suluhisho

\[\begin{align} \lim \limits _{x \to 3}(2x+5) &= \lim \limits _{x \to 3} (2x)+\lim \limits _{x \to 3}(5) && \text{Sum of functions property} \\ &=2 \lim \limits_{ x \to 3}(x)+\lim \limits _{x \to 3}(5) && \text{Constant times a function property} \\ &=2(3)+5 && \text{Evaluate} \\ &=11 \end{align} \nonumber \]

Zoezi$\PageIndex{1}$:

Tathmini kikomo kinachofuata:\[\lim \limits_{x \to −12}(−2x+2). \nonumber \]

Suluhisho

Kupata Limit ya Polynomial

Sio kazi zote au mipaka yao inahusisha kuongeza rahisi, kuondoa, au kuzidisha. Baadhi yanaweza kujumuisha polynomials. Kumbuka kwamba polynomial ni kujieleza yenye jumla ya maneno mawili au zaidi, ambayo kila moja ina mara kwa mara na kutofautiana kukulia kwa nguvu zisizo na negative muhimu. Ili kupata kikomo cha kazi ya polynomial, tunaweza kupata mipaka ya masharti ya mtu binafsi ya kazi, na kisha uwaongeze pamoja. Pia, kikomo cha kazi ya polynomial kama$x$ mbinu$a$ ni sawa na kutathmini tu kazi kwa$a$.

jinsi ya: Kutokana na kazi iliyo na polynomial, pata kikomo chake

Tumia mali ya mipaka ya kuvunja polynomial katika maneno ya mtu binafsi.
Pata mipaka ya masharti ya mtu binafsi.
Kuongeza mipaka pamoja.
Vinginevyo, tathmini kazi kwa$a$.

Mfano$\PageIndex{1}$: Evaluating the Limit of a Function Algebraically

Tathmini\[ \lim \limits_{x \to 3}(5x ^2). \nonumber \]

Suluhisho

\[\begin{align} \lim \limits_{x \to 3}(5x^2) &= 5 \lim \limits_{x \to 3}(x^2) && \text{Constant times a function property} \\ &=5(3^2) && \text{Function raised to an exponent property} \\&=45 \end{align} \nonumber \]

Zoezi$\PageIndex{1}$:

Tathmini\[ \lim \limits_{x \to 4} (x^3−5). \nonumber \]

Suluhisho

Mfano$\PageIndex{2}$: Evaluating the Limit of a Polynomial Algebraically

Tathmini\[ \lim \limits_{x \to 5} (2x^3−3x+1). \nonumber \]

Suluhisho

\[\begin{align} \lim \limits_{x \to 5}(2x^3−3x+1) &= \lim \limits_{x \to 5}(2x3)−\lim \limits_{x \to 5}(3x)+\lim \limits_{x \to 5} (1) && \text{Sum of functions}\\ &= 2 \lim \limits_{x \to 5}(x^3)−3 \lim \limits_{x \to 5}(x)+\lim \limits_{x \to 5}(1) && \text{Constant times a function} \\ &=2(5^3)−3(5)+1 && \text{Function raised to an exponent} \\ &=236 &&\text{Evaluate} \end{align} \nonumber \]

Zoezi$\PageIndex{2}$:

Tathmini kikomo kinachofuata:\[\lim \limits_{x \to −1}(x^4−4x^3+5). \nonumber \]

Suluhisho

Kupata Kikomo cha Nguvu au Mizizi

Wakati kikomo kinajumuisha nguvu au mizizi, tunahitaji mali nyingine kutusaidia kutathmini. Mraba wa kikomo cha kazi ni sawa na kikomo cha mraba wa kazi; hiyo inakwenda kwa mamlaka ya juu. Vivyo hivyo, mizizi ya mraba ya kikomo cha kazi inalingana na kikomo cha mizizi ya mraba ya kazi; hiyo inashikilia kweli kwa mizizi ya juu.

Mfano$\PageIndex{3}$: Evaluating a Limit of a Power

Tathmini\[ \lim \limits_{x \to 2}(3x+1)^5. \nonumber \]

Suluhisho

Tutachukua kikomo cha kazi kama$x$ mbinu 2 na kuongeza matokeo kwa nguvu ^ya 5.

\[\begin{align} \lim \limits_{x \to 2} (3x+1)^5 &= (\lim \limits_{x \to 2}(3x+1))^5 \\ &=(3(2)+1)^5 \\ &=7^5 \\ &=16,807 \end{align} \nonumber \]

Zoezi$\PageIndex{3}$:

Tathmini kikomo kinachofuata:$ \lim \limits_{x \to −4}(10x+36)^3.$

Suluhisho

-64

Swali & A: Kama hatuwezi kutumia moja kwa moja mali ya kikomo, kwa mfano katika$\lim \limits_{x \to 2}(\frac{x^2+6x+8}{x−2})$, can we still determine the limit of the function as $x$ approaches $a$?

Ndiyo. Baadhi ya kazi inaweza kuwa algebraically upya ili mtu anaweza kutathmini kikomo cha kilichorahisishwa sawa fomu ya kazi.

Kupata Limit ya Quotient

Kupata kikomo cha kazi iliyoonyeshwa kama quotient inaweza kuwa ngumu zaidi. Mara nyingi tunahitaji kuandika upya kazi algebraically kabla ya kutumia mali ya kikomo. Kama denominator kutathmini kwa 0 wakati sisi kuomba mali ya kikomo moja kwa moja, ni lazima kuandika upya quotient katika fomu tofauti. Njia moja ni kuandika quotient katika fomu factored na kurahisisha.

Mfano$\PageIndex{4}$: Evaluating the Limit of a Quotient by Factoring

Tathmini\[\lim \limits_{x \to 2} (\frac{x^2−6x+8}{x−2}). \nonumber \]

Suluhisho

Factor inapowezekana, na kurahisisha.

\[\begin{align} \lim \limits_{x \to 2} (\dfrac{x^2−6x+8}{x−2}) &= \lim \limits_{x \to 2}(\dfrac{(x−2)(x−4)}{x−2}) && \text{Factor the numerator.} \\ & = \lim \limits_{x \to 2}(\dfrac{\cancel{(x−2)}(x−4)}{\cancel{x−2}}) && \text{Cancel the common factors.} \\ &= \lim \limits_{x \to 2}(x−4) && \text{Evaluate.} \\ & =2−4=−2 \end{align} \nonumber \]

Uchambuzi

Wakati kikomo cha kazi ya busara hakiwezi kutathminiwa moja kwa moja, aina za hesabu na denominator zinaweza kurahisisha kwa matokeo ambayo yanaweza kutathminiwa.

Angalia, kazi

\[f(x)=\dfrac{x^2−6x+8}{x−2} \nonumber \]

ni sawa na kazi

\[f(x)=x−4,x≠2. \nonumber \]

Kumbuka kwamba kikomo ipo hata kama kazi si defined katika$x = 2$.

Zoezi$\PageIndex{4}$

Tathmini kikomo kinachofuata:\[\lim \limits_{x \to 7} \left( \dfrac{x^2−11x+28}{7−x} \right) . \nonumber \]

Suluhisho

$−3$

Mfano$\PageIndex{5}$: Evaluating the Limit of a Quotient by Finding the LCD

Tathmini\[\lim \limits_{x \to 5} \left( \dfrac{\frac{1}{x}−\frac{1}{5}}{x−5} \right) . \nonumber \]

Suluhisho

Pata LCD kwa denominators ya maneno mawili katika nambari, na ubadili sehemu zote mbili kuwa na LCD kama denominator yao.

Uchambuzi

Wakati wa kuamua kikomo cha kazi ya busara ambayo ina masharti yaliyoongezwa au yaliyotolewa katika namba au denominator, hatua ya kwanza ni kupata denominator ya kawaida ya maneno yaliyoongezwa au yaliyoondolewa; kisha, kubadilisha maneno yote kuwa na denominator hiyo, au kurahisisha kazi ya busara kwa kuzidisha numerator na denominator na denominator angalau kawaida. Kisha angalia ili uone kama nambari ya kusababisha na denominator ina mambo yoyote ya kawaida.

Zoezi$\PageIndex{5}$:

Tathmini\[\lim \limits_{x \to −5} \left( \dfrac{\frac{1}{5}+\frac{1}{x}}{10+2x} \right). \nonumber \]

Suluhisho

$−\frac{1}{50}$

jinsi ya: Kutokana na kikomo cha kazi iliyo na mizizi, tumia conjugate kutathmini

Kama quotient kama aliyopewa si katika$(\frac{0}{0})$ fomu indeterminate, tathmini moja kwa moja.
Vinginevyo, andika upya jumla (au tofauti) ya quotients mbili kama quotient moja, kwa kutumia denominator angalau kawaida (LCD).
Ikiwa namba inajumuisha mizizi, rationalize nambari; kuzidisha nambari na denominator kwa conjugate ya nambari. Kumbuka kwamba$a±\sqrt{b}$ ni conjugates.
Kurahisisha.
Tathmini kikomo kilichosababisha.

Mfano$\PageIndex{6}$: Evaluating a Limit Containing a Root Using a Conjugate

Tathmini\[ \lim \limits_{x \to 0} \left( \dfrac{\sqrt{25−x} −5}{x} \right) . \nonumber \]

Suluhisho

\[\begin{align} \lim \limits_{x \to 0} \left( \dfrac{\sqrt{25−x}−5}{x} \right) &= \lim \limits_{x \to 0} \left( \dfrac{(\sqrt{25−x}−5)}{x}⋅\frac{(\sqrt{25−x}+5)}{(\sqrt{25−x}+5)} \right) && \text{Multiply numerator and denominator by the conjugate.} \\ &= \lim \limits_{x \to 0} \left( \dfrac{(25−x)−25}{x(\sqrt{25−x}+5)} \right) && \text{Multiply: } (\sqrt{25−x} −5)⋅(\sqrt{25−x}+5)=(25−x)−25. \\ & = \lim \limits_{x \to 0} \left( \dfrac{−\cancel{x}}{\cancel{x}(25−x+5)} \right) && \text{Combine like terms.} \\ & =\lim \limits_{x \to 0} \left( \dfrac{−\cancel{x}}{\cancel{x}(\sqrt{25−x}+5)} \right) && \text{Simplify }\dfrac{−x}{x}=−1. \\ & =\dfrac{−1}{\sqrt{25−0}+5} && \text{Evaluate.} \\ & =\dfrac{−1}{5+5}=−\dfrac{1}{10} \end{align} \nonumber \]

Uchambuzi

Wakati wa kuamua kikomo cha kazi na mizizi kama moja ya maneno mawili ambapo hatuwezi kutathmini moja kwa moja, fikiria juu ya kuzidisha namba na denominator kwa conjugate ya masharti.

Zoezi$\PageIndex{6}$

Tathmini kikomo kinachofuata:$\lim \limits_{h \to 0} \left( \dfrac{\sqrt{16−h}−4}{h} \right) $.

Suluhisho

$−\frac{1}{8}$

Mfano$\PageIndex{7}$: Evaluating the Limit of a Quotient of a Function by Factoring

Tathmini\[\lim \limits_{x \to 4} \left( \frac{4−x}{\sqrt{x−2}} \right). \nonumber \]

Suluhisho

\[\begin{align} \lim \limits_{x \to 4} (\dfrac{4−x}{\sqrt{x}−2}) & = \lim \limits_{x \to 4} (\dfrac{(2+\sqrt{x})(2−x)}{\sqrt{x}−2}) && \text{Factor.} \\ &= \lim \limits_{x \to 4} ( \dfrac{(2+\sqrt{x})(\cancel{2−\sqrt{x}})}{−\cancel{(2−\sqrt{x})}}) && \text{Factor −1 out of the denominator. Simplify.} \\ & = \lim \limits_{x \to 4}−(2+x) && \text{Evaluate.} \\ &=−(2+ \sqrt{4}) \\ &=−4 \end{align} \nonumber \]

Uchambuzi

Kuongezeka kwa conjugate bila kupanua nambari; kuangalia badala ya mambo katika nambari. Nne ni mraba kamili ili nambari iko katika fomu

\[a^2−b^2 \nonumber \]

na inaweza kuwa na sababu kama

\[(a+b)(a−b). \nonumber \]

Zoezi$\PageIndex{7}$

Tathmini kikomo kinachofuata:\[\lim \limits_{x \to 3} \left( \frac{x−3}{\sqrt{x}−\sqrt{3} }\right). \nonumber \]

Suluhisho

$2\sqrt{3}$

jinsi ya: Kutokana na quotient na maadili kamili, kutathmini kikomo chake

Jaribu factoring au kutafuta LCD.
Ikiwa kikomo hakiwezi kupatikana, chagua maadili kadhaa karibu na upande wowote wa pembejeo ambapo kazi haijulikani.
Tumia ushahidi wa nambari ili kukadiria mipaka kwa pande zote mbili.

Mfano$\PageIndex{8}$: Evaluating the Limit of a Quotient with Absolute Values

Tathmini\[\lim \limits_{x \to 7} \frac{|x−7|}{x−7}. \nonumber \]

Suluhisho

Kazi haijulikani$x=7$, kwa hiyo tutajaribu maadili karibu na 7 kutoka kushoto na kulia.

Kikomo cha mkono wa kushoto:\[\frac{|6.9−7|}{6.9−7}=\frac{|6.99−7|}{6.99−7}=\frac{|6.999−7|}{6.999−7}=−1 \nonumber \]

Kikomo cha mkono wa kulia:\[\frac{|7.1−7|}{7.1−7}=\frac{|7.01−7|}{7.01−7}=\frac{|7.001−7|}{7.001−7}=1 \nonumber \]

Kwa kuwa mipaka ya mkono wa kushoto na wa kulia si sawa, hakuna kikomo.

Zoezi$\PageIndex{8}$

Tathmini\[ \lim \limits_{x \to 6^+} \frac{6−x}{| x−6 |}. \nonumber \]

Suluhisho

Dhana muhimu

Mali ya mipaka inaweza kutumika kufanya shughuli kwa mipaka ya kazi badala ya kazi wenyewe. Angalia Mfano.
Kikomo cha kazi ya polynomial kinaweza kupatikana kwa kutafuta jumla ya mipaka ya masharti ya mtu binafsi. Angalia Mfano na Mfano.
Kikomo cha kazi ambayo imefufuliwa kwa nguvu inalingana na nguvu sawa ya kikomo cha kazi. Njia nyingine ni badala ya moja kwa moja. Angalia Mfano.
Kikomo cha mizizi ya kazi ni sawa na mizizi inayofanana ya kikomo cha kazi.
Njia moja ya kupata kikomo cha kazi iliyoelezwa kama quotient ni kuandika quotient katika fomu factored na kurahisisha. Angalia Mfano.
Njia nyingine ya kupata kikomo cha sehemu ngumu ni kupata LCD. Angalia Mfano.
Kikomo kilicho na kazi iliyo na mizizi kinaweza kupimwa kwa kutumia conjugate. Angalia Mfano.
Mipaka ya kazi fulani iliyoonyeshwa kama quotients inaweza kupatikana kwa kuzingatia. Angalia Mfano.
Njia moja ya kutathmini kikomo cha quotient iliyo na maadili kamili ni kwa kutumia ushahidi wa nambari. Kuiweka juu ya kipande inaweza pia kuwa na manufaa. Angalia Mfano.

faharasa

mali ya mipaka: mkusanyiko wa theorems kwa ajili ya kutafuta mipaka ya kazi kwa kufanya shughuli za hisabati kwenye mipaka

Mara kwa mara, k	\(\lim \limits_{x \to a} k=k \)
Mara kwa mara kazi	\(\lim \limits_{x \to a} [k⋅f(x)]=k \lim \limits_{x \to a} f(x)=kA\)
Jumla ya kazi	\(\lim \limits_{x \to a} [f(x)+g(x)]= \lim \limits_{x \to a}f(x)+ \lim \limits_{x to a} g(x)=A+B\)
Tofauti ya kazi	\(\lim \limits_{x \to a} [f(x)−g(x)]= \lim \limits_{x \to a} f(x)− \lim \limits_{x \to a} g(x)=A−B\)
Bidhaa ya kazi	\( \lim \limits _{x \to a}[f(x)⋅g(x)]= \lim \limits _{x \to a}f(x)⋅ \lim \limits_{x \to a} g(x)=A⋅B\)
Quotient ya kazi	\(\lim \limits _{x \to a} \frac{f(x)}{g(x)}= \frac{\lim \limits _{x \to a}f(x) }{\lim \limits _{x \to a}g(x)}=\frac{A}{B},B≠0\)
Kazi alimfufua kwa exponent	\(\lim \limits _{x \to a}[f(x)]^n=[\lim \limits _{x \to ∞}f(x)]^n=A^n\),\(n\) wapi integer chanya
Katika mizizi ya kazi, ambapo n ni integer chanya	\(\lim \limits _{x \to a}f(x) \sqrt[n]{f(x)} = \sqrt[n]{ \lim \limits _{x \to a}[ f(x) ]}=\sqrt[n]{A}\)
Kazi ya polynomial	\( \lim \limits _{x \to a} p(x)=p(a)\)